Photonic bandgap engineering using second-order supersymmetry

Abstract

First-order supersymmetry (SUSY) adapted from quantum physics to optics manipulates the transverse refractive index of guided-wave structures using a nodeless ground state to obtain intended modal content. Second-order SUSY can be implemented using excited states as a seed function, even with the presence of nodes. We apply second-order SUSY to the coupled-mode equations by recasting them as the Dirac equation. This enables the engineering of non-uniform surface corrugation of waveguide gratings and coupling potential, which encapsulates the Bragg interaction between counterpropagating modes. We show that the added bound states appear as transmission resonances inside the bandgap of the finite grating. The probability density of each state provides the longitudinal modal energy distribution in the waveguide grating. The smooth modal energy distribution of the states obtained by SUSY can mitigate longitudinal spatial hole burning in high power laser operation. We demonstrate that degenerate second-order SUSY allows the insertion of two states, which can coalesce into Friedrich-Wintgen type bound states in the continuum (BIC) for one-dimensional grating. We show that the eigenfunctions of BIC states are doubly degenerate with opposite parity, and the corresponding transmission resonances have phase changes of 2π across these states. One-dimensional BIC states can find application as robust high-speed all-optical temporal integrators by lifting restrictions on the length of various sections in the phase-shifted grating.

Introduction

Photonic integrated circuits (PICs) provide a robust platform for data communications^1,2, quantum technologies^3,4,5, and various sensing applications^6,7. Optical waveguides coupled to a resonator are vital components in devices such as filters, add-drop (de-)multiplexers, and distributed feedback (DFB) lasers for PICs. These devices rely on engineering the geometry or arrangement of materials within the waveguide to achieve intended functionalities.

Inverse design^8,9 and machine learning¹⁰ are at the forefront of the design techniques for modern photonic structures. These methods achieve the targeted optical response by optimizing parameters in the design space, but often fail to provide the insight behind physical processes in the optimized structure. On the contrary, supersymmetric (SUSY) transformations, which originated in quantum physics and were recently adapted to photonics, offer a robust, physics-based approach to design photonic structures¹¹. In quantum mechanics, SUSY allows the design of a potential and its eigenfunctions simultaneously from a known potential¹². The equivalence of Helmholtz and Schrödinger equations has allowed the application of first-order SUSY (1-SUSY) in optics to design the transverse refractive index profile of waveguides and their modal content^11,13. Engineering the transverse refractive index using SUSY has enabled design of digital multimode devices¹⁴, mode sorter¹⁵, and lasers¹⁶.

The behavior of guided modes is tailored by engineering the refractive index or geometry of the waveguide in the direction of propagation. Recently, metasurfaces on top of waveguides have emerged as an attractive method to manipulate guided waves and tailor the coupling of guided waves to free-propagating waves^17,18. The advancement in fabrication techniques for such hybrid structures has made it possible to realize complex geometries experimentally¹⁹. However, an intuitive physics-based approach to design such structures is currently missing. We demonstrate that the second-order SUSY (2-SUSY) offers an efficient approach to design waveguides with engineered surface corrugation to obtain desired functionalities.

Commonly used 1-SUSY transforms the potential V₀ of the Hamiltonian ${H}_{0}=-{\partial }_{z}^{2}+{V}_{0}$ in its nonsingular partner potential V₁ whose spectra can differ at most in the ground state energy level. This type of transformation is known as unbroken SUSY and is defined by first-order intertwining operator ${\mathbb{A}}={\partial }_{z}+W(z)$, where W(z) is the superpotential. For an arbitrary solution u(z) to the initial Hamiltonian at the energy value ϵ such that $[-{\partial }_{z}^{2}+{V}_{0}]u(z)=\epsilon u(z)$, the superpotential becomes W(z) = ∂_z[u(z)]. The corresponding partner potential then becomes ${V}_{1}={V}_{0}-2{\partial }_{z}^{2}[\mathrm{ln}\,u]$. It is evident that V₁ is nonsingular in a given region if the generating function u(z) does not vanish in this region. Thus, generating function either equal to ground states energy E₀ or lower ϵ ≤ E₀ can be used in the 1-SUSY transformation. In optics, each SUSY operation transforms the refractive index distribution (potential) and the propagating modes (eigenfunctions) using a nodeless fundamental mode (ground state). Broken SUSY produces a potential isospectral to the initial potential, which has been utilized to produce photonic configurations with identical reflection and transmission characteristics²⁰ and complex potentials with real eigenvalue spectrum²¹. Isospectrality of 1-SUSY has also been utilized to preserve bandgaps while transforming ordered potential to potentials analogous to Brownian motion²².

The main limitation of 1-SUSY is the inability to modify the excited part of the eigenspectrum for a nonsingular partner potential. 2-SUSY is implemented through second-order intertwining operator ${\mathbb{B}}$, which is obtained by two generating functions u₁ and u₂. The generating functions are solutions of the initial Hamiltonian $[-{\partial }_{z}^{2}+{V}_{0}]{u}_{1,2}(z)={\epsilon }_{1,2}{u}_{1,2}$, which are not required to satisfy the boundary conditions. The relationship for ϵ₁ and ϵ₂ is used to classify the types of 2-SUSY. If the two energies are unequal and real ${\epsilon }_{1}\;\ne\; {\epsilon }_{2}\in {\mathbb{R}}$, then the 2-SUSY transformed potential is ${V}_{1}={V}_{0}-2{\partial }_{z}^{2}[\ln\,[W({u}_{1},{u}_{2})]]$, where the Wronskian W(u₁, u₂) = u₁∂_zu₂ − ∂_zu₁u₂^23,24. When the energies are equal and real ${\epsilon }_{1}={\epsilon }_{2}\in {\mathbb{R}}$, then the partner potential is given by ${V}_{1}={V}_{0}+{\partial }_{z}[{u}_{\epsilon }^{2}/({w}_{0}-\int {u}_{\epsilon }^{2}{\mathrm{d}}z)]$, where w₀ is an arbitrary constant²⁵. If ϵ₁ is complex, then for a nonsingular partner potential ${\epsilon }_{2}={\epsilon }_{1}^{* }$ and the partner potential becomes ${V}_{1}={V}_{0}-{\partial }_{z}[2\,{\text{Im}}\,({\epsilon }_{1})| {u}_{1}{| }^{2}/W({u}_{1},{u}_{1}^{* })]$²⁶. We have provided an extended analysis of 2-SUSY for potential in the Schrödinger equation in Supplementary Note 1. It is evident that the partner of 2-SUSY is obtained by the Wronskian of the two generating functions. Thus, the partner potential is nonsingular when the Wronskian is nodeless rather than the generating functions. We discuss the critical differences in the partner potentials generated by 1-SUSY and 2-SUSY for infinite square well in the section “Results”.

Recently, the equivalence between Maxwell’s and Dirac equation has been applied to understand the electromagnetic spin and orbital angular momentum²⁷, and examine the relationship between interface states and topology²⁸. The Dirac equation is a set of coupled first-order differential equations, and a matrix intertwining operator relates two Dirac equations. The matrix form of the intertwining operators form a second-order polynomial in Hamiltonian, which is a hallmark of second-order or nonlinear SUSY²⁹. Here, we show that the 2-SUSY can design the optical response of any system described by the coupled-mode equations by rewriting them as the Dirac equation. We study the amplitude and phase of the transmission spectrum for the states added by 2-SUSY at prescribed detuning (eigenvalue) by modifying the coupling parameter (potential). We use the extra degree of freedom provided by 2-SUSY to insert two states at the same eigenvalue in one dimension with opposite parity. We show that the degenerate states in waveguide gratings coalesce to form bound states in the continuum (BIC) strictly in one dimension. We discuss the practical applications of gratings obtained using 2-SUSY transformation.

Results

Key differences between 1-SUSY and 2-SUSY

We illustrate the key differences between 1-SUSY and 2-SUSY through the example of the infinite square well potential. In Fig. 1a, we show the 1-SUSY partner of the infinite square well potential shown in Fig. 1b. In Fig. 1c, we present a 2-SUSY partner of the infinite square well where the ground state at the energy E₀ and the first excited state at the energy E₁ are deleted by using unequal and real factorization energy. 2-SUSY allows manipulation of two adjacent eigenstates, and new states can be inserted at any position between two states. In Fig. 1d, we have deleted the first excited state at the energy E₁ and inserted a new state at the energy value E = 3.2 (a.u.). In Fig. 1e, we have deleted the ground state at the energy E₀ and inserted a new state at the energy value E = 2 (a.u.). Thus, in both cases, we have effectively moved one state of the potential to an arbitrary position. This type of transformation is not achievable by 1-SUSY as it would produce an isospectral potential. In Fig. 1f, we have presented an isospectral potential obtained by 2-SUSY when the factorization energies are complex. In Supplementary Fig. 1, we have presented the 2-SUSY partner potential for harmonic oscillator potential.

Fig. 1: First- and second-order supersymmetry (SUSY) transformation of an infinite square well potential.

a The partner potential of an infinite square well potential (b) is obtained by first-order SUSY (1-SUSY) transformation. The eigenfunctions for initial potential and SUSY partner are transformed into each other using operator ${\mathbb{A}}$ and ${{\mathbb{A}}}^{\dagger }$. The second-order SUSY (2-SUSY) transformation is performed using operators ${\mathbb{B}}$ and ${{\mathbb{B}}}^{\dagger }$. c Two adjacent eigenstates are deleted simultaneously by a single 2-SUSY transformation. d 2-SUSY allows removal of the first excited state of the infinite square well potential and insertion of a new state in the partner potential at energy E = 3.2 (a.u). e 2-SUSY partner after deleting the ground state and adding a new state at energy E = 2 (a.u). f The 2-SUSY transformation also produces isospectral partner potential similar to 1-SUSY in the broken regime.

Optical-quantum analogy

Light propagation and interaction in the waveguide with non-uniform surface corrugation or index variation is described by a set of first-order coupled differential equations. The physical mechanism of wave propagation in such media is called DFB or Bragg reflection, which results from the cumulative reflection from each surface of the structure. The physical interaction in a non-uniform structure is characterized by the coupling parameter varying longitudinally along the waveguide.

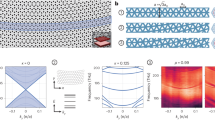
We design a one-dimensional DFB cavity formed by weak corrugation of the height of the waveguide, as shown in Fig. 2a. In the cavity, uniform periodic perturbation results in constant interaction between counter-propagating modes, which is characterized by constant coupling potential given by Fig. 2b. The coupling leads to formation of a bandgap in the transmission spectrum and the dispersion of the cavity as shown in Fig. 2c. The cavity can be modified to sustain n discrete modes by introducing nonuniformity in the surface perturbation, see Fig. 2e. Figure 2d shows the dispersion of unperturbed waveguides, forming the scattering (transmission) continuum for the localized modes. The field intensity in the nth mode is confined in the longitudinal direction along the cavity. Each mode decays independently into both waveguides 1 and 2 with the decay rate given by the sum of the two processes. The transmitted field intensity consists of the superposition of the input electromagnetic energy and the field originating from the decay of the localized states. The transmitted field intensity in waveguide 2 originates entirely from the decay of the localized states. Thus, for frequencies at which localized modes are supported, we observe a peak in the transmission spectrum.

Fig. 2: One-dimensional cavity-waveguide system.

a Schematic of a resonator coupled to a waveguide. Light is injected on the left at the input port and propagates in the z direction through the resonator to the output port. A uniform periodic perturbation with period Λ in the waveguide of height h₀ couples two counter-propagating modes described by the coupling parameter q₀. b In a uniform grating, the coupling is constant along the grating region with N periods leading to the length L = NΛ, and the light gets reflected near the Bragg frequency. The coupling potential that depends on the effective refractive index of the waveguide n_eff for a frequency ω determines the size of the bandgap in the transmission spectrum. Engineering the corrugation height Δh with SUSY designed envelope function α(z) allows the cavity to support discrete modes by changing the coupling potential. c When resonators supporting discrete states in the bandgap are connected to an unperturbed waveguide (d) with continuous dispersion, they form a scattering channel for the decay of the confined photonic states. e Surface corrugation envelope (orange) of resonators supporting three states in the bandgap obtained by 2-SUSY. The corrugation has been magnified for visualization.

The average height of the waveguide is h₀. The corrugated region has a finite length L, and the profile is $h(z)={h}_{0}+{{\Delta }}h\alpha (z)\cos [2\pi z/{{\Lambda }}+\theta (z)]$ for 0 < z < L, where Λ is the grating period. The slow variation of the amplitude and the phase of the grating is described by α(z) and θ(z). The perturbation in the height of the waveguide introduces a coupling between the two counter-propagating modes at the same optical frequency ω, near the Bragg frequency ω_B = c₀π/n₀Λ. The electric field of the propagating modes around a Bragg frequency (ω_B) is given by $E(z,t)=[u(z){\mathrm{e}}^{-i(\omega t-{k}_{\mathrm{B}}z)}+v(z){\mathrm{e}}^{-i({\omega }_{\mathrm{B}}t+{k}_{\mathrm{B}}z)}+{\mathrm{{c.c.}}}]$, where u(z) and v(z) are the envelopes of the two counter-propagating waves, k_B is the Bragg wave number, and c.c. stands for complex conjugate. The slowly varying envelopes for a weak grating strength (Δh/h₀ < < 1) satisfy the following coupled-mode equations³⁰:

$$\left[\begin{array}{ll}i{\partial }_{z}&-q(z)\\ -q(z)&-i{\partial }_{z}\end{array}\right]\left[\begin{array}{l}u(z,\delta )\\ v(z,\delta )\end{array}\right]=\delta \left[\begin{array}{l}u(z,\delta )\\ v(z,\delta )\end{array}\right],$$

(1)

where δ = k − k_B is detuning from Bragg frequency, the coupling is described using coupling constant of uniform grating q₀ by parameter as q(z) = q₀α(z)e^−iβ(z)31. The coupling constant for a uniform grating is given by ${q}_{0}=\frac{\pi }{\lambda }\frac{{{\Delta }}h}{{h}_{{\mathrm{{eff}}}}}\frac{{n}_{\mathrm{w}}^{2}-{n}_{{\mathrm{{eff}}}}^{2}}{n_{\mathrm{eff}}}$, where h_eff is the effective height of the corrugated region, n_w is the refractive index of the waveguide, and n_eff is the effective index of the planar waveguide. The coupling parameter q(z), which depends on the waveguide refractive index, and variation in the height of the grating forms the potential in the eigenvalue equation and detuning from the Bragg frequency is the eigenvalue. The size of the bandgap for a uniform coupling potential is given by (∣δ∣ < q₀), which is identical to the gap between electron and positron states of Dirac particle.

The coupled-mode equation forms an eigenvalue equation of the form h₀Φ = δΦ, where, Φ = (u, v)^T is a two-component spinor (see Supplementary Note 2). Unitary transformation (see Supplementary Note 3) is used to convert the eigenvalue equation into the Dirac equation. Such transformations have been used to show Klein tunneling of light³² and photonic realization of Dirac oscillator³³. Equation (1) is transformed into a one-dimensional Dirac Hamiltonian by unitary transformation ${\mathrm{e}}^{i\frac{\pi }{4}{\sigma }_{1}}{h}_{0}{\mathrm{e}}^{-i\frac{\pi }{4}{\sigma }_{1}}$ which gives h_s = iσ₂∂_z + q(z)σ₁, where σ₁, σ₂, σ₃ are Pauli matrices and q(z) is the scalar potential³⁴. The spinor ϕ also transforms into ${\mathrm{e}}^{i\frac{\pi }{4}{\sigma }_{1}}\phi =\frac{1}{\sqrt{2}}{[u+iv,iu+v]}^{t}$. However, due to the properties of unitary transformation, the eigenvalue spectrum, and the distribution of the modal energy given by the probability density, (∣u(z)∣² + ∣v(z)∣²) remains unchanged.

Thus, SUSY formalism for the Dirac equation is equivalent to application of SUSY in the coupled-mode equation. SUSY acts as an inverse design method to obtain transformed coupling potential required for the desired transmission spectrum and modal energy distribution simultaneously. As the Dirac equation describes a relativistic particle, the potential is classified as a scalar, vector, and pseudoscalar according to the behavior under Lorentz transformation. We can define another unitary operator ${\mathbb{U}}=\frac{1}{\sqrt{2}}({\bf{1}}+{\sigma }_{2})$ to obtain a new Dirac Hamiltonian ${h}_{p}={{\mathbb{U}}}^{\dagger }{h}_{s}{\mathbb{U}}$, where the coupling parameter is pseudoscalar potential. Next, we describe the differences in the spectrum for the two types of potentials.

SUSY design of cavity

Improvements in experimental methods in realizing Dirac materials have led to enormous theoretical activity regarding exact solutions of Dirac-like equations. The bound state spectrum of the Dirac equation with scalar potential has received attention with interest in the topological phase of matter³⁵. The position-dependent mass plays the role of a system parameter to obtain a topologically protected edge state, which are the bound states of a scalar potential at the zero crossings³⁶.

2-SUSY modifies the coupling potential to support bound states and desired frequency in the bandgap by engineering a single defect region. The inhomogeneity introduced by the transformation makes the effective index real at that frequency, allowing a sustained cavity mode. In Fig. 3a, we show the coupling parameter as scalar potential, which is transformed to support two states in the positive and negative detuning. SUSY transformation of scalar potentials produces a symmetric transmission spectrum where the positive states are mirrored in the negative spectrum. The pseudoscalar interpretation of the coupling potential provides greater freedom for the insertion of states. Figure 3b shows the coupling potential and modal energy distribution for two mirrored bound states in addition to a state at zero detuning. The initial function can be modified to produce an asymmetric spectrum for the pseudoscalar case. In Fig. 3c, d, we present the grating design corresponding to the coupling potentials obtained in the scalar and pseudoscalar case. If the cavity is lossless, then the energy stored by the modes couples evanescently into the scattering (transmission) channel. The cavity loss for a corrugated waveguide is controlled by tuning the strength of perturbation or changing the length of the perturbed region. As field intensity distribution decays exponentially away from the defect region, the finite length of the corrugated region leads to coupling between confined energy to the transmission continuum. The leakage of energy combined with any distributed loss in the cavity creates resonances with finite spectral linewidth. We observe a phase change of π across each state, which is a typical characteristic of a resonance. The SUSY method’s flexibility enables the design of frequency combs and the energy distribution for each cavity mode in one shot. Dirac-type equations have two associated Schrödinger equation. Thus, the coupled-mode-equations can be recast into the Helmholtz equation to apply first-order SUSY³⁷, which restricts the variety of spectrum obtained.

Fig. 3: Coupling potential and field distribution obtained by SUSY transformation.

a The coupling potential (shaded gray) derived by the SUSY method supports four modes at frequencies in the stopband. The modal energy distribution, which is the probability density of eigenfunction, is shown in red. The inserted states appear as transmission peaks and the corresponding phase change of π. Phase wrapping from [−π, π] leads to the sharp features at some resonant states. The finite length of the grating truncates the potential, which leads to the finite linewidth of each state. b An equivalent representation of the coupled-mode equation, where the coupling is pseudoscalar potential. It enables the design of a grating that supports states at the center of the stopband. c, d The design of grating with an envelope was obtained using SUSY transformation in a and b, respectively. The grating period has been magnified for visualization. e Pseudoscalar potentials produce grating with adiabatic taper (g), leading to a phase shift for the zero detuning state. The modal energy distribution is smooth in the defect region. f In contrast, modal energy distribution in phase-shifted grating has an abrupt change (h), which leads to longitudinal hole burning in high-power applications.

For a cavity with gain, the modes inserted can be used for lasing. For a state inserted at zero detuning, the coupling obtained by SUSY reverses the sign at the center of the corrugated region, similar to a phase-shifted grating. However, the smooth change in the sign of the coupling contrasts the phase-shift layer, which acts as a point defect in the periodic structure that results in abruptness in the intra-cavity field distribution, as shown in Fig. 3e, f. The advantage of smooth modal energy distribution is evident for high-power operation where irregular field distribution in phase-shifted DFB grating leads to longitudinal spatial hole burning. Various approaches, such as multiple phase shifts and chirped grating periods, lower the abruptness, reducing the fabrication tolerances. The smooth variation of fields near the defect region allows the devices to have easier fabrication, especially additive manufacturing techniques. Figure 3g, h illustrates the difference between a waveguide grating obtained using SUSY to insert state at zero detuning and phase-shifted grating. SUSY requires one defect region for multiple states, which is less cumbersome to fabricate than multiple defects at precise locations for traditional methods.

Bound states in the continuum

The inverse method to obtain a potential, which supports BICs from the wavefunction result in weakly localized potentials that oscillate at infinity³⁸. These potentials are unrealistic for application in photonic systems as they are highly sensitive to errors introduced during fabrication³⁹. Friedrich and Wintgen (FW)⁴⁰ proposed interference of two resonances at the same frequency in the continuum where one of the resonances becomes decoupled from the continuum. The degeneracy of resonances has been utilized to demonstrate BIC in two-dimensional photonic crystals^41,42. One-dimensional structure lacks degeneracy for any potential, which does not allow traditional methods to create FW BICs. So far, BICs in one-dimensional photonic structures are obtained at the second Bragg bandgap using guided-mode resonant gratings⁴³ or by mixing two polarizations with an anisotropic layer in the defect layer in photonic crystals⁴⁴.

Here, we show the inverse method based on SUSY enables the construction of potentials with two eigenvalues separated by an infinitesimal parameter ϵ. The analytical nature of the formalism prevents any numerical error that might occur in the analysis of these eigenvalues using a computational intensive inverse method. As this parameter is set to zero, the eigenvalues coalesce, creating degenerate resonances in the scattering spectrum of the optical structure. Similar method is used to create potential with degenerate eigenvalues in Schrödinger equation on half-axis⁴⁵ and full axis⁴⁶. However, these potentials are oscillatory and have singularity on the full axis, creating hurdles for realizing the photonic system.

Similarly, degenerate SUSY is applied to the coupled-mode equation, which creates overlapping resonances. Under the degenerate limit, SUSY adds two states at δ₁ and δ₁ + ϵ, where ϵ → 0. The coupling potential is obtained using Taylor expansions of second seed spinor at δ₁ + ϵ to avoid indeterminate solution as shown in the section “Methods”. For a waveguide, finite-length corrugation connected to input–output waveguides enables interference of the resonances coupled to the same continuum. The interference of two degenerate states as shown in Fig. 4a produces a BIC, where the transmission coefficient is real, and the phase change across the state is zero. Figure 4a shows the coupling potential obtained after degenerate SUSY transformation in coupled-mode equations. The amplitude of the transmission coefficient at the BIC frequency is unity, and the corresponding phase change is 2π. Effectively the phase does not change across the BIC state in the DFB grating cavity. The finite length grating shown in Fig. 4b leads to the apodization of the potential. Thus, the transmission peak corresponding to the BIC has a finite width, allowing the coupling of the light in these states. In the ideal case, without the grating apodization, the lifetime of the BIC state will be infinite and zero phase difference across the state.

Fig. 4: Bound states in the continuum.

a Coupling potential obtained by degenerate SUSY for two degenerate states shown in black and blue. Both states decay into the same channel, two states at the same frequency can interfere, leading to Friedrich–Wintgen BIC. For a finite grating, the transmission amplitude for BIC states is one, and the phase shift across the state sweeps 2π. In the ideal case for an infinite grating, the phase does not change. b The structure of grating for coupling potential supporting degenerate states. The increase in height is still within the weak grating limit. The grating period has been magnified for visualization. c Comparison of the temporal response of zero detuning state and the BIC state. The ideal temporal integrator has a unit step impulse response. However, the leakage of energy reduces the temporal bandwidth and imposes a strict restriction on the different sections of the grating. As the localization of fields in the BIC state occurs due to interference, the BIC integrators do not have length restrictions.

In practice, BIC states in photonic structures appear extremely narrow resonances which have found applications for lossless propagating PICs⁴⁷ and laser design⁴⁸. BICs in strictly one-dimensional structures have a promising application as photonic temporal integrators⁴⁹. According to signal processing theory, a temporal integrator is implemented using a linear filtering device with a unit step temporal impulse response. In electronics, a capacitor is used for temporal integration. The electric charge accumulates at the capacitor, and the integrated signal is proportional to the voltage measured. In practice, the voltage at the capacitor decays exponentially. This property is used to design an optical temporal integrator using phase-shifted grating⁴⁹. However, the length of both sections of phase-shifted grating must be equal, which restricts the central frequency of the integrator to the zero detuning. As the BIC state is a result of interference, the confinement of light does not depend on the location of the defect but the asymptotic behavior. Figure 4c compares the temporal response of the integrator formed by zero detunings and the BIC state. The BIC integrator provides a longer integration time window, which leads to higher processing speed⁵⁰ for an all-optical temporal integrator.

Discussion

SUSY transformation to design of quasi-isospectral refractive index landscape allows for global phase matching critical to wave devices. First-order SUSY is limited to the manipulation of the ground state of the potential. Second-order SUSY enables the design of the excited part of the spectrum and arbitrary control of insertion of new states. The extra degree of freedom provided by second-order SUSY can pave the path for a new class of SUSY designed optical structures. We have applied second-order SUSY to coupled-mode equations by rewriting them into Dirac-form to design non-uniform corrugation based on the desired spectral response. Waveguide-resonator systems underpin PICs that provide a robust platform for fast optical information processing. The grating-based device is engineered by extra degrees of freedom provided by slowly varying nonuniform gratings, where the local period or depth of modulation varies longitudinally. We have investigated the amplitude and phase characteristics of the transmission spectrum for various cavity engineered from its coupling parameter. The SUSY method provides an elegant single-step procedure to simultaneously derive the structure of the grating and the modal energy distribution as compared to the synthesis of waveguide grating from the coupling parameter using the layer peeling method⁵¹. We observe that the bound states of the coupling potential appear as the resonant state for a finite photonic cavity. The phase of transmission resonances changes by π over the small frequency range. The lifetime can be tuned by engineering the strength of the waveguide for optical filters.

Second-order SUSY allows manipulation of excited states and insertion of a new state at an arbitrary position between two adjacent energy levels. This transformation cannot be achieved by first-order SUSY as the insertion of new states lead to isospectral potentials. This property of the second-order SUSY method can be utilized to add overlapping resonances in the grating. We observe that the transmission coefficient in the finite cavity is real, and the phase changes abruptly by 2π across the BIC state, which contrasts the infinite case where the phase does not change. The high transmission over a narrow spectrum allows the realization of all-optical temporal integrator.

Coupled-mode equations have been generalized to include higher-order effects, which become essential in deeper gratings⁵². We have demonstrated the method by using shallow corrugation on the grating surface, but the formalism used to obtain the profile is very generic. Hence the method described can be adapted for designing a strongly interacting photonic crystal. Additionally, coupled first-order differential equations describe the evolution of the modal amplitudes of two states, which evolve either in time or with propagation distance⁵³. Thus, the SUSY method described can be used to obtain the new design for a large number of photonic systems. SUSY procedure of BIC can be repeated to design any number of states with degenerate eigenvalues to create resonance with exceptionally low spectral linewidth. The (1 + 1) Dirac equation also appears in the Ablowitz–Kaup–Newell–Segur (AKNS) hierarchy for the Lax eigenvalue equation of the nonlinear evolution equations⁵⁴. The formalism of degenerate Darboux transformation can be also used to create FW BICs in one dimension is also used to study the generation of higher-order rogue waves⁵⁵.

Methods

Theoretical background

One-dimensional (1 + 1) Dirac equation with a generic (2 × 2) matrix potential (V₀) with well-defined eigenvalues (E) and spinors (Φ) for particle of mass (m)

$$\left[i{\sigma }_{2}{\partial }_{z}+(m+S(z)){\sigma }_{1}+P(z){\sigma }_{3}\right]{{\Phi }}=E{{\Phi }},$$

(2)

where S(z) is the Lorentz scalar potential, and P(z) is the pseudoscalar potential. In coupled-mode equations the potential V₀ is replaced by coupling potential q₀. We define an intertwining operator $({\mathbb{L}})$ relating two Dirac Hamiltonians (h₀ = −iσ₂∂_z + q₀(z)) and (h₁ = −iσ₂∂_z + q₁(z)), such that ${\mathbb{L}}{h}_{0} ={h}_{1}{\mathbb{L}}$. In the simplest form, the intertwining operator can be be assumed to of form ${\mathbb{L}}={\bf{A}}{\partial }_{z}+{\bf{B}}$, where A and B are two (2 × 2) z-dependent matrices. Upon substitution, in the intertwining relation, we obtain three relationships. First is a restriction on the matrix elements A, where only two elements can be arbitrarily chosen, and others need to be derived using Aσ₂ − σ₂A = 0. Second, a difference of matrix potentials D = q₁ − q₀ = (Aq₀ − q₀A + iBσ₂ − iσ₂B − iσ₂∂_zA)A⁻¹, where A is an invertible matrix. The third equation is used to determine the matrix B. We obtain the matrix form of Riccati equation similar to Schrödinger case shown in Supplementary Note 1 upon substitution B = AG,

$${\partial }_{z}{q}_{0}-i{\sigma }_{2}{\partial }_{z}{\bf{G}}+{\bf{G}}{q}_{0}-{q}_{0}{\bf{G}}+(i{\sigma }_{2}{\bf{G}}-i{\bf{G}}{\sigma }_{2}){\bf{G}}=0.$$

(3)

Similar to Schrödinger case, Riccati equation is linearized upon substituting matrix G = −∂_zUU⁻¹, and we get an equation in U,

$$-i{\sigma }_{2}{\partial }_{z}{\bf{U}}+{q}_{0}{\bf{U}}={{\Lambda }}{\bf{U}}.$$

(4)

This equation is similar to the Dirac equation where the eigenpair is a spinor and a number. However, in this case the eigenpair U and Λ are matrices. The solution of Eq. (4) is obtained by choosing U is composed of two spinors (Φ₁, Φ₂) which are solution of the Dirac equation corresponding to eigenvalues, δ₁ and δ₂, respectively, h₀Φ_1,2 = δ_1,2Φ_1,2.

In principle, the eigenstates must be formal solutions regardless of boundary and normalization conditions.

$${\bf{U}}=({{{\Phi }}}_{1},{{{\Phi }}}_{2})=\left(\begin{array}{ll}{\phi }_{11}&{\phi }_{12}\\ {\phi }_{21}&{\phi }_{22}\end{array}\right),\,\,\,\text{and}\,\,\,{{\Lambda }}=\left(\begin{array}{ll}{\delta }_{1}&0\\ 0&{\delta }_{2}\end{array}\right).$$

(5)

The Darboux transformation is then defined with matrix A is identity as ${\mathbb{L}}={\bf{1}}{\partial }_{z}-{\bf{U}}{{\bf{U}}}^{-1}$ and the eigenfunction is transformed to $\psi ={\mathbb{L}}{{\Phi }}$.

Repeated transformations

In order to illustrate the steps required to repeat the SUSY transformation, the eigenfunction is rewritten as ψ = U[∂_z(U⁻¹Φ)]. We can substitute the

$${{\bf{U}}}^{-1}\Phi =\frac{1}{W({\Phi }_{1},{\Phi }_{2})}\left[\begin{array}{l}W(\Phi ,{\Phi }_{2})\\ W({\Phi }_{1},\Phi )\end{array}\right],$$

(6)

where W(Φ₁, Φ₂) = Φ₁₁Φ₂₂ − Φ₁₂Φ₂₁ is the Wronskian. Using the identities of matrix algebra, we can obtain the transformed eigenfunction

$$\psi =\frac{1}{W({\Phi }_{1},{\Phi }_{2})}{\left[\begin{array}{ll}\left|\begin{array}{lll}{\phi }_{11}&{\phi }_{21}&{\phi }_{1}\\ {\phi }_{21}&{\phi }_{22}&{\phi }_{2}\\ {\partial }_{z}{\phi }_{11}&{\partial }_{z}{\phi }_{21}&{\partial }_{z}{\phi }_{1}\end{array}\right|&\left|\begin{array}{lll}{\phi }_{11}&{\phi }_{21}&{\phi }_{1}\\ {\phi }_{21}&{\phi }_{22}&{\phi }_{2}\\ {\partial }_{z}{\phi }_{21}&{\partial }_{z}{\phi }_{22}&{\partial }_{z}{\phi }_{2}\end{array}\right|\end{array}\right]}^{t}.$$

(7)

Similarly, the potential is derived by q₁ = q₀ + D₁σ₂ − σ₂D₁, where

$${{\bf{D}}}_{{\bf{1}}}=\frac{1}{W({\Phi }_{1},{\Phi }_{2})}\left[\begin{array}{ll}\left|\begin{array}{ll}{\partial }_{z}{\phi }_{11}&{\partial }_{z}{\phi }_{21}\\ {\phi }_{21}&{\phi }_{22} \end{array}\right | & \left|\begin{array}{ll}{\phi }_{11}&{\phi }_{21}\\ {\partial }_{z}{\phi }_{11}&{\partial }_{z}{\phi }_{12} \end{array}\right | \\ \left | \begin{array}{ll} {\partial }_{z}{\phi }_{21}&{\partial }_{z}{\phi }_{22}\\ {\phi }_{21}&{\phi }_{22}\end{array}\right| & \left | \begin{array}{ll} {\phi }_{11}&{\phi }_{21}\\ {\partial }_{z}{\phi }_{21}&{\partial }_{z}{\phi }_{22}\end{array}\right|\end{array}\right].$$

(8)

Thus, multiple (n) SUSY transformation produces the potential q₁ = q₀ + D_nσ₂ − σ₂D_n, where the four determinants are constructed from W(Φ₁₁, Φ₂₁, ⋯, Φ_n1) by replacing the 2nth line with the nth derivatives of the first element of the spinors and (2n − 1)th line with the nth derivatives of the second element of the spinors.

Second-order SUSY in Dirac equation

Dirac-type Hamiltonian is by definition a first-order differential equation and the intertwinning operator and its adjoint form a second-order matrix differential operator ${\mathbb{L}}{{\mathbb{L}}}^{\dagger }$ and ${{\mathbb{L}}}^{\dagger }{\mathbb{L}}$. Upon substitution of the form of operator ${\mathbb{L}}$ and ${{\mathbb{L}}}^{\dagger }$, it is shown that

$${{\mathbb{L}}}^{\dagger }{\mathbb{L}}=({h}_{0}-{\epsilon }_{1})({h}_{0}-{\epsilon }_{2}),$$

(9)

$${\mathbb{L}}{{\mathbb{L}}}^{\dagger }=({h}_{1}-{\epsilon }_{1})({h}_{1}-{\epsilon }_{2}).$$

(10)

Thus, the superalgebra is given by 4 × 4 matrix Hamiltonian and supercharges, respectively,

$${\bf{H}}=\left(\begin{array}{ll}{h}_{0}&0\\ 0&{h}_{1}\end{array}\right),\,\,Q=\left(\begin{array}{ll}0&{\mathbb{L}}\\ 0&0\end{array}\right),\,\,\,\text{and}\,\,\,{Q}^{\dagger }\left(\begin{array}{ll}0&0\\ {{\mathbb{L}}}^{\dagger }&0\end{array}\right).$$

(11)

Superalgebra takes quadratic form that differs from the usual SUSY for Schrödinger equation. The superhamiltonian and supercharges commute [H, Q] = [H, Q^†] = 0.

$$\{Q,{Q}^{\dagger }\}=({\bf{H}}-{\epsilon }_{1})({\bf{H}}-{\epsilon }_{2}),\,\,\{Q,Q\}=\{{Q}^{\dagger },{Q}^{\dagger }\}=0.$$

(12)

Thus, the SUSY formalism is associated with the Dirac equation of the second order or nonlinear form.

Supersymmetry in coupled-mode equations

The coupled-mode equation rewritten as Dirac equation h_s becomes

$${h}_{s}{{\Phi }}=\left[\begin{array}{ll}0&-{\partial }_{z}+q(z)\\ -{\partial }_{z}+q(z)&0\end{array}\right]{{\Phi }}=\delta {{\Phi }}$$

(13)

Upon comparison, the coupling parameter for a uniform corrugation q₀ acts as the mass for the Dirac particle and in the absence of the scalar potential. Thus, the deforming envelope α(z) is derived as the scalar potential ss q(z) = q₀(1 + S(z)/q₀). For eigenvalues (detuning with the bandgap) δ_1,2 = ±δ, the eigenspinors for free Dirac Hamiltonian are ${\Phi}_{1}={(\cosh (\gamma z),\cosh (\gamma z + 2p))}^{t}$ and Φ₂ = −σ₃Φ₁ with $\gamma =\sqrt{{q}_{0}^{2}-{\delta}^{2}}$ and $p=0.5{\mathrm{ln}}\,(\sqrt{({q}_{0}-\gamma )/({q}_{0}+\gamma)})$. Using these spinors the SUSY transformation is applied to obtain the desired number of states in the bandgap and the modal energy distribution. The pseudoscalar potential (mσ₃ + P(z)σ₁) is equivalent to the scalar potential for massless Dirac particle; hence, the SUSY transformation produces potentials with new properties. The DT for pseudoscalar potential is carried out by choosing the following two spinors corresponding to the eigenvalues δ₁ = ∣q₀∣ and δ₂ < ∣q₀∣, ${\phi }_{1}={(1,0)}^{t}\,\,\,{\text{and}}\,\,\,{\phi }_{2}={\left(\frac{k\sinh (kz)}{\delta_2 -| {q}_{0}| },\cosh (kz)\right)}^{t},$ where $k=\sqrt{({q}_{0}^{2}-{\delta }_{2}^{2})}$.

Degenerate SUSY transformation

Application of SUSY twice for the same eigenvalue does not produce two states. In addition, the potential obtained after two SUSY transformations for the same eigenvalue has an indeterminate form. However, the issue can be resolved by applying the SUSY of two eigenvlaues for δ₁ and δ₁ + ϵ. As the parameter ϵ is infinitesimal, we can use Taylor expansion of seed eigenfunctions and elements of the determinant for DT. For an infinitesimal ϵ, the eigenfunction Φ₂ is approximated by the Taylor expansion Φ₂(δ₁ + ϵ) = Φ₂(δ₁) + [∂_ϵΦ₂(δ₁ + ϵ)]ϵ + O(ϵ). Similarly, potential requires an element-wise Taylor expansion of the 2n × 2n matrix D_n give by ${\partial }_{\epsilon }^{{n}_{i}}{{\bf{D}}}_{{{\bf{n}}}_{ij}}({\delta }_{1}+\epsilon )$, where n_i is the floor of the function [(i + 1)/2], and [i]. After transformation has been applied to insert states at δ₁ and δ₁ + ϵ, we let ϵ → 0 in the expression for potential and eigenfunctions.