A potential all-electronic route to the charge-density-wave phase in monolayer vanadium diselenide

Abstract

The transition metal dichalcogenides offer significant promise for the tunable realisation and application of correlated electronic phases. However, tuning their properties requires an understanding of the physical mechanisms underlying their experimentally observed ordered phases, and in particular the extent to which lattice vibrations are a necessary ingredient. Here we present a potential mechanism for charge-density-wave formation in monolayers of vanadium diselenide in which the key role at low energies is played by a combination of electron–electron interactions and nesting. There is a competition between superconducting and density-wave fluctuations as sections of the Fermi surface are tuned to perfect nesting. This competition leads to charge-density-wave order when the effective Heisenberg exchange interaction is comparable to the effective Coulomb repulsion. When all effective interactions are purely repulsive, it results instead in d-wave superconductivity. We discuss the possible role of lattice vibrations in enhancing the effective Heisenberg exchange during the earlier stages of the renormalisation group flow.

Introduction

Since the isolation and characterisation of graphene in 2004¹, the field of two-dimensional materials has seen an explosion in research activity², and a search has begun for two-dimensional materials that can be tuned to exhibit a wider range of properties than graphene. Of particular interest in this regard are monolayers of the transition metal chalcogenides FeX (X = Se, Te) and transition metal dichalcogenides MX₂ (M = Ti, V, Nb, Mo, Ta, W; X = S, Se, Te)³. The transition metal dichalcogenides (TMDs) display an especially wide range of behaviours, including Mott-insulating, semi-metallic, charge-density-wave (CDW), excitonic, and superconducting phases. The development of van der Waals heterostructures made from two or more TMDs⁴ is expected to further increase the range of strongly correlated physics that can be realised in this family of materials.

However, tuning the properties of TMDs requires an understanding of the way in which variations in microscopic parameters affect their phase diagrams. This, in turn, necessitates an understanding of the physical mechanisms that underlie the experimentally observed ordered phases. For several of the ordered states of monolayer TMDs, especially the CDW phases, the mechanism remains the subject of debate.

Many TMDs exhibit CDW phases with rather high critical temperatures, which are often further enhanced in the monolayer limit⁵. One well known route to CDW formation is via Fermi surface nesting: here sections of the Fermi surface lie parallel to each other, giving an enhanced particle-hole susceptibility at a non-zero wavevector Q^6,7,8,9,10. This is an inherently electronic mechanism. However, there are other candidate mechanisms for the CDW phases in the TMDs, including the Rice-Scott saddle band mechanism¹¹, the softening of phonon modes¹², and a mechanism based on the transition to an exciton insulator¹³. It is often assumed that there must be significant influence of the phonon sector in driving the CDW transitions in monolayer TMDs; however, recent evidence of electronically driven density-wave transitions in other correlated materials¹⁴ motivate us to ask whether a mechanism dominated by the electronic sector might be operative here as well.

We focus on the 1T structural isomer of vanadium diselenide, VSe₂, in the monolayer limit. Theoretical and experimental attempts to determine the low-temperature Fermi surface of this material do not all agree. Several studies show column-like Fermi surface pockets protruding from the edge of the Brillouin zone^15,16,17,18; others show a Fermi surface with large triangular pockets around the K and $\,\text{K}\,^{\prime}$ points of the Brillouin zone with an additional small Fermi surface pocket at the Γ point^19,20. Which of these Fermi surfaces is realised appears to depend on the exact position of the chemical potential with respect to a van Hove singularity in the band structure²⁰. Such singularities are usually associated with an enhancement of the susceptibilities to various forms of ordered phase, with superconductivity typically dominant^21,22.

This variation in the predicted Fermi surface leads to a disagreement over the predicted Q-vector of any CDW, and thus also over the reconstructed unit cell. Some studies propose a Q-vector perpendicular to the Brillouin zone edge^19,23,24, in the k_y direction; however, others propose alternative nesting vectors parallel to the Brillouin zone edges^17,25. These studies agree on a renormalisation to flat Fermi surface sections in the low-temperature and low-dimensional limit.

In this article we consider an idealised model of monolayer 1T-VSe₂. For definiteness, we assume column-like Fermi surfaces^17,25, though the patch scheme we employ should also be applicable to the triangular Fermi surface case with appropriate modifications to intra- and inter-pocket scattering and the definitions of superconducting symmetries. Starting from an effective model for the intermediate-energy (~10 meV) physics in the conduction-electron sector, we implement a renormalisation group (RG) analysis retaining both particle-particle and particle-hole channels. We are thus able to capture the interplay of superconducting and density-wave fluctuations, and the effect of Fermi surface nesting on both^26,27, as the eventual ordered state is approached.

Results

Renormalisation group flow equations

(For the meaning of the coupling constants and other details of our model, please see the ‘Methods’ section below.) We define the RG flow parameter $y=\mathrm{log}\,\left(\frac{{k}_{c}}{{{\Omega }}}\right)$ which diverges to infinity as Ω → 0. Introducing the rescaled interaction parameters ${g}_{i}\to \frac{{k}_{c}}{2{\pi }^{2}}{g}_{i}$ we perform a one-loop RG analysis including terms that contribute with a divergent susceptibility at low energies^26,27. We find the following RG flow equations:

$${\dot{g}}_{1}=2{d}^{\varepsilon }(y)\left(-{g}_{1}^{2}+{g}_{5}{g}_{6}-{g}_{6}^{2}\right),$$

(1)

$${\dot{g}}_{2}=-{d}^{\varepsilon }(y){g}_{1}^{2},$$

(2)

$${\dot{g}}_{3}=-2\beta {g}_{3}^{2}-2(1-\beta ){g}_{3}{g}_{4}-2{g}_{5}{g}_{6},$$

(3)

$${\dot{g}}_{4}=-(1-\beta ){g}_{4}^{2}-{g}_{5}^{2}-{g}_{6}^{2},$$

(4)

$${\dot{g}}_{5}=-{g}_{3}{g}_{6}-{g}_{4}{g}_{5}+2{d}^{\varepsilon }(y){g}_{2}{g}_{5},$$

(5)

$${\dot{g}}_{6}=-{g}_{3}{g}_{5}-{g}_{4}{g}_{6}+2{d}^{\varepsilon }(y)({g}_{1}{g}_{5}+{g}_{2}{g}_{6}-2{g}_{1}{g}_{6}),$$

(6)

where ${\dot{g}}_{i}$ denotes the derivative $\frac{d{g}_{i}}{dy}$. The y-dependence of the couplings g_i has been suppressed for brevity. The function d^ε(y) is defined as

$${d}^{\varepsilon }(y)\equiv \frac{d{{{\Pi }}}_{\,\text{ph}\,}^{{{\bf{Q}}}_{1}}}{d{{{\Pi }}}_{\,\text{pp}\,}^{0}},$$

(7)

i.e. it measures the relative strengths of the Q₁ particle-hole susceptibility and the q = 0 particle-particle susceptibility in terms of the flow parameter y and nesting parameter ε.

Solving these differential equations, we find that the couplings diverge at a critical value of y. In order to allow a numerical solution we stop the flow when the largest of the couplings g_i becomes equal to 1; this defines a critical value y = y_c. At this point a subset of the couplings have already become several orders of magnitude larger than their initial values, signalling the breakdown of our perturbation theory and the onset of order. The finite critical value y_c is an artefact of the one-loop RG; higher-loop corrections should shift the divergence to y_c → ∞. We consider that no phase transition occurs if no coupling has reached 1 by the time y = 1/(N₀U_eff), where N₀ = k_c/(2π²) is the density of states.

In the limit y → 0 with ε small, one may show from (7) that ${d}^{\varepsilon }\approx 1-\frac{{\varepsilon }^{2}}{3\mathrm{log}\,2}$. In the large-y limit d^ε(y) takes the form d^ε(y → y_c) =((1 − ε²)e^y)/((1 + e^y)(1 + ε²e^y)). We therefore use the following approximation to d^ε(y):

$${d}^{\varepsilon }(y)=\frac{d{{{\Pi }}}_{\,\text{ph}\,}^{{{\bf{Q}}}_{1}}}{d{{{\Pi }}}_{\,\text{pp}\,}^{0}}\approx \frac{1-\frac{{\varepsilon }^{2}}{3\mathrm{log}\,2}}{1+{\varepsilon }^{2}{e}^{y}},$$

(8)

which interpolates between the y → 0 and y → y_c limits. The exact form of this interpolation function is selected for calculational convenience and is not unique; however, the properties of the RG flow should not depend strongly on the details of the choice we make here.

Initial conditions

The initial conditions for the couplings are approximated by

$${V}_{1}\approx {U}_{{\rm{eff}}}+{V}_{{\rm{eff}}}-\frac{7}{4}{J}_{{\rm{eff}}},{V}_{2}\approx {U}_{{\rm{eff}}}+3{V}_{{\rm{eff}}}-\frac{5}{4}{J}_{{\rm{eff}}}.$$

(9)

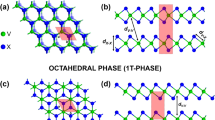
We find the initial conditions at y = 0 for the couplings to be ${g}_{1}^{0}\approx {g}_{3}^{0}\approx {g}_{6}^{0}\approx {V}_{1}$ and ${g}_{2}^{0}\approx {g}_{4}^{0}\approx {g}_{5}^{0}\approx {V}_{2}$ in our approximation. The effect of this approximation is to split the solutions into three regions: (i) V₁, V₂ > 0, all couplings repulsive in the ultraviolet; (ii) V₂ > 0, V₁ < 0; and (iii) V₁, V₂ < 0, i.e., all couplings attractive. In a more general microscopic model the values of the couplings ${g}_{i}^{0}$ would be independent. The mapping between the intermediate-scale effective couplings J_eff and V_eff and the RG couplings V₁ and V₂ is illustrated in Fig. 1.

Fig. 1: Phase diagrams of our extended Hubbard model for monolayer 1T-VSe₂.

a An illustration of the mapping between the effective nearest-neighbour Coulomb repulsion V_eff and the effective Heisenberg exchange interaction J_eff and the coupling constants V₁ and V₂, defined in (9). b–d Calculated phase diagrams for our model of monolayer 1T-VSe₂. The assumed degree of Fermi surface nesting increases from left to right (ε = 10⁻¹, 10⁻², 10⁻³), and the parameter β that represents the finite length of the nested sections is set to 1/2. As well as the metallic phase, we find regions of s-wave superconductor (s-SC), p-wave superconductor (p-SC), d-wave superconductor (d-SC), and a charge density-wave with wavevector Q₁ (Q₁−CDW).

Identification of ordered phases

Additionally we must calculate the susceptibilities of the possible order parameters. We therefore introduce test vertices for all possible two-particle correlators and calculate the corresponding one-loop vertex corrections. In the particle-particle channel the eigenvectors Δ_s = Δ(1, 1, 1, 1)^T/2, Δ_d = Δ(−1, 1, −1, 1)^T/2, Δ_p = Δ(−1, −1, 1, 1)^T/2, and Δ_f = Δ(1, −1, −1, 1)^T/2 define the pairing symmetry. The corresponding eigenvalues are given in equations (10)–(13). The SDW and CDW susceptibilities are calculated via ${\chi }_{\,\text{SDW}\,}^{{\bf{q}}}={\chi }_{\uparrow \uparrow }^{{\bf{q}},\,\text{ph}\,}-{\chi }_{\downarrow \downarrow }^{{\bf{q}},\,\text{ph}\,}$, ${\chi }_{\,\text{CDW}\,}^{{\bf{q}}}={\chi }_{\uparrow \uparrow }^{{\bf{q}},\,\text{ph}\,}+{\chi }_{\downarrow \downarrow }^{{\bf{q}},\,\text{ph}\,}$²⁷.

We refer to the possible superconducting symmetries using their continuum analogues, despite the fact that our system is on a lattice and we furthermore only utilise a discrete set of patches. To make the meanings of these order parameters clear, we note that the s-wave eigenvector predicts an isotropic gap, while the d-wave eigenvector leads to four nodes on each Fermi surface pocket. The p-wave and f-wave eigenvectors each give two nodes per pocket; however, the p-wave order parameter naïvely changes sign twice as a function of angle in the Brillouin zone, whereas the f-wave order parameter changes sign six times.

Due to our patch approximation we can predict neither the relative phases of the superconducting order parameter between pockets nor which vector(s) Q_i will form the CDW. To calculate the latter, a multi-component order parameter theory is required²⁵.

Given the divergence of the couplings at y_c we introduce the asymptotic form g_i = G_i/(y_c − y). As y → y_c we can express the divergences of order parameter susceptibilities in the power-law form ${\chi }_{j}={({y}_{c}-y)}^{-j}$, with j ∈ {${\alpha }_{\,\text{SC}\,}^{s}$, ${\alpha }_{\,\text{SC}\,}^{d}$, ${\alpha }_{\,\text{SC}\,}^{p}$, ${\alpha }_{\,\text{SC}\,}^{f}$, ${\alpha }_{\,\text{SDW}\,}^{{{\bf{Q}}}_{1}}$, ${\alpha }_{\,\text{CDW}\,}^{{{\bf{Q}}}_{1}}$, ${\alpha }_{\,\text{SDW}\,}^{2{{\bf{K}}}_{1+}}$, ${\alpha }_{\,\text{CDW}\,}^{2{{\bf{K}}}_{1+}}$}. The exponents are given by the following equations:

$${\alpha }_{\,\text{SC}\,}^{s}=-{G}_{3}-{G}_{4}-{G}_{5}-{G}_{6},$$

(10)

$${\alpha }_{\,\text{SC}\,}^{d}=-{G}_{3}-{G}_{4}+{G}_{5}+{G}_{6},$$

(11)

$${\alpha }_{\,\text{SC}\,}^{p}={G}_{3}-{G}_{4}+{G}_{5}-{G}_{6},$$

(12)

$${\alpha }_{\,\text{SC}\,}^{f}={G}_{3}-{G}_{4}-{G}_{5}+{G}_{6},$$

(13)

$${\alpha }_{\,\text{SDW}\,}^{{{\bf{Q}}}_{1}}={d}^{\varepsilon }({y}_{c})\left({G}_{2}+{G}_{5}\right),$$

(14)

$${\alpha }_{\,\text{CDW}\,}^{{{\bf{Q}}}_{1}}={d}^{\varepsilon }({y}_{c})\left(-2{G}_{1}+{G}_{2}+{G}_{5}-2{G}_{6}\right),$$

(15)

$${\alpha }_{\,\text{SDW}\,}^{2{{\bf{K}}}_{1+}}=\beta {G}_{4},$$

(16)

$${\alpha }_{\,\text{CDW}\,}^{2{{\bf{K}}}_{1+}}=\beta \left({G}_{4}-2{G}_{3}\right).$$

(17)

Due to the nature of our patch scheme, ferromagnetic instabilities cannot be investigated: they require the full Fermi surface to calculate the susceptibilities. Ferromagnetic phases have been observed experimentally in monolayer VSe₂²⁸. However, there is evidence to suggest that ferromagnetism is suppressed near the CDW phase as our nested approximation would suggest²⁹.

Considering the alternative triangular Fermi surface case, the definitions of intra- vs. inter-pocket scattering have to be altered. This does not change the CDW nesting vectors; however, the f-wave superconductivity would be replaced by an s_±-like order parameter.

Phase diagrams

Solving (1–6) numerically with the initial conditions ${g}_{i}(y=0)={g}_{i}^{0}$, and utilising the definitions of the divergent susceptibilities, we can investigate the phase diagram of the model. When the effective interaction is of pure contact form, for which V_eff = J_eff = 0, only two instabilities are predicted: s-wave superconductivity for an initially attractive interaction and d-wave superconductivity for an initially repulsive one. For V_eff and J_eff non-zero, the phase diagrams for a range of nesting strengths (ε = 10⁻¹, 10⁻², 10⁻³) are plotted in Fig. 1. When all effective interactions are initially repulsive the predicted instability is again to d-wave superconductivity. As some of the initial effective interactions become attractive, regions of s-wave and p-wave superconductivity arise. As the nesting strength is increased, these regions become occupied by a CDW phase.

Discussion

The tuning of the Fermi surface nesting is a control parameter in our analysis. Our analysis is therefore complementary to that of Jang et al.²⁵, and predicts CDW formation without any mean-field assumption, taking into account the competition of superconducting and density-wave fluctuations.

Our CDW phase emerges in the limit of strong nesting. There is evidence in the literature that supports this limit: for example, taking into account self-energy corrections to the patch dispersions, a flow to perfect nesting is predicted by some previous RG calculations^25,30,31. Other analyses, however, show^10,32 a Fermi surface that retains a power-law curvature at the hot-spots and is not perfectly nested. However, given the relatively robust nature of our predicted CDW phase, we do not expect the incorporation of such curvature effects to alter our resulting phase diagrams qualitatively.

It is also worth noting that in our analysis, following Jang et al.²⁵, we have—for technical reasons—considered hot-spots displaced from the boundary of the Brillouin zone. It is of course important to ask what effect this has. Moving our four hot-spots on pocket 1 towards the zone edge would suppress those fluctuation channels in which the converging hot-spots have different phases, i.e., the d- and f-wave superconducting channels. However, since these are not the channels in direct competition with the Q₁ CDW phase, we do not expect major alterations in our resulting phase diagrams in the range where the CDW phase occurs.

It might seem surprising that a strong effective exchange coupling J_eff should lead to CDW formation, since one might have expected that it would favour a magnetically ordered state. However, this intuition is too ‘local moment’: in our itinerant model, where the kinetic energy scales dominate over the bare interaction energies, the development of order is determined by the interplay between the different channels of fluctuation as the temperature is lowered rather than by the mean-field ground state of any single interaction term.

The fact that some of the intermediate-scale effective interactions must be attractive for a CDW phase to be favoured is an interesting result in the context of a purely electronic calculation. It is well known that electron-phonon interactions lead to an effective attractive interaction between electrons. Whether the inclusion of such electron-phonon interactions in the high-energy flow is necessary to arrive at the values of J_eff that provoke a charge-density-wave transition, or whether these could be reached by a (theoretical) purely electronic high-energy flow, is beyond the scope of this calculation to determine.

The Q₁ CDW wavevector is favoured as the chosen instability, even with the artificial enhancement of the q₁ channel due to lack of curvature corrections to the dispersions. Thus this behaviour again agrees with that seen by Jang et al.²⁵, and gives a potential all-electronic mechanism for CDW formation in the monolayer TMDs.

To analyse the effect of Fermi surface nesting on CDW formation in the TMDs, we have performed an RG analysis of an effective extended Hubbard model for monolayer 1T-VSe₂, retaining both particle-particle (superconducting) and particle-hole (density-wave) channels. In the region of intermediate-energy effective coupling strengths where some or all of the effective two-particle interactions are attractive, regions of superconductivity give way to CDW order as the strength of Fermi surface nesting is increased.

Methods

Since the Fermi surface of 1T-VSe₂ is derived from one of the vanadium d-bands^20,33, we adopt a single-band model to describe the physics of monolayer 1T-VSe₂^17,25. We separate the development of correlations as the temperature is lowered into two different regimes: high-energy flow (from scales of ~ 1 eV down to ~ 10 meV), and low-energy flow (below scales of ~ 10 meV). We know from experiment that the high-energy flow tends to increase the degree of nesting of opposite sides of the Fermi surface pockets; it will also renormalise the on-site Coulomb repulsion U, the nearest-neighbour Coulomb repulsion V, and the nearest-neighbour magnetic exchange J from their microscopic values. Since we cannot describe the high-energy flow quantitatively, we take the nesting parameter ε and the effective interactions at a scale of ~ 10 meV — U_eff, V_eff, and J_eff — as input parameters of our electronic model. The resulting Hamiltonian is

$$\begin{array}{ll}H=\sum _{\sigma =\uparrow ,\downarrow }\sum _{i,j}{t}_{{\rm{eff}},ij}{c}_{i\sigma }^{\dagger }{c}_{j\sigma }+{U}_{{\rm{eff}}}\sum _{i}{n}_{i\uparrow }{n}_{i\downarrow }\\ \qquad\qquad+\ {V}_{{\rm{eff}}}\sum _{\sigma \sigma ^{\prime} }\sum _{\langle i,j\rangle }{n}_{i\sigma }{n}_{j\sigma ^{\prime} }+{J}_{{\rm{eff}}}\sum _{\langle i,j\rangle }{{\bf{S}}}_{i}\cdot {{\bf{S}}}_{j}.\end{array}$$

(18)

Here the operator ${c}_{i\sigma }^{\dagger }$ creates an electron with spin-projection σ on vanadium site i; ${n}_{i\sigma }={c}_{i\sigma }^{\dagger }{c}_{i\sigma }$ is the number operator for electrons on vanadium site i with spin-projection σ, while ${{\bf{S}}}_{i}=\frac{1}{2}{\sum }_{\sigma \sigma ^{\prime} }{c}_{i\sigma }^{\dagger }{{\boldsymbol{\tau }}}_{\sigma \sigma ^{\prime} }{c}_{i\sigma ^{\prime} }$ is the operator for the spin on site i, where ${\boldsymbol{\tau }}={({\tau }_{x},{\tau }_{y},{\tau }_{z})}^{\text{T}}$ is the vector of Pauli matrices. t_eff,ij denotes the effective hopping matrix elements for our single-band model of VSe₂, which already incorporate the increase in nesting resulting from the high-energy flow. U_eff and V_eff are the effective strengths of the on-site and nearest-neighbour parts of the Coulomb repulsion respectively, and J_eff is the effective Heisenberg exchange coupling. As noted above, these effective couplings, applicable at scales ~ 10 meV, are renormalised from those in the microscopic model due to the high-energy stage of the flow. 〈i, j〉 indicates that the sum runs over all pairs of nearest-neighbour sites.

At low energies it is sufficient to linearise the non-interacting dispersion relation around the Fermi level, and thus we do not need to know the precise form of the matrix elements t_eff,ij. A schematic non-interacting Fermi surface is shown in Fig. 2. As discussed above, nested sections of the Fermi surface arise at lower temperatures. Since these dominate the relevant susceptibilities, we can safely use a simplified form of the dispersion relation that agrees with the true dispersion in these nested regions.

Fig. 2: Schematic Fermi surface of monolayer 1T-VSe₂.

a Schematic Fermi surface of monolayer 1T-VSe₂ with non-nested Fermi surfaces. In the low-temperature limit sections of the Fermi surface become nested. We adopt the notation of Jang et al.²⁵ to describe the patch scheme and nesting vectors. b Schematic change in one pocket of the Fermi surface of monolayer 1T-VSe₂ as the temperature T is lowered. c A zoomed view of the left-hand side of that pocket in our linearised approximation.

We utilise the patch scheme of Jang et al.²⁵. This scheme consists of twelve patches that lie on sections of the Fermi surface that become nested at low temperatures, as shown in Fig. 2. The absolute wavevector of the centre of patch 1 + is denoted K₁₊, and similarly for the other patches. In each patch we linearise the dispersion relation, i.e., we write the single-electron energy (measured with respect to the Fermi energy) as a linear function of the components of k, the wavevector measured relative to the centre of the patch. For the four patches labelled ‘1’, this gives ${\xi }_{1}^{\pm }=\pm {\!}{k}_{x}+\varepsilon {k}_{y}$ and ${\xi }_{\overline{1}}^{\pm }=-{\xi }_{1}^{\pm }$, in units where both ℏ and the Fermi velocity v_F are set to 1. The parameter ε controls the nesting of the Fermi surface, with the limit ε → 0 corresponding to perfect nesting. We use only the bare effective dispersions in our calculations as fermion self-energy corrections are independent of the renormalisation of interactions at one-loop³⁴.

The effective dispersions on the second and third pockets n = 2, 3 may be obtained from a similar expression, ${\xi }_{n}^{\pm }\equiv {\xi }^{\pm }({k}_{x}^{(n)},{k}_{y}^{(n)})=\pm {\!}{k}_{x}^{(n)}+\varepsilon {k}_{y}^{(n)}$, where the wavevector k⁽ⁿ⁾ is obtained by an appropriate rotation:

$$\left(\begin{array}{l}{k}_{x}^{(n)}\\ {k}_{y}^{(n)}\end{array}\right)=\left(\begin{array}{ll}\cos (n-1)\frac{\pi }{3}&\sin (n-1)\frac{\pi }{3}\\ -\sin (n-1)\frac{\pi }{3}&\cos (n-1)\frac{\pi }{3}\end{array}\right)\left(\begin{array}{l}{k}_{x}\\ {k}_{y}\end{array}\right),$$

(19)

together with the relation ${\xi }_{\overline{n}}^{\pm }=-{\xi }_{n}^{\pm }$.

We can then use these dispersions to calculate the particle-particle and particle-hole susceptibilities for all possible nesting vectors between patches

$${{{\Pi }}}_{\,\text{pp}\,}^{{\bf{q}}}({{\Omega }})={\int_{k}}G(\omega ,{\bf{k}})G({{\Omega }}-\omega ,{\bf{q}}-{\bf{k}}),$$

(20)

$${{{\Pi }}}_{\,\text{ph}\,}^{{\bf{q}}}({{\Omega }})=-{\int_{k}}G(\omega ,{\bf{k}})G(\omega +{{\Omega }},{\bf{k}}+{\bf{q}}),$$

(21)

with $G(\omega ,{\bf{k}})={(i\omega -{\xi }_{{\bf{k}}}+\mu )}^{-1}$. The range of integration is ω ∈ (−∞, ∞) and k_x, k_y ∈ (− k_c, k_c), where k_c is an ultraviolet momentum cutoff²⁷. In the presence of near-perfect nesting, these susceptibilities both have similarly strong divergences. The nature of the eventual low-temperature ordered state is thus determined by a rather intricate competition between various superconducting and density-wave fluctuation channels, which must be tracked carefully as the energy scale is lowered from ~ 10 meV where we take the low-energy flow to begin.

The complete particle-hole susceptibility at wavevector Q₁ = K₁₊ − K₁₋ is

$$\begin{array}{ll}{{{\Pi }}}_{\,\text{ph}\,}^{{{\bf{Q}}}_{1}}({{\Omega }})=\frac{{k}_{c}}{2{\pi }^{2}}+\frac{{k}_{c}}{4{\pi }^{2}}\mathrm{log}\,\left(\frac{{{{\Omega }}}^{2}+4{k}_{c}^{2}}{{{{\Omega }}}^{2}+4{\varepsilon }^{2}{k}_{c}^{2}}\right)\\ \qquad \quad -\frac{{{\Omega }}}{4{\pi }^{2}\varepsilon }\arctan \left(\frac{2{k}_{c}\varepsilon }{{{\Omega }}}\right).\end{array}$$

(22)

The Fermi surface nesting parameter ε cuts off the Ω → 0 divergence of the logarithm in this channel, and the height of the Ω = 0 peak in the susceptibility reduces as ε is increased. By contrast, the particle-particle susceptibility at zero momentum in the low-energy limit has the usual logarithmic dependence, independent of ε, ${{{\Pi }}}_{\,\text{pp}\,}^{{\bf{0}}}({{\Omega }})\approx \frac{{k}_{c}}{2{\pi }^{2}}\mathrm{log}\,\left(\frac{{k}_{c}}{{{\Omega }}}\right)$. Here we have discarded contributions from non-divergent $\arctan$ terms as they are negligible as ${{{\Pi }}}_{\,\text{pp}\,}^{0}({{\Omega }})$ becomes large at low energies.

The particle-particle susceptibility ${{{\Pi }}}_{\,\text{pp}\,}^{{{\bf{q}}}_{1}}({{\Omega }})$ with q₁ = K₁₊ + K₁₋ is logarithmically divergent and dependent on the nesting parameter ε; indeed, ${{{\Pi }}}_{\,\text{pp}\,}^{{{\bf{q}}}_{1}}({{\Omega }})={{{\Pi }}}_{\,\text{ph}\,}^{{{\bf{Q}}}_{1}}({{\Omega }})$. The particle-hole susceptibility ${{{\Pi }}}_{\,\text{ph}\,}^{2{{\bf{K}}}_{1+}}({{\Omega }})$ is always perfectly nested for the case of linear dispersion. However, the nested sections of the VSe₂ Fermi surface are finite in length and there will be curvature corrections to the dispersion which will cutoff the divergence of the integral. We therefore introduce an additional parameter β with 0 ⩽ β ⩽ 1 to reduce the magnitude of this susceptibility and emulate the effect of finite length nested sections: ${{{\Pi }}}_{\,\text{ph}\,}^{2{{\bf{K}}}_{1+}}({{\Omega }})=\beta {{{\Pi }}}_{\,\text{pp}\,}^{0}({{\Omega }})$.

Interactions between Fermi surface patches belonging to different pockets do not give divergent contributions, since the particle-particle bubble has non-zero q and there is no particle-hole nesting between patches on separate pockets. Therefore in our low-energy model we retain only one of the Fermi surface pockets, thereby reducing the number of patches to four. This greatly simplifies our effective Lagrangian; however, we lose information about the relative phase of the superconducting order parameter between different Fermi surface pockets and the competition of particle-hole nesting vectors.

After calculating the divergent susceptibilities, we find that only six of the nine possible interaction terms flow as the theory is renormalised. Retaining only these terms, we obtain the following imaginary-time effective Lagrangian:

$${\mathcal{L}}= \sum _{\sigma =\uparrow ,\downarrow }\sum _{a=1,\overline{1}}\sum _{s=\pm }{\overline{\psi }}_{as\sigma }(i\omega -{\xi }_{a}^{s}){\psi }_{as\sigma }\\ -{g}_{1}\sum _{\sigma \sigma ^{\prime} }\sum _{a}{\overline{\psi }}_{a+\sigma }{\overline{\psi }}_{a-\sigma ^{\prime} }{\psi }_{a+\sigma ^{\prime} }{\psi }_{a-\sigma }\\ -{g}_{2}\sum _{\sigma \sigma ^{\prime} }\sum _{a}{\overline{\psi }}_{a+\sigma }{\overline{\psi }}_{a-\sigma ^{\prime} }{\psi }_{a-\sigma ^{\prime} }{\psi }_{a+\sigma }\\ -\frac{{g}_{3}}{2}\sum _{\sigma \sigma ^{\prime} }\sum _{a}\sum _{s}{\overline{\psi }}_{as\sigma }{\overline{\psi }}_{\overline{a}s\sigma ^{\prime} }{\psi }_{as\sigma ^{\prime} }{\psi }_{\overline{a}s\sigma }\\ -\frac{{g}_{4}}{2}\sum _{\sigma \sigma ^{\prime} }\sum _{a}\sum _{s}{\overline{\psi }}_{as\sigma }{\overline{\psi }}_{\overline{a}s\sigma ^{\prime} }{\psi }_{\overline{a}s\sigma ^{\prime} }{\psi }_{as\sigma }\\ -\frac{{g}_{5}}{2}\sum _{\sigma \sigma ^{\prime} }\sum _{a}\left[{\overline{\psi }}_{a+\sigma }{\overline{\psi }}_{\overline{a}+\sigma ^{\prime} }{\psi }_{a-\sigma ^{\prime} }{\psi }_{\overline{a}-\sigma }+\,\text{H.c.}\,\right]\\ -\frac{{g}_{6}}{2}\sum _{\sigma \sigma ^{\prime} }\sum _{a}\left[{\overline{\psi }}_{a+\sigma }{\overline{\psi }}_{\overline{a}+\sigma ^{\prime} }{\psi }_{\overline{a}-\sigma ^{\prime} }{\psi }_{a-\sigma }+\,\text{H.c.}\,\right],$$

(23)

where $\overline{a}$ denotes the patch with opposite momentum to a. The two-particle scattering processes described by the various interaction terms are shown in Fig. 3.

Fig. 3: The six types of two-particle interaction in our low-energy theory of monolayer 1T-VSe₂.

We illustrate these here for the four patches in group 1. g₁ and g₂ are exchange and density-density interactions between patches separated by the wavevector Q₁, g₃ and g₄ are exchange and density-density interactions between patches with opposite momenta, and g₅ and g₆ are the two possible exchange interactions that involve all four patches.