Abstract
The realization of Bose-Einstein condensation in ultracold trapped gases has led to a revival of interest in this fascinating quantum phenomenon. This experimental achievement necessitated both extremely low temperatures and sufficiently weak interactions. Particularly in reduced spatial dimensionality even an infinitesimal interaction immediately leads to a departure to quasi-condensation. We propose a system of strongly interacting bosons, which overcomes those obstacles by exhibiting a number of intriguing related features: (i) The tuning of just a single control parameter drives a transition from quasi-condensation to complete condensation, (ii) the destructive influence of strong interactions is compensated by the respective increased mobility, (iii) topology plays a crucial role since a crossover from one- to ‘infinite’-dimensionality is simulated, (iv) a ground state gap opens, which makes the condensation robust to thermal noise. Remarkably, all these features can be derived by analytical and exact numerical means despite the non-perturbative character of the system.
Similar content being viewed by others
Introduction
Bose–Einstein condensation (BEC) is one of the most striking quantum phenomena in nature1,2,3,4. While its theoretical prediction dates back almost one hundred years ago it has more recently seen a revival of interest due to its realization in trapped gases5,6,7. The accurate study of BEC by theoretical and computational approaches particularly for systems with strong quantum correlations is rather challenging. This has been the reason why most studies of BEC so far were concerned with weakly interacting bosons (corresponding to the experimental situation for ultracold gases) or even ideal Bose gases, eventually allowing for feasible mean-field approaches. Prime examples are the Bogoliubov theory8 for uniform systems, Gross–Pitaevskii theory9,10,11 for general inhomogeneous systems, and perturbation theoretical approaches12,13,14,15,16,17,18. Although these widely used approaches have led to a deeper understanding of BEC, their range of validity is limited. To go beyond that limitation, various methods were developed19,20,21,22.
Since the experimental realization of BEC, the respective field of ultracold gases has become one of the most exciting fields of research with a fruitful interplay between theory and experiment. It allowed for the experimental verification of numerous other theoretical predictions as well, stimulated further theoretical investigations of trapped particles19, and even revealed phenomena not observed before such as the crossover from BEC-superfluidity to BCS-superconductivity23,24,25,26. One of the most promising recent avenues has been the study of effectively one-dimensional quantum systems27,28,29,30,31,32,33. Their most striking difference to three-dimensional systems is probably the absence of BEC: already an infinitesimally weak interaction between the N bosons leads to a “sublinear” behavior of the number of condensed bosons, N0(N) ~ Nα34,35, even at zero temperature, for homogeneous gases as well for gases in a harmonic trap and regardless of the form of the interaction35,36,37,38,39,40,41,42. A prominent system giving rise to this phase called “quasi-condensation”35 is the Lieb–Liniger model43,44, a ring system with N spinless bosons interacting via a δ-potential. Tuning the coupling constant to infinity leads to impenetrable bosons (Tonk–Girardeau gas)45 with the proven scaling \({N}_{0}(N) \sim \sqrt{N}\)34.
Thermodynamic phase transitions (at finite temperatures) in D = 3 dimensions have been studied for more than a century. However, the study of quantum phase transitions (at zero temperature)46, and particularly of the entanglement close to that transition47,48 have attracted much attention in recent years, only. The latter studies were performed mostly for low-dimensional lattice models. They have revealed a striking similarity between the behavior of the order parameter and of quantum informational quantities, like entanglement entropy. As discussed above, at zero-temperature an interacting Bose gas exhibits two qualitatively different phases, a quasi-condensate in D = 1 and a true BE-condensate in D ≥ 3. Therefore, it is of interest to search for a model that exhibits a transition (or a crossover) between these two phases, and in particular, allows to check whether this special transition has common properties with general quantum phase transitions.
BEC was explored in cylindrical or toroidal trap geometries, both experimentally27,28,29,30,31,32,33 and theoretically49,50,51. But, changing the radial dimension of the confinement, neither the transition from the sublinear N-dependence of N0(N) of the quasi-condensate to the linear dependence of the true condensate, nor its entanglement properties have been investigated. The only systematic study of such a transition was performed for a one-dimensional Bose gas in a harmonic trap52. However, that transition occurs only at temperatures T > 0.
It is the challenge of the present work to propose and investigate a lattice model for strongly interacting bosons that allows one to drive such a transition by changing just a single parameter, s/t, which is the ratio of the model’s two hopping rates s and t, as explained below. One of our major results is to establish by this model a mechanism which can generate “infinite” range hopping by increasing s/t. This is important since enhancing the boson’s mobility allows overcompensating the destructive effects of the repulsive interactions, leading finally to maximal possible condensation, despite infinitely strong repulsion. A further important feature of our model is the generation of an excitation gap in the N-particle spectrum for s/t > 0. This makes BEC even robust to thermal noise and quantum fluctuations and thus may allow experimentalists to overcome the typical obstacles faced while realizing BEC. The other important result concerns the application of tools from quantum information theory. We show that the mutual information possesses the qualitatively similar dependence on s/t as the number N0(N) of condensed bosons. This supports the connection between the behavior of an order parameter and of entanglement at a quantum phase transition even for the transition (or crossover) from a quasi-condensate to a true one.
All these key findings will be derived by analytical or exact numerical means despite the nonperturbative character of our system.
Results
Model Hamiltonian
To motivate our model, let us first recall that the possible presence of BEC depends in general not only on the spatial dimensionality and temperature but also on the ratio between kinetic and interaction energy. In the case of systems, which are inhomogeneous, e.g., due to the presence of an external field or disorder, the occurrence of BEC will also depend on these quantities. Concerning the ratio between kinetic and interaction energy, lattice systems have the great advantage that the kinetic energy can be manipulated by varying the hopping range between the lattice sites. The most prominent lattice model for bosons is the widely studied Bose–Hubbard model53
where \({b}_{i}^{\dagger },{b}_{i}\) creates/annihilates a spinless boson at site i, \({\hat{n}}_{i}\equiv {b}_{i}^{\dagger }{b}_{i}\) and tij is the hopping rate between sites i and j. It was shown that the Bose–Hubbard model can be experimentally realized by ultracold bosonic atoms in an optical lattice54.
The conflict between interaction and mobility is maximized in the limit of strong interactions U → ∞ in which the bosons become hard-core55,56. By employing respective hard-core boson (HCB) creation(\({h}_{i}^{\dagger }\)) and annihilation operators(hi) (1) takes the compact form \({\hat{H}}_{hc}=-{\sum }_{i,j}{t}_{ij}{h}_{i}^{\dagger }{h}_{j}\). Particularly the case of HCBs makes clear the important role of the hopping range, since for infinite-range hopping (a kind of mean-field limit53) HCBs exhibit BEC even at finite temperatures, despite their infinitely strong repulsion57,58,59.
Moreover, the effect of the interaction on BEC is distinctively destructive in one-dimensional systems. At zero temperature even an infinitesimally weak interaction already leads to a departure from BEC to the phase of quasi-condensation. This raises a fundamental question which our work shall answer in an affirmative and constructive way: after having confined a 3D Bose gas to one dimension, is it possible to tweak in an experimentally feasibly way this one-dimensional system with the effect of enhancing the mobility of the interacting bosons to reintroduce BEC? From a general point of view, one is immediately tempted to negate this question. The hopping amplitudes tij namely resemble the overlap of Wannier orbitals at sites i, j which in turn decays exponentially as a function of the spatial separation ∣i − j∣. Screening effects reduce the hopping even further and eventually motivate the common restriction of tij in the Bose–Hubbard model to just nearest neighbors. The potential physical significance of long-range hopping has motivated experimentalists in recent years to realize at least effectively hopping terms beyond nearest neighbors. Despite a remarkable effort, the regime of infinite-range hopping has been out of reach but only the typical decay of tij could be slowed down to an algebraic dipolar- and van der Waals-type one60,61. It will be one of our key achievements to propose a model that eventually would allow one to enhance mobility even to infinite-range.
In contrast to the rather involved experimental realization of algebraically decaying hopping rates our proposal to realize “infinite”-range hopping will be surprisingly simple. As it is illustrated in Fig. 1, we consider N HCBs on a lattice consisting of a ring with d sites, lattice constant a, and one additional site at its center. The ring gives rise to hopping between nearest neighbors at a rate t > 0. The crucial point is now that the ring’s topology allows hopping between the central site and any ring site at a rate s ≥ 0. Accordingly, the central site has an effect similar to an impurity, making the lattice inhomogeneous.
We remind the reader that proposing and studying this model shall be seen as one of our key achievements. It is also worth noticing that various other studies of BEC for inhomogeneous lattices differ significantly from ours. They either consider the rather trivial case of ideal bosons62,63,64,65,66,67,68 or restrict to the mean-field regime69,70. At the same time, our model could be particularly appealing to experimentalists since the underlying graph emerges from a Mexican hat potential (see below) and HCBs can be realized experimentally31,71 by tuning the interactions at the Feshbach resonance72,73,74,75.
Accordingly, the Hamiltonian of our proposed model of bosons with hard-core interaction reads
where \({h}_{c}^{\dagger },{h}_{c}\) denote the corresponding operators for the central site. For s/t → 0, \(\hat{H}\) reduces to the pure ring-model (left of Fig. 1) and the limit s/t → ∞ leads to the star-model (right of Fig. 1). The solution of the eigenvalue problem for these two limiting cases is known. For s = 0 it follows from the solution for impenetrable bosons43,44,45 which only exhibits quasi-condensation, and s = ∞ was solved in ref. 76 proving the existence of true BEC with maximal possible number N0(N, d) = N(d − N + 1)/d of condensed bosons. For finite values of s/t the Hamiltonian (2) interpolates between the ring-lattice and the star-lattice (cf. Fig. 1). Hence, changing the single parameter s/t allows us to investigate in a systematic way the crossover from the regime of quasi-condensation to maximally possible condensation, eventually leading to a number of remarkable insights.
Spectral properties, BEC, and entanglement
The present section contains only the crucial steps. Technical details can be found in “Methods” and particularly in the “Supplementary Methods.”
Since the central site couples to the (N − 1)- and N-particle state-space on the ring, a simple and fully analytic solution does not exist. Yet, after implementing a number of steps, the eigenvalue problem for Hamiltonian (2) can be rewritten as
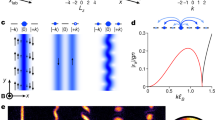
where E is the eigenvalue and {Aν} are amplitudes of the unperturbed (i.e., corresponding to s = 0) N-particle eigenstates \(\left|{\psi }_{{\boldsymbol{\nu }}}^{0}(N)\right\rangle\) on the ring. Although this equation cannot be solved analytically for the entire regime of s, it allows us to derive in a nontrivial way important qualitatively correct features of the spectrum. The unperturbed (N − 1)- and N-particle spectrum forms a band of discrete levels (see Fig. 2a) which becomes continuous for d → ∞. The hopping between the central site and the ring introduces a “hybridization” of these two spectra leading on one hand to a shift of order 1/d of the unperturbed band-levels. On the other hand, some energy levels (marked by crosses) of the smaller (N − 1)-particle band (assuming n = N/d < 1/2, which is not a restriction due to the particle-hole duality) are found to disappear. These levels, however, reappear as new discrete eigenvalues symmetrically below and above the perturbed N-particle band(see open circles in Fig. 2b). The larger s and N, the more of those new discrete energy levels occur. As a matter of fact, they follow from the eigenvalues of an effective Hamiltonian for N HCBs with “infinite”-range hopping: \({\hat{H}}^{{\rm{eff}}}={\tilde{s}}^{2}(1/d)\mathop{\sum }\nolimits_{i,j = 1}^{d}{h}_{i}^{\dagger }{h}_{j}\). Here, the parameter \(\tilde{s}=(s/t)\sqrt{d}\) is a scaled dimensionless hopping rate. This mapping of the original model to an effective one holds for \(\tilde{s}\gg 2\sqrt{2}\,\pi /\sqrt{d}\) for the diluted gas (n ≪ 1) and in the case of finite n for \(\tilde{s}\gg (4/\pi )\sqrt{d}\sin( \pi n)/\sqrt{n(1-n)}\).
a The unperturbed band spectrum of (N − 1) hard-core bosons (red dashed lines) and N hard-core bosons (blue solid lines). The crosses mark those levels which disappear under the perturbation. b The perturbed spectrum consisting of the shifted unperturbed levels (dashed red and solid blue lines) and the crosses mark those levels of the unperturbed (N − 1)-particle spectrum which has disappeared. The open circles are the new levels generated by the perturbation.
Most importantly, these findings imply also the opening of an energy gap \({{\Delta }}E={E}_{{\rm{low}}}^{0}-{E}_{0}\) between the perturbed ground state energy E0 and \({E}_{{\rm{low}}}^{0}\), the lower edge of the N-particle band:
Also, the number N0 of condensed HCBs can be derived analytically since it is related to the largest eigenvalue of Heff. We obtain
where the prefactor ∣β∣2 of the 1/N-correction is given in the Supplementary Eq. (S30).
In order to support these analytical results and to extend those for finite d to small and intermediate values of \(\tilde{s}\) we have performed large-scale density matrix renormalization group computations (DMRG)77,78,79. The corresponding results together with the analytical ones are presented in Figs. 3 and 4. The log–log representation of the gap \({{\Delta }}E(\tilde{s})\) in Fig. 3 reveals a distinctive crossover from a \({\tilde{s}}^{2}\)-dependence for \(\tilde{s}\ll 1\) to the linear dependence on \(\tilde{s}\) for \(\tilde{s}\gg 1\). For the diluted gas, i.e., n ≪ 1, the analytical and DMRG results in the \({\tilde{s}}^{2}\)- and \(\tilde{s}\)-regime are in good agreement. When the density is increased this agreement remains excellent in the linear regime while it gets worse in the complementary range. Figure 4 illustrates clearly for the diluted gas (Fig. 4a) and for higher densities (Fig. 4b) the crossover from a quasi-condensate with \({N}_{0} \sim \sqrt{N}\) to the maximally possible condensation N0(N, n) ≃ N(1 − n). The deviation from the \(\sqrt{N}\)-dependence for small \(\tilde{s}\) and higher densities (see lower panel) is an effect of the lattice-discreteness. In the regime in which the mapping to the effective Hamiltonian is valid (see above) the analytical and DMRG results agree well.
Log–log plot for the excitation gap as a function of \(\tilde{s}\) for d = 199 and various filling factors n. Results from density matrix renormalization group calculations (symbols) and the analytical result (Eq. (4)) (solid lines). The dashed-dotted and dashed lines represent slope two and one, respectively.
a N0 as a function of \({\mathrm{log}}\,(\tilde{s})\) for fixed low-density n ≃ 0.05 and various site numbers d. b N0 as a function of \({\mathrm{log}}\,(\tilde{s})\), various numbers of particles N, and a fixed number of sites d = 199. The dots on the vertical axis represent N(1 − n). Symbols: results from density matrix renormalization group calculations, dashed lines: a guide for the eye, solid lines: analytical result (Supplementary equation S28). The dotted lines mark the asymptotic values for finite N, s = 0, d → ∞ obtained by the exact numerical calculation of a Toeplitz determinant39.
To explore a possible relationship between BEC and the entanglement structure of the ground state we have used DMRG for calculating the mutual information between the central site c and any ring site i (Ii∣c) and between two ℓth nearest neighbor ring sites (Ii∣i+ℓ) (see “Methods”). The corresponding results for d = 199 and n ≃ 0.05 are shown in Fig. 5. The change in the respective pattern related to the crossover from quasi-BEC to genuine BEC is clearly visible through the mutual information, as well. The correlation between the central and any ring site, Ii∣c, vanishes for \(\tilde{s}\) small while it saturates to a finite value in the limit of large \(\tilde{s}\) when the model exhibits “infinite”-range hopping. \(I_{i|i+\ell}\) saturates also with increasing \(\tilde{s}\) to a constant value for all ℓ demonstrating the growth of long-range correlations. This relates to the generation of BEC. For \(\tilde{s}=0\), Ii∣i+ℓ decays algebraically with increasing ℓ which reflects the algebraic dependence of the quasi-condensate on N. Whereas for finite values of \(\tilde{s}\) its decay becomes exponential as the gap opens, and saturates to finite value for very large ℓ values.
Potential experimental realization
As a possible experimental realization of our model (2) we propose in a first step to confine N ultracold bosonic atoms into two dimensions subject to a Mexican-hat-type potential V(x, y) with d local wells (Fig. 6a) in complete analogy to several recent years’ experiments80,81,82,83,84. Then, one may tune the interaction at the Feshbach resonance to realize HCBs in the same way as reported in ref. 31 for cigar-shaped confinement to realize quasi-condensation of HCB with N0(N) ∝ N1/2. Next, the creation of a local well at the hat’s center (Fig. 6b) and increasing its depth more and more would strongly enhance the mobility of the HCBs due to their possible transitions back and forth between any ring-well and the central one. This would significantly change the physical behavior and BEC would occur with N0(N) ~ N. In order for this to happen already for finite d it must be \(s/t\gg 2\sqrt{2}\pi /d\) in case of a diluted gas (see the previous section) which is the regime relevant for ultracold gases. The hopping occurs due to tunneling between the corresponding wells. Let (Vr, lr = a) and (Vc, lc = ad/(2π)) denote the potential barrier and tunneling distance, respectively, between two adjacent ring-wells and between a ring-well and the central one. Use of the WKB tunneling rate yields the estimate \(s/t\approx ({\gamma }_{c}/{\gamma }_{r})\exp [-\sqrt{m{a}^{2}/{\hslash }^{2}}(\sqrt{{V}_{c}}d/(2\pi )-\sqrt{{V}_{r}})]\) with m the particle’s mass and γα, α = c, r the so-called attempt frequency related to the zero-point oscillation frequency in the corresponding well. For instance, if d = 79 and N = 4 (one data set in Fig. 4a) “BEC”-like behavior should occur for s/t > 1. This can be satisfied if Vc/Vr ≈ (2π/d)2 or if a compared to \(\hslash /\sqrt{m\,\max \{{V}_{c},{V}_{r}\}}\) is small enough, provided γc/γr ≈ 1.
a Realization of the ring lattice for d = 10 by a Mexican-hat-potential. b Realization of the wheel lattice for d = 10 by a Mexican-hat-like potential with a local well at its center. Loading hard-core bosons into the potential landscape in (a) and creating a local well as shown in (b) generates a crossover from quasi to complete Bose–Einstein condensation.
If the trap potential in Fig. 6 is chosen such that it represents a good experimental realization of the “wheel” lattice (cf. Fig. 1) there is true condensation for sufficiently large s/t. In particular, since only a single one-particle state (zero-momentum state) is macroscopically occupied, no fragmented condensation exists per definition. This is consistent with the expectation that homogeneous bosonic systems with purely repelling pair interactions do not exhibit fragmented condensation4. Although the presence of the central well (central site) makes the system inhomogeneous it can not generate fragmentation, because it accommodates maximally one HCB, only. But increasing the width of the central well in Fig. 6b such that it can accommodate a macroscopic number of bosons of an ultracold gas, a situation similar to the double-well-like trap potential in one dimension occurs85. As shown in that work, fragmented condensation may then occur if the barrier height of the double-well is high enough.
It is worth noticing that according to the DMRG results (see also Fig. 4) one would not need to realize a macroscopically large ring to observe our crossover. Yet, in the case of experimentalists could even realize our model with a huge number d of sites on a ring of fixed size (i.e., the limit d → ∞, a → 0 with ad fixed) this would generate a true Mexican-hat potential with continuous rotational invariance and the HCBs would become a Tonks–Girardeau gas. Again, creating a central well would generate genuine Bose–Einstein condensation.
Discussion
We proposed and comprehensively studied a physical model of strongly interacting bosons that allows one to drive a non-trivial transition from quasi-condensation to maximal BEC. It is particularly appealing that this necessitates the tuning of just a single control parameter which changes the underlying topology in such a distinctive way that the “infinite” range hopping model is simulated. The enhanced mobility of the bosons then compensates for the destructive effects of the strong interaction to generate BEC. Without solving the model’s eigenvalue equation exactly, our kind of analytical approach (see the section “Spectral properties, BEC, and entanglement” above and also the “Supplementary Methods”) allows us to show on a qualitative level why an excitation gap occurs in the N-particle spectrum, which usually is highly demanding. Similarly to, e.g., superconductivity, the quantum Hall effect, and the Haldane phase the existence of such a gap has an enormous influence on the physical behavior, e.g., making the BE-condensate robust to thermal noise and perturbations in general.
It is worth highlighting the striking potential of our mechanism for generating BEC. As a matter of fact, it is conceptually quite different from the well-known generation of BEC at finite temperatures for non-interacting bosons. The latter is either merely due to the opening of a gap in the “one-particle” spectrum or deformation of the density of states (in analogy to the transition from D ≤ 2 to D = 3)62,63,64,65,66,67,68. The same effect applies to the experimental27,28,29,30,31,32,33 and theoretical studies49,50,51 in which the cylindrical or toroidal confinement is relaxed to reach the mean-field regime. In our system, however, it is the interplay between mobility and interaction within the “non-perturbative” regime which generates genuine BEC (see the rather involved derivation in the Supplementary Methods). The non-trivial influence of the interaction is also well illustrated by the analytical result for the ground state gap (Eq. (4)) which in the regime of maximal BEC differs from one of the non-interacting bosons by the crucial factor \(\sqrt{1-n}\). Remarkably, 1 − n is nothing else than the universal reduction of the maximal possible degree of condensation due to the hard-core constraint76, which is the quantum depletion. In the case of finite on-site interactions, this depletion factor ν(n) is expected to interpolate between both extremal cases of hard-core and ideal bosons, 1 − n ≤ ν(n) ≤ 1. This would provide a remarkable exact relation between the ground state gap, quantum depletion, and the interaction strength of the ultracold atoms. Since the latter can systematically be tuned at the Feshbach resonance72,73,74,75 this would open an avenue for steering ground state gaps and controlling the number of bosons in BEC.
Finally, inspired by the fruitful interplay of theory and experiments in the field of ultracold gases our work based on analytical and exact large-scale DMRG calculations shall be understood as a proposal to the experimentalists as well. Our model could be particularly appealing since the underlying graph emerges from a Mexican-hat-type potential and the entire transition can be driven by tuning just a single control parameter. It is then exactly the respective central site, which can be probed to confirm that transition. At the same time, this would also exploit the fruitful link47,48 between quantum phase transitions and entanglement or related promising quantum informational theoretical concepts, as illustrated in Fig. 5.
Methods
Eigenvalue problem
The central site generates for the N-particle state a superposition \(\left|{{{\Psi }}}_{N}\right\rangle =\alpha {\left|{\phi }_{N}\right\rangle }_{r}\otimes {\left|0\right\rangle }_{c}+\beta {\left|{\varphi }_{N-1}\right\rangle }_{r}\otimes {\left|1\right\rangle }_{c}\) of an N- and (N − 1)-particle ring-state. Expansion of these states with respect to the unperturbed (N − 1)- and N-particle ring-states allows decoupling of the original eigenvalue problem. This leads to a nonintegrable eigenvalue problem on the ring itself. Straightforward manipulation allows deriving Eq. (3). For details see the Supplementary Methods.
Density matrix renormalization group
The DMRG calculations were performed for d ≤ 199 and N ≤ 98. In the DMRG procedure, we have performed calculations using the dynamic block state selection approach86. We have set a tight error bound on the diagonalization procedure, i.e., we set the residual error of the Davidson method to 10−9 and used ten DMRG sweeps. We have checked that the various quantities of interest are practically insensitive to the bond dimension being larger than 1024.
Besides calculating energy eigenvalues and the one-(ρi) and two-site(ρij) reduced density matrices we have also determined one- and two-site von Neumann entropies si and sij, respectively, as well as the two-site mutual information, Ii∣j, given as Ii∣j = si + sj − sij87,88. Here \({s}_{i}=-{\rm{Tr}}{\rho }_{i}{\mathrm{ln}}\,{\rho }_{i}\) and \({s}_{ij}=-{\rm{Tr}}{\rho }_{ij}{\mathrm{ln}}\,{\rho }_{ij}\).
Data availability
The data used in this manuscript are available from the corresponding author upon reasonable request.
References
Griffin, A., Snoke, D. W. & Stringari, S. Bose–Einstein Condensation. (Cambridge University Press, Cambridge, 1995).
Pethick, C. & Smith, H. Bose–Einstein Condensation in Dilute Gases. (Cambridge University Press, Cambridge, 2002).
Leggett, A. Quantum Liquid: Bose Condensation and Cooper Pairing in Condensed-Matter Systems. (Oxford University Press, Oxford, 2006).
Pitaevskii, L. P. & Stringari, S. Bose–Einstein Condensation and Superfluidity. (Oxford University Press, Oxford, 2016).
Anderson, M. H., Ensher, J. R., Matthews, M. R., Wieman, C. E. & Cornell, E. A. Observation of Bose–Einstein condensation in a dilute atomic vapor. Science 269, 198 (1995).
Bradley, C. C., Sackett, C. A., Tollett, J. J. & Hulet, R. G. Evidence of Bose–Einstein condensation in an atomic gas with attractive interactions. Phys. Rev. Lett. 75, 1687 (1995).
Davis, K. B. et al. Bose–Einstein condensation in a gas of sodium atoms. Phys. Rev. Lett. 75, 3969 (1995).
Bogoliubov, N. N. On the theory of superfluidity. J. Phys. USSR 11, 23 (1947).
Gross, E. Structure of a quantized vortex in boson systems. Nuovo Cim. 20, 454 (1961).
Gross, E. Hydrodynamics of a superfluid condensate. J. Math. Phys. 4, 195 (1963).
P., P. L. Vortex lines in an imperfect bose gas. Sov. Phys. JETP 13, 451 (1961).
Lee, T. D. & Yang, C. N. Many-body problem in quantum mechanics and quantum statistical mechanics. Phys. Rev. 105, 1119 (1957).
Lee, T. D., Huang, K. & Yang, C. N. Eigenvalues and eigenfunctions of a Bose system of hard spheres and its low-temperature properties. Phys. Rev. 106, 1135 (1957).
Brueckner, K. A. & Sawada, K. Bose–Einstein gas with repulsive interactions: general theory. Phys. Rev. 106, 1117 (1957a).
Brueckner, K. A. & Sawada, K. Bose–Einstein gas with repulsive interactions: hard spheres at high density. Phys. Rev. 106, 1128 (1957b).
Beliaev, S. T. Energy-spectrum of a non-ideal Bose gas. Sov. Phys. JETP 34, 299 (1958).
Hugenholtz, N. M. & Pines, D. Ground-state energy and excitation spectrum of a system of interacting bosons. Phys. Rev. 116, 489 (1959).
Lieb, E. H. Simplified approach to the ground-state energy of an imperfect Bose gas. Phys. Rev. 130, 2518 (1963).
Dalfovo, F., Giorgini, S., Pitaevskii, L. P. & Stringari, S. Theory of Bose–Einstein condensation in trapped gases. Rev. Mod. Phys. 71, 463 (1999).
Andersen, J. O. Theory of the weakly interacting Bose gas. Rev. Mod. Phys. 76, 599 (2004).
Cazalilla, M. A., Citro, R., Giamarchi, T., Orignac, E. & Rigol, M. One dimensional bosons: from condensed matter systems to ultracold gases. Rev. Mod. Phys. 83, 1405 (2011).
Lode, A. U. J., Lévêque, C., Bojer Madsen, L., Streltsov, A. I. & Alon, O. E. Multiconfigurational time-dependent Hartree approaches for indistinguishable particles. Rev. Mod. Phys. 92, 011001 (2020).
Greiner, M., Regal, C. A. & Jin, D. S. Emergence of a molecular Bose–Einstein condensate from a fermi gas. Nature 426, 537 (2003).
Bartenstein, M. et al. Crossover from a molecular Bose–Einstein condensate to a degenerate fermi gas. Phys. Rev. Lett. 92, 120401 (2004).
Zwierlein, M. W. et al. Condensation of pairs of fermionic atoms near a Feshbach resonance. Phys. Rev. Lett. 92, 120403 (2004).
Bourdel, T. et al. Experimental study of the BEC-BCS crossover region in lithium 6. Phys. Rev. Lett. 93, 050401 (2004).
Greiner, M., Bloch, I., Mandel, O., Hänsch, T. W. & Esslinger, T. Exploring phase coherence in a 2D lattice of Bose–Einstein condensates. Phys. Rev. Lett. 87, 160405 (2001).
Dettmer, S. et al. Observation of phase fluctuations in elongated Bose–Einstein condensates. Phys. Rev. Lett. 87, 160406 (2001).
Görlitz, A. et al. Realization of Bose–Einstein condensates in lower dimensions. Phys. Rev. Lett. 87, 130402 (2001).
Orzel, C., Tuchman, A. K., Fenselau, M. L., Yasuda, M. & Kasevich, M. A. Squeezed states in a Bose–Einstein condensate. Science 291, 2386 (2001).
Paredes, B. et al. Tonks–Girardeau gas of ultracold atoms in an optical lattice. Nature 429, 277 (2004).
Kinoshita, T., Wenger, T. & Weiss, D. S. Observation of a one-dimensional Tonks–Girardeau gas. Science 305, 1125 (2004).
Stöferle, T., Moritz, H., Schori, C., Köhl, M. & Esslinger, T. Transition from a strongly interacting 1D superfluid to a mott insulator. Phys. Rev. Lett. 92, 130403 (2004).
Lenard, A. Momentum distribution in the ground state of the one-dimensional systems of impenetrable bosons. J. Math. Phys. 5, 930 (1964).
Popov, V. N. On the theory of the superfluidity of two- and one-dimensional bose systems. Theor. Math. Phys. 11, 565 (1972).
Widom, H. Toeplitz determinants with singular generating functions. Am. J. Math. 95, 333 (1973).
Schwartz, M. Off-diagonal long-range behavior of interacting Bose systems. Phys. Rev. B 15, 1399 (1977).
Girardeau, M. D. & Wright, E. M. Bose–Fermi variational theory of the Bose–Einstein condensate crossover to the Tonks gas. Phys. Rev. Lett. 87, 210401 (2001).
Forrester, P. J., Frankel, N. E., Garoni, T. M. & Witte, N. S. Finite one-dimensional impenetrable bose systems: occupation numbers. Phys. Rev. A 67, 043607 (2003).
Gangardt, D. M. Universal correlations of trapped one-dimensional impenetrable bosons. J. Phys. A 37, 9335 (2004).
Rigol, M. & Muramatsu, A. Universal properties of hard-core bosons confined on one-dimensional lattices. Phys. Rev. A 70, 031603R (2004).
Rigol, M. & Muramatsu, A. Emergence of quasicondensates of hard-core bosons at finite momentum. Phys. Rev. Lett. 93, 230404 (2004).
Lieb, E. H. & Liniger, W. Exact analysis of an interacting Bose gas. I. The general solution and the ground state. Phys. Rev. 130, 1605 (1963).
Lieb, E. H. Exact analysis of an interacting Bose gas. II. The excitation spectrum. Phys. Rev. 130, 1616 (1963b).
Girardeau, M. Relationship between systems of impenetrable bosons and fermions in one dimension. J. Math. Phys. 1, 516 (1960).
Sachdev, S. Quantum Phase Transitions. (Cambridge University Press, Cambridge, 1999).
Osterloh, A., Amico, L. & Fazio, R. Scaling of entanglement close to a quantum phase transition. Nature 416, 608 (2002).
Osborne, T. J. & Nielsen, M. A. Entanglement in a simple quantum phase transition. Phys. Rev. A 66, 032110 (2019).
Das, K. K., Girardeau, M. D. & Wright, E. M. Crossover from one to three dimensions for a gas of hard-core bosons. Phys. Rev. Lett. 89, 110402 (2002).
Salasnich, L., Parola, A. & Reatto, L. Transition from three dimensions to one dimension in Bose gases at zero temperature. Phys. Rev. A 70, 013606 (2004).
Salasnich, L., Parola, A. & Reatto, L. Quasi-one-dimensional bosons in three-dimensional traps: from strong-coupling to weak-coupling regime. Phys. Rev. A 72, 025602 (2005).
Petrov, D. S., Shlyapnikov, G. V. & Walraven, J. T. M. Regimes of quantum degeneracy in trapped 1D gases. Phys. Rev. Lett. 85, 3745 (2000).
Fisher, M. P. A., Weichman, P. B., Grinstein, G. & Fisher, D. S. Boson localization and the superfluid-insulator transition. Phys. Rev. B 40, 546 (1989).
Jaksch, D., Bruder, C., Cirac, J. I., Gardiner, C. W. & Zoller, P. Cold bosonic atoms in optical lattices. Phys. Rev. Lett. 81, 3108 (1998).
Matsubara, T. & Matsuda, H. A lattice model of liquid helium, I. Prog. Theor. Phys. 16, 569 (1956).
Matsuda, H. & Matsubara, T. A lattice model of liquid helium, II. Prog. Theor. Phys. 17, 19 (1957).
Tóth, B. Phase transitions in an interacting bose system. an application of the theory of Ventsel’ and Freidlin. J. Stat. Phys. 61, 749 (1990).
Penrose, O. Bose–Einstein condensation in an exactly soluble system of interacting particles. J. Stat. Phys. 63, 761 (1991).
Kirson, M. W. Bose–Einstein condensation in an exactly solvable model for strongly interacting bosons. J. Phys. A: Math. Gen. 33, 731 (2000).
Günter, G. et al. Observing the dynamics of dipole-mediated energy transport by interaction-enhanced imaging. Science 342, 954 (2013).
Schempp, H., Günter, G., Wüster, S., Weidemüller, M. & Whitlock, S. Correlated exciton transport in rydberg-dressed-atom spin chains. Phys. Rev. Lett. 115, 093002 (2015).
Burioni, R. et al. Bose–Einstein condensation in inhomogeneous Josephson arrays. Europhys. Lett. 52, 251 (2000).
Burioni, R., Cassi, D., Rasetti, M., Sodano, P. & Vezzani, A. Bose–Einstein condensation on inhomogeneous complex networks. J. Phys. B 34, 4697 (2001).
Buonsante, P., Burioni, R., Cassi, D. & Vezzani, A. Bose–Einstein condensation on inhomogeneous networks: mesoscopic aspects versus thermodynamic limit. Phys. Rev. B 66, 094207 (2002).
Brunelli, I., Giusiano, G., Mancini, F., Sodano, P. & Trombettoni, A. Topology-induced spatial Bose–Einstein condensation for bosons on star-shaped optical networks. J. Phys. B 37, S275 (2004).
Vidal, E. J. G. G., Lima, R. P. A. & Lyra, M. L. Bose-Einstein condensation in the infinitely ramified star and wheel graphs. Phys. Rev. E 83, 061137 (2011).
de Oliveira, I. N., dos Santos, T. B., de Moura, F. A. B. F., Lyra, M. L. & Serva, M. Critical behavior of the ideal-gas Bose–Einstein condensation in the Apollonian network. Phys. Rev. E 88, 022139 (2013).
Lyra, M. L., de Moura, F. A. B. F., de Oliveira, I. N. & Serva, M. Bose–Einstein condensation in diamond hierarchical lattices. Phys. Rev. E 89, 052133 (2014).
Buonsante, P., Burioni, R., Cassi, D., Penna, V. & Vezzani, A. Topology-induced confined superfluidity in inhomogeneous arrays. Phys. Rev. B 70, 224510 (2004).
Halu, A., Ferretti, L., Vezzani, A. & Bianconi, G. Phase diagram of the Bose–Hubbard model on complex networks. Europhys. Lett. 99, 18001 (2012).
DePue, M. T., McCormick, C., Winoto, S. L., Oliver, S. & Weiss, D. S. Unity occupation of sites in a 3D optical lattice. Phys. Rev. Lett. 82, 2262 (1999).
Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885 (2008).
Chin, C., Grimm, R., Julienne, P. & Tiesinga, E. Feshbach resonances in ultracold gases. Rev. Mod. Phys. 82, 1225 (2010).
Weidemüller, M. & Zimmermann, C. Interactions in Ultracold Gases: From Atoms to Molecules (John Wiley, Sons, 2011) https://doi.org/10.1002/3527603417.
Zürn, G. et al. Fermionization of two distinguishable fermions. Phys. Rev. Lett. 108, 075303 (2012).
Tennie, F., Vedral, V. & Schilling, C. Universal upper bounds on the Bose–Einstein condensate and the Hubbard star. Phys. Rev. B 96, 064502 (2017).
White, S. R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863 (1992).
White, S. R. Density-matrix algorithms for quantum renormalization groups. Phys. Rev. B 48, 10345 (1993).
Schollwöck, U. The density-matrix renormalization group. Rev. Mod. Phys. 77, 259 (2005).
Amico, L., Osterloh, A. & Cataliotti, F. Quantum many particle systems in ring-shaped optical lattices. Phys. Rev. Lett. 95, 063201 (2005).
Franke-Arnold, S. et al. Optical Ferris wheel for ultracold atoms. Opt. Express 15, 8619 (2007).
Ramanathan, A. et al. Superflow in a toroidal Bose–Einstein condensate: an atom circuit with a tunable weak link. Phys. Rev. Lett. 106, 130401 (2011).
Amico, L. et al. Superfluid qubit systems with ring shaped optical lattices. Sci. Rep. 4, 4298 (2014).
Bell, T. A. et al. Bose–Einstein condensation in large time-averaged optical ring potentials. New J. Phys. 18, 035003 (2016).
Sakmann, K., Streltsov, A. I., Alon, O. E. & Cederbaum, L. S. Reduced density matrices and coherence of trapped interacting bosons. Phys. Rev. A 78, 023615 (2008).
Legeza, O. & Sólyom, J. Quantum data compression, quantum information generation, and the density-matrix renormalization-group method. Phys. Rev. B 70, 205118 (2004).
Rissler, J., Noack, R. M. & White, S. R. Measuring orbital interaction using quantum information theory. Chem. Phys. 323, 519 (2006).
Szalay, S. et al. Tensor product methods and entanglement optimization for ab initio quantum chemistry. Int. J. Quant. Chem. 115, 1342 (2015).
Acknowledgements
We gratefully acknowledge critical comments on the present manuscript by P. van Dongen, F. Gebhard, J. Marino, and L. Pollet. We also would like to thank P.J. Forrester and T.M. Garoni for providing the exact results obtained directly from the Toeplitz determinant for the number of condensed particles in one dimension for small N. This work has been supported in part by the Hungarian National Research, Development and Innovation Office (grant no. K120569 and K134983), and the Hungarian Quantum Technology National Excellence Program (project no. 2017-1.2.1-NKP-2017-00001). Ö.L. acknowledges financial support from the Alexander von Humboldt foundation. M.M. has been supported by the ÚNKP-19-3 Hungarian New National Excellence Program of the Ministry for Innovation and Technology. The development of the DMRG libraries was supported by the Center for Scalable and Predictive methods for Excitation and Correlated phenomena (SPEC), which is funded from the Computational Chemical Sciences Program by the U.S. Department of Energy (DOE), at Pacific Northwest National Laboratory. C.S. acknowledges financial support from the UK Engineering and Physical Sciences Research Council (Grant EP/P007155/1) and Deutsche Forschungsgemeinschaft (Grant SCHI 1476/1-1).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
The authors Ö.L., M.M., C.S., R.S., and M.Y. have all contributed equally to this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Máté, M., Legeza, Ö., Schilling, R. et al. How creating one additional well can generate Bose-Einstein condensation. Commun Phys 4, 29 (2021). https://doi.org/10.1038/s42005-021-00533-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00533-3
This article is cited by
-
Symmetry-protected Bose-Einstein condensation of interacting hardcore bosons
Communications Physics (2023)
-
Numerical algorithms for corner-modified symmetric Toeplitz linear system with applications to image encryption and decryption
Journal of Applied Mathematics and Computing (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.