Abstract
Gravitational waves from the neutron star coalescence GW170817 were observed from the inspiral, but not the high frequency postmerger nuclear matter motion. Optomechanical white light signal recycling has been proposed for achieving broadband sensitivity in gravitational wave detectors, but has been reliant on development of suitable ultra-low loss mechanical components. Here we show demonstrated optomechanical resonators that meet loss requirements for a white light signal recycling interferometer with strain sensitivity below 10−24 Hz−1/2 at a few kHz. Experimental data for two resonators are combined with analytic models of interferometers similar to LIGO to demonstrate enhancement across a broader band of frequencies versus dual-recycled Fabry-Perot Michelson detectors. Candidate resonators are a silicon nitride membrane acoustically isolated by a phononic crystal, and a single-crystal quartz acoustic cavity. Optical power requirements favour the membrane resonator, while thermal noise performance favours the quartz resonator. Both could be implemented as add-on components to existing detectors.
Similar content being viewed by others
Introduction
Since the detection of gravitational waves (GW) from binary black holes and neutron stars1,2,3,4, there is increasing interest in improving the sensitivity and bandwidth of detectors to allow better characterization of gravitational wave sources. Detectors such as the proposed Einstein Telescope5 and Cosmic Explorer6 aim for improved low frequency sensitivity to dramatically increase the number of observable cycles from compact binary coalescence events. Other detectors focus on multimessenger astronomy from neutron star coalescences, targeting a strain sensitivity of h ~ 10−24 Hz−1/2 in the 1–5 kHz band. Observation of the normal modes of newborn hypermassive neutron stars will provide insight into the complex hydrodynamics of nuclear matter moments before its collapse into a black hole7. Other sources of GWs in the range 1–5 kHz include the final moments of black hole coalescence, normal modes of newborn black holes with mass 5–20 M⊙ and core collapse supernovae.
The current sensitivity of GW detectors has so far been insufficient to characterise binary neutron star postmerger remnants8. High frequency sensitivity in interferometric GW detectors is currently limited by quantum shot noise9,10,11 with strain sensitivity of a few times 10−23 Hz1/2. A straightforward way to reduce the quantum shot noise level is to increase the laser power inside the detector. In addition, configurations based on detuning and strongly coupled signal recycling12 can produce a broadband response at high frequency, but achieving target sensitivity h ~ 10−24 Hz1/2 still requires arm power levels an order of magnitude higher than the best attained to date.
In general, signal recycling improves detector sensitivity by resonant enhancement of the signal rather than suppression of shot noise at the detection port. However, in conventional systems the resonance response creates a trade-off between sensitivity gain and bandwidth13. In principle, the sensitivity-bandwidth tradeoff can be overcome by the method of white light signal recycling (WLSR). While travelling across the long interferometer arms, the GW signal sidebands experience a phase delay relative to the carrier. A negative dispersion medium inside the signal recycling cavity can compensate for the signal sideband phase delay, creating a broadband resonance called a white light cavity14,15. The energetic quantum limit of the cavity is lowered via quantum amplification16,17,18,19, indicating that the interferometer supports a non-classical state and physical laws are not violated.
A succession of papers20,21,22,23 have shown that WLSR can be implemented by using an optomechanically coupled negative dispersion filter. The filter consists of a mechanical resonator placed inside a Fabry-Perot cavity with optical resonance ω0 equal to the interferometer carrier frequency. The cavity pump light has blue detuning equal to the mechanical resonance ωm, and is stabilized by feedback20. The negative dispersion filter can be seen as a blue-detuned analogue of optomechanically-induced transparency, where the GW signals act as the near-resonant probe. Parametric interaction between the signal, pump light, and mechanical resonator stores the signal with a frequency dependent phase compensation, creating the negative dispersion effect.
To maintain quantum amplification, noises introduced by the mechanical resonator must be kept low. It has been shown that the mechanical resonator must have a quality factor Qm and operate at temperature T such that T/Qm < 10−9 K, in order for thermal noise not to dominate the detector noise budget20. In addition, vacuum noise sidebands at ω0 + 2ωm ± Ω are present inside the detuned cavity and create extra quantum noise at GW signal sideband frequencies. High ωm is required to keep the extra sidebands far detuned from the interferometer, and their impact can be further mitigated using a high finesse filter cavity23. Further elaboration on the origin of the WLSR parameter space is given in Supplementary Note 1.
The proposed solution to the mechanical resonator thermal and quantum noise issues has been to use optical dilution to increase the resonant frequency and Q-factor of mechanically soft micro-pendulums21,22,24. However, optical dilution for the purpose of GW detection is technically demanding. The mechanical resonators need to be very small, and yet able to operate at high optical power densities. The trapping power required to achieve sufficient Qm results in coupling to other loss mechanisms, placing an upper limit on the viable ωm. Optical dilution must be balanced against thermoelastic loss, acceleration loss, and beam size. This leaves a very small volume of parameter space in which the necessary performance might be achieved21.
Here we show the possibility of optomechanical negative dispersion using existing resonator structures, without having to resort to optical dilution. The two candidate resonators are (i) a silicon nitride membrane isolated from the external environment by a phononic crystal (henceforth referred to as “phononic crystal” resonator or PNC) and (ii) a plano convex lens constructed from single-crystal quartz, known as a bulk acoustic wave (BAW) resonator due to its characteristic of bulk longitudinal phonons with extremely high quality factor. In combination with 10 dB frequency dependent squeezing of quantum noise, the resulting WLSR interferometer can achieve a sensitivity floor of h ~ 5.0 × 10−25 Hz−1/2, with the BAW configuration being slightly lower. The design and resulting sensitivity spectrum are shown in Fig. 1. Compared to a specialised high frequency dual-recycled Fabry–Perot Michelson interferometer25, the WLSR interferometer produces a broader band of frequency enhancement in the neutron star GW regime 1–5 kHz, and can maintain h ≤ 10−24 Hz−1/2 for GWs up to 4.9 kHz. For the PNC resonator, the required blue-detuned pump light is 42.2 mW. The BAW resonator requires in excess of 10 kW, but the very low optical losses of quartz mean that the dissipated power could be manageable.
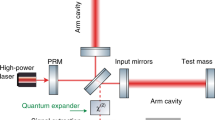
a Gravitational waves (GW) of frequency Ω modulate the interferometer carrier ω0, producing sidebands at ω0 ± Ω. The input test mass (ITM) and signal extraction mirror (SEM) are impedance matched for maximum sideband transmission. The signal recycling mirror (SRM) couples the interferometer dark port, filter cavity and output photodetector. The filter cavity is pumped with light blue detuned by the mechanical resonance ωm. The cavity itself is 5 cm long but may be contained inside a larger housing. b Illustration of the phononic crystal (PNC) resonator consisting of a silicon nitride membrane in a phononic lattice. The colour scale represents out-of-plane mechanical mode displacement. The inset shows a magnified view of the resonator. (Image acknowledgement: E.C. Langman, Neils Bohr Institute) c Quantum noise-limited sensitivity curves of various GW detectors. “Advanced LIGO” denotes the nominal design sensitivity shown in the ref. 49 at 800 kW arm cavity power. “Sloshing SR” refers to a detector where the signal recycling cavity is tuned to achieve an optical resonance at a specific frequency25. WLSR setups using the PNC and bulk acoustic wave (BAW) resonator are denoted with their respective abbreviations. The curve “BAW Ultra-low loss” shows the speculative improvement when the BAW resonator is cooled to 1 K. Apart from “Advanced LIGO”, all curves use 4.0 MW arm cavity power and 10 dB frequency dependent squeezing.
Results
White light signal recycling interferometer configuration
In our WLSR interferometer design we use the PNC resonator characterised by Mason, et al., who have maintained a ωm/(2π) = 1.135 MHz out-of-plane vibrational mode at Qm = 1.03 × 109 and T = 10 K for a 20 nm thick Si3N4 membrane shielded with an acoustic bandgap of 1.07–1.28 MHz26. The PNC resonator can be optomechanically coupled by using it in a “membrane-in-the-middle” (MIM) configuration as characterised by Thompson et al.27.
For the BAW resonator, we refer to Galliou, et al., who have measured ωm/(2π) = 204 MHz and Qm = 8 × 109 at 4 K for the 65th longitudinal mode of a 30 mm diameter, 1 mm thick plano-convex quartz crystal28. Kharel et al. have demonstrated strong optomechanical coupling in BAW resonators using Brillouin scattering29. However, Brillouin scattering using near-infrared light in quartz requires a mechanical mode of 18 GHz, which would have surface scattering losses that exceed the strict thermal noise requirements for WLSR28,30. Instead, we use optomechanical coupling to the antiphase surface motion of the 204 MHz mode. We also estimate that Qm = 1.5 × 1010 is possible by operating at 1 K, and the resulting thermal noise reduction is indicated in Fig. 1. Details of the temperature scaling of the BAW resonator Qm are given in Supplementary Note 2.
The WLSR interferometer layout is shown in Fig. 1. In the interferometer, impedance matching of the arm cavity to the signal extraction mirror allows for enhanced transmission of GW sidebands into the signal recycling cavity. The signal recycling mirror couples the interferometer dark port, negative dispersion filter, and output photodiode. Frequency dependent squeezing may be applied by injecting squeezed vacuum at the output Faraday isolator31. The negative dispersion filter is cooled to temperatures of 1–4 K and contained inside a radiation shield to minimise radiation heating and scattered light noise. A model of the PNC resonator is shown in Fig. 1, embedded in a 2-dimensional phononic lattice. High Qm has been demonstrated for silicon nitride PNC resonators of size 87–346 μm32. Other resonator properties relevant to WLSR are shown in Table 1.
Optomechanical coupling in negative dispersion filters
The interaction Hamiltonian inside the negative dispersion filter suggests correlated two-photon exchange20:
where \(\hat{a}\) and \(\hat{b}\) are the annihilation operators of the optical and mechanical modes inside the filter cavity, respectively, and g is the optomechanical coupling rate. Using this Hamiltonian, the negative dispersion filter is shown to have the following input–output relation:
where \({\hat{a}}_{{\rm{in}}}\) and \({\hat{a}}_{{\rm{out}}}\) are the annihilation operators of the input and output optical fields, respectively, and γopt is the optomechanical anti-damping. Across the detector’s arm length Larm, the GW signal sidebands acquire phase delay ΩLarm/c, which can be compensated when γopt = c/Larm so long as we remain in the linear negative dispersion regime Ω ≪ γopt. For a 4 km interferometer, γopt/(2π) = 12 kHz. The pumping power necessary to achieve γopt is determined by γopt = g2/γf, where γf is the filter cavity bandwidth. The optomechanical coupling rate can be expanded into \(g=\frac{{\rm{d}}\omega }{{\rm{d}}q}{x}_{{\rm{zpf}}}\)\(\bar{a}\), where \(\frac{{\rm{d}}\omega }{{\rm{d}}q}\) is the optical frequency shift per unit of generalised mechanical displacement q, xzpf is the mechanical zero-point displacement fluctuation and \({\bar{a}}^{2}\) is the mean intracavity photon number. The circulating power requirement for negative dispersion becomes:
where Meff is the effective mass of the mechanical resonator, Lf the filter cavity length and ωp = ω0 + ωm the pump frequency of the filter.
The optomechanical coupling for the PNC resonator is found from the relation of optical resonant frequency versus membrane displacement for a MIM cavity, given as27,33:
where rm is the membrane amplitude reflectivity and x is the membrane displacement. The optical frequency ω(x) is periodic with x in the MIM cavity. A 20 nm layer of silicon nitride with refractive index \({n}_{{\rm{SiN}}}=1.98\) will have a power reflectivity of \({r}_{{\rm{m}}}^{2}=0.03\) at λ = 1064 nm wavelength (see Fig. 6.1 in ref. 34). This is low compared to dielectric-stack Bragg reflectors, but nevertheless is still sufficient for WLSR.
We take dω/dq of Eq. (4), where q in this case is equivalent to the membrane displacement x. Substituting into Eq. (3) gives the filter cavity power requirements shown in Fig. 2. We choose filter cavity input transmission Tf = 300 ppm to balance pumping power and quantum noise requirements, resulting in 42.2 mW circulating power. It has been shown that silicon nitride membrane resonators can maintain incident optical power approaching 0.1 W at T ~ 10 K26, so the power requirement is plausible for maintaining low T/Qm.
For the BAW resonator, we find dω/dq by solving for the resonant field when the crystal is placed inside an optical cavity while the opposing faces of the crystal move antiphase. For example, the maximum coupling when λ = 1064 nm, ωm/(2π) = 204 MHz and Lf = 5 cm is seen to be dω/dq = 2π × 0.0075 GHz nm−1. Further details are given in “Methods” section. At Lf = 5 cm, the low optomechanical coupling results in required light intensity of 17 MW cm−2. Quartz has been shown to withstand optical intensities greater than 1 GW cm−2 35,36, and crystalline AlGaAs/GaAs coatings planned for use in GW detector optics have been shown to withstand 64 MW cm−2 37. While maintaining high Qm at such high power has not been tested, quartz has an extremely low absorption coefficient of less than 1 ppm cm−1 at 1064 nm38. Supplementary Note 3 contains further justification for operation of both candidate resonators at their respective power level. In the BAW case, we make an initial estimate that absorption heating could be maintained at less than 1 K increase, based approximately on the size of conductive contacts that have been used with the BAW resonator at Qm = 8 × 109 28.
There are a few strategies to mitigate the BAW resonator power requirement. We can use an alternate WLSR configuration that sacrifices some bandwidth broadening for a tenfold reduction in γopt and Pf. Second, increasing the reflectivity of the BAW resonator with high refractive index materials or a single layer of high-Q reflective coating can increase dω/dq. Third, γopt and Pf are inversely proportional to Larm, so BAW optomechanics may be more suited to detectors such as Cosmic Explorer or Einstein Telescope with arm lengths of 10 km or greater. These strategies are further discussed in Supplementary Notes 4–7.
Calculated noise spectrum of white light signal recycling interferometers
We calculate the noise spectrum of Fig. 1 using the two photon quantum optics formalism of Caves and Schumaker39,40,41. Cavity components are represented as transfer matrices which incorporate optomechanical interaction20,41. The basis vector consists of the amplitude and phase quadratures of the light field. Transfer matrices of the cavity components are then multiplied to obtain an overall transfer function. We assume homodyne phase quadrature measurement of the interferometer output beam with no detuning of the signal recycling cavity.
Thermal noise from the mechanical resonator is introduced as displacement (phase) noise imparted onto the beam inside the filter cavity. Optical losses are input as uncorrelated vacuum in both the amplitude and phase quadratures. We introduce optical losses in the arm cavity, filter cavity, output train and beamsplitter cavity. Beamsplitter cavity losses are dependent upon the incident power on the interferometer beamsplitter, while other losses are assumed to be power-independent. Quantum noise from filter cavity sidebands at ω0 + 2ωm ± Ω is also present, and its effect on the interferometer signal is suppressed using a high finesse filter cavity and high ωm. This particular GW detector configuration uses 4 MW arm cavity power, 10 dB frequency dependent squeezing and superior optical loss performance compared to the planned near-future upgrade of the current Advanced LIGO network known as A+42. Further details of the calculation formalism are presented in “Methods” section, and input parameters are given in Table 1 and Supplementary Table S1.
WLSR using our candidate resonators is seen to reach strain sensitivity levels below h ~ 10−24 Hz−1/2 at GW signal frequencies up to 4.9 kHz, with a peak sensitivity h ~ 5 × 10−25 Hz−1/2 across a broad band, as seen in Fig. 1. The peak sensitivity is limited by thermal noise coupling, set by the experimentally measured Qm of each resonator. At frequencies of 1–5 kHz, we are also concerned with optical loss from the filter cavity. The PNC sensitivity curve is set with 10 ppm filter cavity round trip loss as a desirable target. Previously reported measurements of silicon nitride absorption indicate that 1–4 ppm or lower absorption is possible in the case of a 20 nm thick resonator and 1064 nm wavelength light34,43. The relative contributions of the aforementioned noise sources to the total sensitivity are shown in Supplementary Note 6.
In a dual-recycled Fabry-Perot Michelson interferometer it has been shown that by tuning the transmissivity and length of the signal recycling cavity, an optical “sloshing” resonance at 2.5 kHz with bandwidth 1.5 kHz could be created in order to amplify neutron star signals25. Figure 1 compares our WLSR scheme with the sloshing resonance design at similar levels of interferometer optical loss, arm cavity power, and optical squeezing, showing superior gain/bandwidth enhancement of quantum noise limited sensitivity in the 1–5 kHz range. The WLSR interferometer has an additional advantage of being able to maintain a short signal recycling cavity of much less than 100 m.
In longer interferometers, quantum shot noise scales with \(1/\sqrt{{L}_{{\rm{arm}}}}\), whereas classical displacement noises scale with 1/Larm. Breaking the sensitivity/bandwidth compromise using WLSR is a potential strategy to bring quantum noise down to the level of classical noises in future detectors that plan to use arms of 10 km or longer. However, the filter cavity thermal noise requirement is proportional to the unmodified interferometer bandwidth, and is thus stricter for longer arms. Also, disregarding free spectral range effects, the high frequency strain sensitivity contribution from the beamsplitter cavity loss is length-independent, setting a limit on the length increase benefit. Further exploration of WLSR in longer and shorter detectors is given in Supplementary Note 7, but we note that a 10 km configuration is still beneficial even with increased levels of arm, signal recycling and filter cavity optical loss.
When the pumping power is not perfectly matched to γopt, the quantum noise spectrum exhibits a small region of enhanced high frequency sensitivity at the expense of some lower frequency sensitivity, as shown in Fig. 3. This provides an additional advantage for the detection of binary neutron star gravitational waves, since the exact frequency of the kilohertz ringdown is unknown. WLSR presents the possibility of shifting the optimal detection frequency of the interferometer without changing the interferometer hardware or detuning the signal recycling cavity. However, this is contingent on maintaining a low contribution of filter cavity optical loss.
Adjustment of the quantum noise curve is achieved by changing the filter cavity pump power Ppump relative to Pf, which is the power required to achieve negative dispersion as per Eq. (3). This is useful for tuning the location of peak sensitivity in the neutron star detection band without changing interferometer hardware or detuning the signal recycling cavity.
Discussion
There are several technical concerns not directly considered above, but will be important for implementing WLSR.
Parametric interaction between the two light fields and mechanical motion in the filter cavity results in optomechanical instability that must be controlled. A state space demonstration of filter cavity controllability has been shown20, but it was later seen that the effect of time delay would hinder the global control system. Local sensing control can eliminate the time delay issue. Readout noise may arise from the addition of local control, but it is indicated that this can be cancelled by optimal postprocessing combination of the unstable filter and interferometer control signals23. Another possibility is to use coherent quantum feedback with parity-time symmetry to eliminate the instability at a fundamental level44.
Mode mismatch between the interferometer and filter introduces signal recycling cavity loss. While the noise budgets shown in Fig. 1 account for general signal recycling loss, the specific contribution of mode matching and angular alignment control have yet to be investigated. However, it is expected that the contribution will be significant given the beam size in the filter. From a selection of PNC resonators sufficient for WLSR, the largest is 350 μm wide32, requiring a beam waist of 80–100 μm to reduce optical diffraction losses. For the BAW resonator, the effective radius of the 204 MHz longitudinal mode is 260 μm. The beam waist in the Advanced LIGO output mode cleaner is ~500 μm45, and Advanced LIGO target 1–2% mode matching losses for the next generation of 4 km detectors42. The BAW resonator’s larger beam size requirement is advantageous in reducing potential mode matching loss. In an A+ type detector with 800 kW arm cavity power, signal recycling loss of ~1% contributes roughly equal to unsqueezed WLSR quantum noise in the 100–5000 Hz band. Supplementary Notes 6–7 illustrate that bandwidth broadening is still possible for detectors similar to the current generation with higher optical loss, low levels of squeezing and arm cavity power < 1 MW. In Fig. 1 we use 0.1% signal recycling loss, which contributes below the limiting noises of filter thermal, filter cavity optical loss and beamsplitter cavity noise.
Scattered light rejoining the interferometer beam can contaminate the signal with phase noise acquired from moving objects. An estimate can be obtained by analysing the degree of freedom along the optical axis. The mechanical resonator motion must be controlled, so the dominant contribution is from the filter cavity vacuum enclosure. Assuming that the motion is typical of LIGO isolated tables, the maximum tolerable light power rejoining the interferometer beam is approximately 0.5 ppm of light power incident upon the filter cavity46. In Fig. 1, a large window to the cryogenic component is avoided for this reason.
Silicon nitride phononic crystal resonators provide a first realistic means of creating a white light signal recycling interferometer, using experimentally demonstrated values of mechanical loss, optical absorption and incident laser power. Single crystal bulk acoustic wave resonators also have promising thermal noise properties, but the required levels of optical power are untested. Proposed long-arm detectors such as Einstein Telescope and Cosmic Explorer will relax the optical power requirement, giving us more flexibility in future designs. The University of Western Australia is developing optomechanical negative dispersion filters using both mechanical resonator types described in this paper. The properties of silicon nitride phononic crystal resonators make them ideal for promptly achieving practical broadband enhancement of GW detector sensitivity, allowing greater investigation of neutron star coalescence.
Methods
Calculation of optomechanical coupling of the bulk acoustic wave resonator to the filter cavity
Optomechanical coupling of BAW resonators has been demonstrated using three-mode Brillouin scattering of optical waves to coherent acoustic phonons29. In order to achieve three-mode Brillouin scattering in the BAW resonator, two energy transfer conditions must be met. First, the optical frequencies must be separated by the mechanical frequency, which is achieved through design of the filter cavity. Second, the phase matching requirement states that \({q}_{{\rm{m}}}={k}_{{{\rm{j}}}^{\prime}}+{k}_{{\rm{j}}}\), where qm is the mechanical wavenumber and \({k}_{{\rm{j}},{{\rm{j}}}^{\prime}}\) are the optical wavenumbers of the GW signal and blue detuned pump. For a three mode system in a quartz crystal, phase matching is satisfied when ωm = 2ω0nQvQ/c, where nQ is the refractive index of quartz and vQ is the speed of sound in quartz29. Using the properties shown in Table 1, the resulting mechanical frequency requirement of ωm/(2π) ~ 18 GHz is a factor of 89 higher than the 204 MHz mode with optimal Qm. Since we wish to formulate a means of negative dispersion using the experimentally demonstrated Q-factor and frequency shown by Galliou et al.28, we must resort to another mechanism of optomechanical coupling.
In our calculations, the negative dispersion filter couples the optical modes of the cavity to the antiphase surface motion of the planar and convex faces of the BAW resonator crystal. This allows access to the highest measured Q-factor mode at 204 MHz. To model coupling of the light field to the surface vibrations of the BAW resonator, we consider a BAW resonator crystal situated inside a Fabry–Perot cavity, as shown in Fig. 4. Using the boundary conditions of electromagnetic fields at the cavity end mirrors and crystal surfaces we obtain equations of the electric field as functions of crystal surface position. For given values of the cavity length Lf and crystal center position xp, we can obtain the cavity resonance frequency as a function of generalised displacement q, which in this case is the crystal thickness. Using electric and magnetic boundary conditions at the interface points x = 0, x1, x2, Lf, we then construct a system of equations in terms of nQ, Lf, the electric fields E1,2,3,4, optical wavenumber k.
The following cavity parameters are used in the calculation of optomechanical coupling to BAW resonator antiphase surface motion. The BAW resonator position is denoted using x1 at the flat face and x2 at the apex of the curved face. The electric field amplitude in the vacuum spaces is denoted by E1 and E4. The electric field inside the crystal is composed of a superposition of E2 and E3.The cavity length is denoted as Lf.
The coordinates x1 and x2 are rearranged into crystal center position xp = (x2 + x1)/2 and crystal thickness q = x2 − x1, and the system of equations reduces to:
We then solve the wavenumber in terms of the generalised displacement q. Selected solutions are obtained in proximity to ω0/(2π) = 2.82 × 1014 Hz, corresponding to a 1064 nm wavelength. The dependence of optical resonance frequency with crystal thickness is shown in Fig. 5. Over micron-scale motion, there is an approximately linear negative dω/dq, and an appropriate optical mode can be selected such that there is a linear negative dω/dq within −50 nm < q − q0 < 50 nm. Local frequency variation is due to the sloshing between the left coupled cavity, the crystal itself and the right coupled cavity. The free spectral range between modes varies sinusoidally, which is consistent with studies on BAW resonator coupled cavities29. The coupling dω/dq decreases with cavity length for a small cavity of Lf = 5 mm, the maximum coupling is dω/dq = 2π × 0.061 GHz nm−1, while a longer cavity Lf = 20 mm results in maximum dω/dq = 2π × 0.018 GHz nm−1. The maximum single photon coupling rates \(\frac{{\rm{d}}\omega }{{\rm{d}}q}{x}_{{\rm{zpf}}}\) are 2π × 0.10 Hz and 2π × 0.031 Hz, respectively. As expected, surface optomechanical coupling is small compared to optomechanical coupling to the bulk longitudinal mechanical mode, where Kharel et al. demonstrated a near-infrared single photon coupling rate of 24 Hz in a BAW resonator at similar effective mass29. Micro-pendulums used in previous proposals21 have estimated single photon coupling rates of ~40 Hz, though at much lower effective mass (~10 ng) and mechanical frequency (~100 kHz).
Calculation of effective mass of the bulk acoustic wave resonator mechanical mode
To obtain the pumping power necessary to produce negative dispersion, we must find the effective mass of the relevant mechanical mode. We use the following formula given by Goryachev30:
where the crystal radius rc and density ρ are given in Table 1. The coupling factors ηx,y quantify the trapping of the Gaussian longitudinal mode within the crystal and are given by:
where R is the radius of curvature of the curved surface of the BAW. \({\mathcal{M}}\) and \({\mathcal{P}}\) are material dependent transverse elastic parameters which are only well known at room temperature. Goryachev estimates \({c}_{{\rm{z}}}/{\mathcal{M}} \sim {c}_{{\rm{z}}}/{\mathcal{P}} \sim 0.4\) for cryogenic quartz crystals30. This results in ηx ~ ηy ~ 5.08. The effective mass for the m = 65, ωm/(2π) = 204 MHz mode is M65,0,0 = 0.56 mg. In addition, the optical plane wave corresponding to this effective mass has area \(A=\frac{{M}_{{\rm{eff}}}}{\rho {q}_{0}}\) giving an appropriate optical beam radius of 260 μm to match to the mechanical mode.
Quantum noise matrix calculation for white light signal recycling interferometer
Noise budgets of WLSR interferometers are calculated using the two photon formalism of Caves and Schumaker39,40,41, where cavity components are represented as transfer matrices which can also incorporate optomechanical interaction20,41. For example, a beam travelling distance Lfree and reflected from a moving mirror in free space can be represented as:
where α and β respectively represent the input and output beams, and subscripts a and p the amplitude and phase quadratures. The amplitude and phase quadratures of light are related to the sideband creation and annihilation operators by:
where \({\hat{\alpha }}_{+}({{\Omega }})\) is the annihilation operator of the upper sideband at frequency + Ω with respect to the reference and \({\hat{\alpha }}_{-}^{\dagger }({{\Omega }})\) is the creation operator of the lower sideband at frequency − Ω with respect to the reference. As such the two-photon formalism is naturally used in cases where modulation produces paired sidebands. Optomechanical coupling is incorporated in the frequency of mirror motion Ω and the coupling factor κ = 8P0ω0/(McLfree), where P0 is the incident power and M is the mass of the mirror. 2 × 2 transfer matrices in the two-photon basis can also be built up for tuned and detuned optomechanical cavities in a similar manner to Eq. (12). We obtain an overall sensitivity spectrum by looking at the input-output relation at the output photodetector. For this transfer matrix method it is simple to calculate the sensitivity spectrum for the measurement of any linear combination of amplitude and phase quadrature, though for the purpose of this paper we only require measurement of the phase quadrature.
Additional noise sidebands are produced by the filter cavity, as illustrated by Fig. 6. The calculation considers the GW signal sidebands at optical frequencies of ω0 ± Ω along with the noise sidebands ω0 + 2ωm ± Ω that arise as a result of radiation pressure interactions of the GW sidebands within the detuned filter cavity. Doing so requires expanding the optomechanical transfer matrix from 2 × 2 to 4 × 4, and for the detuned filter cavity, we also switch from the two-photon picture to the sideband creation/annihilation picture. The basis vector incorporates each of the sidebands shown in Fig. 6. As such, we produce a transfer function:
where M4×4 is the transfer matrix of an optomechanical cavity detuned from ω0 by ωm, and the argument ω denotes the separation of sidebands that appear centered around ω0 + ωm, as per Fig. 6. For example, sideband 1 in Fig. 6, the lower GW signal sideband, is separated from the center frequency by ω = ωm + Ω. An appropriate transfer matrix can be constructed by taking the two-photon transfer matrix of an optomechanical cavity detuned by ωm, with GW sidebands occurring at ω = ωm ± Ω, transforming to the sideband basis using the matrix in Eq. (13), and arranging the appropriate entries into a 4 × 4 matrix according to the following basis:
The gravitational wave (GW) signal sidebands, labelled “1” and “2”, are detuned from the interferometer carrier frequency ω0 by the GW signal frequency Ω. The resonance peak of the interferometer and filter cavity is shown centered around ω0. The filter cavity is pumped by light that is blue detuned from the carrier by the mechanical frequency ωm. Additional noise sidebands “3” and “4” are present at ω0 + 2ωm ± Ω, which couple to the GW signal sidebands “1” and “2”, introducing extra quantum noise at ω0 ± Ω.
Conjugating the second and third rows of the transfer matrix M4×4 represents changing the second entry of the basis vector to an annihilation operator and the third entry to a creation operator. This allows us to use the following transformation matrix:
where the frequency of the argument is now written with respect to the carrier frequency ω0 instead of the blue-detuned pumping frequency ω0 + ωm. The first two rows represent the amplitude and phase quadrature of signal sidebands generated about ω0 ± Ω, while the third and fourth rows represent the quadratures of light generated about ω0 + 2ωm ± Ω. The transfer matrix M4×4 can thus give the two-photon transfer function for the quantum noise from sidebands at ω0 + 2ωm ± Ω. For simplicity, we assume that the sidebands at ω0 + 2ωm ± Ω are far enough detuned from the interferometer resonance to be simply reflected back into the signal recycling optics.
As a consequence of keeping propagation phase factor such as that shown in Eq. (12), the calculation also takes into effect cavity free spectral range, which has a significant impact on the audio band sensitivity of GW detectors 10 km and above in length.
An initial impression dictates that γopt/(2π) is set to 12 kHz in order to cancel the phase delay accumulated by GW signals in the 4 km interferometer arms. However, by slightly offsetting the optomechanical anti-damping, the calculated quantum noise response curve extends further into the 1–5 kHz band at a slight cost in peak sensitivity, as indicated by Fig. 3. For the main results in this paper, we actually use γopt/(2π) = 11.5 kHz.
Optical loss calculation for white light signal recycled interferometer
Optical losses from various sources introduce uncorrelated vacuum noise to the GW signal sidebands. Optical loss from the negative dispersion filter is treated as transmission of uncorrelated vacuum through the end mirror of the filter cavity. Likewise, optical loss in the interferometer arms is introduced as transmission of uncorrelated vacuum through the end test mass. Loss from the output optics to the photodiode is introduced between the signal recycling mirror (SRM) and output Faraday isolator. It behaves similar in frequency dependence to the quantum noise curve, but is actually caused by the homodyne detection process as described by Kimble et al.31. Similar to Martynov et al., we consider the effect of resonantly enhanced optical losses inside the interferometer beamsplitter cavity, which is dominated by power-dependent thermal lensing noise25. This is due to absorption of optical power onto the input test mass (ITM) and beamsplitter, causing heat gradients that distort the carrier wave from its desired shape. These losses are then resonantly enhanced inside the beamsplitter cavity. In the WLSR configuration of Fig. 1, this resonant enhancement of arm power-dependent optical loss occurs inside the cavity formed by the ITM and signal extraction mirror (SEM). The wavefront distortion contributions from the ITM and beam splitter scale approximately as25,47:
where αITM,BS represent optical absorption, κITM,BS the compensation factor from various systems that reduce thermal lensing and PBS the incident power on the beamsplitter. The total signal extraction loss ϵse = ϵITM + (ϵBS/2) is introduced as uncorrelated vacuum between the main beamsplitter and SEM. Resonant enhancement causes significant contribution of signal extraction loss in the 1–5 kHz band.
Introducing the SEM also causes impedance matching of losses between the signal recycling cavity and the arm cavity. As such, losses occurring in the signal recycling cavity (SRC) are combined with arm cavity losses into one total loss ϵarm, which is introduced as uncorrelated vacuum inside the SRC. The shot noise amplitude spectrum of this loss behaves similarly to that of quantum noise in a simple Michelson at high frequency, scaling inversely proportional to Larm. As such, the contribution of impedance matched arm losses is reduced in longer interferometers.
Data availability
Datasets are used in Supplementary Figs. S1 and S2 and are available at figshare repository https://doi.org/10.6084/m9.figshare.1335266948.
Code availability
Calculations regarding the noise budget of WLSR interferometers as described in Methods were performed using Mathematica. Annotated code is available from the corresponding author upon request.
References
Abbott, B. P. et al. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116, 061102 (2016).
Abbott, B. P. et al. GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 119, 161101 (2017a).
Abbott, B. P. et al. GWTC-1: a gravitational-wave transient catalog of compact binary mergers observed by ligo and virgo during the first and second observing runs. Phys. Rev. X 9, 031040 (2019a).
Abbott, B. P. et al. GW190425: observation of a compact binary coalescence with total mass ~3.4 M⊙. Astrophys. J. Lett. 892, L3 (2020).
Punturo, M. et al. The Einstein telescope: a third-generation gravitational wave observatory. Class. Quantum Gravity 27, 194002 (2010).
Abbott, B. P. et al. Exploring the sensitivity of next generation gravitational wave detectors. Class. Quantum Gravity 34, 044001 (2017b).
Clark, J., Bauswein, A., Stergioulas, N. & Shoemaker, D. Observing gravitational waves from the post-merger phase of binary neutron star coalescence. Class. Quantum Gravity 33, 085003 (2016).
Abbott, B. et al. Properties of the binary neutron star merger GW170817. Phys. Rev. X 9, 011001 (2019b).
Aasi, J. et al. Enhanced sensitivity of the LIGO gravitational wave detector using squeezed states of light. Nat. Photonics 7, 613 (2013).
Barsotti, L., Harms, J. & Schnabel, R. Squeezed vacuum states of light for gravitational wave detectors. Rep. Prog. Phys. 82, 016905 (2018).
Tse, M. et al. Quantum-enhanced advanced LIGO detectors in the era of gravitational-wave astronomy. Phys. Rev. Lett. 123, 231107 (2019).
Buonanno, A. & Chen, Y. Quantum noise in second generation, signal-recycled laser interferometric gravitational-wave detectors. Phys. Rev. D 64, 042006 (2001).
Mizuno, J. et al. Resonant sideband extraction: a new configuration for interferometric gravitational wave detectors. Phys. Lett. A 175, 273 (1993).
Wicht, A. et al. White-light cavities, atomic phase coherence, and gravitational wave detectors. Opt. Commun. 134, 431 (1997).
Zhou, M., Zhou, Z. & Shahriar, S. M. Quantum noise limits in white-light-cavity-enhanced gravitational wave detectors. Phys. Rev. D. 92, 082002 (2015).
Braginsky, V. B., Gorodetsky, M. L., Khalili, F. Y. & Thorne, K. S. Energetic quantum limit in large-scale interferometers, in AIP Conference Proceedings Vol. 523, 180–190 (AIP, 2000).
Braginsky, V. & Khalili, F. In Quantum Measurement (ed. Thorne, K. S.) (Cambridge University Press, 1992).
Tsang, M., Wiseman, H. M. & Caves, C. M. Fundamental quantum limit to waveform estimation. Phys. Rev. Lett. 106, 090401 (2011).
Miao, H., Adhikari, R. X., Ma, Y., Pang, B. & Chen, Y. Towards the fundamental quantum limit of linear measurements of classical signals. Phys. Rev. Lett. 119, 050801 (2017).
Miao, H., Ma, Y., Zhao, C. & Chen, Y. Enhancing the bandwidth of gravitational-wave detectors with unstable optomechanical filters. Phys. Rev. Lett. 115, 211104 (2015).
Page, M. et al. Enhanced detection of high frequency gravitational waves using optically diluted optomechanical filters. Phys. Rev. D 97, 124060 (2018).
Miao, H., Yang, H. & Martynov, D. Towards the design of gravitational-wave detectors for probing neutron-star physics. Phys. Rev. D 98, 044044 (2018).
Bentley, J., Jones, P., Martynov, D., Freise, A. & Miao, H. Converting the signal-recycling cavity into an unstable optomechanical filter to enhance the detection bandwidth of gravitational-wave detectors. Phys. Rev. D 99, 102001 (2019).
Ma, Y. et al. Narrowing the filter-cavity bandwidth in gravitational-wave detectors via optomechanical interaction. Phys. Rev. Lett. 113, 151102 (2014).
Martynov, D. et al. Exploring the sensitivity of gravitational wave detectors to neutron star physics. Phys. Rev. D 99, 102004 (2019).
Mason, D., Chen, J., Rossi, M., Tsaturyan, Y. & Schliesser, A. Continuous force and displacement measurement below the standard quantum limit. Nat. Phys. 15, 745 (2019).
Thompson, J. et al. Strong dispersive coupling of a high-finesse cavity to a micromechanical membrane. Nature 452, 72 (2008).
Galliou, S. et al. Extremely low loss phonon-trapping cryogenic acoustic cavities for future physical experiments. Sci. Rep. 3, 2132 (2013).
Kharel, P. et al. High frequency cavity optomechanics using bulk acoustic phonons. Sci. Adv. 5, eaav0582 (2019).
Goryachev, M. & Tobar, M. E. Effects of geometry on quantum fluctuations of phonon-trapping acoustic cavities. N. J. Phys. 16, 083007 (2014).
Kimble, H. J., Levin, Y., Matsko, A. B., Thorne, K. S. & Vyatchanin, S. P. Conversion of conventional gravitational-wave interferometers into quantum nondemolition interferometers by modifying their input and/or output optics. Phys. Rev. D 65, 022002 (2001).
Tsaturyan, Y., Barg, A., Polzik, E. & Schliesser, A. Ultracoherent nanomechanical resonators via soft clamping and dissipation dilution. Nat. Nanotechnol. 12, 776 (2017).
Jayich, A. et al. Dispersive optomechanics: a membrane inside a cavity. N. J. Phys. 10, 095008 (2008).
Wilson, D. J. Cavity Optomechanics with High-Stress Silicon Nitride Films Ph.D. thesis, https://resolver.caltech.edu/CaltechTHESIS:06122012-123343193 (California Institute of Technology, 2012).
Gao, X., Li, Q., Chi, H. & Lin, J. 355 nm and 1064 nm laser damage of quartz glass. In Third International Symposium on Laser Interaction with Matter Vol. 9543, 124–128 (SPIE, 2015).
Said, A. et al. Measurement of the optical damage threshold in fused quartz. Appl. Opt. 34, 3374 (1995).
Koch, P. et al. Thickness uniformity measurements and damage threshold tests of large-area GaAs/AlGaAs crystalline coatings for precision interferometry. Opt. Express 27, 36731 (2019).
Loriette, V. & Boccara, C. Absorption of low-loss optical materials measured at 1064 nm by a position-modulated collinear photothermal detection technique. Appl. Opt. 42, 649 (2003).
Caves, C. M. & Schumaker, B. L. New formalism for two-photon quantum optics. I. Quadrature phases and squeezed states. Phys. Rev. A 31, 3068 (1985).
Schumaker, B. L. & Caves, C. M. New formalism for two-photon quantum optics. II. Mathematical foundation and compact notation. Phys. Rev. A 31, 3093 (1985).
Corbitt, T., Chen, Y. & Mavalvala, N. Mathematical framework for simulation of quantum fields in complex interferometers using the two-photon formalism. Phys. Rev. A 72, 013818 (2005).
Lantz, B. et al. Instrument Science White Paper 2019, Tech. Rep. LIGO-T1900409-v5 (LIGO Scientific Collaboration, 2019) https://dcc.ligo.org/LIGO-T1900409-v4/public.
Sankey, J., Yang, C., Zwickl, B., Jayich, A. & Harris, J. Strong and tunable nonlinear optomechanical coupling in a low-loss system. Nat. Phys. 6, 707 (2010).
Li, X. et al. Broadband sensitivity improvement via coherent quantum feedback with PT symmetry, LIGO document P2000452 https://dcc.ligo.org/LIGO-P2000452 (2020).
Fricke, T. T. et al. DC readout experiment in enhanced LIGO. Class. Quantum Gravity 29, 065005 (2012).
Yamamoto, H. Transfer Functions of Scattered Lights in AdvLIGO COC, Tech. Rep. LIGO-T060073 (LIGO Scientific Collaboration, 2006).
Brooks, A. F. et al. Overview of Advanced LIGO adaptive optics. Appl. Opt. 55, 8256 (2016).
Page, M. A. et al. Gravitational wave detectors with broadband high frequency sensitivity—data, Figshare data repository https://doi.org/10.6084/m9.figshare.13352669 (2020).
Aasi, J. et al. Advanced LIGO. Class. Quantum Gravity 32, 074001 (2015).
Acknowledgements
This research was primarily supported by the Australian Research Council (ARC) Centre of Excellence for Gravitational Wave Discovery OzGrav CE170100004 and Discovery Project DP170104424. In addition, C.D. Blair is funded by the ARC Discovery Early Career Researcher Award DE190100437. The work of D. Mason, M. Rossi, and A. Schliesser was supported by the European Research Council project Q-CEOM (grant no. 638765) and the EU H2020 FET proactive project HOT (grant no. 732894). M. Goryachev and M.E. Tobar are supported by the ARC Centre of Excellence for Engineered Quantum Systems EQuS CE170100009. Y. Chen is supported by the US National Science Foundation Grants PHY-1708212 and PHY-1708213, and by the Simons Foundation (Award Number 568762). H. Miao is supported by UK Science and Technology Facilities Council Ernest Rutherford Fellowship (grant no. ST/M005844/11). M.A. Page would like to acknowledge the Japan Society for the Promotion of Science Postdoctoral Fellowship Program (grant no. P20713). We thank Eric C. Langman of Neils Bohr Institute and Carl Knox of ARC OzGrav at Swinburne University of Technology for their assistance in providing illustrations of phononic crystal resonators.
Author information
Authors and Affiliations
Contributions
Calculations and models regarding GW detector interferometry and filter cavity optomechanics were performed by M.A. Page, and discussed and verified by H. Miao, Y. Ma, Y. Chen and C. Zhao. C.D. Blair and D.G. Blair provided discussion on the integration of WLSR in GW detectors. D. Mason, M. Rossi and A. Schliesser provided information regarding measured data of PNC resonators. M. Goryachev and M.E. Tobar provided information regarding measured data of BAW resonators. C. Zhao, L. Ju and D.G. Blair were the main supervisors of the project. The paper was drafted by M.A. Page, M. Goryachev, Y. Chen, A. Schliesser, and D.G. Blair, edited by M.A. Page and commented by all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Page, M.A., Goryachev, M., Miao, H. et al. Gravitational wave detectors with broadband high frequency sensitivity. Commun Phys 4, 27 (2021). https://doi.org/10.1038/s42005-021-00526-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00526-2
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.