Abstract
The strong coupling of a superconductor to a spinful quantum dot results in Yu–Shiba–Rusinov discrete subgap excitations. In isolation and at zero temperature, the excitations are sharp resonances. In transport experiments, however, they show as broad differential conductance peaks. Here we obtain the lineshape of the peaks and their temperature dependence in superconductor–quantum dot–metal nanowire-based devices. Unexpectedly, we find that the peaks shift in energy with temperature, with the shift magnitude and sign depending on ground state parity and bias voltage. Additionally, we empirically find a power-law trend of the peak area versus temperature. These observations are not explained by current models.
Similar content being viewed by others
Introduction
In a quantum dot–superconductor system, the exchange interaction of an unpaired, Coulomb-blockaded electron in the quantum dot with quasiparticles in the superconductor detaches discrete excitations from the edge of the superconducting gap1, as first explained by Yu, Shiba and Rusinov (YSR) for classical spins2,3,4. When the coupling of the quantum dot to the superconductor is increased, the Kondo temperature, TK, rises above the superconducting gap, Δ, prompting a doublet → singlet ground state transition marked by zero excitation energy5,6,7. While the lineshape and temperature dependence of the normal-state spin-1/2 Kondo effect have been thoroughly characterized8,9,10,11, its YSR superconducting analog is yet to be subjected to the same degree of scrutiny.
At finite temperature, the spectral weight of YSR excitations is characterized by an approximately Gaussian lineshape12,13. In a realistic setup, in which the intrinsic superconductor-impurity system is probed by a scanning tunneling tip14,15,16,17,18,19 or a metallic contact6,20,21,22,23,24, the excitations are measured as peaks in the differential conductance25, and various mechanisms may obscure their intrinsic lineshape. On one hand, the peaks can be dressed with a Lorentzian form in the presence of a relaxation channel for quasiparticles, which can be provided, for example, by a soft superconducting gap; i.e., a pseudogap populated by quasiparticle density of states up to the Fermi level26. On the other hand, as by-product of the metallic lead, the normal-state spin-1/2 Kondo effect can emerge and distort the peak lineshape when \(T\, <\, {T}_{{\rm{K}}}^{{\rm{N}}}\), where the superscript N here is used to distinguish the Kondo temperature of the normal lead from TK, the one of the superconducting lead, and T is the temperature27. In addition, photon assisted tunneling can broaden the superconducting density of states28,29, though this issue may be solved by increasing the capacitance of the junction29.
In planar semiconductor/superconductor devices, in which the gate tunability of the semiconductor is employed to define a quantum dot in close proximity to the superconductor30, a deteriorated interface between the superconductor and the semiconductor has been related to a soft superconducting gap31,32,33,34,35. Earlier measurements of the temperature dependence of YSR excitations on soft-gapped devices reported no significant effects at kBT ≪ Δ36,37,38. However, the use of a superconducting lead in place of a normal one led to non-equilibrium features at high temperatures36,37,38.
The interface improvement gained by the in-situ deposition of Al on InAs nanowires yields a hard gap—i.e., a gap devoid of quasiparticle density of states—in tunnel spectroscopy32,39. Using these nanowires, we define superconductor–quantum dot–metal (S-QD-N) devices by either 1) etching Al39 or 2) shadowing in-situ33 to obtain a bare semiconductor channel. At base temperature, the devices are shown to have a hard gap, with Δ nearly temperature-independent in the temperature range explored. At temperatures significantly smaller than Δ, we observe a ground-state and bias-voltage dependent shift of the YSR subgap excitations, in apparent contradiction to recent calculations developed for the simpler S-QD system12,13. The shift occurs irrespective of the conductance of the YSR peaks, implying a negligible role of the normal lead in this effect, and excluding a possibly lurking Kondo effect.
Results
Device description
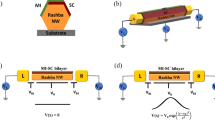
A sketch of the system in consideration is shown in Fig. 1a. From left to right, we show a normal metal lead with a Fermi–Dirac distribution at the electron temperature Te, separated from a spinful quantum dot level by a tunnel barrier of coupling ΓN. The exchange interaction of the spin 1/2 with virtually excited quasiparticles in the superconductor via the barrier of coupling ΓS produces sharp YSR resonances (δ peaks) inside the gap, while the finite but low temperature leads to additional interaction with a small population of thermally fluctuated quasiparticles and produces broadened peaks at the δ-peak position12. In our setup, the dilution refrigerator temperature T is lower than Te (at base, T = 20–30 mK while Te ≈ 80 mK), as it is typically the case40,41. A doped-Si substrate backgate increases the lead capacitance (C ≈ 10 pF) of our devices, which has been shown to reduce environmentally-assisted tunneling29. The backgate, Vbg, is also used as an additional tuning knob of the quantum dots. Al is covering three facets of the nanowire, and Au is used as contact to the bare facets. In Methods, we show details of device fabrication and evidence of hard gap in our devices. The differential conductance, dI/dVsd, of the devices is measured with a lock-in amplifier, where Vsd is the source-drain bias voltage.
a Sketch of the superconductor–quantum dot–metal (S-QD-N) system. b Scanning electron micrograph of the device. Bottom and side gates are false-colored in yellow and orange, respectively. The superconducting three-facet Al lead appears in blue. The normal Au lead is on the top section of the micrograph and appears in green. The section of bare InAs wire in which the QD is defined appears in red. Scale bar is 100 nm. c Fit of YSR peaks from differential conductance, dI/dVsd, data to the sum of two Gaussian (Lorentzian) curves, shown in blue (black). Δ corresponds to the edge of the superconducting gap25, and agrees with the measured gap singularities (see Methods). d dI/dVsd colormap of YSR peaks vs. plunger gate voltage, VP, and bias voltage, Vsd. Other gates are set to VN = −6.82 V, VS1 = −6.56 V, Vbg = −20 V. The color scale has been saturated to highlight the subgap features.
We first focus on the device in which Al was etched, shown in Fig. 1b. Being directly below the region of bare InAs wire closest to Au, bottom gate VN controls ΓN, the coupling of the QD to Au, while bottom and side gate VS1, in proximity to the region of bare InAs wire closest to Al, adjusts the coupling of the QD to Al, ΓS. Bottom and side gate VS2 was kept at −5.5 V throughout the experiment. Bottom gate VP acts as QD plunger gate, controlling the charge occupation.
Shifts of YSR resonances induced by temperature
In our setup, YSR dI/dVsd peaks present in Vsd − dI/dVsd traces can be fitted to the sum of two Gaussian lineshapes over a range of gate voltages and temperatures. This allows us to extract values for the position, height, and full-width at half-maximum (FWHM) of the peaks against these variables. Figure 1c shows a trace exemplifying the fit in comparison to the sum of two Lorentzians. The tails of the Lorentzians drop too slowly to account for the data around zero bias, an effect observed for all the fitted data.
Figure 1d shows a map of subgap dI/dVsd as function of VP and Vsd. The two small loops identified by X and Y correspond to YSR doublet → singlet excitations. We independently corroborate their doublet ground state nature through their evolution in an external magnetic field20,21 (see Methods). The charging energies corresponding to these spinful charge states are U = 3.1 meV and U = 2.7 meV, respectively, obtained from Coulomb-diamond spectroscopy, whereas the gap singularities appear at ∣Δ∣ = 0.27 meV. The condition U ≫ Δ places the system within the YSR regime1. The trace in Fig. 1c was acquired at the electron-hole (e-h) symmetry point of charge state Y, indicated by a vertical arrow in Fig. 1d.
Figure 2a–c show three examples of the effect of changing VS1 for charge state Y. From plots 2a to 2c, the YSR loop shrinks and opens again as the same ground-state changes from doublet to singlet via gate control of ΓS20,21. Figure 2d–f show in turn the temperature dependence of the YSR peaks at the e-h symmetry point of the respective colormaps in Fig. 2a–c. As the temperature increases, the pair of peaks which corresponds to doublet ground state and is closer to Δ in low-temperature bias position splits apart (Fig. 2d). Still in the doublet phase, Fig. 2e shows that, when the initial bias position is closest to zero, the peaks instead come together with temperature. At a similar low-temperature bias position, but in the singlet phase, Fig. 2f shows that the peaks move also towards zero bias, albeit with a faster rate. In contrast, Numerical Renormalization Group (NRG) calculations of the spectral weight of YSR peaks in the single-impurity Anderson model with a conventional superconducting lead have predicted a temperature-independent peak position for a constant gap12, and the opposite behavior to our observations for a temperature-dependent Δ12,13. To the best of our knowledge, no current models account for this behavior.
a–c Differential conductance, dI/dVsd, colormaps of YSR peaks in charge state Y vs. plunger gate voltage, VP, and bias voltage, Vsd, at increasing coupling to the superconducting lead. d–f Temperature dependence of YSR peaks at the electron-hole symmetry point of maps (a–c), indicated by an arrow. Bottom and side gate VS1 is set to (a) VS1 = −6.42 V, (b) VS1 = −6.76 V, (c) VS1 = −6.94 V. VP is compensated for the change in VS1. Bottom gate VN and backgate Vbg are kept at −6.82 V and −20 V, respectively.
To obtain a quantitative description of the variation of the peak position against temperature, we fitted to a Gaussian the YSR peak at positive bias from the three datasets in Fig. 2d–f and from five more datasets taken at intermediate peak positions; all of them at the e-h symmetry point of charge state Y. The temperature range covered by the fit (from 22 mK to ≈ 550 mK, or from 0.01Δ to ≈ 0.17Δ) corresponds to the low-temperature regime12, where Δ is constant (T ≪ Tc = 2.2 K) and significant quasiparticle thermal excitation is not expected to occur. At 22 mK (550 mK), the quasiparticle density in the Al lead is theoretically estimated as \(D({E}_{{\rm{F}}})\sqrt{2\pi \Delta {k}_{{\rm{B}}}T}exp(-\Delta /{k}_{{\rm{B}}}T) \sim 1{0}^{-65}\) nm−3 (~10−5 nm−3), where D(EF) = 23 eV−1nm−3 is the density of states of Al at the Fermi energy42,43,44. We observe, however, that the finite-bias subgap conductance increases with temperature, indicating non-negligible quasiparticle thermal excitation (see Methods).
Figure 3a shows the extracted evolution in temperature of the position of the peaks, five of which correspond to doublet ground state (in red) and three to singlet ground state (in blue). Black circles pair datasets of singlet and doublet ground states whose initial bias position roughly match. The qualitative picture extracted from Fig. 2 is corroborated for such pairs; namely, when having approximately the same initial bias position, datasets of singlet ground state shift faster towards zero bias than datasets of doublet ground state. In addition, a new detail is worth mentioning. The curvature of the datasets of doublet ground state changes from positive to negative as Vsd → 0; i.e., as the peaks are biased away from Δ. In the case of the datasets of singlet ground state, the curvature becomes more negative as Vsd → 0 for the data available.
a Temperature dependence of peak position at the electron-hole symmetry point across the doublet (red) → singlet (blue) ground state (GS) transition. The datasets have been fitted to parabolas y = a0 + a1T + a2T2 (solid lines) in order to indicate that they do not change faster than T2. b Peak position corresponding to the lowest and highest temperature data points in each of the datasets from a vs. g ~ J, the exchange coupling. Shifts towards the bias voltage (Vsd) points Vsd = Δ (Vsd = 0) are indicated by green (red) arrows. Solid lines end at the temperature above which the Gaussian fit cannot be reliably carried out, corresponding to the highest temperature shown in a for each dataset. The arrows are extended beyond that as dotted lines up to the final position of the YSR peaks at 1.2 K. c Temperature dependence of bias position of YSR peaks of doublet GS in a normalized by their bias position values at 22 mK. This plot brings forward the non-monotonic behavior observed closest to the doublet–singlet GS transition from the doublet side. The same symbols as in a are used. d Peak position vs. plunger gate voltage, VP, at different temperatures. Error bars in a, c and d correspond to standard deviation.
This ground-state and bias-position dependent behavior can be parametrized by the exchange coupling, J. In Fig. 3b, we plot the endpoints of each dataset in Fig. 3a as a function of g = πJSD(EF), where S is the spin. We convert YSR peak position to g using \({E}_{{\rm{YSR}}}=\Delta \frac{1-{g}^{2}}{1+{g}^{2}}\), valid in the classical spin limit1,27. YSR peaks of doublet ground state whose low-temperature bias position is closer to Δ, corresponding to small g, shift towards Δ as the temperature is increased. The shift direction is reversed when g is tuned towards the doublet–singlet ground state transition. The reversal occurs between g = 0.7–0.85, when the YSR peak of doublet ground state of lowest bias position shifts towards zero bias. When g = 1.2–1.5, after the transition occurs and the ground state is a singlet, the remaining datasets shift towards zero bias.
To highlight the puzzling behavior of the YSR peak of doublet ground state closer to zero bias at 22 mK (Vsd = 44 ± 1 μV, g ≈ 0.85), we plot in Fig. 3c the datasets of doublet ground state from Fig. 3a normalized by their base-temperature bias positions. This way of plotting proportionally reduces the rate of change with temperature of the peaks whose 22-mK bias position is further away from zero bias, downplaying their changes in curvature, while exaggerating the non-monotonic behavior of the peak closest to zero bias. As the temperature increases, the peak closest to zero bias initially follows the other peaks in their upwards motion above 1, but then it departs from the rest at around 150 mK, quickly moving downwards below 1. At 150 mK, 3.5kBT = 45 μV, which is of the same order of the bias position, leading to possible overlap with the excited singlet state due to thermal broadening in the metallic lead. However, the YSR peak at the next lowest bias position, Vsd ≈ 90 μV, does not exhibit a similar inflexion point at 300 mK nor at any other temperature, nor does the following peak. Therefore, this non-monotonic behavior cannot be explained by thermally-induced overlap between the ground and the excited states, alone. In Supplementary Fig. 1, we show data for charge state X which is qualitatively similar to Fig. 3a–c. Note, however, that the apparent bunching of the data shown in Fig. 3c does not occur in this additional dataset, indicating that it may be coincidental.
In Fig. 3d, the YSR peak position across charge state Y is shown to shift towards larger bias with temperature, indicating that the observed temperature-shifting behavior is not exclusive of the e-h symmetry point. The dataset used to extract the plunger gate dependence of the peak position at various temperatures is shown under Methods.
Power-law trend of the temperature dependence of peak area
We now turn our attention to the peak height and width dependence in temperature against an increase of the coupling of the quantum dot to the normal lead. We plot in Fig. 4a–c three examples of the effect of changing VN within charge state X in the doublet ground state. From left to right plots, the conductance of the subgap states is significantly enhanced. We interpret the enhancement of the conductance as stemming from a decrease in the ΓN, ΓS asymmetry r from ΓN ≪ ΓS to ΓN ~ ΓS due to an increase of ΓN. We can offer an order of magnitude of this asymmetry from the relation peak height = 2e2/h × 4r/(1 + r)2, where r = ΓN/ΓS20,45. By fitting YSR peaks with Gaussians at the e-h symmetry point of charge states X and Y across the entire gate space (VN, VS1) explored, we obtain a peak height range of 0.003e2/h → 1.5e2/h, or ΓN/ΓS ~ 8 × 10−4 → 0.3.
a–c Differential conductance, dI/dVsd, colormaps of YSR peaks in charge state X (of doublet ground state) vs. plunger gate voltage, VP, and bias voltage, Vsd, at increasing peak conductance. d–f Temperature dependence of YSR peaks at the electron-hole symmetry point of maps (a–c), indicated by an arrow. Bottom gate VN is set to (a) VN = −6.77 V, (b) VN = −6.22 V, (c) VN = −5.7 V. VP is compensated for the change in VN. Bottom and side gate VS1 and backgate Vbg are kept at −6.4 V and −11.55 V, respectively.
Figure 4d–f show colormaps of the temperature dependence of YSR peaks at the e-h symmetry point of each of the examples from Fig. 4a–c. In confirmation of our previous observation, the YSR peaks, which are of doublet ground state and away from zero bias, split apart as the temperature is increased. We highlight another observation; as the temperature rises the peak height is decreased and the peak width is increased.
In Fig. 5 we summarize quantitative data on this effect. Figure 5a, b show, respectively, plots of decreasing peak height curves and increasing FWHM curves as temperature is increased. These were acquired from a fit of the positive-bias YSR peak in the three datasets of Fig. 4d–f plus four additional datasets, all taken at the e-h symmetry point of charge state X of doublet ground state. All curves were fitted to parabolas y = a0 + a1T + a2T2, to indicate that they do not change faster than T2. For comparison, we plot the linear broadening 3.5kBT due to the Fermi–Dirac distribution of the normal lead. The slope of the FWHM data is smaller than 3.5kBT below 0.2 K, and larger than 3.5kBT above 0.4 K, while its magnitude is larger than 3.5kBT, indicating that thermal broadening by the metallic lead is not the only broadening mechanism.
Extracted (a) peak height and (b) Full width at half maximum (FWHM) vs. temperature at the electron-hole symmetry point of charge state X of doublet ground state. c Temperature dependence of the product of peak height and FWHM obtained from a and b normalized by their values at 22 mK. Datasets from a, b and c are color-coded in the same way. Error bars indicate standard deviation.
While the upper bound of the theoretical conductance of YSR peaks is 2e2/h26, in the presence of a finite quasiparticle relaxation tunneling rate to a continuum of states, an increase of relaxation rate or temperature leads to a decrease in peak conductance as ~1/(Γ + T), where the lifetime Γ includes the relaxation rate22,26. In the same formalism, the FWHM scales as ~(Γ + T). Therefore, the product of FWHM and peak height, which provides the area of the peak, is a constant independent of temperature. The constant is equal to 1 if the product is normalized by its value at T = 0. Surprisingly, the products of the peak height and FWHM of the seven datasets in Fig. 5a, b scaled by their values at 22 mK appear to follow best a quadratic trend, as shown in Fig. 5c. This occurs despite of widespread change in peak height (of about 2 orders of magnitude), FWHM (from 0.3Δ to 0.5Δ) and peak position (from 0.3Δ to 0.7Δ). For comparison, a constant dashed line equal to 1, predicted by the relaxation formalism, is also shown.
Results from a second device
Finally, we report results from a second device fabricated from a nanowire shadowed during in-situ Al deposition by a thick and shorter nanowire. The resulting Al/nanowire heterostructure, shown in Fig. 6a, eliminates the need to etch Al to form the junction. Figure 6b shows a scanning electron micrograph of the device. Side gate VG1 was used as plunger gate, while side gate VG2 and a substrate backgate Vbg were used to bring the wire close to charge depletion. YSR excitations of doublet ground state form loops identified by their smaller size than their adjacent counterparts, as exemplified in the dI/dVsd(Vsd, VG1) map of Fig. 6c. From Coulomb-diamond spectroscopy, we determined the charging energy of the associated spinful charge state indicated by Z as U = 1.1 meV, and Δ = 0.195 meV. As in the previous device, the sum of two Gaussians fits YSR peaks in dI/dVsd(Vsd) traces up to the gap edge. An instance of this is shown in Fig. 6d.
Scanning electron micrograph of (a) a typical set of as-grown wires and (b) the device. Scale bars are (a) 500 nm and (b) 100 nm. c Differential conductance, dI/dVsd, colormap of Yu–Shiba–Rusinov (YSR) subgap peaks evolving in plunger gate voltage, VP, and bias voltage, Vsd, across spinful charge state Z. Arrows indicate the position of the gap singularities. d Fit to Gaussians of YSR peaks at the electron-hole (e-h) symmetry point of Z. Temperature dependence of (e) peak position and (f) peak height, full width at half maximum (FWHM) extracted from fitting YSR peaks at the e-h symmetry point of four different charge states of doublet ground state, including Z. All datasets have been fitted to parabolas of the form y = a0 + a1T + a2T2, to indicate that they do not change faster than T2. g Temperature dependence of the product of peak height and FWHM scaled by their values at 30 mK. Error bars in e, f and g correspond to standard deviation.
In Fig. 6e, f we show the YSR peak position, height and FWHM extracted from fitting the temperature dependence of four charge states of doublet ground state at their e-h symmetry points, including state Z. The qualitative similarities of the data in both devices is noticeable. As before, the peak-position datasets in Fig. 6e exhibit a bias-dependent change of curvature with temperature. Similarly, in Fig. 6f the FWHM and peak height vs. temperature datasets obey opposite trends, while the FWHM shows a curvature increase with respect to 3.5kBT.
Nonetheless, there is a quantitative difference. In Fig. 6g, we plot the product of peak height and FWHM normalized by their values at 30 mK, the lowest temperature at which data was recorded for this device. The four datasets follow best a T3 dependence instead of the T2 trend displayed by previous device. In Supplementary Fig. 2a we show that, when data from both devices is put together in the same plot, the data for the second device grows faster with temperature than the data of the first one.
Discussion
As commented above, a Kondo singlet with Kondo temperature \({T}_{{\rm{K}}}^{{\rm{N}}}\) can form with the normal lead in the N-QD part of the S-QD-N system27. To address this possibility, we estimate the temperature of the Kondo resonance in the isolated N-QD system. \({T}_{{\rm{K}}}^{{\rm{N}}}\) then depends on gate voltage through the level position, ϵ0, of the QD as \({T}_{{\rm{K}}}^{{\rm{N}}}=\frac{\sqrt{\Gamma U}}{2}{e}^{\pi {\epsilon }_{0}({\epsilon }_{0}+U)/\Gamma U}\), where Γ is the linewidth of the level10. Due to the sensitivity of the exponent to changes in Γ = ΓN, a small variation in ΓN at the e-h symmetry point results in a large change in \({T}_{{\rm{K}}}^{{\rm{N}}}\). At the singlet-doublet transition point5, kBTK = 0.3Δ = 81μeV for U = 3.1 meV, which we can use to estimate ΓS = 1 meV and an upper bound of \({T}_{{\rm{K}}}^{{\rm{N}}}\approx 1.7\) mK for the YSR peaks of doublet ground state of largest conductance (r = 0.3). Such a small \({T}_{{\rm{K}}}^{{\rm{N}}}\) indicates that, in the isolated N-QD system, the Kondo effect of the normal lead is not playing an important role at the e-h symmetry point. However, in the full S-QD-N system, it has been predicted that the coupling to the superconductor can enhance \({T}_{{\rm{K}}}^{{\rm{N}}}\) in the doublet phase, particularly close to the doublet–singlet ground state transition from the doublet side27,46. This prediction concerns the most the data corresponding to the YSR resonance of doublet ground state closest to Vsd = 0, which is the one exhibiting a strikingly different behavior from the rest of the doublets in Fig. 3a, b, c and Supplementary Fig. 1. The signature of this prediction is the presence of a zero bias peak in the differential conductance46, which is absent in our data in both singlet and doublet phases in the temperature (0.022 K < T < 1.2 K) and magnetic field ranges (B < 0.75 T) explored. The absence of this signature also excludes the Kondo effect in the superconducting lead. Indeed, the weakening of superconductivity and the appearance of residual subgap conductance due to an external magnetic field has been shown to result in the emergence of a zero-bias peak attributed to a Kondo resonance34, which is not the case here. To end our discussion of the Kondo effect in the superconducting lead, we point out that, either deep in the doublet phase, when T ≳ TK, or past the ground state transition in the singlet phase, when T ≪ TK ~ 1 K, YSR resonances shift with temperature at a rate of the same order of magnitude (of about 100 μVK−1), indicating that the ratio T/TK is not playing a significant role. Instead, as evidenced by the change of shift direction in Fig. 3a–c and Supplementary Fig. 1, the determinant factor in the temperature-shifting behavior seems to be the closeness to the transition from the doublet side.
In view of this, the role of the N-QD part of the system is reduced to a non-perturbing tunnel probe, and an explanation for the ground-state and peak-position dependent YSR peak behavior against temperature is to be found in the remaining part of the system, S-QD. In this regard, it is important to discuss a possible temperature dependence of ΓS, which is the tunnel coupling responsible for the position of YSR resonances. While the universal temperature scaling of the conductance by the Kondo temperature found in Refs. 47,48,49,50 would imply a temperature-independent tunnel coupling to the metallic reservoir, a quadratic temperature dependence of the tunnel coupling has been found in work related to Fano resonances51, leaving the issue open to discussion. A trivial reduction of ΓS with temperature, which would increase monotonically the energy of the singlet state, either in the excited or ground state configuration, is ruled out based on the non-monotonic behavior of the curvature of the peak-position vs. temperature datasets depending on initial Vsd position, as seen in Fig. 3a and Supplementary Fig. 1.
In turn, the f(T) = Tα dependence extracted from the normalization of the peak area has a less evident origin. Phonon-mediated quasiparticle relaxation could in principle provide temperature-dependent broadening in our S-QD-N setup52,53, but has so far only been used phenomenologically in analyzing the outcome of the S-YSR setup, in which an additional superconductor probes YSR excitations, leading to the need of deconvolving intrinsic YSR effects from those of the superconducting probe54. To explain the increase in normalized peak area with temperature, the combined effect of thermal broadening from the metallic lead, thermal modification of the density of states of the superconductor (see Methods), together with the known intrinsic thermal modification of YSR excitation width found by Žitko12, may need to be considered. A monotonic change of ΓN with temperature, while broadening the YSR peak width, would also lead to a decrease of the same order in the peak height, possibly resulting in a constant temperature dependence unlike the one observed22,51.
At present, the reason for a different exponent α in the power-law temperature dependence of the normalized peak area of the two devices is unclear. We note that, besides the fabrication method, there are other differences between the two devices. The U/Δ ratio is ≈ 10 in the etched device, compared to ≈ 5 in the shadowed device, which means the former is deeper into the YSR regime than the latter. In addition, Δ is 30% smaller in the shadowed device, which results in a smaller Δ/kBT ratio and therefore in more significant quasiparticle thermal excitation for a given temperature. In Supplementary Fig. 2, we plot Tα data for positive and negative YSR peaks for the two devices, showing that the scaling kBT/Δ2 brings the 22 datasets closer together. Additionally, we point out that distinguishing between a T2 or T3 dependence of the normalized peak area in the negative-bias data is less clear due to larger spreading of the data. A statistical analysis based on more samples may be needed to elucidate the specific power-law dependence or its universality.
In the presence of a significant relaxation tunneling rate from YSR subgap resonances to a continuum of states, an asymmetry of the height of the peaks in positive-negative bias voltage is expected26. However, this additional tunneling rate theoretically results in a Lorentzian YSR peak lineshape26, while we observe Gaussian lineshapes. In addition, the temperature dependence of the YSR peak area remarkably deviates from the expected dependence given by the relaxation model presented by Grove-Rasmussen et al., and by Martin and Mozyrsky22,26. Despite these inconsistencies, the height of the YSR conductance peaks is asymmetric in bias voltage even at the e-h symmetry point, as it is readily seen from Figs. 1 and 6, in apparent agreement with an important relaxation tunneling rate22,26. It is unclear which of these observations are determinant arguments in favor or against the existence of a finite relaxation tunneling rate in our devices.
Majorana zero-modes, which can arise in Rashba semiconductor nanowires coupled to superconductors under a properly oriented magnetic field, can give rise to zero-bias differential conductance peaks in tunnel spectroscopy55. Nevertheless, peaks from YSR states bear distinctive features from those from Majorana modes. While the lineshape of Majorana peaks is a Lorentzian56,57, our data indicate that well-separated YSR peaks have a Gaussian lineshape. Note, however, that when two YSR peaks collapse into a single zero-bias peak (e.g., at a singlet-doublet transition), the Lorentzian lineshape might be harder to rule out (see Methods). Additional differences may be found in the change of their FWHM with temperature in comparison to 3.5kBT.
To summarize, we have simplified the complex S-QD-N system by employing a hard superconducting gap and non-invasive N probes, while exploiting the gate tunability of YSR excitation and ground-state energies. We have extensively characterized the temperature dependence of YSR resonances in two devices, establishing a basis for further experimental and theoretical work. In particular, the origin of shifts in bias voltage of the resonances against temperature is not explained by current models12,13.
Methods
Below we provide additional details of the fit and of device fabrication, as well as an independent corroboration of the ground state of the S-QD-N system.
Fabrication of the devices
To fabricate the first device, a 110-nm wide InAs epitaxially half-shell Al-covered nanowire was deterministically deposited on a bed of local bottom gates and additional side-gates were defined during contact deposition. By etching-off the 7-nm-thick Al from the top half of the nanowire and contacting the resulting bare wire with Ti/Au, a S-QD-N junction was defined with a 250 nm channel of bare wire. The Au contact on the Al-lead side was 400 nm away from the channel. The leads ended in large-area bonding pads with a capacitance of ≈ 10 pF estimated by a simple parallel-plate capacitor model to the Si backgate through 200 nm of Si oxide.
To fabricate the second device, a shadowed 90-nm wide InAs wire was deterministically deposited on a Si substrate of similar characteristics as the previous device, leading to similar leads capacitance. Side-gates were defined during evaporation of the ohmic contacts to the bare wire. The bare-wire channel between the 20-nm thick Al film and the Ti/Au contact was 450 nm long. The Au contact on the Al-lead side was 500 nm away from the channel.
Measurements
The devices were voltage-biased. The DC current was acquired using a digital multimeter, while the dI/dVsd signal was recorded using standard lock-in amplifier techniques. To obtain dI/dVsd an excitation of 3 μV on top of Vsd was applied at a frequency of 116.69 Hz for the device in which Al was etched, and of 132.7 Hz for the device in which Al was shadowed.
The full gating effect on YSR states by VS1 and VN is shown in Supplementary Figs. 3 and 4. Note that, while VN has a monotonic effect on peak height, the effect of VS1 on peak position is non-monotonic. As VS1 is increased, YSR states go from the singlet to the doublet phase, and then back to the singlet phase. This behavior is typical of gated nanowire devices (for another example, see Jellinggaard et al.21). For clarity, however, we ordered the maps in Supplementary Fig. 3 by peak position instead of VS1 value, indicating the VS1 value in each plot.
Details of the fit
We fitted dI/dVsd(Vsd) curves to Gaussians
where A+ (A−) represents the height of the positive (negative) bias peak, Vsd+ (Vsd−) represents the position of the positive (negative) bias peak, and ≈2.35c+ (≈ 2.35c−) represents the width of the positive (negative) bias peak. The fit is good up to the quasiparticle continuum, where the peaks lose weight to it. The fits were done below a temperature at which it was not possible to distinguish the edge of the gap Δ, or below a temperature at which the two YSR peaks merged into one (whichever was the lowest). This temperature limit varied within datasets. The temperature used in the analysis was measured at zero bias simultaneously with the recording of the differential conductance. However, to obtain a rectangular grid of constant spacing for easier plotting of temperature vs. Vsd colormaps in Figs. 2, 4 and Supplementary Figs. 3, 4 and 5, we used in those cases the temperature set by the command given to the temperature controller. The measured and set temperatures can be slightly different (difference typically below 20 mK). Across one dataset, we kept fixed the bias range in which the fit was performed. Before analyzing the data, a series resistance of 8.24 kΩ due to the measurement setup was removed from Vsd and dI/dVsd. In the measurements made on the etched device, the voltage source had an offset of −9 μV. In the case of the shadowed device, the offset was +4 μV. These offsets were not taken into account in the analysis of the YSR peak position, unless stated otherwise. Data from fits to negative-bias YSR peaks is shown in Supplementary Figs. 6 and 7.
Figure 7a–d show a typical example of the same pair of YSR peaks at different temperatures. The fit quality does not deteriorate with an increase in temperature. Additionally, Fig. 7e shows an example of the fit at a YSR crossing. To verify the robustness of the parameters extracted from the fit, we compare in Fig. 7f, g the maximum of the peak and its position to the peak height and peak position extracted from the fit. Due to data noise (in Fig. 7d, fluctuations in conductance at the positive-bias YSR peak with respect to the Gaussian fit are 3 × 10−3e2/h), these two values are slightly different, but follow the same trend.
a–d Robustness of the fit against temperature. Differential conductance, dI/dVsd vs. bias voltage, Vsd data extracted from Supplementary Fig. 4c. e Zero-bias dI/dVsd peak obtained from the crossing of two YSR peaks at the right doublet–singlet crossing of state Y in Fig. 1d (at VP = −0.006 V) fitted to a single Lorentzian (black) and Gaussian (blue) curves. While the Gaussian curve captures better the tail at positive bias of the crossed YSR peaks, it fails to do so at negative bias due to the presence of the superconducting gap edge. A slight offset in the voltage source which displaces the curve away from zero bias was corrected. f Peak maximum and fitted peak height against temperature. g Position of peak maximum and fitted peak position against temperature. Error bars in f and g correspond to standard deviation.
Gap hardness
A soft superconducting gap is expected to provide additional relaxation channels which should result in extrinsic YSR peak broadening leading to a Lorentzian-shaped peak26. In our two devices, the gap at base temperature is hard as evidenced by the subgap conductance suppression, while the experimentally extracted YSR peak lineshape is Gaussian. Figure 8 shows dI/dVsd(Vsd) traces of the gap in linear and logarithmic scale measured in deep Coulomb blockade in the regime ΓN, ΓS ≪ U, in which YSR and Kondo physics are suppressed. The FWHM of the positive-bias gap singularity is 50 μV for the etched device, and 40 μV for the shadowed one. These numbers are slightly smaller than the FWHM of the narrowest positive-bias YSR peak measured at e-h symmetry points in each device, which corresponds to 65 μV for the etched device, and 50 μV for the shadowed one.
Variation of the gap against temperature
A decrease of the gap against temperature can produce motion of the position of the YSR peaks within the gap in the opposite direction as observed in the experiment12,13. In both the etched and shadowed devices we observe a decrease of the gap of no more than 5%. In both cases, we determined this through the temperature dependence of the YSR peaks in the charge state of singlet ground state next to one of the examined doublets. In even charge states, the S-QD-N junction behaves effectively as a co-tunneling junction without subgap YSR excitations, making this procedure feasible25. Figure 9 shows that the Δ peaks remain constant in bias from 22 mK to 590 mK, despite losing weight. Note that the gap progressively fills with quasiparticle density of states as the temperature is increased.
a–e Colormaps of differential conductance, dI/dVsd, vs. plunger gate voltage, VP, and bias voltage, Vsd, showing the evolution of Fig. 1d in temperature. The dashed lines indicate the position of Yu–Shiba–Rusinov peaks in the charge state of singlet ground state between charge states X and Y, which are related to the edges of the gap25. These do not move with temperature. f Positive-bias linecuts through the center of the even singlet sector, representing the temperature dependence of the gap.
Determination of the ground state by Zeeman-split spectroscopy
As found before by Lee et al., and by Jellinggaard et al.20,21, in a finite external magnetic field, B, the states of singlet ground state show two excitations corresponding to two spin-resolved excited doublets. This provides a way to distinguish them from states of doublet ground state, which show only one excitation. We verified the ground state of the charge states X and Y to which the datasets of Figs. 1–5 correspond by observing the Zeeman splitting of the YSR peaks with B. Figure 10a–c shows that the X and Y loops of doublet ground state expand with B without any visible peak splitting. Explained schematically in Fig. 10d, this growth is due to doublet splitting, as the energy of the spin-down doublet state is decreased. However, adjacent charge states of singlet ground state to the left and right of X and Y show peak splitting with B, with peaks splitting parallel-wise to their edges. We also corroborated the ground state of the Y charge state once it was tuned into a singlet ground state. Figure 10e, f shows splitting with magnetic field of the characteristic YSR peaks of singlet ground state20,21. Due to the lower critical field of the shadowed sample, this verification could not be performed for the datasets shown in Fig. 6.
a–c Differential conductance, dI/dVsd, colormap of Fig. 1d depicting YSR subgap peaks vs. plunger gate voltage, VP, and bias voltage, Vsd at increasing magnetic field, B. The scale is saturated to highlight Zeeman splitting. d Sketch of Zeeman splitting and allowed excitations of YSR states. e, f Zeeman splitting of charge state Y when tuned into a singlet ground state.
Data availability
All data needed to evaluate the conclusions in the paper are present in the paper. Raw data used to produce the Figures and Supplementary Figures from the paper can be found at the repository ERDA of the University of Copenhagen at https://doi.org/10.17894/ucph.9e36093c-bf0d-47e7-8062-3919ab7eb1ce.
References
Kiršanskas, G., Goldstein, M., Flensberg, K., Glazman, L. I. & Paaske, J. Yu-Shiba-Rusinov states in phase-biased superconductor–quantum dot–superconductor junctions. Phys. Rev. B 92, 235422 (2015).
Yu, L. Bound state in superconductors with paramagnetic impurities. Acta Phys. Sin. 21, 75–91 (1965).
Shiba, H. Classical spins in superconductors. Prog. Theor. Phys. 40, 435–451 (1968).
Rusinov, A. Theory of gapless superconductivity in alloys containing paramagnetic impurities. Sov. Phys. JETP 29, 1101–1106 (1969).
Satori, K., Shiba, H., Sakai, O. & Shimizu, Y. Numerical renormalization group study of magnetic impurities in superconductors. J. Phys. Soc. Jpn. 61, 3239–3254 (1992).
Deacon, R. S. et al. Tunneling spectroscopy of andreev energy levels in a quantum dot coupled to a superconductor. Phys. Rev. Lett. 104, 076805 (2010).
Lee, E. J. H. et al. Scaling of subgap excitations in a superconductor-semiconductor nanowire quantum dot. Phys. Rev. B 95, 180502 (2017).
van der Wiel, W. G. et al. The Kondo effect in the unitary limit. Science 289, 2105–2108 (2000).
Cronenwett, S. M., Oosterkamp, T. H. & Kouwenhoven, L. P. A tunable Kondo effect in quantum dots. Science 281, 540–544 (1998).
Goldhaber-Gordon, D. et al. From the Kondo regime to the mixed-valence regime in a single-electron transistor. Phys. Rev. Lett. 81, 5225–5228 (1998).
Nygård, J., Cobden, D. H. & Lindelof, P. E. Kondo physics in carbon nanotubes. Nature 408, 342–346 (2000).
Žitko, R. Spectral properties of Shiba subgap states at finite temperatures. Phys. Rev. B 93, 195125 (2016).
Liu, C., Huang, Y., Chen, Y. & Ting, C. S. Temperature-dependent spectral function of a Kondo impurity in an s-wave superconductor. Phys. Rev. B 99, 174502 (2019).
Yazdani, A., Jones, B. A., Lutz, C. P., Crommie, M. F. & Eigler, D. M. Probing the local effects of magnetic impurities on superconductivity. Science 275, 1767–1770 (1997).
Franke, K. J., Schulze, G. & Pascual, J. I. Competition of superconducting phenomena and Kondo screening at the nanoscale. Science 332, 940–944 (2011).
Kezilebieke, S., Dvorak, M., Ojanen, T. & Liljeroth, P. Coupled Yu–Shiba–Rusinov states in molecular. Nano Lett. 18, 2311 (2018).
Malavolti, L. et al. Tunable Spin–Superconductor coupling of spin 1/2 vanadyl phthalocyanine molecules. Nano Lett. 18, 7955–7961 (2018).
Ruby, M., Heinrich, B. W., Peng, Y., von Oppen, F. & Franke, K. J. Wave-function hybridization in Yu-Shiba-Rusinov Dimers. Phys. Rev. Lett. 120, 156803 (2018).
Cornils, L. et al. Spin-resolved spectroscopy of the Yu-Shiba-Rusinov states of individual atoms. Phys. Rev. Lett. 119, 197002 (2017).
Lee, E. J. H. et al. Spin-resolved Andreev levels and parity crossings in hybrid superconductor-semiconductor nanostructures. Nat. Nanotechnol. 9, 79–84 (2013).
Jellinggaard, A., Grove-Rasmussen, K., Madsen, M. H. & Nygård, J. Tuning Yu-Shiba-Rusinov states in a quantum dot. Phys. Rev. B 94, 064520 (2016).
Grove-Rasmussen, K. et al. Yu–Shiba–Rusinov screening of spins in double quantum dots. Nat. Commun. 9, 1–6 (2018).
Gramich, J., Baumgartner, A. & Schönenberger, C. Andreev bound states probed in three-terminal quantum dots. Phys. Rev. B 96, 195418 (2017).
Estrada Saldaña, J. C. et al. Supercurrent in a double quantum dot. Phys. Rev. Lett. 121, 257701 (2018).
Koerting, V., Andersen, B. M., Flensberg, K. & Paaske, J. Nonequilibrium transport via spin-induced subgap states in superconductor/quantum dot/normal metal cotunnel junctions. Phys. Rev. B 82, 245108 (2010).
Martin, I. & Mozyrsky, D. Nonequilibrium theory of tunneling into a localized state in a superconductor. Phys. Rev. B 90, 100508 (2014).
Žitko, R., Lim, J. S., López, R. & Aguado, R. Shiba states and zero-bias anomalies in the hybrid normal-superconductor Anderson model. Phys. Rev. B 91, 045441 (2015).
Ast, C. R. et al. Sensing the quantum limit in scanning tunnelling spectroscopy. Nat. Commun. 7, 1–8 (2016).
Pekola, J. P. et al. Environment-assisted tunneling as an origin of the dynes density of states. Phys. Rev. Lett. 105, 026803 (2010).
De Franceschi, S., Kouwenhoven, L., Schönenberger, C. & Wernsdorfer, W. Hybrid superconductor-quantum dot devices. Nat. Nano. 5, 703 (2010).
Zhang, H. et al. Ballistic superconductivity in semiconductor nanowires. Nat. Commun. 8, 1–7 (2017).
Krogstrup, P. et al. Epitaxy of semiconductor–superconductor nanowires. Nat. Mater. 14, 400–406 (2015).
Gazibegovic, S. et al. Epitaxy of advanced nanowire quantum devices. Nature 548, 434–438 (2017).
Lee, E. J. H. et al. Zero-bias anomaly in a nanowire quantum dot coupled to superconductors. Phys. Rev. Lett. 109, 186802 (2012).
Takei, S., Fregoso, B. M., Hui, H.-Y., Lobos, A. M. & Das Sarma, S. Soft superconducting gap in semiconductor Majorana nanowires. Phys. Rev. Lett. 110, 186803 (2013).
Kumar, A. et al. Temperature dependence of Andreev spectra in a superconducting carbon nanotube quantum dot. Phys. Rev. B 89, 075428 (2014).
Li, S., Kang, N., Caroff, P. & Xu, H. Q. 0−π phase transition in hybrid superconductor-InSb nanowire quantum dot devices. Phys. Rev. B 95, 014515 (2017).
Island, J. O. et al. Proximity-induced shiba states in a molecular junction. Phys. Rev. Lett. 118, 117001 (2017).
Chang, W. et al. Hard gap in epitaxial semiconductor–superconductor nanowires. Nat. Nanotechnol. 10, 232–236 (2015).
Torresani, P. et al. Nongalvanic primary thermometry of a two-dimensional electron gas. Phys. Rev. B 88, 245304 (2013).
Feshchenko, A. V. et al. Tunnel-junction thermometry down to Millikelvin temperatures. Phys. Rev. Appl. 4, 034001 (2015).
Higginbotham, A. P. et al. Parity lifetime of bound states in a proximitized semiconductor nanowire. Nat. Phys. 11, 1017–1021 (2015).
Saira, O.-P., Kemppinen, A., Maisi, V. F. & Pekola, J. P. Vanishing quasiparticle density in a hybrid Al/Cu/Al single-electron transistor. Phys. Rev. B 85, 012504 (2012).
Wilson, C. M., Frunzio, L. & Prober, D. E. Time-resolved measurements of thermodynamic fluctuations of the particle number in a nondegenerate fermi gas. Phys. Rev. Lett. 87, 067004 (2001).
Meir, Y. & Wingreen, N. S. Landauer formula for the current through an interacting electron region. Phys. Rev. Lett. 68, 2512–2515 (1992).
Domański, T., Weymann, I., Barańska, M. & Górski, G. Constructive influence of the induced electron pairing on the Kondo state. Sci. Rep. 6, 1–12 (2016).
van der Wiel, W. G. et al. The Kondo effect in the unitary limit. Science 289, 2105–2108 (2000).
Kretinin, A. V. et al. Spin-\(\frac{1}{2}\) Kondo effect in an InAs nanowire quantum dot: unitary limit, conductance scaling, and Zeeman splitting. Phys. Rev. B 84, 245316 (2011).
Grobis, M., Rau, I. G., Potok, R. M., Shtrikman, H. & Goldhaber-Gordon, D. Universal scaling in nonequilibrium transport through a single channel Kondo dot. Phys. Rev. Lett. 100, 246601 (2008).
Scott, G. D., Natelson, D., Kirchner, S. & Muñoz, E. Transport characterization of Kondo-correlated single-molecule devices. Phys. Rev. B 87, 241104 (2013).
Zacharia, I. G. et al. Temperature dependence of Fano line shapes in a weakly coupled single-electron transistor. Phys. Rev. B 64, 155311 (2001).
Kozorezov, A. G. et al. Inelastic scattering of quasiparticles in a superconductor with magnetic impurities. Phys. Rev. B 78, 174501 (2008).
Hijmering, R. A. et al. Modeling of local trapping states in superconductor tunnel junctions with Kondo impurities. IEEE Trans. Appl. Supercond. 19, 423–427 (2009).
Ruby, M. et al. Tunneling processes into localized subgap states in superconductors. Phys. Rev. Lett. 115, 087001 (2015).
Deng, M. T. et al. Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science 354, 1557–1562 (2016).
Zazunov, A., Egger, R. & Levy Yeyati, A. Low-energy theory of transport in Majorana wire junctions. Phys. Rev. B 94, 014502 (2016).
Setiawan, F., Liu, C.-X., Sau, J. D. & Das Sarma, S. Electron temperature and tunnel coupling dependence of zero-bias and almost-zero-bias conductance peaks in Majorana nanowires. Phys. Rev. B 96, 184520 (2017).
Acknowledgements
The authors are grateful to Dr. Rok Žitko, Dr. Jens Paaske and Gorm Steffensen for fruitful discussions and to Mikelis Marnauza and Dags Olsteins for experimental assistance. The project received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 832645. We acknowledge additional financial support from the Carlsberg Foundation, the Independent Research Fund Denmark, QuantERA ‘SuperTop’ (NN 127900), Villum Foundation project No. 25310, the Danish National Research Foundation and the Sino-Danish Center for Education and Research. P. K. acknowledges support from Microsoft and the ERC starting grant No. 716655 under the Horizon 2020 programme.
Author information
Authors and Affiliations
Contributions
J.C.E.S., K.G.R. and J.N. conceived the experiments, J.C.E.S., A.V. and V.S. conducted the experiments, T.K., P.K. and J.N. developed the nanowires. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Estrada Saldaña, J.C., Vekris, A., Sosnovtseva, V. et al. Temperature induced shifts of Yu–Shiba–Rusinov resonances in nanowire-based hybrid quantum dots. Commun Phys 3, 125 (2020). https://doi.org/10.1038/s42005-020-0392-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-0392-5
This article is cited by
-
Excitations in a superconducting Coulombic energy gap
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.