Abstract
Strong spin–orbit semiconductor nanowires coupled to a superconductor are predicted to host Majorana zero modes. Exchange (braiding) operations of Majorana modes form the logical gates of a topological quantum computer and require a network of nanowires. Here, we utilize an in-plane selective area growth technique for InSb–Al semiconductor–superconductor nanowire networks. Transport channels, free from extended defects, in InSb nanowire networks are realized on insulating, but heavily mismatched InP (111)B substrates by full relaxation of the lattice mismatch at the nanowire/substrate interface and nucleation of a complete network from a single nucleation site by optimizing the surface diffusion length of the adatoms. Essential quantum transport phenomena for topological quantum computing are demonstrated in these structures including phase-coherence lengths exceeding several micrometers with Aharonov–Bohm oscillations up to five harmonics and a hard superconducting gap accompanied by 2e-periodic Coulomb oscillations with an Al-based Cooper pair island integrated in the nanowire network.
Similar content being viewed by others
Introduction
Indium-antimonide (InSb) and Indium-arsenide (InAs) nanowires are promising candidates for realizing Majorana-based topological quantum computers1. InSb, in particular, is interesting for its high electron mobility, strong spin–orbit coupling and large Landé g-factor2,3,4,5. Over the past years, extensive efforts have been made to improve the quality of InSb nanowires, grown by the vapor–liquid–solid (VLS) mechanism6,7. A major achievement is the clean and epitaxial semiconductor–superconductor interface relying on in situ metal evaporation and complex substrate processing8,9. This has been critical for showing high quality Majorana zero-modes, a milestone toward braiding experiments10. To braid these Majorana states, scalable nanowire networks with a high degree of interconnectivity are required11. Recently, out-of-plane growth of InSb nanowire networks has been demonstrated by merging multiple wires during VLS growth. Phase-coherent and ballistic transport have been observed, demonstrating the high quality of these network structures8,12. This technique, however, requires predefined positioning of the nanowires with nanometer accuracy in order to form networks, leading to a drastic decrease in yield with increasing network complexity. Moreover, merging of VLS nanowires inevitably forms a widening of the nanowire diameter at and around the junction with a 75% chance of a defect forming at the junction, which negatively affects the one-dimensionality of the system8.
A more scalable approach, would be to use an in-plane selective area growth (SAG) technique (i.e., parallel to the substrate surface), that relies on a template or mask to selectively grow one semiconductor material on top of another13,14,15,16,17,18,19. This technique has several advantages over out-of-plane growth. First, the flexibility of network designs is significantly enhanced, as the preferred design can be written and etched directly into a mask, enabling complex structures. Second, the growth can be confined within the mask, keeping the entire structure one-dimensional with an easily controllable and constant cross-section size. Finally, the technique excels in scalability, readily allowing for the growth of complex structures suggested for Majorana braiding experiments in a variety of theoretical proposals11,20,21. The large lattice mismatch between InSb and any other III–V semiconductor substrate material22, however, poses an important challenge making it difficult to grow defect-free InSb nanowires on large-bandgap or insulating substrates. Furthermore, the disorder created by the lattice mismatch can be detrimental to the topological protection of Majorana states23. Most of the previous SAG studies have focused on an InAs-based material system for nanowire networks14,15,16,17,19, which has a smaller lattice mismatch with InP or GaAs substrates. InSb nanowires have been grown by SAG using molecular beam epitaxy (MBE)18,24. Here, we demonstrate an in-plane SAG technique for scalable and high-quality InSb nanowire networks, which shows all the relevant quantum transport properties (e.g., long coherence length and excellent-induced superconducting properties) necessary for topological qubits.
Results
Growth of in-plane selective area InSb networks
In this study, we use InP as a substrate because it has a type I band alignment with InSb and becomes semi-insulating at low temperatures. The large bandgap of 1.34 eV compared to 0.17 eV of InSb ensures good confinement25. The lattice mismatch between these materials is 10.4%, making large-scale defect-free growth of InSb a challenge26. It is important to have defect-free single crystalline material to obtain a high carrier mobility by reducing electron scattering27. On a (100) substrate, many stacking faults are expected to form inclined to the substrate (along the {111} planes) to relax the lattice strain13. To avoid the formation of these inclined defects, we use InP (111)B as the growth substrate. We will show that strain from the lattice mismatch is relieved directly at the substrate/nanowire interface. Moreover, atomically flat twin planes can form parallel to the substrate, above which the nanowires grow without extended defects, separating the mismatch-induced disorder from the nanowire top part. On a (111)B substrate, growth nuclei with an odd and even number of horizontal twins will have a 180°-rotated crystallographic orientation, with respect to each other. When these nuclei merge by lateral growth, an inclined defect is formed at the interface; details of the atomic structure of such a defect can be found in Supplementary Fig. 1. These defects may act as scattering sites for electrons and can be found in many reported SAG studies13,17,19,27. Therefore, it is important to enable growth of a complete, in-plane network structure from a single nucleation site, which is difficult to achieve for MBE-grown InSb18,24. For this, a large surface diffusion length of the precursor material is required, as well as a low nucleation probability. Here, we show that metalorganic vapor-phase epitaxy (MOVPE)-grown InSb in-plane selective area networks (InSANe) can indeed generate complicated 1D networks from a single nucleation site.
First, the desired structures are etched into a 20-nm-thick SixNy mask (Supplementary Fig. 2), aligned to four different crystal directions, the [−211], [−101], [−1–12], and [0–11], on an InP (111)B substrate (Fig. 1a). These four orientations are all three-fold symmetric, such that networks can be grown with angles of 30, 60, and 90 degrees between two nanowires (Supplementary Fig. 3). The growth starts by forming a nucleus in one of the lines, which develops into an InSb island over time (Fig. 1b, Supplementary Fig. 4). All nuclei are terminated with a {111}B top facet and {110} side facets (Fig. 1b), regardless of the line orientation, implying that surface growth kinetics and lateral growth rates are identical for all <110> and <112> growth directions. For longer growth times, the growth continues, starting from this single nucleus, in the lateral direction following the mask opening by growing {110} facets, as evidenced by atomic force microscopy and transmission electron microscopy (TEM). When the structure is fully grown in the in-plane direction, the growth continues in the vertical <111>B direction. The height of the InSb network can be precisely tuned by the growth time (Supplementary Fig. 5). Under ideal conditions, a yield of up to 80% can be achieved for structures several microns in length (Supplementary Fig. 6). When the InSb grows higher than the mask, it also starts to expand in the lateral direction, especially at acute corners of the structure (Supplementary Fig. 7), which is not ideal for transport measurements as the one-dimensional confinement is lost. An example of a network is shown in Fig. 1c (and Supplementary Fig. 8), whose structure corresponds to the proposed geometry of a four-topological-qubit device20. The {110} planes of the original growth fronts are visible on the convex corners of this structure (Fig. 1d). These facets do not form on the concave corners due to the connection with another branch of the network (Supplementary Fig. 7). Our platform provides freedom of design and scalability for a plethora of device structures (Supplementary Fig. 9).
a The four growth directions on a (111)B substrate suitable for in-plane nanowire growth. b Time evolution for growth of an in-plane InSb (red) nanowire network on an InP (111)B substrate (gray) with a 20 nm thick SixNy mask (light blue) for selectivity. The growth fronts remain the same during the growth of the network. Schematics of the cross-sections below show the relative height of the InSb compared to the height of the mask. The network grows much faster in the in-plane direction than the out-of-plane direction (Supplementary Fig. 5). c The in-plane InSb nanowires controllably grow in the <112> and the <110> families of crystal directions. Scale bar is 1 µm. d Zoom-in on the corners of the structure in c. Scale bar is 50 nm. The {110} facets that form the growth fronts are still visible at these edges.
In order to minimize the formation of inclined defects, the number of nucleation sites in the mask openings per unit length (n) is investigated as a function of the input V/III ratio of the tri-methyl-indium (TMIn) and tri-methyl-antimony (TMSb) precursors. For this purpose, InSb is grown for a short time (1 min) to observe the early stages of nucleation and understand the nucleation probability as a function of V/III ratio. n is determined for growth in the <112> and <110> oriented trenches for different V/III ratios (Fig. 2). Datapoints are averages of ten 40 nm wide and 50 µm long lines on each sample. The results show a clear decrease of n, and thus an increase of the diffusion length of the adatoms on the InP surface, with increasing V/III ratio. At the highest TMSb pressures, the nucleation of InSb islands is completely inhibited. The inset in Fig. 2a is a logarithmic plot of the same data up to a V/III ratio of 20,000, showing a decrease of n with increasing V/III ratio. We note that there is no parasitic growth on the mask under any of these conditions. The red circle and black square (blue and green triangle) datapoints are all taken with the same TMIn (TMSb) partial pressure and varying TMSb (TMIn) partial pressure, respectively. Figure 2a shows that these datapoints all follow the same trend, indicating that not the total flow but the V/III ratio is important in the studied range. Figure 2b shows a scanning electron microscopy (SEM) image of nuclei grown using a low V/III ratio. The InSb islands are only tens of nanometers long and ~20 nm thick. Figure 2c shows an SEM image of a representative nucleus grown with a very high V/III ratio. Here, the InSb island is much longer (300 nm) and <20 nm high. The time series in Supplementary Fig. 5 shows that the InSb structures nucleate from a single site and over time, during growth under the same growth conditions, no new nucleation sites appear as all grown segments in a single structure are connected at all times. From these results, we conclude that Sb changes the surface energy on the InP substrate and enhances the surface diffusion of the In precursor material28. For the growth of large networks, a high V/III ratio is thus beneficial to have a minimum number of nucleation events. By integrating over the total volume of all nuclei in a 50 µm long line structure, we find that the lateral growth rate is determined by the TMIn flux (with higher flux giving faster growth rates) and the V/III ratio (with higher V/III ratio giving slower growth rates). The largest single crystalline networks we have fabricated with our method have a wire diameter of ~60 nm with lengths of up to 11 µm (Supplementary Fig. 9d).
a The average number of nucleation points n per micrometer trench length as a function of the V/III ratio during the growth for different crystal directions of the mask openings ([110] and [112]). The datapoint averages are gathered by analyzing 500 µm length of mask opening (ten lines, each 50 µm long) and error bars represent the standard deviation. Varying the TMSb (TMIn) flow with constant TMIn (TMSb) flow leads to the same value for n as a function of V/III, showing that the total flow does not influence the nucleation of the InSb on the InP. At a ratio of 40,000, the nucleation of InSb is completely inhibited by Sb adatoms on the InP surface. Inset: logarithmic plot of the data up to a V/III ratio of 20,000. b, c Top-view SEM image showing the different morphologies of, and distance between, InSb islands for low b and high c V/III ratios. Scale bar in b, c is 200 nm.
Physical characterization
The structural quality of the in-plane wires has been investigated by TEM. Focused ion beam (FIB) sample preparation was used to cut out cross-sections parallel and perpendicular to the long axis of in-plane [−211] and [0–11] oriented nanowires. Figure 3a shows a cross-sectional view of a nanowire grown along the [−211] direction. The energy-dispersive X-ray spectroscopy (EDX) elemental mapping (Fig. 3b) shows the InP substrate (green) with the InSb nanowire (red) grown slightly higher than the SixNy mask (blue, top indicated by a white dash on the right). An inverse fast Fourier transform (IFFT) of a zoom-in on the InSb/InP interface (Fig. 3c) shows misfit dislocations (Supplementary Note 1.1) and their confinement to the interface between the two materials. This real space image was constructed by filtering for the (110) periodicity in the fast Fourier transform (FFT) pattern of a high-resolution scanning TEM (STEM) image and subsequently creating an IFFT image. In this image, the ratio of the number of InP/InSb atomic columns is 96/87 = 1.1034. The 10.34% decrease in vertical lattice planes is in good agreement with the reported value of a 10.4% lattice mismatch between InSb and InP4, indicating that the heterostructure is fully relaxed (inelastically) at the interface in the lateral direction. Here, it should be mentioned that when imaging orthogonally to this crystal direction the InP/InSb interface cannot be imaged accurately due to the slight recess of the wire into the substrate. Most likely, along the long axis, misfit dislocation planes will also be present with the dislocation lines located at the interface, as we do not see vertically extending defects orthogonal to the long axis of the wires in TEM studies. An FFT of the InSb, the InSb/InP interface, and the InP regions of the high-resolution STEM image (Fig. 3d in green, blue, and purple box, respectively) show that the InSb and the InP are both single crystalline, while the FFT pattern of the interface region displays a combination of two single crystalline patterns with a different lattice constant, indicating that the materials are fully relaxed. To visualize the presence of horizontal twin planes (Supplementary Note 1.4) in the InSb structures, we investigate a cross-section of a nanowire grown along the <110> direction (Fig. 3e). A zoom-in on the bottom part (Fig. 3f) reveals a set of two twin boundaries a few nanometers above the InP/InSb interface (Fig. 3g). Horizontal twin planes have in total been observed in 12 out of 17 TEM samples (six in perpendicular cuts of <110> grown wires and six in parallel cuts of <112> grown wires, the other five TEM samples did not show horizontal twin planes). The twin planes are always located within a few nanometers above the InSb/InP interface and a single crystalline InSb transport channel always forms above the horizontal twin. Once a twin plane is formed in a nucleus it will be extended into the rest of the network by lateral growth. We note that antiphase boundaries (Supplementary Note 1.2) and inclined twin planes (Supplementary Note 1.3) are absent in these structures. The complete relaxation of lattice strain at the nanowire/substrate interface (bottom part) followed by horizontal twin planes helps to separate the electron wavefunctions in the active region of the device from the interface disorder29. This effect allows us to fabricate in-plane InSb nanowires on InP that have quantum transport properties comparable to free-standing structures, as demonstrated by the high-quality quantum transport in the next section.
a Cross-section transmission electron microscope (TEM) image of an in-plane selective area (InSANe) InSb nanowire grown and imaged along the [−211] direction. Scale bar is 20 nm. b EDX map of a with P (green), Sb (red), and Si (blue) depicted showing the InSb nanowire, the InP substrate, and the SixNy mask. The top of the mask is indicated by a white dash on the right; note that SiOx has been deposited on top of the sample to protect it during focused ion beam sample preparation. Scale bar is 20 nm. c Zoom-in on the InSb/InP interface in a (blue square) focusing on the atomic columns using an inverse fast Fourier transform (FFT) procedure filtered for the (110) periodicity. Scale bar is 1 nm. The vertical lines represent the columns of atoms which, at the interface of InSb/InP, show misfit dislocations, encircled in red. Counting the ratio of InSb columns and InP columns gives a lattice mismatch of 10.34%. d Fast Fourier transform of the InSb nanowire (a, green), the InSb/InP interface (a, blue), and the InP substrate (a, purple), demonstrating that the InSb and InP regions are both single crystalline. The FFT of the InSb/InP interface region shows double spots indicating two different lattice parameters. e Cross-section TEM image of an InSANe InSb nanowire grown and imaged along the [0–11] direction. Scale bar is 20 nm. f Zoom-in of e where a pair of horizontal twin planes can be observed a few nanometers above the InP/InSb interface. Scale bar is 5 nm. g Cut along a <112> direction grown wire, looking in the perpendicular <110> zone axis. A few nanometers above the InP/InSb interface, a horizontal twin plane can be observed along the entire observed length of the wire, indicated here by a red arrow. Scale bar is 20 nm.
Quantum transport
We now turn to the quantum transport properties of our InSb InSANe system to demonstrate its feasibility for topological quantum information processing. The key ingredient in the measurement-based gate operation and topological qubit readout is the phase coherence, which can be revealed by the Aharonov–Bohm (AB) effect11,20. The magneto-conductance in Fig. 4a reveals the AB oscillations in a fabricated InSANe device shown in the inset of Fig. 4b. The oscillation amplitude is ~20% of e2/h at 20 mK, about an order of magnitude larger than for previously reported InSb VLS nanowire network structures8. Therefore, higher harmonics (up to the third) in the FFT are observed (Fig. 4b). This means that the electron’s interference due to phase coherence remains measurable after circulating through the loop 1.5 times, translating to ~9 microns in this device. We note that the precise value of the phase-coherence length is not crucial, and that a large AB amplitude, especially higher orders of AB oscillations, presents the qualitative advancement in this work compared to previous studies. A second device shows an even larger AB amplitude (~60% of e2/h in Fig. 4c) and up to five harmonics in the FFT spectrum (Fig. 4d), with the SEM image of the device shown in the inset of Fig. 4d. The measured AB period matches the loop area in all measured devices, i.e., their periods equal h/ne (for the nth harmonic). This result corroborates that the lattice mismatch-induced disorder at the nanowire–substrate interface has negligible effect on the phase-coherent transport. Finally, we observe a sharp weak anti-localization (WAL) peak in the magneto-conductance of this device around zero-magnetic field (Fig. 4e), indicating the strong spin–orbit nature of the InSb nanowire. Fitting this WAL curve requires a new theoretical model applicable for nanowire networks, which will be developed in future studies.
a Magneto-conductance of device A shows Aharonov–Bohm (AB) oscillations with a period of ~2 mT. b Fast Fourier transform (FFT) spectrum of the AB oscillations from device A, indicating the frequency peaks up to the third-order harmonic. Inset, false-color scanning electron microscopy (SEM) image of the device. An InSb nanowire loop (red) is in contact with normal metal electrodes Cr/Au (yellow) with an out-of-plane magnetic field and a fridge temperature of 20 mK. The device has a global top gate that is not shown in the SEM image. Scale bar is 1 µm. The measured AB period matches the loop area of ~2 µm2. c Magneto-conductance of device B shows a larger AB period and oscillation amplitude (~0.6 e2/h), due to its smaller loop area compared to device A. The arrows indicate oscillations due to higher AB harmonics. d FFT spectrum of device B (SEM in inset with scale bar 1 µm) showing up to five harmonic peaks. e Magneto-conductance of device B (ensemble averaged) shows a sharp WAL peak at B = 0 T.
The next important step is to introduce superconductivity in the InSb InSANe system. In order to form superconducting contacts for the creation of Majorana zero modes, the InSANe InSb samples, after growth, are transferred from an MOVPE to an MBE system. Here, the surface oxides are removed using atomic hydrogen cleaning under (ultra-high vacuum) UHV conditions followed by 7 nm aluminum deposition at a sample temperature of ~120 K, leading to a clean and smooth InSb–Al interface (Supplementary Fig. 10)8.
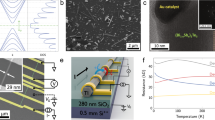
Since in situ shadowing methods to selectively grow superconductors on these InSb in-plane structures are not yet developed, we exploit a reliable selective etching recipe to selectively etch Al on InSb. This novel fabrication recipe enables us to define the positions of tunnel barriers and the Al film by lithography, facilitating flexible device designs. Figure 5a shows such a device where part of the Al is selectively etched away, and a tunnel gate electrode is added to deplete the InSb wire locally. A super-gate is deposited on the superconducting region of the nanowire whose cross-section is shown in Fig. 5b. The differential conductance on this normal–nanowire–superconductor (N-–NW–S) device reflects the quasi-particle density-of-states in the proximitized nanowire segment, i.e., the induced superconducting gap as shown in Fig. 5c with a line-cut in Fig. 5d. The sub-gap conductance reaches zero, indicating a hard gap, a necessary condition for topological protection. Magnetic field dependence of accidental quantum dot levels reveals an effective g-factor of 18.6 (Supplementary Fig. 11), smaller than the bare InSb g-factor of ~50 (Supplementary Fig. 12), but significantly larger than that of Al (|g| = 2), indicating the wavefunction hybridizes between InSb and Al29,30. The measured hard gap with a gap size close to Al bulk, together with the effective g-factor defined by the coupling between Al and InSb, suggest that the electron wavefunction is mainly distributed near the top of the wire (close to Al) where the wire is single crystalline with no noticeable disorder31,32,33. This again supports that disorder at the InP/InSb interface has a negligible effect (see Supplementary Fig. 13, a cross-section TEM of a typical device).
a False-color scanning electron microscopy (SEM) of a typical normal–nanowire–superconductor (N–NW–S) device for illustration purpose, with a schematic of the device cross-section b at the position indicated by the black arrow in a. The InSb nanowire (red) is covered by a 7 nm thick Al layer (green, covered by the etch mask). Part of the Al film on the nanowire is selectively etched before normal metal electrodes deposition (yellow, Cr/Au), and gate-tuneable tunnel barrier. The tunnel- and super-gates are Ti/Au (blue and purple, respectively), deposited on top and separated from the wire by a SixNy dielectric layer as seen in the cross-section schematic on the right. Scale bar is 500 nm. Fridge temperature is 20 mK. c Differential conductance (dI/dV) as a function of bias voltage (V) and super-gate voltage in the tunneling regime, resolving a hard superconducting gap (Δ~250 μeV) with the line-cuts (both linear and logarithmic scale) shown in d at gate voltage indicated by black bar in c. The sub-gap/above-gap conductance suppression reaches two orders of magnitude. e: False-color SEM of the superconducting island device. The Al island on the nanowire is ~1 µm long, with a top plunger gate (purple) to tune the electron density, and two tunnel-gates (blue) to control the tunnel coupling to the two leads. Scale bar is 500 nm. f Differential conductance of the island device as a function of bias and plunger-gate voltage resolving the Coulomb blockade diamonds. The horizontal line-cut at zero bias (black curve) shows 2e-periodic Coulomb oscillations where each peak corresponds to adding/removing two electrons (one Cooper pair), suggesting negligible quasi-particle poisoning. At higher bias voltage where quasi-particle can be excited, the Coulomb oscillations become 1e-periodic. g Magnetic field dependence of the Coulomb oscillations at zero bias voltage with the field direction along the wire. The 2e-peaks split into 1e-peaks at ~0.3 Tesla, indicating a sub-gap state crosses zero energy. h Even (Se red) and odd (So blue) peak spacing extracted from g, with error bars indicated with shaded areas, showing possible Majorana or Andreev oscillations.
Finally, we explore the transport of a hybrid InSb/Al island device (Fig. 5e), with a finite charging energy. The charging energy of the hybrid island can mediate the coupling between the two Majorana states for qubit operations and readout11,20,34. If the charging energy is less than the superconducting gap, the system ground state energetically ‘favors’ even number of electrons, i.e., all electrons on the island form Cooper pairs in the superconducting condensate35. In transport, each Coulomb blockade diamond then corresponds to two electrons (one Cooper pair), as shown in Fig. 5f, as well as in Supplementary Fig. 14. The 2e-periodic Coulomb oscillation at zero bias (black curve) indicates negligible quasi-particle poisoning. A higher bias voltage can excite quasi-particles, resulting in the regular 1e-periodic Coulomb oscillations (red curve). Applying a magnetic field along the nanowire splits the 2e-peaks into 1e-peaks (Fig. 5g), with oscillating even/odd peak spacing (Fig. 5h). This 2e–1e transition might be interpreted as the appearance of two Majorana states, which allows the coherent ‘teleportation’ of a single electron35. The oscillating peak spacing could be attributed to overlapping Majorana wavefunctions36. We note that a trivial explanation for the 2e–1e transition based on Andreev bound states cannot be ruled out at this point37,38,39.
Discussion
We have studied the growth dynamics of in-plane InSb nanowires on InP (111)B substrates. Despite the large mismatch between the wires and the substrate, single crystalline transport channels, free from extended defects, are formed due to immediate strain relaxation at the nanowire–substrate interface. Correspondingly, these in-plane InSb-based devices show high-quality quantum transport, with long phase-coherence length, a hard superconducting gap, 2e-Coulomb blockade peaks, and possible Majorana/Andreev signatures. The next step is to establish Majorana zero modes in these structures by performing key experiments like correlation and Majorana braiding40.
Data availability
Materials and data that support the findings of this research are available within the paper. The raw data have been deposited at https://zenodo.org/record/4589484#.YEoEOy1Y7Sd.
Change history
20 March 2021
A Correction to this paper has been published: https://doi.org/10.1038/s42005-021-00578-4.
24 March 2021
A Correction to this paper has been published: https://doi.org/10.1038/s42005-021-00578-4
References
Lutchyn, R. M. et al. Majorana zero modes in superconductor–semiconductor heterostructures. Nat. Rev. Mater. 3, 52–68 (2018).
Madelung, O. in Semiconductors Group IV Elements and III-V Compounds (ed Poerschke, R.) 124 (Springer-Verlag, Berlin, 1991).
van Weperen, I. et al. Spin-orbit interaction in InSb nanowires. Phys. Rev. B 91, 201413 (2015).
Vurgaftman, I., Meyer, J. R. & Ram-Mohan, L. R. Band parameters for III–V compound semiconductors and their alloys. J. Appl. Phys. 89, 5815–5875 (2001).
Bommer, J. D. S. et al. Spin-orbit protection of induced superconductivity in Majorana nanowires. Phys. Rev. Lett. 122, 187702 (2019).
Plissard, S. R. et al. From InSb nanowires to nanocubes: looking for the sweet spot. Nano Lett. 12, 1794–1798 (2012).
Car, D., Wang, J., Verheijen, M. A., Bakkers, E. P. A. M. & Plissard, S. R. Rationally designed single-crystalline nanowire networks. Adv. Mater. 26, 4875–4879 (2014).
Gazibegovic, S. et al. Epitaxy of advanced nanowire quantum devices. Nature 548, 434–438 (2017).
Chang, W. et al. Hard gap in epitaxial semiconductor–superconductor nanowires. Nat. Nanotechnol. 10, 232 (2015).
Zhang, H. et al. Quantized Majorana conductance. Nature 556, 74 (2018).
Karzig, T. et al. Scalable designs for quasiparticle-poisoning-protected topological quantum computation with Majorana zero modes. Phys. Rev. B 95, 235305 (2017).
Fadaly, E. M. T. et al. Observation of conductance quantization in InSb nanowire networks. Nano Lett. 17, 6511–6515 (2017).
Schmid, H. et al. Template-assisted selective epitaxy of III–V nanoscale devices for co-planar heterogeneous integration with Si. 106, 233101 (2015).
Aseev, P. et al. Selectivity map for molecular beam epitaxy of advanced III-V quantum nanowire networks. Nano Lett. https://doi.org/10.1021/acs.nanolett.8b03733 (2018).
Krizek, F. et al. Field effect enhancement in buffered quantum nanowire networks. Phys. Rev. Mater. 2, 093401 (2018).
Fahed, M., Desplanque, L., Troadec, D., Patriarche, G. & Wallart, X. Selective area heteroepitaxy of GaSb on GaAs (001) for in-plane InAs nanowire achievement. Nanotechnology 27, 505301 (2016).
Friedl, M. et al. Template-assisted scalable nanowire networks. Nano Lett. 18, 2666–2671 (2018).
Desplanque, L., Bucamp, A., Troadec, D., Patriarche, G. & Wallart, X. Selective area molecular beam epitaxy of InSb nanostructures on mismatched substrates. J. Cryst. Growth 512, 6–10 (2019).
Lee, J. S. et al. Selective-area chemical beam epitaxy of in-plane InAs one-dimensional channels grown on InP(001), InP(111)B, and InP(011) surfaces. Phys. Rev. Mater. 3, 084606 (2019).
Plugge, S., Rasmussen, A., Egger, R. & Flensberg, K. Majorana box qubits. New J. Phys. 19, 012001 (2017).
Aasen, D. et al. Milestones toward majorana-based quantum computing. Phys. Rev. X 6, 031016 (2016).
Straumanis, M. E. & Kim, C. D. Lattice parameters, thermal expansion coefficients, phase width, and perfection of the structure of GaSb and InSb. 36, 3822–3825 (1965).
Gül, Ö. et al. Ballistic Majorana nanowire devices. Nat. Nanotechnol. 13, 192–197 (2018).
Aseev, P. et al. Ballistic InSb nanowires and networks via metal-sown selective area growth. Nano Lett. 19, 9102–9111 (2019).
Mattias Borg, B. & Wernersson, L.-E. Synthesis and properties of antimonide nanowires. Nanotechnology 24, 202001 (2013).
Oh, J. E., Bhattacharya, P. K., Chen, Y. C. & Tsukamoto, S. Molecular‐beam epitaxial growth of high‐quality InSb on InP and GaAs substrates. 66, 3618–3621 (1989).
Schroer, M. D. & Petta, J. R. Correlating the nanostructure and electronic properties of InAs nanowires. Nano Lett. 10, 1618–1622 (2010).
Badawy, G. et al. High mobility stemless InSb nanowires. Nano Lett. 19, 3575–3582 (2019).
de Moor, M. W. A. et al. Electric field tunable superconductor-semiconductor coupling in Majorana nanowires. N. J. Phys. 20, 103049 (2018).
Vaitiekėnas, S., Deng, M. T., Nygård, J., Krogstrup, P. & Marcus, C. M. Effective g factor of subgap states in hybrid nanowires. Phys. Rev. Lett. 121, 037703 (2018).
Mikkelsen, A. E. G., Kotetes, P., Krogstrup, P. & Flensberg, K. Hybridization at superconductor-semiconductor interfaces. Phys. Rev. X 8, 031040 (2018).
Antipov, A. E. et al. Effects of gate-induced electric fields on semiconductor majorana nanowires. Phys. Rev. X 8, 031041 (2018).
Woods, B. D., Stanescu, T. D. & Das Sarma, S. Effective theory approach to the Schrödinger-Poisson problem in semiconductor Majorana devices. Phys. Rev. B 98, 035428 (2018).
Vijay, S. & Fu, L. Teleportation-based quantum information processing with Majorana zero modes. Phys. Rev. B 94, 235446 (2016).
Albrecht, S. M. et al. Exponential protection of zero modes in Majorana islands. Nature 531, 206 (2016).
Das Sarma, S., Sau, J. D. & Stanescu, T. D. Splitting of the zero-bias conductance peak as smoking gun evidence for the existence of the Majorana mode in a superconductor-semiconductor nanowire. Phys. Rev. B 86, 220506 (2012).
Chiu, C.-K., Sau, J. D. & Das Sarma, S. Conductance of a superconducting Coulomb-blockaded Majorana nanowire. Phys. Rev. B 96, 054504 (2017).
Shen, J. et al. Parity transitions in the superconducting ground state of hybrid InSb–Al Coulomb islands. Nat. Commun. 9, 4801 (2018).
Cao, Z. et al. Decays of Majorana or Andreev oscillations induced by steplike spin-orbit coupling. Phys. Rev. Lett. 122, 147701 (2019).
Zhang, H., Liu, D. E., Wimmer, M. & Kouwenhoven, L. P. Next steps of quantum transport in Majorana nanowire devices. Nat. Commun. 10, 5128 (2019).
Acknowledgements
This work has been supported by the European Research Council (ERC HELENA 617256 and Synergy), the Dutch Organization for Scientific Research (NWO), and Microsoft Corporation Station-Q. We acknowledge Solliance, a solar energy R&D initiative of ECN, TNO, Holst, TU/e, imec and Forschungszentrum Jülich, and the Dutch province of Noord-Brabant for funding the TEM facility. The work at University of California, Santa Barbara was supported in part by Microsoft Research. We also acknowledge the Department of Energy (DE-SC0019274) and the use of facilities within the National Science Foundation Materials Research and Science and Engineering Center (DMR 11–21053) at the University of California, Santa Barbara. We thank Ghada Badawy and Ksenia Korzun for their careful reading of the manuscript.
Author information
Authors and Affiliations
Contributions
R.L.M.O.H.V., S.M.E.P., J.J., C.T., and E.P.A.M.B. carried out the substrate processing and the InSb synthesis. D.X., V.S., Q.W., M.W.A.d.M., B.H., K.V., J.D.S.B., L.P.K., and H.Z. fabricated the devices and performed the transport measurements. J.S.L., M.P., and C.J.P. have deposited the superconductor. S.K. and J.J. have performed the FIB cuts for the TEM lamella and M.A.V. is responsible for the TEM analysis. A.S., A.M., and L.M. performed the theoretical modeling of defect formations. R.L.M.O.H.V., D.X., M.A.V., H.Z., and E.P.A.M.B. have authored the paper, with contributions from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Op het Veld, R.L.M., Xu, D., Schaller, V. et al. In-plane selective area InSb–Al nanowire quantum networks. Commun Phys 3, 59 (2020). https://doi.org/10.1038/s42005-020-0324-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-0324-4
This article is cited by
-
Correlation between two distant quasiparticles in separate superconducting islands mediated by a single spin
Nature Communications (2024)
-
Cryogenic multiplexing using selective area grown nanowires
Nature Communications (2023)
-
Recent progress on Majorana in semiconductor-superconductor heterostructures—engineering and detection
Science China Physics, Mechanics & Astronomy (2023)
-
Majorana-like Coulomb spectroscopy in the absence of zero-bias peaks
Nature (2022)
-
Doping Dependent Magnetic Behavior in MBE Grown GaAs1-xSbx Nanowires
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.