Abstract
Experiments with the crossover superconductors between standard types I and II revealed exotic magnetic flux patterns where Meissner domains coexist with islands of the vortex lattice as well as with vortex clusters and chains. Until now a comprehensive theory for such configurations has not been presented. We solve this old-standing fundamental problem by developing an approach which combines the perturbation expansion of the microscopic theory with statistical simulations and which requires no prior assumption on the vortex distribution. Our study offers the most complete picture of the interchange of the superconductivity types available so far. The mixed state in this regime reveals a rich manifold of exotic configurations, which reproduce available experimental results. Our work introduces a pattern formation mechanism that originates from the self-duality of the theory that is universal and not sensitive to the microscopic details.
Similar content being viewed by others
Introduction
Magnetic response of a superconductor is one of its most important characteristics crucial for many applications. By their magnetic properties superconducting materials are divided into two types, I and II, depending on whether the magnetic field is fully expelled (Meissner state) or penetrates the superconducting condensate forming the mixed Shubnikov state. The magnetic flux enters a superconductor in the form of Abrikosov vortices, which carry a single flux quantum each and are mutually repulsive, tending to arrange themselves in a periodic lattice1. This dual classification is related with the ratio κ = λL/ξ of the magnetic London penetration depth λL and condensate coherence length ξ- type I takes place at κ ≲ 1 and type II does at κ ≳ 1. The Ginzburg-Landau (GL) theory for superconductors offers an exact critical value \({\kappa }_{0}=1/\sqrt{2}\) at which the types interchange.
Detailed investigations of the magnetic response revealed a class of materials with κ ~ 1 whose magnetic properties belong to neither of these two common types2,3,4,5,6,7,8,9. Experiments demonstrated that such crossover or inter-type (IT) materials develop the so-called intermediate mixed state (IMS), where the magnetic field penetrates a superconductor but forms a rich manifold of exotic spatial configurations made of Meissner domains coexisting with islands of the vortex lattice, vortex clusters, chains, etc. Observed configurations were sensitive to variations in the temperature and magnetic field but generally not to material characteristics pointing to the universality of the underlying physics.
Earlier theory studies linked unconventional flux patterns of the IMS to non-monotonic interactions between vortices, attractive at long and repulsive at short distances10,11,12,13,14,15,16,17, which lead to an instability of Abrikosov lattices towards their fragmentation into clusters16,18,19,20. In order to distinguish the IT regime from the standard type II superconductivity the name type II/1 was proposed. However, it has been recently demonstrated21,22,23 that the physics of the IT regime cannot be fully explained by the pairwise non-monotonic vortex interactions. The physical grounds of this regime are in the proximity to the critical Bogomolnyi (B) point (κ0, Tc)24, where Tc is the superconducting transition temperature. This point, which separates type I and type II superconductivity at T → Tc, is specified by the self-dual and infinitely degenerate condensate state, which hosts all possible, including exotic, flux-condensate configurations. At T < Tc the degeneracy is removed and those exotic configurations shape the properties of the IMS in a finite IT domain in the κ–T phase diagram. This mechanism has a variety of physical consequences, including strong many-vortex interactions23, totally missing in the type-II/1 concept.
Although the IT regime is long known and appears a fundamental property, which essentially amends the existing dual classification of superconductivity types, comprehensive theoretical studies of its IMS flux configurations are still absent. The main reason for this lack of progress is that the calculations must be done beyond the GL theory since the latter fails for this regime in bulk superconductors. Numerical solution of the microscopic equations is very demanding because the IMS is inhomogeneous and highly irregular rendering conventional a priori assumptions on the vortex distribution, e.g., the Abrikosov lattice, useless. Owing to these difficulties theory efforts focused on studying properties of few-vortex systems, such as the pair vortex interaction12,13,15,16,17 or on the analysis of stability of the periodic Abrikosov lattice16,18,19,20 in order to determine boundaries of the IT domain.
This work presents a comprehensive theoretical study that classifies flux-condensate patterns in the IMS and their interchange across the IT domain. This is achieved by advancing the approach that combines the perturbation expansion for the microscopic equations in the B-point vicinity with statistical simulations. The method requires no prior assumption on vortex distributions and can be regarded as first principle calculations for the vortex matter.For the calculations we use the standard Bardeen-Cooper-Schrieffer (BCS) model with the s-wave paring on a spherical Fermi surface and without impurities. However, universality of the physical mechanism behind the IT regime ensures the qualitative results do not depend on the microscopic details, in particular, on the symmetry of the Cooper pairing and on the band structure.
Results
Universality of vortex configurations
In the limit T → Tc the BCS theory reduces to the GL equations which have the critical point κ = κ0 separating the superconductivity types I and II. This defines the critical B point (κ0, Tc) for the BCS theory on the κ–T plane. A peculiar feature of this point is the degeneracy of its condensate state—the Gibbs free energy of the condensate, calculated within the GL theory at κ0, is the same for all configurations of the mixed state. However, when T < Tc the GL and BCS deviate one from another, the degeneracy is removed and the Gibbs free energy becomes configuration dependent. Nevertheless, the proximity to the B point still affects the condensate state in a finite domain in the κ–T plane—the IT domain21. The physics of this domain can be captured by employing the perturbation expansion for the microscopic superconductivity theory with the small parameters being the proximity to the critical temperature τ = 1 − T∕Tc12,21,25,26,27 and the deviation from the critical GL parameter δκ = κ − κ016,17,21. The expansion yields a remarkably simple expression for the leading contributions to the Gibbs free energy21
where GM is the energy of the uniform Meissner state, Hc and λL are the thermodynamic critical field and the magnetic penetration depth of the GL theory, L is the sample size in the z direction. Constants C1 and C2 are combinations of the coefficients of the perturbation expansion for the Gibbs free energy, and \({\mathcal{I}}\) and \({\mathcal{J}}\) are calculated from the solution of the scaled dimensionless GL theory (see Methods section)
The Gibbs free energy difference in Eq. (1) depends on the microscopic parameters of the model via the prefactor Λ and two constants C1 and C2. For the chosen single-band model (no impurities) with a spherical Fermi surface one obtains C1 ≈ −0.41 and C2 ≈ 0.68.
It is important that the structure of the IT domain in the κ-T plane is, in fact, qualitatively independent of the microscopic structure of the bands or of the details of the pairing in general. The prefactor Λ in Eq. (1) merely determines the energy scale. At the same time the integral \({\mathcal{I}}\) and \({\mathcal{J}}\) are obtained from the dimensionless GL Eq. (4), which are model independent. To trace the role of the remaining constants C1 and C2, we consider the boundaries of the IT domain, \({\kappa }_{\max }\) and \({\kappa }_{\min }\), determined, respectively, by the appearance of the long-range vortex attraction and by the possibility of the flux to create the mixed state21. This yields the IT interval as δκ∕(τκ0) ∈ [C1, 2C2 + C1]. It is non-zero if C2 > 0 and also the internal structure of the IT domain is preserved in this case.
One sees that the appearance of the finite IT domain, facilitated by removing the B-point degeneracy, depends only on a sign of a single parameter C2. However, details of the removal microscopic mechanism, which are formally encoded in the perturbative corrections to the GL theory, are not important if qualitative characteristics of the IT domain are of interest—the latter depend only on the GL solution. In this way the theory of the IT domain in this work has the same generality as the GL theory itself.
IMS vortex patterns
We now investigate IMS vortex configurations in the IT interval \({\kappa }_{\min } \, < \, \kappa \, < \, {\kappa }_{\max }\). This interval depends on temperature T as well as on the constants Λ, C1 and C2 in Eq. (1). However, as discussed above, the structure of the IT domain in the vicinity of the B point is universal, while the constants affect only the axis scaling on the κ-T phase diagram of the IMS states. Thus we are free to take the results obtained for the spherical Fermi surface model. For the same reason we can take arbitrary τ, here we set it τ = 1–the IT interval is then δκ∕κ0 ∈ [−0.41, 0.95]. The remaining free parameter of the system is the magnetic field which determines the number of vortices.
Most energetically favorable vortex configurations are found by using the following three steps (details of the calculations are given in Methods section): (1) we obtain the N-vortex solution of the GL theory with the vortex positions (xi, yi) (i = 1…N), (2) the solution is substituted into Eq. (2) and then into Eq. (1) to calculate the energy of the vortex state, (3) finally, the dependence of the energy obtained in (1) and (2) is used in the statistical Monte-Carlo (Metropolis) minimization algorithm28 in order to find the vortex configuration with the minimal energy. This combination of the perturbation expansion around the B point, the GL theory and the Metropolis algorithm offers a practical tool to study vortex configurations in the IT domain and is expected to yield quantitatively correct results down to relatively low temperatures21. It does not require any prior knowledge of the vortex distribution and may thus be regarded as the first principle calculations for the vortex matter.
The results are summarized in Fig. 1, which shows colour density plots for the spatial profiles of the condensate density ∣Ψ(x, y)∣2 of the stable vortex configurations. Columns in the figure are obtained for δκ in the interval [−0.3, 0.3]—the values are shown on the horizontal δκ axis. The rows correspond to different values of the averaged field B, shown on the vertical axis in the units of the critical field Hc. Selected values of δκ are chosen to represent all types of IMS vortex configurations and their evolution across the IT domain. The most left column is calculated for δκ = −0.3, which corresponds to a type I superconductor.
Columns show the density profiles calculated for different values of the Ginzburg-Landau (GL) parameter difference δκ = κ − κ0 chosen in the interval [−0.3, 0.3], rows demonstrate the density profiles for different average values of the magnetic field B selected in the interval [0.05, 1.0] (in the units of the critical field Hc).
Above the upper boundary of the IT domain, \(\delta \kappa \, > \, \delta {\kappa }_{\max }\), the superconductivity is of type II allowing only for Abrikosov repulsive single-quantum vortices, which form a standard triangular Abrikosov lattice. Below this boundary, \(\delta \kappa \, < \, \delta {\kappa }_{\max }\), the vortex–vortex interactions become attractive at large and (initially) repulsive at short distances. The interaction potential has thus a minimum at some distance r023 so that the lattice becomes unstable towards formation of vortex clusters with the average inter-vortex distance close to r0. However, the clustering takes place only when the vortex density in the system is less then \({r}_{0}^{-2}\), so that the Abrikosov lattice remains stable at \(B \, \gtrsim \, {\Phi }_{0}/{r}_{0}^{2}\) (Φ0 denotes the magnetic flux quantum). Notice, that r0 grows when δκ approaches the upper boundary, so that r0 → ∞ in the limit \(\delta \kappa \to \delta {\kappa }_{\max }\). Consequently, the clustering is observed at progressively smaller fields for larger δκ (which requires larger samples).
This is seen in Fig. 1 by comparing results for different values of δκ. For example, for δκ = 0.3κ0 the clustering is visible only at B = 0.05Hc whereas for δκ = 0.13κ0 it is observed (vortex islands embedded in the Meissner phase) already at B = 0.1Hc. At δκ = 0.1κ0 the clustering persists up to B = 0.2Hc. For yet smaller δκ one can trace a complete evolution of vortex patterns with increasing field - from few-vortex clusters embedded in the Meissner state to small Meissner islands surrounded by vortex matter. Between these two limiting cases, there is also a regime where Meissner islands are separated by vortex chains. In Fig. 1 the vortex chains can be observed at δκ = 0 and δκ = 0.03. At sufficiently large fields Meissner islands eventually disappear and the Abrikosov lattice occupies all available space. These transformations of the vortex matter agree with available experimental results on IMS vortex patterns2,3,4,5,6,7,8,9.
Results at large fields in Fig. 1 show that when B approaches the critical value Hc, the vortex lattice distorts and then melts, becoming a liquid. The distortion starts at B ≃ 0.7Hc and the liquid state appears for B ≳ 0.8Hc. When the field further increases up to B ≃ 0.9Hc, normal phase islands are formed inside the IMS. At the critical field B = Hc the superconductivity disappears, however, Fig. 1 still demonstrates isolated domains of the superconducting phase. Melting of the Abrikosov lattice and formation of droplets of the normal phase at B ~ Hc were investigated earlier for type II superconductors and can be explained by many physical reasons, including temperature fluctuations29,30. Here the distortion of the lattice is induced by a near degeneracy of the vortex matter close to the energy minimum. The degeneracy takes place when the system reaches the critical field and it is also strongly enhanced by the proximity to the degenerate B point. As a consequence, the algorithm yields a vortex state in a local energy minimum, which needs very large convergence time to achieve. Obtained configurations can thus be seen as instantaneous snapshots of a typical fluctuation configuration.
Figure 1 reveals another important feature—even at lower fields the vortex matter changes from a solid to a liquid phase at δκ ≈ −0.05. For δκ ≳ −0.05 the vortex matter appears in the form of clusters and islands with a hexagonal Abrikosov lattice inside them. The average distance between vortices in these clusters is close to r0, which reduces when δκ decreases23. At δκ ≲ −0.05 the pairwise vortex–vortex interaction becomes fully attractive with r0 = 0 and the vortex distribution inside clusters and islands changes qualitatively—the lattice is replaced by a vortex liquid. This crossover is also accompanied by the appearance of notable differences of vortex structure inside the clusters and at their boundaries. This fact manifests itself in the presence of the surface tension (surface layer) in the liquid phase. This tension grows when δκ decreases and, as a result, vortex clusters approach a circular shape typical for liquid droplets. This transformation is seen in Fig. 1 at δκ = −0.15κ0 and −0.2κ0. The vortex packing in the liquid phase increases at smaller δκ, which is manifested, e.g., in that droplets of the Meissner phase survive up to larger fields when δκ decreases: at δκ = −0.2κ0 droplets of the Meissner phase are observed up to B = 0.7Hc, at δκ = −0.25κ one sees them up to B = 0.8Hc, and at δκ = −0.28κ0 they persist even up to B = 0.9Hc.
The appearance of the liquefied vortex matter is a clear manifestation of the inadequacy of the type II/1 concept for the IT regime and its central assumption that the non-monotonic pairwise vortex interaction is the main underlying mechanism for the formation of the IMS. Indeed, the results demonstrate that the vortex matter liquefies when the pairwise interaction becomes fully attractive and thus, according to the type II/1 concept, vortex clusters should always be unstable towards merging into giant multi-quantum vortices. The fact that large vortex clusters-droplets are still stable is a confirmation for the earlier conclusion23 that the vortex matter is shaped by many-vortex interactions which remain repulsive at short distances for larger clusters. In Fig. 1 the dominant role of the many-vortex interactions is illustrated by the transformation of giant vortices into vortex clusters taking place at small δκ. Giant multi-quantum vortices (lamellas) appear as a precursor of the type I regime for δκ = −0.2κ0, −0.25κ0, and −0.28κ0. One sees that multi-quantum vortices are formed at smaller fields and their size (flux) increases with the field. However, when giant vortices reach a threshold size, they are turned into liquid droplets of single-quantum vortices. When the system approaches type I the threshold size increases such that vortex clusters disappear altogether at the lower boundary of the IT domain and the standard intermediate state of type I replaces the IMS.
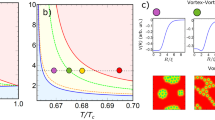
The results can also be represented by the phase diagram on the κ–T plane. Such a diagram cannot show all configurations observed at different magnetic fields and we consider only low field patterns [Fig. 2]. In this diagram the IT domain originates in the B point (red) and is limited by the boundaries \({\kappa }_{\min }\) and \({\kappa }_{\max }\). It contains the upper part (κ ≳ κ0), with the “solid” vortex matter, and the lower part (κ ≲ κ0), where the vortex matter liquefies, with the division line κ ≈ κ0 marking the onset of the stability of single vortex states21,22. Until now experimental studies dealt with the materials in the upper part of the diagram, such as Nb9 and ZrB128, and our results fully explain observed solid vortex clusters. However, the vortex liquid and giant vortices in the lower part of the diagram remain to be studied experimentally.
on the κ-T plane, where κ is the Ginzburg-Landau (GL) parameter and T is the temperature (in the units of the critical temperature Tc); the representative vortex configurations are shown in the insets. The lower and upper boundaries of the intertype domain, \({\kappa }_{\min }\) and \({\kappa }_{\max }\), are calculated for a conventional s-wave superconductor with a single spherical Fermi surface.
Discussion
This work presents a first universal theory of IMS vortex configurations in superconductors between types I and II. Three fundamental ingredients of the theory are the perturbative correction to the GL theory, the Bogomolnyi equations, and the Metropolis algorithm. The self-duality of the Bogomolnyi equations makes it possible to represent the free energy as a function of the vortex positions and to employ the Metropolis algorithm to find stable vortex configurations.
The calculations reveal a rich variety of qualitatively different vortex patterns: vortex lattices, clusters of solid and liquid vortex matter embedded in the Meissner state, vortex chains separating condensate islands, and giant vortices as a precursor of the type I regime. Results of the work offer a deeper understanding of fundamentals of the superconductivity phenomenon by revealing details of the interchange between conventional superconductivity types via the IT regime. This regime is independent of peculiarities of the microscopic model and can be regarded as a separate generic IT superconductivity type, that can be observed in many superconducting materials.
The work demonstrates typical IMS vortex patterns, however, without detailed analysis of their quantitative characteristics, such as vortex density correlation functions and related form factors. Such a study requires a more specialized analysis beyond the scope of this work. Similarly, we did not touch a question on whether the interchange of different vortex configurations are accompanied by phase transitions. Also, although the applied formalism is known to yield quantitatively correct results down to relatively low temperatures T ~ 0.5Tc21, it is not yet clear whether the obtained IMS patterns change in the limit of T → 0. The results do not depend on details of the superconductivity model and thus apply to a wide class of materials. In particular, a similar approach applies for the case of many contributing carrier bands and consequently such multiband superconductors should have a similar IT domain with the IMS configurations, at least near the critical temperature. Whether this applies for the entire temperature range and, in particular, at temperatures below the hidden criticality31, remains to be seen. We believe that further more detailed theoretical studies in this directions will soon shed light of these fundamental problems.
Finally, we note that our work introduces a new mechanism for the pattern formation, that originates from the self-duality of the theory and complements existing pattern formation models32,33,34. We expect that this mechanism can apply to other systems, in condensed matter and beyond, where vortex patterns appear as the result of breaking the self-duality. Notice that there are many examples of self-dual gauge theories35, including, in particular, those used to describe planar condensed matter systems36.
Methods
Self-dual GL theory
At κ = κ0 the GL theory becomes self-dual, which implies that the condensate function Ψ and the field B (after an appropriate scaling21) are related algebraically as
At this point the GL theory simplifies and, by representing the condensate function as Ψ = e−φΦ with φ being the magnetic scalar potential, can be written in the form of the Bogomolnyi equations
also known as Sarma equations, which are to be solved in order to obtain \({\mathcal{I}}\) and \({\mathcal{J}}\) in Eq. (2).
N-vortex solutions
To find the solution to the GL equations in the form of Eq. (4) we first note that any analytical function Φ(ζ) of the complex argument \(\zeta =x+{\mathbb{i}}y\) satisfies the second of Eq. (4). To obtain the N-vortex solution one takes \(\Phi (\zeta )=\prod _{i=1}^{N}(\zeta -{\zeta }_{i})\) that has N zeros at the vortex positions \({\zeta }_{i}={x}_{i}+{\mathbb{i}}{y}_{i}\). We note in passing that without the self-duality condition (3), Eq. (4) describe the Landau ground state of a charged particle in the magnetic field B (obtained from φ)37. When vortices are arranged in a periodic lattice, this ansatz yields the famous Abrikosov ansatz for the vortex lattice1. In the actual numerical calculations it is more convenient to represent the N-vortex condensate function as
where Ψ(1)(ζ) is the solution of Eq. (4) for an isolated single-quantum vortex located at the coordinates origin while δφ satisfies the equation
which must be solved with the asymptotic boundary condition δφ → 0 far from the vortex cores. The calculations are done on a square d × d with the periodic boundary conditions, where d = L/λL is chosen sufficiently large so that vortex configurations are not affected by the boundaries. The obtained Ψ is then used to calculate \({\mathcal{I}}\) and \({\mathcal{J}}\) and then \({\frak{G}}\).
Metropolis algorithm
The energy of the vortex state is calculated using Eq. (1) where the N-vortex solution, obtained above, is substituted. This gives the Gibbs energy difference \({\frak{G}}(\{{\zeta }_{j}\})\) as a function of the vortex positions. When the total flux is fixed this quantity can be used as the free energy of the vortex system.
The energy \({\frak{G}}(\{{\zeta }_{j}\})\) is minimized by the statistical Metropolis algorithm28. The minimum of the functional is found by varying sequentially all vortex positions \({\zeta }_{i}^{{\rm{new}}}={\zeta }_{i}^{{\rm{old}}}+\delta {\zeta }_{i}\) and then calculating the corresponding energy change \(\Delta {\frak{G}}={{\frak{G}}}_{{\rm{old}}}-{{\frak{G}}}_{{\rm{new}}}\). When \(\Delta {\frak{G}} \, < \, 0\), the move is accepted; when \(\Delta {\frak{G}} \, > \, 0\), one compares a random number p ∈ [0, 1] with the exponential weight \(w=\exp (-\Delta {\frak{G}}/{T}^{* })\)—the move is accepted for p < w and rejected if p > w. The effective “temperature” T * as well as the variations δζi are chosen to ensure better convergence of the algorithm. Notice that the prefactor Λ in the expression for \({\frak{G}}\) in Eq. (1) is absorbed in T * and can be omitted.
Data availability
The data and the code that support the findings of this study are available from the corresponding author upon a reasonable request.
References
Abrikosov, A. A. On the magnetic properties of superconductors of the second Group. Sov. Phys. JETP 5, 1174–1182 (1957).
Brandt, E. H. & Das, M. P. Attractive vortex interaction and the intermediate-mixed state of superconductors. J. Supercond. Nov. Magn. 24, 57–67 (2011).
Laver, M. et al. Structure and degeneracy of vortex lattice domains in pure superconducting niobium: a small-angle neutron scattering study. Phys. Rev. B 79, 014518 (2009).
Pautrat, A. & Brûlet, A. Temperature dependence of clusters with attracting vortices in superconducting niobium studied by neutron scattering. J. Phys.: Condens. Matter 26, 232201 (2014).
Ge, J.-Y. et al. Direct visualization of vortex pattern transition in ZrB12 with Ginzburg-Landau parameter close to the dual point. Phys. Rev. B 90, 184511 (2014).
Reimann, T. et al. Visualizing the morphology of vortex lattice domains in a bulk type-II superconductor. Nature Commun. 6, 8813 (2015).
Reimann, T. et al. Domain formation in the type-II/1 superconductor niobium: interplay of pinning, geometry, and attractive vortex-vortex interaction. Phys. Rev. B 96, 144506 (2017).
Ge, J.-Y. et al. Paramagnetic Meissner effect in ZrB12 single crystal with non-monotonic vortex-vortex interactions. New J. Phys. 19, 093020 (2017).
Backs, A. et al. Universal behavior of the intermediate mixed state domain formation in superconducting niobium. Phys. Rev. B 100, 064503 (2019).
Krägeloh, U. Flux line lattices in the intermediate state of superconductors with Ginzburg Landau parameters near \(1/\sqrt{2}\). Phys. Lett. A 28, 657–658 (1969).
Essmann, U. Observation of the mixed state. Physica 55, 83–93 (1971).
Jacobs, A. E. Interaction of vortices in type-II superconductors near T = Tc. Phys. Rev. B 4, 3029–3034 (1971).
Leung, M. C. Attractive interaction between vortices in type-II superconductors at arbitrary temperatures. J. Low Temp. Phys. 12, 215–235 (1973).
Auer, J. & Ullmaier, H. Magnetic behavior of type-II superconductors with small Ginzburg-Landau parameters. Phys. Rev. B 7, 136–145 (1973).
Kramer, L. Interaction of vortices in type II superconductors and the behavior near Hc1 at arbitrary temperature. Z. Physik 258, 367–380 (1973).
Luk’yanchuk, I. Theory of superconductors with κ close to \(1/\sqrt{2}\). Phys. Rev. B 63, 174504 (2001).
Mohamed, F., Troyer, M., Blatter, G. & Lukýanchuk, I. Interaction of vortices in superconductors with κ close to \(1/\sqrt{2}\). Phys. Rev. B 65, 224504 (2002).
Klein, U., Kramer, L., Pesch, W., Rainer, D. & Rammer, J. Microscopic calculations of vortex structure and magnetization curves for type II superconductors. Acta Physica Hungarica 62, 27–30 (1987).
Klein, U. Microscopic calculations on the vortex state in type II superconductors. J. Low Temp. Phys. 69, 1–36 (1987).
Miranović, P. & Machida, K. Thermodynamics and magnetic field profiles in low-κ type-II superconductors. Phys. Rev. B 67, 092506 (2003).
Vagov, A. et al. Superconductivity between standard types: Multiband versus single-band materials. Phys. Rev. B 93, 174503 (2016).
Wolf, S. et al. BCS-BEC crossover induced by a shallow band: pushing standard superconductivity types apart. Phys. Rev. B 95, 094521 (2017).
Wolf, S., Vagov, A., Shanenko, A. A., Axt, V. M. & Albino Aguiar, J. Vortex matter stabilized by many-body interactions. Phys. Rev. B 96, 144515 (2017).
Bogomolnyi, E. B. The stability of classical solutions. Sov. J. Nucl. Phys. 24, 449–454 (1976).
Shanenko, A. A., Milošević, M. V., Peeters, F. M. & Vagov, A. Extended Ginzburg-Landau formalism for two-band superconductors. Phys. Rev. Lett. 106, 047005 (2011).
Vagov, A., Shanenko, A. A., Milošević, M. V., Axt, V. M. & Peeters, F. M. Extended Ginzburg-Landau formalism: systematic expansion in small deviation from the critical temperature. Phys. Rev. B 85, 014502 (2012).
Vagov, A., Shanenko, A. A., Milošević, M. V., Axt, V. M. & Peeters, F. M. Two-band superconductors: extended Ginzburg-Landau formalism by a systematic expansion in small deviation from the critical temperature. Phys. Rev. B 86, 144514 (2012).
Leach, A. R. Molecular modelling: principles and applications (Harlow, England, 2001).
Varlamov, A. A., Galda, A. & Glatz, A. Fluctuation spectroscopy: from Rayleigh-Jeans waves to Abrikosov vortex clusters. Rev. Mod. Phys. 90, 015009 (2018).
Blatter, G., Feigel’man, M. V., Geshkenbein, V. B., Larkin, A. I. & Vinokur, V. M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 66, 1125–1175 (1994).
Komendová, L., Chen, Y., Shanenko, A. A., Milošević, M. V. & Peeters, F. M. Two-band superconductors: hidden criticality deep in the superconducting state. Phys. Rev. Lett. 108, 207002 (2012).
Seul, M. & Andelman, D. Domain shapes and patterns: the phenomenology of modulated phases. Science 267, 476–483 (1995).
Aranson, I. S. & Tsimring, L. S. Patterns and collective behavior in granular media: theoretical concepts. Rev. Mod. Phys. 78, 641–692 (2006).
Stoop, N., Lagrange, R., Terwagne, D., Reis, P. M. & Dunkel, J. Curvature-induced symmetry breaking determines elastic surface patterns. Nature Mat. 14, 337–342 (2015).
Tarantello, G. Selfdual Gauge Field Vortices, an Analytical Approach (Birkhäuser, Boston, 2007) .
Dunne, G. Self-Dual Chern-Simons Theories (Springer, Berlin, 1995).
Dubrovin, B. A. & Novikov, S. P. Ground states of two-dimensional electron in a periodic magnetic field. Sov. Phys. JETP 52, 511–516 (1980).
Acknowledgements
Support by the CAPES/Print Grant, process No. 88887.333666/2019-00 (Brazil), is acknowledged. A.V. thanks the Department of Physics at the Federal University of Pernambuco for the hospitality during his stay in Brazil. A.V. also acknowledges a support from the Russian Science Foundation Project 18-12-00429.
Author information
Authors and Affiliations
Contributions
A.V. and A.A.S. developed the formalism, S.W. created the numerical code, S.W. and A.V. performed the calculations and did initial interpretations of the results, A.V. and A.A.S. wrote the article, with the support of M.D.C. who helped to clarify several important features related to inhomogeneous vortex states.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vagov, A., Wolf, S., Croitoru, M.D. et al. Universal flux patterns and their interchange in superconductors between types I and II. Commun Phys 3, 58 (2020). https://doi.org/10.1038/s42005-020-0322-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-0322-6
This article is cited by
-
Intertype superconductivity evoked by the interplay of disorder and multiple bands
Frontiers of Physics (2024)
-
Intertype superconductivity in ferromagnetic superconductors
Communications Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.