Abstract
Zero-angle refraction of elastic waves in metamaterials has attracted attention for its extraordinary wave collimation properties. However, earlier implementations relied on the specific flat equifrequency curve of the phononic crystals suffer from a narrow range of incident angles or operating bandwidths, which severely hinders the exploration and design of functional devices. Here, we propose an elastic near-zero refractive index metamaterial of a triangular lattice to realize topological zero refraction with arbitrary angles of incidence and wide working frequency range. Topological robustness of the zero-angle refraction of pseudospin-Hall edge state against defects is experimentally demonstrated. Furthermore, tunable wave mode conversion associated with the zero-angle refraction is revealed and discussed. These results provide a paradigm for the simultaneous control of the refraction properties of longitudinal and transverse waves that can be employed for designing the topological elastic antennas and elastic wave collimator.
Similar content being viewed by others
Introduction
Elastic metamaterials (EMMs) have become an attractive research focus based on their unusual properties1,2,3,4,5,6. These specially designed composite structures have demonstrated a variety of intriguing effects and promising applications, including zero-index metamaterials (ZIM)7,8, wave transformation9, and negative refraction10,11,12,13,14. Especially, EMMs exhibiting zero-angle refraction have garnered attention because of their potential prospects in information processing and detection for medical and industrial purposes. The collimating properties of zero-angle refraction open a new possibility for achieving directional signal emission and reception in communication field. Recently, several successful theoretical and experimental demonstrations of zero-angle refraction of elastic waves depended on square-shaped equifrequency curves (EFCs) have been reported15,16,17,18. However, the specific flat EFCs of the phononic crystals (PCs) fundamentally restrict the direction of the incident wave beam and the working frequency range. Moreover, since the waveform conversion between longitudinal and transverse waves is pervasive during elastic wave propagation and elastic phonons found in solids possess the defect-sensitive characteristics compared with fluid/airborne ones, realizing wide-band all-angle zero refraction with defect immunity in a solid structure remains a great challenge. It is highly desirable to develop a novel scheme for elastic wavefront manipulations that can overcome these obstacles in both physics and engineering.
On the other hand, the exploration of topologically ordered states in photonic and PCs has renewed our understanding of condensed matter physics and has inspired a number of unique properties like backscattering-immune and defect-insensitive transport19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39. Very recently, these concepts have been extended to the field of electromagnetic40,41 and acoustic communication42,43,44,45,46. It is especially the case in the phononic world, the out-coupling of topological edge states has attracted an enormous interest due to its promising application for directional antennas46. In contrast to ordinary plane-wave refraction at the Brewster angle, topological protected refraction rests on out-coupled edge states with near-perfect efficiency upon entering into free space. Besides, owing to the topological effects of the edge modes, this form of refraction possesses the abilities to immunize against defects and is independent of the input field. These performance superiorities thus open up a new way to study topological zero refraction in PCs. To date, intensive research effort has been devoted to achieve topological positive and negative refraction in the scalar (longitudinal wave) system of fluid airborne acoustic42,43,44,45,46, whose practical role is largely limited. Therefore, it is of great practical value to realize topological zero refraction of elastic waves with both longitudinal and transverse polarizations, especially in the solid PCs that can be scaled accordingly for future chip-scale applications with highly directional collimated beams.
In this paper, we report the experimental realization of topologically protected zero refraction for in-plane waves in pseudospin-Hall PCs, which feature an extremely wide operating frequency range and irrespective of the input field. We show that by inhomogeneously changing the ellipse orientation in a triangular lattice, an elastic near-zero refractive index metamaterial (NZIM) can be obtained that possesses a double Dirac cone with fourfold degeneracy at the center of the Brillouin zone. Moreover, the wave mode separation analysis is systematically investigated to reveal the in-plane-wave mode conversion of the zero refraction behaviors. Our research provides a robust way to manipulate the refraction characteristics of longitudinal and transverse waves simultaneously and has potential applications in elastic wave collimation and underwater communications.
Results
Design of NZIM
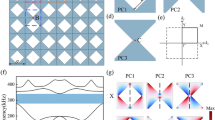
The two-dimensional (2D) solid PCs considered in this work are consisting of elliptical tungsten cylinders arranged in a triangular lattice embedded in an epoxy matrix. The lattice constant is as = 15 mm. The major axis and the minor axis of the ellipse are a = 1.644 mm and b = 1.370 mm, respectively. We then introduce a topological modification into a unit cell by rotating individual elliptical rod in different directions. The angle between the major axis of an ellipse and the horizontal axis is set to \(\theta \;{\mathrm{ = }}\;{\mathrm{k}}\varphi + C\), where φ represents the polar angle of the center position of the ellipse, k = 1 is the topological charge, and C is the initial phase. Figure 1a shows the topological transition process in the solid PCs, where the eigenfrequencies of the p- and d-type states at the Г point vary with the band gap closure and opening. The evolution of the unit cell when varying C is depicted in the inset of Fig. 1a, where pattern I corresponds to the radical configuration (C = 0°) with the nontrivial phase and pattern ш corresponds to the azimuthal configuration (C = 90°) with the trivial phase (see Supplementary Note 1). When C = 47.5° (indicated by pattern ∏), a double Dirac cone appears at the hexagonal Brillouin zone (BZ) center and the corresponding band structure of in-plane modes is calculated, as shown in Fig. 1b. To further explore the physical properties of the eigenmodes at the Dirac point, we show the in-plane displacement field distributions of the four degenerate eigenstates at point A in the inset of Fig. 1b. According to the group theory analysis, the eigenmode is a combination of the doubly degenerate dipolar and doubly degenerate quadrupolar Bloch states. This indicates that the double Dirac cones can emerge as a consequence of the degeneracy of the dipolar and quadrupolar states at the Γ point47,48. To illustrate the double Dirac cone intuitively, the three-dimensional dispersion surfaces near the Dirac point frequency are plotted in Fig. 1c. Figure 1d shows the EFCs in 2D reciprocal space for the top band that touches at the Dirac point, and illustrates that the linear dispersion is highly isotropic around the Γ point. Therefore, an effectively elastic NZIM can be achieved using the solid PC with the quadruple Dirac degeneracy at the Γ point7. It is worth emphasizing that the four degeneracy bands which forms the double Dirac cone are the mixed longitudinal-transverse polarization modes with a predominantly transverse polarization38, implying that the solid PCs should have the intriguing wave manipulation properties of the NZIM.
a Band edge frequencies of the d- and p-type eigenstates at the Г point as a function of the initial phase C. The evolution of the unit cell is depicted in the inset, where pattern I corresponds to C = 0°, pattern Π corresponds to C = 47.5°, and pattern ш corresponds to C = 90°. The nontrivial and trivial band gaps are marked with orange and cyan, respectively. b Band structure for the case of C = 47.5° with fourfold-degenerate Dirac cone formed at the Г point. Insets show the displacement field distributions for the four degenerate states at point A, the lattice array of the solid phononic crystals (PCs) and its irreducible Brillouin zone (BZ). c The three-dimensional dispersion surfaces near the Dirac point frequency. d The equifrequency curves (EFCs) in 2D reciprocal space for the high-frequency branch of the double Dirac cone.
To precisely explore the in-plane wave transport behaviors of the elastic NZIM and reveal its relationship with the double Dirac cone, we study the in-plane phase evolutions of the Uy displacement field in the PC slab with the propagation direction along the ΓM direction, as shown in Fig. 2a–c. The periodic (perfectly matched layer) boundary conditions are imposed on the y (x) direction. When a transverse wave at the Dirac point frequency fD = 89.692 kHz impinges on the PC slab from the left, the displacement fields in all the unit cells of the solid PC oscillate in phase, as illustrated in Fig. 2b. This is what an elastic NZIM is expected to behave. However, in the case of panels a and c, when the incident wave frequency is detuned away from fD, there is an accumulated phase change along the propagation direction. This is better interpreted in Fig. 2d, where we plot the corresponding phase diagrams at equivalent sampling points in each unit cell [marked by the white dots in Fig. 2a–c]. It can be seen that the phases change linearly as a function of the propagation distance.
a–c The simulated phase distributions of the Uy displacement field for a transverse wave incidence from the left along the x direction (ΓM), at f = 89.830, 89.692, and 89.560 kHz, respectively. d Phase of the displacement field at the marked points by white dots in figures of a–c. e Total displacement field distributions of near-zero index phononic crystals (PCs) surrounded by aluminum. f Same as e, except that the simulated triangular region is replaced by a homogeneous zero refractive index medium. g In-plane displacement (acoustic pressure) field of near-zero index PCs surrounded by water. A point source is placed at the center of a triangular region (marked by black dot), at the Dirac frequency fD = 89.692 kHz. Black arrows denote the propagation direction of the waves.
As demonstrated in the above, the in-plane waves do not experience any phase change as they propagate inside the elastic NZIM. Such unique properties can be exploited to realize intriguing wave manipulation effects. To test the directional emission of in-plane waves by utilizing the elastic NZIM, we construct a finite triangular PC structure whose boundaries are normal to the ΓM direction, surrounded by aluminum, as illustrated in Fig. 2e. When the in-plane waves at fD = 89.692 kHz are excited by a point source placed in the middle of the triangular region, the highly directive and collimated radiation beams outside of the solid PC are obtained along three directions. For comparison, we consider a homogeneous triangular region with relative parameters \(\rho = 0.0001\rho _{\mathrm{{Al}}}\), \(\kappa = \kappa _{\mathrm{{Al}}}\), and \(1/\mu = 0.0001(1/\mu _{\mathrm{{Al}}})\) surrounded by aluminum, as depicted in the Fig. 2f. It can be found that the corresponding displacement field distribution exhibits a similar emission pattern as that of Fig. 2e, and also match well with the simulation of the same PC structure immersed in water shown in the Fig. 2g. One difference worth noting is the fact that in the Fig. 2e there is low radiation energy outside of the PC, which arises from the impedance mismatch between the solid PC and the aluminum surrounding medium. These results unambiguously confirm that the triangular PC can be effectively described as an elastic NZIM near the Dirac point frequency. Furthermore, owing to the coexistence of longitudinal and transverse modes in bulk elastic waves, tunable control of the mode conversion for longitudinal and transverse waves can be realized by introducing the defect into the elastic NZIM to modulate their transmission properties (see Supplementary Note 2). The directive emission and tunable mode conversion phenomena demonstrated here suggest potential applications in the elastic wave energy industry for the simultaneous manipulation of the longitudinal and transverse wave energy.
Topological zero refraction
Next, we investigate the topological protected refraction of the pseudospin-polarized edge states (see Supplementary Note 3) entering into free space through a zigzag termination. To this end, we construct two topologically protected waveguides (TPWGs) of opposite configuration surrounded by aluminum, as illustrated in Fig. 3a, b. A harmonic force excitation with 45° inclination, \({\mathbf{F}}({t}) = [F_{{x}}(t),F_y(t)] = [1,1]F{\mathrm{e}}^{ - i\omega t}\), is applied at the left end of the domain wall (indicated by the green star). The total displacement field distributions at f = 89.4 kHz show that the in-plane waves propagate along the termination normal upon exiting the TPWG. This is characteristic of zero-angle refraction behavior. Compared with the conventional refraction without topological effect15,16,17,18, such topological zero refraction is independent of the input field, because the topological transports of the edge states are not affected by the direction of the excitation force49 (see Supplementary Note 4). The important difference to note here is that the out-coupled edge states always undergo zero-angle refraction for the topological channels in arbitrary direction (see Supplementary Note 5). In addition, the topological zero refraction for armchair termination are demonstrated (see Supplementary Note 6). We also note that, the presence of the impedance mismatch between the TPWG and the background medium induces the relatively low radiation energy of the outgoing beam. To verify the directivity of the refracted beams, we numerically scan the out-space field pattern along a cutline parallel to the termination (white solid line in Fig. 3b) at different frequencies within the topological band gap. Figure 3c illustrates the profile of the normalized displacement amplitude along the y direction of the cutline. It is very convincing that the energy of the refracted waves is indeed concentrated on the termination normal, which demonstrates unambiguously the presence of a nearly normal outgoing beam and therefore of zero-angle refraction occurring within the entire frequency range of the topological band gap.
a, b The total real displacement fields at f = 89.4 kHz along the domain wall with a C = 0° (nontrivial) above and C = 90° (trivial) below; b C = 90° (trivial) above and C = 0° (nontrivial) below. c In-plane displacement field amplitude of a cutline (white solid line) along the y direction at various frequencies. Plots d–e give the real longitudinal and transverse polarized displacement gradient at f = 89.4 kHz, respectively. The green star indicates a harmonic force excitation. The white dashed line denotes the normal to the interface. The white dotted lines highlight the domain wall and the termination. The arrows represent the directions of the propagating beams. f The S/P ratio as a function of the frequency, extracted by the output energy of three equally spaced dots A, B and C on the termination normal in d–e. g The corresponding k-space analysis on the out-coupling of the edge states through the zigzag termination. The Brillouin zone (BZ) is depicted by the black solid line. The green (blue) dashed circles indicate the dispersions of longitudinal (transverse) waves in aluminum. The black dashed lines represent the condition of conservation of the wave vector components parallel to the zigzag termination.
Due to the vector nature of in-plane waves, the refracted waves can be separated into the longitudinal and transverse components upon exiting the TPWG. To resolve the individual waves, i.e., longitudinal (P) and transverse (S) polarized waves, the divergence and curl of the in-plane displacement gradient fields are calculated by the Helmholtz decomposition (see Supplementary Note 7). Figure 3d, e plots the real longitudinal and transverse polarized displacement gradients, which denote the longitudinal and transverse wave component of the in-plane waves, respectively. It is interesting to note that the refracted wave field distribution of the transverse wave mode is more intense than that of the longitudinal wave mode. This implies that a wave mode conversion between the longitudinal waves and the transverse waves has occurred on the zigzag termination due to the zero-angle refraction15,16. To quantitatively analyze the wave mode conversion efficiency for the outgoing waves, the ratio between the output power of the refracted S and P waves is numerically calculated as a function of the frequency, as shown in Fig. 3f. It can be found that the S/P ratio is around 2.8 at f = 89.4 kHz and decreases with the increase of frequency, which indicates that the mode conversion of transverse wave to longitudinal wave is highly frequency dependence. To further interpret this zero-angle refraction behavior and its co-existed refracted longitudinal and transverse wave modes, we apply the phase-matching conditions at the termination, as shown in Fig. 3g. The pseudospin-polarized edge states leave from the PCs and obey the conservation of momentum parallel to the zigzag termination, thus the refracted wave vectors kout in free space satisfy \({\mathbf{k}}_{\mathrm{{out}}} \cdot {\mathbf{e}}_{\mathrm{{zig}}} = {\mathbf{k}}_{\Gamma \Gamma } \cdot {\mathbf{e}}_{\mathrm{{zig}}}\). The EFCs of longitudinal (transverse) waves in free space (green (blue) dashed circles in Fig. 3g) are determined by \(| {{\mathbf{k}}_{\mathrm{{out}}}} | = 2\pi {f}/c_{\mathrm{l}}({c}_{\mathrm{{t}}})\), where f represents the excitation frequency, \(c_{\mathrm{l}}(c_{\mathrm{t}})\) is the longitudinal (transverse) wave velocity of aluminum. By matching the wave vector of the incident edge states \({\mathbf{k}}_{\Gamma \Gamma }\) on the EFCs of free space, one is able to find the radiation direction of the refracted beams. The refraction angle γ can be quantitatively determined by \({\mathrm{|}}{\mathbf{k}}_{\mathrm{{out}}}{\mathrm{|}} \cdot \cos(90^ \circ + \gamma ) = {\mathrm{|}}{\mathbf{k}}_{\Gamma \Gamma }{\mathrm{|}} \cdot \cos90^ \circ\) and be obtained as \(\gamma _{\mathrm{l}} = \gamma _{\mathrm{t}} = 0^ \circ\). As graphically solved in Fig. 3g, zero-angle refraction for both the longitudinal and transverse modes can be identified at the frequency f = 89.4 kHz, which agrees well with the simulation results. It is worth noting that, different from the topological refraction phenomena induced by valley-polarized edge states40,41,43,44,45,46, this zero-angle refraction is independent of the placement of the trivial/nontrivial regions according to the phase-matching condition. Compared with other classical waves in fluid matrix PCs42,43,44,45,46, our solid/solid system can be coupled to various background mediums, so that different types of topological refraction and beam splitting can be realized in the epoxy surrounding medium and fluid environments respectively (see Supplementary Notes 8 and 9). In addition, the transmission and the refraction characteristics of out-of-plane modes are discussed theoretically (see Supplementary Note 10), and it is proved that our PC system can achieve the simultaneous manipulation of the out-coupling of in-plane and out-of-plane wave.
To validate the robustness of the zero refraction behavior at the zigzag termination, we introduce different types of non-spin-mixing defects including the sharp bends, randomly distributed cavities and disorders into the TPWG. Figure 4a, b shows both the schematics and the simulated total displacement field distributions of the perturbed TPWG under a harmonic excitation applied at left port. Owing to the topological protection, the in-plane waves can propagate robustly along the domain wall without notable scattering losses and undergo zero-angle refraction upon exiting the TPWG. These results also confirm that the cavities near and far from the exit of the TPWG have no impact on the radiation directivity, in contrast to the traditional non-topological waveguides15,16,17,18. In addition, the influences on the radiation directionality caused by the perturbations to the domain wall and the termination are investigated. As illustrated in the Fig. 4c, we cut through the elliptical cylinders above the domain wall to introduce the spin-mixing defects, and thereby resulting in the breaking of the trivial/nontrivial interface symmetry50. It can be seen that the energy amplitude and refraction direction of the exiting in-plane waves maintain perfectly well. Remarkably, the topological zero refraction is still robust to the separation between the two PCs and the oblique-cut truncation at the zigzag termination, as depicted in the Fig. 4d. The overall results demonstrate the robustness of the topological refraction against various kinds of perturbations, which is drastically different from ordinary plane-wave refraction without topological effects. Thus, this topological refracted patterns can be leveraged to design the elastic directional antennas with high efficiency and stability.
Schematics of the perturbations are depicted at the upper right corner in each figure. Simulated in-place displacement field distributions at f = 89.0 kHz with a bends, b cavities and disorders, c spin-mixing defects, d separation and truncation. The green star indicates a harmonic force excitation. The white dashed line denotes the normal to the interface. The arrows represent the directions of the propagating beams.
Experimental confirmation of topological robustness
To characterize experimentally the transmission and the refraction properties of in-plane waves, we design a solid PC composed of elliptical steel cylinders embedded in an epoxy resin matrix (see Methods section). The corresponding topological mode inversions and band dispersions of the edge states are presented in Supplementary Fig. 11. Figure 5a presents a photograph of the prism-shaped samples of the TPWG surrounded by the aluminum, whose interface is connected by a topological trivial crystal (C = 90°) with a topological nontrivial crystal (C = 0°). As shown in Fig. 5b, the simulated displacement field distribution of the TPWG at f = 98.95 kHz indicates unambiguously the presence of zero-angle refraction at the entrance of the TPWG. Figure 5c further displays the experimentally measured transmission spectra for the TPWG, which indicates the measured ∼15 dB transmittance increase of the normal end compared with the positive or negative side of the termination normal. The experiment results are in good agreement with the simulation results shown in Fig. 5b. The overall lower transmission intensity can result from the transverse-to-longitudinal mode conversion and the impedance mismatch to the background medium. To further verify the robustness of the topological zero refraction, as displayed in Fig. 5d, we intentionally introduce sharp bends to the TPWG. Based on the corresponding in-plane displacement field distribution as illustrated in Fig. 5e, we can conclude that the energy and direction of the refracted beams are robust against the bends. Moreover, the experimental results shown in Fig. 5f confirm the robustness of the zero-angle refraction within the entire frequency range of the topological band gap.
a Photograph of the topologically protected straight waveguide constructed by stacking a topological trivial crystal (C = 90°) with a topological nontrivial crystal (C = 0°). The red dashed lines represent the trivial/nontrivial interfaces. The black solid lines denote normal to the zigzag termination. b Simulated in-plane displacement field distribution of the topologically protected waveguide (TPWG) at f = 98.95 kHz. The white dashed line denotes the normal to the termination. The white dotted lines highlight the domain wall and the termination. The black arrows represent the directions of the refracted beams. c Experimentally measured transmission spectra for the TPWG. The shaded region indicates the topological band gap. d Photograph of the TPWG with bends. e Simulated in-plane displacement field distribution of the TPWG with bends at f = 98.95 kHz. f Experimentally measured transmission spectra for the TPWG with bends.
Discussion
In summary, we have constructed an effectively elastic NZIM using the solid PC with the quadruple Dirac degeneracy at the Brillouin zone center. By introducing elastic pseudospin–orbit coupling into the PCs, the defect-immune topological zero refraction with wide operating frequency range and independent of incident angle is experimentally realized. The strategy rests on out-coupling pseudospin-polarized edge state, which breaks through the limitation of bandwidth and incidence angle for elastic wave collimation in current EMMs. Accompanying the zero-angle refraction, we have also demonstrated the directional emission and the tunable wave mode conversion phenomena for in-plane waves, which are drastically different from the wave manipulation characteristics in electromagnetic and acoustic domains. Moreover, our finding provides a paradigm for the simultaneous manipulation of the refraction properties of in-plane and out-of-plane waves that can be utilized in the design of integrated elastic wave antennas. Such a flexible platform enables the highly efficient and stable control of longitudinal and transverse waves in various fluid and solid environments, paving the way for advance signal processing and underwater communication.
Methods
Simulations
Numerical simulations are performed using a commercial finite-element analysis and solver software COMSOL MULTIPHYSICS. The solid material parameters used for calculation are ρ = 19,100 kg m−3, κ = 354.1 GPa, μ = 131.1 GPa for tungsten; ρ = 1180 kg m−3, κ = 4.35 GPa, μ = 1.59 GPa for epoxy; and ρ = 2730 kg m−3, κ = 77.6 GPa, μ = 28.7 GPa for aluminum, where ρ, κ, and μ are the mass density, bulk modulus, and shear modulus, respectively. The fluid parameters are ρ = 1000 kg m−3, c = 1490 m s−1 for water and ρ = 1594 kg m−3, c = 938 m s−1 for CCl4. When calculating the bulk (edge) band dispersions, Floquet periodic boundary conditions are applied to the periodic surfaces of the unit cell (supercell). Perfectly matched layers (PML) are imposed on the exterior of the whole structures to eliminate the reflected waves from the boundaries.
Experimental setup
The prism-shaped samples consist of elliptical stainless-steel rods with the major axis a = 2.4 mm, the minor axis b = 2 mm, embedded in an epoxy resin, which are surrounded by the aluminum frames. The lattice constant of the PCs is as = 18.6mm and the total size of the parallelepiped block is 220 mm × 140 mm × 70 mm. During the fabrication process, both the PC prism (stainless-steel rods in epoxy) and its environment (aluminum) are built simultaneously as a single block to facilitate their coupling. In experiments, a couple of ultrasonic broadband transducers with a central frequency of 100 kHz and a diameter of 60 mm (OLYMPUS contact transducers type Videoscan No. V1011) are used to act as the emitter and the receiver, launching a probing longitudinal wave signal from the emitter through the composite sample, which is then processed at the receiver. The emitter is excited with an ultrasonic emission source (OLYMPUS model 5073PR) producing a short-duration large-amplitude pulse. The receiver transducer is mounted on the motorized stage to scan the output signals at a step of 1 mm along the exit termination of the samples. The transmission signals of the positive or negative side of the termination normal are averaged over 50 data acquisitions. Finally, the signal acquired by the receiver is postamplified and then digitized with a Tektronix digital oscilloscope with real-time fast Fourier transform capability to produce the transmission power spectrum.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Lai, Y., Wu, Y., Sheng, P. & Zhang, Z. Q. Hybrid elastic solids. Nat. Mater. 10, 620 (2011).
Liu, Z. et al. Locally resonant sonic materials. Science 289, 1734–1736 (2000).
Sridhar, A., Liu, L., Kouznetsova, V. G. & Geers, M. G. D. Homogenized enriched continuum analysis of acoustic metamaterials with negative stiffness and double negative effects. J. Mech. Phys. Solids 119, 104–117 (2018).
Zhou, X. M. & Hu, G. K. Analytic model of elastic metamaterials with local resonances. Phys. Rev. B 79, 195019 (2009).
Wu, Y. & Zhang, Z. Q. Dispersion relations and their symmetry properties of electromagnetic and elastic metamaterials in two dimensions. Phys. Rev. B 79, 195111 (2009).
Fang, X., Wen, J., Bonello, B., Yin, J. & Yu, D. Ultra-low and ultra-broad-band nonlinear acoustic metamaterials. Nat. Commun. 8, 1288 (2017).
Liu, F. & Liu, Z. Elastic waves scattering without conversion in metamaterials with simultaneous zero indices for longitudinal and transverse waves. Phys. Rev. Lett. 115, 175502 (2015).
Liu, F., Lai, Y., Huang, X. & Chan, C. T. Dirac cones at \(\bar k = 0\) in phononic crystals. Phys. Rev. B 84, 224113 (2011).
Hu, J., Chang, Z. & Hu, G. Approximate method for controlling solid elastic waves by transformation media. Phys. Rev. B 84, 201101 (2011).
Wu, Y., Lai, Y. & Zhang, Z. Q. Elastic metamaterials with simultaneously negative effective shear modulus and mass density. Phys. Rev. Lett. 107, 105506 (2011).
Croënne, C. et al. Negative refraction of longitudinal waves in a two-dimensional solid-solid phononic crystal. Phys. Rev. B 83, 054301 (2011).
Zhu, R., Liu, X. N., Hu, G. K., Sun, C. T. & Huang, G. L. Negative refraction of elastic waves at the deep-subwavelength scale in a single-phase metamaterial. Nat. Commun. 5, 5510 (2014).
Liu, X. N., Hu, G. K., Huang, G. L. & Sun, C. T. An elastic metamaterial with simultaneously negative mass density and bulk modulus. Appl. Phys. Lett. 98, 251907 (2011).
Morvan, B., Tinel, A., Hladky-Hennion, A. C., Vasseur, J. & Dubus, B. Experimental demonstration of the negative refraction of a transverse elastic wave in a two-dimensional solid phononic crystal. Appl. Phys. Lett. 96, 101905 (2010).
Vasseur, J. O. et al. Experimental evidence of zero-angle refraction and acoustic wave-phase control in a two-dimensional solid/solid phononic crystal. Phys. Rev. B 86, 134305 (2012).
Swinteck, N. et al. Multifunctional solid/solid phononic crystal. J. Appl. Phys. 112, 024514 (2012).
Morvan, B. et al. Ultra-directional source of longitudinal acoustic waves based on a two-dimensional solid/solid phononic crystal. J. Appl. Phys. 116, 214901 (2014).
Liu, W. & Su, X. Collimation and enhancement of elastic transverse waves in two-dimensional solid phononic crystals. Phys. Lett. A 374, 2968–2971 (2010).
Rechtsman, M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013).
Wu, L.-H. & Hu, X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys. Rev. Lett. 114, 223901 (2015).
Peano, V., Brendel, C., Schmidt, M. & Marquardt, F. Topological phases of sound and light. Phys. Rev. X 5, 031011 (2015).
Yves, S. et al. Crystalline metamaterials for topological properties at subwavelength scales. Nat. Commun. 8, 16023 (2017).
Fleury, R., Khanikaev, A. B. & Alu, A. Floquet topological insulators for sound. Nat. Commun. 7, 11744 (2016).
Yves, S., Fleury, R., Lemoult, F., Fink, M. & Lerosey, G. Topological acoustic polaritons: robust sound manipulation at the subwavelength scale. N. J. Phys. 19, 075003 (2017).
Khanikaev, A. B., Fleury, R., Mousavi, S. H. & Alu, A. Topologically robust sound propagation in an angular-momentum-biased graphene-like resonator lattice. Nat. Commun. 6, 8260 (2015).
Zangeneh-Nejad, F. & Fleury, R. Topological Fano resonances. Phys. Rev. Lett. 122, 014301 (2019).
Peng, Y. G. et al. Experimental demonstration of anomalous Floquet topological insulator for sound. Nat. Commun. 7, 13368 (2016).
Lu, J.-Y. et al. Observation of topological valley transport of sound in sonic crystals. Nat. Phys. 13, 369–374 (2017).
He, C. et al. Acoustic topological insulator and robust one-way sound transport. Nat. Phys. 12, 1124–1129 (2016).
Zhang, Z. et al. Topological creation of acoustic pseudospin multipoles in a flow-free symmetry-broken metamaterial lattice. Phys. Rev. Lett. 118, 084303 (2017).
Ding, Y. et al. Experimental demonstration of acoustic chern insulators. Phys. Rev. Lett. 122, 014302 (2019).
Mousavi, S. H., Khanikaev, A. B. & Wang, Z. Topologically protected elastic waves in phononic metamaterials. Nat. Commun. 6, 8682 (2015).
Süsstrunk, R. & Huber, S. D. Observation of phononic helical edge states in a mechanical topological insulator. Science 349, 47–50 (2015).
Pal, R. K. & Ruzzene, M. Edge waves in plates with resonators: an elastic analogue of the quantum valley Hall effect. N. J. Phys. 19, 025001 (2017).
Yu, S. Y. et al. Elastic pseudospin transport for integratable topological phononic circuits. Nat. Commun. 9, 3072 (2018).
Huo, S., Chen, J., Huang, H. & Huang, G. Simultaneous multi-band valley-protected topological edge states of shear vertical wave in two-dimensional phononic crystals with veins. Sci. Rep. 7, 10335 (2017).
Huo, S. Y., Chen, J. J. & Huang, H. B. Topologically protected edge states for out-of-plane and in-plane bulk elastic waves. J. Phys. Condens. Matter 30, 145403 (2018).
Chen, J. J. et al. Self-ordering induces multiple topological transitions for in-plane bulk waves in solid phononic crystals. Phys. Rev. B 98, 014302 (2018).
Huo, S. Y., Chen, J. J., Feng, L. Y. & Huang, H. B. Pseudospins and topological edge states for fundamental antisymmetric Lamb modes in snowflakelike phononic crystal slabs. J. Acoust. Soc. Am. 146, 729–735 (2019).
Gao, F. et al. Topologically protected refraction of robust kink states in valley photonic crystals. Nat. Phys. 14, 140 (2018).
Ma, T. & Shvets, G. All-Si valley-Hall photonic topological insulator. N. J. Phys. 18, 025012 (2016).
He, H. et al. Topological negative refraction of surface acoustic waves in a Weyl phononic crystal. Nature 560, 61 (2018).
Zhu, Z. et al. Negative refraction and partition in acoustic valley materials of a square lattice. Phys. Rev. Appl. 12, 024007 (2019).
Xie, B. et al. Acoustic topological transport and refraction in a Kekulé lattice. Phys. Rev. Appl. 11, 044086 (2019).
Zhang, Z., Tian, Y., Cheng, Y., Liu, X. & Christensen, J. Experimental verification of acoustic pseudospin multipoles in a symmetry-broken snowflakelike topological insulator. Phys. Rev. B 96, 241306 (2017).
Zhang, Z. et al. Directional acoustic antennas based on valley-Hall topological insulators. Adv. Mater. 30, 1803229 (2018).
Chen, Z. G. et al. Accidental degeneracy of double Dirac cones in a phononic crystal. Sci. Rep. 4, 4613 (2014).
Li, Y., Wu, Y. & Mei, J. Double Dirac cones in phononic crystals. Appl. Phys. Lett. 105, 014107 (2014).
Wang, P., Lu, L. & Bertoldi, K. Topological phononic crystals with one-way elastic edge waves. Phys. Rev. Lett. 115, 104302 (2015).
Deng, Y., Ge, H., Tian, Y., Lu, M. & Jing, Y. Observation of zone folding induced acoustic topological insulators and the role of spin-mixing defects. Phys. Rev. B 96, 184305 (2017).
Acknowledgements
We thank G. L. Huang at University of Arkansas at Little Rock and R. Zhu at Beijing Institute of Technology for helpful discussions. This work is supported by the National Science Foundation of China under Grant No. 11374093 and No. 11672214; and the foundation strengthening program No.2019-JCJQ-00.
Author information
Authors and Affiliations
Contributions
J.C., Z.T., and X.H. initiated the program, oversaw, and directed the whole project. J.C. and H.H. conceived the original idea. H.H. performed the simulations and derived the theory. J.C., H.H., S.H., and L.F. supported the fabrication process of the sample. Z.T., S.H., and L.F. helped in the experiment setup. Z.T. and J.C. carried out experimental measurements. J.C., H.H. and S.H. analyzed the data, prepared the figures, and wrote the manuscript. All authors contributed to scientific discussion of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Huang, H., Tan, Z., Huo, S. et al. Topologically protected zero refraction of elastic waves in pseudospin-Hall phononic crystals. Commun Phys 3, 46 (2020). https://doi.org/10.1038/s42005-020-0314-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-0314-6
This article is cited by
-
Coupled topological rainbow trapping of elastic waves in two-dimensional phononic crystals
Scientific Reports (2024)
-
Ultra-sensitive gas sensor based fano resonance modes in periodic and fibonacci quasi-periodic Pt/PtS2 structures
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.