Abstract
The interest in artificial magnetic media such as magnonic crystals increased substantially in recent years due to their potential applications in information processing at microwave frequencies. The main features of these crystals are the presence of band gaps in the spin-wave spectra, usually formed due to Bragg reflections of spin-waves on the artificially created periodic structures. Here, we study spin-wave propagation in longitudinally magnetized width- and thickness-modulated yttrium iron garnet waveguides by means of Brillouin light scattering and microwave spectroscopy techniques. It is found that the width modulated crystal does not manifest noticeable Bragg reflections, but still demonstrates a pronounced band gap in its transmission characteristic. The phenomenon can be explained by the destructive interference between different frequency-degenerated spin-wave modes excited by the crystal. Such a reflection-less crystal is promising for future design of multi-element magnonic devices.
Similar content being viewed by others
Introduction
In recent years, propagation of spin waves (SWs) in ferromagnetic film structures attracts considerable attention in connection with their applications in novel data transfer and processing technologies1,2. This strong research interest is determined by efficient mechanisms of signal transmission based on the general idea that characteristics of SW quanta—magnons—such as their phase and occupation numbers can be regarded as state variables instead of charge in conventional electronics3,4,5,6,7,8,9. Among different physical phenomena, which shape the mainstream research directions of magnonics2, selective SW propagation is one of the most promising tools for information processing at microwave frequencies10,11,12,13,14. An SW spectrum can be engineered using artificial magnetic media—magnonic crystals (MC)—created by a spatial periodic modulation of a SW-carrying magnetic material15. These structures have recently received a great attention as promising building blocks of linear and nonlinear magnonics10,16,17,18,19,20. A distinctive feature of MCs is the possibility to design a desired functionality for a given application by variation of the magnon band structure10,11. Magnonic crystals have been successfully utilized for the realization of various microwave devices such as magnon transistors4, microwave filters21, phase shifters22, SW logic gates23, magnetic field sensors24, memory cells25, for wavevector-dependent mode selection in SW oscillators26, time reversal27, and other cases.
Magnonic crystals are produced using different types of magnetic materials: metals such as Ni and Co28,29, alloys such as Permalloy (\({{\rm{Ni}}}_{80}{{\rm{Fe}}}_{20}\))28,30,31,32,33 and CoFeB34,35, Heusler compounds such as \({{\rm{Co}}}_{2}({{\rm{Fe}}}_{0.4}{{\rm{Mn}}}_{0.6}){\rm{Si}}\)36,37, and dielectrics like yttrium iron garnet (YIG, \({{\rm{Y}}}_{3}{{\rm{Fe}}}_{5}{{\rm{O}}}_{12}\))11,16,18,20,21,22,23,24,25,26,27,38,39. The main advantages in choosing μm-thick single-crystal YIG films over nm-thick metallic materials such as Permalloy or CoFeB is the small magnetic damping40 and higher group velocity of dipolar SWs. These two properties result in a long SW propagation length, which is crucial for future spintronic and magnonic applications. From the technological point of view, MCs based on epitaxially grown YIG films possess essential advantages: (i) small out-of-band insertion losses; (ii) deep rejection bands; (iii) conventional methods of MC production, ranging from metal deposition, chemical etching, ion implantation, or other methods that produce a periodic variation of a given magnetic parameter3,11,18,23. Among various types of YIG-based MCs, geometrically structured MCs produced by modulation of thickness or width of YIG SW waveguides (see Fig. 1) are most promising candidates to gain broad applications due to their high robustness, predictability of characteristics, stability of parameters, and simplicity of fabrication.
Typically, SWs in periodic magnetic structures undergo Bragg scattering, resulting in the formation of spectral regions with prohibited propagation known as SW band gaps by analogy to photonic41,42 and phononic43,44 crystals. This band formation mechanism has been investigated in detail and is well understood for a variety of MCs with different physical properties and geometries, including thickness-modulated YIG-based waveguides. At the same time, it was predicted that for some cases band gaps can arise due to peculiarities of the SW excitation mechanisms inside an MC45.
In this article, we combine electrical and optical detection of SWs in order to investigate SW propagation in a width-modulated MC (Fig. 1a). We show that transmission characteristics of such a crystal exhibit a single well-pronounced rejection band, which, however, cannot be described in terms of a simple Bragg scattering model. Contrary to a thickness-modulated structure (Fig. 1b), the width-modulated crystal demonstrates no resonant back-scattering of SWs at the central frequency of the band gap. The formation of such unusual rejection band can be associated with destructive interference of different spatial SW components at the MC’s output antenna due to phase shifts accumulated in the course of their propagation through the crystal structure.
Results
Experimental set-up
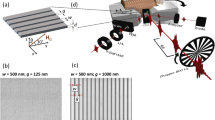
Figure 1a, b shows spatially modulated MCs comprising the longitudinally magnetized periodically structured YIG-film waveguides and attached microstrip antennas serving for inductive excitation and detection of SWs in the GHz frequency range. The magnetization geometry is chosen in a way allowing for the excitation of backward volume magnetostatic spin waves (BVMSWs)38 having reciprocal propagation characteristics46 and demonstrating high scattering efficiency in thickness-modulated MCs47,48.
The optical access to the YIG film was especially ensured for a two-dimensional mapping of the magnon density distribution by means of space- and time-resolved Brillouin Light Scattering (BLS) spectroscopy49,50. The BLS measurements were performed in backward scattering geometry by placing a dielectric mirror below the samples51.
The YIG samples were fabricated in the form of 1.9 mm broad stripes cut out from low-damping (ferromagnetic resonance linewidth is about 0.5 Oe at 5 GHz) single-crystal YIG films, epitaxially grown in the (111) crystallographic plane on a gallium gadolinium garnet substrate. The thickness- and width-modulated samples (see Fig. 1) were produced in Kaiserslautern and St. Petersburg, respectively. Conventional photolithographic and chemical etching techniques were used for the patterning in both cases.
For the fabrication of the grooved (thickness-modulated) crystal (see Fig. 1b) a 5.5-\({\upmu}\)m-thick YIG film was used. The pattern consists of 10 parallel grooves with a width of 50 \({\upmu}\)m spaced by 250 \({\upmu}\)m, so that the lattice constant is 300 \({\upmu}\)m. The grooves were etched to a depth of 1 \({\upmu}\)m, controlled by a surface profilometer.
The width-modulated sample is 26 mm long and 8.5 \({\upmu}\)m thick. The length of the rectangular-modulated area in the middle of the stripe is 6 mm (see Fig. 1a). The spatial modulation period and depth are 600 and 400 \({\upmu}\)m, respectively.
The microwave stripline antennas with a width of 50 \(\upmu\)m were placed at distances of about 3 and 4 mm from the left and right ends of the modulated film area, respectively. The antennas were connected to a vector network analyzer (VNA) for continuous wave (CW) measurements. A circuit consisting of a pulsed microwave single frequency generator, a semiconductor detector, and an oscilloscope was utilized for pulse-regime measurements.
Microwave measurements
Figure 2 illustrates the transmission characteristics of the investigated samples measured by VNA. Here, a bias magnetic field of 120 mT for the width-modulated and 182 mT for the grooved MCs was applied. The input microwave power was \(-30\) dBm that guaranteed a linear regime of SW propagation.
Transmission characteristics of the modulated (blue solid line) and regular (red dashed line) waveguides for the grooved crystal (a) and the width-modulated crystal (b). Orange and green lines indicate the frequencies, where the Brillouin light scattering (BLS) measurements are performed: \({f}_{{\rm{1}}}=5.344\, {\mathrm{{GHz}}}\), \({f}_{{\rm{2}}}=5.373\) GHz, and \({f}_{{\rm{3}}}=7.02\) GHz.
The blue solid curves in Fig. 2 represent the transmission characteristics of the structured waveguides, while the red dashed lines show, for comparison, the characteristics of similar YIG waveguides without periodic structures. One can clearly identify several frequency regions with different SW dynamics in the transmission characteristic of the periodic waveguides.
For the thickness-modulated crystal (see Fig. 2a), we observe the formation of three magnonic band gaps, where the level of attenuation sharply increases by roughly 20 dB. The width of the central band gap is 10 MHz measured at a level of 6 dB above the maximum loss of −50 dB.
The width-modulated MC shows formation of only one pronounced band gap at the center frequency \({f}_{{\rm{1}}}=5.344\) GHz, which is marked by the orange line in Fig. 2b. The region of enhanced microwave attenuation has a width of 5 MHz measured at a level of 6 dB from the maximum loss of \(-46.5\) dB (in our analysis we neglected the fast oscillations of the transmission characteristics caused by the interference of the SW signal and an electromagnetic wave directly passed from the input to the output antenna). In addition, there are regions around the band gap, where BVMSW modes are transmitted with relatively low attenuation. For example, the frequency \({f}_{{\rm{2}}}=5.373\) GHz with loss level of \(-25\) dB is marked by the green line in Fig 2b. The frequencies marked in Fig. 2 by vertical lines are chosen for further analysis of the SW dynamics for the different crystals and different propagation regimes.
Brillouin light scattering measurements
In order to reveal the SW dynamics within the crystal structures and to be able to distinguish between individual responses of different parts of these structures, we performed BLS measurements in a pulsed microwave regime. To this end, we applied 30-ns-long microwave pulses with a power of \(-10\) dBm to the input antennas. Due to the short pulse durations we were able to raise the power of the SW excitation, and thus to increase the signal-to-noise ratio of our optical measurements, without any visible influence from nonlinear SW processes. The repetition rate was 1.5 \({\upmu}\)s to avoid any spurious influence trough heating effects in the magnetic material.
The used BLS technique allowed us to carry out the study of the magnon density distribution with 25 \({\upmu}\)m spatial and 400 ps time resolution. In these measurements, the intensity of the inelastically scattered light is proportional to the magnon occupation number, or, in other words, to the intensity of the SW in the sample.
In Fig. 3, snapshots of the spatial distribution of the SW intensity measured in the central rejection band (\({f}_{{\rm{3}}}\) = 7.02 GHz) of the grooved structure are shown. The pictures are plotted in a linear color scale, and the SW intensity is normalized in each frame. High SW intensities are indicated as red and low ones as blue. The selected time frames illustrate how the SW packet enters the grooved area, stops due to the Bragg reflection around the fourth groove (grooves are indicated by the vertical gray lines) and gets entirely reflected out of the crystal. The observed behavior perfectly corresponds with the conventional SW dynamics expected in the frame of the Bragg reflection model.
The same measurements were also performed for the width-modulated crystal at the carrier frequencies that correspond to the rejection band (\({f}_{{\rm{1}}}=5.34\) GHz) and pass band (\({f}_{{\rm{2}}}=5.373\) GHz). The resulting snapshots are shown in Fig. 4a for the rejection band frames and in Fig. 4b for the pass band frames. The color scale is the same as in Fig. 3.
Two-dimensional plots of the time-resolved spin-wave intensity distributions in periodic width-modulated waveguides for the frequencies \({f}_{{\rm{1}}}=5.34\) GHz (rejection band (a)) and \({f}_{{\rm{2}}}=5.373\) GHz (pass band (b)). The dotted white lines show the motion of the center of the spin-wave (SW) packet excited within the rejection band. The positions of the input and output microstrip microwave antennas are outside of the measurement area of the sample at 0 and 13 mm. The dashed red lines in the top frames represent the virtual antennas used for later analysis of the SW pulse intensity by comparing a vector network analyzer and Brillouin light scattering measurements.
The main feature of the measured SW intensity distributions in the width-modulated waveguide is obvious: In contrast to conventional MCs, this crystal exhibits nearly zero reflected SW intensity within both the rejection and pass bands (see Fig. 4a, b).
In the absence of any visible Bragg reflection, the physical mechanisms responsible for the formation of the rejection band in Fig. 2b might be related to, e.g., some non-resonant or resonant SW decay caused by enhanced magnon–magnon scattering processes in the rejection band frequency range. In order to clarify this issue, the magnon decay was analyzed for both cases presented in Fig. 4. The instantaneous spatial distributions of the measured magnon densities were integrated over a moving window containing the propagating SW packet and over the whole YIG-film region accessible for the BLS probing. The obtained integral data were fitted with an exponential decay function.
It was found that the lifetimes of both SW packets are about 1.6 times shorter than the lifetimes of the secondary magnons (note the spatially structured noise behind the SW packets in Fig. 4a, b) generated due to scattering of these packets from the notched waveguide edges. However, the lifetimes of the SW packets propagating within the rejection and pass bands differ only by 11%, being equal to 73 and 82 ns, respectively. Such a small difference in decay rates cannot explain the observed reduction of the transmitted SW power within the rejection band. The difference in group velocities and, respectively, in the SW propagation times is also rather small (compare the measured positions of the SW packets in Fig. 4): the experimentally determined group velocities are \(3.88\times 1{0}^{4}\ {\rm{m}}\ {{\rm{s}}}^{-1}\) in the pass band and \(3.65\times 1{0}^{4}\ {\rm{m}}\ {{\rm{s}}}^{-1}\) in the rejection band. Being the same both in the MC and in unstructured parts of the YIG waveguide, these values correspond well with theoretically calculated velocities of the first width BVMSW mode in a regular 1.9-mm-wide YIG waveguide (\(3.83\times 1{0}^{4}\) and \(3.65\times 1{0}^{4}\ {\rm{m}}\ {{\rm{s}}}^{-1}\), respectively). Together, the differences in the decay rates and group velocities may account for only two-fold reduction of SW power within the rejection band compared to the pass band, while the experimentally observed reduction exceeds 20 dB (see Fig. 2b).
Comparison of BLS results and pulsed microwave measurements
For further analysis of the pulsed SW dynamics in the width-modulated MC and for comparison with the microwave signals detected at the output antenna, we used the BLS data shown in Fig. 4 to calculate the dependence of the SW pulse energy (defined as an integral of the magnon density over the waveguide width and magnon arrival time) on the propagation distance. The results of this analysis are presented in Fig. 5. As one can see, the spatial decay of SW pulses within both the pass and rejection bands can be accurately described by a simple exponential function (see solid lines in Fig. 5) with slightly different decay rates. Being extended to the position of the output microwave antenna, these exponential fits provide the estimated two-fold relative decay in the SW pulse within the rejection band compared to the SW pulse within the pass band. At the same time, the experimental microwave measurements of the output pulses demonstrate much stronger (6 times; see data points at 13 mm in Fig. 5) decay. Note that the observed decay of the microwave output from a pulsed 30-ns-long SW signal differs from the decay of CW signals shown in Fig. 2 because of the finite spectral width of the SW pulses used in the experiments. Thus, our experiments clearly demonstrate the substantial difference in the output signal power within the MC’s rejection band measured by the BLS and microwave techniques.
The main panel shows the energy of the spin-wave (SW) pulses at different positions along the magnonic crystal (MC). Solid circles and triangles—experimental data as measured by the Brillouin light scattering (BLS) technique; solid lines—exponential fits; the shaded area between the dashed lines indicate the 3-sigma confidence interval of the decay fit parameter. Solid squares at 13 mm correspond to the results of microwave measurements. The errorbars in the x-dimension are given through the measurement scale to 0.1 mm, while the error in y-dimension is given through the noise in the signal, which is too small to be visible in the graph. Inset: Temporal profiles of the SW pulses at the input and output of the MC, as measured by BLS, in comparison with signals measured by the output microwave antenna.
As a possible nature of this discrepancy we could assume a destructive interference between different components of the SW packet, namely, different frequency-degenerated width and thickness SW modes co-propagating in the waveguide. The role of the width-modulated crystal in this mechanism is to partially transfer the SW energy from the lowest SW modes (which are primarily excited by the input microwave antenna) to highest ones and, also, to introduce additional phase shift between different SW modes. The output microwave antenna integrates the SW amplitude over the waveguide width (e.g., sums different SW components with account of mutual phase relations) and, if the phase relation between different SW modes is destructive, the output microwave signal will be substantially attenuated. At the same time, the spectroscopic BLS measurements are insensitive to the phases of individual SW modes and measure the total SW energy. Thus, this mechanism naturally explains appearance of a rejection band in microwave measurements accompanied by the absence of pronounced reflection or additional damping in the BLS measurements.
The proposed mechanism of reflection-less formation of rejection band lead to one additional unexpected consequence. Thus, higher-order SW modes, created by the MC, propagate in the unstructured portion of the waveguide with slightly different phase velocities. As a result, mutual phase relations between different SW components will change during propagation of the SW pulse and the rejection frequency, measured by the microwave technique, should depend on the position of the output antenna. We have verified this prediction in an additional experiment with movable output antenna, while keeping all other parameters of the microwave measurement system the same. We observed the gradual shift of the central band gap frequency (see orange line in Fig. 2b) up to 17 MHz as a function of the distance between antennas (see Fig. 6). This result strongly supports the proposed mechanism and, also, provides an additional way to control transmission properties of this type of MCs.
Relative shift of the band gap frequency as a function of the distance between the antennas. The error in the band gap shift is estimated as the full-width half-maximum value of the central frequency in the rejection band, while the error of the antenna distance is given through the measurement scale to 0.1 mm.
Discussion
Based on the results of the BLS and microwave electric measurements, we have found that the longitudinally magnetized width-modulated MC does not manifest Bragg reflections, but still demonstrates well-pronounced frequency band gaps in the microwave measurements. The formation of such a reflection-less rejection band can be explained by the destructive interference of different frequency-degenerated SW modes excited by the MC. At the same time, our results significantly differ from the results of the experiments and the simulations presented in refs. 30,52,53 for micro-sized width-modulated MCs, where the classical Bragg-gaps were clearly observed. And there is a fundamental reason behind it. The MC under consideration in this work is macroscopic. Relatively large width results in a very dense spectrum of width modes, which are separated only by a few MHz. This fact allows direct two-magnon scattering between these modes. This process allows for both backward and forward scattering in relation to the direction of original wave propagation. Since the wavevector difference is also very small, the preferred scattering direction is forward. A number of forward-scattered waves with different phases and group velocities interfere with each other at the output antenna, producing the observed rejection bands without appearance of Bragg reflections. In the case of microscopic MCs the frequency gap between neighboring width modes is very large. Such a spectrum allows only back-scattering, which results in the Bragg-type band gaps.
We believe, that the reflection-less SW propagation is a general property of the macroscopic width-modulated MCs. As we showed above, the appearance of the rejection bands is the result of interference of different width modes. The spectral content of the output SW packet strongly depends on mutual positions of the scattering centers (period of width modulation) as well as on scattering efficiencies. Thus, in general, the number and the depth of the rejection bands should be described by some non-monotonic function of the crystal geometry. Also, rejection band positions of such width-modulated MCs depend strongly on the position of the receiving antenna (see Fig. 6). The detailed study of properties of width-modulated MCs falls outside of the scope of this manuscript. However, we believe that it deserves to be a subject for another research paper and we sincerely hope that our paper will become a trigger for such studies.
From the practical point of view, such a reflection-less artificial crystal looks very promising for cascading of magnonic-crystal-based devices in magnonics circuits due to the significant reduction of back-coupling between the contiguous cascades. The position dependence of the effective rejection frequency can be used for development of simple MC-based frequency multiplexers and demultiplexers.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Kruglyak, V. V., Demokritov, S. O. & Grundler, D. Magnonics. J. Phys. D Appl. Phys. 43, 264001 (2010).
Chumak, A. V., Vasyuchka, V. I., Serga, A. A. & Hillebrands, B. Magnon spintronics. Phys. Rev. Lett. 109, 160401 (2012).
Khitun, A., Bao, M. & Wang, K. L. Spin-wave magnetic nanofabric: a new approach to spin-based logic circuitry. IEEE Trans. Magn. 44, 2141–2152 (2008).
Chumak, A. V., Serga, A. A. & Hillebrands, B. Magnon transistor for all-magnon data processing. Nat. Commun. 5, 4700 (2014).
Brächer, T. et al. Phase-to-intensity conversion of magnonic spin currents and application to the design of a majority gate. Sci. Rep. 6, 38235 (2016).
Csaba, G., Papp, A. & Porod, W. Perspectives of using spin waves for computing and signal processing. Phys. Lett. A 381, 1471–1476 (2017).
Fischer, T. et al. Experimental prototype of a spin-wave majority gate. Appl. Phys. Lett. 110, 152401 (2017).
Dobrovolskiy, O. V. et al. Spin-wave phase inverter upon a single nanodefect. ACS Appl. Mater. Interfaces 11, 17654–17662 (2019).
Bozhko, D. A. et al. Bogoliubov waves and distant transport of magnon condensate at room temperature. Nat. Commun. 10, 2460 (2019).
Krawczyk, M. & Grundler, D. Review and prospects of magnonic crystals and devices with reprogrammable band structure. J. Phys. Condens. Matter 26, 123202 (2014).
Chumak, A. V., Serga, A. A. & Hillebrands, B. Magnonic crystals for data processing. J. Phys. D Appl. Phys. 50, 244001 (2017).
Heussner, F. et al. Frequency-division multiplexing in magnonic logic networks based on caustic-like spin-wave beams. Phys. Stat. Sol. RRL 12, 1800409 (2018).
Gieniusz, R. et al. The switching of strong spin wave beams in patterned garnet films. Sci. Rep. 7, 8771 (2017).
Vogel, M., Hillebrands, B. & von Freymann, G. Spin-wave optical elements: towards spin-wave Fourier optics. Preprint at https://arxiv.org/abs/1906.02301 (2019).
Nikitov, S. A., Taihades, P. & Tsai, C. S. Spin waves in periodic magnetic structures–magnonic crystals. J. Magn. Magn. Mater. 236, 320 (2001).
Ustinov, A. B., Drozdovskii, A. V. & Kalinikos, B. A. Multifunctional nonlinear magnonic devices for microwave signal processing. Appl. Phys. Lett. 96, 142513 (2010).
Lenk, B., Ulrichs, H., Garbs, F. & Münzenberg, M. The building blocks of magnonics. Phys. Rep. 507, 107 (2011).
Ustinov, A. B., Kalinikos, B. A., Demidov, V. E. & Demokritov, S. O. Formation of gap solitons in ferromagnetic films with a periodic metal grating. Phys. Rev. B 81, 180406 (2010).
Liu, X. M., Ding, J., Kakazei, G. N. & Adeyeye, A. O. Magnonic crystals composed of \({{\rm{Ni}}}_{80}{{\rm{Fe}}}_{20}\) film on top of \({{\rm{Ni}}}_{80}{{\rm{Fe}}}_{20}\) two-dimensional dot array. Appl. Phys. Lett. 103, 062401 (2013).
Kłos, J. W., Krawczyk, M., Dadoenkova, Y. S., Dadoenkova, N. N. & Lyubchanskii, I. L. Photonic-magnonic crystals: multifunctional periodic structures for magnonic and photonic applications. J. Appl. Phys. 115, 174311 (2014).
Sadovnikov, A. V., Gubanov, V. A., Sheshukova, S. E., Sharaevskii, Y. P. & Nikitov, S. A. Spin-wave drop filter based on asymmetric side-coupled magnonic crystals. Phys. Rev. Appl. 9, 051002 (2018).
Zhu, Y., Chi, K. H. & Tsai, C. S. Magnonic crystals-based tunable microwave phase shifters. Appl. Phys. Lett. 105, 022411 (2014).
Nikitin, A. A. et al. A spin-wave logic gate based on a width-modulated dynamic magnonic crystal. Appl. Phys. Lett. 106, 102405 (2015).
Inoue, M. et al. Investigating the use of magnonic crystals as extremely sensitive magnetic field sensors at room temperature. Appl. Phys. Lett. 98, 132511 (2011).
Chumak, A. V. et al. Storage-recovery phenomenon in magnonic crystal. Phys. Rev. Lett. 108, 257207 (2012).
Karenowska, A. D., Chumak, A. V., Serga, A. A., Gregg, J. F. & Hillebrands, B. Magnonic crystal based forced dominant wavenumber selection in a spin-wave active ring. Appl. Phys. Lett. 96, 082505 (2010).
Chumak, A. V. et al. All-linear time reversal by a dynamic artificial crystal. Nat. Commun. 1, 141 (2010).
Gubbiotti, G. et al. Brillouin light scattering studies of planar metallic magnonic crystals. J. Phys. D. Appl. Phys. 43, 264003 (2010).
Mruczkiewicz, M. et al. Spin-wave nonreciprocity and magnonic band structure in a thin permalloy film induced by dynamical coupling with an array of Ni stripes. Phys. Rev. B 96, 104411 (2017).
Chumak, A. V. et al. Spin-wave propagation in a microstructured magnonic crystal. Appl. Phys. Lett. 95, 262508 (2009).
Obry, B. et al. A micro-structured ion-implanted magnonic crystal. Appl. Phys. Lett. 102, 202403 (2013).
Kakazei, G. N., Liu, X. M., Ding, J. & Adeyeye, A. O. \({{\rm{Ni}}}_{80}{{\rm{Fe}}}_{20}\) film with periodically modulated thickness as a reconfigurable one-dimensional magnonic crystal. Appl. Phys. Lett. 104, 042403 (2014).
Dobrovolskiy, O. V. et al. Magnon-fluxon interaction in a ferromagnet/superconductor heterostructure. Nat. Phys. 15, 477 (2019).
Schwarze, T. & Grundler, D. Magnonic crystal wave guide with large spin-wave propagation velocity in CoFeB. Appl. Phys. Lett. 102, 222412 (2013).
Mansurova, M. et al. Magnetization dynamics in magnonic structures with different geometries: interfaces, notches and waveguides. J. Phys. Condens. Matter 29, 214001 (2017).
Mizukami, S. & Serga, A. A. Advancement in Heusler compounds and other spintronics material designs and applications. J. Phys. D Appl. Phys. 48, 160301 (2015).
Langer, M. et al. Parameter-free determination of the exchange constant in thin films using magnonic patterning. Appl. Phys. Lett. 108, 102402 (2016).
Serga, A. A., Chumak, A. V. & Hillebrands, B. YIG magnonics. J. Phys. D Appl. Phys. 43, 264002 (2010).
Langner, T. et al. Spin-wave propagation through a magnonic crystal in a thermal gradient. J. Phys. D Appl. Phys. 51, 344002 (2018).
Mihalceanu, L. et al. Temperature dependent relaxation of dipolar-exchange magnons in yttrium-iron-garnet films. Phys. Rev. B 97, 214405 (2018).
Lu, L., Joannopoulos, J. D. & Soljačić, M. Topological photonics. Nat. Photonics 8, 821 (2014).
Sakoda, K. Optical Properties of Photonic Crystals (Springer, Heidelberg, 2014).
Brun, M., Movchan, A. B. & Jones, I. S. Phononic band gap systems in structural mechanics: finite slender elastic structures and infinite periodic waveguides. J. Vib. Acoust. 135, 041013 (2013).
Hussein, M. I., Leamy, M. J. & Ruzzene, M. Dynamics of phononic materials and structures: Historical origins, recent progress, and future outlook. Appl. Mech. Rev. 66, 040802 (2014).
Polushkin, N. I. Forward mode coupling and bandgap formation in magnonic crystals. Phys. Lett. A 377, 2221 (2013).
Schneider, T., Serga, A. A., Neumann, T., Hillebrands, B. & Kostylev, M. Phase reciprocity of spin-wave excitation by a microstrip antenna. Phys. Rev. B 77, 214411 (2008).
Chumak, A. V., Serga, A. A., Wolff, S., Hillebrands, B. & Kostylev, M. P. Scattering of surface and volume spin waves in a magnonic crystal. Appl. Phys. Lett. 94, 172511 (2009).
Mohseni, M. et al. Backscattering immunity of dipole-exchange magnetostatic surface spin waves. Phys. Rev. Lett. 122, 197201 (2019).
Demokritov, S. O., Hillebrands, B. & Slavin, A. N. Brillouin light scattering studies of confined spin waves: linear and nonlinear confinement. Phys. Rep. 348, 441–489 (2001).
Sandweg, C. W. et al. Wide-range wavevector selectivity of magnon gases in Brillouin light scattering spectroscopy. Rev. Sci. Instrum. 81, 073902 (2010).
Bozhko, D.A., et al. Unconventional spin currents in magnetic films. Preprint at https://arxiv.org/abs/1904.12610 (2019).
Lee, Ki-Suk, Han, Dong-Soo & Kim, Sang-Koog Physical origin and generic control of magnonic band gaps of dipole-exchange spin waves in width-modulated nanostrip waveguides. Phys. Rev. Lett. v.102, 127202 (2009).
Wang, Q. et al. Voltage-controlled nano-scale reconfigurable magnonic crystal. Phys. Rev. B 95, 134433 (2017).
Acknowledgements
The work was supported in part by the Deutsche Forschungsgemeinschaft (DFG) within projects B01 and B04 of the Transregional Collaborative Research Centre (SFB/TRR) 173 “Spin+X”, by the Ministry of Science and Higher Education of the Russian Federation, by the EU Horizon 2020 research, by the ERC Starting Grant 678309 MagnonCircuits and innovation program within the CHIRON project (contract number 801055), by DAAD-FCT project “Spin-wave detection beyond the limit of inductive methods”, and by the grants Nos. EFMA-1641989 and ECCS-1708982 from the NSF of the USA. D. A. Bozhko acknowledges support from the Alexander von Humboldt Foundation. S. A. Bunyaev and G. N. Kakazei acknowledge the Network of Extreme Conditions Laboratories-NECL and Portuguese Foundation of Science and Technology (FCT) support through Project Nos. NORTE-01-0145-FEDER-022096, POCI-0145-FEDER-030085, and EXPL/IF/00541/2015 (to S.A.B.).
Author information
Authors and Affiliations
Contributions
A.A.N. and A.B.U. designed and created the width-modulated sample, while A.V.C. produced the thickness-modulated sample. P.F. performed the experiments on the width-modulated sample in collaboration with A.A.N. and S.A.B. and analyzed the experimental data. F.C. and A.V.C. performed the experiments on the thickness-modulated sample. A.A.S., D.A.B., V.S.T. and Q.W. created the interpretation. P.F., A.A.N. and A.A.S. wrote the paper with contribution from all the authors. A.B.U., A.A.S., G.N.K., B.A.K. and B.H. contributed to the experimental idea, planned, and supervised the project. All authors analyzed the experimental data and discussed the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Frey, P., Nikitin, A.A., Bozhko, D.A. et al. Reflection-less width-modulated magnonic crystal. Commun Phys 3, 17 (2020). https://doi.org/10.1038/s42005-020-0281-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-0281-y
This article is cited by
-
Intrinsic topological magnons in arrays of magnetic dipoles
Scientific Reports (2022)
-
Sensitivity enhancement in magnetic sensor using CoFeB/Y3Fe5O12 resonator
Scientific Reports (2022)
-
Advances in coherent magnonics
Nature Reviews Materials (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.