Abstract
The Floquet state, which is a periodically and intensely light-driven quantum state in solids, has been attracting attention as a novel state that is coherently controllable on an ultrafast time scale. An important issue has been to demonstrate experimentally novel electronic properties in the Floquet state. One technique is light scattering spectroscopy, which offers an important clue to clarifying the symmetries and energy structures of the states through symmetry analysis of the polarization selection rules. Here, we determine circular and linear polarization selection rules of light scattering in a mid-infrared-driven Floquet system in monolayer MoS2 and provide a comprehensive understanding in terms of the “dynamical symmetry” of the Floquet state.
Similar content being viewed by others
Introduction
Floquet engineering is a potential concept for coherent control of electronic states under a strong light field1,2,3,4,5,6,7. The Floquet theoretical approach is useful for describing strong light–matter interactions at energy scales beyond which perturbation theory works8. In this nonperturbative regime, intense light is predicted to change the symmetry and topology of the states and in turn the electronic properties of solids1,2.
The Floquet state in solids has been verified through time and angle-resolved photoemission spectroscopy3,4, time-resolved absorption spectroscopy5,6, and time-resolved transport measurements7. Its properties, such as nonperturbative electron dynamics during the period of the driving laser, can also be explored by using high-order harmonic generation (HHG)9,10,11, which is a coherent emission process from a Floquet system12,13,14,15,16.
Here, we examine light scattering in a Floquet system by injecting an additional probe pulse. Compared with HHG, tuning of the polarization and frequency of the probe light may provide more detailed information about the symmetries and electronic structures. This process is nothing but high-order sideband generation (HSG)17,18,19,20.
Below, we systematically present polarization selection rules, which is fundamental to probe the symmetry of the electronic states, for HSG in monolayer MoS2 under a mid-infrared (MIR) driving field. In a Floquet system, the electronic properties are described by a unique class of symmetries, called “dynamical symmetries” (DSs), which unify the symmetries of the spatio-temporal profiles of the laser field and material3,12,14,15,16,21. It has been experimentally confirmed that DSs govern the band crossings of surface electrons in a light-driven topological insulator3 and determines the polarization selection rules for HHG in a circularly polarized light-driven crystalline solid15. Here, we introduce a new interpretation, i.e., HSG as “Raman scattering” of the MIR-driven Floquet state, and use the DS concept to achieve a full understanding of the polarization selection rules.
Results
HSG spectra from monolayer MoS2
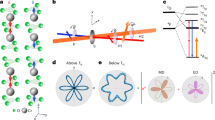
We prepared monolayer MoS2 grown with the CVD method (see “Methods” section). This atomically thin semiconductor is an ideal experimental HSG platform on which to avoid propagation effects10,11,22,23,24,25. Figure 1 shows a schematic diagram of the HSG measurement setup. We used intense MIR pulses (photon energy: ħωMIR = 0.26 eV, pulse duration: 60 fs) to create a Floquet state in monolayer MoS2. To achieve a nonperturbative regime without damaging the monolayer, we set the photon energy of the pulses to a much lower energy than the bandgap energy of the monolayer (1.8 eV)11. In addition, we injected weak near-infrared (NIR) pulses nearly resonant with the bandgap energy (photon energy: ħωNIR = 1.55 eV, pulse duration: 110 fs) into the MIR-driven system. We controlled the polarizations of the MIR and NIR pulses by using liquid crystal retarders and resolved the polarization of the sidebands by using wave plates and polarizers. The sideband spectra were detected by a spectrometer equipped with a CCD camera (see “Methods” section). Throughout this paper, we denote the zigzag direction of monolayer MoS2 as X and armchair direction as Y.
We observed HHG spectra at photon energies of mħωMIR (m: integer) by irradiating the monolayer with MIR pulses and observed the HSG spectra at photon energies of ħωNIR + mħωMIR (m: integer) by simultaneously applying NIR pulses. Therefore, we obtained the HSG contribution by subtracting the HHG component from the spectra (Supplementary Note 1). Figure 2 shows polarization-unresolved HSG spectra under linearly and circularly polarized excitation with a MIR-pulse peak intensity of 0.5 TW cm−2 and NIR-pulse peak intensity of 0.5 GW cm−2. Here, sidebands up to seventh order appear under linearly polarized excitations. In contrast, sidebands only up to third-order appear under circularly polarized excitation. This difference may arise from the different resultant kinetic energies that coherent electron–hole pairs obtained from linearly and circularly polarized laser fields18,20.
Polarization-unresolved HSG spectra measured under linearly polarized (cyan, X-polarized near-infrared (NIR) and mid-infrared (MIR) pulses) and circularly polarized excitation (red, σ+-polarized NIR and MIR pulses). The intensity of the cyan spectrum is multiplied by 100 for clarity. The black arrow shows the photon energy of the NIR pulses.
Nonperturbative aspects induced by MIR light appear in both the spectral shape and excitation power dependence. One such aspect is the non-exponential decay with increasing order in the spectra. The excitation power dependence is shown in Supplementary Fig. 1. Moreover, the MIR power dependence deviates from the power-law derived from perturbation theory under both linearly and circularly polarized excitations (Supplementary Fig. 1a, b). On the other hand, the intensity of the sideband is proportional to the NIR probe power (Supplementary Fig. 1c, d). This indicates the NIR pulses can be treated as a perturbation.
Polarization selection rule of HSG
The observed selection rules are shown in Fig. 3. Figure 3a–d shows circular (σ+, σ−) polarization-resolved sideband spectra obtained from different combinations of σ+-polarized and σ−-polarized excitations. The polarization of the sideband depends on the order and the polarization of the excitation pulses. Since we obtained the same result from monolayer MoSe2, which has the same crystal structure, the selection rules are determined only by the symmetry of the crystal and polarization of the light (Supplementary Fig. 2).
a–d Circular polarization-resolved HSG spectra. Red and blue shaded areas indicate σ+-polarized and σ−-polarized spectra, respectively. The sidebands are generated by a σ+-polarized near-infrared and σ+-polarized mid-infrared pulses (σ+, σ+), b (σ+, σ−), c (σ−, σ+), d (σ−, σ−). e–h Linear polarization-resolved HSG spectra. Cyan and yellow areas indicate X-polarized and Y-polarized spectra, respectively. The sidebands are generated by e (X, X), f (X, Y), g (Y, X), h (Y, Y). Each order of the sideband is scaled with the indicated number.
Furthermore, we systematically examined the linear polarization selection rules. Figure 3e–h shows linear polarization-resolved sideband spectra obtained from different combinations of X and Y-polarized excitations. In particular, when MIR-driving pulses are X-polarized (Fig. 3e, g), odd-order sidebands are emitted with a perpendicular polarization to that of NIR pulses and even-order sidebands are emitted with a parallel polarization. On the other hand, when the MIR-driving pulses are Y-polarized (Fig. 3f, h), the polarization of the sideband is parallel to that of NIR pulses for all orders.
Discussion
To explain these selection rules, we propose a simple scheme for symmetry analysis of HSG using the “Raman tensor” and DSs. In the previous report, HSG selection rules were explained in terms of the symmetry of microscopic intraband dynamics of electron–hole pairs in momentum space20. However, it is difficult to extend this microscopic explanation to the circular polarization case or to polarization selection rules in other materials.
Below, we show that DS gives us a general tool for symmetry analysis of HSG. To justify the “Raman-scattering” description, we consider a microscopic model of HSG. We start with a general Hamiltonian of an electron interacting with an electric field in a solid. We apply the Floquet theorem by assuming periodicity of the MIR-driving field and perturbation theory for the weak NIR pulses (Supplementary Note 2). We calculated the polarization current in the MIR-driven Floquet system perturbed by additional NIR pulses, which emits sideband light as follows:
Here, \(\hat J_\mu = \partial \hat H_0\left( t \right)/\partial A_\mu \left( t \right)\) is the current operator in the velocity gauge, \(\hat H_0\left( t \right)\) is the Hamiltonian of the system of a crystalline solid and external MIR laser field, |iF〉 and |eF〉 are initial and intermediate Floquet eigenstates, \(\hbar \omega _{ei} = {\it{\epsilon }}_{e_{\mathrm{F}}} - {\it{\epsilon }}_{i_{\mathrm{F}}}\) is the difference in quasi-energy between each Floquet eigenstate and \(\delta {\mathbf{A}}_{{\mathrm{NIR}},j}\) is the vector potential of the additional NIR pulses (see Supplementary Note 2). Equation (1) justifies the “Raman scattering” process description depicted in Fig. 4. A NIR photon coherently excites an electron from the initial to an intermediate Floquet state, and the electron simultaneously relaxes back to the initial state by emitting a sideband photon. In this interpretation, the high-order sideband corresponds to “multi-photon anti-Stokes Raman scattering”. The second rank tensor \(\chi _{\mu ,\nu }^{e_{\mathrm{F}}}\left( {t,t^{\prime} } \right) = \left\langle {i_{\mathrm{F}}\left( t \right)} \right|\hat J_\mu \left| {e_{\mathrm{F}}\left( t \right)} \right\rangle \times \left\langle {e_{\mathrm{F}}\left( {t^{\prime} } \right)} \right|\hat J_\nu \left| {i_{\mathrm{F}}\left( {t^{\prime} } \right)} \right\rangle\) corresponds to the response function of the Floquet system, which gives the relation between JSG(t) and δANIR(t). It should be noticed that not the polarization current JSG(t) but \(\chi _{\mu ,\nu }^{e_{\mathrm{F}}}\left( {t,t^{\prime} } \right)\) follows the DS of the MIR-driven Floquet system in the case of HSG selection rule. This is in contrast with the case of HHG selection rules16, where the current has the same DS as the Floquet system.
The energies of the incident near-infrared (NIR) photon and scattered mth order sideband photon are written as ħωNIR and ħωNIR + mħωMIR, respectively. The vertical arrows represent electronic transitions between the initial Floquet state |iF〉 and intermediate Floquet state |eF〉. Ladder-like levels with spacing of the MIR photon energy (ħωMIR) denote the quasi-energy levels of the Floquet states.
One simple way to describe the symmetry restriction on JSG(t) and δANIR(t) is to consider a second rank tensor \({\mathbf{J}}_{{\mathrm{SG}}}\left( t \right)\delta {\mathbf{A}}_{{\mathrm{NIR}}}^\dagger \left( t \right)\). One can derive the invariance of this tensor under the DS operation when δANIR(t) is an “eigenvector” of the DS operation (Supplementary Note 3). JSG(t) and δANIR(t) are directly related to the electric fields of the mth order sideband ESG,m(t) and the NIR light ENIR(t). Therefore, the symmetry restriction can be written in terms of a “Raman tensor” as follows:
where \(E_{{\mathrm{SG}},m,x}\,{\mathrm{and}}\,E_{{\mathrm{NIR}},x}\ ( {E_{{\mathrm{SG}},m,y}\,{\mathrm{and}}\,E_{{\mathrm{NIR}},y}} )\) denote the X (Y) component of the electric fields of the mth order sideband and NIR light, respectively. Here, the direction of the electric field is reduced to being in a two-dimensional space parallel to the monolayer sample in our experimental setup. The “Raman tensor” satisfies the DS of the Floquet system:
where \(\hat X\) is a DS operation. Equation (3) determines the polarization selection rules of HSG.
This equation also supplies a physical insight of HSG selection rules, where the DS of the Floquet system determines the relation between incident and scattered lights. This is similar to the conventional Raman scattering in crystalline solids, where the tensor has the symmetry of the solid and determines the selection rules.
The DS operation of the Floquet system is determined by the symmetry of the monolayer MoS2 and the MIR-driving field. Thus, the DS of the system under circularly polarized MIR light is different from that under linearly polarized MIR light. Under circularly polarized light, the DS operator that determines the selection rule is
where σM = ±1 is the polarization of the MIR-driving pulses, \(\hat \tau _n\) is a temporal translation by T/n (T: the period of the MIR light field) and \(\hat R_3\) is a spatial rotation by 2π/3. The angle of 2π/3 reflects the three-fold rotational symmetry of the crystal (Supplementary Note 4). From Eqs. (3) and (4), the circular polarization selection rule of the mth order sideband is derived as
where \(\sigma _{\mathrm{N}},\sigma _{\mathrm{S}}^m =\pm\! 1\) denotes the polarization of the NIR and mth order sideband, respectively, and N is an integer (Supplementary Note 5). Equation (5) is consistent with all experimental results in Fig. 3a–d. It is noteworthy that this equation cannot be derived from the DS of the MIR-driven and NIR-driven crystal using the same analysis as that in the HHG selection rule16 (see Supplementary Note 6).
Equation (5) represents the angular momentum conservation rule of light modified in crystalline solids15,26,27. The σ+ (σ−)-polarized light can be considered to have spin +ħ (−ħ). The left-hand side of Eq. (5) shows the difference between the total spin of the incident photons and the spin of the emitted mth order sideband photon. Although the right-hand side should be zero in isotropic media, 3Nħ is allowed in monolayer MoS2, which has three-fold rotational symmetry, due to the rotational analog of the umklapp process.
The linear polarization selection rule can be derived similarly. The DS of the Floquet system depends on whether the polarization of the MIR pulses is in the X or Y direction, reflecting the mirror symmetry with respect to the Y direction of monolayer MoS2. The following DS operations determine the selection rules, respectively:
where \(\hat \sigma _{\mathrm{y}}\) means reflection with respect to the Y direction. Because of the temporal term in Eq. (6), the polarizations of the odd-order and even-order sidebands are perpendicular to each other in the X-polarized case. On the other hand, all sidebands have the same polarization in the Y-polarized case (Supplementary Notes 4 and 5). This is consistent with the experimental results in Fig. 3e–h. Table 1 summarizes the polarization selection rules in each configuration.
Odd-order sidebands in monolayer WSe2 with Y-polarized MIR pulses were not observed in the previous report, although they were observed in our experiment20. This fact does not contradict our selection rules. The difference in the intensity of odd-order sidebands may be attributed to the microscopic electron dynamics depending on the frequency of the excitation pulses. In previous works17,18,19,20, the driving field is considered only to induce intraband acceleration of electron–hole pairs. In this work, due to the relatively higher frequency of the MIR pulse, the driving field may also contribute to coherent electron–hole pair creation, i.e., interband transition, giving rise to the increase of the odd-order harmonics intensity. In terms of the “Raman scattering” description, the driving field may create a different Floquet state depending on its frequency and determine the efficiency of the scattering process.
In our theoretical formalism, dephasing and relaxation is not included, which may affect the time-translation symmetries similarly to HHG28. However, the effect of the dephasing on DS should be negligible as the selection rules are well explained by the DS without dephasing in this study. The dephasing effect should be more important and relevant for HHG and HSG in the metallic or strongly correlated electronic system where the electron–electron scattering takes place much faster than that in semiconductors.
In conclusion, we have systematically determined the circular and linear polarization selection rules of HSG in monolayer MoS2. By combining the concepts of Floquet and perturbation theory, we devised a new description of HSG as a “Raman scattering” in the MIR-driven Floquet state and revealed that the selection rules of HSG can be comprehensively understood in terms of DS. DS has the potential to describe topological phases and classify Floquet systems such as Floquet topological insulators2,21. Thus, our results pave the way for experimental studies of electronic structures and their topological properties of Floquet systems through light-scattering experiments and DS analyses.
Methods
Sample preparation
Monolayer MoS2 and MoSe2 were grown on sapphire substrates by chemical vapor deposition. The monolayer flake size of MoS2 was typically 100 μm and MoSe2 was typically tens of micrometers. The MoS2 monolayers were prepared by using the method reported by Kojima et al.29. The monolayer MoSe2 was purchased from 2d Semiconductors, Inc.
Experiments
The experimental setup for the HSG measurements is shown in Supplementary Fig. 4. Ultrafast laser pulses (photon energy 1.55 eV, 35 fs pulse duration, 1 kHz repetition rate, 7 mJ pulse energy) were derived from a Ti:sapphire-based regenerative amplifier. Some of the total pulse energy (1 mJ) was used to generate signal and idler beams by an optical parametric amplifier (OPA, TOPAS-C, Light Conversion). The MIR pulses (photon energy 0.26 eV) were obtained by difference frequency generation (DFG) of the signal and idler beams in a AgGaS2 crystal. After the DFG, the signal and idler beams were blocked by a longpass filter (LPF) with a cutoff wavelength of 4 μm. Another part of the ultrafast laser pulses was passed through a band pass filter (BPF) centered at 800 nm (band width 10 nm) and used as the NIR probe pulses. The polarizations of the NIR and MIR pulses were controlled by a wire grid polarizer (WGP), a Glan laser polarizer (GLP), and liquid crystal variable retarders (LCR). The MIR pulses were focused by a ZnSe lens to a spot 60 μm in diameter (full width at half maximum). The NIR pulses were passed through a fused-silica lens and reflected by a D-shaped mirror placed below the MIR beam. The NIR pulses were focused onto the sample almost coaxially with the MIR beams (~4° between the two beams). The pulse durations of NIR and MIR pulses were estimated to be 110 and 60 fs (full width half maximum (FWHM)), respectively, as noted in Supplementary Methods. The generated harmonics and sidebands were collected by fused-silica lens and their spectra were analyzed by a grating spectrometer (iHR320, Horiba) equipped with a Peltier-cooled Si charge-coupled device camera (Syncerity CCD, Horiba). The NIR light was blocked by 750 and 550 nm short pass filter (SPF) in front of the spectrometer. The polarization of the sidebands was resolved by a quarter wave plate and a wire grid polarizer. The obtained spectra were corrected for the total efficiency including mirrors, a spectrometer and a CCD camera. All the experiments were performed in the air at room temperature.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Oka, T. & Aoki, H. Photovoltaic Hall effect in graphene. Phys. Rev. B 79, 081406 (2009).
Lindner, N. H., Refael, G. & Galitski, V. Floquet topological insulator in semiconductor quantum wells. Nat. Phys. 7, 490–495 (2011).
Wang, Y. H., Steinberg, H., Jarillo-Herrero, P. & Gedik, N. Observation of Floquet–Bloch states on the surface of a topological insulator. Science 342, 453–457 (2013).
Mahmood, F. et al. Selective scattering between Floquet–Bloch and Volkov states in a topological insulator. Nat. Phys. 12, 306–310 (2016).
Sie, E. J. et al. Valley-selective optical Stark effect in monolayer WS2. Nat. Mater. 14, 290–294 (2015).
Uchida, K. et al. Subcycle optical response caused by a terahertz dressed state with phase-locked wave functions. Phys. Rev. Lett. 117, 277402 (2016).
McIver, J. W. et al. Light-induced anomalous Hall effect in graphene. Nat. Phys. 16, 38–41 (2020).
Shirley, J. H. Solution of the schrödinger equation with a hamiltonian periodic in time. Phys. Rev. 138, B979 (1965).
Ghimire, S. et al. Observation of high-order harmonic generation in a bulk crystal. Nat. Phys. 7, 138–141 (2011).
Yoshikawa, N., Tamaya, T. & Tanaka, K. High-harmonic generation in graphene enhanced by elliptically polarized light excitation. Science 356, 736–738 (2017).
Yoshikawa, N. et al. Interband resonant high-harmonic generation by valley polarized electron–hole pairs. Nat. Commun. 10, 3709 (2019).
Ben-Tal, N., Moiseyev, N. & Beswick, A. The effect of Hamiltonian symmetry on generation of odd and even harmonics. J. Phys. B 26, 3017–3024 (1993).
Faisal, F. H. M. & Kamiński, J. Z. Floquet–Bloch theory of high-harmonic generation in periodic structures. Phys. Rev. A 56, 748–762 (1997).
Alon, O., Averbukh, V. & Moiseyev, N. Selection rules for the high harmonic generation spectra. Phys. Rev. Lett. 80, 3743–3746 (1998).
Saito, N. et al. Observation of selection rules for circularly polarized fields in high-harmonic generation from a crystalline solid. Optica 4, 1333–1336 (2017).
Neufeld, O., Podolsky, D. & Cohen, O. Floquet group theory and its application to selection rules in harmonic generation. Nat. Commun. 10, 405 (2019).
Zaks, B., Liu, R. B. & Sherwin, M. S. Experimental observation of electron–hole recollisions. Nature 483, 580–583 (2012).
Langer, F. et al. Lightwave-driven quasiparticle collisions on a subcycle timescale. Nature 533, 225–229 (2016).
Banks, H. B. et al. Dynamical birefringence: electron–hole recollisions as probes of Berry curvature. Phys. Rev. X 7, 041042 (2017).
Langer, F. et al. Lightwave valleytronics in a monolayer of tungsten diselenide. Nature 557, 76–80 (2018).
Morimoto, T., Po, H. C. & Vishwanath, A. Floquet topological phases protected by time glide symmetry. Phys. Rev. B 95, 195155 (2017).
Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 10, 343–350 (2014).
Ghimire, S. et al. Generation and propagation of high-order harmonics in crystals. Phys. Rev. A 85, 043836 (2012).
Vampa, G., You, Y. S., Liu, H., Ghimire, S. & Reis, D. A. Observation of backward high-harmonic emission from solids. Opt. Express 26, 12210–12218 (2018).
Xia, P. et al. Nonlinear propagation effects in high harmonic generation in reflection and transmission from gallium arsenide. Opt. Express 26, 29393–29400 (2018).
Konishi, K. et al. Polarization-controlled circular second-harmonic generation from metal hole arrays with threefold rotational symmetry. Phys. Rev. Lett. 112, 135502 (2014).
Seyler, K. L. et al. Electrical control of second-harmonic generation in a WSe2 monolayer transistor. Nat. Nanotechnol. 10, 407–411 (2015).
Baudisch, M. et al. Ultrafast nonlinear optical response of Dirac fermions in graphene. Nat. Commun. 9, 1018 (2018).
Kojima, K. et al. Restoring the intrinsic optical properties of CVD-grown MoS2 monolayers and their heterostructures. Nanoscale 11, 12798–12803 (2019).
Acknowledgements
This work was supported by a Grant-in-Aid for Scientific Research (S) (Grant No. 17H06124). K.N. was supported by a JSPS fellowship (Grant No. JP20J14428). K.U. was supported by a Grant-in-Aid for Early-Career Scientists (Grant No. 19K14632). N.Y. was supported by a JSPS fellowship (Grant No. 16J10537). Y.M. acknowledges support from JST CREST (Grant No. JPMJCR16F3) and a Grant-in-Aid for Scientific Research (B) (Grant No. JP18H01832) from the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan.
Author information
Authors and Affiliations
Contributions
K.N., N.Y., and K.T. conceived the experiments. K.N., K.U., and N.Y. built the experimental setup. K.N. and N.Y. carried out the experiments. T.E. and Y.M. fabricated the samples. K.N., K.U., and K.T. constructed the theoretical framework and wrote the manuscript. All the authors contributed to the discussion and interpretation of the results.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nagai, K., Uchida, K., Yoshikawa, N. et al. Dynamical symmetry of strongly light-driven electronic system in crystalline solids. Commun Phys 3, 137 (2020). https://doi.org/10.1038/s42005-020-00399-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-020-00399-x
This article is cited by
-
Phonon-dressed states in an organic Mott insulator
Communications Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.