Abstract
Short ballistic graphene Josephson junctions sustain superconducting current with a non-sinusoidal current-phase relation up to a critical current threshold. The current-phase relation, arising from proximitized superconductivity, is gate-voltage tunable and exhibits peculiar skewness observed in high quality graphene superconductors heterostructures with clean interfaces. These properties make graphene Josephson junctions promising sensitive quantum probes of microscopic fluctuations underlying transport in two-dimensions. We show that the power spectrum of the critical current fluctuations has a characteristic \(1/f\) dependence on frequency, \(f\), probing two points and higher correlations of carrier density fluctuations of the graphene channel induced by carrier traps in the nearby substrate. Tunability with the Fermi level, close to and far from the charge neutrality point, and temperature dependence of the noise amplitude are clear fingerprints of the underlying material-inherent processes. Our results suggest a roadmap for the analysis of decoherence sources in the implementation of coherent devices by hybrid nanostructures.
Similar content being viewed by others
Introduction
Graphene Josephson junctions (GJJs) in the regime of ballistic transport emerged in the past few years as unique hybrid systems allowing investigation of fundamental quantum phenomena related to proximitized superconductivity in a two-dimensional (2D) material. High-quality graphene superconductor heterostructures with clean interfaces, realized by encapsulating graphene in hexagonal boron nitride (hBN) with one-dimensional edge contacts to superconducting leads, allowed the observation of ballistic transport of Cooper pairs over micron-scale lengths, of gate-tunable supercurrents that persist at large parallel magnetic fields1,2,3 and of different features of 2D Andreev physics4,5,6.
In a short ballistic GJJ, a dissipationless supercurrent flows in equilibrium through the proximitized normal metal region. The coherent flow of Cooper pairs in this structure is due to successive Andreev reflections at the graphene–superconductor interfaces. In the ballistic limit, where the junction channel length \(L\) is much shorter than the mean free path \({l}_{{\rm{mfp}}}\), well-defined Andreev bound states are formed inside the superconducting gap, \(\Delta \equiv \Delta (T)\). The corresponding energies depend on the phase difference \(\phi \) of the superconducting order parameters on the two sides of the junction. Each Andreev level with energy \(\varepsilon (\phi )\), carries a supercurrent \((1/{\Phi }_{0})\partial \varepsilon (\phi )/\partial \phi \), where \({\Phi }_{0}=\hslash /2e\). In the short junction limit (\(L\ll \xi ,W\), where \(\xi =\hslash {v}_{{\rm{D}}}/\Delta \) is the superconducting coherence length, \(W\) is the channel width, and \({v}_{{\rm{D}}}\) is the graphene monolayer Fermi velocity \({v}_{{\rm{D}}}\approx 1{0}^{6}{\rm{m}}{{\rm{s}}}^{-1}\)), the supercurrent is mediated by a single bound state, \(\varepsilon ({q}_{n},\phi )\), per transversal mode \({q}_{n}=(n+1/2)\pi /W\). This mechanism results in a strongly non-sinusoidal current–phase relation (CPR), whose skewness and maximal supercurrent, \({I}_{{\rm{c}}}\), viz., critical current, depend on temperature and gate voltage7,8,9,10,11,12,13, nonvanishing even at the Dirac point, despite the zero carrier concentration resulting from the linear dispersion of graphene.
Experimental evidence of strong Josephson coupling in planar ballistic GJJ has been recently reported14,15,16. Very recent experimental studies integrated graphene-based van der Waals heterostructures into circuit quantum electrodynamics systems17,18,19. Spectroscopy and coherent quantum control in a graphene-based “gatemon”17, together with microwave performances18 and resilience to strong magnetic fields19, make short ballistic GJJs a promising platform for the implementation of coherent quantum circuits in hybrid architectures. Understanding material-inherent microscopic noise sources possibly limiting the phase-coherent behavior of GJJ-based quantum circuits represents an essential, still unexplored, prerequisite. Indications of the possible presence of spurious two-level systems embedded in the heterostructure have been reported in refs. 17,20.
An especially relevant issue is understanding the impact on ballistic GJJs of fluctuations responsible for current noise with \(1/f\) power spectrum, which is observed in a variety of graphene devices21. Low frequency noise with \(1/f\) power spectrum is an intriguing phenomenon occurring in a variety of materials and over different scales. Investigation of decoherence due to \(1/f\) noise in superconducting quantum devices based on conventional Josephson junctions provides relevant insights into microscopic noise sources22. This has allowed developing quantum control strategies to reduce its effects toward the implementation of efficient building blocks for quantum hardware.
Although detrimental in many of its manifestations, \(1/f\) noise offers also opportunities for materials characterization. Graphene, with its inherent bi-dimensional nature and linear ambipolar dispersion, is a unique material in the context of \(1/f\) noise, which has been observed even in clean graphene samples23,24,25,26. \(1/f\) noise is in fact a versatile probe to study fluctuations affecting charge transport properties, as density fluctuations and dielectric screening, which cannot be directly accessed by resistivity measurements. Remarkably, because of their strongly non-sinusoidal CPR with gate voltage-tunable skewness and critical current, ballistic GJJs are potentially flexible quantum probes of microscopic fluctuations underlying transport 2D materials.
A number of investigations on \(1/f\) current (or equivalently resistance) noise in graphene21, and recently in graphene tunnel junctions27, pointed out the relevant role of carrier density fluctuations due to charge trapping and release processes between graphene and carrier traps in the underlying substrate. This noise mechanism, typical of conventional semiconducting field-effect transistor, is commonly described by the McWorther model28. Each trap can be empty or occupied by an electron, and it randomly switches between these two states. Typical switching times between the two states are much longer than the relaxation time of the crystal, thus trapping–recombination traces are modeled as Markovian random telegraph processes. A spatially uniform distribution of independent generation–recombination centers determines a logarithmic distribution of the switching rates, \(1/\tau \), of the noise sources in the interval \([1/{\tau }_{{\rm{max}}},1/{\tau }_{{\rm{min}}}]\). This yields \(1/f\) noise spectrum in the same frequency range21,22,28,29,30,31, the actual low-frequency cut-off \(1/{\tau }_{{\rm{max}}}\) being in practice hardly detectable. This is also the basis of our description of critical current noise in short ballistic GJJs.
In this work, we show that fluctuations with \(1/f\) power spectrum of the critical current of a short ballistic GJJ directly probe carrier density fluctuations of the graphene channel induced by the presence of charge traps in the nearby substrate. Fluctuations of carrier density in the graphene insert are responsible for fluctuations of Andreev levels manifesting themselves as noise in the critical current of the ballistic GJJ. Tunability with the Fermi level, close to and far from the charge neutrality point (CNP), and temperature dependence of the noise amplitude are clear fingerprints of the underlying material-inherent processes. The considered noise mechanism results from proximitized superconductivity of the normal metal forming the junction. It has, therefore, a broader validity beyond GJJ. As a difference, in conventional tunnel Josephson junctions, switching charge traps in the insulating barrier randomly block tunneling channels thus modulating the junction area and inducing \(1/f\) critical current noise22. Our results also provide relevant figures of merit in view of the implementation of coherent quantum circuits in hybrid architectures.
Results
Model
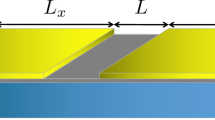
The system considered in this work is schematically shown in Fig. 1a. A graphene layer (gray), partially covered by two superconducting electrodes (yellow), is deposited on a substrate (blue) under which a metal gate (green) allows electrical tuning of the doping level in graphene. Carrier traps, randomly distributed in the substrate, are represented by cyan circles.
a displays the side view, from bottom to top there are a metal gate (green), a substrate (blue), a monolayer graphene (gray), and two superconducting electrodes (yellow). Electron traps are represented with cyan circles randomly distributed inside the substrate. b displays the top view, gray region represents the stripe in normal phase and yellow sides are the regions covered by superconductors. Here \(L\) represents the junction channel and \(W\) is the length of the device along the invariant direction.
We model the ballistic GJJ within the Dirac–Bogoliubov–de Gennes approach where superconducting metal stripes induce on the underlying graphene layer very large doping and superconductivity by proximity effect7,11,12. In the short junction limit, the supercurrent is expressed as
where the Andreev eigenenergies depend on the phase difference \(\phi \) and on the normal-state transmission amplitude \(\tau ({q}_{n})\) as
Here \({k}_{{\rm{F}}}={\mu }_{0}/(\hslash {v}_{{\rm{D}}})\) is the Fermi wavenumber expressed in terms of the Fermi level \({\mu }_{0}\) and the graphene monolayer Fermi velocity \({v}_{{\rm{D}}}\). For a wide and short normal region (see Fig. 1b), \(L\ll W,\xi \), the summation in Eq. (1) can be replaced by an integral. Recently, ballistic devices in this limit have been experimentally realized by using graphene encapsulated in hBN3,15,16. Maximization of Eq. (1) with respect to \(\phi \) gives the junction’s critical current, \({I}_{{\rm{c}}}({\mu }_{0},T)\). Because of the dependence of the Fermi level on the carrier density, both the CPR and the critical current are tunable with the gate voltage. At zero temperature, \({I}_{{\rm{c}}}\) at the CNP, \({\mu }_{0}=0\), is approximately given by \(1.33e{\Delta }_{0}W/(\pi \hslash L)\), where \({\Delta }_{0}\) is the zero-temperature superconducting gap, \({\Delta }_{0}=\Delta (T=0)\)7. The finite supercurrent, in the absence of free carriers in the graphene channel, is due to evanescent modes. With increasing values of doping level \(| {\mu }_{0}| \), the critical current increases due to the contribution of propagating modes, independently of the sign of carriers because of electron–hole symmetry. Its dependence on the Fermi level changes from parabolic close to the CNP to the linear asymptote, \(1.22e{\Delta }_{0}W| {\mu }_{0}| /(\pi {\hslash }^{2}{v}_{{\rm{D}}})\), for large doping \(| {\mu }_{0}| \gg \hslash {v}_{{\rm{D}}}/L\). Small amplitude Fabry–Perot oscillations appear for finite doping due to the interference of reflected carriers at the graphene–superconductor interfaces, characteristic of the ballistic regime7.
Critical current noise
Whenever the Fermi level deviates from the equilibrium value \({\mu }_{0}\), the critical current fluctuations can be approximated as
where
Close to the CNP, where the critical current first derivative vanishes, the dominant contribution to current fluctuations is quadratic in the fluctuations of the Fermi level, whereas for large dopings the leading contribution is linear in \(\delta \mu (t)=\mu (t)-\langle \mu (t)\rangle =\mu (t)-{\mu }_{0}\). In the following, we relate fluctuations of the Fermi level to the carrier density fluctuations due to trapping/recombination processes within the McWorther model and evaluate the critical current power spectrum
where the current–current correlation function is written in terms of second- and higher-order correlators of \(\delta \mu (t)\)
In our model, fluctuations of the Fermi level stem from carriers trapped in the substrate. Charge traps are randomly distributed in the substrate beneath the graphene layer32,33, as sketched in Fig. 1. Charge carrier tunneling between the graphene electron channel and the substrate traps induces a fluctuating voltage34, \({V}_{{\rm{T}}}(t)\), which contributes to the (fixed) voltage drop between the metal gate and the graphene layer, \({V}_{{\rm{G}}}\),
where \({W}_{{\rm{f}}}\) is the work function difference between the gate and graphene. The other two terms are the geometric and quantum capacitance contributions due to charge carriers in the graphene layer, \(d\) and \({\epsilon }_{{\rm{r}}}\) being, respectively, the width and the dielectric constant of the substrate, and \(n(t)\) the instantaneous carrier density in graphene. The equilibrium carrier density \({n}_{0}\) is related to the Fermi level \({\mu }_{0}\), in particular at zero temperature \({\mu }_{0}=\hslash {v}_{{\rm{D}}}\ \sqrt{\pi | {n}_{0}| }\)35. Being a disordered system, charge traps are spatially randomly distributed in the substrate layer and have an unknown distribution in energies \(\epsilon \) (with respect to the CNP, \({\mu }_{0}=0\)). If we assume that the spatial distribution of carrier traps is quasiuniform along the \(\hat{{\boldsymbol{x}}}\) and \(\hat{{\boldsymbol{y}}}\) directions36,37, the voltage drop \({V}_{{\rm{T}}}(t)\) can be written as
where \({\boldsymbol{R}}=({\boldsymbol{r}},z)\) and \({{\mathcal{N}}}_{{\rm{T}}}(\epsilon ,{\boldsymbol{R}},t)\) denotes the density of populated traps per unit volume and energy. In equilibrium, it reads \({{\mathcal{N}}}_{{\rm{T0}}}(\epsilon ,{\boldsymbol{R}})={f}_{{\rm{D}}}(\epsilon -{\mu }_{0}){\mathcal{D}}(\epsilon ,{\boldsymbol{R}})\), where \({\mathcal{D}}(\epsilon ,{\boldsymbol{R}})\) is the number of trap states per unit of energy and volume whose occupation probability is given by the Fermi distribution \({f}_{{\rm{D}}}(x)=1/[{e}^{x/({k}_{{\rm{B}}}T)}+1]\). Since the time scale of fluctuations of carriers in graphene is much shorter than the time scale of the charge fluctuations in the traps31, we assume that charge carriers (as well as Fermi level) in graphene adjust instantaneously to fluctuations of the trapped carriers entering \(\delta {V}_{{\rm{T}}}(t)\). Under these conditions, expansion of Eq. (8) around the equilibrium values gives
where \({C}_{\parallel }={C}_{{\rm{g}}}+{C}_{{\rm{Q}}}\), \({C}_{{\rm{g}}}\equiv {\epsilon }_{{\rm{r}}}/(4\pi d)\) is the geometric capacitance, and \({C}_{{\rm{Q}}}\) is the quantum capacitance
and \(\delta {V}_{{\rm{T}}}(t)\) represents the deviations of the trap voltage drop from the equilibrium value due to population fluctuations of the trap density with respect to \({{\mathcal{N}}}_{{\rm{T}}0}(\epsilon ,{\boldsymbol{R}})\)
where \(\delta {{\mathcal{N}}}_{{\rm{T}}}(\epsilon ,{\boldsymbol{R}},t)={{\mathcal{N}}}_{{\rm{T}}}(\epsilon ,{\boldsymbol{R}},t)-{{\mathcal{N}}}_{{\rm{T0}}}(\epsilon ,{\boldsymbol{R}})\) can be expressed as
and \(X(i,t)\) is a random telegraph process, being one (zero) when the trap \(i\) is filled (empty)31. Switching between the occupied/empty state of trap \(i\) occurs with a rate depending on the trap position along the direction perpendicular to the graphene layer21,28
where we distinguish tunneling processes related to the graphene channel, characterized by \({\gamma }_{0}\) and \(\ell \), and tunneling process related to the gate channel, characterized by \({\gamma }_{0}^{{\prime} }\) and \({\ell }^{{\prime} }\). Typical orders of magnitude of the tunneling parameters are \({\gamma }_{0},{\gamma }_{0}^{{\prime} } \sim 1{0}^{10}\,{{\rm{s}}}^{-1}\) and \(\ell ,{\ell }^{{\prime} } \sim 1\,\) Å21. The Fermi level correlators entering \({I}_{{\rm{c}}}\)’s fluctuations in Eq. (7) are therefore related to correlators of various orders of the population of traps. Exploiting Markovianity, assuming that traps are uncorrelated and \(\langle X(i,t)\rangle ={f}_{{\rm{D}}}({\epsilon }_{i}-{\mu }_{0})\), the correlators up to the fourth order in the population fluctuations of trapped electron density are written as
and \(\langle \delta {{\mathcal{N}}}_{{\rm{T}}}(\epsilon ,{\boldsymbol{R}},t)\rangle =0\) (see details in Supplementary Note 1). By using Eq. (10) with Eq. (12) and the correlators in Eq. (15a–c), considering that \(d\ll \ell ,{\ell }^{{\prime} }\) in the switching rates, Eq. (14), the critical current spectrum, Eq. (6), for frequencies \(\omega \ll {\gamma }_{0},{\gamma }_{0}^{{\prime} }\) takes the characteristic form \({{\mathcal{S}}}_{{I}_{{\rm{c}}}}(\omega )={{\mathcal{A}}}_{{I}_{{\rm{c}}}}/\omega\) with amplitude
where \({\varepsilon }_{{\rm{Q}}}={e}^{2}/({C}_{\parallel }LW)\) and
having assumed that the density of trap states does not depend on \({\boldsymbol{R}}\) and indicated it as \({\mathcal{D}}(\epsilon )\). The critical current power spectrum with amplitude given by Eq. (16) is the main result of this work. The three contributions entering the noise amplitude arise from correlators of the trapped electron density populations of different orders. The term proportional to \({F}_{0}\) derives from second-order correlator, while the terms in \({F}_{1}\) and \({F}_{2}\) derive from correlators of the third and fourth order (see Supplementary Note 1). Their contribution to the noise amplitude depends on the doping level, \({\mu }_{0}\), and on temperature. In the undoped case, being \(d{I}_{{\rm{c}}}/d{\mu }_{0}{| }_{{\mu }_{0}=0}=0\), the spectrum reduces to
and for large doping
Thus by tuning the doping level, the GJJ’s critical current spectrum probes either the power spectrum (large doping) or higher-order correlators of the trapped electron density population. At the CNP, the \({I}_{{\rm{c}}}\) spectrum is a measure of the fourth-order correlator. These correlators sensitively depend on the trap energy distribution \({{\mathcal{D}}}_{\Gamma }(\epsilon )\), entering the functions \({F}_{j}\)s, Eq. (17).
In our phenomenological model, we consider a Lorentzian distribution around a central energy \({\epsilon }_{{\rm{T}}}\) and with width \(\Gamma \)
In the limit \(\Gamma \to 0\) the distribution tends to a Dirac delta function \({\rho }_{{\rm{T}}}\delta (\epsilon -{\epsilon }_{{\rm{T}}})\), describing degenerate traps, whereas for large \(\Gamma \) we model a uniform distribution, \({\rho }_{{\rm{T}}}/(\pi \Gamma )\). In these two limiting cases, the power spectrum can be evaluated in analytic form (see Supplementary Note 1). From now on, in order to compare our results with realistic devices, we fix \(d=0.1\,\upmu {\rm{m}}\), \(L=0.2\,\upmu {\rm{m}}\), and \(W=3\,\upmu {\rm{m}}\). Moreover, we set the relative dielectric constant at \({\epsilon }_{{\rm{r}}}=4.4\) and the gap energy at \(\Delta =0.1\hslash {v}_{{\rm{D}}}/L\), which ensures the validity of the short junction limit, \(\xi \sim \hslash {v}_{{\rm{D}}}/\Delta \gg L\).
The dependence of the amplitude \({{\mathcal{A}}}_{{I}_{{\rm{c}}}}\) on the doping level is reported in Fig. 2a for \(T=0.1\Delta /{k}_{{\rm{B}}}\) and trap energy distribution centered at the CNP, \({\epsilon }_{{\rm{T}}}=0\), for different widths \(\Gamma \). The noise amplitude is symmetric around the resonance condition, \({\mu }_{0}={\epsilon }_{{\rm{T}}}=0\). For a narrow trap energy distribution, \(\Gamma \ll \hslash {v}_{{\rm{D}}}/L\), noise is nonvanishing and takes large values only for low doping. For a broader trap energy distribution, the doping range where the amplitude is nonvanishing increases and reflects \({I}_{{\rm{c}}}\)’s Fabry–Perot oscillations, characteristic of the ballistic transport regime7. The behavior of \({{\mathcal{A}}}_{{I}_{{\rm{c}}}}\) close to the CNP and the contributions from different correlators (dashed lines) of the trapped electron density are reported in Fig. 2b–d. Correlators of orders larger than the second have a substantial impact on the critical current power spectrum in proximity of the CNP where it has an M-shaped trend independently of \(\Gamma \). For larger dopings, the amplitude \({{\mathcal{A}}}_{{I}_{{\rm{c}}}}\) is dominated by the second-order correlator, see Eq. (19).
Amplitude of the critical current noise, \({{\mathcal{A}}}_{{I}_{{\rm{c}}}}\), as a function of the doping level \({\mu }_{0}\) for trap energy distributions centered at the charge neutrality point (CNP), \({\epsilon }_{{\rm{T}}}=0\). The amplitude is expressed in units of \({{I}_{{\rm{c}}}^{* }}^{2}{N}_{{\rm{T}}}\), where \({I}_{{\rm{c}}}^{* }=e\Delta W/(\hslash L)\), \({N}_{{\rm{T}}}={\rho }_{{\rm{T}}}WL\ell \) is the number of traps in a slab of the substrate of depth \(\ell \) under the graphene layer, and \(W\) and \(L\) are the width and the length of the junction channel, respectively. Other parameters are \({k}_{{\rm{B}}}T=0.1\Delta \) and \(\Delta =0.1\hslash {v}_{{\rm{D}}}/L\). Colored lines correspond to different widths of the trap energy distribution \(\Gamma \): \(\Gamma =0.01\hslash {v}_{{\rm{D}}}/L\) (red solid line), \(\Gamma =0.1\hslash {v}_{{\rm{D}}}/L\) (green solid line), and \(\Gamma =\hslash {v}_{{\rm{D}}}/L\) (blue solid line). a compares the amplitudes of the critical current power spectrum for the considered \(\Gamma \). The inset shows a sketch of the graphene band with electronic states occupied up to a generic doping level (gray) and the Lorentzian trap energy distribution centered at the CNP. In b–d, the width is fixed to \(\Gamma =0.01\hslash {v}_{{\rm{D}}}/L\), \(\Gamma =0.1\hslash {v}_{{\rm{D}}}/L\), and \(\Gamma =\hslash {v}_{{\rm{D}}}/L\), respectively. Each panel compares the amplitude (solid line) with the corresponding correlators of second order (red dashed line), third order (green dashed line), and fourth order (blue dashed line) in proximity of \({\mu }_{0}=0\).
Charge carrier density noise
Since both critical current and carrier density fluctuations are induced by trapping–recombination processes, it is worth addressing also the carrier density spectrum. An independent detection of the two spectra could be used for a cross-check of the considered noise mechanism. Carrier density fluctuations in GJJ could be inferred from Hall voltage fluctuation measurements, similarly to the recent experiment on graphene38. Fluctuations of charge carrier density and of the doping level are related by
where
where \({n}_{0}\) represents the charge carrier density at equilibrium. Using Eqs. (14) and (15a–c), in the limit \(d\ll \ell ,{\ell }^{{\prime} }\), the charge carrier density power spectrum for frequencies \(\omega \ll {\gamma }_{0},{\gamma }_{0}^{{\prime} }\) reads
Remarkably, the two spectra have the same structure with \(d{I}_{{\rm{c}}}/d{\mu }_{0}\) in \({{\mathcal{S}}}_{{I}_{{\rm{c}}}}(\omega )\), Eq. (16), replaced with the quantum capacitance, \({C}_{{\rm{Q}}}\), in \({{\mathcal{S}}}_{n}(\omega )\). This quantity does not vanish at the CNP, where \({C}_{{\rm{Q}}}={C}_{{\rm{Q}}}{| }_{{\mu }_{0}=0}=4\mathrm{ln}(2){e}^{2}{k}_{{\rm{B}}}T/(\pi {\hslash }^{2}{v}_{{\rm{D}}}^{2})\), whereas \(d{C}_{{\rm{Q}}}/d{\mu }_{0}{| }_{{\mu }_{0}=0}=0\). Therefore, as a difference with \({I}_{{\rm{c}}}\)’s spectrum, the charge carrier density spectrum at the CNP consists of the second-order correlator in the trapped carrier density fluctuations,
The dependence of the amplitude \({{\mathcal{A}}}_{n}\) on the doping level is reported in Fig. 3a, for the same temperature and trap energy distribution of Fig. 2a. The amplitude \({{\mathcal{A}}}_{n}\) shows an M-shaped trend independently of \(\Gamma \), whereas exactly at the CNP \({{\mathcal{A}}}_{n}\propto {F}_{0}\), the impact of the correlators of orders larger than the second is substantial in proximity of the CNP where the size of the central dip at \({\mu }_{0}=0\) is sensitive to the trap energy distribution width \(\Gamma \), see Fig. 3b–d. For larger doping, the second-order correlator dominates again
If the trap energy distribution instead of being centered at the CNP is centered in the conduction band, both critical current and carrier density spectra are dominated by the second-order correlators. The amplitudes are asymmetric with respect to the resonance condition \({\mu }_{0}={\epsilon }_{{\rm{T}}}\), due to the electron–hole asymmetry, see Fig. 4. Fabry–Perot oscillations in the amplitude of the current power spectrum appear clearly by increasing the width \(\Gamma \) of the trap energy distribution, Fig. 4a. The amplitude of the charge carrier density noise maintains instead a bell-shaped profile around \({\epsilon }_{{\rm{T}}}\), of larger width with broadening of the trap energy distribution, Fig. 4b.
Amplitude of the charge carrier density noise, \({{\mathcal{A}}}_{n}\), in units of \({N}_{{\rm{T}}}/{L}^{4}\), as a function of the doping level \({\mu }_{0}\), for \({k}_{{\rm{B}}}T=1{0}^{-2}\hslash {v}_{{\rm{D}}}/L\) and trap energy distribution centered at the charge neutrality point (CNP), i.e., \({\epsilon }_{{\rm{T}}}=0\) (\({N}_{{\rm{T}}}={\rho }_{{\rm{T}}}WL\ell \) is the number of traps in a slab of the substrate of depth \(\ell \) under the graphene layer and \(W\) and \(L\) are the width and the length of the junction channel, respectively). Colors correspond to different values of width \(\Gamma \): \(\Gamma =0.01\hslash {v}_{{\rm{D}}}/L\) (red solid line), \(\Gamma =0.1\hslash {v}_{{\rm{D}}}/L\) (green solid line), and \(\Gamma =\hslash {v}_{{\rm{D}}}/L\) (blue solid line). a compares the amplitudes \({{\mathcal{A}}}_{n}\) for the considered \(\Gamma \). The left-top inset shows a sketch of the electron structure with the shaded region below a generic doping level and the Lorentzian trap energy distribution centered at the CNP. In b–d, the trap energy widths are \(\Gamma =0.01\hslash {v}_{{\rm{D}}}/L\), \(\Gamma =0.1\hslash {v}_{{\rm{D}}}/L\), and \(\Gamma =\hslash {v}_{{\rm{D}}}/L\): each panel compares the amplitude (solid line) with the corresponding correlators of second (red dashed line), third (green dashed line), and fourth order (blue dashed line) in proximity of \({\mu }_{0}=0\).
Critical current noise amplitude \({{\mathcal{A}}}_{{I}_{{\rm{c}}}}\), in units of \({{I}_{{\rm{c}}}^{* }}^{2}{N}_{{\rm{T}}}\) in a, and charge carrier noise amplitude \({{\mathcal{A}}}_{n}\), in units of \({N}_{{\rm{T}}}/{L}^{4}\) in b, as a function of the doping level \({\mu }_{0}\) (\({I}_{{\rm{c}}}^{* }=e\Delta W/(\hslash L)\), \({N}_{{\rm{T}}}={\rho }_{{\rm{T}}}WL\ell \) is the number of traps in a slab of the substrate of depth \(\ell \) under the graphene layer, and \(W\) and \(L\) are the width and the length of the junction channel, respectively). The trap energy distribution is centered at \({\epsilon }_{{\rm{T}}}=5\hslash {v}_{{\rm{D}}}/L\) and widths are \(\Gamma =0.01\hslash {v}_{{\rm{D}}}/L\) (red solid line, scaled to improve visibility), \(\Gamma =0.1\hslash {v}_{{\rm{D}}}/L\) (green solid line), and \(\Gamma =\hslash {v}_{{\rm{D}}}/L\) (blue solid line). The left-top inset shows a sketch of the electron structure with the shaded region below a generic doping level and the Lorentzian trap energy distribution centered in the conduction band.
Temperature dependencies
Charge trapping–release processes lead to peculiar temperature dependencies of both noise amplitudes. We consider low temperatures \({k}_{{\rm{B}}}T\ll {\Delta }_{0}\) and approximate \(\Delta (T)\approx {\Delta }_{0}\). Figure 5a and c [b and d] display, respectively, the amplitudes \({{\mathcal{A}}}_{{I}_{{\rm{c}}}}\) and \({{\mathcal{A}}}_{n}\) as a function of temperature, with the Fermi level and center of the trap energy distribution fixed at \({\mu }_{0}={\epsilon }_{{\rm{T}}}=0\) [\({\mu }_{0}={\epsilon }_{{\rm{T}}}=5\hslash {v}_{{\rm{D}}}/L\)]. At the CNP, the two amplitudes reflect the different temperature dependencies of the fourth- and second-order correlator of the trapped carrier density fluctuations, as given by Eqs. (18) and (24). The linear temperature behavior of \({{\mathcal{A}}}_{{I}_{{\rm{c}}}}\) for \(T\to 0\) derives from the approximate form \({F}_{2}\to {\rho }_{{\rm{T}}}{k}_{{\rm{B}}}T/(3\pi \Gamma )\) approached in the limit \(\Gamma \to \infty \). In Fig. 5, amplitudes have been scaled of a factor \(0.01\hslash {v}_{{\rm{D}}}/(L\Gamma )\), so that in the linear temperature regime all curves superpose. For larger temperatures \(T\lesssim \Gamma /{k}_{{\rm{B}}}\), \({F}_{2}\) decreases monotonically. This regime is clearly visible in Fig. 5a for the smallest \(\Gamma \) value considered (red dots). The carrier density noise amplitude is approximately given by \({{\mathcal{A}}}_{n}\propto {T}^{2}{F}_{0}\), where the quadratic temperature dependence is due to the quantum capacitance. For \(T\ll \Gamma /{k}_{{\rm{B}}}\), \({F}_{0}\to {\rho }_{{\rm{T}}}{k}_{{\rm{B}}}T/(\pi \Gamma )\), leading to \({{\mathcal{A}}}_{n}\propto {T}^{3}\). With increasing temperature, \(T\gtrsim \Gamma /{k}_{{\rm{B}}}\), \({{\mathcal{A}}}_{n}\) approaches \({{\mathcal{A}}}_{n}\propto {T}^{2}{F}_{0}=({\rho }_{{\rm{T}}}/4){T}^{2}\). If the trap energy distribution center and the Fermi level are in the conduction band, both amplitudes are related to correlators of the second order in the trapped carrier density fluctuations, see Eqs. (19) and (25). The case \({\mu }_{0}={\epsilon }_{{\rm{T}}}=5\hslash {v}_{{\rm{D}}}/L\) is shown in Fig. 5b and d. In the considered temperature range, the critical current derivative with respect to the Fermi energy does not depend on the temperature and the parallel capacitance is dominated by the geometric capacitance, i.e., \({C}_{\parallel }\approx {C}_{{\rm{g}}}\), thus both amplitudes follow the linear temperature dependence of \({F}_{0}\). Owing to the Fabry–Perot oscillations of \({I}_{{\rm{c}}}\), the ratio \({{\mathcal{A}}}_{{I}_{{\rm{c}}}}/{{\mathcal{A}}}_{n}={(d{I}_{{\rm{c}}}/d{\mu }_{0})}^{2}/(2{C}_{{\rm{g}}}^{2}/{e}^{4})\) is to a certain extent tunable with the doping level. Moreover, we note that both \({{\mathcal{A}}}_{{I}_{{\rm{c}}}}\) and \({{\mathcal{A}}}_{n}\) are considerably larger than at the CNP. For the carrier density noise, the scale factor is related to the capacitances’ ratio \({({C}_{{\rm{g}}}/{C}_{{\rm{Q}}})}^{2}\), from Eqs. (24) and (25).
Critical current noise amplitude \({{\mathcal{A}}}_{{I}_{{\rm{c}}}}\), in units of \({{I}_{{\rm{c}}}^{* }}^{2}{N}_{{\rm{T}}}\) (a, b), and carrier density noise amplitude \({{\mathcal{A}}}_{n}\), in units of \({N}_{{\rm{T}}}/{L}^{4}\) (c, d), as a function of temperature for \({\Delta }_{0}=0.1\hslash {v}_{{\rm{D}}}/L\) and fixed Fermi level \({\mu }_{0}={\epsilon }_{{\rm{T}}}\). a, c refer to a trap energy distribution at the charge neutrality point (CNP), \({\epsilon }_{{\rm{T}}}=0\), in b, d the distribution is centered in the conduction band \({\epsilon }_{{\rm{T}}}=5\hslash {v}_{{\rm{D}}}/L\). Different curves correspond to \(\Gamma =0.01\hslash {v}_{{\rm{D}}}/L\) (red circles), \(\Gamma =0.1\hslash {v}_{{\rm{D}}}/L\) (green squares), and \(\Gamma =\hslash {v}_{{\rm{D}}}/L\) (blue triangles). Green and blue data have been scaled of \(0.01\hslash {v}_{{\rm{D}}}/(L\Gamma )\) for the corresponding \(\Gamma \) value. In a, the solid gray lines represent contributions from correlators of the fourth order in the trapped carrier density fluctuations, see Eq. (18), while in b–d the solid black lines are contributions from correlators of the second order in the trapped carrier density fluctuations. In particular, in c this corresponds to Eq. (24). Left-top insets show a sketch of the electron structure with a shaded region below the doping level placed at the center of trap energy distribution and the Lorentzian trap energy distribution. (\({I}_{{\rm{c}}}^{* }=e\Delta W/(\hslash L)\), \({N}_{{\rm{T}}}={\rho }_{{\rm{T}}}WL\ell \) is the number of traps in a slab of the substrate of depth \(\ell \) under the graphene layer, and \(W\) and \(L\) are the width and the length of the junction channel, respectively).
Discussion
Our analysis points out that short ballistic GJJs are sensitive probes of microscopic noise underlying ballistic transport in 2D. In particular, we have shown that critical current noise probes either the second- or higher-order correlators of charge trapping center fluctuations by tuning the doping level or the temperature. This result, obtained within a simple phenomenological model for discrete charge density fluctuations, highlights the GJJ potentialities to characterize non-Gaussian noise sources22,39,40. Independent measurements of critical current noise and carrier density noise could provide valuable insights on the underlying microscopic mechanisms and a cross-check of the McWorther’s model applicability to GJJs. Charge carrier density noise may be probed via Hall voltage fluctuation measurements, an approach adopted in graphene38. Newly developed GJJ-based qubits may instead be employed as quantum sensors of critical current noise41. An important outcome of our analysis is the prediction of a linear \(T\) dependence of the critical current noise amplitude at sufficiently low temperatures, independently of the details of the trap state energy distribution included in the density \({{\mathcal{D}}}_{\Gamma }(\epsilon )\). This behavior arises in the regime \({k}_{{\rm{B}}}T\ll \min [{\Delta }_{0},\Gamma ]\) from the factors \({F}_{j}\), defined by Eq. (17), when the critical current is approximately given by the zero doping value \(1.33e{\Delta }_{0}W/(\pi \hslash L)\). For characteristic values of GJJs on hBN, the fractional noise amplitude at the CNP is approximately given by \({{\mathcal{A}}}_{{I}_{{\rm{c}}}}/{I}_{{\rm{c}}}^{2} \sim 2\pi \times 1{0}^{-7}\times ({N}_{{\rm{T}}}\Delta /\Gamma )\times (T/{T}_{{\rm{c}}})\), where \({T}_{{\rm{c}}}\) is the critical temperature and noise is measured in Hz\({}^{-1}\). For finite doping instead the fractional amplitude is approximately one order of magnitude larger, \({{\mathcal{A}}}_{{I}_{{\rm{c}}}}/{I}_{{\rm{c}}}^{2} \sim 2\pi \times 1{0}^{-6}\times ({N}_{{\rm{T}}}\Delta /\Gamma )\times (T/{T}_{{\rm{c}}})\). An analogous temperature dependence observed in Al/AlO\({}_{x}\)/Al and Nb/AlO\({}_{x}\)/Nb Josephson junctions, scaling with the inverse junction area down to \({A}_{0}\approx 0.04\,\upmu {{\rm{m}}}^{2}\), has been attributed to ensembles of two-level fluctuators in the oxide barrier42,43. Superconducting qubits are one of the forefront platforms for quantum state processing. In view of the relevance of hybrid superconducting circuits for quantum technologies, it is interesting to benchmark critical current noise in short ballistic GJJ with figures in AlO\({}_{x}\)-based Josephson junctions, where \({{\mathcal{A}}}_{{I}_{{\rm{c}}}}/{I}_{{\rm{c}}}^{2}\approx 1{0}^{-11}\times T/{T}_{{\rm{c}}}\) for junction’s area \( \sim {A}_{0}\)42. Assuming a featureless \(1/f\) spectrum due to \({N}_{{\rm{T}}} \sim 10\) traps, a fractional noise amplitude comparable to the one in conventional Josephson junctions would imply a wide distribution of trap energies, \(\Gamma \sim 1{0}^{6}\times \Delta \) (for finite doping \(\Gamma \sim 1{0}^{5}\times \Delta \)). Within our phenomenological model, the number of traps involved, \({N}_{{\rm{T}}}\), and the width of their energy distribution, \(\Gamma \), are unknown parameters, which could be estimated by fitting experimental data.
Methods
In this work, we deal with the critical current noise of short and wide GJJs as a function of temperature and doping level. In this regime, the supercurrent, defined in Eq. (1), can be expressed as7
where the summation over the transverse modes in Eq. (1) is replaced by the integration. The integration above has been performed with Python numerical routines, in particular we have used the free and open-source library SciPy44. Similarly, to calculate the functions \({F}_{j}\)s defined in Eq. (17) we have used the numerical integration routines included in SciPy.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Calado, V. E. et al. Ballistic Josephson junctions in edge-contacted graphene. Nat. Nanotechnol. 10, 761–764 (2015).
Ben Shalom, M. et al. Quantum oscillations of the critical current and high-field superconducting proximity in ballistic graphene. Nat. Phys. 12, 318–322 (2016).
Borzenets, I. V. et al. Ballistic graphene Josephson junctions from the short to the long junction regimes. Phys. Rev. Lett. 117, 237002 (2016).
Allen, M. T. et al. Observation of electron coherence and Fabry-Perot standing waves at a graphene edge. Nano Lett. 17, 7380–7386 (2017).
Amet, F. et al. Supercurrent in the quantum Hall regime. Science 352, 966–969 (2016).
Bretheau, L. et al. Tunnelling spectroscopy of Andreev states in graphene. Nat. Phys. 13, 756–760 (2017).
Titov, M. & Beenakker, C. W. J. Josephson effect in ballistic graphene. Phys. Rev B 74, 041401 (2006).
Black-Schaffer, A. M. & Doniach, S. Self-consistent solution for proximity effect andJosephson current in ballistic graphene SNS Josephson junctions. Phys. Rev. B 78, 024504 (2008).
Black-Schaffer, A. M. & Linder, J. Strongly anharmonic current-phase relation in ballistic grapheneJosephson junctions. Phys. Rev. B 82, 184522 (2010).
Hagymási, I., Kormányos, A. & Cserti, J. Josephson current in ballistic superconductor-graphene systems. Phys. Rev. B 82, 134516 (2010).
Takane, Y. & Imura, K.-I. Josephson current through a planar junction of graphene. J. Phys. Soc. Jpn. 80, 043702 (2011).
Takane, Y. & Imura, K.-I. Quasiclassical theory of the Josephson effect in ballistic graphene junctions. J. Phys. Soc. Jpn. 81, 094707 (2012).
Guarcello, C., Valenti, D. & Spagnolo, B. Phase dynamics in graphene-based Josephson junctions in the presence of thermal and correlated fluctuations. Phys. Rev. B 92, 174519 (2015).
English, C. D. et al. Observation of nonsinusoidal current-phase relation in grapheneJosephson junctions. Phys. Rev. B 94, 115435 (2016).
Nanda, G. et al. Current-phase relation of ballistic graphene Josephson junctions. Nano Lett. 17, 3396–3401 (2017).
Park, J. et al. Short ballistic Josephson coupling in planar graphene junctions with inhomogeneous carrier doping. Phys. Rev. Lett. 120, 077701 (2018).
Wang, J. I.-J. et al. Coherent control of a hybrid superconducting circuit made with graphene-based van der Waals heterostructures. Nat. Nanotechnol. 14, 120–125 (2018).
Kroll, J. G. et al. Magnetic field compatible circuit quantum electrodynamics with graphene Josephson junctions. Nat. Commun. 9, 4615 (2018).
Schmidt, F. E., Jenkins, M. D., Watanabe, K., Taniguchi, T. & Steele, G. A. A ballistic graphene superconducting microwave circuit. Nat. Commun. 9, 4069 (2018).
Wang, J. I.-J. et al. Tunneling spectroscopy of graphene nanodevices coupled to large-gap superconductors. Phys. Rev. B 98, 121411 (2018).
Balandin, A. A. Low-frequency 1/f noise in graphene devices. Nat. Nanotechnol. 8, 549–555 (2013).
Paladino, E., Galperin, Y. M., Falci, G. & Altshuler, B. L. 1/f noise: Implications for solid-state quantum information. Rev. Mod. Phys. 86, 361–418 (2014).
Kumar, C., Kuiri, M., Jung, J., Das, T. & Das, A. Tunability of 1/f noise at multiple dirac cones in hBN encapsulated graphene devices. Nano Lett. 16, 1042–1049 (2016).
Kumar, M., Laitinen, A., Cox, D. & Hakonen, P. J. Ultra low 1/f noise in suspended bilayer graphene. Appl. Phys. Lett. 106, 263505 (2015).
Stolyarov, M. A., Liu, G., Rumyantsev, S. L., Shur, M. & Balandin, A. A. Suppression of 1/f noise in near-ballistic h-BN-graphene-h-BN heterostructure field-effect transistors. Appl. Phys. Lett. 107, 023106 (2015).
Kayyalha, M. & Chen, Y. P. Observation of reduced 1/f noise in graphene field effect transistors on boron nitride substrates. Appl. Phys. Lett. 107, 113101 (2015).
Puczkarski, P. et al. Low-frequency noise in graphene tunnel junctions. ACS Nano 12, 9451–9460 (2018).
McWhorter, A. L. in Semiconductor Surface Physics (ed. Kingston, R. H.) 207 (University of Philadelphia Press, Philadelphia, PA, 1957).
Dutta, P. & Horn, P. M. Low-frequency fluctuations in solids: 1/f noise. Rev. Mod. Phys. 53, 497–516 (1981).
Weissman, M. B. 1/f noise and other slow, nonexponential kinetics in condensed matter. Rev. Mod. Phys. 60, 537–571 (1988).
Kogan, Sh Electronic Noise and Fluctuations in Solids (Cambridge University Press, Cambridge, 1996).
Hooge, F. N., Kleinpenning, T. G. M. & Vandamme, L. K. J. Experimental studies on 1/f noise. Rep. Prog. Phys. 44, 479–532 (1981).
Fernandez-Rossier, J., Palacios, J. J. & Brey, L. Electronic structure of gated graphene and graphene ribbons. Phys. Rev. B 20, 205441 (2007).
Fu, H. S. & Sah, C. T. Theory and experiments on surface 1\(/\) f noise. IEEE Trans. Electron. Devices 19, 273–285 (1972).
Giuliani, G. F. & Vignale, G. Quantum Theory of the Electron Liquid (Cambridge University Press, Cambridge, 2005).
Brews, J. R. Surface potential fluctuations generated by interface charge inhomogeneities in MOS devices. J. Appl. Phys. 43, 2306 (1972).
Pellegrino, F. M. D., Falci, G. & Paladino, E. Charge carrier density noise in graphene: effect of localized/delocalized traps. J. Stat. Mech. 2019, 094015 (2019).
Lu, J. et al. Negative correlation between charge carrier density and mobility fluctuations in graphene. Phys. Rev. B 90, 085434 (2014).
Galperin, Y. M., Altshuler, B. L., Bergli, J. & Shantsev, D. V. Non-Gaussian low-frequency noise as a source of qubit decoherence. Phys. Rev. Lett. 96, 097009 (2006).
Paladino, E., Faoro, L., Falci, G. & Fazio, R. Decoherence and 1/f noise in Josephson qubits. Phys. Rev. Lett. 88, 228304 (2002).
Pellegrino, F. M. D., Falci, G. & Paladino, E. Graphene Josephson junction quantum circuits for noise detection. Proceedings 12, 33 (2019).
Nugroho, C. D., Orlyanchik, V. & Van Harlingen, D. J. Low frequency resistance and critical current fluctuations in Al-based Josephson junctions. Appl. Phys. Lett. 102, 142602 (2013).
Pottorf, S., Patel, V. & Lukens, J. E. Temperature dependence of critical current fluctuations in Nb/AlO\({}_{x}\)/Nb Josephson junctions. Appl. Phys. Lett. 94, 043501 (2009).
Jones, E. et al. SciPy: open source scientific tools for python http://www.scipy.org/ (2001).
Acknowledgements
The authors thank G. G. N. Angilella, R. Fazio, S. Kubatkin, M. Polini, F. Taddei, I. Torre, and D. Vion for illuminating discussions and fruitful comments on various stages of this work. E.P. acknowledges hospitality of the Kavli Institute for Theoretical Physics, UC Santa Barbara where this work was finished thanks to partial support by the National Science Foundation under Grant No. NSF PHY-1748958. This research was funded by the project “Linea di intervento 2” of Dipartimento di Fisica e Astronomia “Ettore Majorana”, Università di Catania.
Author information
Authors and Affiliations
Contributions
All the authors conceived the work, agreed on the approach to pursue, and analyzed and discussed the results. F.M.D.P. performed the analytical and numerical calculations, E.P. originally conceived the project, and E.P. and G.F. supervised the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pellegrino, F.M.D., Falci, G. & Paladino, E. 1/f critical current noise in short ballistic graphene Josephson junctions. Commun Phys 3, 6 (2020). https://doi.org/10.1038/s42005-019-0275-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0275-9
This article is cited by
-
Open-loop quantum control of small-size networks for high-order cumulants and cross-correlations sensing
Scientific Reports (2024)
-
Effect of dilute impurities on short graphene Josephson junctions
Communications Physics (2022)
-
Critical current fluctuations in graphene Josephson junctions
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.