Abstract
Unconventional superconductivity arises at the border between the strong coupling regime with local magnetic moments and the weak coupling regime with itinerant electrons, and stems from the physics of criticality that dissects the two. Unveiling the nature of the quasiparticles close to quantum criticality is fundamental to understand the phase diagram of quantum materials. Here, using resonant inelastic x-ray scattering (RIXS) and \({\rm{Fe}}-{{\rm{K}}}_{\beta }\) emission spectroscopy (XES), we visualize the coexistence and evolution of local magnetic moments and collective spin excitations across the superconducting dome in isovalently-doped BaFe\({}_{2}\)(As\({}_{1-x}\)P\({}_{x}\))\({}_{2}\) (0.00 \( \le \) x \(\le 0.52\)). Collective magnetic excitations resolved by RIXS are gradually hardened, whereas XES reveals a strong suppression of the local magnetic moment upon doping. This relationship is captured by an intermediate coupling theory, explicitly accounting for the partially localized and itinerant nature of the electrons in Fe pnictides. Finally, our work identifies a local-itinerant spin fluctuations channel through which the local moments transfer spin excitations to the particle-hole (paramagnons) continuum across the superconducting dome.
Similar content being viewed by others
Introduction
It is now well established that unconventional superconductivity (SC) originates from a unique and augmented manifestation of the electronic correlation properties that arises as the system is driven towards a quantum critical region via various tuning parameters, such as doping and pressure1,2,3,4,5,6,7,8,9,10,11. On one side of the superconducting dome, the correlation strength is strongly enhanced, leading to diverse quantum many-body effects, such as the Mott insulating state, non-Fermi-liquid behaviour and magnetic orders (see Fig. 1a, b)3,4,12,13,14. On the other side of the dome, the correlation strength is often substantially suppressed, and the low-energy physics can be described by a more conventional Fermi-liquid theory11. The transition region between these two limits of correlation holds a quantum critical point (QCP) barely understood. Generally, SC is optimised in this intermediate region where the cooperation of a strongly enhanced non-Fermi-liquid behaviour, and the presence of a quantum criticality leads to unconventional and not understood physics11. This generic phase diagram suggests that intertwined electronic and magnetic instabilities, arising from the intermediate correlation strength close to this critical region, induce strong Cooper pairing3,4,15.
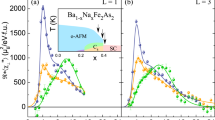
Phase diagram, structure and excitations of BaFe2(As1−xPx)2. a Phase diagram of BaFe2(As1−xPx)2. The black squares represent the doping levels and temperature measured in our work. As blue line, we schematically depict the expected behaviour of the fluctuating moment. b Schematic real space magnetic structure of BaFe2As2. c–f Density of states (DOS) as a function of quasiparticle energy. Non-interacting c, weak-coupling random-phase approximation (RPA) d, strong coupling e and intermediate coupling momentum-resolved density-fluctation theory (MRDF) f. g Excitation spectrum of the spin excitations arising from weak, strong and intermediate coupling
The physics that determines the evolution of the spin excitations is crucially dependent on the interaction strength of the electrons compared with their bandwidth. We explain this phenomenon schematically in Fig. 1c–g. The non-interacting density of states (DOS) of electrons (Fig. 1c) is renormalised by the interaction in the two extreme limits as (i) the bands become sharper in the weak-coupling quasiparticle picture (Fig. 1d), and (ii) split into two Mott-like bands characterised by local moments in the strong-coupling limit (Fig. 1e). (i) In the weak-coupling limit, the low-energy spin excitations (\({\chi }_{{\mathrm{ii}}}\), see Fig. 1d) are very fragile and mix with the particle–hole continuum, failing to form a localised moment. (ii) In the strong-coupling limit, the spin excitations across the Mott bands (\({\chi }_{{\mathrm{ll}}}\), see Fig. 1e) feature a gapped behaviour on the order of the on-site energy U without the particle–hole continuum13,14. However, as the correlation strength is tuned to the intermediate coupling region (Fig. 1f), the correlated DOS co-hosts the quasiparticle DOS at low energy and Mott states at high energy. In this way, a new spin-excitation channel (\({\chi }_{{\mathrm{il}}}\) see Fig. 1g) appears, through which the local moment can now decay to the particle–hole (paramagnon) channels across the magnetic QCP. Fe pnictides (FePns) can be placed in this intermediate region where the interplay of local and itinerant electronic states leads to high-temperature SC1,2,11,15. An important open question in this context is how local magnetic moments and collective spin excitations are evolving across the superconducting dome in FePns.
FePns have a layered structure that reduces dimensionality, and the parent compounds exhibit a spin-density wave with collinear antiferromagnetic (AF) order (see Fig. 1b), which gives way to SC via doping as outlined in Fig. 1a1,2,3,4,5,6,7,8,9,10,11. The origin of the magnetism is poised between being itinerant, as in Cr, and localised, as in cuprates or heavy fermion materials1,2,5,6,7,8,9,10,11,16 producing an uncommon behaviour that has important consequences for the properties of FePns. Theoretical models proposed that the pairing interaction leading to the superconducting phase is provided by residual AF fluctuations persisting upon doping3,4,15. Yet, owing to the contribution of the AF fluctuations from local and itinerant states, a complex interplay between them arises, which is believed to play a crucial role in shaping the superconducting dome. Thus, the experimental study of magnetism across the phase diagram of high-temperature superconductors is of vital importance to provide a solid basis for testing these theories.
Inelastic neutron scattering (INS) is the traditional technique of choice to study magnetism, being able to detect magnetic fluctuations in the full Brillouin zone (BZ)8,9. Recently, resonant inelastic X-ray scattering (RIXS) has emerged as a complementary technique to INS by detecting spin excitations in FePns close to the \(\Gamma\) point as summarised in Refs. 17,18,19,20,21,22. The detection of spin excitations is enabled in RIXS thanks to the spin–orbit coupling of the intermediate state mixing the quantum numbers L and S, thereby activating a channel for the detection of magnetic excitations23,24. An important consideration when comparing RIXS with INS is the portion of BZ probed by the two techniques, close to the \(\Gamma\) point in the case of RIXS and at the AF wave vector for the case of INS. Depending on the case, these two positions in momentum space can be equivalent or not. Moreover, it is hard to estimate and compare the absolute weight of magnetic excitations in these two regions of BZ, but it is generally accepted that the intensity at the AF wave vector is higher than close to the \(\Gamma\) point.
In this article, we use RIXS to systematically unveil the persistence and gradual hardening of the spin excitations in isovalently doped BaFe2(As1−xPx)2 across the phase diagram (see Fig. 1a for a graphical description of the doping levels). Upon doping and without nominally injecting charge carriers, the spectral weight of the spin excitations increases. Our RIXS measurements are complemented with theory placing the Fe-based superconductors in the intermediate region of correlations and well describing the evolution of the spin excitations with the spin susceptibility (\({\chi }_{s}\)). In addition, an investigation of the local fluctuating magnetic moment unravels a decrease in the local moment (\({\mu }_{{\mathrm{bare}}}\)) as a function of doping. This apparent dichotomy implies that there is a transfer of magnetic spectral weight from localised to itinerant as imposed by sum rule relations. We argue that the balance between localised and itinerant states is the key to achieve SC and plays an important role for the physics of criticality in BaFe2(As1−xPx)2.
Results
RIXS
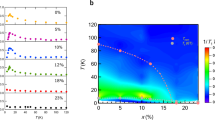
In Fig. 2, we show a selection of raw RIXS spectra and fitting of the elastic line, fluorescence background and spin excitations for all the doping levels. The RIXS spectra display a low-energy mode ascribed to spin excitations dispersing as a function of in- plane momentum transfer (q\({}_{//}\))17,18,19,20,21. The bandwidth, better appreciated at high momentum transfer (top row in Fig. 2), gradually increases with doping along both (H, 0) and (H, H) as summarised for the highest q points in Fig. 3. The doping increases the width (damping) of the spin excitations, leading to broader dispersing modes at high doping levels. This is expected as the hardening of the spin excitations coupled to electron–hole pair excitations naturally leads to further broadening of the spin excitations25. Our main results are presented in Fig. 4a, where we report the doping dependence of the dispersion of the spin excitations extracted from RIXS experiments as dots with error bars, and overlaid on the calculated dynamical spin susceptibility (\({\chi }_{s}\)). All the doping levels investigated display dispersive spin excitations as shown in Fig. 2 and 4a and in Supplementary Fig. 6. Upon doping the spin excitations, observed in our RIXS experiments, harden in energy by about 45 meV between the parent (x = 0.0) compound and the most doped compound (x = 0.52) at (0.44, 0). The hardening for the same doping levels at (0.32, 0.32) is on the order of 65 meV as summarised in Fig. 3.
Resonant inelastic X-ray scattering (RIXS) spectra at low-energy loss for BaFe2(As1−xPx)2 along (0, 0)\(\to\)(H, 0). Momentum dependence of RIXS spectra along (0, 0)\(\to\)(0.44, 0) for \(x=0.00\), 0.15, 0.22, 0.28, 0.38, 0.48 and 0.52. The incoming photons are \(\pi\) polarised, and the energy is tuned to the maximum of the Fe L\({}_{3}\) absorption edge. Experimental data are shown as black dots, background and elastic peak as purple dashed lines and magnetic peaks as green dashed lines. The sum of background, elastic and magnetic peaks is depicted as a red solid line. At low q\({}_{//}\) a fitting is unreliable, so no fitting was attempted
Summary of spin excitations. a Dots with error bars: maximum of the spin excitations’ peak detected by resonant inelastic X-ray scattering (RIXS) at (0.44, 0). b Dots with error bars: maximum of the spin excitations’ peak detected by RIXS at (0.32, 0.32). The error bars are defined by the uncertainty of locating the zero-energy position in the raw RIXS spectra. We took conservatively 30 meV (one pixel of our detector), which is much larger than the error resulting from the fitting analysis
Evolution of spin excitations. a Colour map: spin susceptibility (\({\chi }_{s}\)) calculated by means of momentum-resolved density-fluctuation theory (MRDF) self-energy corrected density functional theory (DFT) calculations. Black dots with error bars: maximum of the spin excitation peak detected by resonant inelastic X-ray scattering (RIXS). The error bars are defined by the uncertainty of locating the zero-energy position in the raw RIXS spectra. We took conservatively 30 meV (one pixel of our detector), which is much larger than the error resulting from the fitting analysis. b Evolution of the excitation spectrum with doping in the MRDF framework at (0.44, 0). c Peak of spin excitations from RIXS for \(x=0.00\), 0.15, 0.28 and 0.52 at (0.44, 0). d Difference of the spin excitations between doped and parent compound of RIXS spectra and MRDF calculations
The hardening of the spin excitations has been observed by INS for BaFe\({}_{2}\)(As\({}_{0.7}\)P\({}_{0.3}\))\({}_{2}\)26. At the zone boundary, INS observed a hardening of the spin excitations from 180 meV (x = 0) to 220 meV (x = 0.3) very similar to what is detected in our RIXS data (180 meV to ~205 meV at [0.44, 0]). The small difference between INS and RIXS emerges from slightly different positions in reciprocal space ([0.5, 0] vs. [0.44, 0]) and doping levels (x = 0.3 vs. x = 0.28). The comparison to these INS measurements establishes that RIXS probes spin excitations in FePns similarly to INS, even if mixing with other channels such as charge and orbital needs to be considered27,28. The broadening effects as a function of doping detected by our RIXS experiments have been observed by INS as well, where the local susceptibility clearly shows a synergy of hardening and broadening for x = 0.3.
The persistence of spin excitations along the superconducting dome was previously observed in both electron- and hole-doped FePns but with different effects on the energy of these modes. In hole-doped Ba\({}_{1-x}\)K\({}_{x}\)Fe\({}_{2}\)As\({}_{2}\), the spin excitations soften upon doping due to the increase in the electronic correlations as demonstrated by theoretical calculations and accurate measurements of the Sommerfeld constant29,30,31. In electron-doped FePns, a different behaviour has been detected with the spin excitations being unaffected by doping in their bandwidth but with a decrease in spectral weight29,32. In our present work, we uncover that the energy of the spin excitations increases upon isovalent doping and does not directly correlate with the critical temperature (T\({}_{c}\)). This indicates that T\({}_{c}\) is likely connected to other microscopic details aside the effective exchange constant. Thus, the case of isovalent BaFe2(As1−xPx)2 reveals an unprecedented behaviour, in stark contrast to hole- and electron-doped BaFe\(_{2}\)As\(_{2}\), adding new features to the large diversity in the doping effects and magnetism in FePns.
The persistence of spin excitations in unconventional superconductors outside the antiferromagnetic parent compound is also a hallmark of the cuprates33,34,35,36,37, where paramagnons have been observed across all the phase diagrams. In cuprates, the energy evolution of the spin excitations upon doping is different than the case of FePns: in hole-doped cuprates, there is a more or less constancy of the bandwidth along the antinodal direction, whereas electron-doped cuprates display hardening of the magnetic excitations35,36,37.
Momentum-resolved density fluctuation theory
One approach able to describe the regime of intermediate coupling is momentum-resolved density fluctuation (MRDF) theory. MRDF dissects the electronic spectrum into strongly renormalised, incoherent ‘local’ states, and low-energy, itinerant Bloch states as displayed in Fig. 1f. The back reaction of the quantum fluctuations to the electronic states leads to momentum, energy and orbital-dependent renormalisation as well as lifetime broadening. Within the quantum field theory, these effects are captured by the real and imaginary part of the self-energy correction38. MRDF theory self-consistently computes the dynamical correlation functions and the corresponding self-energy in the full momentum and energy space15,38. This theory captures the momentum and energy-dependent evolution of the localised states as well as the dispersive quasiparticle states, resulting in an anisotropic pairing symmetry, compatible with what is observed experimentally3,4.
To describe the spin excitations probed by RIXS, the dynamical susceptibility (\(\chi\)) has been calculated and decomposed into the spin (\({\chi }_{s}\)) and charge (\({\chi }_{c}\)) channels with both the random-phase approximation (RPA) and MRDF method. The intensity of \({\chi }_{s}\) dominates over \({\chi }_{c}\) in agreement with a previous work20. Density functional theory (DFT)–RPA calculations fail to distribute the spectral weight between the local and itinerant states and overestimate the peak energy of the spin excitations compared with our experimental data (see Supplementary Figs. 10 and 11 and Supplementary Notes 1 and 2). The reason for this is that DFT–RPA underestimates the electronic correlation strength placing the spin excitations at too high energy. Moreover, these RPA calculations cannot account for the hardening of the dispersion of spin excitations observed upon doping. In Fig. 1g, we show an idealised scheme of the excitation pattern achieved in the intermediate coupling region comprising local–local (\({\chi }_{{\mathrm{ll}}}\)), local–itinerant (\({\chi }_{{\mathrm{il}}}\)) and itinerant–itinerant excitations (\({\chi }_{{\mathrm{ii}}}\)). The low-energy \({\chi }_{{\mathrm{ii}}}\) excitations have an energy in the order of the spin gap (\(\approx\)1–10 meV) and are not observable by RIXS due to current limitations of the energy resolution but are observed in INS8,9. The high-energy \({\chi }_{{\mathrm{ll}}}\) appears at energies of 900–1500 meV and are not detectable by RIXS due to the intense fluorescence background. The \({\chi }_{{\mathrm{il}}}\) excitations are the (para)-magnon excitations and can be qualitatively compared with our RIXS measurements as a function of doping.
In Fig. 4b, c, we depict the doping dependence of \({\chi }_{s}\) directly extracted from the MRDF calculations as well as the RIXS spectra at (0.44, 0). To better visualise the renormalisation in energy of the magnetic excitations, we also take the difference between the selected doping levels and the parent compound and present the results in Fig. 4d for both theory and experiments. The agreement between theory and experiment is remarkable individuating the MRDF, and more in general the intermediate coupling approach as appropriate to describe the magnetism and electronic structure of FePns. In previous works, DFT–RPA has been employed to successfully describe the spin excitations in overdoped cuprates39,40,41. The failure of DFT–RPA to account for the spin excitations in BaFe2(As1−xPx)2 implies that the FePns are not weakly correlated systems and cannot be compared with overdoped cuprates with reduced electronic correlations but rather need to be placed in the family of multi-orbital correlated systems similarly to heavy fermion materials16,39.
X-ray emission spectroscopy
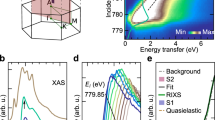
To complement our measurements of the spin excitations and assess the local magnetism of BaFe2(As1−xPx)2, we employed X-ray emission spectroscopy (XES)—a classical technique that has been established as a sensitive probe of the local magnetic moment (\({\mu }_{{\mathrm{bare}}}\))19,42,43,44,45,46,47,48. XES is sensitive to the local fluctuating magnetic moment and does not require a net magnetisation or ordering, such as X-ray magnetic circular dichroism (XMCD) or neutron diffraction, but detects directly the paramagnetic moment44,45,46. In this technique, a photon (h\(\nu =7140\) eV) excites an Fe-1s core electron into the continuum, creating a core hole that is filled by a Fe-3p electron with the consequent emission of a photon (h\(\nu =7040\)–7065 eV). The final Fe-3p\({}^{5}\) state has a wave function partly overlapped with the Fe-3d orbitals, and is, thereby, affected by the spin of the valence band through the exchange interaction19,42,43,44,45,47,48,49. The femtosecond timescale of this technique allows for the measurement of fast fluctuations of \({\mu }_{{\mathrm{bare}}}\)5,42,43,49, and by means of normalisation and calibration [carried out with FeCrAs (0 \({\mu }_{B}\)) and BaFe\(_{2}\)As\(_{2}\) (set arbitrarily to one to define a relative scale)] \({\mu }_{{\mathrm{bare}}}\) can be determined42,43,49.
In Fig. 5a, b, we show XES spectra for BaFe2As2, and BaFe2(As1−xPx)2 (x = 0.52), and FeCrAs and the respective difference spectra. Clearly, a gradual decrease in \({\mu }_{{\mathrm{bare}}}\) is inferred from the difference spectra depicted in Fig. 5c. The values of \({\mu }_{{\mathrm{bare}}}\), presented in Fig. 5d, e are continuously reduced, (e.g., \({\mu }_{{\mathrm{bare}}}=\) 1.0\(\pm 0.1\) for \(x=0.00\), \({\mu }_{{\mathrm{bare}}}=0.6\pm 0.1\) for \(x=0.28\) and \({\mu }_{{\mathrm{bare}}}=0.4\pm 0.1\) for \(x=0.52\)), but not fully quenched by doping, despite the complete disappearance of the ordered magnetic moment observed by neutron scattering50,51. This evidence is remarkable in light of the constancy of the Fe oxidation state observed in XAS (see Supplementary Fig. 2) with isovalent doping driving the antiferromagnetically long-range ordered BaFe2As2 into a paramagnetic phase.
Fe-K\({}_{\beta }\) X-ray emission spectroscopy (XES) and difference spectra for BaFe2(As1−xPx)2. K\({}_{\beta }\) XES for \(x=0.00\), and 0.52 (a, b as black lines) and reference spectrum of FeCrAs (a, b as red lines). The integrated area difference (IAD) is displayed as grey line. c Summary of IADs for all the samples. d Values of local magnetic moment extracted from XES compared with theoretical estimates of the Fermi surface (FS) nesting strength. The nesting strength is calculated integrating the static susceptibility at the nesting wavevector. The error bars on the values of \({\mu }_{{\mathrm{bare}}}\) are systematic due to the normalisation and subtraction steps; thus, all the values have an error of \(\pm\)0.1 with respect to the values assumed by the parent compound. e Summary of local magnetic moment from XES (orange) and intensity of spin excitations (green) integrating the fitting from the resonant inelastic X-ray scattering (RIXS) spectra at high momenta (three highest momenta) along (H, 0) and (H, H) as a function of doping across the phase diagram of BaFe2(As1−xPx)2. In order to visualise the reciprocal redistribution of local magnetic moments and spin excitations, we represent the superconducting dome as a purple shaded area in the background. The error bars on the intensity of the spin excitations have been quantified in \(\pm\)0.1 with respect to the value of the parent compound. The fitting error is actually smaller, but the sum procedure at different q points produces a propagation of the errors, so we set a slightly higher upper boundary
We compare the doping dependence of the local moment with the strength of the Fermi surface (FS) nesting at the antiferromagnetic wavevector. In Fig. 5d, the theoretical data are presented as \(\Delta \chi\)(x) = \(\chi\)(x) – \(\chi\)(0.6), where \(\chi\)(x) is the computed static susceptibility at the antiferromagnetic wavevector at doping x [we normalise \(\Delta \chi\) (x = 0) = 1]. Note that this comparison is only qualitative, and a self-consistent estimation of the static magnetic moment is computationally expensive. Similar doping dependence of the magnetic instability arising from the FS nesting and the observed local moment indicates an electronic mechanism of the magnetic ground state in this system.
Discussion
Our XES results are puzzling, and assuming spectral weight sum rules, there has to be spectral weight transfer from localised moments into spin excitations as probed by RIXS. In Fig. 5e, we report the integrated spectral weight of the spin excitations determined from our RIXS spectra. Within error bars, the spin excitation intensities detected in the portion of BZ pertinent to RIXS possibly show gradual transfer of spectral weight upon doping. However, additional enhancement of spectral weight in different regions of the BZ could be observed. On this aspect, further combined studies of RIXS and high-energy INS as a function of doping are required to shed light on the redistribution of spectral weight in the complete BZ. In Fig. 5e, we observe the gradual transfer of spectral weight from local magnetic moments into collective spin excitations across the superconducting dome. This spectral redistribution signals that SC is optimised by a balance of these types of interactions.
In summary, we unveiled the persistence and hardening of magnetic excitations along the superconducting dome of BaFe2(As1−xPx)2 with a concomitant decrease in local magnetic moments. The spectral weight of the spin excitations observed with RIXS slightly increases, corroborating that SC emerges from a balance of localised and itinerant electronic interactions. The experimental results agree well with intermediate coupling calculations placing the FePns in the family of multi-orbital correlated systems and uncovering clearly the mixed electronic and magnetic interactions present with optimal SC.
Methods
Sample preparations
Single crystals of BaFe2(As1−xPx)2 were grown either by stoichiometric melt52 or Ba\({}_{2}\)As\({}_{3}\)/Ba\({}_{2}\)P\({}_{3}\) self-flux method53. The samples were characterised either with resistivity or magnetisation measurements. For \(x=0.15\), 0.22, 0.27 and 0.48, crystals grown by the stoichiometric melt technique were used for the RIXS experiments, while for \(x=0.38\) and 0.52 we use the crystals grown by the self-flux technique. Supplementary Fig. 1 shows the temperature dependence of the resistivity on crystals selected from the same batches. For \(x\, > \, {0.3}\) the spin-density wave (SDW) long-range order is completely suppressed52,53.
X-ray absorption spectroscopy and RIXS
X-ray absorption spectra (XAS) and RIXS experiments were performed at the ADRESS beamline of the Swiss Light Source, Paul Scherrer Institut, Villigen PSI, Switzerland54,55. In agreement with previous works17,18,19,20,56, the samples were mounted with the ab plane perpendicular to the scattering plane and the c axis lying on it (sketch in Supplementary Fig. 2) and post cleaved in situ at a pressure better than 2.0 × 10−10 mbar. The reciprocal space directions studied are (0, 0)\(\to\)(1, 0) and (0, 0)\(\to\)(1, 1) according to the orthorhombic unfolded crystallographic notation. The values of in-plane momentum transferred are expressed as relative lattice units (RLU) (q\({}_{//}=2\pi\)/a). We use the convention of 1 Fe per unit cell. All the measurements were carried out at 13 K by cooling the manipulator with liquid helium. XAS spectra were measured in both total fluorescence yield (TFY) and total electron yield (TEY) modes. No difference was observed between TEY and TFY, which indicates the sample integrity across the thickness probed in our experiment. We measured Fe L\({}_{2,3}\) XAS spectra for all samples at 15° of incidence angle relative to the sample surface. All the XAS spectra are reported in Supplementary Fig. 3 and display the constancy of the iron oxidation state. There are small spectral differences at around 710 eV that are possibly due to a different covalency between the FeAs and FeP.
The RIXS spectrometer was set to a scattering angle of 130°, and the incidence angle on the samples surface was varied to change the in-plane momentum-transferred (q\({}_{//}\)) from (0, 0) to (0.44, 0) and from (0, 0) to (0.31, 0.31). All RIXS measurements in this paper were recorded in grazing-incidence configuration as depicted in Supplementary Fig. 2. The zero-energy loss of our RIXS spectra was determined by measuring spectra in \(\sigma\) polarisation. The total energy resolution was measured by employing the elastic scattering of carbon-filled acrylic tape and is around 110 meV.
RIXS spectra were normalised to unity, and the main emission line was fitted according to Refs. 17,18,19,20,56 employing the following formulas:
with
and
In the first formula, the first part is a second-order polynomial function describing the emission line at low-energy loss, the second part is an exponential decay describing the emission line at high-energy loss. The two behaviours are swapped into each other by the g\({}_{\gamma }\) term. The third term is a Gaussian curve (G) observed at around –4.2-eV energy loss. An exemplary fitting of the full RIXS spectra is shown in Supplementary Fig. 4 for BaFe2As2 at (0.44, 0.0).
In Supplementary Fig. 5, we show RIXS spectra over an extended range of energy loss. Overall, the three spectra resemble a metallic system with the lineshape not being affected by doping. Due to changes in the band structure upon doping, small energy shifts and changes in the RIXS intensity are detected.
We complemented the momentum dependence along (0, 0)\(\to\)(1, 0) with (0, 0)\(\to\)(1, 1) and display the raw data for all the dopings and momenta with the fitting in Supplementary Fig. 6.
K\({}_{\beta }\) emission spectroscopy
We performed the Fe-K\({}_{\beta }\) X-ray emission (XES) experiments at BL11XU of SPring-8, Japan. The incoming beam was monochromatised by a Si (111) double crystal and a Si (400) secondary channel-cut crystal. The energy was calibrated by measuring X-ray absorption of a Fe foil and set to 7.140 keV with \(\pi\) polarisation. We employed three spherical diced Ge (620) analysers and a detector in Rowland geometry at 2-m distance. The total combined resolution was about 400 meV estimated from full width half maximum (FWHM) of the elastic line. We scanned the absolute emission energy between 7.02 keV and 7.08 keV and normalised the intensity by the incident flux monitored by an ionisation chamber. We carried out the measurements at 15 K. The experimental geometry of the experiment is depicted in Supplementary Fig. 7. The determination of \({\mu }_{{\mathrm{bare}}}\) was performed by employing the integrated absolute difference (IAD) method described by Vanko et al.45. The areas of the XES spectra were normalised to unity as shown in Supplementary Fig. 8a–f. To overcome problems of alignment of the absolute energy between different samples, we estimated the centre of mass of the spectra and aligned the energy to have the same centre of mass as described by Glatzel et al.44. Then the difference with the spectrum of the FeCrAs reference was taken as displayed in Supplementary Fig. 8a–f and summarised in Supplementary Fig. 8g. The integration of this difference gives the IAD, which is directly proportional to \({\mu }_{{\mathrm{bare}}}\)45.
Doping-dependent band structure
Two extreme doping regimes of the BaFe2(As1−xPx)2 samples, namely BaFe\({}_{2}\)As\({}_{2}\) (\(x=0.00\)) and BaFe\({}_{2}\)P\({}_{2}\) (\(x=1.00\)), have been studied within DFT57. Also accurate tight-binding models are available to reproduce the DFT band structure, consistent with angle-resolved photoemission spectroscopy (ARPES) data (after including renormalisation effects). However, P-doping effects on the As site, which do not change the carrier concentration, are neither trivial to accurately calculate within the DFT framework, nor within a simple rigid band shift technique that works reasonably well for electron- and hole-doping cases58. Since P atom is smaller in size compared with As atoms, P doping is expected to decrease the lattice volume. Indeed, both X-ray52 and neutron51 diffraction analysis revealed that all three lattice constants as well as the pnictogen atomic coordinates in the unit cell (z\({}_{Pn}\)) and the pnictogen height from the Fe plane (h\({}_{Pn}\)) decrease monotonically with P doping. Among them, the c-axis lattice constant decreases drastically from \(\approx\)13 Å at \(x=0.00\) to \(\approx\)12.4 Å at \(x=1.00\). This explains why the three-dimensionality of the sample (i.e., k\({}_{z}\) dispersion) increases considerably with doping, as consistently demonstrated in both ARPES59 as well as in de Haas–van Alphen measurements60,61. It is shown that throughout the entire doping range, the Fermi surface (FS) topology remains very similar and consists of hole pockets at the \(\Gamma\)-point and electron pockets at the M-point. At \(x=0.00\), there are three concentric hole pockets, which reduce to only two remaining hole pockets at \(x=1.00\), with the smaller pocket disappearing at some intermediate doping. The electron-like FS consists of two elliptic electron pockets interpenetrating to each other11. Among all the FS pockets, the outermost hole pocket shows most dominant and drastic changes with doping: it is very close to cylindrical as a function of k\({}_{z}\) at \(x=0.00\), but gradually becomes corrugated with increasing doping. The other pockets acquire comparatively less k\({}_{z}\) dispersion59,60,61. This could be quantified by calculating the nesting strength via the integration of the static susceptibility at the nesting wave vector. The nesting strength has been shown to decrease upon doping11,58,60. Projected orbital symmetries on each FS reveal that the hole pockets are dominated by the d\({}_{xz}\)/d\({}_{yz}\) orbitals, while the electron pockets are made of hybridisation between the d\({}_{xz}\)/d\({}_{yz}\) orbitals with the d\({}_{xy}\) orbitals. The d\({}_{{z}^{2}}\) orbital has little contribution at \(x=0.00\), while it grows with doping. d\({}_{{z}^{2}}\) basically contributes to the strongly k\({}_{z}\) dispersive parts of the outermost hole pocket60.
Based on the aforementioned experimental observations on the band structure evolution with doping, we construct an effective five-orbital tight-binding (TB) model to reproduce the low-energy dispersion and FS topology across the entire phase diagram. The 2 Fe unit cell incorporates two Fe sublattices producing a ten-band model. We start with a five-orbital TB model as derived in Ref. 57 for BaFe\({}_{2}\)As\({}_{2}\). The intra-orbital dispersions are defined by \({\xi }_{k}^{i}={\epsilon }_{k}^{i}+{\Delta }^{i}-{\epsilon }_{F}\), where k is the crystal momentum and \(i=1-5\) is the orbital index. \({\epsilon }_{k}^{i}\) is the momentum-dependent part of the dispersion that arises from the nearest, next and higher neighbour hoppings between the same orbitals, \({\Delta }^{i}\) is the corresponding on-site potentials and \({\epsilon }_{F}\) is the chemical potential. As the unit cell volume decreases monotonically with P doping, it is expected that the electron hopping amplitude increases monotonically with doping. We model this effect by a simple renormalisation factor \(\lambda\) as \({\epsilon }_{k}^{i}\to \lambda {\epsilon }_{k}^{i}\), where \(\lambda\) increases with doping. Similarly, due to the monotonic increase in the pnictogen coordinate and the height (z\({}_{Pn}\), h\({}_{Pn}\)), the on-site potential also changes. Interestingly, we find that an orbital-dependent modification of the on-site potential is required to properly reproduce the experimental behaviour of the k\({}_{z}\) dispersion and FS changes. We set \({\Delta }^{i}\to {\Delta }^{i}+\delta\) for d\({}_{xz}\)/d\({}_{yz}\) orbitals, \({\Delta }^{i}\to {\Delta }^{i}-\delta\) for d\({}_{{x}^{2}-{y}^{2}}\) and d\({}_{z}^{2}\) orbitals and \({\Delta }^{i}\to {\Delta }^{i}-2\delta\) for d\({}_{xy}\) orbital, where \(\delta (x)=0.08x\), with \(x\) being the doping value. The chemical potential is adjusted at each doping to keep the same number of electrons. Such a model was also invoked earlier to model the FS topological transition in KFe\({}_{2}\)Se\({}_{2}\) under pressure62. The corresponding FS topologies at three representative dopings are shown in Supplementary Fig. 9.
Data availability
Data that support the findings of this study are available upon reasonable request from the corresponding authors.
References
Johnston, D. C. The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides. Adv. Phys. 59, 803–1061 (2010).
Stewart, G. R. Superconductivity in iron compounds. Rev. Mod. Phys. 83, 1589–1652 (2011).
Chubukov, A. Pairing mechanism in Fe-based superconductors. Annu. Rev. Condens. Matter Phys. 3, 57–92 (2012).
Scalapino, D. J. A common thread: the pairing interaction for unconventional superconductors. Rev. Mod. Phys. 84, 1383–1417 (2012).
Mannella, N. The magnetic moment enigma in Fe-based high temperature superconductors. J. Phys.: Condens. Matter 26, 473202 (2014).
Inosov, D. S. Spin fluctuations in iron pnictides and chalcogenides: from antiferromagnetism to superconductivity. C. R. Phys. 17, 60 (2016).
Tranquada, J. M., Xu, G. & Zaliznyak, I. A. Superconductivity, antiferromagnetism, and neutron scattering. J. Magn. Magn. Mater. 350, 148–160 (2014).
Dai, P. Antiferromagnetic order and spin dynamics in iron-based superconductors. Rev. Mod. Phys. 87, 855–896 (2015).
Dai, P., Hu, J. & Dagotto, E. Magnetism and its microscopic origin in iron-based high-temperature superconductors. Nat. Phys. 8, 709–718 (2012).
Lumsden, M. D. & Christianson, A. D. Magnetism in Fe-based superconductors. J. Phys.: Condens. Matter 22, 203203 (2010).
Shibauchi, T., Carrington, A. & Matsuda, Y. A quantum critical point lying beneath the superconducting dome in iron pnictides. Annu. Rev. Condens. Matter Phys. 5, 113–135 (2014).
Lee, P. A., Nagaosa, N. & Wen, X.-G. Doping a Mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006).
Yin, Z. P., Haule, K. & Kotliar, G. Kinetic frustration and the nature of the magnetic and paramagnetic states in iron pnictides and iron chalcogenides. Nat. Mater. 10, 932–935 (2011).
de Medici, L., Hassan, S. R., Capone, M. & Dai, X. Orbital-selective Mott transition out of band degeneracy lifting. Phys. Rev. Lett. 102, 126401 (2009).
Chubukov, A. V. Itinerant electron scenario for Fe-based superconductors. Springer Series in Mater. Sci. 211, 255–329 (2015).
Yang, W. L. et al. Evidence for weak electronic correlations in iron pnictides. Phys. Rev. B 80, 014508 (2009).
Zhou, K.-J. et al. Persistent high-energy spin excitations in iron-pnictide superconductors. Nat. Commun. 4, 1470 (2013).
Pelliciari, J. et al. Presence of magnetic excitations in SmFeAsO. Appl. Phys. Lett. 109, 122601 (2016).
Pelliciari, J. et al. Local and collective magnetism of EuFe\({}_{2}\)As\({}_{2}\). Phys. Rev. B 95, 115152 (2017).
Pelliciari, J. et al. Intralayer doping effects on the high-energy magnetic correlations in NaFeAs. Phys. Rev. B 93, 134515 (2016).
Rahn, M. C. et al. Paramagnon dispersion in \(\beta\)-FeSe observed by Fe L-edge resonant inelastic x-ray scattering. Phys. Rev. B 99, 014505 (2019).
Garcia, F. A. et al. Anisotropic magnetic excitations and incipient Neel order in Ba(Fe\({}_{1-x}\)Mn\({}_{1-x}\))\({}_{1-x}\)As\({}_{1-x}\). Phys. Rev. B 99, 115118 (2019).
Ament, L. J. P., van Veenendaal, M., Devereaux, T. P., Hill, J. P. & van den Brink, J. Resonant inelastic x-ray scattering studies of elementary excitations. Rev. Mod. Phys. 83, 705–767 (2011).
Jia, C., Wohlfeld, K., Wang, Y., Moritz, B. & Devereaux, T. P. Using RIXS to uncover elementary charge and spin excitations. Phys. Rev. X 6, 021020 (2016).
Tohyama, T., Tsutsui, K., Mori, M., Sota, S. & Yunoki, S. Enhanced charge excitations in electron-doped cuprates by resonant inelastic x-ray scattering. Phys. Rev. B 92, 014515 (2015).
Hu, D. et al. Spin excitations in optimally P-doped BaFe\({}_{2}\)(As\({}_{2}\)P\({}_{2}\))\({}_{2}\) superconductor. Phys. Rev. B 94, 094504 (2016).
Nomura, T. et al. Resonant inelastic x-ray scattering study of entangled spin-orbital excitations in superconducting PrFeAsO\({}_{0.7}\). Phys. Rev. B 94, 035134 (2016).
Kaneshita, E., Tsutsui, K. & Tohyama, T. Spin and orbital characters of excitations in iron arsenide superconductors revealed by simulated resonant inelastic x-ray scattering. Phys. Rev. B 84, 020511 (2011).
Wang, M. et al. Doping dependence of spin excitations and its correlations with high-temperature superconductivity in iron pnictides. Nat. Commun. 4, 2874 (2013).
Eilers, F. et al. Strain-driven approach to quantum criticality in AFe\({}_{2}\)As\({}_{2}\) with A=K, Rb, and Cs. Phys. Rev. Lett. 116, 237003 (2016).
Charnukha, A. et al. Intrinsic charge dynamics in high-T\({}_{c}\) AFeAs(O,F) superconductors. Phys. Rev. Lett. 120, 087001 (2018).
Luo, H. et al. Electron doping evolution of the magnetic excitations in BaFe\({}_{2-x}\)Ni\({}_{2-x}\)As\({}_{2-x}\). Phys. Rev. B 88, 144516 (2013).
Dean, M. P. M. et al. Persistence of magnetic excitations in La\({}_{2-x}\)Sr\({}_{2-x}\)CuO\({}_{2-x}\) from the undoped insulator to the heavily overdoped non-superconducting metal. Nat. Mater. 12, 1019–1023 (2013).
Le Tacon, M. et al. Intense paramagnon excitations in a large family of high-temperature superconductors. Nat. Phys. 7, 725–730 (2011).
Lee, W. S. et al. Asymmetry of collective excitations in electron- and hole-doped cuprate superconductors. Nat. Phys. 10, 883–889 (2014).
Ishii, K. et al. High-energy spin and charge excitations in electron-doped copper oxide superconductors. Nat. Commun. 5, 3714 (2014).
Dellea, G. et al. Spin and charge excitations in artificial hole- and electron-doped infinite layer cuprate superconductors. Phys. Rev. B 96, 115117 (2017).
Das, T., Markiewicz, R. S. & Bansil, A. Intermediate coupling model of the cuprates. Adv. Phys. 63, 151–266 (2014).
Monney, C. et al. Resonant inelastic x-ray scattering study of the spin and charge excitations in the overdoped superconductor La\({}_{1.77}\)Sr\({}_{1.77}\)CuO\({}_{1.77}\). Phys. Rev. B 93, 075103 (2016).
Guarise, M. et al. Anisotropic softening of magnetic excitations along the nodal direction in superconducting cuprates. Nat. Commun. 5, 5760 (2014).
Dean, M. P. M. et al. Itinerant effects and enhanced magnetic interactions in Bi-based multilayer cuprates. Phys. Rev. B 90, 220506 (2014).
Gretarsson, H. et al. Spin-state transition in the Fe pnictides. Phys. Rev. Lett. 110, 047003 (2013).
Gretarsson, H. et al. Revealing the dual nature of magnetism in iron pnictides and iron chalcogenides using x-ray emission spectroscopy. Phys. Rev. B 84, 100509 (2011).
Glatzel, P. & Bergmann, U. High resolution 1s core hole X-ray spectroscopy in 3d transition metal complexesâĂŤelectronic and structural information. Coord. Chem. Rev. 249, 65–95 (2005).
Vanko, G. et al. Probing the 3d spin momentum with X-ray emission spectroscopy: the case of molecular-spin transitions. J. Phys. Chem. B 110, 11647–11653 (2006).
Yamamoto, Y. et al. Origin of pressure-induced superconducting phase in K\({}_{x}\)Fe\({}_{x}\)Se\({}_{x}\) studied by Synchrotron X-ray diffraction and spectroscopy. Sci. Rep. 6, 30946 (2016).
Lafuerza, S. et al. Evidence of Mott physics in iron pnictides from x-ray spectroscopy. Phys. Rev. B 96, 045133 (2017).
Pelliciari, J. et al. Magnetic moment evolution and spin freezing in doped BaFe\({}_{2}\)As\({}_{2}\). Sci. Rep. 7, 8003 (2017).
Vilmercati, P. et al. Itinerant electrons, local moments, and magnetic correlations in the pnictide superconductors CeFeAsO\({}_{1-x}\)F\({}_{1-x}\) and Sr(Fe\({}_{1-x}\)Co\({}_{1-x}\))\({}_{1-x}\)As\({}_{1-x}\). Phys. Rev. B 85, 220503 (2012).
Hu, D. et al. Structural and magnetic phase transitions near optimal superconductivity in BaFe\({}_{2}\)(As\({}_{2}\)P\({}_{2}\))\({}_{2}\). Phys. Rev. Lett. 114, 157002 (2015).
Allred, J. M. et al. Coincident structural and magnetic order in BaFe\({}_{2}\)(As\({}_{2}\)P\({}_{2}\))\({}_{2}\) revealed by high-resolution neutron diffraction. Phys. Rev. B 90, 104513 (2014).
Kasahara, S. et al. Evolution from non-Fermi- to Fermi-liquid transport via isovalent doping in BaFe\({}_{2}\)(As\({}_{2}\)P\({}_{2}\))\({}_{2}\) superconductors. Phys. Rev. B 81, 184519 (2010).
Nakajima, M. et al. Growth of BaFe\({}_{2}\)(As\({}_{2}\)P\({}_{2}\))\({}_{2}\) single crystals (0\({}_{2}\)x\({}_{2}\)1) by Ba\({}_{2}\)As\({}_{2}\)/Ba\({}_{2}\)P\({}_{2}\)-Flux method. J. Phys. Soc. Japan 81, 104710 (2012).
Strocov, V. N. et al. High-resolution soft X-ray beamline ADRESS at the Swiss Light Source for resonant inelastic X-ray scattering and angle-resolved photoelectron spectroscopies. J. Synchrotron Radiat. 17, 631–643 (2010).
Ghiringhelli, G. et al. SAXES, a high resolution spectrometer for resonant x-ray emission in the 400–1600 ev energy range. Rev. Sci. Instrum. 77, 113108 (2006).
Hancock, J. N. et al. Evidence for core-hole-mediated inelastic x-ray scattering from metallic Fe\({}_{1.087}\)Te. Phys. Rev. B 82, 020513 (2010).
Graser, S., Maier, T. A., Hirschfeld, P. J. & Scalapino, D. J. Near-degeneracy of several pairing channels in multiorbital models for the Fe pnictides. New J. Phys. 11, 025016 (2009).
Richard, P., Sato, T., Nakayama, K., Takahashi, T. & Ding, H. Fe-based superconductors: an angle-resolved photoemission spectroscopy perspective. Rep. Prog. Phys. 74, 124512 (2011).
Yoshida, T. et al. Two-dimensional and three-dimensional Fermi surfaces of superconducting BaFe\({}_{2}\)(As\({}_{2}\)P\({}_{2}\))\({}_{2}\) and their nesting properties revealed by angle-resolved photoemission spectroscopy. Phys. Revi. Lett. 106, 117001 (2011).
Arnold, B. J. et al. Nesting of electron and hole Fermi surfaces in nonsuperconducting BaFe2P2. Phys. Rev. B 83, 220504 (2011).
Analytis, J. G., Chu, J.-H., McDonald, R. D., Riggs, S. C. & Fisher, I. R. Enhanced Fermi-surface nesting in superconducting BaFe\({}_{2}\)(As\({}_{2}\)P\({}_{2}\))\({}_{2}\) revealed by the de Haas–van Alphen effect. Phys. Rev. Lett. 105, 207004 (2010).
Das, T. & Balatsky, A. V. Origin of pressure induced second superconducting dome in A\({}_{y}\)Fe\({}_{y}\)Se\({}_{y}\) [A = K, (Tl, Rb)]. New J. Phys. 15, 093045 (2013).
Acknowledgements
J.P. and T.S. acknowledge financial support through the Dysenos AG by Kabelwerke Brugg AG Holding, Fachhochschule Nordwestschweiz and the Paul Scherrer Institut. J.P. also acknowledges financial support by the Swiss National Science Foundation Early Postdoc Mobility fellowship project number P2FRP2_171824 and PostDoc Mobility project number P400P2_180744. We acknowledge Y. Shimizu for the support during the experiments at SPring-8 and D. Casa for fabrication of the Ge (620) analysers. The Fe-K\({}_{\beta }\) emission experiments were performed at BL11XU of SPring-8 with the approval of the Japan Synchrotron Radiation Research Institute (JASRI) (Proposals No. 2014A3502 and 2014B3502). RIXS experiments have been performed at the ADRESS beamline of the Swiss Light Source at Paul Scherrer Institut. Part of this research has been funded by the Swiss National Science Foundation through the Sinergia network Mott Physics Beyond the Heisenberg (MPBH) model (SNSF Research grant numbers CRSII2_141962 and CRSII2_160765) and the D-A-CH programme (SNSF Research Grant No. 200021L_141325). The research leading to these results has received funding from the European Community’s Seventh Framework Programme (FP7/2007–2013) under Grant Agreement No. 290605 (COFUND: PSIFELLOW). Work in Japan was supported by Grant-in-Aids for Scientific Research (KAKENHI) from Japan Society for the Promotion of Science (JSPS), and by the ‘Topological Material Science’ and ‘Quantum Liquid Crystals’ Grant-in-Aid for Scientific Research on Innovative Areas from the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan. The work at IOP-CAS is supported by NSF and MOST through research projects.
Author information
Authors and Affiliations
Contributions
Th.Sc. conceived the project. J.P., K.I., Y.H. and Th.Sc. conducted XES experiments. J.P., Y.H., M.D., P.O.V., X.L. and Th.Sc. performed RIXS experiments with the assistance of V.N.S. S.K., Y.M. and Ta.Sh. prepared and characterised P-doped BaFe\(_{2}\)As\(_{2}\). L.X., X.W. and C.J. prepared the reference sample for XES. T.D. performed the calculations. J.P., K.I., T.D. and Th.Sc. together planned the project phases. J.P., T.D. and Th.Sc. wrote the paper with input from all the authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pelliciari, J., Ishii, K., Huang, Y. et al. Reciprocity between local moments and collective magnetic excitations in the phase diagram of BaFe2(As1−xPx)2. Commun Phys 2, 139 (2019). https://doi.org/10.1038/s42005-019-0236-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0236-3
This article is cited by
-
Spin-excitation anisotropy in the nematic state of detwinned FeSe
Nature Physics (2022)
-
Dispersionless orbital excitations in (Li,Fe)OHFeSe superconductors
npj Quantum Materials (2022)
-
Evolution of spin excitations from bulk to monolayer FeSe
Nature Communications (2021)
-
Tuning spin excitations in magnetic films by confinement
Nature Materials (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.