Abstract
The complex interactions between orbital angular momentum (OAM) of light and atoms are particularly intriguing in the areas of quantum optics and quantum information. Building a versatile high-dimensional quantum network needs broad spiral-bandwidth for preparing higher-quanta OAM mode and resolving the bandwidth mismatch in spatial space. Here, we demonstrate a broad spiral-bandwidth quantum-interface between photon and memory. Through twisted fields of the writing and reading, the correlated OAM distribution between photon and memory is significantly broadened. This broad spiral-bandwidth quantum-interface could be spanned in multiplexing regime and could work in high-quanta scenario with capability of \(\vert l\vert =\) 30, and we demonstrate the entanglement within 2-D subspace with a fidelity of 80.5 ± 4.8% for high \(l\). Such state-of-the-art technology to freely control the spatial distribution of OAM memory is very helpful to construct high-dimensional quantum networks and provides a benchmark in the field of actively developing methods to engineer OAM single photon from matters.
Similar content being viewed by others
Introduction
Light beams with orbital-angular-momentum (OAM)1 have a helical phase structure, where the phase winds azimuthally around the optical axis resulting in a characteristic null intensity at the center due to destructive interference. The interaction between OAM structured light and matters has many intriguing applications2, including trapping of particles3,4 and measuring rotation angular5,6, OAM-based imaging7 and optical communications8. In quantum information, light carried with OAM could significantly enhance the information capacity, thus advancing the developments of the high-dimensional (high-D) quantum networks, especially in OAM entanglement generation9,10,11,12, OAM-based quantum memory13,14,15,16,17,18,19, and OAM-based teleportation20. One block of constructing a high-D quantum network is how to establish a versatile high-D OAM quantum interface between photon and memory21.
Building a high-D OAM quantum interface could be based on the protocol of Duan–Lukin–Cirac–Zoller (DLCZ)22 where the probabilistically generated OAM photon is entangled with memory13,23. There are many parameters to characterize the performance of the interface between photon and memory24,25, such as lifetime, efficiency, and fidelity25,26,27. The most unique parameter of high-D OAM quantum interface could be the spiral-bandwidth \(\delta l\), which characterizes the mode-matching bandwidth window28,29. The adjacent nodes in high-dimensional quantum networks may be diverse and different in spatial mode, spiral-bandwidth, etc., for example, one is encoded in \(\pm l\) OAM spaces and the other one is in \(\pm (l+m)\) OAM spaces, here \(l\) and \(m\) represent the topological number of orthogonal OAM modes; or one mode can be encoded in the spacial bandwidth of \(\delta l\) and another in \(\delta (l+m)\), requiring a technology to make the quantum interface be more flexible and controllable in order for the nodes to be connected freely30. There are many efforts towards shaping the spatial bandwidth or spectrum of photon pairs, for example, increasing the pump beam waist, shaping the pump beam, and changing the OAM spectrum of pump28,31,32,33,34,35 in spontaneous parametric down conversion (SPDC) process, but no reports on shaping the spectrum of photon–atom interface. Shaping the OAM spectrum of the photon–atom interface from the third-order spontaneously four-wave mixing (SFWM) process is different from the second-order SPDC process, because there are two pumps in the SFWM process that we can individually modulate.
In this paper, we experimentally demonstrate a broad spiral-bandwidth OAM interface between photon and memory in a delayed SFWM process by shaping the write- and read-laser beams individually, it makes the joint of correlation against \(l\) modes broadened because the interaction length is increased in transverse azimuthal direction. This offers the ability to control the spatial distribution, including entangled OAM eigenmode \(\pm l\) and the spiral bandwidth \(\delta l\). Based on that, we demonstrate a potential application for OAM multiplexing, and obtain an obvious contrast data with inputting \(\Delta l=10\). We also have achieved high-D entanglement with \(l\) up to 16 and high-\(l\) 2-D OAM entanglement with \(l\) up to 30, all of which obey the entanglement properties. The reported results are useful for realizing broad spiral bandwidth and high-D quantum memory and increasing the capacity of quantum communication, and also is a benchmark of searching ways to explore versatile quantum interfaces.
Results
Experimental setup details
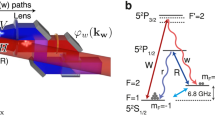
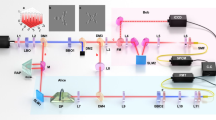
The experimental media is an optically thick atomic ensemble of Rubidium 85 (\({}^{85}{\mathrm{Rb}}\)) that is trapped in two-dimensional magneto-optic trap (MOT). The involved schematic of the energy levels and the experimental setup are shown in Fig. 1a and b. We firstly establish the correlation between a collective spin excited state (spin wave, also called as atomic memory) and a single photon (Signal 1) through spontaneous Raman scattering (SRS) in atomic ensemble. In this process, the write-laser is set to blue-detuned with atomic transition \(\vert 2\rangle\to \vert 3\rangle\). After reflecting from spatial light modulator (SLM) 1 (Holoeye LETO LCoS, \(1920\times 1080\) pixel) as depicted in Fig. 1b, the write-laser has carried on the OAM phase message loaded by a computer. Then, a 4-f image system with unequal arms, which is consisted of two lenses L1 and L2 with focal length of 300 and 500 mm, respectively, is utilized to map the OAM phase of the write-laser to the center of atomic ensemble accurately. The Signal 1 photon emitted from atomic ensemble is mapped onto another SLM 2 for detecting the OAM modes. Due to the angular momentum is conserved in SRS process, hence the spatial modes of the spin wave and Signal 1 are entangled in OAM degree of freedom. This OAM correlation can be flexibly demonstrated by mapping and checking the OAM modes on SLM 1 and SLM 2, respectively.
Overview of experiment. a The relevant energy level diagram. Write and Read represent write-laser pulse and read-laser pulse respectively; S1 and S2 are Signal 1 photon and Signal 2 photon. States \(\vert 1\rangle,\vert 2\rangle,\vert 3\rangle\), and \(\vert 4\rangle\) correspond to \({}^{85}{\mathrm{Rb}}\) atomic levels of \(5{S}_{1/2}(F=2)\), \(5{S}_{1/2}(F=3)\), \(5{P}_{1/2}(F=3)\), and \(5{P}_{3/2}(F=3)\), respectively. \(\Delta\) represents the detuning of write-laser pulse, which is set to be \(+2\pi \times 70\ {\rm{MHz}}\). The part in below is the time sequence of experiment. b Experimental setup. MOT is magneto-optical trap, \({\rm{L}}1-{\rm{L}}8\) represent a series of lenses, \({\rm{\lambda }}/4\) is quarter-wave plate, \({\rm{\lambda }}/2\) is half-wave plate and PBS is polarization beam splitter. SLM \(1 \sim 4\) are spatial light modulators
The OAM-based DLCZ quantum memory is built when the entanglement between the spin wave and Signal 1 photon is created. After a storage time of \(\Delta t\), we use another SLM 3 to load OAM structured light to read the spin wave out to Signal 2, the Signal 2 is also mapped onto another SLM 4. Ultimately, in order to check the quantum correlation between Signal 1 and atomic spin wave, we measure the coincidence counts between Signal 1 and Signal 2 by projecting them onto SLM 2 and SLM 4, respectively, in which the different phase structures on both of SLM 2 and 4 are loaded for measurement. Here, two couples of 4-f systems with unequal arms are used to map the OAM phase of signal photons to SLM accurately, see “Method” sections. The reflected photons from SLMs are collected into two single-mode fibers, which are detected by two detectors (avalanche diode, PerkinElmer SPCM-AQR-16-FC, 60% efficiency, maximum dark count rate of 25/s), respectively.
OAM conservation
In previous work18 for high-D OAM quantum interface with Gaussian mode input, it is difficult to generate higher-D entanglement because the correlated coincidences decrease dramatically against \(l\). Here, we modulate the OAM quanta of write- and read-beams to change the OAM spectrum of the interface. We input the write-laser with OAM quanta of \({l}_{{\rm{W}}}\). Due to the fact that SRS process conserves angular momentum, we have created OAM entanglement between Signal 1 and atomic memory, which can be specified by the formula
here, \(\vert {c}_{l}{\vert }^{2}\) represents excitation probability, \(\vert l\rangle _{{\rm{S1}}}\) is the OAM eigenmode of Signal 1 with quanta of \(l\). \(\vert {l}_{{\rm{W}}}-l\rangle _{{\rm{a}}}\) is the OAM eigenmode of atomic memory with quanta of \({l}_{{\rm{W}}}-l\). The spiral-bandwidth \(\delta l\) defined as the full width at half maximum of the correlated OAM spectrum describes how many orthogonal modes could be entangled. Through this method, the atomic memory could carry the arbitrary OAM topological charge with the term of \({l}_{{\rm{W}}}-l\), thus resulting in the redistributed quantum interface, that is an asymmetric distribution because \(\vert {l}_{{\rm{a}}}\vert \ne \vert {l}_{{\rm{S}}1}\vert\) with nonzero \({l}_{{\rm{W}}}\).
After a programmed time of storage, we check photon-atom entanglement by inputting read-laser with OAM quanta of \({l}_{{\rm{R}}}\), and checking the entanglement between Signal 1 and Signal 2. The entanglement between Signal 1 and Signal 2 can be written as \(\vert \psi \rangle _{{\rm{photon-photon}}}^{{l}_{{\rm{W}}},{l}_{{\rm{R}}}}={\sum }_{l=-\infty }^{l=\infty }{c}_{l}^{^{\prime} }\vert l\rangle _{{\rm{S1}}}\otimes \vert {l}_{{\rm{W}}}+{l}_{{\rm{R}}}-l\rangle _{{\rm{S2}}}\), here \(\vert {c}_{l}^{^{\prime} }{\vert }^{2}\) represents overall probability depending on write and read processes. At first, we set \({l}_{{\rm{W}}}=2\) and \({l}_{{\rm{R}}}=0\), it means using OAM quanta of 2 and 0 to write and read, respectively. Thus, the photonic entangled state is a sum of \(\vert l\rangle _{{\rm{S1}}}\otimes \vert 2-l\rangle _{{\rm{S2}}}\) with different \(l\), this is a modulated asymmetric OAM entangled state. Here, we only post-select the OAM mode of entangled state into 2-D subspace \(\vert 0\rangle _{{\rm{S1}}}\vert 2\rangle _{{\rm{S2}}}\) and \(\vert 2\rangle _{{\rm{S1}}}\vert 0\rangle _{{\rm{S2}}}\), that is \(\vert \psi \rangle _{{\rm{photon-photon}}}^{2,0}=1/2\sqrt{2}\left({\vert 0\rangle}_{{\rm{S1}}}{\vert 2\rangle}_{{\rm{S2}}}+{\vert 2\rangle}_{{\rm{S1}}}{\vert 0\rangle}_{{\rm{S2}}}\right)\). To characterize the OAM entanglement between Signal 1 and Signal 2, we reconstruct the density matrices by projecting Signal 1 and Signal 2 onto OAM bases of \(\vert 0\rangle\), \(\vert 2\rangle\), \(\left(\vert 0\rangle-i\vert 2\rangle\right)/{2}^{1/2}\), \(\left(\vert 0\rangle+\vert 2\rangle\right)/{2}^{1/2}\) for demonstrating quantum tomography. Then we use the obtained 16 coincidence rates to reconstruct the density matrix of state as shown in Fig. 2a and b. According to the formula \(F={\rm{Tr}}{(\sqrt{\sqrt{\rho }{\rho }_{{\rm{ideal}}}\sqrt{\rho }})}^{2}\), which compares the constructed density matrix \(\rho\) with the ideal density matrix \({\rho }_{{\rm{ideal}}}\), we obtain the fidelity of \(83.3\pm 3.5\)%. We also try another data set of \({l}_{{\rm{W}}}=1\) and \({l}_{{\rm{R}}}=2\), and detect the photonic entangled state \(\vert \psi \rangle _{{\rm{photon-photon}}}^{1,2}=1/\sqrt{2}\left({\vert 0\rangle}_{{\rm{S1}}}{\vert 3\rangle}_{{\rm{S2}}}+{\vert 3\rangle}_{{\rm{S1}}}{\vert 0\rangle}_{{\rm{S2}}}\right)\). Similarly, we reconstruct the density matrix of this state, the real and imaginary parts of reconstructed density matrix are shown in Fig. 2c and d, with fidelity of \(81.1\pm 4.2\)%.
Reconstructed density matrices for modulated orbital-angular-momentum (OAM) entanglement. The real (a, b) and imaginary (c, d) parts of density matrices for photonic OAM entangled state \(\vert \psi \rangle _{{\rm{photon-photon}}}^{2,0}\) and \(\vert \psi \rangle _{{\rm{photon-photon}}}^{1,2}\). Each data for reconstructing density matrices are recorded in 1000 s
Spiral-bandwidth broadening
Due to the broadening effect of spiral bandwidth with larger \(l\) laser beam input, the distribution of generated OAM signal 1 and memory would be redistributed in more flat range. This is because the generated OAM modes are dependent on the interaction length and the waist of the write- and read-beams36. The vector mismatching \(\Delta k\) from transverse azimuthal phase would increase the value of \(\Delta k\cdot L\), where \(L\) is the interaction length. This effect is very promising because it is regarded as a concentration operation. In order to achieve a broad spiral-bandwidth OAM interface, we utilize the above method to extend the quanta of write-laser, we set \({l}_{{\rm{W}}}=10\). In addition, we set \({l}_{{\rm{R}}}=-10\) for reading process. The writing and reading process of DLCZ quantum memory is essentially a delayed SFWM process. Based on the unique advantages of individually modulating write- and read-beams of SFWM (not like a single pump field used in SPDC process), the write- and read-laser beams can be individually loaded OAM modes with opposite signs whilst the input total angular momentum can be zero, thus making the joint spectrum of correlation broadened. We map different OAM phases onto SLM 2 and SLM 4, and record the coincidence between Signal 1 and Signal 2 photons. The spiral bandwidth of OAM entanglement is measured in the red line in Fig. 3a. The spiral bandwidth of generated single photons becomes much flater than the scheme with inputting Gaussian mode. The spiral bandwidth of Gaussian mode is \(\delta l=11.4\pm 2.3\), whilst for \({l}_{{\rm{W}}}=-{l}_{{\rm{R}}}=10\) the spiral bandwidth is \(\delta l=27.0\pm 1.8\) obviously enhanced by a factor of \(\sim 2.2\). This transverse vector mismatch would lead to decrements on detecting \({l}_{{\rm{S1}}}={l}_{{\rm{S2}}}=0\) when using larger-\(l\) OAM to write and read. In Fig. 3b, we use \({l}_{{\rm{W}}}=-{l}_{{\rm{R}}}=-30\) to measure the correlated OAM spectrum of signal photons, we obtain a modulated OAM distribution in which the coincidence peak appears at \({l}_{{\rm{S1}}}=-{l}_{{\rm{S2}}}=-23\pm 7\) not at \({l}_{{\rm{S1}}}={l}_{{\rm{S2}}}=0\). In addition, in this process, we found that the coincidence counts at \({l}_{{\rm{S1}}}=-{l}_{{\rm{S2}}}=30\) is very small; this is because the nonlinearity in the SRS process becomes weak when the vector mismatch between write and signal 1 photon is larger.
The measured correlated orbital-angular-momentum (OAM) distribution under different OAM modes of write- and read-beams. a The correlated OAM distribution with \({l}_{{\rm{W}}}=-{l}_{{\rm{R}}}=0\) (black line) and \({l}_{{\rm{W}}}=-{l}_{{\rm{R}}}=10\) (red line). The black data are fitted by the function \(y={y}_{0}+2bw/[\pi (4{(x-{x}_{c})}^{2}+{w}^{2})]\) with parameters (\({y}_{0}=15.8\), \(w=11.4\pm 2.3\), \(b=5501\), \({x}_{c}=0\)). The red data are fitted by the function \(y=\frac{A}{w* \sqrt{\pi /2}}{\mathrm{exp}}[\left.-2{(\frac{(x-{x}_{c})}{w})}^{2}\right)]\) with parameters (\(w=27.0\pm 0.7,A=8363\), \({x}_{c}=-1.0\)). b The correlated OAM distribution with \({l}_{{\rm{W}}}=-{l}_{{\rm{R}}}=-30\), the red line is the smooth line guided for eyes. Error bars represent \(\pm\) one standard deviation
High-D OAM entanglement
We also check the high-D OAM entanglement with a broad spiral-bandwidth, and give a high-D entanglement properties with OAM quanta up to \(\Delta l=16\). In order to demonstrate the high-D entanglement between Signal 1 and atomic memory at high-\(l\), we avoid the crosstalk between neighboring OAM modes and select the modes of \(l=0,\,4,\,8,\,12,\,16\) in which three modes between adjacent terms are removed for better isolation, see the correlated coincidence counts in Fig. 4a. We read the photon-atom entanglement out to photon–photon entanglement for verification. So, the entangled photonic state is \(\vert \psi \rangle _{{\rm{photon-photon}}}^{{\rm{10}},-{\rm{1}}0}={c}_{0}^{^{\prime} }\vert 0\rangle _{{\rm{S1}}}\vert 0\rangle _{{\rm{S2}}}+{c}_{4}^{^{\prime} }\vert -4\rangle _{{\rm{S1}}}\vert 4\rangle _{{\rm{S2}}}+{c}_{8}^{^{\prime} }\vert -8\rangle _{{\rm{S1}}}\vert 8\rangle _{{\rm{S2}}}+{c}_{12}^{^{\prime} }\vert -12\rangle _{{\rm{S1}}}\vert 12\rangle _{{\rm{S2}}}+{c}_{16}^{^{\prime} }\vert -16\rangle _{{\rm{S1}}}\vert 16\rangle _{{\rm{S2}}}\) here, \({c}_{0}^{^{\prime} } \sim {c}_{16}^{^{\prime} }\) are the corresponding amplitudes of different terms \(\vert 0\rangle _{{\rm{S1}}}\vert 0\rangle _{{\rm{S2}}} \sim \vert {\rm{-16}}\rangle _{{\rm{S1}}}\vert {\rm{16}}\rangle _{{\rm{S2}}}\). To verify the high-D state, we use high-D entanglement dimensionality witness12,37 to characterize the entanglement. The entanglement dimensionality witness is expressed as \({W}_{d}=3D(D-1)/2-D(D-d)\), here, \(D\) is the number of measured OAM modes, and \(d\) is associated with the dimensions of entanglement. If \(W> {W}_{d}\), the two photons entangled in at least \(d+1\) dimensions, where \(W\) is obtained from calculating the sum \(N={V}_{x}+{V}_{y}+{V}_{z}\) of each visibility of two-photon interference in the diagonal/anti-diagonal \({\sigma }_{{\rm{{x}}}}\), left-circular/right-circular \({\sigma }_{y}\) and horizontal/vertical \({\sigma }_{z}\) bases respectively, in which \({V}_{i}=\vert \langle{\sigma }_{i}\otimes {\sigma }_{i}\rangle\vert ,i=x,y,z\). Here, the OAM modes are selected from l = 0, 4, 8, 12, 16. We calculate the value W is \(21.93\pm 0.55\), which violates the bound \({W}_{d}\) of 20 revealing at least a 4-D OAM entanglement between Signal 1 and Signal 2 photons, the sum visibility in each \(2\times 2\) subspace is given in Fig. 4b. In these measurements, the atom-photon entangled states are both detected in photonic regime, we assume the fidelity of reading out from ensembles is near unit. Although there are definitely some noise or inefficient elements from reading process, making the degree of the measured entanglement lower than that existed in ensembles.
High-dimensional entanglement. a The post-selected correlated orbital-angular-momentum (OAM) matrix between Signal 1 and Signal 2 photons with OAM modes difference \(\vert \Delta l\vert\) up to 16. b The sum \(N\) of visibilities for \(2\times 2\) subspaces for calculating the high-D entanglement dimensionality witness \(W\)
OAM multiplexing
Broad spiral-bandwidth interface allow us to demonstrate a potential application for OAM multiplexing. If we select \({l}_{{\rm{W}}}=10\) for writing and \({l}_{{\rm{R}}}=-10\) for reading out, we can detect the correlated coincidence; while for \({l}_{{\rm{W}}}=10\), \({l}_{{\rm{R}}}=0\) given in Fig. 5a, there would be almost no coincidence counts exhibiting orthogonality-like property shown by Fig. 5b. The nonlinearity of the interleaved OAM modes is strongly dependent on the overlap of beam profiles of write- and read-beams, it would become small if the mismatch between write- and read-beams is large, then the coincidence counts would jump down. The detected contrast \(({C}_{\text{same}}-{C}_{\text{diff}})/({C}_{\text{same}}+{C}_{\text{diff}})\) is \(0.85\pm 0.03\) (where \({C}_{\text{same}}\) and \({C}_{\text{diff}}\) are defined as coincidence counts with same (\(\vert {l}_{{\rm{W}}}\vert =\vert {l}_{{\rm{R}}}\vert\)) and different (\(\vert {l}_{{\rm{W}}}\vert \ne \vert {l}_{{\rm{R}}}\vert\)) write- and read-beam OAM modes). In this process, the storage lifetime is almost the same for \({l}_{{\rm{W}}}=0\) and \({l}_{{\rm{W}}}=10\), see Fig. 5c. The atomic dephasing along the azimuthal direction in cold atomic cloud is not obvious, while the dephasing along the azimuthal direction is strong in hot vapor cell38. This is because the velocity of cold atoms is smaller than that of the hot atoms. Furthermore, we map the different OAM modes in the inner (\({l}_{{\rm{in}}}\)) and outer rings (\({l}_{{\rm{out}}}\)) to detect the multiplexing property along radial direction, see Fig. 5d. Since the nonlinearity of interleaved OAM modes (for example \({l}_{{\rm{W}}}=0\) and \({l}_{{\rm{W}}}=10\)) in the center of ensemble can be distinguished by inputting distinct OAM modes (Fig. 5e), this may result in multiplexing along radial direction. For a superposition composite OAM state along radial direction, \(\vert \varphi \rangle=\alpha \vert l\rangle _{{\rm{in}}}+\beta \vert l\rangle _{{\rm{out}}}\), where \(\alpha\) and \(\beta\) are mode weight coefficients obeying a relation of \(\vert \alpha {\vert }^{2}+\vert \beta {\vert }^{2}=1\). We map the different OAM modes with \(\Delta l=1,2\ldots 10\) in inner and outer rings (\(\Delta l={l}_{{\rm{out}}}-{l}_{{\rm{in}}}\)) and detect the correlation given in Fig. 5e. The crosstalk between different OAM modes is detected by setting same/different phase structures. The contrast of coincidence counts is increased against with \(\Delta l\) because the different topological numbers \({l}_{{\rm{W}}}\), \({l}_{{\rm{R}}}\) make the strong mismatch between write- and read-beams decreasing the correlation (Fig. 5f), which is in agreement with the above analysis. This whole process could be regarded as the multiplexing of two OAM spectra, which are created by inputting two distinct OAM writing and reading (\({l}_{{\rm{out}}}\), \({l}_{{\rm{in}}}\)), thus achieving higher capacity quantum communications with one OAM spectra docking to another OAM spectrum.
Orthogonality and multiplexing orbital-angular-momentum (OAM) modes. a The orthogonality with different OAM modes of write- and read-lasers. The cross and check marks in up/down equation shows the weak/strong correlation under the different (\(\vert {l}_{{\rm{W}}}\vert \ne \vert {l}_{{\rm{R}}}\vert\)) /same OAM orders (\(\vert {l}_{{\rm{W}}}\vert =\vert {l}_{{\rm{R}}}\vert\)). b The coincidence counts for the different situations of \(\vert {l}_{{\rm{W}}}\rangle=\vert 0\rangle/\vert 10\rangle\), \(\vert {l}_{{\rm{S1}}}\rangle=\vert 0\rangle/\vert 10\rangle\), \(\vert {l}_{{\rm{R}}}\rangle=\vert 0\rangle/\vert -10\rangle\), \(\vert {l}_{{\rm{S2}}}> =\vert 0\rangle/\vert -10\rangle\). c The memory decay function with different OAM modes (black for \(\vert {l}_{{\rm{W}}}\vert =0\), red for \(\vert {l}_{{\rm{W}}}\vert =10\)). The memory decays exponentially with storage lifetime of \(\tau =1655\ {\rm{ns}}\). The fitted functions are \(y={y}_{0}+A{e}^{-\frac{t}{\tau }}\) with parameters of \({y}_{0}=-3.3\), \(A=104.6\), \(\tau =1655\) for black data and \({y}_{0}=-7.6\), \(A=73.5\), \(\tau =1655\) for red data. d The multiplexing in radial direction with different OAM modes in inner and outer rings. When the OAM orders in the inner and outer rings are different (up equation), the correlation is weak; on the contrary, the correlation is strong when the OAM orders are same (down equation). e The normalized coincidence counts with \(\vert {l}_{{\rm{W}}}\rangle=\vert 0\rangle+\vert 10\rangle\), \(\vert {l}_{{\rm{R}}}\rangle=\vert -10\rangle+\vert 0\rangle\), and \(\vert {l}_{{\rm{W}}}\rangle=\vert 0\rangle+\vert 10\rangle,\vert {l}_{{\rm{R}}}\rangle=\vert 0\rangle+\vert -10\rangle\) in the left two bars. The right two bars are the corresponding OAM mode of \(\vert {l}_{{\rm{W}}}\rangle=\vert 0\rangle+\vert 9\rangle\), \(\vert {l}_{{\rm{R}}}\rangle=\vert -9\rangle+\vert 0\rangle\), and \(\vert {l}_{{\rm{W}}}\rangle=\vert 0\rangle+\vert 9\rangle\), \(\vert {l}_{{\rm{R}}}\rangle=\vert 0\rangle+\vert -9\rangle\). f The detected contrast of coincidence counts against different \(\Delta l\), here \(\Delta l={l}_{{\rm{W}}}-{l}_{{\rm{R}}}\). The storage time is set to be 500 ns. The different signs of OAM quanta set in (a) and (d) are required to maintain OAM conservation. Error bars represent \(\pm\) one standard deviation
High-\(l\) OAM entanglement
At last, broad spiral-bandwidth offers an ability for demonstrating interface toward high-\(l\). For this, we set \({l}_{{\rm{W}}}=30\), \({l}_{{\rm{R}}}=-30\), the storage time is set to be twice of the width of write pulse, the decoherence from the transverse azimuthal momentum mismatch between write-laser and the Signal 1 photons is ignored. The third-order nonlinearity of the DLCZ process at large quanta \(l\) is relatively small and the generation rate of the two correlated photons is decreased with large quanta l, we then only consider the two OAM modes for verifying entanglement. We choose the OAM modes of \(l=28,32\) to verify the high-quanta OAM entanglement. The photonic entangled state is expressed as
Through quantum state tomography, we obtain the reconstructed density matrix as shown in Fig. 6a and b. The fidelity of reconstructed density matrix is calculated as \(80.5\pm 4.8 \%\) by comparing with the ideal density matrix. We also check the violation of Clauser–Horne–Shimony–Holt (CHSH) inequality39,40,41 to demonstrate the nonlocality of the entangled state. The CHSH parameter S42 is represented as following
Here, the correlation function \(E\left({\theta }_{{\rm{S2}}},{\theta }_{{\rm{S1}}}\right)\) can be calculated from the rates of coincidence at several particular orientations
\({\theta }_{{\rm{S1}}}/{\theta }_{{\rm{S2}}}\) represents the angle of phase distribution on the surface of SLM 2/SLM 4. We select \({\theta }_{{\rm{S2}}}=0\), \({\theta }_{{\rm{S1}}}=\pi /8\), \({\theta }_{{\rm{S}}{2}^{^{\prime} }}=\pi /4\), and \({\theta }_{{\rm{S}}{1}^{^{\prime} }}=3\pi /8\). The calculated S is \(2.22\pm 0.07\) which is larger than 2 violating the CHSH inequality, thus it demonstrates the real entanglement between Signal 1 and Signal 2 photons.
Discussion
High-fidelity quantum memory for high OAM is indispensable element for establishing a quantum network in high-dimensional space. In addition, the unitary quantum efficiency and sufficient storage lifetime are required to establish a long distance quantum communication. In order to solve these benchmark problems, one needs increase the optical depth of atomic cloud to get a unitary quantum efficiency for different OAM modes. There are two limiting factors for storage time, including the residual magnetic field and atomic motion. Storage lifetime can be improved by compensating for the magnetic field or by using magnetic field-insensitive states. The transverse momentum from OAM would contribute the dephasing, which could be eliminated by reducing atomic motion with an optical lattice.
In this work, we demonstrate a broad spiral-bandwidth OAM interface between photon and memory, the OAM distribution and the quanta of OAM quantum interface are freely manipulated. In this state-of-the-art quantum interface, we have achieved high-D OAM entanglement with OAM modes difference \(\Delta l\) up to 16, the OAM quanta can be accessible to \(l=\pm 30\) in 2-D subspace. The experiment reported here would be very promising to demonstrate high-quanta OAM quantum interface and study the fundamental physics in OAM-based light and matter interaction.
Methods
Experimental time sequence
The repetition rate of our experiment is \(100\ {\rm{Hz}}\), and the MOT trapping time is 8.7 ms. Besides, the operation window of 1.3 ms consists of 2600 cycles with a cycle time of 500 ns. Write-laser and read-laser are pulsed by acousto-optic modulator with pulse width of 50 and 200 ns, respectively in each cycle. The optical depth in MOT is about 40. The storage time is controlled by changing the delay time between write- and read-laser through an arbitrary function generator. The magnetic field for trapping is shut down in the experiment window.
4-F image system for four SLMs
The SLM 1 acts as a mask plane, and the center of atomic ensemble in MOT is the image plane. Two lenses L1 and L2 with focal length of 300 and 500 mm are utilized to map the phase message of SLM 1 to the atomic ensemble. Due to the phase matching condition \({k}_{W}-{k}_{S1}={k}_{R}-{k}_{S2}\), the imaging system can be easily optically aligned. The Signal 1 and Signal 2 fields are collinear, the Signal 1 beam is completely overlapped by the write beam through demonstrating electromagnetically induced transparency effect. Here, the write-laser carrying high OAM quanta diffracts very strongly and results in the waist of laser beam too large in the center of atomic ensemble, which results in weak interaction between write-laser and atomic ensemble. Through the 4-f image system with unequal arms, we can not only map the OAM phase message to the center of atomic ensemble accurately but also decrease the waist of write-laser with high OAM quanta. Similarly, the single photon carried with OAM phase message from the center of atomic ensemble is retrieved to project on SLM 1 via the other 4-f image system, and ultimately we collect photons by single-mode fibers.
Theoretical analysis
In the interaction picture, despite the decay of spin wave, the effective Hamiltonian for the delayed four-wave mixing process is written as36,43
where \({\varepsilon }_{0}\) is the vacuum permittivity, \(H.c.\) means the Hermitian conjugate, \({\chi }^{(3)}\) is the third-order nonlinear susceptibility for resonant signal 2 photon. For our experimental conditions, the distribution of atomic cloud is assumed to be Gaussian, so the effective nonlinearity44: \({\chi }^{(3)} \sim {\rm{exp}}[-\frac{{r}^{2}}{{w}_{a}^{2}}]\), here, \({w}_{a}\) is the effective size of the cloud of atoms in the transverse plane.
As the SLM planes are imaged to the center of the atomic cloud, the write, read, signal 1 and signal 2 fields in the the center of the atomic cloud can be expressed as \({\overrightarrow{E}}_{x}(r)=\sqrt{2/\pi }\exp (-{r}^{2}/{w}_{x}^{2}){\rm{exp}}(-i\overrightarrow{{k}_{r}^{x}}\overrightarrow{r})\), where \({w}_{x}\) is the beam waist, \(\overrightarrow{{k}_{r}^{x}}\) is the transverse wave vector of the \(x\) field, \(x\) represents write, read, signal 1 and signal 2 fields. Because a perfect Gaussian beam loading a helical phase \(\mathrm{exp}(-il\theta )\) experiences the evolution of Collins diffraction45, this offers the fields with the ability of carrying transverse wave vector \({q}_{s1}\) and \({q}_{s2}\). The spatial quantum state of the generated pair of photon can be written as the following expression44,46
here, the mode function \(\Phi\) here is \(\sim \int d{q}_{W}d{q}_{R}{\overrightarrow{E}}_{W}(r){\overrightarrow{E}}_{R}(r)\mathrm{exp}[-{a}_{0}^{2}{({q}_{S2}-{q}_{S1})}^{2}/2]{,}\) \({a}_{0}\) corresponds to the width of the Gaussian distribution. When the quantum number \(l\) of write and read fields is small, the Gaussian distribution of photon pairs dominates. While for the quantum number \(l\) is large, the mismatch between write and read fields would result in a dip in the spectrum distribution when detecting \({l}_{S1}={l}_{S2}=0\).
2-D high-\(l\) entanglement and state tomography
If we considered the OAM modes of \(a\) and \(b\) with \(l\) = 32 and 28, the Signal 1 and Signal 2 are entangled in OAM space and entangled state is expressed as
here, \(\vert -28\rangle _{{\rm{S1}}}\) represents the Signal 1 carrying with OAM quanta of −28. By using two computers, we project two photons onto two SLMs respectively and four state of \(\vert {\phi }_{1 \sim 4}\rangle\) (\(\vert -28\rangle\), \(\vert -32\rangle\), \(\left(\vert -28\rangle-i\vert -32\rangle\right)/{2}^{1/2}\), \(\left(\vert -28\rangle+\vert -32\rangle\right)/{2}^{1/2}\)) are programmed onto SLM 2 and \(\vert {\varphi }_{1 \sim 4}\rangle\) (\(\vert 28\rangle\), \(\vert 32\rangle\), \(\left(\vert 28\rangle-i\vert 32\rangle\right)/{2}^{1/2}\), \(\left(\vert 28\rangle+\vert 32\rangle\right)/{2}^{1/2}\)) are programmed onto SLM 4. Then, we obtain a set of 16 data for reconstructing the density matrix given in the main text. The error bars in our experiment are estimated by Poisson statistics and using Monte Carlo simulations with the aid of Mathematica software.
Data availability
The data sets generated during the current study are available from the corresponding author on reasonable request.
References
Allen, L., Beijersbergen, M. W., Spreeuw, R. J. C. & Woerdman, J. P. Orbital angular momentum of light and the transformation of laguerre-gaussian laser modes. Phys. Rev. A 45, 8185 (1992).
Padgett, M. J. Orbital angular momentum 25 years on, Orbital angular momentum 25 years on. Opt. Express 25, 11265–11274 (2017).
He, H., Friese, M. E. J., Heckenberg, N. R. & Rubinsztein-Dunlop, H. Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity. Phys. Rev. Lett. 75, 826 (1995).
He, X., Xu, P., Wang, J. & Zhan, M. Rotating single atoms in a ring lattice generated by a spatial light modulator. Opt. Express 17, 21007–21014 (2009).
Courtial, J., Dholakia, K., Robertson, D. A., Allen, L. & Padgett, M. J. Measurement of the rotational frequency shift imparted to a rotating light beam possessing orbital angular momentum. Phys. Rev. Lett. 80, 3217 (1998).
Lavery, M. P. J., Speirits, F. C., Barnett, S. M. & Padgett, M. J. Detection of a spinning object using lightas orbital angular momentum. Science 341, 537–540 (2013).
Fürhapter, S., Jesacher, A., Bernet, S. & Ritsch-Marte, M. Spiral phase contrast imaging in microscopy. Opt. Express 13, 689–694 (2005).
Wang, J. et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. photonics 6, 488 (2012).
Mair, A., Vaziri, A., Weihs, G. & Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 412, 313 (2001).
Dada, A. C., Leach, J., Buller, G. S., Padgett, M. J. & Andersson, E. Experimental high-dimensional two-photon entanglement and violations of generalized bell inequalities. Nat. Phys. 7, 677 (2011).
Fickler, R. et al. Quantum entanglement of high angular momenta. Science 338, 640–643 (2012).
Krenn, M. et al. Generation and confirmation of a (100\(\times\) 100)-dimensional entangled quantum system. Proc. Natl Acad. Sci. 111, 6243–6247 (2014).
Inoue, R., Yonehara, T., Miyamoto, Y., Koashi, M. & Kozuma, M. Measuring qutrit-qutrit entanglement of orbital angular momentum states of an atomic ensemble and a photon. Phys. Rev. Lett. 103, 110503 (2009).
Ding, D.-S., Zhou, Z.-Y., Shi, B.-S. & Guo, G.-C. Single-photon-level quantum image memory based on cold atomic ensembles. Nat. Commun. 4, 2527 (2013).
Nicolas, A. et al. A quantum memory for orbital angular momentum photonic qubits. Nat. Photonics 8, 234 (2014).
Zhou, Z.-Q. et al. Quantum storage of three-dimensional orbital-angular-momentum entanglement in a crystal. Phys. Rev. Lett. 115, 070502 (2015).
Ding, D.-S. et al. Quantum storage of orbital angular momentum entanglement in an atomic ensemble. Phys. Rev. Lett. 114, 050502 (2015).
Ding, D.-S. et al. High-dimensional entanglement between distant atomic-ensemble memories. Light 5, e16157 (2016).
Zhang, W. et al. Experimental realization of entanglement in multiple degrees of freedom between two quantum memories. Nat. Commun. 7, 13514 (2016).
Wang, X.-L. et al. Quantum teleportation of multiple degrees of freedom of a single photon. Nature 518, 516 (2015).
Krenn, M., Malik, M., Erhard, M. & Zeilinger, A. Orbital angular momentum of photons and the entanglement of laguerre-gaussian modes. Philos. Trans. R. Soc. A 375, 20150442 (2017).
Duan, L.-M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413 (2001).
Inoue, R. et al. Entanglement of orbital angular momentum states between an ensemble of cold atoms and a photon. Phys. Rev. A 74, 053809 (2006).
Bussie`res, F. et al. Prospective applications of optical quantum memories. J. Mod. Opt. 60, 1519–1537 (2013).
Heshami, K. et al. Quantum memories: emerging applications and recent advances. J. Mod. Opt. 63, 2005–2028 (2016).
Ma, L., Slattery, O. & Tang, X. Optical quantum memory based on electromagnetically induced transparency. J. Opt. 19, 043001 (2017).
Brennen, G., Giacobino, E. & Simon, C. Focus on quantum memory. New J. Phys. 17, 050201 (2015).
Torres, J. P., Alexandrescu, A. & Torner, L. Quantum spiral bandwidth of entangled two-photon states. Phys. Rev. A 68, 050301 (2003).
Offer, R. F., Stulga, D., Riis, E., Franke-Arnold, S. & Arnold, A. S. Spiral bandwidth of four-wave mixing in rb vapour. Commun. Phys. 1, 84 (2018).
Kimble, H. J. The quantum internet. Nature 453, 1023 (2008).
Romero, J. et al. Orbital angular momentum correlations with a phase-flipped gaussian mode pump beam. J. Opt. 14, 085401 (2012).
Kovlakov, E. V., Bobrov, I. B., Straupe, S. S. & Kulik, S. P. Spatial bell-state generation without transverse mode subspace postselection. Phys. Rev. Lett. 118, 030503 (2017).
Liu, S. et al. Coherent manipulation of a three-dimensional maximally entangled state. Phys. Rev. A 98, 062316 (2018).
Kovlakov, E. V., Straupe, S. S. & Kulik, S. P. Quantum state engineering with twisted photons via adaptive shaping of the pump beam. Phys. Rev. A 98, 060301 (2018).
Torres, J. P., Deyanova, Y., Torner, L. & Molina-Terriza, G. Preparation of engineered two-photon entangled states for multidimensional quantum information. Phys. Rev. A 67, 052313 (2003).
Du, S., Wen, J. & Rubin, M. H. Narrowband biphoton generation near atomic resonance. JOSA B 25, C98–C108 (2008).
Agnew, M., Leach, J. & Boyd, R. W. Observation of entanglement witnesses for orbital angular momentum states. Eur. Phys. J. D 66, 156 (2012).
Shi, S. et al. Transverse azimuthal dephasing of a vortex spin wave in a hot atomic gas. Phys. Rev. A 95, 033823 (2017).
Clauser, J. F., Horne, M. A., Shimony, A. & Holt, R. A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23, 880 (1969).
Freedman, S. J. & Clauser, J. F. Experimental test of local hidden-variable theories. Phys. Rev. Lett. 28, 938 (1972).
Clauser, J. F. & Horne, M. A. Experimental consequences of objective local theories. Phys. Rev. D 10, 526 (1974).
Leach, J. et al. Violation of a bell inequality in two-dimensional orbital angular momentum state-spaces. Opt. Express 17, 8287–8293 (2009).
Wen, J. & Rubin, M. H. Transverse effects in paired-photon generation via an electromagnetically induced transparency medium. I. Perturbation theory. Phys. Rev. A 74, 023808 (2006).
Osorio, C. I., Barreiro, S., Mitchell, M. W. & Torres, J. P. Spatial entanglement of paired photons generated in cold atomic ensembles. Phys. Rev. A 78, 052301 (2008).
Zhou, Z.-Y. et al. Quantum twisted double-slits experiments: confirming wavefunctionsaphysical reality. Sci. Bull. 62, 1185–1192 (2017).
Lee, J.-C., Park, K.-K., Zhao, T.-M. & Kim, Y.-H. Einstein–Podolsky–Rosen entanglement of narrow-band photons from cold atoms. Phys. Rev. Lett. 117, 250501 (2016).
Acknowledgements
Dong-Sheng Ding and Ming-Xin Dong contributed this paper equally. We thank Guo-Yong Xiang professor for loaning a SLM. This work was supported by National Key R&D Program of China (2017YFA0304800), Anhui Initiative in Quantum Information Technologies (AHY020200), the National Natural Science Foundation of China (Grant nos. 61525504, 61722510, 61435011, 11174271, 61275115, and 11604322), and the Youth Innovation Pro motion Association of Chinese Academy of Sciences under Grant no. 2018490.
Author information
Authors and Affiliations
Contributions
D.S.D. conceived the idea. M.X.D. carried out the experiments with assistance from W.Z, S.S., Y.C.Y., and Y.H.Y. All authors contributed to the discussions and analysis of results. D.S.D. and M.X.D. wrote the paper. D.S.D., B.S.S., and G.C.G. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ding, DS., Dong, MX., Zhang, W. et al. Broad spiral bandwidth of orbital angular momentum interface between photon and memory. Commun Phys 2, 100 (2019). https://doi.org/10.1038/s42005-019-0201-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0201-1
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.