Abstract
Recent years have brought an explosion of activities in the research of topological aspects of condensed-matter systems. Topological phases of matter are accompanied by protected surface states or exotic degenerate excitations such as Majorana modes or Haldane’s localized spinons. Topologically protected degeneracies can, however, also appear in the bulk. An intriguing example is provided by Weyl semimetals, where topologically protected electronic band degeneracies and exotic surface states emerge even in the absence of interactions. Here we demonstrate experimentally and theoretically that Weyl degeneracies appear naturally in an interacting quantum dot system, for specific values of the external magnetic field. These magnetic Weyl points are robust against spin–orbit coupling unavoidably present in most quantum dot devices. Our transport experiments through an InAs double-dot device placed in magnetic field reveal the presence of a pair of Weyl points, exhibiting a robust ground-state degeneracy and a corresponding protected Kondo effect.
Similar content being viewed by others
Introduction
Mathematical tools borrowed from topology find more and more applications in contemporary condensed-matter physics1,2,3. In Weyl semimetals4,5, e.g., the electronic band structure exhibits isolated degeneracy points6, where two bands touch; this effect is also accompanied by exotic surface states5,7. In three-dimensional systems, these degeneracy points can be protected by topology—and classified by a suitably chosen Chern number: continuous perturbations may displace these Weyl points in momentum space, but cannot break their degeneracy. Weyl point-related degeneracies of electronic states in molecules termed conical intersections are also thought to play a fundamental role in various phenomena in photochemistry8. They have also been predicted to appear in the context of multi-terminal Josephson junctions9, and that of photonics10, and have also been engineered and demonstrated in coupled superconducting qubits11,12.
The simplest example of a Weyl point arises when a spin-1/2 electron is placed in a homogeneous magnetic field (see Fig. 1a–c). In this example, the parameter space is spanned by the magnetic-field vector B = (Bx, By, Bz) and the two energy eigenstates are degenerate at B = 0. We can associate a nonzero topological charge to this degeneracy point: the ground-state Chern number \(C({\cal{S}}) = 1\) evaluated on an arbitrary closed surface \({\cal{S}}\) surrounding the degeneracy point (see Methods for details). This nonzero Chern number promotes this B = 0 degeneracy point to a Weyl point and underlines the robustness of its (Kramers) degeneracy against perturbations.
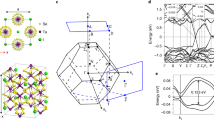
Geometries of degeneracy points for simple spin systems in a Zeeman field. a–c A single spin-1/2. d–f Two interacting S = 1/2 spins with isotropic antiferromagnetic exchange. g–i Two interacting S = 1/2 spins subject to spin–orbit interaction, where μB is the Bohr magneton, B is the magnetic field, S, SL/R are the spin operators, \(g\), \(\widehat {\mathbf{g}}_{{\mathrm{L}}/{\mathrm{R}}}\) are the corresponding g-factors/g-tensors, and \(J\) and \(\widehat {\mathbf{J}}\) are the exchange coupling between the spins. b, e, h, Characteristic magnetic-field dependence of the energy spectrum, T are the triplets, and S is the singlet solution. Red dots mark the ground-state degeneracy points. c, f, i, Geometry of the magnetic-field values where the ground state is degenerate
Let us now turn to the case of two coupled interacting spins and investigate the fate of Weyl points in the presence of—possibly strong—spin–orbit interaction (SOI)13,14. In the most general case, this system is described by the Hamiltonian H = HZ + Hint, where \(H_{\mathrm{Z}} = \mathop {\sum}_{\alpha ,\beta } {\mu _{\mathrm{B}}} B_\alpha (\hat g_{\mathrm{L}}^{\alpha \beta }S_{\mathrm{L}}^\beta + \hat g_{\mathrm{R}}^{\alpha \beta }S_{\mathrm{R}}^\beta )\) describes the Zeeman coupling and \(H_{{\mathrm{int}}} = \mathop {\sum}_{\alpha ,\beta } {\hat J^{\alpha \beta }} {\mkern 1mu} S_{\mathrm{L}}^\alpha S_{\mathrm{R}}^\beta\) is just the exchange interaction. The SOI appears here through the anisotropic and dot dependent g-tensors, \(\widehat {\mathbf{g}}_{{\mathrm{L}}/{\mathrm{R}}}\), and the anisotropic exchange coupling tensor, \(\widehat {\mathbf{J}}\).
In the absence of SOI (Fig. 1d–f), the g-tensors as well as the exchange coupling are just scalars, \(\widehat {\mathbf{g}}_{{\mathrm{L}}/{\mathrm{R}}} \to g_{{\mathrm{L}}/{\mathrm{R}}}\) and \(\widehat {\mathbf{J}} \to J\). The energy spectrum (Fig. 1e) is therefore isotropic as a function of the magnetic field. For an antiferromagnetic coupling, the ground state becomes degenerate at a sphere of radius B = J/(μBg), where a singlet to triplet transition occurs (Fig. 1f).
According to naive expectations, a small SOI should mix the singlet and triplet states close to the sphere of degeneracies, and thereby remove the degeneracy immediately (Fig. 1g–i). Simple models, however, indicate that this may not be the case. For example, quasi-two- and quasi-one-dimensional quantum dots are often described in terms of a Rashba field, Bso \(\Vert\)E × p, with E a substrate- or gate-induced (usually) vertical electric field, and p the momentum of the carriers15. In such models, singlet–triplet mixing is found to be absent if the external field is aligned with the effective Rashba fields, whereas the degeneracy is lifted in other external field directions.
Unfortunately, the somewhat simplistic Rashba-field model is not quite appropriate for three-dimensional or disordered quantum dots, similar to ours: it fails to account, e.g., for the strongly distorted, dot-dependent g-tensors measured earlier in InAs nanowire double quantum dots (DQDs)16,17, as well as in our device, which are neither aligned with each other nor correlated with the geometry of the sample.
In this work, we consider two interacting spins confined in a spin–orbit-coupled DQD. Theoretically, we study a generic Hamiltonian with spin-dependent tunneling and distorted g-tensors, and use topological considerations to provide the conditions for the existence of ground-state degeneracy points in the three-dimensional magnetic-field parameter space. Experimentally, we demonstrate the presence of two such magnetic Weyl points by doing transport spectroscopy in an InAs DQD as we explore the magnetic-field parameter space. Furthermore, we show that these degeneracies lead to a two-electron Kondo effect. Our results establish generic, robust, topologically protected degeneracy points, insensitive to microscopic details, in spin–orbit-coupled interacting spin systems.
Results
Magnetic Weyl points are topologically protected
We show now that the presence of degeneracy points is not a consequence of an oversimplified description or the simple dot geometries, but is rooted in topology. To show this, we consider first the most generic spin–orbit-coupled two-spin Hamiltonian H above. Consider a sphere in the magnetic parameter space, centered at the origin, with a radius approaching infinity, and calculate the corresponding ground-state Chern number, C∞. In this limit, each spin follows just the external field, yielding a Chern number, \(C_\infty = {\mathrm{sign}}\,{\mathrm{det}}(\widehat {\mathbf{g}}_{\mathrm{L}}) + {\mathrm{sign}}\,{\mathrm{det}}(\widehat {\mathbf{g}}_{\mathrm{R}}) \equiv C_\infty ^{\mathrm{L}} + C_\infty ^{\mathrm{R}}\). As long as both g-tensor determinants are positive, we simply obtain C∞ = 2. As, by definition, C∞ counts the total topological charge carried by the degeneracy points in the entire magnetic field space, the finiteness of C∞ signals the existence of ground-state degeneracies with nonzero topological charge, typically located at single points, which we call magnetic Weyl points. Time reversal constrains the locations of these points (see Methods): a degeneracy point at B0 must have a partner at −B0, carrying the same topological charge.
By these topological considerations, we expect that two Weyl points at ±B0 carry the total topological charge C∞ = 2. Using random spin Hamiltonians, we have numerically verified that this scenario of two magnetic Weyl points is generic and is indeed realized in cca. 98% of randomly generated two-spin Hamiltonians. In the remaining cca. 2% of cases, the number of Weyl points is six, but the sum of their topological charges remains two.
Experimental observation of magnetic Weyl points
To demonstrate experimentally the existence of magnetic Weyl points in a spin–orbit-coupled interacting two-spin system, we carried out low-temperature electric transport measurements through a serial InAs nanowire DQD16,18,19,20,21 in the temperature range 60–300 mK. The setup is sketched in Fig. 2a (for sample fabrication and characterization see Methods and Supplementary Note 1). Alternative experimental techniques to explore these magnetic Weyl points are Landau–Zener22,23,24 or electrically driven spin resonance spectroscopy15, as well as Pauli-blockade spectroscopy21, as applied to various two-electron double-dot devices.
Detecting magnetic Weyl points through the conductance of a two-electron double quantum dot. a Device layout, showing the nanowire (black), and the metallic electrodes (gold) including the contacts NL, NR, and the finger gates below the nanowire. The gate-controlled electric double-well potential (red) confines one electron (blue) in each well. b Charge stability diagram: zero-bias conductance at zero magnetic field as a function of two gate voltages. Labels such as (1,1) specify the number of electrons on each dot. c Finite-bias differential conductance at zero magnetic field along the dotted horizontal line in b at VgR = 0.236 V, indicating an exchange splitting ΔE ≈ J0 ≈ 0.055 meV. The white curve shows a cut along the vertical dotted line at VgL = 0.526 V. d–f Magnetic-field dependence of the finite-bias conductance in the (1,1) charging state. d Data taken in a generic direction (here θ = 60° and ϕ = 90°) exhibit no ground-state degeneracy. Solid gray lines are ground-state energy gaps obtained from theoretical fits (see Methods). e In the “sweet” direction, θ ≈ 130° and ϕ ≈ 90°, a ground-state degeneracy (a magnetic Weyl point) emerges at B ≈ 70 mT. f θ dependence of the gap for ϕ = 90° and a magnetic field very close to the Weyl point, B = 75 mT ≈ B0. Time-reversed Weyl points emerge at θ ≈ 130° and θ ≈ 310°. g Visualization of the calculated ground-state Berry curvature vector field in the vicinity of the two magnetic Weyl points (red). The outward oriented hedgehog patterns indicate that the two Weyl points carry the same topological charge. h Magnetic-field and θ dependence of the zero-bias magnetoconductance, ΔG(B) = G(B) − G(B = 0) along the lines indicated on the left sketch by colored lines. The maximum at B ≈ 70 mT in the bottom right panel indicates a magnetic Weyl point, also marked on the surface of the sphere
In the experiments, we focused on the (1,1) charge configuration of the device (see Fig. 2b), where the DQD contains two spatially separated and exchange-coupled spins. In this region, we expect that the ground state of the system is a singlet and the first excited state separated by ΔE ≈ J0 is a triplet (see Supplementary Note 2). The finite exchange splitting J0 ≈ 0.055 meV is demonstrated by the bias-dependent differential conductance data presented in Fig. 2c. At the center of the (1,1) configuration, i.e., along the vertical dashed line, the conductance is suppressed at small biases, but increases once the bias is sufficiently high to induce inelastic co-tunneling processes populating the triplet states. The differential conductance G = dI/dVbias (white curve) has therefore two finite-bias peaks (white lines) placed symmetrically at the first excited state of the DQD, at eVbias = ±ΔE ≈ ± J0. The asymmetry G(Vbias) ≠ G(−Vbias) can be attributed to asymmetric coupling to the leads.
We now switch on the magnetic field to tune the relative energies of the ground and excited states, and explore by the co-tunneling spectroscopy outlined above, how the energy gap ΔE = ΔE(B) between the ground and first excited states varies with the field (Fig. 1h)25,26,27. Two examples are shown in Fig. 2d, e, where we present the conductance G(B, Vbias) for magnetic fields B = B(sinθ cosϕ, sinθ sinϕ, cosθ) oriented along two different directions (see reference frame in Fig. 2a).
In Fig. 2d, e, the magnetic-field dependence of the gap ΔE(B) is traced by the large-conductance features close to zero bias, also indicated by solid lines. The observed behavior is markedly different in the two cases: Fig. 2d displays a behavior in line with the naive singlet–triplet mixing argument and the gap remains open for all values of B. In Fig. 2e, however, the gap closes at around B0 = 70 mT, where a zero-bias conductance peak develops (white continuous line), suggesting that this magnetic-field vector corresponds to a magnetic Weyl point.
The scenario of the two magnetic Weyl points at opposite magnetic fields ±B0, fits perfectly our experimental observations. To demonstrate this, we display the conductance G(θ, Vbias) in Fig. 2f for a fixed magnetic-field length B = 75 mT and ϕ = 90°, while varying the polar angle θ over a range of 360° (see also Supplementary Note 3 for additional data). Our data indicate ground-state degeneracies at two opposite isolated points, θ ≈ 130° and θ ≈ 310°, but a finite gap otherwise. The solid lines in Fig. 2d–f, indicating the gap, are not only guides to the eye: they were computed from a two-site Hubbard model (see Methods), with parameters adjusted to yield a good overall match to experimental observations. Figure 2g visualizes the Berry curvature fields (see Methods) and the associated topological charges at the two Weyl points, as computed numerically from this two-site Hubbard model.
We support further the scenario of the two magnetic Weyl points by showing a more complete scan of the zero-bias magnetoconductance ΔG(B) = G(B) − G(B = 0) in Fig. 2h. The four panels of Fig. 2h correspond to four azimuthal angles, ϕ ∈ {−45°, 0°, 45°, 90°} of the magnetic field, as depicted in the sketch on the left side of panel h. Each panel of Fig. 2h displays the zero-bias magnetoconductance ΔG(θ, B) as the function of the polar angle θ and strength B of the magnetic field. The most prominent local maximum in the bottom right panel of Fig. 2h indicates that the two-electron double dot has a magnetic Weyl point close to that region, ϕ ≈ 90°, θ ≈ 130°, and B ≈ 70 mT (also seen in Fig. 2e).
Two-electron Kondo effect at the Weyl points
In our device, the observed ground-state degeneracy is accompanied by an increased zero-bias conductance in the vicinity of the magnetic Weyl points (see white curve on Fig. 2e). This increased conductance is due to a two-electron Kondo effect25,26,27,28,29, as clearly revealed by the temperature and voltage dependence of our transport data in Fig. 3, complying with the Kondo behavior seen in other experiments30,31,32. The differential conductance at the Weyl point exhibits, in particular, a pronounced zero-bias Kondo peak with a height increasing upon decreasing temperature (see Fig. 3a). This increased low-temperature conductance appears to be characteristic of the whole charge (1,1) domain, as demonstrated in Fig. 3b, presenting the temperature dependence of the zero-bias conductance along the diagonal dashed line in Fig. 2b. In contrast, in the regions corresponding to (2,0) and (0,2) charge configurations, the ground state is unique; there the conductance shows thermal activation and is suppressed with decreasing temperatures.
Protected two-electron Kondo effect in a double quantum dot. a Temperature-dependent conductance in the center of the (1,1) charge configuration (corresponding to VgL = 0.523 V, VgR = 0.236 V), at the magnetic Weyl point (B = 60 mT, θ = 130°, ϕ = 90°). Inset: temperature scaling of the Kondo peak38,39, using Kondo temperature TK = 0.95 K. b Temperature- and gate-voltage dependence of the zero-bias conductance along the diagonal dashed line in Fig. 2b. Magnetic field as specified above
Discussion
So far, we have argued that for two interacting spins, the appearance of ground-state degeneracies at a pair of time-reversed magnetic Weyl points is generic and robust due to topological protection. The two Weyl points can change their positions in the magnetic-field space as the two-spin Hamiltonian is modified, but they cannot disappear, i.e., the corresponding degeneracy cannot split. Of course, this protection carries over to the observed Kondo effect.
In our experiments, we have tested the robustness of the Weyl points in two different ways. (1) We have also investigated other double-dot charge states and verified that the signatures of two Weyl points are indeed present there too, as predicted, although the quantum dot parameters as well as the location of the Weyl points changed considerably. (2) We have modified the microscopic parameters within the same charge state by varying the gate potentials. The Weyl points were displaced but have never disappeared (for further details, see Supplementary Notes 4 and 5).
Interestingly, in our simulations, we can find cases where four additional Weyl points emerge. In such cases, four out of the six Weyl points have a topological charge +1, whereas two of them have charge −1, adding up to a total topological charge +2, in agreement with our sum rule. This is shown in Fig. 4a, where the red (blue) spheres represent Weyl points with Chern number +1 (−1). As discussed below, this case—never realized in the simple Rashba-field model—may be relevant, e.g., in Si double dots33,34.
Magnetic Weyl points in spin–orbit-coupled few-spin systems. a An example of evolution and annihilation of Weyl points with opposite charges (red with Chern number +1, blue with −1) upon continuous deformation of a spin–orbit-coupled two-spin Hamiltonian. b, c Statistics of the number of magnetic Weyl points for randomly chosen spin–orbit-coupled Hamiltonians for b a two-spin system and c a three-spin system
The numerical simulation in Fig. 4a illustrates further topological protection: Weyl points can move around upon continuous deformation of the Hamiltonian and degeneracies of opposite topological charge can annihilate each other, but the total topological charge remains unchanged and assures the presence of degeneracies. A particular example of an annihilation process is presented in Fig. 4a, where arrows indicate the motion of degeneracy points, while their colors refer to their charge (see Supplementary Note 6 for a description of the deformation protocol).
The creation and annihilation of magnetic Weyl points should be observable in double-dot devices. Although using completely random parameters the probability of finding six Weyl points is only cca. 2% as illustrated of Fig. 4b, engineering the parameters allows for increasing ratio of six Weyl points. An analysis of our InAs double-dot setup using the experimentally determined g-tensors and the ratio of spin-conserving and spin-rotating tunnel amplitudes (see Supplementary Note 6) yields that the probability of creating additional Weyl points is still low, cca. 10–20%. However, in other experimental systems with lower spin-rotating tunneling amplitude, the likelihood of finding six Weyl points can increase significantly (50–100%) (see Supplementary Note 6). Silicon devices33,34 or bent carbon nanotubes could be promising candidates in this regard.
Remarkably, the argument applied to two coupled spins can be generalized to interacting multi-spin systems, such as magnetic trimers35, atomic clusters, or multi-dot arrangements. In fact, the total topological charge for N non-interacting spins with size 1/2 and isotropic g-tensors36 is C∞ = N. This suggests that for a generic N-spin system there are N magnetic-field values where Weyl points of topological charge +1 appear and the ground state is degenerate. For even values of N, these degeneracies must appear as time-reversed pairs, whereas for an odd number of spins a Weyl point must appear at B = 0, as also implied by Kramers’ theorem. These arguments can be readily extended to systems of spin S impurities as well, where the total topological charge adds up to C∞ = 2S N.
These general considerations have direct experimental implications. To demonstrate this, we generated an ensemble of random Hamiltonians for a spin–orbit-coupled three-spin quantum dot system (see Supplementary Note 6) and analyzed the statistics of the number of magnetic Weyl points (Fig. 4c). We dominantly observe three Weyl points of charge +1 (~75%), but with a 25% likelihood, additional pairs of degeneracy points appear. From the trend observed in Fig. 4b, c, we anticipate that the more complex the interacting spin system, the easier it is (1) to find more Weyl points than the number of spins and (2) to measure the controlled creation and annihilation of Weyl points.
We thus established that magnetic Weyl degeneracies are generic in interacting quantum dot devices in the presence of SOI. The precise location and structure of these degeneracies may depend on microscopic details, but their presence is assured by topology. Their robustness has important physical implications such as the corresponding topologically protected Kondo effect observed.
Methods
Sample fabrication and measurement details
An array of Cr/Au (with 5/25 nm thickness) bottom gates (see Fig. 2a) with a width of 40 nm and a period of 100 nm was prepared by e-beam lithography and e-beam evaporation on a Si/SiO2 substrate. Exfoliated hexagonal boron-nitride (hBN) flakes with a thickness of 20 nm were positioned on top of the bottom gates by a transfer microscope to electrically isolate the bottom-gate electrodes from the nanowire. The 80 nm diameter InAs nanowire was placed on the hBN by a micromanipulator setup. The nanowire and the bottom gates were contacted by Ti/Au electrodes (10/80 nm), defined in a second e-beam lithography and e-beam evaporation step.
The sample was measured in Leiden Cryogenics CF-400 cryo-free dilution refrigerator, equipped with a two-dimensional vector magnet. To vary the magnetic field in three dimensions, the sample holder probe was rotated manually to four different orientations ϕ ∈ {−45°, 0°, 45°, 90°}. After each rotation, the base temperature was different due to the different thermal contact between the probe and the cryostat. The differential conductance of the DQD was measured in a two-point geometry by lock-in technique at 237 Hz with 10 μV ac excitation with a home-built I/V converter. The conduction band was not fully depleted by the gates: charge-configuration labels in Fig. 2b therefore correspond to the number of electrons above closed shells in each quantum dot holding an unknown, large number of electron pairs.
Berry curvature and Chern number
Consider the ground-state manifold ψ0(B) of a family of Hamiltonians H(B) parametrized by the magnetic field B. Assuming that ψ0 is differentiable in the vicinity of B, we define the Berry connection vector field \({\cal{A}} = ({\cal{A}}_x,{\cal{A}}_y,{\cal{A}}_z)\) as
The Berry curvature vector field \({\cal{B}} = ({\cal{B}}_x,{\cal{B}}_y,{\cal{B}}_z)\) is defined as the curl of the Berry connection,
It is noteworthy that although the Berry connection \({\cal{A}}\) is gauge dependent, the Berry curvature \({\cal{B}}\) is not.
Consider now a closed surface \({\cal{S}}\) in the magnetic-field space, such that the ground state is non-degenerate at any point of \({\cal{S}}\). The (ground state) Chern number associated with this surface is then
For details, see Supplementary Note 7.
Magnetic Weyl points form time-reversed pairs
If there is a magnetic Weyl point at B0, then—by time reversal—there is also one at −B0. This follows from the properties of time reversal, τ. (i) τ is an anti-unitary operator, i.e., 〈τφ|τψ〉 = 〈φ|ψ〉* for any φ and ψ. (ii) τ changes the sign of each spin operator; hence, \(\tau H({\mathbf{B}})\tau ^\dagger = H( - {\mathbf{B}})\). (iii) From (ii) it follows that if H(B)|ψ〉 = E|ψ〉, then H(−B)τ|ψ〉 = Eτ|ψ〉. Thus, apart from an overall phase, τ|ψ(B)〉 = |ψ(−B)〉. Thus a degeneracy at B0 implies a degeneracy at −B0, and at non-degenerate points \({\cal{B}}({\mathbf{B}}) = - {\cal{B}}( - {\mathbf{B}})\).
Two-site Hubbard model of the double quantum dot
Theoretical results in Fig. 2d–f, h were produced by a spin–orbit-coupled two-site Hubbard model, with Hamiltonian H = H0 + HZ. Here, the Hamiltonian in the absence of magnetic field is
with UL/R the strength of the Coulomb interaction on the left/right dot, nL/R the occupation numbers, εL/R the gate-controlled on-site energies, and \(t^{ss\prime } = t_0\delta _{ss\prime } - i\mathop {\sum}\nolimits_{\alpha = (x,y,z)} {t_\alpha } \sigma _{ss\prime }^\alpha\) a spin-rotating hopping term37, with real-valued hopping amplitudes t0, tx, ty, tz. The σα here denote Pauli matrices and are related to the spin operators in the usual way, e.g., \(S_{\mathrm{L}}^x = \mathop {\sum}\nolimits_{ss\prime } {c_{{\mathrm{L}}s}^\dagger } \sigma _{ss\prime }^xc_{{\mathrm{L}}s\prime }\). In an external magnetic field, we also add the Zeeman terms \(H_{\mathrm{Z}} = \mu _{\mathrm{B}}{\mathbf{B}} \cdot \left( {\widehat {\mathbf{g}}_{\mathrm{L}}{\mathbf{S}}_{\mathrm{L}} + \widehat {\mathbf{g}}_{\mathrm{R}}{\mathbf{S}}_{\mathrm{R}}} \right)\). The spin-rotating interdot hopping as well as the nontrivial g-tensors can be attributed to strong SOI in the InAs nanowires16,18,19,21.
We have determined the values of the model parameters to provide a good overall agreement with the experimentally observed. For the methodology, see Supplementary Note 2. These parameters were then used to derive the theoretical results in Fig. 2d–f, h. The g-tensors used were as follows:
Hoppings were set to t0 = 0.0525 meV, tx = −0.0151 meV, ty = 0.0565 meV, tz = −0.0697 meV, and Coulomb energies to UL = 1 meV, UR = 0.6 meV. The on-site energies corresponding to the center of the (1, 1) hexagon of the charge stability diagram in Fig. 2b read εL = −UL/2 and εR = −UR/2.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Lutchyn, R. M., Sau, J. D. & Das Sarma, S. Majorana Fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys. Rev. Lett. 105, 077001 (2010).
Oreg, Y., Refael, G. & von Oppen, F. Helical liquids and majorana bound states in quantum wires. Phys. Rev. Lett. 105, 177002 (2010).
Haldane, F. D. M. Nonlinear field theory of large-spin Heisenberg antiferromagnets: semiclassically quantized solitons of the one-dimensional easy-axis Néel state. Phys. Rev. Lett. 50, 1153 (1983).
Turner, A. & Vishwanath, A. in Topological Insulators (eds Franz, M. & Molenkamp, L.) Ch. 11, 294–324 (Elsevier, Oxford, 2013).
Armitage, N. P., Mele, E. J. & Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 90, 015001 (2018).
Herring, C. Accidental degeneracy in the energy bands of crystals. Phys. Rev. 52, 365 (1937).
Murakami, S. Phase transition between the quantum spin Hall and insulator phases in 3D: emergence of a topological gapless phase. New J. Phys. 9, 356 (2007).
Yarkony, D. R. Diabolical conical intersections. Rev. Mod. Phys. 68, 985 (1996).
Riwar, R.-P., Houzet, M., Meyer, J. S. & Nazarov, Y. V. Multi-terminal Josephson junctions as topological matter. Nat. Commun. 7, 11167 (2016).
Gao, W. et al. Photonic Weyl degeneracies in magnetized plasma. Nat. Commun. 7, 12435 (2016).
Schroer, M. D. et al. Measuring a topological transition in an artificial spin-1/2 system. Phys. Rev. Lett. 113, 050402 (2014).
Roushan, P. et al. Observation of topological transitions in interacting quantum circuits. Nature 515, 241 (2014).
Nowack, K. C., Koppens, F. H. L., Nazarov, Y. V. & Vandersypen, L. M. K. Coherent control of a single electron spin with electric fields. Science 318, 1430 (2007).
Nadj-Perge, S., Frolov, S. M., Bakkers, E. P. A. M. & Kouwenhoven, L. P. Spin-orbit qubit in a semiconductor nanowire. Nature 468, 1084 (2010).
Nadj-Perge, S. et al. Spectroscopy of spin-orbit quantum bits in indium antimonide nanowires. Phys. Rev. Lett. 108, 166801 (2012).
Schroer, M. D., Petersson, K. D., Jung, M. & Petta, J. R. Field tuning the g factor in InAs nanowire double quantum dots. Phys. Rev. Lett. 107, 176811 (2011).
d’Hollosy, S., Fabian, G., Baumgartner, A., Nygard, J. & Schonenberger, C. g-factor anisotropy in nanowire-based InAs quantum dots. AIP Conf. Proc. 1566, 359 (2013).
Fasth, C., Fuhrer, A., Samuelson, L., Golovach, V. N. & Loss, D. Direct measurement of the spin-orbit interaction in a two-electron InAs nanowire quantum dot. Phys. Rev. Lett. 98, 266801 (2007).
Pfund, A., Shorubalko, I., Ensslin, K. & Leturcq, R. Suppression of spin relaxation in an InAs nanowire double quantum dot. Phys. Rev. Lett. 99, 036801 (2007).
Fasth, C., Fuhrer, A., Björk, M. T. & Samuelson, L. Tunable double quantum dots in InAs nanowires defined by local gate electrodes. Nano Lett. 5, 1487 (2005).
Wang, J.-Y. et al. Anisotropic Pauli spin-blockade effect and spin-orbit interaction field in an InAs nanowire double quantum dot. Nano Lett. 18, 4741 (2018).
Reilly, D. J. et al. Suppressing spin qubit dephasing by nuclear state preparation. Science 321, 817 (2008).
Petta, J. R., Lu, H. & Gossard, A. C. A coherent beam splitter for electronic spin states. Science 327, 669 (2010).
Fogarty, M. A. et al. Integrated silicon qubit platform with single-spin addressability, exchange control and single-shot singlet-triplet readout. Nat. Commun. 9, 4370 (2018).
Jeong, H., Chang, A. M. & Melloch, M. R. The Kondo effect in an artificial quantum dot molecule. Science 293, 2221 (2001).
Chorley, S. J. et al. Tunable Kondo physics in a carbon nanotube double quantum dot. Phys. Rev. Lett. 109, 156804 (2012).
Spinelli, A. et al. Exploring the phase diagram of the two-impurity Kondo problem. Nat. Commun. 6, 10046 (2015).
Sasaki, S. et al. Kondo effect in an integer-spin quantum dot. Nature 405, 764 EP (2000).
Nygård, J., Cobden, D. H. & Lindelof, P. E. Kondo physics in carbon nanotubes. Nature 408, 342 EP (2000).
Goldhaber-Gordon, D. et al. Kondo effect in a single-electron transistor. Nature 391, 156 (1998a).
van der Wiel, W. G. et al. The Kondo effect in the unitary limit. Science 289, 2105 (2000).
Kouwenhoven, L. & Glazman, L. Spins in few-electron quantum dots. Phys. World 14, 33 (2001).
Veldhorst, M. et al. Spin-orbit coupling and operation of multivalley spin qubits. Phys. Rev. B 92, 201401 (2015).
Jock, R. M. et al. A silicon metal-oxide-semiconductor electron spin-orbit qubit. Nat. Commun. 9, 1768 (2018).
Jamneala, T., Madhavan, V. & Crommie, M. F. Kondo response of a single antiferromagnetic chromium trimer. Phys. Rev. Lett. 87, 256804 (2001).
Gritsev, V. & Polkovnikov, A. Dynamical quantum Hall effect in the parameter space. Proc. Natl Acad. Sci. USA 109, 6457 (2012).
Danon, J. & Nazarov, Y. V. Pauli spin blockade in the presence of strong spin-orbit coupling. Phys. Rev. B 80, 041301 (2009).
Goldhaber-Gordon, D. et al. From the Kondo regime to the mixed-valence regime in a single-electron transistor. Phys. Rev. Lett. 81, 5225 (1998b).
Grobis, M., Rau, I. G., Potok, R. M., Shtrikman, H. & Goldhaber-Gordon, D. Universal scaling in nonequilibrium transport through a single channel Kondo dot. Phys. Rev. Lett. 100, 246601 (2008).
Acknowledgements
We acknowledge J. Asbóth, Á. Butykai, W. Coish, K. Grove-Rasmussen, B. Hensen, R. Maurand, P. Nagy, J. Paaske, F. Pollmann, and T. Tanttu for valuable discussions, and M. H. Madsen and C. B. Sørensen for technical support. This work was supported by the National Research Development and Innovation Office of Hungary within the Quantum Technology National Excellence Program (Project Number 2017-1.2.1-NKP-2017-00001), under OTKA Grants 124723 and 127900, the New National Excellence Program of the Ministry of Human Capacities, CA16218 nanocohybri COST Action, QuantERA SuperTop 127900, FET Open AndQC, the Danish National Research Foundation, and the Elemental Strategy Initiative conducted by the MEXT, Japan, and the CREST (JPMJCR15F3), JST.
Author information
Authors and Affiliations
Contributions
Experiments were designed by S.C. Wires were developed by J.N. and hBN crystals by K.W. and T.T. Devices were developed and fabricated by G. Frank, I.L., B.F., G. Fülöp, and S.C. Measurements were carried out and analyzed by Z.S., G. Frank, and S.C. Theoretical analysis was given by A.P., Z.S., G. Frank, and G.Z. A.P., Z.S. and G.Z. prepared the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Scherübl, Z., Pályi, A., Frank, G. et al. Observation of spin–orbit coupling induced Weyl points in a two-electron double quantum dot. Commun Phys 2, 108 (2019). https://doi.org/10.1038/s42005-019-0200-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0200-2
This article is cited by
-
Uncovering topographically hidden features in 2D MoSe2 with correlated potential and optical nanoprobes
npj 2D Materials and Applications (2020)
-
Mixed topological semimetals driven by orbital complexity in two-dimensional ferromagnets
Nature Communications (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.