Abstract
Complex 3D magnetic textures in nanomagnets exhibit rich physical properties, e.g., in their dynamic interaction with external fields and currents, and play an increasing role for current technological challenges such as energy-efficient memory devices. To study these magnetic nanostructures including their dependency on geometry, composition, and crystallinity, a 3D characterization of the magnetic field with nanometer spatial resolution is indispensable. Here we show how holographic vector field electron tomography can reconstruct all three components of magnetic induction as well as the electrostatic potential of a Co/Cu nanowire with sub 10 nm spatial resolution. We address the workflow from acquisition, via image alignment to holographic and tomographic reconstruction. Combining the obtained tomographic data with micromagnetic considerations, we derive local key magnetic characteristics, such as magnetization current or exchange stiffness, and demonstrate how magnetization configurations, such as vortex states in the Co-disks, depend on small structural variations of the as-grown nanowire.
Similar content being viewed by others
Introduction
Novel synthesis methods and the discovery of emerging magnetic phenomena (e.g., topological non-trivial textures) at the nanoscale triggered an expansion of nanomagnetism into three dimensions (3D) focusing on unconventional magnetic configurations with unprecedented properties1. These nanomagnetic configurations are interesting for prospected2 and realized applications in field sensing3, magnetic memory, and spintronics2,4,5. Indeed, even trivial magnetic systems such as homogeneously magnetized domains adopt a 3D modulation near surfaces due to ubiquitous surface anisotropies and the role of dipolar interactions as the demagnetizing field. Surface-induced modulations play a crucial role in the formation and the dynamics of different classes of domain walls in magnetic nanowires (NWs; transverse-vortex and Bloch point domain walls5,6). Similarly, surfaces of chiral magnets characterized by a non-zero antisymmetric Dzyaloshinskii–Moriya interaction (DMI)7 exhibit 3D surface twists8, chiral bobbers9,10, and other 3D textures. Conceptually similar to DMIs, handed magnetic coupling can occur in curvilinear surfaces, which can be considered as a frozen and frustrated gauge background induced by the spatially varying frame of reference. As a consequence, a family of curvature-driven effects are predicted including magnetochiral effects and topologically induced magnetization patterning, e.g., skyrmion multiplet states in bumpy films11. Another example pertains to magnetically frustrated 3D configurations found in (artificial) spin ice12, where the magnetic dipole interaction is the driving force for highly degenerated ground states.
To gain insight into 3D magnetic textures in nanomagnets, tomographic magnetization mapping techniques with spatial resolution approaching the nanometer regime are highly desired. There are, however, a limited number of contrast mechanisms, which allow to record projections of the magnetic field suitable for a tomographic reconstruction, notably, (soft) X-ray techniques and transmission electron microscopy (TEM)-based phase reconstruction techniques. Both techniques are still in their infancy with only a few studies reported so far. Soft X-ray tomography has been employed to retrieve spin textures13 on curved magnetic films at a spatial resolution approaching 50 nm, with challenges facing the further reduction of resolution and the limited penetration depth. This could recently be solved by employing hard X-rays to tomographically reconstruct either one magnetization component14, or two via a dual-axis approach, enabling estimation of the third15.
The first TEM-based proof-of-principle 3D reconstruction of one Cartesian component of the magnetic induction (flux density) B by employing electron holographic tomography (EHT) dates back already 25 years16. However, due to instrumental and computational limitations, progress in this research field was only little until 5 years ago, when a quantitative reconstruction of one B-component in- and outside magnetic nanoscale materials was achieved17,18,19. The spatial resolution obtained in these studies is better than 10 nm. However, further improvements in resolution will be very challenging because of fundamental detection limits for electron holography (EH) of the magnetic signal20,21 and experimental challenges in electron tomography. The full reconstruction of all three Cartesian components, which we here refer to as holographic vector field electron tomography (VFET), remains challenging due to the complexity of acquisition and reconstruction involved. Notwithstanding, isolated studies have been reported with large regularization and reduced spatial resolution22 or angular sampling23. Another challenge is to characterize the specimen in terms of magnetization M instead of the B-field reconstructed by EHT. Therefore, micromagnetic modeling has been included in the tomographic reconstruction to retrieve the full magnetic configuration24,25.
In off-axis EH, the phase shift φ in the object plane (x, y) with respect to a vacuum reference acquired by an electron wave passing through a magnetic sample along z direction is given by the Aharonov–Bohm phase shift26
Here, v is the electron velocity, V(x, y, z) the 3D electrostatic potential, e the elementary charge, ħ the reduced Planck constant, and Az(x, y, z) the 3D component of the magnetic vector potential parallel to the electron beam direction z. Accordingly, the first term can be considered as electric phase shift φel and the second one as magnetic phase shift φmag. By converting the latter to the magnetic flux enclosed between interfering paths of object and reference wave, the directional spatial derivatives of the phase are
proportional to the projected in-plane B-components. The last line of the above relation also holds for inline holographic techniques, such as transport of intensity holography22,27,28. Inline techniques, however, act spatially similar to high-pass filters28, i.e., are ill-conditioned for reconstructing low spatial frequencies. To separate electric and magnetic contributions in the total phase shift (φ = φmag + φel), two phase images with reversed magnetic induction are required29. Subtracting both allows to remove the electric phase shift, which does not change sign under time-reversal as opposed to the magnetic one. To reconstruct the 3D distribution of B from their projections, we collect a series of projections at different angles (tilt series) and employ tomographic reconstruction algorithms to this tilt series. By tilting about a particular axis, say x, we obtain a complete set of projections of the component Bx, whereas the remaining two components mix in their contribution to the magnetic flux as a function of tilt angle. Consequently, three tilt series around perpendicular axes are required to reconstruct the vector field B. Commercially available TEM specimen holder allow tilting only about two independent axes. Therefore, we have to exploit the solenoidal character of the B-field (Gauss’s law for magnetism), i.e.,
to obtain the third component Bz (see Supplementary Note 1).
In the following, we combine all these strands, facilitating the 3D reconstruction of the magnetic induction as well as the 3D magnetization and related magnetic properties. More specifically, we demonstrate the 3D reconstruction of all three B-field components with sub-10 nm resolution and derive magnetization currents and exchange energy contributions. We correlate the magnetic configuration to the chemical composition from the mean inner potential (MIP) 3D distribution reconstructed in parallel by holographic VFET. In addition, we show how to derive M from B by involving micromagnetic considerations. Within the case study of a multilayered NW composed of alternating magnetic Co and non-magnetic Cu disks, we observe a range of different magnetic configurations including vortex states. Such structures are model systems of spintronics devices such as spin valves or spin-torque-based microwave devices, for which the knowledge and control of the initial magnetic state is crucial for applications.
Results
Workflow of holographic vector field electron tomography
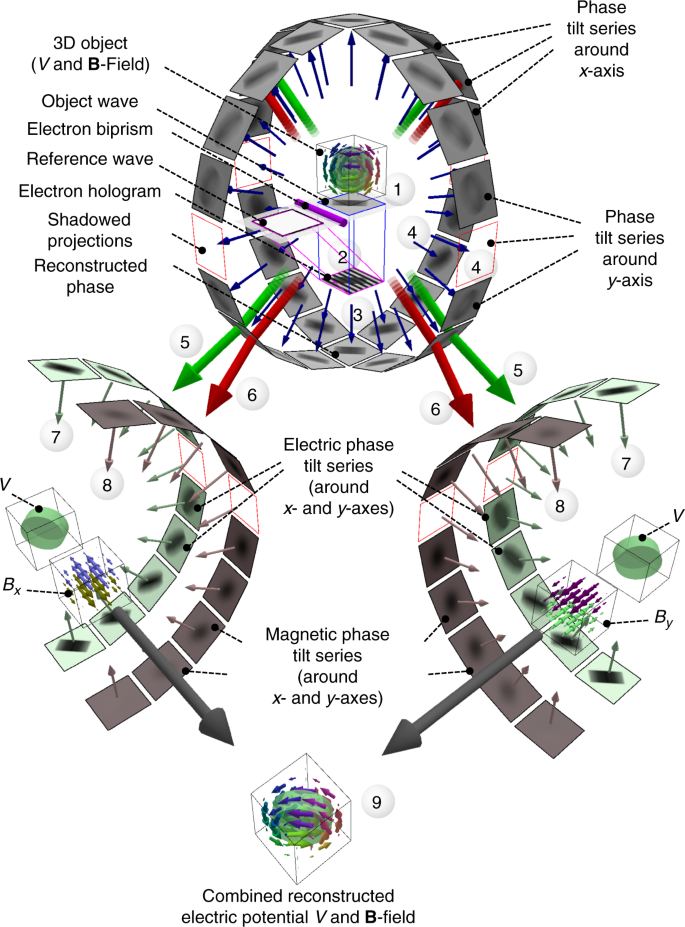
Holographic VFET, illustrated in Fig. 1, starts with the electron hologram acquisition (1, 2) and ensuing phase image reconstruction out of it (3). Then, these three steps are repeated at each tilt direction for the collection of two orthogonal tilt series of phase images (4). The latter two are separated in their electric (5) and magnetic (6) parts, and reconstructed by tomographic techniques yielding the 3D distributions of electric potential (7) as well as the two magnetic B-field components Bx and By (8). Finally, the third magnetic B-field component Bz is computed from ∇ · B = 0 (9). In order to perform the crucial separation of electric and magnetic phase shifts (5, 6), each tilt series (ideally 360° is split into two sub-tilt series (ideally 180°). However, even by using dedicated tomography TEM sample holders, in many cases the specimen and holder geometry may de facto limit the tilt range to usually 140°. Thus, the second sub tilt series with the corresponding opposite projections has to be recorded after the sample was turned upside-down outside the electron microscope. Consequently, tomograms reconstructed from those tilt series with incomplete tilt range suffer from a direction-dependent reduction of resolution leading to so-called missing wedge artifacts30. The details about acquisition, holographic reconstruction, the elaborate post-processing of projection data, tomographic reconstruction, and computation of the Bz-component are given in the Methods section at the end.
Principle of holographic vector field electron tomography. 1 Electron waves pass through the magnetic sample represented by both electrostatic potential V and magnetic B-field. 2 Underneath the sample, an electrostatic biprism brings the modulated part (object wave) of the electron waves to interference with an unmodulated part (reference wave) resulting in an electron hologram at the detector plane. 3 The hologram is reconstructed numerically yielding the amplitude and phase shift of the object wave. 4 Rotating and recording the object around two tilt axes, x and y, provides for each tilt axis a 360° phase tilt series. A few projections might be missing due to technical and space limitations of the experiment. 5, 6 Half the sum/difference of opposite projections (green/red arrow) results in the electric/magnetic part of the phase shift; thus, two 180° tilt series for the tilt axes x and y. 7 The electric potential is reconstructed in 3D from the electric phase tilt series around x- or y-axis, or both results are averaged. 8 The two magnetic B-field components Bx and By are reconstructed in 3D from the magnetic phase tilt series around x- and y-axis, respectively. 9 Finally, the 3D Bzcomponent is obtained by solving ∇ · B = 0
3D magnetic induction mapping of a layered Cu/Co nanowire
Figure 2 depicts the 3D reconstruction of a multilayered Co/Cu NW using holographic VFET. The bright-field TEM image shown in Fig. 2a reveals the nanocrystalline structure of the NW, but does not visualize the alternating Co and Cu segments as intended by template-based electrodeposition growth (Fig. 2b). Figure 2c shows the 3D B-field reconstructed from the magnetic phase shift in combination with the MIP obtained from the electric phase-shift distribution reflecting the composition of the NW. The positions of the stacked Co and Cu disks (visible due to the difference in the MIP between Co and Cu) are also confirmed by energy-filtered TEM (EFTEM) on exactly the same NW (see Supplementary Note 2). Previous quantitative EFTEM investigations on similar NWs have also demonstrated the presence of 15% of Cu in the Co disks resulting from the electrodeposition31. We obtained MIP values for the Co (including 15% Cu) and Cu disks of \(V_0^{{\mathrm{Co}}} = \left( {21 \pm 1} \right){\mathrm{V}}\) and \(V_0^{{\mathrm{Cu}}} = \left( {17.5 \pm 1} \right){\mathrm{V}}\), respectively, by determining the peak maximum and width in the histograms evaluated at the corresponding tomogram regions. The MIP tomogram (Fig. 2c and Supplementary Movie 1) already provides an important contribution for a better analysis of magnetic properties, because it reveals that the Co disks not only deviate slightly from their nominal thickness of 25 nm and their cylindrical shape intended by electrodeposition synthesis (see Methods section for the details), but also vary to some degree in the inclination angle along the growth direction. Therefore, to illustrate the 3D distribution of the B-field within the individual Co disks, we selected cross-sections oriented parallel to their inclined base surface (Fig. 2c, d and Supplementary Movie 2). Accordingly, two different magnetic configurations were observed: a homogeneously in-plane magnetized state and a vortex state. The latter shows both clockwise and counter-clockwise rotation without noticeable correlation of the rotation between the Co-disks (i.e., coupling between different rotational directions). At the center of the vortex, the magnetization (and hence the B-field) is expected to rotate out-of-plane within a core radius < 10 nm (see further below for details), which is, however, difficult to resolve unambiguously in the vector tomogram at the present spatial and signal resolution. These out-of-plane magnetized vortex cores together with other out-of-plane components, such as Co bridges in the Cu (e.g., between disks 1 and 2, 7 and 8 in Fig. 2e) and asymmetries of the vortices with respect to the NW axis, may, however, contribute to an Aharonov–Bohm phase shift in the vacuum region around the NW. This is demonstrated in Supplementary Note 3, where the reconstructed 3D magnetic structure is correlated with a corresponding phase image: an inspection of the vacuum region in the phase image reveals that the core polarities are mutually aligned by their long-range dipole interaction (producing a net flux density along the NW), whereas the in-plane states (disks 2 and 7) emanate particularly strong stray fields. We finally observe some out-of-plane modulations outside of the core region as indicated by yellow and black color in (Fig. 2d), which will be discussed in detail further below. Turning to the longitudinal cross-section (Fig. 2e) we notice the strong reduction of the magnetic induction between the vortex state discs (producing small stray fields only). Correspondingly, significant B-fields are visible in the vicinity of the in-plane magnetized discs producing large stray fields. The longitudinal section also exhibits the out-of-plane modulations of the vortex states and indicates a complicated configuration in the NW tip, which will not be discussed further in detail. In order to examine the reliability and fidelity of these delicate findings, we measured the spatial resolution of the tomograms by Fourier shell correlation (FSC)32. As described in Supplementary Note 4, we determined with FSC a spatial resolution of about 7 nm for the 3D reconstructions of both Bx and By, and of about 5 nm in case of the 3D electrostatic potential. In addition, we verified the fidelity of the reconstructed B-field by applying our holographic VFET reconstruction on a simulated magnetic Co disk with similar magnetization, dimension, orientation, configuration (vortex and in-plane magnetized), and sampling as in the experiment (Supplementary Note 5). The resulting B-field tomograms agree very well with their simulated input data, even though a limited tilt range is used (±70°). Our VFET analysis can thus unambiguously reveal the 3D magnetic structure of a complex system, highlight the various magnetic configurations, and determine magnetic characteristics such as the vorticity and out-of-plane modulations of a vortex.
3D reconstruction of multilayered Co/Cu nanowire (NW). a Bright-field transmission electron micrograph of the NW. b Idealized model of the NW as intended by template-based electrodeposition growth. c The volume rendering of the NW’s mean inner potential (MIP) displays Co in red and Cu in bluish white (as illustrated in b). The arrow plots represent the field lines of magnetic induction (B-field) sliced through eight Co disks, where the direction of the normal B-field component is color-coded in black and yellow. Please note that the coordinate system is rotated with respect to the experimental setup: The Bx component is now parallel to the NW axis (=out-of-plane component of disks). d Slices through the Co disks as indicated in c: Co disks 2, 7 show in-plane magnetization, 1, 3, 5, 6 show counter-clockwise, and 4, 8 show clockwise vortex magnetization. e Same viewing direction as c, but arrow plot taken in axial NW direction. The inset illustrates where the arrow plot intersects the NW
Magnetization current exchange density
In the following we elaborate on the relation of other important magnetic quantities to the B-field, in order to comprehensively characterize the nanomagnetic properties of the NW. We first note that the conservative (longitudinal) and solenoidal (transverse) part of the Helmholtz decomposition of the magnetization (with scalar magnetic potential Φ and vector potential A)
directly correspond to the magnetic field and magnetic induction. As holographic VFET reconstructions cannot reconstruct the conservative part (i.e., H, which is typically large at boundaries, interfaces but also in Néel textures), the magnetization M cannot be unambiguously retrieved from VFET without additional knowledge about the magnetism of the sample. In order to elaborate on this crucial point, we first compute the total current density \({\mathbf{j}} = \mu _0^{ - 1}\nabla \times {\mathbf{B}}\), i.e., the vorticity of the magnetic induction. If we decompose j into free and magnetization (or bound) currents (j = jf + jb) and take into account that the former can be neglected in the magnetostatic limit, we obtain the magnetization current from
which appears in various energy terms of the micromagnetic free energy. In our case, the three most important micromagnetic energy contributions determining the remanent state in the stacked NW are the exchange, demagnetizing field, and crystallographic anisotropy energy
The magnetization current contributes among others to the exchange energy (see Supplementary Note 6 for detailed expressions of Ed and Ea)
with exchange stiffness A and saturation magnetization Ms. Therein, the first term denotes the magnetic charge contribution (ρm = −∇ · M = ΔΦ) and additional terms describing surface contributions not written out here (see Methods section and Supplementary Note 6 for further details). Consequently, exchange energy minimization favors suppression of both magnetic charge and magnetization current in the volume. The 3D distribution of the magnetization current exchange density |jb|2 in the Co/Cu NW is computed from the reconstructed B-field using Eq. (5) and correlated with the MIP tomogram (Fig. 3a). As a result, the current exchange density is effectively minimized in the homogeneously magnetized parts (slices 2, 7 in Fig. 3b, c). In contrast, it is significantly larger in the vortex regions (slices 1, 3–6, 8 in Fig. 3b, c), which is, of course, compensated by the decrease in demagnetizing field and energy in the total energy functional.
Magnetization current exchange density. a 3D mean inner potential tomogram of the Co/Cu nanowire with bounding box indicating the region where the current exchange density is computed. b Volume rendering of the current exchange density. c Slices through Co disks 1–8, in which the Co disks with a vortex state (1, 3–6, and 8) exhibit a localized maximum in the current exchange density
Comparison with micromagnetic simulations
The above considerations now open a way to derive M from B by incorporating micromagnetic undefined. At the example of the symmetric magnetic exchange energy (Eq. (7), see Supplementary Note 6 for the other energy contributions), we see that the micromagnetic energy functional can be reduced to a functional of a scalar field (i.e., the magnetostatic potential Φ), Etot[M] → Etot[Φ], if B (and hence jb) is known (from the experiment). This significantly reduces the degrees of freedom and hence the complexity of the micromagnetic minimization problem of Etot, which can be exploited in various ways for retrieving M. First, micromagnetic simulations can be used to compute B from a given M and iterate over different magnetization configurations until agreement with the reconstructed data is reached. We use this approach below to obtain information about the exchange stiffness and magnetocrystalline anisotropy in the stacked NW. Second, micromagnetic simulation can be adapted such to directly minimize the energy as a function of the scalar field Φ. Such adapted micromagnetic schemes, which even allow to analytically derive the total magnetization M for highly symmetric magnetic configurations, are further discussed in Supplementary Note 6.
In the light of the above discussion, we now employ micromagnetic simulations to gain more insight into the complex magnetic structure of the Co/Cu NW (see Methods section and Supplementary Note 7 for details). In order to foresee which kind of magnetic remanent states could be obtained in such layers, we first simulated the remanent state phase diagram of a single Co disk as a function of thickness and diameter (Fig. 4a). To mimic the experimental conditions, remanent states were calculated after saturation with 1T close to the wire axis. Simulations were performed with the magnetic parameters of ref. 31 and a tilt angle of the layers of about 10° with respect to the wire axis. Depending on the ratio of thickness and diameter, the remanent states of a single layer can be out-of-plane, in-plane, or vortices with the core either being out-of-plane or tilted with respect to the normal of the layers. The Co disks of the investigated NW are at the boundary of the in-plane and vortex configurations, which agrees well with the coexistence of both configurations in the experiment. Additional contributions such as dipolar coupling between the discs, multiple grains including magnetocrystalline and surface anisotropies, coupling to defects, irregular disc shapes, and chemical gradients further influence the magnetic state of a real Co disc. In particular, the contribution of the crystallographic anisotropy is very complex in the Co (alloyed with 15% Cu) disks including randomly oriented nanoscaled grains of predominant fcc symmetry (i.e., cubic anisotropy). Using TEM, the nano-crystallinity can be observed by local diffraction contrast of the nanometer-sized grains when they are oriented in low-index zone axis with respect to the electron beam direction. This is visible in the bright-field TEM image (Fig. 2a) and also in the original electron holograms, from which the tomograms are reconstructed (Supplementary Note 8). Therefore, to go deeper in the analysis of the magnetic properties of the layers, we performed simulations of the eight Co layers shown in Fig. 4b, c. Within the simulations, the magnetization amplitude Ms, exchange constant A, and crystalline anisotropy HK of each Co layer were changed until the best fit to the experiment was achieved. A crucial step is to implement the 3D morphology of the layers extracted from the MIP tomogram into the micromagnetic simulations (see Methods section and Supplementary Note 7) in order to take into account the geometrical symmetry breaking and inhomogeneity of the Co layers in the calculations. This valuable input significantly reduces the numbers of unknown parameters to reproduce the magnetic configurations in the simulations and allowed to extract magnetic parameters for all individual layers within a range for Ms (1000–1200) Am−1, A (12–20)10−12 Jm−1, and HK (50–130)103 Jm−3 (see Supplementary Table 2 for values of each layer). The variation of these intrinsic parameters from one layer to the other reflects the large impact of the individual disc shapes in the formation of the magnetic configurations. Note, however, the magnetization is found to be between 20% and 30% overestimated in our simulations (Fig. 4c), which indicates that the magnetization amplitude and most probably the exchange constant for each layer can be decreased even further. Such low values of magnetic constants due to the Cu impurities in the Co layers were also observed in a recent work33 on electrodeposited Co/Cu multilayers grown in a single bath, especially when decreasing the thickness of the layer.
Micromagnetic simulations. a Simulated magnetic phase diagram of regular Co disks/cylinders obtained by variation of diameter and thickness. Each point (square) corresponds to the resulting magnetic state obtained from one micromagnetic simulation. The region of the investigated nanowire (NW) is highlighted around 60 nm diameter and 25 nm thickness. b Comparison of the By component between the simulated and experimental Co/Cu NW. In the simulation, the irregular morphology of the Co disks obtained from the mean inner potential tomogram was taken into account. Note the different blue–red color-coding range between simulation and experiment according to the color bars. c Slices through the Co disks 1–8 as indicated in b superimposed by an arrow plot indicating the magnetic state. The opposite out-of-plane directions are distinguished by black and green as also shown in the arrowplots in b
Discussion
We have demonstrated the successful 3D reconstruction of both the magnetic induction vector field and 3D chemical composition of a complex real nanomaterial with sub-10 nm spatial resolution using holographic VFET. Crucial steps are the semi-automated holographic acquisition of dual-axis tilt series within a tilt range of 280°, holographic phase reconstruction, precise image alignment, separation of electric and magnetic phase shift, the tomographic reconstruction of all three B-field components exploiting the constraint ∇ · B = 0. Moreover, we elaborated on the extraction of magnetic properties such as the solenoidal magnetic exchange energy from the tomographic data. The results obtained from a multilayered Co/Cu NW paint a complex picture of the 3D magnetization behavior, e.g., the coexistence of vortex and in-plane magnetized states. This allows to set up a micromagnetic model including the exact geometry of the Co nanodisks that matches the experimental B-field tomogram, from which magnetic parameters of individual layers can be derived. Indeed, micromagnetic simulations of nano-objects are generally performed considering “ideal” systems, which can lead to false predictions of the magnetic states. Avoiding problems of geometrical uncertainties as well as providing additional data in terms of 3D B-field distribution for optimizing micromagnetic simulation are therefore a great advance for a precise analysis of the magnetic properties of nano-objects. We anticipate further improvements by including additional tilt series (e.g., uitilzing improved three-tilt axis tomography holders), increased signal-to-noise ratio (SNR) at long exposure times using automated feedback of the microscope34, improved vector field reconstruction schemes, and adapted micromagnetic modeling of the magnetostatic potential, explicitly exploiting the a priori knowledge of the B-field. The technique holds large potential for revealing complex 3D nanomagnetization patterns, e.g., in chiral magnets, nanomagnets (e.g, NWs), and frustrated magnets, currently not possible with other methods at the required spatial resolution.
Methods
Nanowire synthesis
NWs are grown via template-based electrodeposition technique. The thereby used template was a commercial polycarbonat membrane (Maine Manufacturing, LLC). NWs with diameter ranging from 55 to 90 nm are obtained by electrodeposition in pulse mode from a single bath containing both Co and Cu ions. The deposition potentials for Co and Cu are −1 and −0.3 V, respectively. Lower deposition potential of the Co leads to about 15% of Cu impurities inside the Co layers31. The duration of the deposition potential pulses was adjusted to 1 s for Co and 10 s for Cu, to achieve nominal layer thicknesses of 25 nm Co and 15 nm Cu. In order to be transferred onto a holey carbon grid for TEM experiments, the membrane surrounding the wires was removed by immersion of the sample in dichloromethane. All details about the growth and cleaning processes are given in ref. 31 and references therein. Prior to the tomography experiments, the NWs were saturated in a 1 T magnetic field oriented roughly at 10° from the wire axis direction.
Acquisition of holographic tilt series
The holographic tilt series was recorded at the FEI Titan 80–300 Holography Special Berlin TEM instrument, in image-corrected Lorentz-Mode (conventional objective lens turned off) operated at 300 kV. We employed the two electron bisprism setup35 that was adjusted by an upper biprism voltage of 35 V, a lower biprism voltage of 100 V, and an intermediate X-lens (extra lens between the two biprisms) excitation of −0.36. For acquisition of electron holgrams, a 2 k by 2 k slow scan CCD camera (Gatan Ultrascan 1000 P) was used. The high tilt angles and the manual in-plane rotation of the sample in between the two tilt series (one to reconstruct Bx and one to reconstruct By) were achieved by means of a dual-axis tomography holder (Model 2040 of E. A. Fischone Instruments, Inc.). The acquisition process was performed semi-automatically with an in-house developed software package for an efficient collection of holographic tilt series consisting of object and object-free empty hologram36. The latter is required for correction purposes as explained below. For the first tilt series, the specimen was rotated in-plane, such that an angle between NW axis and tilt axis of +44.5° was obtained. For the second tilt series, the specimen was rotated further in-plane by 91° (ideal is 90°) resulting in an angle between NW axis and tilt axis of −46.5°. After turning the sample upside down ex-situ, two more holographic tilt series were recorded that represent the flipped version of the first two tilt series. The tilt range of each tilt series was from −69° to +66° in 3° steps. The electon holograms had an average contrast of 14% in vacuum, a fringe spacing of 3.3 nm, a field of view of 1 μm, and a pixel size of 0.48 nm.
Reconstruction and processing of projection data
The elaborate image data treatment was mainly accomplished using in-house developed scripts and software plugins for Gatan Microscopy Suite. Amplitude and phase images were reconstructed by filtering out one sideband of the Fourier transform of the electron hologram, e.g., described in ref. 37). Likewise, amplitude and phase images were reconstructed from empty holograms for correction of imaging artifacts, such as distortions of camera and projective lenses. In detail, we used a soft numerical aperture with a full width at half maximum of 1/9 nm−1 and zero-damping the signal at 1/4.5 nm−1. Accordingly, the resolution (reconstructed pixel size) of the image wave after inverse Fourier transformation (FT) of the cut sideband is in the range from 4.5 to 9 nm depending on the SNR. After holographic reconstruction of all four tilt series, phase images were unwrapped with automatic phase unwrapping algorithms (Goldstein or Flynn)38. Possible artifacts after application of these algorithms at regions, where the phase signal is too noisy or undersampled, are corrected by manual treatment of using preknowledge of the phase shift (e.g., from adjacent projections)39. All four phase tilt series were pre-aligned separately by cross-correlation to correct for coarse displacements between successive projections. Furthermore, those two tilt series, where the sample was flipped before acquisition, were flipped back numerically yielding for each tilt angle a pair of phase images with equal electric but opposite magnetic phase shift. Then, each pair of phase images was aligned by applying a linear affine transformation on the “flipped” phase image, which considers displacements, rotation, and direction-dependent magnification changes18. After this step, the separation of electric and magnetic phase shifts was performed for these pairs of phase images as illustrated in Fig. 1, steps (5) and (6). To finally employ the fine alignment (i.e., the accurate determination of the tilt axis and correction for subpixel displacement), we used a self-implemented center-of-mass method for correction of displacements perpendicular to the tilt axis and the common line approach40 for the correction of displacements parallel to the tilt axis. We applied these procedures initially on the electric phase tilt series, which has a higher SNR than the magnetic one, and used the thereby determined displacements for alignment of magnetic phase tilt series. Before computation of the derivatives, the magnetic phase images were smoothed slightly by a non-linear anisotropic diffusion41 filter using the Avizo software package (ThermoFisher Scientific Company). Following Eq. (2), we calculated the projected Bx- and By-components from the derivatives of the magnetic phase images in y- and x-direction.
Tomographic reconstruction
The tomographic reconstruction of electrostatic potential, Bx- and By-component from their aligned tilt series (projections) was conducted with the weighted simultaneous iterative reconstruction technique (W-SIRT)42. As the W-SIRT involves a weighted (instead of a simple) back-projection for each iteration step, it convergences faster than a conventional SIRT algorithm. The number of iterations was determined to five, by visually inspecting the trade-off between spatial resolution and noise. In addition, we reduced the missing wedge artifacts in the tomograms at low spatial frequencies by a finite support approach, explained in ref. 43.
Calculation of the third magnetic B-field component
In order to determine the third B-field component Bz not directly obtainable from one of the two tilt series around x or y, two strategies may be applied. First, it is possible to solve third Maxwell’s law divB = 0 with appropriate boundary conditions on the surface of the reconstruction volume. Second, it is possible to compute the projected component of the B-field perpendicular to the tilt axis in one tilt series (say around x), which is a mixture of the y and z component in the non-rotated laboratory frame and substitute the y component with the reconstruction from the second tilt series around y. The second approach may be implemented in both a field- and vector potential-based reconstruction scheme (automatically implying divB = 0)44. Indeed, the two strategies to determine Bz are identical as demonstrated in the Supplementary Note 1.
The most straight-forward way to calculate Bz from Eq. (3) is by integration along the z-coordinate, that is,
However, to reduce accumulation of errors while integrating along z, we employed periodic boundary conditions for solving this differential equation, which reads in Fourier space
Here \({\cal{F}}\){} and \({\cal{F}}^{ - 1}\){} denote the forward and inverse 3D FT, and kx., ky, kz the reciprocal coordinates in 3D Fourier space. The zero frequency component (integration constant) was fixed by setting the average of Bz to zero on the boundary of the reconstruction volume.
Micromagnetics
Micromagnetic simulations of the remanent magnetic states were performed with Object Oriented Micromagnetic Framework software package45 solving the non-linear minimization problem (non-linear constraint |M| = Ms) of the energy functional (Eq. (6)) containing the exchange, demagnetizing field and crystalline anisotropy energy as the main contributions in our case. The details of the single disc simulations are given in the Supplementary Note 7. The 3D morphology of the Co/Cu layers is revealed from MIP tomogram by assigning each voxel to a different material region. The NW’s 3D shape is segmented by a MIP threshold of 11.0 V to distinguish between NW and vacuum, whereas a MIP threshold of 18.5 V was employed to distinguish between Co (>18.5 V) and Cu (≤18.5 V). Then, the 3D data array is interpolated to a grid with voxels of 2 × 2 × 2 nm3 (grid dimension: 960 × 160 × 200 nm3). Each Co layer is attributed to an individual set of magnetic parameters such as magnetization Ms, exchange constant A, and uniaxial crystal anisotropy HK (see Supplementary Table 2). Here, the assumption of uniaxial anisotropy relies on the polycrystalline nature of the layers, which may be approximated by an average anisotropy in a first-order approximation. The magnetic induction B in each layer is obtained summing the calculated magnetization components and the demagnetization field H.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Fernandez-Pacheco, A. et al. Three-dimensional nanomagnetism. Nat. Commun. 8, 15756 (2017).
Parkin, S. S., Hayashi, M. & Thomas, L. Magnetic domain-wall racetrack memory. Science 320, 190–194 (2008).
Karnaushenko, D. et al. Self-assembled on-chip-integrated giant magneto-impedance sensorics. Adv. Mater. 27, 6582–6589 (2015).
Hoffmann, A. & Bader, S. D. Opportunities at the frontiers of spintronics. Phys. Rev. Appl. 4, 047001 (2015).
Fruchart, O. et al. Bloch-point-mediated topological transformations of magnetic domain walls in cylindrical nanowires, arXiv:1806.10918 [cond-mat-mes-hall] (2018).
Biziere, N. et al. Imaging the fine structure of a magnetic domain wall in a ni nanocylinder. Nano Lett. 13, 2053–2057 (2013).
Bogdanov, A. N. & Yablonskii, D. A. Thermodynamically stable “vortices” in magnetically ordered crystals. the mixed state of magnets. Zh. Eksp. Teor. Fiz. 95, 178–182 (1989).
Rybakov, F. N., Borisov, A. B. & Bogdanov, A. N. Three-dimensional skyrmion states in thin films of cubic helimagnets. Phys. Rev. B Condens. Matter Mater. Phys. 87, 094424 (2013).
Rybakov, F. N., Borisov, A. B., Blügel, S. & Kiselev, N. S. New spiral state and skyrmion lattice in 3D model of chiral magnets. New J. Phys. 18, 045002 (2016).
Zheng, F. et al. Experimental observation of chiral magnetic bobbers in b20-type fege. Nat. Nanotechnol. 13, 451–455 (2018).
Kravchuk, V. P. et al. Multiplet of skyrmion states on a curvilinear defect: Reconfigurable skyrmion lattices. Phys. Rev. Lett. 120, 067201 (2018).
Nisoli, C., Moessner, R. & Schiffer, P. Colloquium: Artificial spin ice: Designing and imaging magnetic frustration. Rev. Mod. Phys. 85, 1473–1490 (2013).
Streubel, R. et al. Retrieving spin textures on curved magnetic thin films with full-field soft x-ray microscopies. Nat. Commun. 6, 7612 (2015).
Suzuki, M. et al. Three-dimensional visualization of magnetic domain structure with strong uniaxial anisotropy via scanning hard X-ray microtomography. Appl. Phys. Express 11, 036601 (2018).
Donnelly, C. et al. Tomographic reconstruction of a three-dimensional magnetization vector field. New J. Phys. 20, 083009 (2018).
Lai, G. et al. Three-dimensional reconstruction of of magnetic vector fields using electron-holographic interferometry. J. Appl. Phys. 75, 4593–4598 (1994).
Lubk, A. et al. Nanoscale three-dimensional reconstruction of electric and magnetic stray fields around nanowires. Appl. Phys. Lett. 105, 173110 (2014).
Wolf, D. et al. 3d magnetic induction maps of nanoscale materials revealed by electron holographic tomography. Chem. Mater. 27, 6771–6778 (2015).
Simon, P. et al. Synthesis and three-dimensional magnetic field mapping of co2fega heusler nanowires at 5 nm resolution. Nano Lett. 16, 114–120 (2016).
Lichte, H. Performance limits of electron holography. Ultramicroscopy 108, 256–262 (2008).
Röder, F., Lubk, A., Wolf, D. & Niermann, T. Noise estimation for off-axis electron holography. Ultramicroscopy 144, 32–42 (2014).
Phatak, C., Petford-Long, A. K. & De Graef, M. Three-dimensional study of the vector potential of magnetic structures. Phys. Rev. Lett. 104, 253901 (2010).
Tanigaki, T. et al. Three-dimensional observation of magnetic vortex cores in stacked ferromagnetic discs. Nano Lett. 15, 1309–1314 (2015).
Caron, J. Model-based reconstruction of magnetisation distributions in nanostructures from electron optical phase images, volume 177 of Key Technologies (Forschungszentrum Jülich GmbH Zentralbibliothek, Verlag Jülich, 2018) http://hdl.handle.net/2128/19740.
Mohan, K. A., Kc, P., Phatak, C., De Graef, M. & Bouman, C. A. Model-based iterative reconstruction of magnetization using vector field electron tomography. IEEE Trans. Comput. Imaging 4, 432–446 (2018).
Aharonov, Y. & Bohm, D. Significance of electromagnetic potentials in the quantum theory. Phys. Rev. 115, 485–491 (1959).
Teague, M. Deterministic phase retrieval: a Green’s function solution. J. Opt. Soc. Am. 73, 1434–1441 (1983).
Lubk, A. Holography and tomography with electrons: From Quantum States to Three-Dimensional Fields and Back. In Advances in Imaging and Electron Physics, vol 206, 1–14 (Elsevier, 2018).
Kasama, T., Dunin-Borkowski, R., Beleggia, M. Electron Holography of Magnetic Materials (InTech, 2011).
Midgley, P. A. & Weyland, M. 3d electron microscopy in the physical sciences: the development of z-contrast and eftem tomography. Ultramicroscopy 96, 413–431 (2003).
Reyes, D., Biziere, N., Warot-Fonrose, B., Wade, T. & Gatel, C. Magnetic configurations in co/cu multilayered nanowires: Evidence of structural and magnetic interplay. Nano Lett. 16, 1230–1236 (2016).
van Heel, M. & Schatz, M. Fourier shell correlation threshold criteria. J. Struct. Biol. 151, 250–262 (2005).
Ogrodnik, P. et al. Field-and temperature-modulated spin diode effect in a GMR nanowire with dipolar coupling. J. Phys. D Appl. Phys. 52, 065002 (2019).
Gatel, C., Dupuy, J., Houdellier, F. & Hytch, M. J. Unlimited acquisition time in electron holography by automated feedback control of transmission electron microscope. Appl. Phys. Lett. 113, 133102 (2018).
Harada, K., Tonomura, A., Togawa, Y., Akashi, T. & Matsuda, T. Double-biprism electron interferometry. Appl. Phys. Lett. 84, 3229–3231 (2004).
Wolf, D., Lubk, A., Lichte, H. & Friedrich, H. Towards automated electron holographic tomography for 3d mapping of electrostatic potentials. Ultramicroscopy 110, 390–399 (2010).
Lehmann, M. & Lichte, H. Tutorial on off-axis electron holography. Microsc. Micro. 8, 447–466 (2002).
Ghiglia, D. C. & Pritt, M. D. Two-Dimensional Phase Unwrapping: Theory, Algorithms and Software. (Wiley & Sons, New York NY, 1998).
Lubk, A. et al. Nanometer-scale tomographic reconstruction of three-dimensional electrostatic potentials in gaas/algaas core-shell nanowires. Phys. Rev. B 90, 125404 (2014).
Penczek, P. A., Zhu, J. & Frank, J. A common-lines based method for determining orientations for n > 3 particle projections simultaneously. Ultramicroscopy 63, 205–218 (1996).
Frangakis, A. S. & Hegerl, R. Noise reduction in electron tomographic reconstructions using nonlinear anisotropic diffusion. J. Struct. Biol. 135, 239–250 (2001).
Wolf, D., Lubk, A. & Lichte, H. Weighted simultaneous iterative reconstruction technique for single-axis tomography. Ultramicroscopy 136, 15–25 (2014).
Wolf, D. et al. Three-dimensional composition and electric potential mapping of iii-v core-multishell nanowires by correlative stem and holographic tomography. Nano Lett. 18, 4777–4784 (2018).
Phatak, C., Beleggia, M. & De Graef, M. Vector field electron tomography of magnetic materials: theoretic development. Ultramicroscopy 108, 503–513 (2008).
Donahue, D. G. & Porter, M. J. OOMMF User’s Guide Version 1.0, Interagency Report NISTIR 6376 (National Institute of Standards and Technology, Gaithersburg, MD, 1999).
Acknowledgements
D.W., A.L., S.S. and J.K. have received funding from the European Research Council (ERC) under the Horizon 2020 research and innovation program of the European Union (grant agreement number 715620). We express our gratitude to M. Lehmann (TU Berlin) for providing access to the FEI Titan 80–300 Holography Special Berlin. The publication of this article was funded by the Open Access Fund of the Leibniz Association.
Author information
Authors and Affiliations
Contributions
D.W., S.S., A.L., C.G., B.W. and T.N. performed the experiments. D.W. aligned, reconstructed, and evaluated the 3D data. T.W., N.B. and D.R. fabricated the samples. N.B. carried out the micromagnetic simulations. A.L. and J.K. contributed to the theoretical foundation of VFET and derivation of magnetic properties. D.W. and A.L. wrote the manuscript. N.B. and C.G. contributed to manuscript writing. E.S. and B.B. helped with the interpretation of the data and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wolf, D., Biziere, N., Sturm, S. et al. Holographic vector field electron tomography of three-dimensional nanomagnets. Commun Phys 2, 87 (2019). https://doi.org/10.1038/s42005-019-0187-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-019-0187-8
This article is cited by
-
Real space iterative reconstruction for vector tomography (RESIRE-V)
Scientific Reports (2024)
-
A fast magnetic vector characterization method for quasi two-dimensional systems and heterostructures
Scientific Reports (2023)
-
Probing of three-dimensional spin textures in multilayers by field dependent X-ray resonant magnetic scattering
Scientific Reports (2023)
-
3D magnetic imaging using electron vortex beam microscopy
Communications Physics (2022)
-
Topological magnetic field textures
Nature Nanotechnology (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.