Chemical potential formalism for polymer entropic forces

Abstract

The entropic force is one of the most elusive interactions in macromolecules. It is clearly defined theoretically, but practically difficult to evaluate, thus restricting our knowledge of it often to a qualitative level. Here, we propose a formula for entropic force, f = f${\hskip0.3pt}^{\rm -{\hskip-4.3pt}o}$ + T ln(α), for confined polymers and demonstrate its mathematical equivalence to the widely used chemical potential formula for solutions, μ = μ$^{\rm -{\hskip-4.3pt}o} +R\tilde T\,{\mathrm{ln}}(a)$. A systematic analysis based on this formalism clarifies the force magnitudes obtained in several recent experiments on polymers and granular chains and elucidates the common force scales for polymers studied in nanoscience and biological systems. This work provides a practical tool for instantaneously evaluating the entropic forces in polymer science and indicates the possibility of using a reference-based strategy to tackle general entropic problems beyond chemical solutions.

Introduction

A wire threaded through a hole might be one of the simplest models one can imagine in physics, which, captures the core scenario in numerous polymer systems in laboratories, industrial applications, and real biological environments. This model has been studied intensively over decades, for polymer translocation and confined polymers in microfluidics, nanotechnology, and single-molecule experiments^1,2,3,4. Although entropic effects are significant for systems scaled down to that size and were already formulated in the earlier theories in this field^5,6,7, the estimation of their strength is challenging, because analytically or numerically solving partition functions is difficult^8,9. Thus, qualitative judgments on entropic effects are more frequently reported than quantitative characterizations.

In contrast to these direct approaches, here we derive an entropic force formula for confined polymers and demonstrate its correspondence to the well-known chemical potential formula for solutions (Fig. 1)¹⁰. The advantage of the latter formula is that one can calculate the chemical potential of a desired solution by summing an easily calculable correction term with a known reference value. In the same spirit, the convenience of the derived force formula is that it can be readily calculated based on the knowledge of the entropic force of a known reference system. The formalism is elucidated in several numerical experiments, including a polymer pulled by an optical tweezer into a two-dimensional (2D) channel and a polymer straddling a 2D channel undergoing a tug-of-war. Different types of entropic forces in those systems are calculated by the Jarzynski equality (JE)¹¹ and a recursion formula (RF) for counting the exact configuration numbers. The highly coincident force magnitudes extracted from these two independent approaches justify the accuracy of the force formula. On the basis of this consistency, the analysis is extended to three-dimensional (3D) circular tubes and slits. The estimated force magnitudes are very close to the experimentally observed ones in 2D strips¹², pillar arrays¹³, and 3D nanoslits¹⁴, and follow the same scaling behavior observed in granular chains¹⁵. More general studies on several polymers threaded through various natural and artificial pores unravel a common force range between femto- and piconewton and indicate a special ratio between the forces of different confinements. The proposed force formula reduces the complex evaluation of partition functions to a simple textbook-level calculation. This allows us to estimate the entropic effects on polymers algebraically by hand without resorting to elaborate computational efforts and perform a systematic analysis on the force scales for a broad class of confined-polymer systems.

Fig. 1

A correspondence between polymer physics and physical chemistry. Owing to a correspondence between the chemical potentials for solutions and the entropic forces for partly confined polymers, solving these two problems is mathematically equivalent. The chemical potential formula for a solution of activity a = rb is μ = μ$^{\rm -{\hskip-4.3pt}o}$ + $R\tilde T\,{\mathrm{ln}}(a)$, with the standard chemical potential μ$^{\rm -{\hskip-4.3pt}o}$, gas constant R, Kelvin temperature $\tilde T$, activity coefficient r, and concentration b of the solution. With this expression one can calculate the μ of a desired solution by summing an easily calculable correction term $R\tilde T\,{\mathrm{ln}}(a)$ with a known reference value μ$^{\rm -{\hskip-4.3pt}o}$. The entropic force formula for a polymer partly confined in a channel is f = f${\hskip0.3pt}^{\rm -{\hskip-4.3pt}o}$ + T ln(α), with a reference force f${\hskip0.3pt}^{\rm -{\hskip-4.3pt}o}$ and a dimensionless temperature T. Here, the “activity” α = γβ depends on the channel width and stiffness, as well as the polymer persistence length and excluded volume. Therein, the “concentration” β is decided by the configuration number of the basic unit to coarse-grain the polymer, such as the commonly adopted beads, rods, or blobs, whereas the “activity coefficient” γ reflects the change in internal freedom in that basic unit when it enters or leaves the channel. If all the basic units along the polymer chain are identical in shape and internal freedom, such as those in a granular chain, then γ = 1 and α = β, which corresponds to the ideal case of dilute solutions with r = 1 and a = c in μ

Results

Configurational entropies

Let us consider a polymer partly confined in a channel. Suppose the polymer segment inside (outside) the channel is coarse-grained as a chain of basic unit (BU) C_I (C_O), where C_I and C_O do not need to be the same (Fig. 2a). For instance, C_I could be a rod in the Odijk regime and C_O could be a Kuhn segment in a free space, or C_I and C_O could have the same shape but different numbers of monomer microstates inside them. The chain can be a non-self-avoiding chain (NSC) or a self-avoiding chain (SC). The channel is assumed to be narrow with respect to C_I. If C_I and C_O are identical beads of size l in a bead-spring model (Fig. 2b, c), let n_I (n_O) be the number of beads inside (outside) the channel and ${\mathrm{\Omega }}_{n_{\mathrm{I}}}$ $\left( {{\mathrm{\Omega }}_{n_{\mathrm{O}}}} \right)$ denote the configuration number of the chain segment of C_I (C_O) inside (outside) the channel. Then the configurational entropy of the whole chain is $S = k_{\mathrm{B}}\,{\mathrm{ln}}\left( {{\mathrm{\Omega }}_{n_{\mathrm{I}}}{\mathrm{\Omega }}_{n_{\mathrm{O}}}} \right)$, with k_B being the Boltzmann constant.

Fig. 2

Three kinds of entropic forces for partly confined polymers. a A chain partly confined by a channel, for which three basic units of C_I (red) appear inside the channel when two basic units of C_O (blue) move into the channel. ${\mathrm{\Phi }}_{n_{\mathrm{I}}}$ $\left( {{\mathrm{\Phi }}_{n_{\mathrm{O}}}} \right)$ is the excess configuration number inside (outside) the channel in Eq. (1), whereas ${\mathrm{\Psi }}_{n_{\mathrm{I}}}$ and ${\mathrm{\Psi }}_{n_{\mathrm{O}}}$ reflect the changes of internal freedoms in basic units in Eq. (3). b The entropic recoiling force f_R for a chain escaping from a two-dimensional (2D) channel is counterbalanced by the drag force f_drag of an optical tweezer. n_I (n_O) is the number of basic unit C_I inside (C_O outside) the channel. c The entropic drift force f_D and tension force f_T for polymer tug-of-war. n_L (n_R) is the number of basic unit C_O in the left (right) space. d A bead (blue circle) of size l is in a channel (black) of width w = l + d, where the lateral free space d is the distance the bead can freely move without touching the boundary. The potential well (blue curve) above the channel describes the bead-wall interaction versus the location of the bead center. The well boundary V(η) = κη²/2 is a function of the penetration depth η and stiffness κ. The probability density of finding the bead in the lateral direction of the channel (green area) has the same area as a uniform probability density of an effective width d + d_e (magenta rectangle). The bead confined by the blue soft potential is analogous to being restricted to a hard potential of an effective width d + d_e

Entropic recoiling forces

The entropic recoiling force describes the tendency of a chain to escape from a channel (Fig. 2b). It is the negative of the change in the entropic free energy, $- \tilde TS$, per shifted distance out of the channel, where $\tilde T$ is the Kelvin temperature. If the distance is l, this force is given by $\tilde f_{\mathrm{R}} = \left( {k_{\mathrm{B}}\tilde T{\mathrm{/}}l} \right){\mathrm{ln}}\left[ {\left( {{\mathrm{\Omega }}_{n_{\mathrm{I}} - 1}{\mathrm{\Omega }}_{n_{\mathrm{O}} + 1}} \right){\mathrm{/}}\left( {{\mathrm{\Omega }}_{n_{\mathrm{I}}}{\mathrm{\Omega }}_{n_{\mathrm{O}}}} \right)} \right]$. Taking the dimensionless temperature $T \equiv \tilde T{\mathrm{/}}\tilde T_{{\mathrm{room}}}$ with respect to the room temperature $\tilde T_{{\mathrm{room}}} = 298$ K, it yields a dimensionless entropic force $f_{\mathrm{R}} \equiv \tilde f_{\mathrm{R}}l{\mathrm{/}}\epsilon$, or

$$f_{\mathrm{R}} = T\,{\mathrm{ln}}\left( {\frac{{{\mathrm{\Omega }}_{n_{\mathrm{I}} - 1}{\mathrm{\Omega }}_{n_{\mathrm{O}} + 1}}}{{{\mathrm{\Omega }}_{n_{\mathrm{I}}}{\mathrm{\Omega }}_{n_{\mathrm{O}}}}}} \right) = T\,{\mathrm{ln}}\left( {\frac{{{\mathrm{\Phi }}_{n_{\mathrm{O}}}}}{{{\mathrm{\Phi }}_{n_{\mathrm{I}} - 1}}}} \right),$$

(1)

with $\epsilon \equiv k_{\mathrm{B}}\tilde T_{{\mathrm{room}}}$. Here, ${\mathrm{\Phi }}_{n_{\mathrm{I}}} \equiv {\mathrm{\Omega }}_{n_{\mathrm{I}} + 1}{\mathrm{/\Omega }}_{n_{\mathrm{I}}}$ $\left( {{\mathrm{\Phi }}_{n_{\mathrm{O}}} \equiv {\mathrm{\Omega }}_{n_{\mathrm{O}} + 1}{\mathrm{/\Omega }}_{n_{\mathrm{O}}}} \right)$ is the excess configuration number caused by an added bead inside (outside) the channel. As ${\mathrm{\Phi }}_{n_{\mathrm{O}}}$ outside the channel is always larger than ${\mathrm{\Phi }}_{n_{\mathrm{I}} - 1}$ inside the channel, we have f_R > 0. The positive sign indicates that the force points to the same direction as an outward-moving bead. If the channel is so narrow that only one straight configuration is allowed inside it, the force will degenerate to $f_{\mathrm{R}} = T\,{\mathrm{ln}}\left( {{\mathrm{\Phi }}_{n_{\mathrm{O}}}} \right)$, because ${\mathrm{\Omega }}_{n_{\mathrm{I}} - 1} = {\mathrm{\Omega }}_{n_{\mathrm{I}}} = 1$ implies ${\mathrm{\Phi }}_{n_{\mathrm{I}} - 1} = 1$.

Let $f_{\mathrm{R}}{\!\!}{\prime}$ be the force of a second chain of the same form as Eq. (1), with ${\mathrm{\Phi }}_{n_{\mathrm{O}}}$, ${\mathrm{\Phi }}_{n_{\mathrm{I}}}$, and l there replaced by ${\mathrm{\Phi }}_{n_{\mathrm{O}}}{\!\!\!\!\!}{\prime}$, ${\mathrm{\Phi }}_{n_{\mathrm{I}}}{\!\!\!\!}{\prime}$, and l′. For a given (n_I, n_O), $f_{\mathrm{R}}{\!\!}{\prime}$ is related to f_R by

$$f_{\mathrm{R}} = f_{\mathrm{R}}{\!\!}{\prime} + T\,{\mathrm{ln}}\left( {\frac{{{\mathrm{\Phi }}_{n_{\mathrm{I}} - 1}{\!\!\!\!\!\!\!\!\!}{\prime} \,\,\,\,\,\,\,{\mathrm{\Phi }}_{n_{\mathrm{O}}}}}{{{\mathrm{\Phi }}_{n_{\mathrm{I}} - 1}{\mathrm{\Phi }}_{n_{\mathrm{O}}}{\!\!\!\!\!}{\prime} }}} \right) = f_{\mathrm{R}}{\!\!}{\prime} + T\,{\mathrm{ln}}\left( {\alpha _{\mathrm{R}}} \right),$$

(2)

with α_R ≡ α_iα_o, where $\alpha _{\mathrm{i}} \equiv {\mathrm{\Phi }}_{n_{\mathrm{I}} - 1}{\!\!\!\!\!\!\!\!\!}{\prime} \,\,\,\,\,\,\,{\mathrm{/\Phi }}_{n_{\mathrm{I}} - 1}$ and $\alpha _{\mathrm{o}} \equiv {\mathrm{\Phi }}_{n_{\mathrm{O}}}{\mathrm{/\Phi }}_{n_{\mathrm{O}}}{\!\!\!\!\!}{\prime}\,\,\,$. Generally, the bead sizes l for f_R and l′ for $f_{\mathrm{R}}{\!\!}{\prime}$ in Eq. (2) are not the same. Therefore, even when the values of f_R and $f_{\mathrm{R}}{\!\!}{\prime}$ of the two systems are identical, the real forces $\tilde f_{\mathrm{R}} = f_{\mathrm{R}}\epsilon {\mathrm{/}}l$ and $\tilde f_{\mathrm{R}}{\!\!}{\prime} = f_{\mathrm{R}}{\!\!}{\prime} \epsilon {\mathrm{/}}l\prime$ may be different.

If C_I and C_O do not have identical shapes or internal freedom, such as those in Fig. 2a, let ${\tilde{\mathrm \Phi }}_{n_{\mathrm{I}}}$ $\left( {{\tilde{\mathrm \Phi }}_{n_{\mathrm{O}}}} \right)$ be the excess “microstate” number caused by an added BU C_I inside (C_O outside) the channel. The “microstates” here include the allowed configurations of C_I and C_O considered in Eq. (1) and the internal freedom inside each individual BU, which are generally hybridized and cannot be decoupled. When a chain segment of length l moves into (out of) a channel, suppose n_i (n_o) BUs of C_I (C_O) appear inside (outside) it. Then, the total excess microstate number of n_i (n_o) added BUs would be $\left( {{\tilde{\mathrm \Phi }}_{n_{\mathrm{I}} - 1}} \right)^{n_{\mathrm{i}}}$ $\left( {\left( {{\tilde{\mathrm \Phi }}_{n_{\mathrm{O}}}} \right)^{n_{\mathrm{o}}}} \right)$, for which the entropic recoiling force in Eq. (1) is generalized to

$$f_{\mathrm{R}} = T\,{\mathrm{ln}}\left( {\frac{{\left( {{\tilde{\mathrm \Phi }}_{n_{\mathrm{O}}}} \right)^{n_{\mathrm{o}}}}}{{\left( {{\tilde{\mathrm \Phi }}_{n_{\mathrm{I}} - 1}} \right)^{n_{\mathrm{i}}}}}} \right),$$

(3)

with ${\tilde{\mathrm \Phi }}_{n_{\mathrm{I}}} \equiv g_{n_{\mathrm{I}} + 1}{\mathrm{\Omega }}_{n_{\mathrm{I}} + 1}{\mathrm{/}}\left( {g_{n_{\mathrm{I}}}{\mathrm{\Omega }}_{n_{\mathrm{I}}}} \right)$ = ${\mathrm{\Psi }}_{n_{\mathrm{I}}}{\mathrm{\Phi }}_{n_{\mathrm{I}}}$ and ${\tilde{\mathrm \Phi }}_{n_{\mathrm{O}}} \equiv g_{n_{\mathrm{O}} + 1}{\mathrm{\Omega }}_{n_{\mathrm{O}} + 1}{\mathrm{/}}\left( {g_{n_{\mathrm{O}}}{\mathrm{\Omega }}_{n_{\mathrm{O}}}} \right)$ =  ${\mathrm{\Psi }}_{n_{\mathrm{O}}}{\mathrm{\Phi }}_{n_{\mathrm{O}}}$. Therein, ${\mathrm{\Phi }}_{n_{\mathrm{I}}}$ $\left( {{\mathrm{\Phi }}_{n_{\mathrm{O}}}} \right)$ is the excess configuration of C_I (C_O) defined in Eq. (1), while $g_{n_{\mathrm{I}}}$ and $g_{n_{\mathrm{O}}}$ as well as ${\mathrm{\Psi }}_{n_{\mathrm{I}}} \equiv g_{n_{\mathrm{I}} + 1}{\mathrm{/}}g_{n_{\mathrm{I}}}$ and ${\mathrm{\Psi }}_{n_{\mathrm{O}}} \equiv g_{n_{\mathrm{O}} + 1}{\mathrm{/}}g_{n_{\mathrm{O}}}$ are correction terms reflecting the difference between the shapes, or internal freedoms, of C_I and C_O. Notice that n_O and n_o as well as n_I and n_i in Eq. (3) have different meanings.

Two forces of the same form as Eq. (3) are related as Eq. (2) with α_R there replaced by $\tilde \alpha _{\mathrm{R}} = G\bar \alpha _{\mathrm{R}}$ where

$$G \equiv \frac{{g_{n_{\mathrm{I}} - 1}\!\!\!\!\!\!\!\!\!{\prime} \,\,\,\,\,\,\,{}^{n_{\mathrm{i}}}g_{n_{\mathrm{O}}}\,{}^{n_{\mathrm{o}}}}}{{g_{n_{\mathrm{I}} - 1}\,{}^{n_{\mathrm{i}}}g_{n_{\mathrm{O}}}{\!\!\!\!\!}{\prime} \,{}^{n_{\mathrm{o}}}}}\,{\mathrm{and}}\,\bar \alpha _{\mathrm{R}} \equiv \frac{{{\mathrm{\Phi }}_{n_{\mathrm{I}} - 1}{\!\!\!\!\!\!\!\!\!}{\prime} \,\,\,\,\,\,\,{}^{n_{\mathrm{i}}}{\mathrm{\Phi }}_{n_{\mathrm{O}}}\,{}^{n_{\mathrm{o}}}}}{{{\mathrm{\Phi }}_{n_{\mathrm{I}} - 1}\,{}^{n_{\mathrm{i}}}{\mathrm{\Phi }}_{n_{\mathrm{O}}}{\!\!\!\!\!}{\prime} \,{}^{n_{\mathrm{o}}}}}.$$

(4)

That is, $\tilde \alpha _{\mathrm{R}}$ is related to the α_R in Eq. (2) by $\tilde \alpha _{\mathrm{R}} = \gamma \alpha _{\mathrm{R}}$ with $\gamma \equiv G\bar \alpha _{\mathrm{R}}{\mathrm{/}}\alpha _{\mathrm{R}}$. Therefore, for general C_I and C_O, Eq. (2) is extended to the form

$$f = f^{\rm -{\hskip-4.3pt}o} + T\,{\mathrm{ln}}\left( \alpha \right),\,{\mathrm{with}}\,\alpha = \gamma \beta ,$$

(5)

with β = α_R. Specifically, if the microstates of a polymer can be decomposed as those inside and outside C_I (C_O), then $g_{n_{\mathrm{I}}}$ $\left( {g_{n_{\mathrm{O}}}} \right)$ is exactly the number of microstates inside C_I (C_O). This decomposition is similar to that in the de Gennes blob, where the Flory statistics inside a blob is independent of the chain properties outside the blob. If C_I and C_O are identical, then $n_{\mathrm{i}} = n_{\mathrm{o}} = g_{n_{\mathrm{I}}} = g_{n_{\mathrm{O}}} = 1$ for all n_I and n_O. In this case, γ = 1 and α is reduced to the β = α_R of an “ideal” confined chain in Eq. (2). Therefore, α, β, and γ play the same role as the activity a = rc, the concentration c, and the activity coefficient r, respectively, in the chemical potential formula μ = μ$^{\rm -{\hskip-4.4pt}o}$ + T ln(a) of a non-ideal solution. Notice that the mathematical equivalence between Eq. (5) and the chemical potential formula for solutions does not mean the former is aimed at understanding polymer solutions.

Entropic drift forces

The above formalism also applies to other entropic forces. For polymer tug-of-war in Fig. 2c, the chain straddling the channel is unstable and will gradually move out of a channel either rightward or leftward. The entropic drift force

$$f_{\mathrm{D}} = T\,{\mathrm{ln}}\left( {\frac{{{\mathrm{\Omega }}_{n_{\mathrm{R}} - 1}{\mathrm{\Omega }}_{n_{\mathrm{L}} + 1}}}{{{\mathrm{\Omega }}_{n_{\mathrm{R}}}{\mathrm{\Omega }}_{n_{\mathrm{L}}}}}} \right) = T\,{\mathrm{ln}}\left( {\frac{{{\mathrm{\Phi }}_{n_{\mathrm{L}}}}}{{{\mathrm{\Phi }}_{n_{\mathrm{R}} - 1}}}} \right)$$

(6)

represents the tendency of the drift of the whole chain from the right to the left space. Here, n_L (n_R) denotes the number of beads in the left (right) space and ${\mathrm{\Phi }}_{n_{\mathrm{L}}} \equiv {\mathrm{\Omega }}_{n_{\mathrm{L}} + 1}{\mathrm{/\Omega }}_{n_{\mathrm{L}}}$ $\left( {{\mathrm{\Phi }}_{n_{\mathrm{R}}} \equiv {\mathrm{\Omega }}_{n_{\mathrm{R}} + 1}{\mathrm{/\Omega }}_{n_{\mathrm{R}}}} \right)$ stands for the excess configuration number caused by an added bead in the left (right) space. ${\mathrm{\Phi }}_{n_{\mathrm{L}}}$ and ${\mathrm{\Phi }}_{n_{\mathrm{R}}}$ are the same function as ${\mathrm{\Phi }}_{n_{\mathrm{O}}}$ in Eq. (1). Since the configuration of an outside segment with fewer beads is more constrained by the half-plane boundary, such segment cannot have a larger excess number, which implies Φ_n−1 ≤ Φ_n for n ∈ {n_O, n_L, n_R} (see a discrete example in Fig. 3). Hence, n_L > n_R − 1 (n_L < n_R − 1) in Eq. (6) implies ${\mathrm{\Phi }}_{n_{\mathrm{L}}} > {\mathrm{\Phi }}_{n_{\mathrm{R}} - 1}$ $\left( {{\mathrm{\Phi }}_{n_{\mathrm{L}}} < {\mathrm{\Phi }}_{n_{\mathrm{R}} - 1}} \right)$ and f_D > 0 (f_D < 0), for which the chain tends to move leftward (rightward). For n_L = n_R − 1, one has ${\mathrm{\Phi }}_{n_{\mathrm{L}}} = {\mathrm{\Phi }}_{n_{\mathrm{R}} - 1}$ and f_D = 0, for which the chain movement does not have a biased direction. The drift force in Eq. (6) can be decomposed as a difference $f_{\mathrm{D}} = f_{{\mathrm{R}},(n_{\mathrm{I}},n_{\mathrm{L}})} - f_{{\mathrm{R}},(n_{\mathrm{I}},n_{\mathrm{R}} - 1)}$ between a leftward recoiling force, $f_{{\mathrm{R}},(n_{\mathrm{I}},n_{\mathrm{L}})}$, and a rightward recoiling force, $f_{{\mathrm{R}},(n_{\mathrm{I}},n_{\mathrm{R}} - 1)}$, with $f_{{\mathrm{R}},(n,n{\prime})} \equiv T\,{\mathrm{ln}}\left[ {\left( {{\mathrm{\Omega }}_{n - 1}{\mathrm{\Omega }}_{n\prime + 1}} \right){\mathrm{/}}\left( {{\mathrm{\Omega }}_n{\mathrm{\Omega }}_{n\prime }} \right)} \right]$ being a generalized expression of Eq. (1). Interestingly, the statistical forces f_D and f_R based on counting configurations also comply with the above subtraction rule as normal non-statistical forces in mechanics. Two drift forces of the same form as Eq. (6) are related as Eq. (2) with α_R there replaced by α_D ≡ α_l/α_r, where $\alpha _{\mathrm{l}} \equiv {\mathrm{\Phi }}_{n_{\mathrm{L}}}{\mathrm{/\Phi }}_{n_{\mathrm{L}}}{\!\!\!\!\!}{\prime} \,\,$ and $\alpha _{\mathrm{r}} \equiv {\mathrm{\Phi }}_{n_{\mathrm{R}} - 1}{\mathrm{/\Phi }}_{n_{\mathrm{R}} - 1}{\!\!\!\!\!\!\!\!\!\!}{\prime} \,\,\,\,\,\,\,$ are the same function as the α_o below Eq. (2).

Fig. 3

Relations between the entropic recoiling forces of different kinds of polymer. a If a non-self-avoiding chain is pulled into a channel by an optical tweezer (as shown in the inset of b), the entropic recoiling forces $f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ calculated by the Jarzynski equality at d = 0.05l, $\kappa {\mathrm{/}}\epsilon = 10^4$, T = 1, and different bead numbers outside the channel, n_O, are depicted by the green points. Increasing the number of systems in the ensemble of the Jarzynski equality approach, the green points will become more concentrated onto the magenta dashed curve. The curve saturates at the maximum magnitude $\bar f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ when n_O > 10. The blue dotted (solid) line denotes the force $\bar f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ calculated by the recursion formula, without (with) the penetration effect, for which the lateral free space in Fig. 2d is d (is d + d_e). b For d = 0.2l at different temperatures, the circles (squares) are the force $\bar f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ $\left( {\bar f_{\mathrm{R}}^{{\mathrm{(SC)}}}} \right)$ of the non-self-avoiding chain (self-avoiding chain) measured via the Jarzynski equality. The dotted (dashed) line denotes the $\bar f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ $\left( {\bar f_{\mathrm{R}}^{{\mathrm{(SC)}}}} \right)$ calculated by the recursion formula without the penetration effect, while the solid (dash-dotted) line represents the $\bar f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ $\left( {\bar f_{\mathrm{R}}^{{\mathrm{(SC)}}}} \right)$ calculated by the recursion formula with that effect, which agrees with the circles (squares). The forces $\bar f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ and $\bar f_{\mathrm{R}}^{{\mathrm{(SC)}}}$ are related by a specific version of formula (5) written in the plot. c The function α_o (blue curve) in Eq. (2) converges to 0.66 (red dashed line). It has a zigzag shape, because α_o behaves differently at even and odd n_O in a lattice space. The error bars in the Jarzynski equality approach vary with the selected ensemble size and are, therefore, not emphasized in b

Entropic tension forces

The entropic tension force in Fig. 2c characterizes the tendency of polymer stretching inside a channel. The simplest version of that force describes the tendency of moving one bead from the channel into the left or the right space,

$$\begin{array}{*{20}{l}} {f_{\mathrm{T}}} \hfill & = \hfill & {T\,{\mathrm{ln}}\left( {\frac{{{\mathrm{\Omega }}_{n_{\mathrm{L}} + 1}{\mathrm{\Omega }}_{n_{\mathrm{I}} - 1}{\mathrm{\Omega }}_{n_{\mathrm{R}}} + \, {\mathrm{\Omega }}_{n_{\mathrm{L}}}{\mathrm{\Omega }}_{n_{\mathrm{I}} - 1}{\mathrm{\Omega }}_{n_{\mathrm{R}} + 1}}}{{{\mathrm{\Omega }}_{n_{\mathrm{L}}}{\mathrm{\Omega }}_{n_{\mathrm{I}}}{\mathrm{\Omega }}_{n_{\mathrm{R}}}}}} \right)} \hfill \\ {} \hfill & = \hfill & {T\,{\mathrm{ln}}\left( {\frac{{{\mathrm{\Phi }}_{n_{\mathrm{L}}} + \, {\mathrm{\Phi }}_{n_{\mathrm{R}}}}}{{{\mathrm{\Phi }}_{n_{\mathrm{I}} - 1}}}} \right).} \hfill \end{array}$$

(7)

Since ${\mathrm{\Phi }}_{n_{\mathrm{L}}},{\mathrm{\Phi }}_{n_{\mathrm{R}}} > {\mathrm{\Phi }}_{n_{\mathrm{I}} - 1}$, f_T is always positive, indicative of a spontaneous trend of stretching, rather than compression, in that system. This trend will eventually be counterbalanced by the increased free energy during stretching caused by other mechanisms, such as bead deformation. Two tension forces of the same form as Eq. (7) can be related as Eq. (2), with α_R there replaced by α_T ≡ α_iα_lr, where $\alpha _{{\mathrm{lr}}} \equiv \left( {{\mathrm{\Phi }}_{n_{\mathrm{L}}} + {\mathrm{\Phi }}_{n_{\mathrm{R}}}} \right){\mathrm{/}}\left( {{\mathrm{\Phi }}_{n_{\mathrm{L}}}{\!\!\!\!\!}{\prime}\,\, + {\mathrm{\Phi }}_{n_{\mathrm{R}}}{\!\!\!\!\!}{\prime} \,\,\,} \right)$ and l = l′ is not required, as in Eq. (2). For large n_L and n_R, ${\mathrm{\Phi }}_{n_{\mathrm{L}}}$, ${\mathrm{\Phi }}_{n_{\mathrm{R}}}$, ${\mathrm{\Phi }}_{n_{\mathrm{L}}}{\!\!\!\!\!}{\prime}\,\,\,$, and ${\mathrm{\Phi }}_{n_{\mathrm{R}}}{\!\!\!\!\!}{\prime}\,\,$ are approximately the same as ${\mathrm{\Phi }}_{n_{\mathrm{O}}}$ at large n_O, which implies $f_{\mathrm{T}} \approx T\,{\mathrm{ln}}\left( {2{\mathrm{\Phi }}_{n_{\mathrm{O}}}{\mathrm{/\Phi }}_{n_{\mathrm{I}}}} \right)$ and $\alpha _{\mathrm{T}} \approx \alpha _{\mathrm{i}}\alpha _{\mathrm{o}} = \alpha _{\mathrm{R}}$.

If C_I and C_O are different, in analogy to Eq. (3), the generalized tension force is $f_{\mathrm{T}}$ = $T\,{\mathrm{ln}}\left( {\left[ {\left( {{\tilde{\mathrm \Phi }}_{n_{\mathrm{L}}}} \right)^{n_{\mathrm{o}}} + \left( {{\tilde{\mathrm \Phi }}_{n_{\mathrm{R}}}} \right)^{n_{\mathrm{o}}}} \right]{\mathrm{/}}\left[ {\left( {{\tilde{\mathrm \Phi }}_{n_{\mathrm{I}} - 1}} \right)^{n_{\mathrm{i}}}} \right]} \right)$. It is related to another tension force of the same form again by Eq. (5) with a slightly different α. For those C_I and C_O, the drift force f_D in Eq. (6) does not need to be generalized, because C_I is absent in that equation and C_O in the left and right spaces are identical. The upper and lower limits of the above forces for NSCs and SCs in various confinements are derived in Supplementary Note 1 and summarized in Table 1), which serve as good candidates for the values of f $^{\rm -{\hskip-4.3pt}o}$ in Eq. (5).

Optical tweezer experiments

To illustrate the above formulas and the analytical results in Table 1, let us carry out the following numerical experiments, with the Hamiltonian described in the Methods section. First, suppose an NSC is pulled into a 2D channel of width w by the drag force f_drag of an optical tweezer, which moves slowly rightward with a constant speed (Fig. 2b, d). The work done by f_drag is converted to the entropic recoiling force $f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ via the JE (Methods section), as depicted by the magenta dashed curve in Fig. 3a. This curve shows that for n_O > 10, $f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ has almost saturated at its maximum value $\bar f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ on a plateau (blue solid line), which is independent of the tail length n_Ol outside the channel. In contrast to other studies in experiments¹³ and simulations^16,17, this tail length independent force is, to our knowledge, first time determined by the JE. For n_O < 10, the curve falls monotonically and drastically with a decreasing n_O to its minimum. The sharp kink around n_O = 5 reveals that after most beads have been pulled into the channel, the rest beads in the tail will surrender and give up to resist, which behaves like a first order phase transition¹⁶. In Fig. 3a, the maximum force $\bar f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ is also calculated by the RF (blue dotted line) (Methods section), which is slightly larger than the magenta dashed curve calculated via the JE.

Table 1 The upper and lower bounds of various entropic forces

To inspect the cause of this slight difference, we raise the temperature from T = 1 ($\tilde T = 298$ K) up to a physically extreme value T = 8 ($\tilde T = 2384$ K) in Fig. 3b. At that T, the $\bar f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ evaluated by the RF (blue dotted line) has deviated 10% from that calculated by the JE (blue circles). However, taking into account the penetration effect by enlarging the channel width w = l + d in the RF approach to w_e = l + d + d_e with d_e being the mean penetration depth in Eq. (8) in the Methods section, the blue dotted line is reduced to the blue solid line in the same plot. The latter passes precisely through all blue circles evaluated by the JE, which justifies the crucial role of the penetration effect and the accuracy of formula (8). Subtracting this effect, the plateau of the magenta dashed curve in Fig. 3a is shifted to the blue dotted line, which is rather close to the magnitude $\bar f_{\mathrm{R}}^{{\mathrm{(NSC)}}} = T\,{\mathrm{ln}}(2\pi l{\mathrm{/}}d)$ predicted in Table 1. Although that analytical magnitude is derived under the strict assumption of $n_{\mathrm{O}} \gg 1$, the simulation in Fig. 3a shows its correctness even for n_O > 10.

If the chain is an SC, the maximum values $\bar f_{\mathrm{R}}^{{\mathrm{(SC)}}}$ of the recoiling force $f_{\mathrm{R}}^{{\mathrm{(SC)}}}$ of that chain are calculated by the JE at different T and depicted by the red squares in Fig. 3b. To determine those values from an NSC by Eq. (2), one needs to evaluate $\bar \alpha _{\mathrm{o}}$, which is the α_o at $n_{\mathrm{O}} \gg 1$. For a 2D half-lattice, our Monte Carlo simulation (Fig. 3c) shows that α_o has almost saturated at its minimum $\bar \alpha _{\mathrm{o}} \approx 0.66$ after n_O = 10, which is slightly smaller than that, $\widehat {\bar \alpha }_{\mathrm{R}} \approx 0.78$, observed in a 3D half-lattice¹⁸. If f_R and $f_{\mathrm{R}}{\!\!}{\prime}$ in formula (2) represent the $\bar f_{\mathrm{R}}^{{\mathrm{(SC)}}}$ of an SC and the $\bar f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ of an NSC, respectively, partly confined in the same channel, α_R there should be equal to $\bar \alpha _{\mathrm{R}} = \bar \alpha _{\mathrm{i}}\bar \alpha _{\mathrm{o}} \approx 0.66$, where $\bar \alpha _{\mathrm{i}} = 1$ due to identical channels (Supplementary Note 1). Using this formula, $\bar f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ (blue dotted line) in Fig. 3b is converted to $\bar f_{\mathrm{R}}^{{\mathrm{(SC)}}}$ (red dashed line), which is the RF calculated force for the SC without the penetration effect. Taking into account that effect by enlarging d to d + d_e, the red dashed line is further shifted down to the red dash-dotted line. The latter is very close to the JE calculated red squares, which confirms the specific version of formula (5) written in Fig. 3b.

In Fig. 4a, the maximum recoiling force $\bar f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ for a channel of width w = l + d at different d is calculated by the RF and depicted by the blue solid curve. It deviates from the force evaluated by the JE when the channel has stiffness $\kappa = 10^3\epsilon$ (diamonds) and $10^4\epsilon$ (triangles). However, after considering the penetration effect by replacing d by d + d_e as before for $\kappa {\mathrm{/}}\epsilon = 10^3$ $\left( {\kappa {\mathrm{/}}\epsilon = 10^4} \right)$, the blue solid curve is shifted to the red dash-dotted (dashed) curve, which precisely passes through the diamonds (triangles) and again justifies the significance of formula (8). All force magnitudes on the blue solid curve agree very well with the analytical results in Table 1, which validates those results at least up to d = 0.6l, far beyond the ideal condition $d \ll l$. In Fig. 4b, the stiffness dependent $\bar f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ calculated by the JE at two different T (squares and circles) coincide precisely with those evaluated by the RF (dashed and solid curves). Both curves show a kink around $\kappa {\mathrm{/}}\epsilon = 10^3$, indicative of a separation between the stiffness effect dominant regime $\left( {\kappa {\mathrm{/}}\epsilon < 10^3} \right)$ and the width effect dominant regime $\left( {\kappa {\mathrm{/}}\epsilon > 10^3} \right)$ for the force. A similar stiffness analysis on a linear channel potential can be found in ref. ¹⁹. In Fig. 4c, the potentials of three different stiffnesses are plotted. The force magnitudes calculated in Fig. 4a, b confirm the specific version of formula (5) written in Fig. 4a.

Fig. 4

Relations between the entropic recoiling forces of different channel sizes and stiffnesses. a The recoiling forces $\bar f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ of a non-self-avoiding chain for $\kappa {\mathrm{/}}\epsilon = 10^3$ and 10⁴ at T = 1 and different d measured by the Jarzynski equality approach are depicted by the diamonds and triangles, respectively. The same force for a hard-wall channel (κ = ∞) calculated by the recursion formula is depicted by the blue solid curve. The divergence of this curve is bounded by a maximum value when d falls into the small area (0, 1/ρ), which is the degenerate force explained below Eq. (1). b The squares (circles) are the $\bar f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ measured by the Jarzynski equality approach, at d = 0.2l, T = 1 (T = 1.1), and different stiffnesses κ scaled by $\epsilon$. The dashed (solid) curve denotes those forces calculated by the recursion formula for the effective channel width w_e = l + d + d_e, in units of l. c The potentials of three different stiffnesses studied in b are plotted on the same length scale. The error bars in the Jarzynski equality approach vary with the selected ensemble size and are, therefore, not emphasized in a, b

Tug-of-war experiments

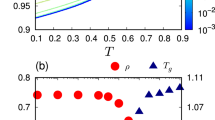
In Fig. 5a, the drift forces $f_{\mathrm{D}}^{{\mathrm{(NSC)}}}$ of an NSC of N′ beads straddling a channel are calculated by the RF, where the translocation ratio ξ ≡ n_L/N, with N = N′ − n_I, is the fraction of the chain segment in the left space. The left (right) ends of the force curves of different N approach their minimum, −T ln 2, (maximum, T ln 2,) as derived in Table 1. These force curves are insensitive to the penetration depth and channel size, in consistent with the absence of ${\mathrm{\Omega }}_{n_{\mathrm{I}}}$ and ${\mathrm{\Phi }}_{n_{\mathrm{I}}}$ in Eq. (6). Integrating these curves leads to the free energy profiles F(ξ) in Fig. 5b. The barriers of F(ξ) can be used to calculate Krammers' escape rate for polymer translocation, if the process is quasi-equilibrium and ergodicity is preserved²⁰. The curves in Fig. 5b will converge to an invariant shape at large N. In Fig. 5c, the tension forces $f_{\mathrm{T}}^{{\mathrm{(NSC)}}}$ of different N start from some initial values close to T ln(3πl/d) at ξ = 0, increase monotonically to their maxima below T ln(4πl/d), and then fall back to their initial values when ξ = 1. For larger (smaller) N, the maxima (minima) of the forces will approach T ln(4πl/d) (T ln(2πl/d)). All these numerical observations agree with the analytical bounds of $f_{\mathrm{T}}^{{\mathrm{(NSC)}}}$ predicted in Table 1 and Supplementary Note 1.

Fig. 5

Entropic drift and tension forces at different chain lengths and translocation ratios. a The drift forces $f_{\mathrm{D}}^{{\mathrm{(NSC)}}}$ of a non-self-avoiding chain of N = 4, 20, and 100 are calculated by the recursion formula at different ξ, and fitted by the black dash-dotted, red dashed, and blue solid curves, respectively. When the chain is pulled leftward to increase its n_L starting from n_L = 0, it will be resisted by a rightward force, $f_{\mathrm{D}}^{{\mathrm{(NSC)}}}(\xi ) < 0$, when ξ < 0.5, but assisted by a leftward force, $f_{\mathrm{D}}^{{\mathrm{(NSC)}}}(\xi ) > 0$, when ξ > 0.5. b The free energy profiles F(ξ) are integrated from the curves in a, where the two ends of those profiles are set to zero. The integration is carried out along the real length n_Ll, and then reexpressed as a function of ξ. Therefore, F(ξ) rises with N, although the areas bounded by the curves $f_{\mathrm{D}}^{{\mathrm{(NSC)}}}(\xi )$ in Fig. 5a decrease with N. c The tension forces $f_{\mathrm{T}}^{{\mathrm{(NSC)}}}$ calculated by the recursion formula are fitted by the black dash-dotted, red dashed, and blue solid curves for N = 4, 20, and 100, respectively. d The free-energy barrier Δ_n measured from the energy profiles in Fig. 5b gives the blue circles, red squares, and black triangles for n = 1, 2, and 3, respectively, where $n_{\mathrm{I}} \gg 1$. The Δ_n calculated by the scaling formula in the main text are the blue solid, red dashed, and black dash-dotted curves, respectively

Let Δ_n be the difference between the entropic free energies of a chain at n_L = n and N/2, where the latter is the position of the maximum of the F(ξ) in Fig. 5b. The value of Δ_n reveals the free energy barrier for a chain translocation starting from n_L = n. According to a scaling argument, the entropic free energy of a chain of n_L = n is $F_n{\mathrm{/}}k_{\mathrm{B}}\tilde T$ = $(1 - r)\, {\mathrm{ln}}(n) + (1 - r)\, {\mathrm{ln}}(N - n)$ when n and $N - n \gg 1$^21,22, where r = 1/2 for NSCs. It implies ${\mathrm{\Delta }}_n$ = $\left( {F_{N/2} - F_n} \right){\mathrm{/}}\left( {k_{\mathrm{B}}\tilde T} \right)$ = $(1{\mathrm{/2}}){\mathrm{ln}}\left[ {(N{\mathrm{/}}2)^2{\mathrm{/}}(n(N - n))} \right]$ for an NSC. In Fig. 5d, the Δ_n calculated by that scaling argument are found to overestimate those measured from the F(ξ) in Fig. 5b. The discrepancy is especially significant in Δ₁ between the solid curve and circles. This is ascribed to the overestimated difficulty of pulling the first few beads into the left space by the scaling formula. It is in echo with the finding in Fig. 3a that $f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ is weaker than expected for chains with few beads outside the channel.

Applications

Suppose we have a double-stranded DNA (dsDNA) of persistence length l_p ≈ 53 nm partly confined in a 2D strip (Fig. 2b, c), a 3D circular tube, or a 3D slit of size w = 110 nm and stiffness κ = ∞ pN nm⁻¹ at $\tilde T = 298$ K. If this system is modeled by an SC of beads of Kuhn length l_K, then l = l_K ≈ 2l_p ≈ 106 nm. According to Eq. (5) (Supplementary Note 2), the maximum real forces are $\left( {\hat f_{\mathrm{R}}^{{\mathrm{(SC)}}},\hat f_{\mathrm{D}}^{{\mathrm{(SC)}}},\hat f_{\mathrm{T}}^{{\mathrm{(SC)}}}} \right)$ ≈ $(0.18,0.01,0.21)$ pN for the strip, (0.35, 0.02, 0.38) pN for the tube, (0.16, 0.02, 0.19) pN for the slit when n_I is so large that an added bead in the slit can freely rotate 2π, and (0.28, 0.02, 0.31) pN if n_I is so small during strong stretching that an added bead can only rotate a small angle around 2π/q = π/16 for q = 32.

In an experiment¹², a dsDNA recoiling from a 90-nm-wide and 100-nm-deep channel is estimated to encounter a force $\hat f_{\mathrm{R}}^{{\mathrm{(exp)}}} \approx 0.22$ pN. It is slightly larger than the value $\hat f_{\mathrm{R}}^{{\mathrm{(SC)}}} \approx 0.18$ pN for a strip of a slightly greater width 110 nm calculated above. In an experiment¹³, a T2 phage dsDNA recoils from an array of nanopillars 35 nm in diameter with a center-to-center spacing of 160 nm. The experimentally estimated recoiling force $\hat f_{\mathrm{R}}^{{\mathrm{(exp)}}} \approx 0.04$ pN in that array was bounded by the force $\hat f_{\mathrm{R}}^{{\mathrm{(SC)}}} \approx 0.12$ pN in a 2D channel of the same width estimated by formula (5) (Supplementary Note 2). This upper bound is reasonable because the confinement of an array is much weaker than that of a channel of the same size. In an experiment¹⁵, a granular chain above a vibrating platform escapes from a channel. The recorded recoiling force follows exactly the same relation f_R ~ −ln(w − l) as in Fig. 4a. In another experiment¹⁴, when a dsDNA straddling a nanoslit is entropically pulled out of the slit, it undergoes (i) a tug-of-war scenario, followed by (ii) a recoiling-retraction scenario. The force, $\tilde f_{{\mathrm{(i)}}}^{{\mathrm{(exp)}}}$, in (i) is similar to the above $\tilde f_{\mathrm{T}}^{{\mathrm{(SC)}}}$, which is counterbalanced by the entropic elasticity of the stretched dsDNA strand inside the nanoslit. The force, $\tilde f_{{\mathrm{(ii)}}}^{{\mathrm{(exp)}}}$, in (ii) is closer to our $\tilde f_{\mathrm{R}}^{{\mathrm{(SC)}}}$, which are dragged by the friction force and the optical tweezer (Fig. 2b), respectively. For a slit 110 nm in height, the forces extracted from the experiment, $\left( {\hat f_{{\mathrm{(i)}}}^{{\mathrm{(exp)}}},\hat f_{{\mathrm{(ii)}}}^{{\mathrm{(exp)}}}} \right)$ ≈ $(0.17,0.30)$ pN, are not far from $\left( {\hat f_{\mathrm{T}}^{{\mathrm{(SC)}}},\hat f_{\mathrm{R}}^{{\mathrm{(SC)}}}} \right)$ ≈ $(0.31,0.28)$ pN of a tightened chain estimated in the previous paragraph. The relation $\hat f_{{\mathrm{(ii)}}}^{{\mathrm{(exp)}}} \approx \, \hat f_{\mathrm{R}}^{{\mathrm{(SC)}}}$ indicates that the allowed rotational angle for beads inside the slit is around π/16. The ordering $\hat f_{{\mathrm{(i)}}}^{{\mathrm{(exp)}}} \, < \, \hat f_{\mathrm{T}}^{{\mathrm{(SC)}}}$ suggests the existence of a non-configurational-entropy effect in $\hat f_{{\mathrm{(i)}}}^{{\mathrm{(exp)}}}$. Indeed, in addition to increasing the configurational entropy, strong chain stretching may also decrease the microstate number inside a bead or deform the bead. The subsequent increase of free energy will weaken $\hat f_{{\mathrm{(i)}}}^{{\mathrm{(exp)}}}$, but not $\hat f_{\mathrm{T}}^{{\mathrm{(SC)}}}$, leading to $\hat f_{{\mathrm{(i)}}}^{{\mathrm{(exp)}}} \, < \, \hat f_{\mathrm{T}}^{{\mathrm{(SC)}}}$. Despite that discrepancy, these two forces are of the same order.

More generally, if a single-stranded DNA (ssDNA) of l_p ≈ 0.75 nm²³, partly confined in a 2D nanochannel or a 3D circular nanotube of width 1.6 nm and κ = ∞ pN nm⁻¹, is modeled by an SC comprising beads of three nucleotide bases²⁴, one obtains l = l_K ≈ 1.5 nm and d ≈ 0.1 nm. This yields $\hat f_{\mathrm{R}}^{{\mathrm{(SC)}}} \approx 11.32$ pN for the nanochannel and 21.76 pN for the nanotube (Supplementary Note 2), which are even larger than the drag force, 5 ~ 6 pN, of a myosin. The increase in the force magnitude from dsDNA to ssDNA is a consequence of the shortened Kuhn length and the narrowed channel width. Owing to the physical limits on these two lengths, 20 pN seems to be close to the maximum entropic force one can observe in nature for a recoiling polymer. For the examples of soft channels, consider a 120-nt ssDNA oligomer²⁵ threaded through an α-hemolysin, which is 10 nm long and has an inner size varying between 1.4 and 4.1 nm¹. If this system is modeled by an NSC of 40 Kuhn segments of l ≈ 1.5 nm²⁴ and threaded through a circular tube of the same width as l, with a hypothesized effective stiffness κ = 1 ~ 10² pN nm⁻¹, then the maximum tension force is $\hat f_{\mathrm{T}} \approx 1.47\sim 14.12$ pN (Supplementary Note 2). This analysis provides an instantaneous check for the consistency between the hypothesized d, κ, and forces.

Discussion

The experimental measurement of polymer entropic forces is challenging. The currently reported “measured” force magnitudes are all indirectly inferred from certain force-velocity or force-extension relations. The observed velocity and extension can be affected by several factors, including interfacial friction, Debye length, osmotic force, dye and salt concentrations, and nature of solvent. Even for the more fundamental polymer characteristics, such as persistence length or width of DNA and RNA, the experimentally measured values are often not unique. Thus, some experimentally measured entropic force was considered an “effective” one¹³. With these technical difficulties and system varieties, a coincidence close to 100% between a theoretically predicted force and an experimentally measured one could be accidental, when these forces are as small as a few piconewtons. However, if coincidences of the same order occur concurrently in several systems, as in the above-mentioned examples, the actual force magnitudes are probably not much different from the experimentally and theoretically determined ones.

The formalism proposed in this work overcomes the problem of directly solving partition functions and provides a less-time-consuming reference-based algorithm to assess entropic contributions. This approach is especially simple when a polymer system can be modeled by an ideal confined chain with γ = 1. Beyond that regime, such as in the de Gennes or Odijk regime, the forces obtained from Eqs. (3) and (5) are as complex as those extracted by other half-analytical approaches (Supplementary Note 3). If other specific interactions, such as the angular and dihedral force-fields, are not coarse-grained in the BUs of a chain model, their entropic contribution has to be derived case by case, as reflected in the widened channel width in Eq. (8), or empirically measured, as the α_o in Fig. 3c. Nevertheless, the forces of a nearby system with γ = 1, calculated by Eq. (5), can readily provide an upper or a lower bound for the desired systems with γ ≠ 1, as the pillar array discussed above. To sharpen these force bounds, the current formalism further serves as a proper framework, for instance, for selecting more sophisticated UBs C_I and C_O or for performing perturbation approaches on Eq. (5) around γ = 1.

Methods

Hamiltonian

For a chain of N identical beads in the bead-spring model in Fig. 2b, let m and l be the mass and the size of a bead, respectively, whereas x_i and ${\dot{\bf x}}_i$ be the position and the velocity of the ith bead, respectively. The Hamiltonian of the chain is H = E_K + E_C + E_V + E_O + E_W, with the kinetic energy $E_{\mathrm{K}} = \mathop {\sum}\nolimits_{i \, = \, 1}^N {\kern 1pt} m{\dot{\bf x}}_i^2{\mathrm{/}}2$, the interaction between consecutive beads $E_{\mathrm{C}} = \mathop {\sum}\nolimits_{i \, = \, 1}^{N - 1} {\kern 1pt} k_{\mathrm{C}}\left( {\left| {{\bf{x}}_i - {\bf{x}}_{i + 1}} \right| - l} \right)^2{\mathrm{/}}2$, the excluded volume interaction between non-consecutive beads $E_{\mathrm{V}} = \mathop {\sum}\nolimits_{i,j = 1{\kern 1pt} (i \, > \, j)}^N {\kern 1pt} k_{\mathrm{V}}\left( {\left| {{\bf{x}}_i - {\bf{x}}_j} \right| - l} \right)^2\sigma _{ij}{\mathrm{/}}2$, the bead-channel interaction $E_{\mathrm{W}} = \mathop {\sum}\nolimits_{i = 1}^N {\kern 1pt} V\left( {\eta _i} \right)$, and the interaction between the last bead and the optical tweezer E_O = k_O|x_N − z|²/2. Here, the natural length of the spring between two consecutive beads is the same as the bead size l. The value σ_ij = 1 for |x_i − x_j| ≤ l and 0 for |x_i − x_j| > l. The position z denotes the location of the optical tweezer. The potential $V(\eta _i) = \kappa \eta _i^2{\mathrm{/}}2$ when the ith bead penetrates a distance η_i into a channel wall (Fig. 2d). Therein, k_C, k_V, k_O, and κ are the force constants in E_C, E_V, E_O, and E_W, respectively. In this system, there is no facial friction and the diffusion coefficient is position independent. For an SC, the bending angle formed by three consecutive beads lies within [0, 2π/3].

Penetration effects

Since the channel is narrow, the slight lateral motion of a bead is less affected by its motion along the channel axis. Therefore, the probability density of finding a bead at some lateral position y follows the Boltzmann distribution $e^{ - U(y)/k_{\mathrm{B}}\tilde T}$, which is depicted by the green area in the upper part of Fig. 2d. Here, the potential well U(y) consists of a zero-potential area flanked by two walls of the form of the above V(η). If that distribution has the same area as an effective uniform distribution (magenta rectangle) of the same height h and of a larger width d + d_e, the equality in area implies $2{\int}_0^\infty h{\kern 1pt} {\mathrm{exp}}\left( { - \kappa \eta ^2{\mathrm{/}}\left( {2k_{\mathrm{B}}\tilde T} \right)} \right)d\eta + hd$ = $h\left( {d + d_{\mathrm{e}}} \right)$. In analogy, for a 3D circular tube, the equality in volume leads to ${\int}_0^\infty {\kern 1pt} 2\pi (\eta + d{\mathrm{/}}2)h\,{\mathrm{exp}}\left( { - \kappa \eta ^2{\mathrm{/}}\left( {2k_{\mathrm{B}}\tilde T} \right)} \right)d\eta$ + $h(d{\mathrm{/}}2)^2\pi$ = $h(d{\mathrm{/}}2 + d_{\mathrm{e}}{\mathrm{/}}2)^2\pi$. Therein, d_e is the mean penetration depth into two strip walls in Fig. 2b, c or into the circular tube wall, which is given by

$$d_{\mathrm{e}} = \left\{ {\begin{array}{*{20}{l}} {\sqrt {2\pi T\epsilon {\mathrm{/}}\kappa } ,} \hfill & {{\mathrm{for}}\,2{\mathrm{D}}\,{\mathrm{strips}};} \hfill \\ {\sqrt {d^2 + B} - d,} \hfill & {{\mathrm{for}}\,{\mathrm{3D}}\,{\mathrm{circular}}\,{\mathrm{tubes}},{\kern 1pt} } \hfill \end{array}} \right.$$

(8)

with $\epsilon$ defined in Eq. (1) and $B \equiv 8\epsilon T{\mathrm{/}}\kappa + 2d\sqrt {2\pi \epsilon T{\mathrm{/}}\kappa }$. Although the above soft potential U can generally be interpreted as a soft channel or a soft bead, the latter requires a more subtle model with a varying bead shape during bead-wall collision, which is not considered here.

Langevin dynamics

With the above Hamiltonian H, the ith bead follows a Langevin equation $m{\ddot{\bf x}}_i = - \nabla _{{\rm x}_i}H - {\mathrm{\Xi }}{\dot{\bf x}}_i + {\mathbf{\zeta }}_i$, where $\nabla _{{\bf{x}}_i}H$ is the derivative of H with respect to x_i, Ξ denotes the friction coefficient, and ζ_i stands for a random force²⁴. That force is Gaussian and white and satisfies the fluctuation-dissipation theorem, with 〈ζ_i(t)〉 = 0 and $\left\langle {{\mathbf{\zeta }}_i(t){\mathbf{\zeta }}_j^{\mathrm{T}}(t\prime )} \right\rangle$ = $4{\mathrm{\Xi }}k_{\mathrm{B}}\tilde T\delta (t - t\prime )\delta (i - j)$, where the superscript T represents the transpose. Since the strength of the above random force changes with temperature, the diffusion of beads is temperature dependent as well. To study general real systems, the above equation can be reduced to a dimensionless one, ${\tilde{m}} {\ddot{\tilde{\mathbf{x}}}}_{i} = - {\nabla}_{\tilde{\mathbf{x}}}{\tilde{H}} - {\tilde{\Xi}} {\dot{\tilde{\mathbf{x}}}}_{i} + {\tilde{\zeta }}_i$, with the dimensionless quantities: $\tilde m = m{\mathrm{/}}M$, ${\tilde{\bf x}}$ ≡ x/l, $\tilde t \equiv t{\mathrm{/}}\tau$, $\tilde H \equiv \left( {\tau ^2{\mathrm{/}}\left( {Ml^2} \right)} \right)H$, $\tilde k_{\mathrm{C}} \equiv \left( {\tau ^2{\mathrm{/}}M} \right)k_{\mathrm{C}}$, $\tilde k_{\mathrm{V}} \equiv \left( {\tau ^2{\mathrm{/}}M} \right)k_{\mathrm{V}}$, $\tilde \kappa \equiv \left( {\tau ^2{\mathrm{/}}M} \right)\kappa$, ${\tilde{\mathrm \Xi }} \equiv (\tau {\mathrm{/}}M){\mathrm{\Xi }}$, and ${\tilde{\mathbf \zeta }} \equiv \left( {\tau ^2{\mathrm{/}}(Ml)} \right){\mathbf{\zeta }}$ in units of some convenient mass M and time τ²⁴. However, to test the consistency between the force formula (5), the JE and RF approaches, and the analytical results in Table 1, it is sufficient to consider some simple parameter values for the original Langevin equation. In this study, we take $(l,m,\Xi ,k_{\mathrm{C}},k_{\mathrm{V}},k_{\mathrm{O}},\kappa {\mathrm{/}}\epsilon )$ = $(1,1,1,10^4,10^4,10^4,0\sim 10^4)$, where units are not specified.

Jarzynski equality

Let $\tilde W$ be the work done by f_drag to pull a bead of length l into the channel in Fig. 2b. Owing to fluctuations, the $\tilde W$ in different pulling realizations will be different, which form a work distribution. According to the JE¹¹, the free energy change, $\Delta \tilde F$, per shifted l is related to $\tilde W$ by $e^{ - {\mathrm{\Delta }}\tilde F/k_{\mathrm{B}}\tilde T} = \left\langle {e^{ - \tilde W/k_{\mathrm{B}}\tilde T}} \right\rangle$, where the ensemble mean 〈⋅〉 is averaged over the whole work distribution. Therefore, the mean force to counterbalance f_drag is the free energy change per shifted bead $\tilde f = - {\mathrm{\Delta }}\tilde F{\mathrm{/}}l = \left( {k_{\mathrm{B}}\tilde T{\mathrm{/}}l} \right){\mathrm{ln}}\left( {\left\langle {e^{ - \tilde W/k_{\mathrm{B}}\tilde T}} \right\rangle } \right)$, which has a dimensionless version $f = \tilde fl{\mathrm{/}}\epsilon = T\,{\mathrm{ln}}\left( {\left\langle {e^{ - W/T}} \right\rangle } \right)$, with the dimensionless work $W = \tilde W{\mathrm{/}}\epsilon$, where $\epsilon$ is defined in Eq. (1). The f measured in our numerical recoiling experiments should be the $f_{\mathrm{R}}^{{\mathrm{(NSC)}}}$ derived in Eq. (1) if the change of internal energy is negligible during pulling, which occurs when the channel has a hard-wall or its soft wall is replaced by an effective hard-wall.

Recursion formulas

A recursion formula can be used to count the configuration number of a chain of n beads based on that of a chain of n − 1 beads. For a one-dimensional NSC consisting of n rods of unit length, let $N_x^n$ be the configuration number when one end of the chain is anchored to the origin and the other end is located at x between −n and + n, where x is an integer. It follows a simple recursion relation $N_x^n = N_{x - 1}^{n - 1} + N_{x + 1}^{n - 1}$ for x = −n, −n + 1, …, n − 1, n, where $N_x^n = 0$ for |x| > n. The solutions of this equation are the binomial coefficients $N_x^n = C_{(n + x)/2}^n$ when x = −n, −n + 2, …, n − 2, n and $N_x^n = 0$ elsewhere. With those $N_x^n$, the total number of the chain configurations of n rods is ${\mathrm{\Omega }}_n = \mathop {\sum}\nolimits_{x = - n}^n {\kern 1pt} N_x^n = 2^n$ and the corresponding configurational entropy is S = k_B lnΩ_n = nk_B ln 2. For a chain of n beads of size l in a high-dimensional off-lattice space, the above RF can be generalized to $N_{\bf{r}}^n = {\int} N_{{\bf{r}}\prime }^{n - 1}\delta \left( {\left| {{\bf{r}}\prime - {\bf{r}}} \right| - l} \right)d{\bf{r}}\prime$, for which the total number of the chain configurations, ${\mathrm{\Omega }}_n = {\int} N_r^nd{\bf{r}}$, is an integration over all end-to-end displacement vectors r of a chain of n beads. To count the configurations of a macrostate of a chain, specified by some (n_I, n_O), in Fig. 2b, first calculate the configuration number ${\mathrm{\Omega }}_{n_{\mathrm{I}}}$ $\left( {{\mathrm{\Omega }}_{n_{\mathrm{O}}}} \right)$ of a chain segment of n_I (n_O) beads inside (outside) the channel when one segment end is anchored to a point on the cross-section of the channel opening. Summing up the product ${\mathrm{\Omega }}_{n_{\mathrm{I}}}{\mathrm{\Omega }}_{n_{\mathrm{O}}}$ over all different points on that cross-section yields the total configuration number needed for calculating the entropy of the whole chain. Notice that although the RF is able to count the chain configurations within a channel, it cannot reflect the stiffness effect of the channel, unless we use Eq. (8) to replace a soft channel by an effective wider hard channel.