Introduction

Electric charge and spin are intrinsic quantum properties of electrons and, so far, are the basis of electronics. Likewise, charge carriers in two-dimensional (2D) hexagonal crystals have an additional electronic degree of freedom, the valley-index, associated to degenerate bands at the inequivalent K and K’ points in the Brillouin zone (BZ). The valleytronic field proposes the creation of a new class of dissipationless electronic devices based on the manipulation of the valley-indices like valley filters and valley valves1,2,3,4. One interesting 2D crystal with useful features for valleytronics is bilayer graphene (BLG). The material is a tunable semiconductor and contains low lattice defects that prevents inter-valley scattering. Moreover, it holds topological properties when its inversion symmetry is broken by the application of transverse electric field. In this condition, a topological invariant is defined, the integer index called Chern number, with important implications on the quantum properties of BLG. For instance, it gives rise to the observation of the valley Hall Effect in graphene5,6,7, which is a topological phase where gapless edge states labeled by opposite valley-indices counter-propagate at the boundaries of the insulating bulk8. One important aspect of the Chern number in BLG is that its sign depends either on the valley-index as well as on the sign of the band gap (interlayer energy difference), which can be changed by inverting the electric field direction or by inverting the stacking order of the material1,8,9,10,11,12. Such control of the band gap of BLG allows the design of topological one-dimensional (1D) interfaces between regions with opposite Chern numbers—a domain wall (DW)—where strongly confined edge states, called kink states, are predicted1,9,10,11,12. The kink states have several useful features for valleytronics. There are two spin-degenerate kink states per valley and they are chiral, meaning that the propagation direction in the DW is defined by the valley-index. Such chiral edge states are robust for almost any kind of boundary configurations of the domains (except perfect armchair) and the topological protection inhibits backscattering from smooth disorder potentials10. If valley-mixing is suppressed in the DW, such as by reducing the short-range disorder like edge defects and substrate corrugation, a dissipationless electrical conduction with conserved valley-index is expected.

To date, there are two routes to investigate kink states in BLG flakes. One exploits DWs formed along stacking faults (AB-BA boundaries). However, so far, such DWs have been only produced in BLG placed on top of rough silicon dioxide (SiO2) substrates13,14 showing limited mean free path. The other possible way is by designing complex gate-controlled topological channels, which requires a very precise alignment of the bottom and top gates15,16. Here, we observe strong evidence of kink states in high-quality DW formed at the curved boundary of a folded bilayer graphene (folded-BLG). Such compact geometry provides several advantages: the DW is atomically narrow, a variety of techniques enable the controlled production of such folded structures17,18 and this architecture simplify the fabrication of valley-filters and valley-valves using fewer metallic gates. Moreover, we show that the topologically protected electronic transport is robust up to room temperature and shows a mean free path (MFP) up to the length of 20 μm at low temperatures, which is one of the longest MFP ever reported in a DW.

Results

Device preparation

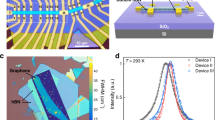
To introduce our valleytronic device, in the Fig. 1a we show a cartoon with some typical components of the device such as the folded-BLG, the metallic gates, and the dielectrics. The folded-BLG is encapsulated in between two hexagonal boron nitride (hBN) crystals. The bottom hBN is placed on top of a SiO2/Si++ wafer, such that the Si++ is a highly p-type doped silicon used as a backgate. The top hBN is covered by a metallic gate composed by Cr/Au. To illustrate our fabrication process, in the Fig. 1b we show a typical heterostructure of a naturally folded-BLG on top of a flat hBN crystal, before patterning the metallic contacts (fabrication details are discussed in Methods, Supplementary Figure 1 and Supplementary Figure 2). The dashed lines in this picture indicate the position of such electric terminals: two of them stand on the curved boundary and two of them are placed on the etched edges. Figure 1c shows a false-color atomic force microscopy (AFM) topography measurement of device 1. Here, we present device 1 after the cleaning process and before encapsulating with a top hBN crystal. From this measurement, we see the high quality and cleanness of the device, which prevents short-range scattering along the 1D channel. These good conditions are provided either by the flat surface of the hBN crystals as well as by the efficacy of the mechanical cleaning method to remove contamination from the fabrication process.

Fig. 1
figure 1

Valleytronic device based on a folded bilayer graphene. a Components of the folded bilayer graphene (folded-BLG) valleytronic device. The folded-BLG is sandwiched by hexagonal boron nitride (hBN) crystals that separate the material from the metallic gates. Under a transverse electric field, the bulk behaves likely semiconductor with band gap and a topological 1D conducting channel forms at the curved boundary, where the valley-index defines the direction of propagation. b Optical image of a folded-BLG transferred on top of the bottom hBN flake. Dashed lines indicate the position of the electric terminals. Scale bar: 4 μm. c A false-color atomic force microscopy (AFM) image of device 1 before the transference of the top hBN. The AFM measurement reveals that the curved boundary is free from contamination of fabrication processes. Scale bar: 1 μm. d Electrostatic potential energy (Δ/2) of the bilayer graphene (BLG) layers, calculated relative to the center of each BLG. The layer energies reverse sign from the bottom BLG to the top BLG and vanish across the curved boundary, where the electric field is parallel to the layers. This variation of the electrostatic potential energy enables the formation of a domain wall at the curved boundary. e Illustration of the pair of kink states localized at inequivalent points K and K’ in the Brillouin zone of BLG, having opposite group-velocities for different valleys. In the domain wall, these edge states propagate in opposite one-dimensional directions due their chiral nature

Full size image

Kink states in a folded bilayer graphene

In the Fig. 1d, we present a scheme that describes the electrostatic conditions imposed to the folded-BLG by application of gate potential. The transverse electric field breaks the inversion symmetry of each BLG (bottom sheet and top sheet of the folded-BLG), which leads to an energy band gap (Δ)19 defined as the layer energy difference between the top graphene layer and the bottom graphene layer of BLG. At the bottom BLG sheet, the top graphene layer acquires a relative energy +Δ/2, calculated relative to the center of the sheet, and the bottom layer acquires a relative energy −Δ/2. This electrostatic energy distribution inverts in the other BLG sheet on top. The bottom graphene layer (former top layer) now acquires a relative energy −Δ/2 and the top layer (former bottom layer) acquires a relative energy +Δ/2. Then, the band gap inverts its sign from the bottom to top BLG and, consequently, a valley at these different BLGs holds opposite Chern numbers. In this condition, the curved boundary of the folded-BLG transforms into a DW. We use the model proposed by Martin et al.1 to demonstrate the emergence of kink states in such topological folded structure (Supplementary Figure 3 and Supplementary Note 1). In the Fig. 1e, we illustrate the pair of spin-degenerate kink states localized at the points K and K’ of the BZ, having opposite group-velocities at different valleys. These chiral edge states propagate in the curved boundary along a 1D direction defined by the valley-index, as illustrated in Fig. 1a.

Two-terminal measurements

One of the main achievements of this work is the measurement of a quantization of the two-terminal resistance (R) along the curved boundary near of the ballistic resistance R = 6.45 kΩ (or R = e2/4h) at B = 0 T and T = 1.2 K. Such result is a remarkable evidence of kink states, since the conductance of the 1D channel is governed by a ballistic transport regime related to a pair of chiral edge states spin-degenerated1,9,10. This result is presented in Fig. 2, which shows raw data of R as a function of the backgate voltage (VBG) and the topgate voltage (VTG) measured at electric contacts placed along the etched edge (Fig. 2a) and along the curved boundary (Fig. 2b). Both measurements exhibit a diagonal line that shows a strong dependence of resistance with gate potentials. Along these diagonal lines, the electrostatic condition defined by the gate potentials set zero charge in the BLGs, called the charge neutrality point (CNP). The resistance at such diagonal lines are defined as follows: for the electric measurements realized on the etched edge it will be called REE,CNP and for the electric measurements realized on the curved boundary it will be called RCB,CNP. A better comparison of REE,CNP and RCB,CNP is present in Fig. 2c, where we plot R as a function of the displacement field D, obtained from the data showed in Fig. 2a, b. We converted the gate potentials to displacement field with the following formula: D = (CTGVTG–CBGVBG)/ε0, where CTG and CBG are, respectively, the capacitances per unit of area and charge of the top capacitor and bottom capacitor, and ε0 is the vacuum permittivity. From data present in Fig. 2c we note that the monotonic increasing of REE,CNP with D reflects a tunable band gap caused by the broken inversion symmetry of BLGs20,21. In contrast, the RCB,CNP saturates near of the ballistic resistance R = h/4e2 for |D|>1.6 V nm−1. This saturation of the resistance reveals that the DW formed at the curved boundary becomes electric isolated from the bulk of the folded-BLG and a ballistic transport regime governs the carrier motion at this 1D region. The quantization of resistance close to the ballistic resistance show a robust valley transport, with backscattering strongly inhibited by the lack of short-range disorder along the channel.

Fig. 2
figure 2

Two-terminal electronic measurements: Evidence of a topological valley transport in the curved boundary of the folded bilayer graphene (folded-BLG). a and b Two-terminal electrical measurements of resistance (R) vs VTG vs VBG in the etched edge (contacts 1–3) and curved boundary (contacts 1–2), respectively, at T = 1.2 K and B = 0 T. The insets show each particular measurement configuration. c R as a function of displacement field (D) from data showed in the Fig. 2a, b. The resistance at the etched edge, REE,CNP, monotonically increases with D indicating a semiconducting regime with a band gap. For sufficient electric insulation of the bulk (achieved at high D) the resistance at the curved boundary, RCB,CNP, saturate close to the ballistic resistance R = h/4e2, an evidence of kink states and the suppression of backscattering in this 1D conducting channel

Full size image

The strong suppression of backscattering in the DW formed along the curved boundary leads to a long MFP. We use the Landauer-Büttiker formula22 R = R0(1 + L/LMFP) to calculate the MFP of the ballistic channel in our two devices. Here, LMFP is the MFP, R0 = h/4e2 is the ballistic resistance and L is the length of the channels: L = 1 μm for device 1 and L = 1.75 μm for device 2 (Supplementary Figure 4 and Supplementary Note 2). As the experiment shows a resistance close to R = e2/4h, we neglected any other residual resistances in this channel. The calculated MFP of the channels are: LMFP ∼ 20 μm for device 1 and LMFP ∼ 17 μm for device 2. Such long MFP show that the DW formed at the folded-BLG is comparable to the best topological channels created by gate-confinement15,16 and at least, two-orders higher than the MFP reported in a DW of BLG on SiO213.

Four-terminal measurements

Further details about the mechanisms of conduction in the folded-BLG are obtained by using a four-terminal electronic configuration. In the Fig. 3, we show the raw data of the longitudinal resistance (Rxx) as a function of the VBG and VTG measured at contacts placed along the etched edge (Fig. 3a) and the curved boundary (Fig. 3b). Again, both measurements show distinct diagonal lines where the resistance strongly depends on the gate potential. These dependence are better visualized in Fig. 3c, where we plot only the longitudinal resistances along the diagonal line as a function of D. Such resistances are called \(R_{{\mathrm{xx}}}^{{\mathrm{EE,CNP}}}\) for the electric measurements realized at the etched edge and \(R_{{\mathrm{xx}}}^{{\mathrm{CB,CNP}}}\) for the electric measurements performed at the curved boundary. We note that similarly to the two-terminal measurements, \(R_{{\mathrm{xx}}}^{{\mathrm{EE,CNP}}}\) continuously increase with the displacement field. It changes from \(R_{{\mathrm{xx}}}^{{\mathrm{EE,CNP}}}\)∼1 kΩ up to \(R_{{\mathrm{xx}}}^{{\mathrm{EE,CNP}}}\)∼12 kΩ, an expected behavior related to the tunable semiconducting nature of the BLGs by the action of the transverse electric field. On the other hand, we measure a different trend at the curved boundary channel. We observe that \(R_{{\mathrm{xx}}}^{{\mathrm{CB,CNP}}}\) decreases with D, changing from \(R_{{\mathrm{xx}}}^{{\mathrm{CB,CNP}}}\)∼400 Ω down to \(R_{{\mathrm{xx}}}^{{\mathrm{CB,CNP}}}\)∼60 Ω for high D. Such small longitudinal resistance is a distinct feature of a ballistic transport regime in a channel with quasi-absence of backscattering. It provides another important evidence that a ballistic charge motion was achieved at the DW in the curved boundary.

Fig. 3
figure 3

Four-terminal electronic measurements and influence of temperature on the kink states. a and b Four-terminal raw data of the longitudinal resistance RXX as a function of VTG and VBG in the etched edge and curved boundary, respectively. The insets show how the electronic measurements are performed. c RXX as a function of D when the bilayer graphenes are at the charge neutrality point (CNP). The resistances measured along the etched edge, \(R_{{\mathrm{xx}}}^{{\mathrm{EE,CNP}}}\), are represented by the red squares and the resistances measured at the curved boundary, \(R_{{\mathrm{xx}}}^{{\mathrm{CB,CNP}}}\), are represented by the blue circles. \(R_{{\mathrm{xx}}}^{{\mathrm{EE,CNP}}}\) increases by one order of magnitude, while under same electrostatic conditions \(R_{{\mathrm{xx}}}^{{\mathrm{CB,CNP}}}\) decreases down to a few tens of ohms, an expected behavior for the longitudinal resistance of a channel on the ballistic regime. d and e RXX in the etched edge and curved boundary, respectively, as a function of VTG for a fixed VBG = −86 V, when the temperature of the system changes from T = 1.2 K up to T = 300 K. Such measurements reveals that different transport mechanisms governs the electric conduction at the etched edge region and at the curved boundary channel

Full size image

Temperature dependence

Next, we investigate the effect of temperature on the electric conduction at the different regions of the folded-BLG in a four-terminal configuration (Details about the temperature dependence of two-terminal measurements are shown on Supplementary Figure 5 and Supplementary Note 3). In Fig. 3d, e we show measurements of RXX as function of VTG, with the backgate voltage fixed at VBG = −86 V, while we changed the temperature of the system from T = 1.2 K up to room temperature (T = 300 K). At low temperatures, the electric conduction in the curved boundary is governed by a ballistic transport regime, revealed by the measurement of a small longitudinal resistance. At same electrostatic condition the BLGs at the etched edge reveal a semiconducting regime. As showed in Fig. 3d, the elevation of temperature in the system let to a decreasing of RXX measured along the etched edge. Clearly, it is the expected behavior of a semiconducting regime dominated by thermally activated processes21. A different feature is observed at the curved boundary, as illustrated in Fig. 3e. The longitudinal resistance of such region increases when temperature goes up. Such behavior revels that temperature promotes valley-mixing by phonon scattering and enhances the scattering of edge states localized at the curved boundary channel to BLG states that may conduct due to charge inhomogeneity. These measurements on different temperatures give a third evidence that chiral edge states at the curved boundary let to a different electronic transport regime when compared to the other regions of the folded-BLG.

Discussion

We perform a set of two-terminal, four-terminal measurements, and temperature dependence to investigate the mechanisms of conduction at the curved boundary and at the bulk of a folded bilayer graphene. We observed that under an external electric field, the bulk becomes a semiconductor with tunable band gap while a topological domain wall forms at the curved boundary. At such a one-dimensional channel, we have evidence of a dissipationless transport mechanism governed by topological edge states—kink states—rather than ordinary ones. The two-terminal electric resistance saturates near of the ballistic resistance R = h/4e2. It shows that both spin and valley are well-preserved quantum numbers. In addition, the four-terminal measurements show the resistance dropping down to a few tens of ohms, confirming the ballistic nature of the electric conduction. On the other hand, the electrical measurements performed along the bulk show that the resistance of two bilayer graphenes placed one on top of the other continuously increases as a function of the electric field, behaving quite similarly gate tunable semiconductors like single bilayer graphene. Finally, from the electrical measurements as a function of temperature, we confirm the different behavior of the bulk states and chiral states of the folded edge. The bulk shows electronic conduction governed by a thermo-activated process typical of semiconductors while the resistance along the curved boundary shows temperature dependence similar to metallic materials, showing that phonons enhance the scattering of conducting edge states.

Our electrical measurements in one valleytronic device show strong evidence of the different mechanisms of conduction along the curved boundary and conduction along the bulk. In order to find more evidence of the topological nature of edge states on the curved boundary, we fabricated a second valleytronic device. At such device, we also observe the two-terminal electric resistance saturating near of the ballistic resistance R = h/4e2 under high electric fields. Such experiments performed at this second device provide further evidence that the topological edge states lie at the curved boundary of a folded bilayer graphene. Finally, we note that the electric resistance of the gapped bulk is smaller than typically resistances observed in single bilayer graphene under similar electric fields. As the bulk and the curved boundary are physically connected, one expects that a small bulk resistance could lead to more scattering of kink states to bulk states. However, our two-terminal resistances on both devices are very close to the ballistic resistance of R = h/4e2 at the curved boundary. It confirms a strong suppression the scattering from kink states to bulk states. We believe that future microscopic measurements could bring more explanation about the nature of such strong protection of the edge conduction.

In summary, our findings show the existence of topological chiral edge states in a domain wall formed at the curved boundary of a folded bilayer graphene. We observe a strong suppression of valley scattering at this high-quality one-dimensional channel that leads to a long-range ballistic conduction at zero-magnetic fields. Such platform contains elements to promote the development of dissipationless valleytronic devices and provides a route to investigate graphene-based superconducting effects23,24 as well as Luttinger liquid interactions25.

Methods

The heterostructures of folded bilayer graphene (folded-BLG) sandwiched between hexagonal boron nitride (hBN) crystals are prepared with the following steps: we first employed the mechanical cleavage method to separate few layers of graphene from graphite flakes on top of a polymeric film of methyl methacrylate (MMA 495 C4). Next, we selected self-folded BLG samples and we transferred such flakes to top of clean hBN crystals supported on a 285-nm thick SiO2/Si++, where Si++ is a highly doped Si wafer used as a metallic backgate. The fabrication of devices is divided into three main steps. First, we fabricated the electric terminals by using conventional electron beam lithography and thermal metalization of Cr/Au (1 nm/40 nm). We also used electron beam lithography and etching processes with oxygen plasma to define and shape our devices. Next, we used a mechanical cleaning method with an atomic force microscopy (AFM) probe26 to remove any contamination of fabrication processes from the surface of the folded-BLG. We finished the fabrication by covering the device with another hBN flake and patterning a metallic top-gate. The electronic measurements are realized inside a cryogen system that enables the application of magnetic field up to B = 7 T. In our electronic measurements we normally operated at T = 1.2 K and we performed the measurements using a low-frequency (f = 17 Hz) Lock-in technique. In the two-terminal measurements we applied a constant bias (Vbias = 1 mV) between the contacts and we measured it electric current. The conductance is calculated by using the formula G = I/V. In the four-terminal measurements, a constant electric current (I = 100 nA) is applied between two electric terminals and a longitudinal voltage (VXX) is measured in between the other electric terminals on the opposite side. The longitudinal resistance is calculated by using the Ohm’s law RXX = VXX/I.