Abstract
The magnetorotational instability (MRI) has long been considered a plausibly ubiquitous mechanism to destabilize otherwise stable Keplerian flows to support radially outward transport of angular momentum. Such an efficient transport process would allow fast accretion in astrophysical objects such as stars and black holes to release copious kinetic energy that powers many of the most luminous sources in the universe. But the standard MRI under a purely vertical magnetic field has heretofore never been directly measured despite numerous efforts over more than a decade. Here we report an unambiguous laboratory demonstration of the spring-mass analogue to the standard MRI by comparing motion of a spring-tethered ball within different rotating flows. The experiment corroborates the theory: efficient outward angular momentum transport manifests only for cases with a weak spring in quasi-Keperian flow. Our experimental method accomplishes this in a new way, thereby connecting solid and fluid mechanics to plasma astrophysics.
Similar content being viewed by others
Introduction
Understanding angular momentum transport in astrophysical disks comprises a long-standing enterprise, spanning planetary, stellar, black hole, galactic, and laboratory astrophysics. The challenge originated 250 years ago1,2,3 with enduring questions about how the angular momentum distribution within the solar system evolved from its original nebular gas4,5,6. In addition, luminous and jetted sources in the universe, including quasars, X-ray binaries7,8,9, pre-planetary nebulae10,11, and gamma-ray bursts12 are likely powered by the conversion of gravitational potential energy into kinetic energy and radiation, as matter accretes onto central engines13. Since accreting plasma typically originates far from the core of the potential well, conserving even a modest initial angular momentum during infall would prevent matter from reaching the engines. Angular momentum must be extracted much faster than microphysical diffusivities alone allow.
Enhanced transport is typically parameterized by a “turbulent viscosity”, allowing practical accretion disk models to be compared with observations14. What mechanisms supply enhanced transport and how to model it are long-standing physics problems of astrophysics15,16. A ubiquitous source of turbulence is thought to be the magnetorotational instability (MRI)17,18 as applied to accretion discs19,20,21,22: while purely hydrodynamic discs require a decreasing angular momentum gradient for linear instability, the MRI in a magnetohydrodynamic (MHD) disk requires only a radially decreasing angular velocity, so magnetized Keplerian disks of astrophysics should be unstable. Growth and saturation of the MRI are widely studied23,24,25,26,27,28,29,30.
The scientific method establishes scientific fact by corroborating theory with experiment, no matter how widely assumed the veracity of a theoretically calculated mechanism may otherwise be. As such, there are substantial efforts to demonstrate the MRI in the laboratory using differentially rotating liquid metals31,32,33 and plasma34, and even polymer fluids35,36 or an elastic beam37. Purely hydrodynamic flow experiments confirm the Rayleigh criterion for stability38,39. Measurements of the MRI in the standard setup with a purely vertical field in liquid metals are challenging, although recent evidence of related helical and azimuthal field MRI has been reported40,41. The result of ref. 32, for example, is now understood to result from boundary effects42. There is further optimism as boundary control improves43,44, but so far, none of these experiments have yet demonstrated the vertical MRI.
Here we take a different approach. We appeal to the known result that the dispersion relation of the MRI for an initially vertical magnetic field also characterizes the motion of two masses tethered by a weak spring16,22. The spring represents the magnetic field and the mass represents a parcel of MHD fluid. It has been speculated16 that this analogue might be experimentally testable in the laboratory, distinct from multi-tethered configurations that have been previously theoretically explored45,46,47.
Below we discuss the design and results from a new tethered ball experiment using the Princeton Taylor–Couette apparatus with water or Hydrodynamic Turbulence Experiment (HTX)48. We compare the radial motion of the ball for cases when the ball is untethered, weakly tethered, and strongly tethered. As predicted by the MRI mechanism, angular momentum is transported efficiently outward only in the cases with a weak spring in quasi-Keplerian flows. The experiment demonstrates a new way to use solid and fluid mechanics to study astrophysical processes in the lab.
Results
Theoretical model and predictions
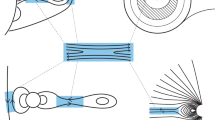
A Keplerian flow with a weak vertical magnetic field, Bz, subjected to perturbations within the horizontal plane (r, θ) exhibits the MRI. The minimalist MHD version of the equations depends only on the displacement of the field lines in the plane perpendicular to the initial magnetic field. Two masses tethered by a weak spring orbiting in a central potential15 then provide an analogue of this local instability, although the minimalist MHD MRI equations most directly correspond to the motion of a single mass tethered to a fixed point in a co-rotating frame16 (Fig. 1a vs. Fig. 1b).
Analogues of standard magnetorotational instability (MRI) in a purely vertical magnetic field. a Conventional MRI analogue using two equal masses (solid blue circles) tethered by a weak spring, under the influence of a central gravitational force. b The MRI analogue that we study in our experiment, depicted in the lab frame. A light mass (solid blue circle) is tethered to a fixed post (solid black circle) moving at angular speed Ω3 through a weak spring embedded in a Taylor–Couette flow, with inner cylinder and outer cylinder rotating at Ω1 and Ω2, respectively. The outward radial pressure gradient, sustained through the flow by the outer rigid wall in b, plays the role of the central gravity of a. If the inner tethered mass in a were much larger than the outer mass (both still being much less than the central mass), the equations for the MRI analogue depicted in the two figures would be identical
Physically, the linear phase of the instability interpreted in the context of Fig. 1b is expected to occur as follows: a light test mass is released from a post that is fixed to orbit with the flow at angular speed Ω3. The mass is tethered to a weak spring. If the spring is weak enough such that oscillation time is significantly longer than an orbit time but still strong enough to couple the post and mass over this time scale, the post will transmit angular momentum to the test mass moving the latter outward. If the spring is too strong, outward motion is limited by the spring tension, effectively retaining the ball as part of the post.
Mathematical correspondence between the minimalist MRI unstable MHD equations and those of tethered mass motion is simplest in local Cartesian coordinates x, y, z in a rotating frame with radius r = r0 + x and r0(θ − θ0) = y, with fixed point at x = y = 0. This point moves in the lab frame with angular velocity Ω3 ≡ Ω(x = 0) and the shear flow away from the fixed point in the rotating frame is given by \(r(\Omega - \Omega _3) \simeq xr\partial _r\Omega |_{r = r_0} = - xq\Omega _3\), with q ≡ −dlnΩ/dlnr. For the MHD case, when the centrifugal force is balanced by gravity and total pressure gradients are ignored, the local 2-D MHD momentum equations are
Dots indicate time derivatives; \(T = 2q\Omega _3^2\) is the coefficient of the tidal force per unit mass; the second terms on the left sides come from the Coriolis force; KA = (kvA)2, arises from magnetic tension where vA is the Alfvén speed associated with the vertical field.
Equations (1) and (2) also approximate motion of a mass tethered to a fixed point x,y = 0 by a spring with spring constant per unit mass KA, as in Fig. 1b. [For Fig. 1a this requires Ω = Ω3 and KA →2 KA16.] The Coriolis and tidal force terms arise whether supplied by gravity without pressure gradients, or by pressure gradients when the mass is embedded in a laboratory quasi-Keplerian (qK) flow without gravity. For initial displacements [x(t)eikz, y(t)eikz] and q < 0, the system is stable. But for q > 0, when KA < T, the MRI instability ensues. For KA = 0 (no spring), the right side of Eq. (2) vanishes and \(\mathop {x}\limits^{...} = \dot x(T - 4\Omega _3^2)\). The behavior then depends on q: the coefficient of \(\dot x\) changes sign at q = 2, and instability occurs only for q > 2—the Rayleigh unstable regime.
Although the Cartesian approximation captures the MRI mechanism, modeling the MRI mechanism with our our Taylor-Couette experiment requires inclusion of the non-linear curvature and damping terms. In cylindrical coordinates, the vector lab-frame equation of motion for a tethered mass in the rotating background flow is
where t is time; \({\mathbf{r}} = r\widehat {\mathbf{e}}_{\mathrm{r}}\) and \({\mathbf{r}}_{\mathrm{p}} = r_0\widehat {\mathbf{e}}_{{\mathrm{r}}_0}\) are the time-dependent position vectors of the ball and its launch locus (the post) respectively; \(\bar K\) is the spring constant divided by the mass of the ball; \({\mathrm{\Omega }}(r) \simeq \Omega _0(r/r_0)^{ - q}\), where q is a constant; and \({\mathbf{f}}_{\mathrm{c}} = - r\Omega ^2(r)\widehat {\mathbf{e}}_r\) is the centripetal force per unit mass on the ball, supplied by the background fluid pressure gradient transmitted from the outer wall. It is equal and opposite in magnitude to the centrifugal force per unit mass of the flow of the local rotating frame when the background flow is in equilibrium. Quantities D1 and D2 are the Stokes and Reynolds drag coefficients49 given by \(D_1 = 6\pi \rho _{\mathrm {H}_{\mathrm {2}}{\mathrm {O}}}\nu _{\mathrm {H}_{\mathrm {2}}{\mathrm {O}}}R/M\) and \(D_2 = C_D\pi \rho _{\mathrm {H}_{\mathrm {2}}{\mathrm {O}}}R^2/2M\), for water density \(\rho _{\mathrm {H}_{\mathrm {2}}{\mathrm {O}}}\), kinematic viscosity \(\nu _{\mathrm {H}_{\mathrm {2}}{\mathrm {O}}}\), test mass radius R, test mass M, and drag coefficient CD. Using R = 1.27 cm and neutrally buoyant test mass, D1 = 0.0284 s−1 and D2 = 15.0 m−1 in our experiments.
Since \({\mathrm {d}}\widehat {\mathbf{e}}_r/{\mathrm {d}}t = \dot \theta \widehat {\mathbf{e}}_\theta\), Eq. (3) contains both the azimuthal and radial components of the force equation. For initial values \(r(0) = r_0;\theta (0) = \theta _{\mathrm{p}}(0) = \theta _0;\dot r_{\mathrm{p}} = 0,\dot \theta _{\mathrm{p}} = \Omega _3\), (where θp is the angular coordinate of the post), the coupled equations for r(t) and θ(t) are given by
where we have used \(\widehat {\mathbf{e}}_r \cdot \widehat {\mathbf{e}}_{r_p} = {\mathrm{cos}}(\theta - \theta _0 - \Omega _3t)\) and \(\widehat {\mathbf{e}}_\theta \cdot \widehat {\mathbf{e}}_{r_p} = {\mathrm{sin}}(\theta - \theta _0 - \Omega _3t).\) Eqs. (4) and (5) reduce to Eqs. (1) and (2) in the linear limit.
For realistic parameters, the D1 term is small. In the linear regime, the D2 term also does not contribute and Eqs. (4) and (5) then predict runaway displacement in the usual MRI unstable regimes, namely \(0 < q < 2\) and \(\bar K > 0\), but not \(0 < q < 2\) and \(\bar K = 0\) (Table 1). By choosing springs with proper strengths, the MRI mechanism can be directly tested using a tethered ball in qK flows.
We emphasize that even when D1 and D2 are small, the ball is still strongly coupled to the flow by the background fluid pressure forces. In the vertical direction the upward pressure force balances gravity to maintain neutral buoyancy which keeps the primary ball motion confined to 2D. The radial pressure force transmitted from the outer wall balances the outward radial force associated with rotation as we have discussed in defining fc above.
Experimental measurements
For solid-body (q = 0) and qK (0 < q < 2) flows, we compare the motion of an untethered ball to that of a ball tethered to a post anchored at a local rotating frame (Ω3 = 80 rpm, clockwise) by a weak or strong spring. These cases are listed in Table 1.
Figure 2 shows polar coordinate and time-dependent ball trajectories in the lab frame. Each solid line of a given color corresponds to a separate experimental run with the same initial conditions. The left and right column panels correspond to qK and solid-body flow cases respectively. For each run in the qK case, the ball is initially held to the post rotating at Ω3 which rotates slightly faster (and has more angular momentum) than the background flow at its radius, to minimize secondary Ekman flow, as in the cases with both caps48. The ball therefore drifts to larger radii, regardless of whether it is tethered or untethered. However, the ball lags behind less in azimuth in the rotating frame for the tethered cases and thus advances ahead to more negative angles in the lab frame (Fig. 2a). The radial and azimuthal drift speeds are also different for tethered versus untethered cases. The radial velocity is lower for the tethered than untethered cases (Fig. 2c). The tethered cases exhibit faster angular speeds, as evidenced by their steeper slopes in Fig. 2e.
Ball trajectories in polar coordinate and their time evolution in the lab frame for two different rotation profiles. a Ball trajectories in the quasi-Keplerian (qK) flows (Ω1, Ω3, Ω2) = (190,80,22) rpm clockwise, for the angular speeds of inner cylinder, local post frame, and outer cylinder, respectively. b Ball trajectories in the solid body flows (Ω1, Ω3, Ω2) = (60, 60, 60) rpm clockwise. c, d Time evolution of radial coordinates for the qK (solid body) flows. e, f Time evolution of azimuthal coordinates for the qK (solid body) flows. Experimental results for untethered, weak spring-tethered, and strong spring tethered, cases are shown in black, red, and blue, respectively. Predictions from solving Eqs. (4) and (5) for each of these cases are shown as corresponding dashed lines
The dashed lines show the corresponding solutions to Eqs. (4) and (5). Amplitudes of oscillation modes across all presented cases are negligible compared to experimental noise. The very early time linear growth rate, within the noise, is consistent with the standard MRI growth rate with negligible Stokes drag D1. At late times, saturation from nonlinear damping by the D2 term is most consistent with the data.
Most telling are the specific angular momentum evolution plots of Fig. 3. Figure 3a shows that for the qK flows, the angular momentum of the ball remains constant for the untethered case (solid black lines) as expected from angular momentum conservation. In contrast, the weak spring tethered ball gains angular momentum (solid red lines) as expected from the MRI. Figure 3c correspondingly shows that the tethered ball gains angular momentum as it moves outward.
Time evolution and radial evolution of the ball’s angular momentum. a, b Time evolution of the ball’s angular momentum in the quasi-Keplerian or qK (solid body) flows. c, d Radial evolution of the ball’s angular momentum in the qK (solid body) flows. Experimental results for untethered, weak spring-tethered, and strong spring tethered, cases are shown in black, red, and blue, respectively. Predictions from solving Eqs. (4) and (5) for each of these cases are shown as corresponding dashed lines. Efficient angular momentum transport occurs only in the case of the qK flows using a weak-spring tether (red). All other cases show little angular momentum transport, as expected. The green dashed line shows the background flow angular momentum profile
For solid body flow, Fig. 2d shows that the ball hardly moves in radius from its initial position for either the weak spring case (red) or the untethered case (black). Correspondingly, Fig. 3b, d show little difference in the red and black lines for solid-body flow runs. The blue lines in the plots of Figs. 2 and 3 show the case of a strong spring where the MRI mechanism is predicted to be ineffective. All of these blue trajectories are consistent with theoretical expectation that outward motion is halted once the strong spring is taut and angular momentum transfer is abated. The initial radial drift and associated angular momentum gain in the strong spring case is due to a limitation of the experimental setup, namely that the spring anchor point is offset from the center of mass of the ball. This does not affect the physics conclusions.
Discussion
While many astrophysical processes are difficult to test and validate in the lab, theory should be experimentally validated when possible and this is one of the core pillars of the discipline of laboratory astrophysics. In this context, neither the standard MRI instability, nor its mechanical analogue have been previously demonstrated in the laboratory, despite their widespread use in theoretical astrophysics. Measurements from our new apparatus now experimentally confirm the mechanism of angular momentum transport by the MRI and thus support its validity.
The measurements are all consistent with the theoretical implications of Eqs. (4) and (5). Specifically, (i) only for the weak spring case with a qK (0 < q < 2) flow, does the MRI-like instability manifest, and sustain angular momentum transport from post to ball; (ii) measured trajectories of the ball agree with non-linear model equations for weak-spring tethered, strong-spring tethered, and untethered cases for qK and solid-body flows; (iii) Reynolds drag eventually balances the spring force to saturate the instability in the tethered case. Larger experiments could better distinguish linear from non-linear regimes and detailed investigations could further delineate the “weak” and “strong” spring transition.
Our spring-ball apparatus highlights use of a novel combination of solid and fluid mechanics to test MHD principles in the lab. The apparatus requires careful choices of the experimental parameters to ensure that the MHD analogue is captured: the dominant forces governing the motion of the ball must directly correspond to the dominant forces governing the motion of a parcel of MHD fluid for the chosen experimental design.
Methods
Apparatus
The experiments were carried out in a modified Taylor–Couette device (Fig. 4) using water and an open top cap. Two co-axial cylinders with height h = 39.7 cm, and radii r1 = 6.9 cm and r2 = 20.3 cm, were driven by motors at two independent angular rotation rates Ω1 and Ω2. qK flows in which Ω1 > Ω2 while \(\Omega _1r_1^2 < \Omega _2r_2^2\) can be established. To minimize secondary Ekman flow, axial boundaries are divided into three annuli. The innermost annulus with r < 8 cm co-rotates with the inner cylinder while the outermost annulus with r > 14 cm co-rotates with the outer cylinder. The intermediate annulus where 8 cm < r < 14 cm is driven by a third motor at a rotation rate Ω3. The secondary flow can be minimized by a suitable choice of Ω3, resulting in an extremely quiescent qK flow48. Our experiments used only the bottom boundary, allowing top access to the interior. To avoid significant fluid height variation that occurs on a rotating free surface, the rotation rates were limited to Ω1 = 190 rpm, Ω3 = 80 rpm, and Ω2 = 22 rpm. Measurements of the azimuthal velocity at the mid-height of the fluid using laser Doppler velocimetry confirmed that the flow had nearly the ideal Couette profile with negligible Ekman effect (as using both axial boundaries48) with q ≤ 2 with little dependence on r and z. Practical limitations on rotation rates and spring constants led us to use 1-inch diameter water-filled plastic spheres, of total mass 8.43 g. With any tethering spring, they were nearly neutrally buoyant. The finite size of the spherical test masses, as compared with r1 and r2 is included in the analysis as discussed above. The test mass was held in place by a clamp attached to a vertical post mounted at r0 = 10.8 cm on the annular ring rotating at Ω3. This radius was originally selected so that Ω3 = ΩTC(r0) where ΩTC(r) is the ideal Couette profile with a Ω1:Ω3:Ω2 = 190:80:22. The height l = 12.7 cm of the vertical post was chosen so that the test mass would sit away from the lower boundary and the top surface at z = 31.1 cm. The clamp release was triggered by hand using a metal arm fixed in the laboratory frame. The test mass was either untethered to the vertical post, or tethered with either a weak or strong spring. The springs had measured spring constants of kweak = 0.636 N m−1 and kstrong = 51.5 N m−1. We estimate the effective Reynolds number of the flow around the ball using \({\mathrm{Re}} = 2{\mathrm{R}}[\dot{r}^{2} + {r}^{2}[\dot{\theta} - \Omega (r)]^2]^{1/2}/\nu _{{\mathrm {H}}_{2}{\mathrm {O}}}\), and find maximum values Re ≈ 5000–20,000 for qK runs and Re ≈ 1 for solid body. The former values are consistent with the importance of the D2 term in Eqs. (4) and (5).
Experimental apparatus and diagnostics. a Schematic of the modified Taylor-Couette device48, with the inner and outer cylinder radii of r1 = 6.9 cm and r2 = 20.3 cm, respectively, and the height of h = 39.7 cm. The device was filled with water to a depth of 31.1 cm and the top was open to allow access. A GoPro HERO4 camera was partially submerged to minimize optical distortion. The camera was supported by an attachment and co-rotated with the ring (yellow) at Ω3. A 1-inch-diameter neutrally buoyant test mass (red) was tethered by an unstretched spring to a vertical post and held by a spring-loaded jaw-clamp. At t = 0 a release line (not shown) was pulled from above allowing the vertical spring to relax, releasing the mass. b Photograph of the test mass and release mechanism. The camera is visible at the top of the image
Diagnostics
We mounted a compact battery-powered, waterproof, video camera in the rotating frame of the vertical post with rotation rate Ω3 so that the test mass appeared stationary until release at t = 0. The camera captured 120 frames per second and the lens was slightly immersed in the water to minimize further optical distortions due to the fluid free surface. After each run, the recorded video was transferred to a computer. The camera uses a “fisheye” lens for a wide field-of-view, but this distortion was readily removed using commonly available software. The location of the center of the test mass in each frame was determined automatically by object identification and tracking software. Cartesian image data were converted into polar coordinates. From the position data, velocities, acceleration, and the vertical component of the angular momentum were calculated. The accuracy of the position data is limited by factors such as motion blur, tracking errors, the abilities to correct for lens distortion and refraction.
Data availability
The digital data for this paper can be found at http://arks.princeton.edu/ark:/88435/dsp01x920g025r.
References
Swedenborg, E. (Principia) Latin: Opera Philosophica et Mineralia (English: Philosophical and Mineralogical Works) I. (1734).
Kant, I. Universal Natural History and Theory of the Heavens; Engl. translation (1968), in KantÕs Cosmogony (ed. W. Ley, W.) (Greenwood Publishing, New York, 1755).
Laplace, P. Exposition du SytŽme du Monde,(Reprinted in the Cambridge Library Collection; 2009). (Cambridge Univ. Press, New York, 1796).
Armitage, P. J. Dynamics of protoplanetary disks. ARAA 49, 195–236 (2011).
Kley, W. & Nelson, R. P. Planet-disk interaction and orbital evolution. ARAA 50, 211–249 (2012).
Morbidelli, A. & Raymond, S. N. Challenges in planet formation. J. Geophys. Res. (Planets) 121, 1962–1980 (2016).
Kylafis, N. D. & Belloni, T. M. in A strophysics and Space Science Library, Vol. 414 (eds Contopoulos, I., Gabuzda, D. & Kylafis, N.) 245 (EDP Sciences, Cham, Switzerland, 2015).
Blaes, O. General overview of black hole accretion theory. Space Sci. Rev. 183, 21–41 (2014).
Romero, G. E., Boettcher, M., Markoff, S. & Tavecchio, F. Relativistic jets in active galactic nuclei and microquasars. Space Sci. Rev. 207, 5–61 (2017).
Bujarrabal, V., Castro-Carrizo, A., Alcolea, J. & Sánchez Contreras, C. Mass, linear momentum and kinetic energy of bipolar flows in protoplanetary nebulae. A&A 377, 868–897 (2001).
Blackman, E. G., Frank, A. & Welch, C. Magnetohydrodynamic stellar and disk winds: application to planetary nebulae. Astrophys. J. 546, 288–298 (2001).
Levan, A. et al. Gamma-ray burst progenitors. Space Sci. Rev. 202, 33–78 (2016).
Frank, J., King, A. & Raine, D. J. Accretion Power in Astrophysics: Third Edition (Cambridge University Press, Cambridge, UK, 2002).
Shakura, N. I. & Sunyaev, R. A. Black holes in binary systems. Observational appearance. A&A 24, 337–355 (1973).
Balbus, S. A. Enhanced angular momentum transport in accretion disks. ARAA 41, 555–597 (2003).
Blackman, E. G. & Nauman, F. Motivation and challenge to capture both large-scale and local transport in next generation accretion theory. J. Plasma Phys. 81, 395810505 (2015).
Velikhov, E. P. Stability of an ideally conducting liquid flowing between cylinders rotating in a magnetic field. Sov. J. Exp. Theor. Phys. 36, 1398–1404 (1959).
Chandrasekhar, S. The stability of non-dissipative couette flow in hydromagnetics. Proc. Natl Acad. Sci. USA 46, 253–257 (1960).
Balbus, S. A. & Hawley, J. F. A powerful local shear instability in weakly magnetized disks. I - linear analysis. II - nonlinear evolution. Astrophys. J. 376, 214–233 (1991).
Hawley, J. F., Gammie, C. F. & Balbus, S. A. Local three-dimensional magnetohydrodynamic simulations of accretion disks. Astrophys. J. 440, 742 (1995).
Brandenburg, A., Nordlund, A., Stein, R. F. & Torkelsson, U. Dynamo-generated turbulence and large-scale magnetic fields in a Keplerian Shear flow. ApJL 446, 741 (1995).
Balbus, S. A. & Hawley, J. F. Instability, turbulence, and enhanced transport in accretion disks. Rev. Mod. Phys. 70, 1–53 (1998).
Guan, X. & Gammie, C. F. Radially extended, stratified, local models of isothermal disks. Astrophys. J. 728, 130 (2011).
Flock, M., Dzyurkevich, N., Klahr, H., Turner, N. J. & Henning, T. Turbulence and steady flows in three-dimensional global stratified magnetohydrodynamic simulations of accretion disks. Astrophys. J. 735, 122 (2011).
Hawley, J. F., Guan, X. & Krolik, J. H. Assessing quantitative results in accretion simulations: from local to global. Astrophys. J. 738, 84 (2011).
Parkin, E. R. Global simulations of magnetorotational turbulence - II. Turbulent energetics. MNRAS 438, 2513–2529 (2014).
Bodo, G., Cattaneo, F., Mignone, A. & Rossi, P. On the convergence of magnetorotational turbulence in stratified isothermal shearing boxes. ApJL 787, L13 (2014).
Nauman, F. & Blackman, E. G. Sensitivity of the magnetorotational instability to the shear parameter in stratified simulations. MNRAS 446, 2102–2109 (2015).
Shi, J.-M., Stone, J. M. & Huang, C. X. Saturation of the magnetorotational instability in the unstratified shearing box with zero net flux: convergence in taller boxes. MNRAS 456, 2273–2289 (2016).
Bhat, P., Ebrahimi, F. & Blackman, E. G. Large-scale dynamo action precedes turbulence in shearing box simulations of the magnetorotational instability. MNRAS 462, 818–829 (2016).
Ji, H., Goodman, J. & Kageyama, A. Magnetorotational instability in a rotating liquid metal annulus. MNRAS 325, L1–L5 (2001).
Sisan, D. R. et al. Experimental observation and characterization of the magnetorotational instability. Phys. Rev. Lett. 93, 114502 (2004).
Ji, H. & Balbus, S. Angular momentum transport in astrophysics and in the lab. Phys. Today 66, 27 (2013).
Flanagan, K. et al. Prospects for observing the magnetorotational instability in the plasma Couette experiment. J. Plasma Phys. 81, 345810401 (2015).
Boldyrev, S., Huynh, D. & Pariev, V. Analog of astrophysical magnetorotational instability in a Couette-Taylor flow of polymer fluids. Phys. Rev. E 80, 066310 (2009).
Bai, Y., Crumeyrolle, O. & Mutabazi, I. Viscoelastic Taylor-Couette instability as analog of the magnetorotational instability. Phys. Rev. E 92, 031001 (2015).
Vasil, G. M. On the magnetorotational instability and elastic buckling. Proc. Math. Phys. Eng. Sci. 471, 20140699 (2015).
Ji, H., Burin, M., Schartman, E. & Goodman, J. Hydrodynamic turbulence cannot transport angular momentum effectively in astrophysical disks. Nature 444, 343–346 (2006).
Schartman, E., Ji, H., Burin, M. J. & Goodman, J. Stability of quasi-Keplerian shear flow in a laboratory experiment. A&A 543, A94 (2012).
Stefani, F. et al. Helical magnetorotational instability in a Taylor-Couette flow with strongly reduced Ekman pumping. Phys. Rev. E 80, 066303 (2009).
Seilmayer, M. et al. Experimental evidence for nonaxisymmetric magnetorotational instability in a rotating liquid metal exposed to an azimuthal magnetic field. Phys. Rev. Lett. 113, 024505 (2014).
Gissinger, C., Goodman, J. & Ji, H. The role of boundaries in the magnetorotational instability. Phys. Fluids 24, 074109 (2012).
Wei, X. et al. Numerical simulations of the Princeton magnetorotational instability experiment with conducting axial boundaries. Phys. Rev. E 94, 063107 (2016).
Caspary, K. J. et al. Effects of axial boundary conductivity on a free Stewartson-Shercliff layer. Phys. Rev. E 97, 063110 (2018).
Breakwell, J. V. Stability of an orbiting ring. J. Guid. Control Dyn. 4, 197–200 (1981).
Beletsky, V. V. & Levin, E. M. Stability of a ring of connected satellites. Acta Astronaut. 12, 765–769 (1985).
Pizarro-Chong, A. & Misra, A. K. Dynamics of multi-tethered satellite formations containing a parent body. Acta Astronaut. 63, 1188–1202 (2008).
Edlund, E. & Ji, H. Nonlinear stability of laboratory quasi-keplerian flows. Phys. Rev. E 89, 021004 (2014).
Landau, L. D. & Lifshitz, E. M. Fluid Mechanics, Second Edition (Course of Theoretical Physics), Vol. 6. (Butterworth-Heinemann, Oxford, UK, 1987).
Acknowledgements
D.H., K.C., E.G., and H.J. acknowledge support from NASA (NNH15AB25I), NSF (AST-1312463), and DoE (DE-AC0209CH11466). E.B. acknowledges support from the Simons Foundation and the Institute for Advanced Study (Princeton) while on sabbatical, and grants NSF-AST-15156489 and HST-AR-13916, the Kavli Institute for Theoretical Physics (KITP) USCB with associated support from grant NSF PHY-1125915. Authors acknowledge technical support by Peter Sloboda.
Author information
Authors and Affiliations
Contributions
E.B. and H.J. initiated the research. D.H. modified the apparatus and conducted the experiments with the help of K.C. and E.G., guided by H.J. and E.B. D.H. analyzed the data, performed theoretical calculations and generated result figures with the guidance of all other authors. H.J. generated analogue diagrams and E.G. generated apparatus figure. E.B., D.H., E.G., and H.J. drafted and revised the manuscript. All authors discussed the results and interpretations.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hung, D.M.H., Blackman, E.G., Caspary, K.J. et al. Experimental confirmation of the standard magnetorotational instability mechanism with a spring-mass analogue. Commun Phys 2, 7 (2019). https://doi.org/10.1038/s42005-018-0103-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-018-0103-7
This article is cited by
-
Identification of a non-axisymmetric mode in laboratory experiments searching for standard magnetorotational instability
Nature Communications (2022)
-
The unusual properties of plasmas
La Rivista del Nuovo Cimento (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.