Abstract
Despite the apparent ease with which sheets of paper are crumpled and tossed away, crumpling dynamics are often considered a paradigm of complexity. This arises from the infinite number of configurations that disordered, crumpled sheets can take. Here we experimentally show that key aspects of axially confined crumpled Mylar sheets have a very simple description; evolution of damage in crumpling dynamics can largely be described by a single global quantity—the total length of creases. We follow the evolution of the damage network in repetitively crumpled elastoplastic sheets, and show that the dynamics are deterministic, depending only on the instantaneous state of the crease network and not on the crumpling history. We also show that this global quantity captures the crumpling dynamics of a sheet crumpled for the first time. This leads to a remarkable reduction in complexity, allowing a description of a highly disordered system by a single state parameter.
Similar content being viewed by others
Introduction
From collapsed hulls of ships to discarded mathematical theorems written on a white piece of paper, many thin sheets end their life cycle as crumpled heaps. Nevertheless, the dynamics by which an initially flat sheet develops into a disordered and elaborate three-dimensional network of folds are often considered a hallmark example of disordered and complex systems1,2,3,4,5,6,7. When a thin sheet is crumpled, elastic energy focuses to point and line singularities termed d-cones and stretching ridges respectively2,8,9,10,11,12. The localization of stresses to individual sharp folds is driven by the local minimization of the elastic deformation energy9,13,14,15,16. However, the crumpled sheet is never at its global energy minimum and the folds’ network structure is determined dynamically; as a sheet is confined, existing defects rearrange and new ones are created17,18. In elastoplastic sheets, the material scars where the localized stress exceeds the plastic yield threshold19,20. In this case, although defects may still migrate, they leave a furrow-like scar in their wake21. Consequently, the detailed history of the crumpling dynamics is written into the intricate pattern of creases observed when the sheet is unfolded. No two crumpled sheets are identical.
Geometrical and mechanical constraints forbid the smooth sheet from folding to a ball without accumulating damage in the form of a disordered network of creases. In principle, once the damage is done, the sheet can capitalize on these existing degrees of freedom and fold back smoothly into a ball, without creating new scars. Nevertheless, despite the tendency of the sheet to bend along preexisting scars, it is impossible to crumple the sheet again without creating new folds. Unless the order of folding is reproduced exactly, the system quickly jams at a state in which it cannot conform to further compression; thus, ridges must break18 and new folds are created. As the process of crumpling and uncrumpling of the sheet is repeated, the network of creases becomes increasingly complex. It is unclear, however, if this tumultuous process continues indefinitely or asymptotes to a maximally crumpled state in which the sheet smoothly folds along existing creases and no new scars are created.
We experimentally examine the evolution of the crease patterns in thin sheets that are repeatedly crumpled n times and find that the change of the total length of all creases, \(\ell\), is not random at all. Instead, it is a deterministic function whose evolution depends only on its current value. Strikingly, the accumulation of damage does not depend on the crumpling history or the structure of the crease network. Thus, \(\ell\) can be interpreted as a state variable of the crumpled sheet. We find that the increase in total crease length, \(\delta \ell\), for a given crumpling iteration, n, decays exponentially with \(\ell\), and that these dynamics are described by a phenomenological equation for the evolution of the damage network. By analyzing this equation in the limit of n = 1, we precisely resolve the dynamics of initial crumpling of a smooth sheet into a ball, a well-studied problem.
Results
Evolution of the crease patterns in thin sheets
The development of damage networks is investigated by repeatedly crumpling elastoplastic thin sheets of Mylar. The mechanical durability of Mylar under repeated crumpling cycles makes it an ideal material for this study: Even after accumulating damage over hundreds of repeated crumpling tests, the Mylar sheet retains its spring-like, crackling characteristic. Square sheets, 30 µm thick with side length of L = 100 mm, are rolled into a cylinder, inserted into a cylindrical container of diameter D = 27 mm, and compressed uniaxially to a given gap Δ < L, as shown schematically in Fig. 1a. The dimensionless compaction parameter \({\tilde{\mathrm \Delta }} \equiv {\mathrm{\Delta }}/L\) can take values between 0 and 1. After compression the sheets are unfolded and their three-dimensional (3D) structure is scanned using a custom laser profilometer4 as demonstrated in Fig. 1b. To deduce the pattern of damage after every crumpling/unfolding iteration, the measured height profiles of the creases are locally fitted to a surface and converted into a map of mean curvatures. As the crumpling dynamics are dominated by the localization of stresses into folds, the curvature map is dominated by sharp valleys (red) and ridges (blue) with high positive and negative curvatures, respectively, as shown in Fig. 1c. Creases are detected with two independent protocols: Canny edge detection algorithm and a Radon transform method. In the main text we apply the Canny edge detection algorithm to the curvature map. Before measuring the length of creases by summing over pixels determined as edges, the data are cleaned by removing small detected edges below a threshold of a minimal number of connected pixels. Our main results are insensitive to the choice of the parameters of the edge detection algorithm, or to the scale over which the height map is fitted. To validate this analysis, in the Supplementary Discussion we compare it with a second approach based on the Radon transform method and show that the results are independent of the data processing method, as shown in Supplementary Figures 1-5. We then track the evolution of the crease network as a function of the number of crumpling/unfolding iterations, n, as shown for a typical example in Fig. 1c and Supplementary Movie. The sheets are carefully flattened between every crumpling iteration to replicate the initial conditions of each crumpling as closely as possible.
Crumpled thin sheets scarred by ridges and valleys. a Mylar sheets are crumpled uniaxially in a cylindrical container to a given gap, Δ. b The 3D topography of an unfolded crumpled sheet. Height maps are obtained with a laser profilometer similar to the one designed by Blair and Kudrolli4. c Mean curvature maps for the scanned surfaces of crumpled thin sheets for n=1, 2, 7, and 15 with \({\tilde{\mathrm \Delta }} = \frac{{\mathrm{\Delta }}}{L} = 0.27.\) Red and blue correspond to positive and negative mean curvatures respectively
When the thin sheet is repeatedly crumpled, the damage network evolves as progressively more creases are created. These dynamics lead to a monotonic increase in the total length of both valleys and ridges, \(\ell _{\mathrm{v}}\) and \(\ell _{\mathrm{r}}\) respectively, as seen for a typical example in Fig. 2a. The rate at which \(\ell _{\mathrm{v}}\) and \(\ell _{\mathrm{r}}\) increase slows down with n, indicating that when more creases are present, the sheet tends to fold along the already existing plastic scars rather than create new folds. Changing \({\tilde{\mathrm \Delta }}\) changes the rate at which creases accumulate, as shown in Fig. 2b for the total length of all creases, \(\ell = \ell _{\mathrm{r}} + \ell _{\mathrm{v}}\), for \({\tilde{\mathrm \Delta }}\) ranging from 0.9 to 0.045 and representing data from 507 individual scans. Despite the random nature of crumpling, the evolution of \(\ell\) with n is strikingly reproducible. This can be seen, for example, by the open yellow markers in Fig. 2b, which show \(\ell (n)\) curves for five different experiments in which sheets are crumpled repetitively to \({\tilde{\mathrm \Delta }} = 0.36\).
The evolution of damage networks. a \(\ell _{\mathrm{r}}(n)\) for ridges (blue) and \(\ell _{\mathrm{v}}(n)\) for valleys (red). Full circles correspond to the four crease patterns shown in Fig. 1c. b \(\ell \left( n \right) = \ell _{\mathrm{r}} + \ell _{\mathrm{v}}\) for \({\tilde{\mathrm \Delta }}\) ranging from 0.9 to 0.045 for 507 scans. Different markers of identical colors correspond to different sheets crumpled to the same values of \({\tilde{\mathrm \Delta }}\). c The a (blue diamonds) and b (red circles) as a function of \({\tilde{\mathrm \Delta }}\). The dashed lines are the respective fits to \(a = c_1(1 - {\tilde{\mathrm \Delta }})\) \(\left( {c_1 = 5200 \pm 200} \right)\) and \(b = c_2/{\tilde{\mathrm \Delta }}\) \(\left( {c_2 = 0.063 \pm 0.005} \right)\). Note that for \({\tilde{\mathrm \Delta }}\)→0, \(\ell\) diverges for any finite n. (inset) Fit (red curve) of a single \(\ell (n)\) curve to \(\ell \left( n \right) = a\;{\mathrm{log}}(1 + b\;n)\). d \(\ell /(1 - {\tilde{\mathrm \Delta }})\) as a function of \(n/{\tilde{\mathrm \Delta }}\) for all data shown in (b) collapse, demonstrating that all \(\ell (n)\) curves follow Eq. 1 (inset)
As the sheet is re-crumpled, preexisting creases, where the material is weakened, function as mechanical hinges along which the sheet may bend without creating new scars. However, as the compression increases, the sheet often deforms into a jammed configuration in which it cannot compress further by only bending along existing creases. This inevitably leads to the creation of new scars, consistent with the curves shown in Fig. 2b, in which the \(\ell \left( n \right)\) curves do not plateau. We find that \(\ell \left( n \right) = a\log \left( {1 + b\;n} \right)\) is a good fit to all \(\ell \left( n \right)\) curves, as shown for a specific value of \({\tilde{\mathrm \Delta }}\) in the inset to Fig. 2c, where a and b are fitting parameters which depend on \({\tilde{\mathrm \Delta }}\), as shown in Fig. 2c.
For large \({\tilde{\mathrm \Delta }}\) creases accumulate at a slower rate, consistent with the observation that a decreases linearly with \({\tilde{\mathrm \Delta }}\) and b decreases as \({\tilde{\mathrm \Delta }}^{ - 1}\), as shown in Fig. 2c. Note that since no creases are created when the sheet is not compressed, \(\left( {\alpha {\tilde{\mathrm \Delta }} = 1} \right)\) = 0, as expected. Thus, \(\ell\) and n can be rescaled by \((1 - {\tilde{\mathrm \Delta }})\) and \({\tilde{\mathrm \Delta }}\) respectively, leading to a remarkable collapse of all \(\ell (n)\) curves, as shown in Fig. 2d. Moreover, all our data can now be replotted and fitted by
with only two fitting parameters \(c_1 = 5200 \pm 200\), and \(c_2 = 0.063 \pm 0.005\) as shown in the inset to Fig. 2d.
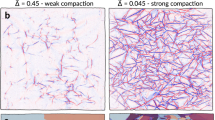
Changing \({\tilde{\mathrm \Delta }}\) varies the rate at which creases accumulate as well as the statistics of the crease pattern, as can be seen by comparing two typical crease patterns with similar \(\ell\) shown in Fig. 3a, b. When crumpling a sheet a few times to a small \({\tilde{\mathrm \Delta }}\) (Fig. 3a), creases tend to be relatively long and uniformly distributed across the sheet. The same \(\ell\) can be obtained by crumpling a sheet many times less vigorously to larger \({\tilde{\mathrm \Delta }}\)s. However, in this case the pattern is dominated by short, more localized creases (Fig. 3b).
Accumulation of damage is not history dependent. a, b Scanned surfaces with almost identical \(\ell\) created with two different crumpling protocols. c \(\ell (n)\) curves for \({\tilde{\mathrm \Delta }}_1 = 0.45\) and \({\tilde{\mathrm \Delta }}_2 = 0.18\) (black circles and diamonds respectively), and \(\ell \left( n \right)\) curve for a sheet crumpled n0 = 11 times to \({\tilde{\mathrm \Delta }}_1\) and subsequently crumpled to \({\tilde{\mathrm \Delta }}_2\) (full green squares). The open green squares correspond to shifting of the n > n0 part of the \(\ell (n)\) data to the \({\tilde{\mathrm \Delta }}_2\) curve. d Same as (c) for \({\tilde{\mathrm \Delta }}_2 > {\tilde{\mathrm \Delta }}_1\) with \({\tilde{\mathrm \Delta }}_1 = 0.18\), \({\tilde{\mathrm \Delta }}_2 = 0.36\) and n0 = 3
So far we only addressed crumpling protocols where one \({\tilde{\mathrm \Delta }}\) was used repeatedly. We test whether the evolution of \(\ell (n)\) is history dependent by implementing a new crumpling protocol with two values of \({\tilde{\mathrm \Delta }}\). \(\ell _{{\tilde{\mathrm \Delta }}_1,{\tilde{\mathrm \Delta }}_2}(n)\) is measured by initially crumpling a sheet n0 times to \({\tilde{\mathrm \Delta }}_1\), and then crumpling the same sheet several times to a different \({\tilde{\mathrm \Delta }}_2\), as shown in Fig. 3c, d. We compare \(\ell _{{\tilde{\mathrm \Delta }}_1,{\tilde{\mathrm \Delta }}_2}\left( n \right)\) to the curves obtained by crumpling a fresh sheet repeatedly to a single \({\tilde{\mathrm \Delta }}_i\),\(\ell _{{\tilde{\mathrm \Delta }}_i}\), and note that \(\ell _{{\tilde{\mathrm \Delta }}_1,{\tilde{\mathrm \Delta }}_2}\left( n \right)\) indeed deviates from \(\ell _{{\tilde{\mathrm \Delta }}_1}(n)\) for n >n0. Remarkably, \(\ell _{{\tilde{\mathrm \Delta }}_1,{\tilde{\mathrm \Delta }}_2}(n > n_0)\) overlaps perfectly with \(\ell _{{\tilde{\mathrm \Delta }}_2}(n)\) by a shift along the n axis, marked by open squares in Fig. 3c, d. The overlap of the two curves demonstrates that when two sheets with similar \(\ell\) but different crumpling histories are crumpled repetitively to the same \({\tilde{\mathrm \Delta }}\), the evolution of \(\ell\) for both is identical. This implies that the evolution of \(\ell\) is independent of the crumpling history. Furthermore, as the crumpling history determines the structure of the crease pattern, this history independence also implies that the evolution of the global quantity \(\ell\) is independent of the local statistics of the structure; hence, the evolution of \(\ell\) is determined solely by its instantaneous value. Drawing an appealing analogy with statistical physics, the history independence of the evolution of \(\ell\) suggests that this observable can be thought of as a macroscopic state variable quantifying the “crumpledness” of a damaged sheet. Identifying a global quantity that evolves independently of the details of the pattern significantly reduces the complexity of this system.
Traditionally, crumpling is considered a random and disordered process. The crease pattern obtained for a given sheet is specific to the details of the crumpling dynamics, and is thus impossible to reproduce perfectly. However, as \(\ell\) is a state variable with a known functional dependence on \({\tilde{\mathrm \Delta }}\) and n, it is a striking corollary that it is possible to fully predict the evolution of \(\ell\) for any arbitrary crumpling sequence. \(\delta \ell _{{\tilde{\mathrm \Delta }}}\) can be estimated by differentiating Eq. 1 with respect to n, yielding
where the second equality is equivalent to Eq. 1. The total length of new creases created at any crumpling iteration, \(\delta \ell _{{\tilde{\mathrm \Delta }}}\), is a function only of \({\tilde{\mathrm \Delta }}\) and of \(\ell\) (measured before the current crumpling cycle) and not a function of n. Note that Eq. 2 is an equation of state for the damage evolution, highlighting that \(\ell\) is always memoryless. Through iterative summations of Eq. 2, \(\ell (n)\) can be predicted for any crumpling protocol given as a sequence of \({\tilde{\mathrm \Delta }}\)’s.
We crumple a sheet 12 times according to the protocol described in Fig. 4a., i.e., we crumple the sheet 6 consecutive times, each time to a smaller volume than the previous crumple (a smaller \({\tilde{\mathrm \Delta }}\)), and then repeat this cycle. The measured \(\ell \left( n \right)\) curve for this crumpling protocol is in excellent agreement with the prediction obtained from Eq. 2, as seen in Fig. 4a (top). Note that there are no fitting parameters used in Fig. 4a, as c1 and c2 are extracted from the data shown in Fig. 2c. This is possible only because \(\ell \left( n \right)\) is a state variable that evolves without memory. Additionally, Eq. 2 indicates that \(\delta \ell _{{\tilde{\mathrm \Delta }}}\) cannot be broken down into two separate functions of \(\ell\) and of \({\tilde{\mathrm \Delta }}\). This nontrivial functional form suggests that the predictive power of Eq. 2 is not likely to result from any artifact of image processing or crease detection.
Crumpling dynamics. a \(\ell \left( n \right)\) (circles) and prediction based on Eq. 2 (solid red line) for a crumpling protocol given as a sequence of \({\tilde{\mathrm \Delta }}\)(n). b \(\ell (n)\) for sheets initially crumpled by hand (black circles and top left inset) or folded in straight lines (yellow squares and bottom right inset) and then subjected to the same crumpling protocol as in (a). Solid red line again shows the prediction based on Eq. 2. Curvature maps are thresholded for clarity. c The surface \(\ell (n,{\tilde{\mathrm \Delta }})\) given by Eq. 1. The pink and red curves correspond to \(\ell (n = 15,{\tilde{\mathrm \Delta }})\) and \(\ell (n = 1,{\tilde{\mathrm \Delta }})\) respectively. d \(\ell (n = 1,{\tilde{\mathrm \Delta }})\) and \(\ell \left( {n = 15,{\tilde{\mathrm \Delta }}} \right)\) (inset) with fit based on Eqs. 3 and 1, respectively. A 1D heuristic model predicts \(\ell\) to depend linearly on \((1 - {\tilde{\mathrm \Delta }})\) for mild compression \(\left( {{\tilde{\mathrm \Delta }} \approx 1} \right)\) (schematic 1) and to scale with \({\tilde{\mathrm \Delta }}^{ - 1}\) for large compression \(\left( {{\tilde{\mathrm \Delta }} \approx 0} \right)\) (schematic 2)
The agreement between experiment and prediction demonstrated in Fig. 4a further indicates that the evolution of \(\ell\) is history independent, and supports the claim that it may be treated as a state variable of crumpling. Such a statement will be more meaningful if it could be applied to a general loading configuration; however, so far we have only considered this history independence for fold networks created by uniaxially crumpling sheets in a cylindrical configuration. We therefore repeat the crumpling protocol shown in Fig. 4a and measure \(\ell \left( n \right)\) for two pre-creased sheets with distinctively different loading histories; one sheet was first hand crumpled into a ball, and the other folded along straight lines to create the initial crease patterns shown in the insets to Fig. 4b. For both sheets, Eq. 2 with c1 and c2 extracted from Fig. 2c still accurately predicts the evolution of \(\ell\), as shown in Fig. 4b.
An equation of state for the evolution of the crease network
The history independence of \(\ell\) for sheets that are repeatedly crumpled allows us to take an unconventional approach to understanding the dynamics of crumpling. By this approach we gain direct insight into the crumpling process, resolving the question regarding the evolution of the crease network as a smooth sheet is confined to an increasingly shrinking volume. That is, how does \(\ell\) depend on \(\widetilde {\mathrm{\Delta }}\)? Rather than tracking the evolution of \(\ell (n)\) as a sheet is repeatedly crumpled to a given \({\tilde{\mathrm \Delta }}\), we now inspect \(\ell ({\tilde{\mathrm \Delta }})\) for a given n. In Fig. 4c we re-plot the data presented in Fig. 2a as the surface \(\ell (n,{\tilde{\mathrm \Delta }})\), where we highlight two \(\ell ({\tilde{\mathrm \Delta }})\) traces. The history independence of the crumpling dynamics corresponds to path independence along the \((n,{\tilde{\mathrm \Delta }})\) phase space; thus, \(\ell ({\tilde{\mathrm \Delta }})\) curves at constant n are mathematically and physically meaningful even though it requires many different sheets, with their unique network of creases, to experimentally generate one such curve.
For large n, \(\ell (n)\) curves are smooth and \(\ell (n = const,\;{\tilde{\mathrm \Delta }})\) curves are traced well by Eq. 1, as seen in the inset to Fig. 4d. By examining Eq. 1 at n = 1 we can obtain a prediction for the accumulation of creases as a smooth sheet is crumpled for the first time. The great advantage of this approach is that the phenomenological Eq. 1 and the two constants c1 and c2 are obtained by fitting the entire \(\ell (n,{\tilde{\mathrm \Delta }})\) surface—a fit dominated by the large n data, where the noise is significantly reduced. As \(c_2 = 0.063,\) for n = 1, Eq. 1 is approximated by
Equation 3 is in striking agreement with the experimental results for n=1, as seen in Fig. 4d.
Equation 3 indicates that for small compression \(({\tilde{\mathrm \Delta }} \approx 1)\), \(\ell _1\) is proportional to the strain applied by the piston \((1 - {\tilde{\mathrm \Delta }})\), while for very large compression \(({\tilde{\mathrm \Delta }} \to 0)\), \(\ell _1\) is inversely proportional to \({\tilde{\mathrm \Delta }}\).
A heuristic one-dimensional (1D) model of crumpling, described schematically in the insets to Fig. 4d, provides intuition for the behavior of \(\ell \left( {n = 1,{\tilde{\mathrm \Delta }}} \right)\) in the two limits. For small compression, the sheet can be compacted by creating a circumferential fold along the sheet, which at this stage of the crumpling is roughly cylindrical. This fold serves as a hinge that the cylinder can bend along without the need to create new folds. The sheet can thus compress continuously, creating new hinges when the freedom of travel provided by the existing hinges runs out, as described in inset schematic 1. In this regime \(\ell\) is proportional to the number of hinges created, leading to a linear relation between \(\ell\) and the distance the piston compressed the sheet, i.e., \(\ell \sim (1 - {\tilde{\mathrm \Delta }})\). For large compression, the sheet is tightly packed and all facets of the sheet must be broken when compression is increased. This breaking of all facets doubles the total length of creases for every halving of \({\tilde{\mathrm \Delta }}\), leading to the observed scaling of \(\ell \sim {\tilde{\mathrm \Delta }}^{ - 1}\), and represented in inset schematic 2.
Discussion
The crumpled state can be thought of as one point in a hyper-dimensional configuration space, where the angle of each individual fold corresponds to a dimension, and the folding dynamics are represented by a trajectory in configuration space. The seemingly unbounded increase of \(\ell\) for large n implies that most of these trajectories lead to a dead-end where the system jams. The sheet cannot smoothly compact by deforming along existing creases; instead, to reach the designated compaction new, energetically expensive creases are created. Because of the complexity of such a configuration space, it is nontrivial that much of this system’s evolution can be captured by a single state equation. In contrast to classical glassy systems, where the dynamics are illustrated as a stroll in a complex energy landscape, our system holds richer dynamics. When our system jams in a local minimum, it supports further confinement by introducing new ridges or valleys, increasing the dimensionality of the system. Furthermore, the energy landscape changes as a result of the interactions between the new and existing folds. It would be meaningful in the future to explore the dynamics of how the energy landscape evolves as folds accumulate. It may also be noteworthy to look for state variables in other systems that evolve under geometric and mechanical constraints. For example, earthquake fault networks evolve via the accumulation and release of tectonic stresses by the formation of new faults or slip along pre-existing faults that are themselves remnants of its seismic history22. More provocatively, we may consider the evolution of functional materials, such as proteins23,24,25, where several recent works suggest that through continuous structural alterations, resulting from cyclic loading, genetic complexity is reduced via evolutionary selection to perform a specific mechanical task.
Data availability
The data that support the findings of this study are available from the authors on reasonable request.
References
Matan, K., Williams, R. B., Witten, T. A. & Nagel, S. R. Crumpling a thin sheet. Phys. Rev. Lett. 88, 076101 (2002).
Witten, T. Stress focusing in elastic sheets. Rev. Mod. Phys. 79, 643 (2007).
Cambou, A. D. & Menon, N. Three-dimensional structure of a sheet crumpled into a ball. Proc. Natl. Acad. Sci. USA 108, 14741–14745 (2011).
Blair, D. L. & Kudrolli, A. Geometry of crumpled paper. Phys. Rev. Lett. 94, 1–4 (2005).
Adda-Bedia, M., Boudaoud, A., Boué, L. & Deboeuf, S. Statistical distributions in the folding of elastic structures. J. Stat. Mech. Theory Exp. 2010, P11027 (2010).
Deboeuf, S., Katzav, E., Boudaoud, A., Bonn, D. & Adda-Bedia, M. Comparative study of crumpling and folding of thin sheets. Phys. Rev. Lett. 110, 104301 (2013).
Stern, M., Pinson, M. B. & Murugan, A. The complexity of folding self-folding origami. Phys. Rev. X 7, 041070 (2017).
Wood, A. Witten’s lectures on crumpling. Phys. A Stat. Mech. Appl. 313, 83–109 (2002).
Cerda, E. & Mahadevan, L. Conical surfaces and crescent singularities in crumpled sheets. Phys. Rev. Lett. 80, 2358 (1998).
Chaïeb, S., Melo, F. & Géminard, J.-C. Experimental study of developable cones. Phys. Rev. Lett. 80, 2354 (1998).
Cerda, E., Chaieb, S., Melo, F. & Mahadevan, L. Conical dislocations in crumpling. Nature 401, 46–49 (1999).
Amar, M. B. & Pomeau, Y. Crumpled paper. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 453, 729–755 (1997).
Cerda, E. & Mahadevan, L. Confined elastic developable surfaces: cylinders, cones and the elastica. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 461, 671–700 (2005).
Lobkovsky, A., Gentges, S., Li, H., Morse, D. & Witten, T. Scaling properties of stretching ridges in a crumpled elastic sheet. Science 270, 1482 (1995).
Venkataramani, S., Witten, T., Kramer, E. & Geroch, R. P. Limitations on the smooth confinement of an unstretchable manifold. J. Math. Phys. 41, 5107–5128 (2000).
Vliegenthart, G. & Gompper, G. Forced crumpling of self-avoiding elastic sheets. Nat. Mater. 5, 216–221 (2006).
Aharoni, H. & Sharon, E. Direct observation of the temporal and spatial dynamics during crumpling. Nat. Mater. 9, 993–997 (2010).
Sultan, E. & Boudaoud, A. Statistics of crumpled paper. Phys. Rev. Lett. 96, 136103–136103 (2006).
Habibi, M., Adda-Bedia, M. & Bonn, D. Effect of the material properties on the crumpling of a thin sheet. Soft matter 13, 4029–4034 (2017).
Tallinen, T., Åström, J. & Timonen, J. The effect of plasticity in crumpling of thin sheets. Nat. Mater. 8, 25–29 (2009).
Gottesman, O., Efrati, E. & Rubinstein, S. M. Furrows in the wake of propagating d-cones. Nat. Commun. 6, 7232 (2015).
Scholz, C. H. The Mechanics of Earthquakes and Faulting 2nd edn (Cambridge University Press, Cambridge, 2002).
Mitchell, M. R., Tlusty, T. & Leibler, S. Strain analysis of protein structures and low dimensionality of mechanical allosteric couplings. Proc. Natl. Acad. Sci. USA 113, E5847–E5855 (2016).
Tlusty, T., Libchaber, A. & Eckmann, J.-P. Physical model of the genotype-to-phenotype map of proteins. Phys. Rev. X 7, 021037 (2017).
Yan, L., Ravasio, R., Brito, C. & Wyart, M. Architecture and coevolution of allosteric materials. Proc. Natl. Acad. Sci. USA 114, 2526–2531 (2017).
Acknowledgements
We thank Efi Efrati and Tom Witten for valuable discussions. This work was supported by the National Science Foundation through the Harvard Materials Research Science and Engineering Center (DMR-1420570). S.M.R. acknowledges support from Alfred P. Sloan research foundation. C.H.R. acknowledges support from the Applied Mathematics Program of the U.S. Department of Energy Office of Advanced Scientific Computing Research under contract DE-AC02-05CH11231.
Author information
Authors and Affiliations
Contributions
O.G. and S.M.R. came up with the concept of the paper. O.G. assembled the profilometer, performed the experiments, and used the Canny edge detection method to analyze all the data. J.A. and C.H.R. developed the Radon transform methods. J.A. analyzed the data with the Radon transform methods and wrote most of the supplementary material. All the authors interpreted the experimental results and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gottesman, O., Andrejevic, J., Rycroft, C.H. et al. A state variable for crumpled thin sheets. Commun Phys 1, 70 (2018). https://doi.org/10.1038/s42005-018-0072-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-018-0072-x
This article is cited by
-
A model for the fragmentation kinetics of crumpled thin sheets
Nature Communications (2021)
-
Curvature-Driven Wrinkling of Thin Elastic Shells
Archive for Rational Mechanics and Analysis (2021)
-
Our second revolution around the sun
Communications Physics (2020)
-
The compressive strength of crumpled matter
Nature Communications (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.