On the manifestation of electron-electron interactions in the thermoelectric response of semicrystalline conjugated polymers with low energetic disorder

Abstract

The development of semicrystalline polymer semiconductors with field-effect mobilities comparable to or even exceeding those of amorphous silicon has exposed limitations of describing charge transport in these materials with disorder-based models developed originally for more disordered, lower mobility polymers. Here, we show that the charge carrier density and temperature dependence of the field-effect electron mobility and Seebeck coefficient in the semicrystalline polymer P(NDI2OD-T2) with varying degrees of crystallinity are incompatible with a description of charge transport being limited by energetic disorder effects. We provide instead direct evidence of low disorder, narrow band conduction. A spatially inhomogeneous density of states and the inclusion of short range electron–electron interactions allow to consistently explain both the measured mobility and Seebeck coefficient. These results provide a rationale for improving thermoelectric efficiency of polymer semiconductors via increasing the extension of the crystalline domains.

Introduction

The charge transport properties of conjugated polymers have experienced tremendous progress in the past decade with the development of low disorder amorphous as well as semicrystalline polymers with charge carrier mobilities that outperform those of amorphous silicon and make these materials suitable candidates for a variety of electronic applications^1,2,3. Most theoretical models of charge transport in conjugated polymers assume transport to be dominated by energetic disorder effects and describe the transport properties in terms of hopping between localized states or delocalized transport above a mobility edge (ME)^4,5,6. These models were initially developed by Mott for transport in strongly disordered inorganic semiconductors and provided an accurate prediction of the temperature and charge carrier dependence of the conductivity, the most prominent feature of amorphous inorganic semiconductors⁷. They have been extensively refined by considering a Gaussian, exponential or more complex density of states (DoS) in order to better describe organic semiconductors⁸. Several types of hopping mechanisms have been considered, most notably those developed by Miller and Abrahams as well as those for polaron transport^9,10,11. Nevertheless, it has to be stressed that some of these models have been employed outside their range of validity. Emin showed, for example, that for both acoustic and optical phonons the Miller-Abrahams hopping rates only emerge at very low temperatures, yet they are used frequently outside this range^12,13. Different approaches were developed to calculate the macroscopic transport coefficients. Among those are numerically solving the Master equation or applying a percolation theory approach^4,6,14.

While such energetic disorder based models describe very well the transport properties of low-mobility conjugated polymers⁴ it has recently been shown that they are not applicable to some high-mobility systems: for nearly amorphous polymers with well-defined near-planar chain conformation the energetic disorder broadening of the DoS can become so low that nearly all repeat units along the polymer chain become thermally accessible for transport and that the charge carrier mobility becomes independent of carrier concentration^2,15. In high-mobility polymers with strong aggregation and semicrystalline microstructure the description of transport is even more challenging^3,16,17,18: one has to consider the heterogeneity of the electronic structure due to the coexistence of crystalline and amorphous domains. There is clear experimental evidence for such inhomogeneities in the DoS but these are usually not considered within disorder based transport models^18,19,20. It was shown recently that energetic disorder models are not consistent with the measured microstructure of semicrystalline polymers²¹. In particular, a common prediction of such models is a stronger charge carrier density dependence of the mobility with stronger energetic disorder. This is in contradiction with observations that a stronger charge carrier density dependence of the mobility is unambiguously tied to an increase in average crystallite size, i.e., a higher degree of structural order²¹.

A better understanding of the transport properties of these polymers is urgently required in order to make further progress on materials and device performance. For this a more powerful, experimental methodology is needed as measurements of the charge carrier mobility and its carrier concentration and temperature dependence alone can often be fitted well by different transport models and different sets of parameters²¹. In this work, we extend such measurements to include simultaneous determination of the thermoelectric Seebeck coefficient and its carrier concentration and temperature dependence which allows us to constrain the possible transport models. We investigate the more complex case of a semicrystalline, high-mobility polymer, in which the DoS cannot be assumed to be uniform. We show that, although common disorder-based transport models can reproduce the temperature and charge carrier density dependence of the mobility correctly, they fail to explain the temperature and charge carrier density dependence of the Seebeck coefficient simultaneously. We measure a temperature independent Seebeck coefficient which exhibits a $\frac{{k_{\mathrm{B}}}}{e}$ ln(10) slope indicative of narrow-band transport in a non-degenerate semiconductor. We show that in order to explain the full set of experimental mobility and Seebeck data on such semicrystalline polymers consistently it is necessary to consider a spatially inhomogeneous DoS and include electron–electron interaction through an explicitly charge density dependent DoS.

Results

Thermoelectric transport in the non-degenerate regime

The Seebeck coefficient represents the entropy transported by a charge carrier divided by its charge²². It allows to directly probe the DoS as well as the relative contribution to charge transport of different conduction channels within the DoS.

The general expression for the Seebeck coefficient in an independent electron model with a spatially homogeneous DoS can be derived from the Boltzmann transport equation^23,24 and reads:

$$S = - \frac{1}{{eT}}\left[ {\frac{{{\int} \left( {E - E_{\mathrm{F}}} \right)\sigma (E){\mathrm{d}}E}}{{{\int} \sigma (E){\mathrm{d}}E}}} \right],$$

(1)

where σ(E) is the energy dependent conductivity function in the expression for the conductivity:

$$\begin{array}{*{20}{l}} \sigma \hfill & = \hfill & {{\int} {\kern 1pt} \sigma (E){\mathrm{d}}E} \hfill \\ {} \hfill & = \hfill & {{\int} {\kern 1pt} e\mu (E)g(E)k_{\mathrm{B}}T\left( { - \frac{{\partial f(E)}}{{\partial E}}} \right){\mathrm{d}}E,} \hfill \end{array}$$

(2)

with f(E) representing the Fermi-Dirac distribution function and g(E) the DoS. In Eq. (1) each charge contributes to the transported energy according to its excess energy with respect to the chemical potential (E − E_F), weighted by the relative contribution of the conduction channel $\frac{{\sigma (E)}}{\sigma }$ to the total conductivity.

It can be shown that if the state occupancy is low, i.e., $\frac{n}{{\overline N }} \ll 1$, where n is the field-induced charge carrier density and $\overline N$ is the total number of states per unit volume (in semicrystalline systems, like the one investigated here, this includes states in both the amorphous as well as the crystalline domains as well as spin degeneracy), the difference in S between two carrier concentrations n₁ and n₂ with n₂ > n₁ just depends on the logarithm of the ratio of the two carrier concentrations. Therefore, S can be expressed in terms of $\tilde N$, the effective DoS that is thermally accessible to charge carriers contributing to transport (a derivation is presented in Supplementary Note 1):

$$\begin{array}{*{20}{l}} {S\left( {n_2} \right)} - {S\left( {n_1} \right)} = {\frac{{k_{\mathrm{B}}}}{e}{\mathrm{ln}}\left( {\frac{{n_2}}{{n_1}}} \right)} \hfill \\ {} \hskip1.7pc \Rightarrow {S(n)} = { - \frac{{k_{\mathrm{B}}}}{e}{\mathrm{ln}}\left( {\frac{{\tilde N}}{n}} \right).} \hfill \end{array}$$

(3)

This formula describes the entropy-of-mixing contribution to the Seebeck coefficient, which is the change of the entropy-of-mixing upon adding a charge carrier^25,26. In this way measurements of the Seebeck coefficient provide direct and powerful insight into the DoS. It has been reported for several high mobility polymer systems such as indacenodithiophene-benzothiadiazole (IDTBT), with a very well defined planar polymer chain conformation that is maintained uniformly despite a nearly amorphous microstructure, that $\tilde N$ is approximately temperature independent via the observation of a temperature independent Seebeck coefficient in the low occupancy regime². Furthermore, it has been shown that the slope extracted from a plot of the field-effect gated Seebeck coefficient against the logarithm of the carrier concentration exhibits a value close to $\frac{{k_{\mathrm{B}}}}{e}{\mathrm{ln}}(10)$².

Structural characterization

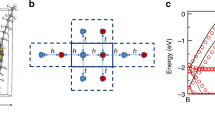
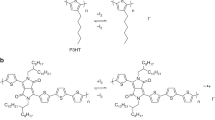
We investigate P(NDI2OD-T2), a widely studied n-type conjugated polymer with a relatively high electron mobility on the order of 0.1 cm² V⁻¹ s⁻¹¹⁶. We have fabricated top-gate, field-effect transistors with an on-chip heater (Fig. 1a, b) to characterize both charge carrier mobility and the Seebeck coefficient in the same device^2,27. P(NDI2OD-T2) was spin-coated from a 5 g l⁻¹ solution in toluene and the gate dielectric was PMMA. It has already been shown how by controlling the processing conditions it is possible to selectively tune the size of the crystalline domains in these films while keeping other properties such as cumulative positional disorder, energetic disorder and polymer chain orientation in the crystalline domains unaffected (microstructure illustrated in Fig. 1c, structural formula shown in Fig. 1d)²¹. Here, we focus on films annealed at 200 °C and films dried in a vacuum oven (as-cast).

Fig. 1

Device architecture and model illustrations. Schematic of the device structure of the thin film transistors with an on-chip heater element (a, b modified dimensions for illustration) as well as the microstructure of the semicrystalline polymer semiconductors (c) and the structural formula of P(NDI2OD-T2) (d) are shown

We characterized the microstructure of each polymer film by 2D grazing incidence wide angle X-ray scattering (GIWAXS) (Fig. 2). Upon annealing we observe an increase in coherence length from 2.1 to 3.5 nm along the π–π stacking direction, from 16.5 to 20.7 nm along the backbone direction and from 20.1 to 38.0 nm along the lamellar stacking direction, indicating an increase in the average volume of crystalline domains by a factor of 4 and the average lamellar area (relevant for charge transport in organic field-effect transistors (OFETs)) by a factor of 2. D-spacings along the three crystallographic directions are not appreciably altered by the annealing (further details are available in Supplementary Note 2).

Fig. 2

2D grazing incidence scattering patterns of P(NDI2OD-T2) polymer films. The GIWAXS patterns for the 200 °C annealed film (a) and the as-cast film (b) are shown. The peak assignments are based on previous reports^48,49. From the diffraction peaks an increase in coherence length in all directions upon annealing is evident. This indicates an increase in the average volume of crystalline domains by a factor of 4 and the average lamellar area (relevant for charge transport in OFETs) by a factor of 2

Electric and thermoelectric characterization

Both charge carrier mobility and Seebeck coefficient have been measured as a function of temperature and charge carrier density, according to the procedure reported in the methods section and Supplementary Note 3. The temperature calibration of the source and drain contacts was performed with a 4-point-probe calibration (Fig. 1b). The temperature dependent saturation mobilities for the annealed and as-cast device were extracted from saturation transfer curves (Supplementary Note 3) according to ref. ²⁸ and are presented in Fig. 3a, b respectively. The extracted mobility is thermally activated for both films with large and small crystalline domains. In contrast to nearly amorphous polymers like IDTBT the annealed sample, with large crystalline domains shows a pronounced charge density dependence of the mobility and an overall higher mobility than the as-cast sample (with small crystalline domains). In the as-cast sample the mobility is independent of the carrier concentration. This behavior is fully consistent with previous mobility measurements on the same system which used normal FET device architectures without integrated heaters²¹.

Fig. 3

Saturation mobility μ and Seebeck coefficient S versus charge carrier density n. Charge carrier density and temperature dependent saturation mobility as well as Seebeck coefficient measurements of the 200 °C annealed (a, c) and as-cast device (b, d). The fits of the Coulomb enhanced charge transport (CET) model²¹ (solid lines) and the ME model⁵ (dashed lines) are shown as well. The fitting parameters for the CET fits are E_barr = 95 meV, $\mu _{{\mathrm{02C}}} = 20 \cdot \frac{{300}}{T}$ cm² V⁻¹ s⁻¹, n = 2 × 10²⁰ cm⁻³ (a–d) and G = 80 meV, μ₀ = 0.75 cm² V⁻¹ s⁻¹ (a, c), respectively G = 120 meV, μ₀ = 1.35 cm² V⁻¹ s⁻¹ (b, d). The fitting parameters for the ME fits are E_deep = −8 eV, W_deep = 0.01 eV, E₀ = −4 eV, E_C = 0.037 eV, N_tot = 2 × 10²⁰ cm⁻³ (a–d) and μ₀ = 0.7 cm² V⁻¹ s⁻¹, N_tail = 5 × 10¹⁹ cm⁻³, W_tail = 0.042 eV, E_a = 0 eV (a, c), respectively μ₀ = 5.2 cm² V⁻¹ s⁻¹, N_tail = 1.8 × 10²⁰ cm⁻³, W_tail = 0.018 eV, E_a = 0.04 eV (b, d). The relative error in the Seebeck coefficient is approx. 7%, calculated from the intrinsic current and voltage measurement errors of the Agilent SPA 4156B as well as the linear regression fit errors from the sensor resistance calibration and the thermal voltage versus temperature difference plots (shown as error bars on the data points)

In addition to these saturation mobility measurements, the charge carrier density and temperature dependent Seebeck coefficient measurements of the annealed and as-cast device are presented in Fig. 3c, d respectively. Within the uncertainty of the measurement (approx. 7%, the full error estimation is reported in Supplementary Note 4), we measured a very similar Seebeck coefficient for the two different samples. We observe a slight increase in the Seebeck coefficient with decreasing temperature, however such increase is within the precision of our measurement: the variation of the Seebeck is less than 14% in the range 180–300 K, and can consequently be considered to be constant in this temperature range. The slope of the Seebeck coefficient versus charge density of 220 μV K⁻¹ decade⁻¹ is close to the ideal slope of $\frac{{k_{\mathrm{B}}}}{e}{\mathrm{ln}}(10)$ (corresponding to 198 μV K⁻¹ decade⁻¹) and a total DoS of $\tilde N = 2 \times 10^{20}$ cm⁻³ is extracted from a fit to the Seebeck data for both annealed and as-cast films, despite the average crystallite size increases upon annealing by a factor of 2. If the increase in crystallite size was connected to a reduction of the amorphous states and an increase of the crystalline ones, it would cause an increase in the Seebeck coefficient of $\frac{{k_{\mathrm{B}}}}{e}{\mathrm{ln}}(2)$ = 60 μV, which we do not observe in our measurements. The fact that $\tilde N$ stays constant indicates that a smaller number of larger crystalline domains are formed upon annealing so that the total number of electronic states is not changed significantly. This is in agreement with the results of UV–Vis spectroscopy, which show that the density of aggregates in the films does not change upon annealing²⁹. The density calculated from the Seebeck coefficient is lower than the one estimated from UV–Vis (approx. 4 × 10²⁰ cm⁻³) but there are several factors that can contribute to such difference. The monomer density is estimated from the lattice spacing of the crystalline fraction, and might lead to an overestimation of the total (crystalline + amorphous) monomer density. UV–Vis spectroscopy probes the bulk of the film, while the transport measurements probe the top surface, and the ratio between crystalline and amorphous domains can be different among the two. A more fundamental issue that will require further analysis is that the estimate from UV–Vis is obtained by probing the neutral molecules and neglects effects related to polaron formation that are instead captured by the Seebeck coefficient measurements¹⁷.

Evidence of low disorder narrow band conduction

From the experimental results we can draw some important general conclusions that do not rely on specific modeling. The observation of a $\frac{{k_{\mathrm{B}}}}{e}{\mathrm{ln}}(10)$-slope and the temperature independence of S is direct evidence that the band in the DoS that contributes to transport is narrow with negligible disorder and that we are in the non-degenerate limit (E_F outside the band). The Seebeck coefficient follows a modified Heikes’ formula³⁰ in which $\tilde N$ is not equal to the total DoS $\overline N = 10^{21}$ cm⁻³ that can be estimated from the density of repeat units of the polymer, but is 5 times smaller. This result is consistent with the semicrystalline microstructure of P(NDI2OD-T2). Our interpretation is that in this system $\tilde N$ reflects the DoS in the crystalline domains N_C, which is the band where most of the charges accumulate²¹. The temperature independence of S indicates that these states are not significantly disorder-broadened. The contribution to the DoS from the amorphous domains is expected to be energetically offset by more than 100 meV from the crystalline states due to the difference in bandgap between crystalline domains and amorphous regions and does not directly contribute to transport and to S²¹.

This raises the question how the strong gate voltage dependence of the mobility in the films annealed at 200 °C can be explained. It is straightforward to show generally that in the independent electron approximation no charge density dependence of the mobility can be observed for a narrow band semiconductor in the non-degenerate limit (full derivation presented in Supplementary Note 5): the observation of a $\frac{{k_{\mathrm{B}}}}{e}{\mathrm{ln}}(10)$-slope in the plot of the Seebeck coefficient versus the logarithm of the charge density is therefore not compatible with a charge density dependent mobility in the independent electron approximation. We would like to emphasize that these conclusions are general, are not obtained from a specific charge transport model and are made possible by the high accuracy with which the Seebeck measurements have been performed. The results rule out the possibility of describing transport using any type of model which is based on the effect of disorder on the DoS, since they rely on the semiconductor being treated as a degenerate system.

This is evident when fitting our results with a mobility edge (ME) model, as we did in Fig. 3 (a detailed description of the fits is presented in Supplementary Note 6)⁵. In the ME model, a tail of trap states extending in the band gap is added to the conduction band and the mobility is calculated from the occupancy ratio between mobile and trapped states. The fits are shown as dashed lines in Fig. 3. Within such a model a stronger charge density dependence of the mobility can be modeled by an increase in disorder and a broadening of the DoS: With increasing charge density, the chemical potential E_F moves higher in the band modifying the trapped (or low mobility) to high mobility charge carrier ratio. Such change is stronger for more disordered systems. To fit the experimental mobility data well a width of the tail states of 18 meV needs to be assumed for the as-cast sample and 42 meV for the annealed one. It was already argued earlier that these values are not consistent with microstructure and spectroscopic characterization, including GIWAXS and photothermal deflection spectroscopy measurements, in which both samples have similar energetic and positional disorder²¹. We can now show more convincingly that these DoS parameters required to fit the mobility data are also not consistent with the measured Seebeck coefficient. The modeled Seebeck coefficient calculated according to Eq. (1) has a much higher value than observed in the experiments, a stronger charge density dependence with a slope significantly higher than $\frac{{k_{\mathrm{B}}}}{e}{\mathrm{ln}}(10)$ and predicts a temperature dependence of the Seebeck coefficient which is much stronger than what could be consistent within the error of our Seebeck measurements. This shows that the agreement observed between fit and experimental mobility curve is just coincidental. The fit to the Seebeck data is closer to the $\frac{{k_{\mathrm{B}}}}{e}{\mathrm{ln}}(10)$-slope for the as-cast sample. Here, the measured charge density dependence of the mobility is much weaker, hence the data can be fit with the ME model using a tail density of N_tail = 1.8 × 10²⁰ cm⁻³. But the accuracy of the fit is still too poor (the model predicts a too large temperature dependence of the Seebeck coefficient) and the reason is that when the band tails extend in the forbidden energy gap the system cannot be considered as a non-degenerate semiconductor at the charge densities we are considering here, hence it is impossible for the model to predict the $\frac{{k_{\mathrm{B}}}}{e}{\mathrm{ln}}(10)$-slope we measure nor the lack of temperature dependence, regardless of the specific choice for the DoS.

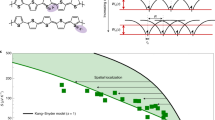
To show that this is a general issue and not specific to the model we chose, we have extended our comparison in Fig. 4a to other disorder based models which are commonly employed to describe charge transport in semicrystalline polymers including the one used in this work, P(NDI2OD-T2) (a detailed description of all fits is presented in Supplementary Notes 6 and 7)^7,21,31,32. The graph shows the measured Seebeck coefficient of the 200 °C annealed device versus conductivity at 300 and 200 K, as well as the fits with the different transport models. To convert the mobility into conductivity we estimated a channel thickness of 2 nm³³. A slightly different value would lead to a small rigid horizontal shift of the data which would not affect any of the conclusions obtained from the analysis. The original ME model by Mott was evaluated following a similar procedure as presented by Glaudell et al., i.e. fitting the temperature dependence of the conductivity at each charge carrier density in an Arrhenius plot, extracting the activation energy E_A = B ln(σ) + C (which was estimated to be equal to the activation energy of the Seebeck coefficient and assumed to be temperature independent), and hence evaluating S = $\frac{{k_{\mathrm{B}}}}{e}\left( {\frac{{B{\kern 1pt} {\mathrm{ln}}(\sigma ) + C}}{{k_{\mathrm{B}}T}}} \right)$ + A, with A ≥ 0 as a free fitting parameter^31,34. The fit fails to follow the temperature dependence because of the predicted 1/T-temperature dependence of the Seebeck coefficient, which is in contrast to the measured values which are temperature independent. The VRH model by Mott was evaluated by fixing γ = $\frac{1}{{d\,+\,1}}$ = $\frac{1}{3}$ according to 2d variable-range hopping, given our essentially 2d charge density profile, in σ = $\sigma _0{\kern 1pt} {\mathrm{exp}}\left[ { - \left( {\frac{{T_0}}{T}} \right)^\gamma } \right]$, extracting T₀ at each charge carrier density and consequently fitting the data with S = $\xi _{\mathrm{d}}T_0^{\frac{2}{{d + 1}}}T^{\frac{{d - 1}}{{d + 1}}}$, leaving the temperature independent numerical factor $\xi _{\mathrm{d}} \propto \left[ {\frac{{\partial {\kern 1pt} {\mathrm{ln}}\overline N (E)}}{{\partial E}}} \right]_{E\,=\,E_{\mathrm{F}}}$ as a free fitting parameter^7,35,36. The variable-range hopping model fails to explain our experimental data as the Seebeck coefficient is predicted to depend on temperature according to $S \propto T^{\frac{1}{3}}$, while the experimental data show a temperature independent Seebeck coefficient. Furthermore, the predicted slope of the Seebeck coefficient with respect to conductivity is too high to resemble the data. Finally, the data has been fit with the model Snyder and coworkers developed for doped conducting polymers by fixing s = 1 or s = 3, obtaining η(T, n) from S(T, n), extracting σ₀(T) from a linear regression fit of s × F_s−1(η) versus σ at each temperature and finally calculating the conductivity according to σ = σ₀(T) × sF_s−1(η), where $F_i(\eta )$ = ${\int}_0^\infty \frac{{\epsilon ^i}}{{1 + {\mathrm{exp}}(\epsilon - \eta )}}{\mathrm{d}}\epsilon$ is the non-normalized complete Fermi-Dirac integral and the Seebeck coefficient according to S = $\frac{{k_{\mathrm{B}}}}{e}\left[ {\frac{{(s + 1)F_s(\eta )}}{{sF_{s - 1}(\eta )}} - \eta } \right]$³². In this case the slope of the Seebeck coefficient versus conductivity curve is far too steep, regardless of the type of conduction considered (s = 1 for acoustic-phonon scattering, s = 3 for ionized-impurity scattering), particularly visible for the 200 K data. Although the model has been shown to work for chemically doped polymer films, we argue that the presence of counterions in molecularly doped polymer films leads to a strong broadening of the DoS, which is not the case for the electrostatically doped semiconductors in this study for which no broadening is observed upon introduction of additional charge carriers (also in consideration of the much lower charge density achievable in an FET geometry)³⁷. We have also investigated a simple two-band, independent electron model with adjustable energy gap between the two states and adjustable total number of states in both bands (details presented in Supplementary Note 8). Similar limitations and shortcomings appear also when using more complex models: Lu et al. have developed a thermoelectric transport model using percolation theory in a disorder broadened Gaussian DoS which shows that in disordered systems the Seebeck coefficient is strongly enhanced with increasing disorder. Our data would indicate negligible disorder (<0.5 k_BT) for both annealed and as-cast films. For such low disorder the model would predict very low charge density dependence of the mobility for both preparation conditions, in clear contrast with our results³⁸. A similar treatment which takes into account also the charge carrier delocalisation also fails to describe our results, as it is not able to simultaneously describe charge density and temperature dependence of Seebeck coefficient and mobility^4,39. The general issue that becomes evident in all these models is that the strong gate voltage dependence of the mobility that is observed experimentally in the annealed sample can be modeled only in the degenerate limit for strong disorder. This is incompatible with the (lack of) temperature dependence and the charge density dependence of the Seebeck coefficient which we experimentally measure.

Fig. 4

Seebeck coefficient S versus conductivity σ as well as Coulomb enhanced charge transport (CET) model illustration. The measured Seebeck coefficient versus conductivity of the 200 °C annealed device at 300 and 200 K, as well as the fits of different transport models are shown in the top (a)^7,21,31,32. The fitting parameters for the CET model (solid black and solid blue line)²¹ are the same as in Fig. 3. For the fits with Snyder and coworkers model the following conductivity prefactors were used: σ₀ = 0.151 S cm⁻¹ (s = 1, 300 K, turquoise dashed line), σ₀ = 2.2 mS cm⁻¹ (s = 3, 300 K, olive dashed line), σ₀ = 0.051 S cm⁻¹ (s = 1, 200 K, purple dashed line) and σ₀ = 0.82 mS cm⁻¹ (s = 3, 200 K, dark green dashed line). For the fits with the VRH Mott model the following parameters were used: γ = 1/3 and ξ_d = 6.15387 nV K⁻² (pink and green dashed dotted lines). A = 0 has been used for the ME Mott fits (orange and dark red dashed lines). The bottom (b) illustrates the two key processes of the CET model. The first process is exemplified as having single independent electrons in a crystalline domain and the second process of two charges in a crystalline domain raised in energy due to their Coulomb interaction

Modeling transport with the inclusion of e⁻e⁻-interactions

Having shown that no disorder based model can explain our results and having demonstrated from basic principles that in an independent electron approximation the non-degenerate limit and the charge density dependence of the mobility are incompatible, we need to revisit the main assumptions behind Eqs. (1) and (2). Two aspects that are neglected in our analysis are (a) the non-homogeneous nature of the DoS and (b) that electrons confined within nanoscale crystalline domains can experience strong local electron-electron interactions. In our system the surface density of crystalline domains is approximately 10¹²−10¹³ cm⁻² (from the GIWAXS measurements with spectroscopic estimates of the total volume fraction between crystalline and amorphous domains (about 1:1)²¹). In our transport regime also the surface electron density is around 10¹² cm⁻². This suggests indeed that multiple occupancy of crystallites cannot be neglected.

We have recently introduced a simple transport model that lifts these two assumptions by incorporating both a non-uniform DoS and taking into account electron–electron interactions due to multiple occupancy of crystallites, which we have improved upon in this work. This Coulomb enhanced charge transport (CET) model is able to consistently explain the mobility data as well as microstructrual and spectroscopic characterization of P(NDI2OD-T2)²¹. It assumes charges to be confined to nanoscale crystalline domains, separated by amorphous regions (Fig. 1c). These regions act as potential barriers for charges moving from a crystallite to an adjacent one. The value for the potential barrier will depend on the local configuration of the molecules at the interface, but is considered as an average value E_barr for our macroscopic electrical measurements. The local Coulomb repulsion between multiple charge carriers accumulated in the same crystalline domain provides additional energy to overcome this energy barrier E_barr and allows a small fraction of the accumulated charges to be transported with much higher mobility. The two processes are illustrated in Fig. 4b, where we exemplify the process as having single independent electrons in a crystalline domain for the first process and two electrons next to each other for the charges experiencing Coulomb interaction. We ignore energetic disorder within the crystalline domains and assume that there are in total N_C isoenergetic states per unit volume within the crystalline domains. N_C can be estimated from the temperature-independent value of $\tilde N$ extracted from the experimental Seebeck data above. We then consider two populations of charges, one for non-interacting electrons for which Coulomb interaction can be neglected (n_1C) and a second one (n_2C) for charges which experience a strong Coulomb interaction increasing the electron energy by a charging energy U_C > E_barr. This effect is modelled by mapping non-interacting and electrostatically interacting electrons into a charge density dependent single electron density of state where we assume that each charge that accumulates in the crystalline domains lifts ν states in energy by U_C, which are available to accommodate a second electron which can then travel with much higher mobility. The total DoS is split into two narrow bands: one band of states at energy E_C with density N_C − νn_1C for low mobility charges and the other band of states at E_2C = E_C + U_C and density N_2C = νn_1C for high mobility charges. The total number of states N_C is fixed but the number of states N_2C increases with increasing charge density, and the two populations can be determined according to the following equation:

$$\begin{array}{*{20}{l}} {g(E)} = {\left[ {N_{\mathrm{C}} - \nu n_{{\mathrm{1C}}}} \right]\delta \left( {E - E_{\mathrm{C}}} \right) + \nu n_{{\mathrm{1C}}}\delta \left( {E - E_{{\mathrm{2C}}}} \right)} \hfill \\ {} \hskip 18pt= {N_{\mathrm{C}} \times \left( {1 - \frac{{\nu f\left( {E_{\mathrm{C}}} \right)}}{{1 + \nu f\left( {E_{\mathrm{C}}} \right)}}} \right)\delta \left( {E - E_{\mathrm{C}}} \right)} \hfill \\ {} \hskip 18pt+ {\frac{{N_{\mathrm{C}}\nu f\left( {E_{\mathrm{C}}} \right)}}{{1 + \nu f\left( {E_{\mathrm{C}}} \right)}}\delta \left( {E - E_{{\mathrm{2C}}}} \right),} \hfill \end{array}$$

(4)

where n_1C and n_2C = νn_1C f(E_2C) are the charge densities of low and high mobility electrons and f(E) is the Fermi-Dirac distribution function. Equation (4) leads to the following occupancy ratio (in the non-degenerate limit):

$$\frac{{n_{{\mathrm{2C}}}}}{{n_{{\mathrm{1C}}}}} = f\left( {E_{\mathrm{C}},E_{\mathrm{F}}} \right)e^{{\mathrm ln}(\nu ) - \frac{{U_{\mathrm{C}}}}{{k_{\mathrm{B}}T}}} \cong \frac{n}{{N_{\mathrm{C}}}}e^{ - \frac{G}{{k_{\mathrm{B}}T}}},$$

(5)

where G = U_C−k_BT ln(ν) is the free energy associated with the interacting charge pair, and n = n_1C + n_2C. The right-hand side shows the main qualitative features of this approach. The population ratio increases with increasing charge density, the feature responsible for the observed charge density dependence of the mobility. An increase in crystallite size results in a decrease in the free energy by both reducing the Coulomb repulsion experienced by the two electrons (hence reducing U_C) and increasing the available states (ν) for the formation of such charge pair.

The two populations of charges can be used to obtain the macroscopic electron mobility from a charge density average considering that high mobility electrons represent the electron of an interacting charge pair which can overcome the energy barrier and travel with a higher mobility, following the same approach used by Emin in the ref. ⁴⁰:

$$\mu = \frac{{n_{{\mathrm{1C}}}\mu _{{\mathrm{1C}}} + n_{{\mathrm{2C}}}\mu _{{\mathrm{2C}}}}}{{n_{{\mathrm{1C}}} + n_{{\mathrm{2C}}}}}.$$

(6)

Here, $\mu _{{\mathrm{1C}}} = \mu _0{\kern 1pt} {\mathrm{exp}}\left( { - \frac{{E_{{\mathrm{barr}}}}}{{k_{\mathrm{B}}T}}} \right)$ is the mobility of low mobility electrons (representative of non-interacting electrons), which is limited by thermal activation across the energy barrier and $\mu _{{\mathrm{2C}}} = \mu _{{\mathrm{02C}}} \times \frac{{300{\kern 1pt} {\mathrm{K}}}}{T}$ is the mobility of high mobility charges (representative of the electron–electron pairs experiencing sufficient Coulomb repulsion), which is assumed to be scattering limited and significantly higher than μ_1C. The mobility pre-factors μ₀ and μ_02C are determined by the microscopic properties of the material. In this model the spatial inhomogeneity is responsible for the temperature activated dependence of the mobility, but the amorphous region is not explicitly included in the DoS as a further parallel conduction channel for simplicity. It would not change in fact any of the fits appreciably. As shown previously, the amount of charges in the high energy amorphous band would always be below 5% of the total charge density, as confirmed experimentally through charge accumulation spectroscopy (CAS) measurements, and well within the uncertainty on the experimentally measured charge density. The changes to the different charge densities upon inclusion of the amorphous band are therefore negligible compared to our experimental sensitivity. Combined with the much lower mobility charges have in the amorphous phase the contribution such charges would give to both mobility and Seebeck calculations would be even less relevant.

In order to calculate the Seebeck coefficient it is paramount to take into account that the two energy bands that form our DoS are not present at the same point in space: if charges are electrostatically interacting only the high energy band is present, if they do not interact only the lower band is present. We cannot plug the DoS in Eq. (4) directly into Eq. (1) as doing so is equivalent to considering the two bands as present in parallel everywhere in space and will lead to a large overestimation of the Seebeck coefficient (further simulations are presented in Supplementary Note 8). The contribution to the Seebeck coefficient of the two charge populations can instead be readily calculated by considering the entropy of such a system and exploiting the definition of the Seebeck coefficient as entropy transported per unit charge, an approach already detailed in the ref. ⁴⁰. The macroscopic Seebeck coefficient is given by:

$$S = - \frac{{k_{\mathrm{B}}}}{q}\left\{ {{\mathrm{ln}}\left[ {\frac{{\left( {N_{\mathrm{C}} - 2n_{{\mathrm{1C}}}} \right)}}{{n_{{\mathrm{1C}}}}}} \right] - \frac{{\partial n_{{\mathrm{2C}}}}}{{\partial n}}{\mathrm{ln}}\left( {\frac{{n_{{\mathrm{2C}}}}}{{n_{{\mathrm{1C}}}}}} \right)} \right\},$$

(7)

where q is the charge transported by each carrier. Considering that the number of doubly occupied crystalline domains is predicted to be always below 5% of the total accumulated charge density $\left( {\frac{{\partial n_{{\mathrm{2C}}}}}{{\partial n}} \cong \frac{{n_{{\mathrm{2C}}}}}{{n_{{\mathrm{1C}}}}} \cong 10^{ - 2}} \right)$ it is readily seen that the inclusion of short range electron–electron interactions has a negligible effect on the Seebeck coefficient. Equation (7) is effectively equal to Heikes’ formula for a system of fermions with forbidden occupancy of the same site (i.e., no bipolaron formation), regardless of the extension of the crystalline domains⁴¹. It is important to note that the Seebeck coefficient in Eq. (7) is not explicitly dependent on the mobility of the two charge populations, since the mobility enhancement is a local effect caused by Coulomb interactions rather than due to different channels present in parallel for charge transport. The fits to the data are reported as solid lines in Figs. 3 and 4a and show the agreement with a slightly modified Heikes’ formula with a $\frac{{k_{\mathrm{B}}}}{e}{\mathrm{ln}}(10)$-slope and no temperature dependence. On the other hand, the impact of sufficiently strong Coulomb interacting electrons on the macroscopic electron mobility is much stronger due to the much higher mobility of this small charge population. The close fit of both datasets is summarized in Fig. 4a where it is shown how the presented model finally allows us to accurately fit the data both in terms of slope and temperature dependence, in agreement with the structural characterization. It is important to note that when fitting mobility and Seebeck data at the same time, only 4 parameters are available to fit the mobility data (E_barr, μ_02C, μ₀, and G), of which only 2, the free energy associated with an interacting charge pair G and the mobility prefactor μ₀ are different between the different preparation conditions. We did not attempt to determine ν from the fits, as we do not have an independent estimate of U_C. However, the Seebeck coefficient provides a direct estimation of the total number of states in the conduction band within the crystalline domains (N_C = 2 × 10²⁰ cm⁻³). We note that this value is approx. one order of magnitude higher than the effective DoS at room-temperature for crystalline silicon (N_C = 2.86 × 10¹⁹ cm⁻³ and N_V = 3.10 × 10¹⁹ cm⁻³)⁴², highlighting the suitability of narrow band polymer semiconductors for thermoelectric applications. Together with the observation that crystallinity can be used to selectively increase the electrical conductivity without affecting the Seebeck coefficient, increasing crystallinity provides a method to improve the power factor of organic based thermoelectric generators⁴³. Our theoretical model shows the importance of introducing a more realistic inhomogeneous DoS and the presence of local electron–electron interactions which are necessary to fully explain the experimental data. This concept was also explored in the limit of infinite temperature in the theoretical work by Beni for charge transport in the correlated electron regime in a narrow-band Hubbard chain at arbitrary electron density⁴⁴. Both approaches predict a Seebeck coefficient resembling a slightly modified Heikes formula with the characteristic $\frac{{k_{\mathrm{B}}}}{e}{\mathrm{ln}}(10)$-slope in the low occupancy limit. One important feature of the Seebeck coefficient in a correlated electron system is a sign change of the Seebeck coefficient at a charge density n < N_sites (for the charging energy $U \gg k_{\mathrm{B}}T$), which is also expected in our treatment (a full analysis is given in Supplementary Note 9). In order to reach such regime however a higher charge density regime needs to be attained and further improvements on the accuracy of the measurement are required.

Discussion

In conclusion, we have demonstrated that charge transport within and between crystalline domains in high-mobility, semicrystalline polymer semiconductors is not determined by energetic disorder effects, but involves a relatively narrow DoS, that manifests itself in a temperature independent Seebeck coefficient approximately following a modified Heikes’ formula. To explain a pronounced carrier concentration dependence of the mobility in this transport regime we have shown that electron-electron interactions between the carriers in the small crystalline domains need to be considered. We have constructed a charge transport model that is able to consistently explain mobility and Seebeck measurements as a function of carrier concentration and temperature. The model is simplistic, in particular, in the way that it takes into account the complex energy spectrum of crystalline domains that are occupied by multiple, Coulomb-interacting charges but it nevertheless provides important insight into how electron-electron interactions affect the structure-property relationships and provides a foundation for further improvements in the carrier mobilities and thermoelectric performance of this important class of conjugated polymers.

Methods

Grazing incident wide angle X-ray scattering

GIWAXS measurements were performed at the SAXS/WAXS beamline at the Australian Synchrotron⁴⁵. 15 keV photons were used with two-dimensional scattering patterns recorded on a Dectris Pilatus 1 M detector. Images shown in the manuscript were acquired at an incident angle close to the critical angle. Such images were chosen from a series of images taken with incident X-ray angle varying from 0.02° to 0.15° in steps of 0.01° with the chosen image showing the highest scattering intensity. The X-ray exposure time was 1 s such that no film damage was identified. The sample-to-detector distance was calibrated using a silver behenate sample. The results were analysed by an altered version of the NIKA 2D⁴⁶ based in IgorPro.

Device preparation

The device structure, a bottom-contact top-gate field-effect transistor structure with an on-chip heater, used to measure the charge carrier density and temperature dependent saturation mobility and Seebeck coefficient of the semicrystalline polymer poly([N,N′-bis(2-octyldodecyl)-naphthalene-1,4,5,8-bis(dicarboximide)-2,6-diyl]-alt-5,5′-(2,2′-bithiophene)) (P(NDI2OD-T2))¹⁶ is shown in Fig. 1a and was adopted from the refs.^2,27. The eight contact pads used for the four-point-probe sensor resistance calibrations as well as the two for the on-chip heater are shown in golden color, the patterned semiconductor in green and the gate in dark gray. The dimensions of the active layer of the device are a width of one millimeter (W = 1 mm), a channel length of fifty micrometer (L = 50 μm) and a spacing between the heater stripe and the hot sensor of twenty micrometer. Chromium/Gold (3 nm/12 nm) contacts are used for the sensors and heater (plus a second double layer of 3 nm/50 nm of chromium/gold for the contact pads to improve contact), while the active layer is an approx. thirty-five nanometer thick film of the semiconducting polymer P(NDI2OD-T2). A layer of approx. 300 nm of poly(methyl methacrylate) (PMMA) is used as the dielectric layer and a 25 nm thick layer of Aluminum is employed for the gate contact. The devices were fabricated as follows: glass slides have been cut to approx. 1.7 cm × 1.7 cm substrates, which subsequently were cleaned in four ultrasonication steps in Decon 90 diluted in deionized (DI) water, DI water, acetone, and 2-propanol for 10 min each, followed by microwave plasma cleaning (250 W for 10 min). The bottom contacts were fabricated via double resist LORB/S1813 photolithography and thermal evaporation of chromium/gold. P(NDI2OD-T2) (Polyera N2200, M_N = 29.3 kg mol⁻¹, M_W = 101.7 kg mol⁻¹, PDI = 3.5) was dissolved in toluene with 5 mg ml⁻¹ concentration, heated for 6 h at 90 °C and spin-coated at 2000 rpm for 60 s. Depending on the desired condition the device was either annealed at 200 °C for 15 min (ann.) or dried in vacuum (as-cast). After the patterning of P(NDI2OD-T2) according to the ref. ⁴⁷, PMMA (M_N = 318 kDa) from Polymer Source was dissolved in n-butyl-acetate with 45 mg ml⁻¹ concentration and spin-coated at 1000 rpm for 120 s. Finally, a 25 nm thick aluminum gate electrode was evaporated using a shadow mask.

Device characterization

The transistor transfer curves, the sensor resistance measurements as well as the thermal voltage measurements were performed within a cryogenic testing chamber BCT-43 MDC Nagase & Co., LTD. with six probes controlled by an Agilent 4156B Semiconductor Parameter Analyser (SPA) (Supplementary Note 3). The transfer curves were measured in a condition V_gs = V_ds + V_on (V_on the onset voltage) at each gate voltage in order to ensure that the transistor is operated in the saturation regime during the entire measurement. V_on was determined by taking several transfer measurements with different values for V_on and choosing the value which lead to a clear onset in the transfer measurement and a drain current on the order of the noise level for voltages V_gs < V_on (at 300 K V_on = −8 V for the annealed sample and V_on = −1 V for the as-cast sample). Consequently, the saturation mobilities were extracted according to ref. ^28. The gate voltages were used to calculate the accumulated charge carrier density via the relationship: n = $\frac{{\epsilon _0 \times \epsilon _{\mathrm{r}}}}{{d \times h}} \times \left( {V_{{\mathrm{gs}}} - V_{{\mathrm{on}}}} \right)$, where $\epsilon _{\mathrm{r}}$ = 3.6 for PMMA, d = 300 nm for the dielectric layer thickness and the height of the accumulation layer was assumed to be h = 2 nm³³. In principle the thermal voltages as well as the temperature differences between the sensors and hence the Seebeck coefficients were measured according to the refs. ^2,27. 4-point-probe resistance measurements were used for the calibration of the sensors in order to get accurate values for the temperature coefficients of the sensor resistances. Further details on the exact measurement procedure are reported in Supplementary Note 3.

Data availability

The data that support the findings of this study are available at the University of Cambridge data repository at https://doi.org/10.17863/CAM.22237.