Abstract
Methylammonium lead iodide is a benchmark hybrid organic perovskite material used for low-cost printed solar cells with a power conversion efficiency of over 20%. Nevertheless, the nature of light–matter interaction in hybrid perovskites and the exact physical mechanism underlying device operation are currently debated. Here, we report room temperature, ultrafast photocurrent generation, and free-space terahertz emission from unbiased hybrid perovskites induced by femtosecond light pulses. The polarization dependence of the observed photoresponse is consistent with the bulk photovoltaic effect caused by a combination of injection and shift currents. Observation of this type of photocurrents sheds light on the low recombination and long carrier diffusion lengths arising from the indirect bandgap in CH3NH3PbI3. Naturally ballistic shift and injection photocurrents may enable third-generation perovskite solar cells with efficiency exceeding the Shockley–Queisser limit. The demonstrated control over photocurrents with light polarization also opens new venues toward perovskite spintronics and tunable THz devices.
Similar content being viewed by others
Introduction
The bulk photovoltaic effect (BPVE) is a striking quantum phenomenon that is observed in non-centrosymmetric crystals1. Unlike the conventional p-n junction-based photovoltaic (PV) mechanisms, the BPVE does not require a built-in electric field. There are two proposed mechanisms of the BPVE: injection and shift. The injection (also sometimes called ballistic2) currents are associated with hot carriers in a crystal and are caused by the asymmetric distribution of their momenta. Photoexcited hot carriers lose their energy and descend to the bottom of conduction band over a free path, which can be hundreds of nanometres1. Injection currents give rise to the circular photogalvanic effect (CPGE), which depends on the helicity of the incident light. The CPGE has been experimentally observed in quantum wells3. It has also been observed in tellurium crystals with significant spin–orbit valence band splitting4, in topological insulators with spin-split surface states5,6 and 2D transition metal dichalcogenides7. In the shift current mechanism, the driving force for the carriers is the coherent evolution of the electron and hole wave functions owing to non-diagonal elements of the density matrix8. The shift currents are responsible for the linear photogalvanic effect (LPGE), which depends on the linear polarization.
On the macroscopic level, both injection (CPGE) and shift (LPGE) currents can be linked to second-order optical nonlinear effects, as
where the Greek letter subscripts refer to the Cartesian coordinates, β σμv is a third-rank photogalvanic tensor, e is the unit vector of light wave polarization and \(E_0^2\) is the light intensity. For both mechanisms, the current dynamics are expected to be on a subpicosecond time scale; thus, BPVE currents are often accompanied by free-space THz emission upon femtosecond optical excitation9. Moreover, hot carrier harvesting enables the generation of a photovoltage that can greatly exceed the band gap10. Therefore, solar cell devices based on the BPVE can theoretically show a power conversion efficiency (PCE) that exceeds the Shockley–Queisser limit11 for excitonic PV cells12.
Methylammonium lead iodide (MAPI) has a tetragonal ABX3 perovskite structure at room temperature with a polar molecular cation CH3NH3+ at each A-site13,14,15,16,17,18,19. It was recently predicted that it is possible to observe the BPVE for the polar configurations of the MAPI crystal structure20,21,22,23. Strong spin–orbit coupling in heavy Pb atom and inversion symmetry breaking (e.g., due to organic cation rotation) lead to Rashba-type spin splitting with a preferred spin orientation orthogonal to the momentum and the direction of inversion symmetry breaking24. Density functional theory (DFT) calculations show that such spin texture can lead to the CPGE, where, due to angular momentum selection rules and spin-momentum locking, interband optical transitions respond asymmetrically to the right- or left-handed circular polarization or light helicity25.
Here, we demonstrate the generation of polarization-sensitive ultrafast photocurrents and free-space terahertz emission in unbiased MAPI at room temperature. By measuring the amplitude and time-domain waveforms of the photocurrents under excitation with different optical polarizations, incidence angles, and wavelengths, we extract the contributions of the injection photocurrents (sensitive to helicity) and shift photocurrents (sensitive to linear polarization) from the overall photocurrent response. The simultaneous observation of both “circular” and “linear” photocurrents is direct evidence of a strong BPVE in MAPI, providing a fundamentally new route for third-generation PV solar energy conversion.
Results
Polarization-dependent photocurrents
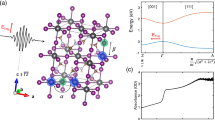
The optical scheme of the experimental setup is shown in Fig. 1a. For these experiments, a 350 nm thick MAPI film was deposited on a soda lime glass substrate with pre-patterned 120 nm thick indium tin oxide (ITO) electrodes (see Methods section). MAPI films were optically excited with either single-beam continuous wave (CW) laser diodes operating at 532 and 650 nm or fundamental (780 nm) and second-harmonic (390 nm) radiation from femtosecond-pulsed lasers (see Methods section). Photoinduced currents were measured as a voltage drop, U ∝ J, across a 50 Ω load resistor and recorded in unbiased samples with a storage oscilloscope. By changing the orientation of the MAPI sample (angle φ in Fig. 1a), we were able to measure the longitudinal (J x , when φ = 0°) and transverse (J y , when φ = 90o) currents with respect to the light incidence plane components of the induced photocurrent. Polarization dependences of the induced J x and J y were identified by measuring the peak-to-peak amplitude of the corresponding photocurrent waveform while rotating a quarter (λ/4) waveplate positioned in front of the sample by an angle α, which varied the state of the laser polarization with a period of 90° and 180o, respectively. Fig. 1b shows the waveforms of J y components obtained at incidence angles of 45° and −45°. Fig. 1c, d shows the dependence of the respective photocurrents J x and J y excited with femtosecond pulses at 390 nm on the λ/4 waveplate angle. This dependence is the most informative for starting our analysis of the photocurrent generation in MAPI because it should contain contributions from all possible mechanisms. The presented data show that both J x and J y components of the photocurrent induced in MAPI by obliquely incident light exhibit strong polarization dependence and change their sign upon reversing the direction of incidence from 45° to −45°.
Polarization dependent photocurrent in unbiased MAPI sample at room temperature. Configuration (a) and temporal profiles of photocurrent response measured (b) at different incidence angles (θ = 45o: red colour; θ = −45o: blue colour) in the transversal (φ = 90°) geometry of the experiment. c and d Excitation beam polarization dependence of correspondingly longitudinal (J x , φ = 0°) and transversal (J y , φ = 90°) components of photocurrent response measured at 45° incidence. The excitation beam polarization state is controlled by rotation of the quarter wave-plate with a step of 5 degrees. 45° and 225° angles correspond to left circular polarization; 135° and 315° correspond to right circular polarization. The open circles are the experimental data. The fitting data with function J = J 0 + C·sin(2α) + L1·cos(4α) + L2·sin(4α) are shown with solid lines
The overall dependence of J on α demonstrates a complex behaviour that is well described by an oscillating function consisting of four components
where D is a polarization-independent offset ascribed to laser-heating gradients or the photo-Dember effect in the sample (we confirm the origin of this offset by sweeping the laser spot across two electrodes with a fixed polarization; see Supplementary Figure 1). This offset is present in all data obtained for both J x and J y components. To prevent the temperature gradient between the contacts necessary for the thermoelectric effect and to minimize the offset D in our measurements, the laser spot was always centred between the contacts. However, owing to the finite size of the laser spot on the sample, some small polarization-independent contribution offset was always observed. The coefficient D varies from measurement to measurement because we used different laser sources and samples. The coefficient C describes the strength of the circular (helicity-dependent) contribution to the photocurrent because the rotation of the λ/4 waveplate causes the light polarization to vary between left (σ−) and right (σ+) circular polarization with the functional form sin(2α). The coefficients L1 and L2 in (1) parameterize the helicity-independent photocurrents caused by the rotation of linear polarization with the functional forms cos(4α) and sin(4α), respectively. For the α angles of 45° and 135° (purely circular polarization), the linear contribution vanishes.
The principal observation made from polarization-dependent measurements is that oblique incidence excitation of the MAPI sample with right and left circularly polarized light leads to the generation of transverse (J y ) photocurrents flowing along opposite directions, while the longitudinal (J x ) photocurrents do not “feel” the helicity of light and depend only on the rotation of linear polarization. The amplitudes of polarization-sensitive J x and J y photocurrents linearly depend on the radiation intensity. We should also note here that the helicity dependence completely vanishes at normal incidence, while minor modulation of J x and J y amplitudes with a change in the linear polarization angle persists even under normally incident light (Supplementary Figure 2).
Analysis of circular and linear polarization-dependent photocurrents
The overall behaviour of the observed photocurrents falls under the class of second-order nonlinear effects, which include circular and linear photogalvanic effects (also known as injection and shift currents or BPVE8) and the photon-drag effect (also known as the AC Hall effect26 or light-induced drift currents27). The fundamentally distinct feature of this class of effects compared to the conventional PV optical effects, where charge carrier separation (photocurrent) is only possible when internal or external fields are applied, is the possibility to observe an intrinsic and instantaneous photocurrent response of excited carriers with no external influence on the carriers. In general, the second-order optical response is allowed in the material if either (i) the spatial inversion symmetry of the material is broken or (ii) second-order conductivities change their sign at spatial inversion [i.e., there is a linear coupling between the current and photon wavevector 8]. The second case is related to the momentum transfer from a photon to the excited carrier. While both circular and linear photogalvanic effects are possible only in systems that lack inversion symmetry, the photocurrent proportional to photon momentum does not require centrosymmetry, and it is therefore allowed in any medium. Similar to the photogalvanic effect, the photon drag effect in principle occurs in response to both linearly and circularly polarized radiation. Thus, these two phenomena show an indistinguishable dependence on light polarization. However, there is a significant difference between the effects in terms of wavevectors. In particular, the photogalvanic effect is an even function of the wavevector (the photoresponse does not change sign when k is replaced with −k), while photon-drag is odd (i.e., the photoresponse does change sign). Therefore, the photocurrents associated with the photogalvanic and photon-drag effects demonstrate distinct behaviour and can be distinguished in the experiment by reversing the excitation beam direction. In the experiment, the reverse of the wavevector direction can be realized by applying front and back illumination of the sample28 (Note that there is no difference between the back and front excitations in terms of the sample geometry. As shown in Supplementary Figure 3, the MAPI film is covered with encapsulation glass of the same quality as the substrate). To elucidate the particular mechanisms of the polarization-sensitive photocurrents generated in the MAPI samples, we further focus on analysing the transverse component J y under the back and front excitations. The experimental dependences of the photocurrent amplitude on the quarter-waveplate angle obtained under front and back illumination of the MAPI sample incident at 45° with a femtosecond laser at 390 nm are summarized in Fig. 2. The data are fitted with Eq. (2), and the percentile contributions of the different types of photocurrents extracted from the fitting are shown on a bar plot on the right side of the figure. Strikingly, at first glance, the photocurrents excited from the front and the back sides of the sample show different dependence on the polarization state, while the average amplitude of the photocurrent signal remains constant. Namely, the photocurrent contribution depending on linear polarization (L1 and L2 coefficients in Eq. (2)) decreases in the case of back excitation. By contrast, the amplitude of the circular photocurrent (C) is larger in this case. To exclude any influence of the pulsed nature of the light on the amplitude and the sign of J y photocurrents excited from the front and back sides, we performed independent measurements with a CW laser. Excitation of the MAPI sample with a CW laser leads to a DC photocurrent response, which can be detected via the occurrence of a constant positive or negative (depending on the sample orientation and incidence polarization) offset on the oscilloscope. The photocurrent traces taken with CW lasers operating at 650 and 532 nm under excitation from both sides of the MAPI sample are shown in Fig. 2. The data taken with the CW laser irradiation are in agreement with the femtosecond data and qualitatively confirm the decrease in linear L1 and L2 contributions and the increase in circular current C upon changing the direction of excitation. A decrease in the linear contribution with the change in the direction of propagation of light provides evidence for the assumption that there are two types of currents responsible for the dependence on linear polarization. Indeed, when exciting the sample from the front side, the dependence on the linear polarization is due to the combination of parallel linear photogalvanic and photon drag currents. When changing the direction of the excitation, these currents become antiparallel: the photon-drag current changes sign, while the direction of the shift current remains the same. If one assumes that the amplitudes of shift and photon-drag currents are the same, in the case of back excitation, they should compensate each other, and in turn, the linear contribution to the photoresponse would become zero. In reality, the amplitudes and temporal dynamics of the shift and photon-drag currents are not equal and might also depend on the excitation wavelength. This qualitative picture is in agreement with the experimental data presented in Fig. 2, where the complete compensation of the linear component is never achieved.
Wavelength dependent contributions of circular and linear polarization sensitive photocurrents. Open circles represent the experimental data obtained from the MAPI sample excited with a a second-harmonic femtosecond Ti:Sa laser (390 nm) and CW laser diodes operating at 532 nm (b) and 650 nm (c). The photocurrents demonstrate different behaviour when the sample is excited from the front (lighter colour) and back (darker colour) sides. The corresponding percentile contributions of different types of photocurrents extracted from fitting are shown as bar plots on figures (d-f). Coefficients C, L1, and L2 are the fitting parameters from Eq. (2). Fitting is shown with solid lines
Terahertz emission
Upon excitation with femtosecond pulses, the duration of the induced AC response obtained from the MAPI sample is determined by the registration system bandwidth rather than by the relaxation time of the excited carriers, while its magnitude represents the time-integrated current. Since the photocurrent is triggered by a sub-picosecond-long laser pulse and the current dynamics are also expected to be on a subpicosecond time scale, the time-varying current J can result in the emission of the THz wave in proportion to ∂J/∂t. Since these photoexcitations occur in the unbiased sample, the transient photocurrents J x and J y or the resultant free-space emission of p- or s-polarized THz radiation, respectively, provides information regarding the internal bias near the sample surface or the relevant electrodynamics parameters. Owing to the limited time resolution in the photocurrent experiments, without information on the transient response of the current, it is difficult to conclude whether the charge current is induced directly by light illumination or indirectly by some other effects, e.g., the photo-Dember or thermo-effect. To detect the instantaneous polarization-sensitive photocurrent response upon excitation with femtosecond light pulses in the MAPI samples, we employed time-resolved THz emission spectroscopy. Typical transient waveforms of the emitted THz radiation detected with electro-optic sampling at the far field under oblique excitation with linear and circular photon polarizations are shown in Fig. 3a. The emitted THz pulses have a picosecond duration and consist of a nearly single cycle oscillation. The shape of the THz waveform remains essentially constant for all incident polarizations and fluences. The THz frequency spectra obtained by Fourier transformation of the corresponding transient waveform are shown in Fig. 3a, b. The frequency of the maximum THz amplitude is ~0.7 THz. Theoretically, the temporal dynamics of the shift currents is different from that of the injection and photon-drag currents29. The shift current directly follows the time-domain profile of the optical pulse intensity, whereas only the front of the other transient currents follows this profile. The decay of injection and photon-drag currents is determined by the momentum relaxation time in the medium. However, in experiment, due to ultrafast momentum scattering of the carriers, the transient dynamics of different currents is indistinguishable on a subpicosecond time scale, which is in agreement with the virtually identical THz time-domain waveforms obtained under excitation with linear and circular polarization (see Fig. 3a).
Polarization-dependent coherent terahertz emission from unbiased MAPI at room temperature. Excitation of the MAPI sample with femtosecond laser pulses leads to efficient emission of THz radiation. The typical transient waveforms of the emitted THz radiation detected with a GaP EO crystal at the far field under oblique excitation with linear (black curve), right circular (red curve), and left circular (blue curve) excitation beam polarization is shown in a. Typical THz frequency spectra obtained by Fourier transform of the transient waveforms for the case of right circular (red curve) and left circular (blue curve) polarizations are shown in b. (c) Photon-polarization dependence of the emitted THz field amplitude and fitting with Eq. (2) are shown with open circles and solid line correspondingly. The fitting results are shown in the bar plot on the right part of c
To additionally confirm that the emitted THz radiation arises from the same mechanism as the photocurrents presented in Fig. 2, we varied the polarization of the pump (second-harmonic) beam using a quarter-waveplate. In Fig. 3c, the y-component of the generated THz electric field is plotted as a function of the polarization state of the incident pump light. The measured polarization dependence resembles those obtained with contact measurements and is well fitted with Eq. (2). The results of fitting are shown in the inset of Fig. 3c.
Discussion
Since all our optical measurements were performed with the same film that is used for the PV cells at room temperature, we believe that our findings can also help to understand the photophysics of perovskite solar cell devices and ultimately engineer devices with record efficiencies that would challenge the S-Q limit. First, from observation of the CPGE, we conclude that MAPI films at room temperature lack inversion symmetry. There could be several reasons why this is the case. For instance, it is possible that the sample surface is supplying the necessary symmetry breaking (which would be consistent with the small response for normal incidence). Indeed, the geometry of the sample (see Supplementary Figure 3) where the top and the bottom surfaces of the MAPI film are inequivalent may lead to a net broken symmetry (even if uniform generation over the layer thickness is assumed). We also note that breaking bulk inversion symmetry in our experiments can be caused by light-induced polarons, which lead to the collective distortion of the crystal lattice30,31. In fact, the presence or absence of polarons in the MAPI films may explain the controversial reports on MAPI polarity32,33.
Second, our experimental data confirm the theoretically predicted Rashba spin-splitting of the bands and a resulting indirect band gap24, which can explain the low recombination rates and high carrier diffusion length observed for MAPI34,35,36,37. This mechanism was recently questioned by T. Etienne et al. who performed DFT calculations for dynamical MAPI systems and concluded that the small splitting magnitude (< 10 meV) might have a marginal effect on the reduction of the carrier recombination (i.e., less than an order of magnitude)38. However, our DFT+U calculations (with Hubbard correction and spin–orbit coupling) of the MAPI band structure in the presence of hole polarons yield much higher splitting values of 30 meV (Supplementary Figure 4). Here, it is worth noting that Rashba spin splitting is caused by the local arrangements of the atoms in the unit cell rather than by the average, long-range symmetry of the crystal39. We would like to note that owing to the technical limitations of the computer cluster, our calculations were done for a 2 × 2 × 2 supercell. A larger MAPI system needs to be considered, for example, in order to compute the polaron radius and effectively estimate the contribution of the polaron effects to β σμv .
Finally, THz emission from MAPI films implies ultrafast photocurrents with response times comparable to the carrier thermalization times (on the order of few ps34). Thus, a high VOC close to the bandgap and even slightly above it can be obtained for perovskite PV cells with appropriate transport layers. Moreover, as recently noted by Spanier et al.12 and Tan et al.21, photoinduced injection and shift currents can be used to construct PV device architectures with power conversion efficiencies that surpass the S–Q limit.
In conclusion, we present experimental evidence for optically stimulated ultrafast injection and shift currents in MAPI films at room temperature. Our measurements confirm inversion symmetry breaking of the MAPI films and an indirect bandgap due to Rashba splitting at room temperature. This result can help understand the device photophysics of highly efficient perovskite solar cells and, in particular, their recombination suppression and long carrier diffusion lengths. Moreover, observed ultrafast photocurrents could enable third-generation perovskite PV cells with efficiencies that break the S–Q limit. Our findings also open new venues for perovskite spintronics, ultrafast photodetectors, and tunable THz emitters.
Methods
Sample fabrication
Following Lee et al., we have adopted the perovskite deposition method using a CH3NH3I + PbCl2 (3:1) solution precursor14. Perovskite precursors and a dimethylformamide (DMF) solvent were purchased from Sigma Aldrich and used as received. Patterned ITO-glass substrates were cleaned via immersing in an ultrasonic bath of 5 wt% Deconex OP121 detergent in a DI water solution for 20 min. After the ultrasonic bath, the substrates were rinsed with DI water, dried at 200 °C for 60 min on a hot plate and treated with oxygen plasma (Harrick Plasma, Pdc-32G) for 5 min. Perovskite film of ~350 nm was formed from a precursor solution (CH3NH3I and PbCl2 at the 3:1 molar ratio dissolved in anhydrous DMF) by spin-casting at 4000 rpm followed by 120 min of annealing at 90 °C. The film was encapsulated with a top recess glass slide with the edges sealed by the NOA68 UV epoxy. This method results in the formation of MAPI films with uniform coverage and long-range crystalline domains. Fabricated with this deposition method, PV cells (ITO/PEDOT:PSS/MAPI/C60/BCP/Al) show a reproducible PCE of 12 ± 2% under 1.5 AM, 100 mW/cm2 illumination, which is comparable to the state-of-the-art PV cells with a similar architecture and film deposition method40 (Supplementary Figure 5). X-ray diffraction (XRD) and scanning electron microscopy (SEM) images of the microcrystalline MAPI film are both consistent with the typical data reported for multicrystalline perovskite films that are highly oriented along the α axis (Supplementary Figure 5).
PV cell fabrication and characterization
Glass substrates with pre-patterned indium tin oxide (ITO) were cleaned by sonication in Deconex OP121 detergent and in DI water and then treated with oxygen plasma. The polymer hole transport layer (PEDOT:PSS CLEVIOS™ P VP AI 4083) was spin coated at 6000 RPMs and then annealed at 150 °C for 10 min resulting in a 30 nm film. Then, an ~350 nm of thick CH3NH3PbI3 perovskite film was deposited. Next, for the electron transport layer, 30 nm of C60 fullerene (Solaris Chem) and 6 nm of bathocuproine (BCP) (Sigma-Aldrich) were sequentially thermally evaporated at the rates of 0.1 and 0.03 nm/s, respectively. Finally, a 100 nm thick Ag cathode was thermally deposited. The residual base pressure during the thermal deposition was <10−7 Torr. The current density–voltage (J–V) characteristics of the fabricated PV cells were recorded using a Keithley 2400 source-measure unit under 100 mW/cm2 illumination (AM 1.5 G). The external quantum efficiency (EQE) was measured using a lock-in amplifier with a current preamplifier under short-circuit conditions after illuminating the cells with a monochromator. SEM imaging was performed using an FEI Helios NanoLab 400. XRD measurements were performed using a Rigaku SmartLab diffractometer.
Photocurrent response measurements
To induce the photocurrents in a MAPI sample, we employed a Ti:Sapphire amplified system (Coherent Elite Pro) delivering 150 fs pulses with 1 kHz repetition rate at 780 nm (1.59 eV) fundamental wavelength and output pulse energy of 2.6 mJ. In the experiments, we used the second harmonic fundamental wavelength centred at 390 nm (3.18 eV) generated in a beta-barium-borate (BBO) crystal. The particular pump energies on the sample were 500 and 30 μJ for fundamental and second harmonics, respectively. The used pump fluencies are well below the damage threshold of our samples and did not result in any damage and/or artefacts in our measurements. To reveal the dependence of photocurrent response on excitation laser wavelength and to confirm the possibility of photocurrent generation under excitation with CW radiation, we also use two different low-power diode lasers operating at 532 nm (2.3 eV) and 650 nm (1.9 eV) with less than 1 mW average power. The induced photocurrents (J) were measured at room temperature across unbiased MAPI samples by the voltage drop on the 50 Ω input impedance of a 600 MHz digital oscilloscope connected to the ITO electrodes under short-circuit conditions, or an AC lock-in amplifier in the case of the excitation with a CW laser. The MAPI sample was excited in two different ways depending on the experiment. In the first case, the pump beam excites the sample from the front side through the cap-glass slide as shown in Fig. 1. The MAPI sample can also be excited from the back side through the glass substrate. By changing the orientation of the MAPI sample, we were able to measure longitudinal (J x ) and transverse (J y ) components with respect to the light incidence plane components of the induced photocurrent. In experiments the unfocused pump beam with diameter ranging from 200 µm to 0.5 cm (depending on the laser used) was directed to the MAPI sample surface at incidence angle Θ. Polarization dependences of the induced J x and J y components of the photocurrents were identified by measuring the peak-to-peak amplitudes of the corresponding photocurrent waveform while rotating half (λ/2) or quarter (λ/4) waveplates positioned before the sample by an angle α, which varied the state of the laser polarization with a period of 90° and 180o, respectively.
Terahertz emission measurements
The terahertz emission experiment was performed using a standard THz time-domain spectroscopy setup based on electro-optic sampling using a (111) oriented 450-μm-thick GaP crystal. In this experiment, we employed as a light source a femtosecond diode-pumped Yb:KGW regenerative amplifier (PHAROS-SP1.5 mJ, Light Conversion, Ltd.) with a central wavelength of 1028 nm, repetition rate of 14.0 kHz, average power of 5.5 W, and pulse duration of 200 fs. The MAPI sample was excited with second harmonic radiation centred at 514 nm generated in a BBO crystal. The emitted THz radiation was collected with a system of golden parabolic mirrors or polytetrafluoroethylene lens in the direction of laser beam reflection as shown in Fig. 1a and Supplementary Figure 6. The orientation of a GaP electro-optic (EO) crystal was chosen in such a way that only s-polarized THz radiation associated with transversal photocurrent J y is detected. The delayed probe beam was used for time-equivalent sampling of the THz time-domain waveforms employing a typical balanced detection scheme. The polarization of the excitation second-harmonic beam was controlled with a quarter-waveplate. All the measurements were performed at room temperature in ambient atmosphere.
DFT computational modelling
Band structure calculations were performed for 2 × 2 × 2 MAPI supercells using a GGA+U Hubbard correction and spin orbital correction implemented in the Vienna Ab initio Simulation package, together with the projected augmented wave method (see Supplementary Figure 4)30. Habbard correction (U parameter) was obtained by ionic force matching between GGA+U and hybrid exchange-correlation functionals (HSE06). A pseudocubic MAPI unit cell was relaxed using generalized gradient approximation (GGA) until forces were less than <2 meV/Å. A 256-point k-mesh (determined from a single 8 × 8 × 8 automatic Monkhorst-Pack k-mesh calculation) was used for self-consistent calculations with a 400 eV kinetic-energy cut-off. For non-self-consistent calculations, a linear k point scheme was used to sample the Brillouin zone in all Cartesian directions away from the R-point. Polarons were studied by first relaxing a charge neutral supercell of MAPI, then removing an electron and relaxing the charged (+1) supercell, effectively searching configuration space to find the lowest energy trapped state, i.e., a hole polaron. The valence band maximum of MAPI is mainly Ip orbital with negligible Pb s orbital coupling. Thus Dudarev’s rotationally invariant method with U = 6 eV was employed for the p orbitals of the I atom.
Data availability
The data that support the findings of this study are available from the authors on reasonable request, see author contributions for specific data sets.
References
Sturman, B. & Fridkin, V. The photovoltaic and photorefractive effects in noncentrosymmetric materials (CRC Press, Boca Raton, FL, 1992).
Belinicher, V. I. & Sturman, B. I. The relation between shift and ballistic currents in the theory of photogalvanic effect. Ferroelectrics 83, 29–34 (1988).
Glazov, M. M. & Ganichev, S. D. High frequency electric field induced nonlinear effects in graphene. Phys. Rep. 535, 101–138 (2014).
Shalygin, Va, Moldavskaya, M. D., Danilov, S. N., Farbshtein, I. I. & Golub, L. E. Circular photon drag effect in bulk tellurium. Phys. Rev. B – Condens. Matter Mater. Phys. 93, 045207 (2016).
McIver, J. W., Hsieh, D., Steinberg, H., Jarillo-Herrero, P. & Gedik, N. Control over topological insulator photocurrents with light polarization. Nat. Nanotechnol. 7, 96–100 (2011).
Braun, L. et al. Ultrafast photocurrents at the surface of the three-dimensional topological insulator B2Se3. Nat. Commun. 7, 13259 (2016).
Yuan, H. et al. Generation and electric control of spin–valley-coupled circular photogalvanic current in WSe2. Nat. Nanotechnol. 9, 851–857 (2014).
Von Baltz, R. & Kraut, W. Theory of the bulk photovoltaic effect in pure crystals. Phys. Rev. B 23, 5590–5596 (1981).
Priyadarshi, S. et al. Terahertz spectroscopy of shift currents resulting from asymmetric (110)-oriented GaAs/AlGaAs quantum wells. Appl. Phys. Lett. 95, 10–13 (2009).
Yang, S. Y. et al. Above-bandgap voltages from ferroelectric photovoltaic devices. Nat. Nanotechnol. 5, 143–147 (2010).
Shockley, W. & Queisser, H. J. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 32, 510 (1961).
Spanier, J. E. et al. Power conversion efficiency exceeding the Shockley-Queisser limit in a ferroelectric insulator. Nat. Photonics 10, 611–616 (2016).
Im, J.-H., Lee, C.-R., Lee, J.-W., Park, S.-W. & Park, N.-G. 6.5% efficient perovskite quantum-dot-sensitized solar cell. Nanoscale 3, 4088–4093 (2011).
Lee, M. M., Teuscher, J., Miyasaka, T., Murakami, T. N. & Snaith, H. J. Efficient hybrid solar cells based on meso-superstructured organometal halide perovskites. Science 338, 643–647 (2012).
Etgar, L. et al. Mesoscopic CH3NH3PbI3/TiO2 heterojunction solar cells. J. Am. Chem. Soc. 134, 17396–17399 (2012).
Crossland, E. J. W. et al. Mesoporous TiO2 single crystals delivering enhanced mobility and optoelectronic device performance. Nature 495, 215–9 (2013).
Heo, J. H. et al. Efficient inorganic–organic hybrid heterojunction solar cells containing perovskite compound and polymeric hole conductors. Nat. Photonics 7, 486–491 (2013).
Yang, W. S. et al. High-performance photovoltaic perovskite layers fabricated through intramolecular exchange. Science 348, 1234–1237 (2015).
Manspeaker, C., Venkatesan, S., Zakhidov, A. & Martirosyan, K. S. Role of interface in stability of perovskite solar cells. Curr. Opin. Chem. Eng. 15, 1–7 (2017).
Zheng, F. et al. First-principles calculation of the bulk photovoltaic effect in CH3NH3PbI3 and CH3NH3PbI3–xCl x . J. Phys. Chem. Lett. 6, 31–37 (2015).
Tan, L. Z. et al. Shift current bulk photovoltaic effect in polar materials—hybrid and oxide perovskites and beyond. NPJ Comput. Mater. 2, 16026 (2016).
Leppert et al. Is CH3NH3PbI3 polar? J. Phys. Chem. Lett. 7, 3683 (2016).
Li, J. & Haney, P. M. Circular photogalvanic effect in organometal halide perovskite CH3NH3PbI3. Appl. Phys. Lett. 109, 193903 (2016).
Zheng, F., Tan, L. Z., Liu, S. & Rappe, A. M. Rashba spin-orbit coupling enhanced carrier lifetime in CH3NH3PbI3. Nano Lett. 15, 7794–7800 (2015).
Li, J. & Haney, P. M. Optical spintronics in organic-inorganic perovskite photovoltaics. Phys. Rev. B – Condens. Matter Mater. Phys. 93, 155432 (2016).
Valov, P. M. et al. Dragging of electrons by photons in intraband absorption of light by free carriers in semiconductors. Sov. Phys. JETP 32, 1038–1041 (1971).
Shalaev, V. M., Douketis, C., Stuckless, J. T. & Moskovits, M. Light-induced kinetic effects in solids. Phys. Rev. B 53, 11388–11402 (1996).
Obraztsov, P. A. et al. Photon-drag-induced terahertz emission from graphene. Phys. Rev. B – Condens. Matter Mater. Phys. 90, 241416 (2014).
Laman, N., Bieler, M. & van Driel, H. M. Ultrafast shift and injection currents observed in wurtzite semiconductors via emitted terahertz radiation. J. Appl. Phys. 98, 103507 (2005).
Welch, E., Scolfaro, L. & Zakhidov, A. Density functional theory + U modeling of polarons in organohalide lead perovskites. AIP Adv. 6, 125037 (2016).
Neukirch, A. J. et al. Polaron stabilization by cooperative lattice distortion and cation rotations in hybrid perovskite materials. Nano Lett. 16, 3809–3816 (2016).
Sharada, G. et al. Is CH3NH3PbI3 polar? J. Phys. Chem. Lett. 7, 2412–2419 (2016).
Kutes, Y. et al. Direct observation of ferroelectric domains in solution-processed CH3NH3PbI3 perovskite thin films. J. Phys. Chem. Lett. 5, 3335–3339 (2014).
Xing, G. et al. Long-range balanced electron- and hole-transport lengths in organic-inorganic CH3NH3PbI3. Science 342, 344–347 (2013).
Dong, Q. et al. Electron-hole diffusion lengths 175 um in solution grown CH3NH3PbI3 single crystals. Science 347, 967–970 (2015).
Stranks, S. D. et al. Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science 342, 341–344 (2013).
Chen, Y. et al. Extended carrier lifetimes and diffusion in hybrid perovskites revealed by Hall effect and photoconductivity measurements. Nat. Commun. 7, 12253 (2016).
Etienne, T., Mosconi, E. & De Angelis, F. Dynamical origin of the Rashba effect in organohalide lead perovskites: a key to suppressed carrier recombination in perovskite solar cells? J. Phys. Chem. Lett. 7, 1638–1645 (2016).
Zhang, X., Liu, Q., Luo, J.-W., Freeman, A. J. & Zunger, A. Hidden spin polarization in inversion-symmetric bulk crystals. Nat. Phys. 10, 387–393 (2014).
You, J. et al. Low-temperature solution-processed perovskite solar cells with high efficiency and flexibility ACS Nano 8, 1674–1680 (2014).
Acknowledgements
This work was partially supported by the Russian Science Foundation (P.O. personal Grant RSF #17-72-10303), the Academy of Finland Grants #299059, #318596, Russian Foundation for Basic Research Grant #16-52-10062 the ACS Petroleum Research Fund Grant #56095-UNI6 (Program Manager Askar Fahr), and the U.S. DoD Contract W911NF-16-1-0518 (Program officer Paul Armistead). This work is also supported by JSPS international joint research program, and the Photon Frontier Network Program funded by the Ministry of Education, Culture, Sports, Science, and Technology(MEXT), Japan.
Author information
Authors and Affiliations
Contributions
P.O. designed and performed all experiments and analyzed results. D.L. designed, prepared, and characterized MAPI films and PV devices. P.C. participated in designing the photocurrent experiments and performed the measurements. K.K., N.N., and K.G. provided the THz facility and participated in discussion of the results. E.W. performed DFT calculations. A.O. initiated the research and analyzed the results. A.Z. coordinated the work. All authors discussed the results and contributed to the manuscript writing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Obraztsov, P.A., Lyashenko, D., Chizhov, P.A. et al. Ultrafast zero-bias photocurrent and terahertz emission in hybrid perovskites. Commun Phys 1, 14 (2018). https://doi.org/10.1038/s42005-018-0013-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-018-0013-8
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.