Abstract
Earth-abundant antimony trisulfide (Sb2S3), or simply antimonite, is a promising material for capturing natural energies like solar power and heat flux. The layered structure, held up by weak van-der Waals forces, induces anisotropic behaviors in carrier transportation and thermal expansion. Here, we used stress as mechanical stimuli to destabilize the layered structure and observed the structural phase transition to a three-dimensional (3D) structure. We combined in situ x-ray diffraction (XRD), Raman spectroscopy, ultraviolet-visible spectroscopy, and first-principles calculations to study the evolution of structure and bandgap width up to 20.1 GPa. The optical band gap energy of Sb2S3 followed a two-step hierarchical sequence at approximately 4 and 11 GPa. We also revealed that the first step of change is mainly caused by the redistribution of band states near the conduction band maximum. The second transition is controlled by an isostructural phase transition, with collapsed layers and the formation of a higher coordinated bulky structure. The band gap reduced from 1.73 eV at ambient to 0.68 eV at 15 GPa, making it a promising thermoelectric material under high pressure.
Similar content being viewed by others
Introduction
The needs for environmentally friendly and sustainable energy supplies are the prerequisites for achieving carbon neutrality. According to Renewables 2020 Global Status Report, renewable technologies like solar, geothermal, and wind power have provided 8.7% of the final world’s primary energy consumption1. The development of solar cells has enjoyed its blossom since the last decade2,3,4,5. However, their broad implications are still restricted by the materials cost, reliability, and power conversion efficiency (PCE)6. Sb2S3 is a promising solar energy absorber with affordable cost, good Earth abundance and non-toxic composition7,8,9. It features a relatively low melting point (550 °C), which helps to synthesize high quality film at below 350 °C10. In particular, Sb2S3 has a high absorption coefficient (a > 104 cm−1)11, and the band gap of 1.7–1.8 eV matching the required Eg values of Si-based solar cells, making its maximum theoretical PCE above 40%12,13. However, its performance is dragged by self-trapping states, which limits the upper approximately maximum open circuit voltage at around 0.8 V and thus, its realistic PCE is still lower than 16%9,14,15,16,17.
Sb2S3 is also regarded as a promising thermoelectric material18. Sb2S3 features a large Seebeck coefficient and relatively low lattice thermal conductivity due to varied activity of Sb electron lone pairs and soft Sb–S bonds18,19. However, on the basis of the intrinsic correlation between the Seebeck coefficient S and the electrical conductivity σ, the large band gap of pure Sb2S3 (1.73 eV) makes it difficult to achieve a significant increase in the power factor20. Energy band engineering, for instance, doping21,22,23 and applying strain24, have been used to decouple S and σ in order to achieve higher power factor and conversion efficiency. Specifically, applying pressure stiffens bonds and alters electronic structures, which can be used as an environmental-friendly method to engineer band gap energy.
Pressure by applying stress directly alters bonding distances, engineers bandgap energies and has recently been used to improve photon efficiencies in many materials5,17,25,26,27. Sb2S3 is an archetypal layered structure that contains parallel Sb4S6 chains formulated in 2 × 1 crumpled sheets28. Two major pressure induce phase transitions were reported below 15 GPa29, despite existing arguments. Within 4–5 GPa, Sorb et al.30 reported that Sb2S3 underwent an isostructural electronic topological phase transition. The results were later confirmed by Dai et al.31 and Efthimiopoulos et al.32 who also found the transition incurred the redistribution of Sb3 + lone-electron pairs. However, Ibañez et al.33 reported that no evidence from the first-principles simulation would support electronic topological transition below 10 GPa. At higher pressures of 10–15 GPa, more controversies regarding the second phase transition processes were observed. Efthimiopoulos et al.32 suggested pressure-induced structural disordering took place at 15 GPa and completed at ~20 GPa, while theoretical studies show Sb2S3 is stabilized in a quasi-3D structural phase transition at similar pressures33. Upon futher compression, Sb2S3 becomes a substituinal alloy34. Since the crystal structure strongly influences the electronic band gap of materials, it is necessary to conduct an updated study and figure out the underlying transition mechanisms.
In this work, we focus on the evolution of the layering structure in Sb2S3 in response to external stress. Detailed structural analysis of Sb2S3 was performed up to 20 GPa, where we found the (Sb4S6)n were completely collapsed. At the same time, we measured the evolution of band gap energies using ultraviolet-visible absorption spectroscopy. Based on experimental results and first-principles simulation using hybrid functionals, we revisited the sterically controlled phase transition at ~4 GPa and 11 GPa. We observed two major discontinuities in band-gap energies, corresponding to the two above mentioned transition points. The transition mechanism can be defined by the onset of a direct-band gap type at ~4 GPa and a fully developed 3-dimentional (3D) Sb2S3 crystal structure at above 11 GPa.
Results and discussion
Crystal structure of compressed Sb2S3
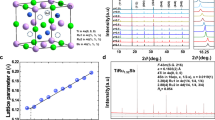
Previous studies on the layered structure of Sb2S3 suggested a set of pressure-induced polymorphic and electronic phase transitions. Here, our first experiment mainly focused on the structural properties of single-crystal Sb2S3. At pressures below 10 GPa, the sample is readily resolved in the conventional way of single-crystal crystallography (e.g., at 1.7 GPa, Table 1). The rocking curves of representative single-crystal diffraction spots became flattened at higher pressure. For data collected above 10 GPa, single-crystal refinement is no longer feasible due to twinning and crushed samples, but we can still treat the patterns as pseudo-Debye-Scherrer rings, which can be resolved using the Rietveld method. We noticed diffraction peaks in the integrated diffraction patterns are consistent through the studied pressure range (Supplementary Fig. 1), indicating Sb2S3 kept the same Pnma space group up to 20.1 GPa. However, by comparing the atomic positions, S atoms involve greater atomic displacement and form new bonds with neighboring Sb atoms (Table 1 and Fig. 1). Consequently, the signature layered chains of SbS5 polyhedral collapsed into a 3D crystal structure within 9.1 to 11.1 GPa, where an isostructural phase transition might have taken place (Fig. 1c).
a Rietveld refinements results of Sb2S3 at 11 GPa. b P–V data is fitted to the third-order Birch-Murnaghan equation. Solid lines were fit to two segments of data while dashed line was fit for the whole range of data with V0 = 120.3(7) Å3/f.u., K0 = 48(6) GPa and K′ = 5.4(9). Volume uncertainties are generally smaller than the size of symbols. c the signature layered chains of SbS5 polyhedral collapsed into a bulky structure in between 9.1 and 11.1 GPa. d Evaluation of crystal structure parameters up to 20.6 GPa. The errorbars in cell volume and lattice parameters were generated by the refinement of X-ray diffraction pattern and the Unitcell fitting process.
It is possible to fit the whole range of data into one equation of state (dashed line in Fig. 1b). However, the collapse of interlayer space motivated us to fit the P–V data to two segments, namely before and after the isostructural phase transition. Therefore, we used two sets of EOS parameters. To characterize the isostructural phase transition, we used the third-order Birch-Murnaghan equation35 to fit the cell volumes over pressure and studied the equation of state:
where B0 and V0 are the bulk modulus and volume at ambient pressure, V is the deformed volume under pressure, and B′ is the derivate of the bulk modulus with respect to pressure. In addition, we plot the Eulerian strain-normalized pressure (F–f) relation in Supplementary Fig. 2 and the evolution of interlayer distance in Supplementary Fig. 3. A clear stiffening of lattice was observed near the isostructural transition point, where the B0 of reconstructed 3D-Sb2S3 is 24% greater (B0 = 54.4 GPa compared to 43.8 GPa for the low-pressure phase). Seeing from the evolution of structural parameters (Fig. 1c, d), the compression in low-pressure phase is mainly achieved by squeezing layers made of Sb–S polyhedral chains. Above the transition point, the material becomes less-compressible as the Sb2S3 features higher atomic coordination described in the 3D structure. A notable jump of the c axis length is observed at 11 GPa, accompanying the shortening of a and b lattice axis and the isostructural transition. This compression anomaly is the signature for the formation of new chemical bonds, which may profoundly change the electronic structure of Sb2S3. Pressure-regulated dynamic stereochemistry has been reported in many layered materials36,37,38,39,40,41. We also characterized the interlayer distance as a function of pressure force (Supplementary Fig. 3 and Supplementary Data 1), which suggest the layer is initially maintained by the van der Waals force and then by covalent bonding upon isostructural transition.
Our x-ray diffraction analysis indicate that the isostructural phase transition is achieved by the reconstruction of bonds and coordination environments. In light of this, we performed Raman spectroscopy which is more sensitive to the change of chemical bonds. The experimental results are summarized in Fig. 2 and compared with the first-principles simulation (Supplementary Fig. 4). The frequencies of modes in our experiments generally agree with the previous experiment by Dai et al.31 and Efthimiopoulos et al.32 Here, we identified each mode on the basis of first-principles calculations and classified them into two groups: interlayer modes (solid red circles in Fig. 2b) and other bulk-like inner-layer modes (open blue circles in Fig. 2b). The interlayer breathing mode ~100 cm−1 was terminated soon after the transition, suggesting the completion of the layer to bulk isostructural phase transition. While both interlayer stretching modes were observed to be softened below ~14 GPa, they robustly shifted to higher frequencies upon the completion of the phase transition. The rest bulk-like inner-layer mode exhibit blueshift over the pressure region. It was also reported that a turning point of electronic conductivity was seen at ~5 GPa31. However, our XRD and Raman experiments alone were unable to identify this phase transition. The electronic phase transition is unlikely due to the collapse of Sb2S3 layers, but may due to changes in the electronic band structures.
a Raman spectra of compressed Sb2S3 in the range of 0–400 cm−1 wavelength. The asterisk peaks were not traceable thus not assigned to specific modes. b Evolution of each Raman mode over pressure. The frequency of peak has maximum uncertainty of 5 cm−1. Mode displacements are derived from the first-principles simulation at low pressure. Inl interlayer.
Ultraviolet–Visible and bandgap analysis
Therefore, we are motivated to measure the electronic band-gap energy in compressed Sb2S3 single crystals. At ambient condition, bulk Sb2S3 has indirect band-gap energy of 1.73 eV, which is suitable for solar cell application, although its self-trapping states substantially inhibit its photon-energy conversion6,14,42. Here, we obtained the ultraviolet-–visible (UV–Vis) spectra and calculated the bandgap by the Kubelka–Munk (K–M) equation43 over the regime of phase transition (Fig. 3a, b and Supplementary Data 1). We also conducted the first-principles calculation on the basis of HSE06 hybrid functionals to find the mechanism. The calculated band-structure confirmed that ambient Sb2S3 has an indirect semiconductor, with its valence band maximum located at Γ (0, 0, 0) and conduction band minimum (CBM) located near Z, at (0,0,0.375) (Fig. 3c). However, the CBM moved to the Γ (0, 0, 0) point of the Brillouin zone once pressure was increased to 5.2 GP and Sb2S3 tuned into a direct bandgap semiconductor. Guided by our simulation results, the bandgap change induced the first discontinuity in our bandgap measurement. Such electronic phase transition was also predicted in layered structures like MoS244 and was known to boost electrical conductivity45. Similarly, the onset of direct band-gap type would be the principal reason of observed higher electrical conductivity in Sb2S3.
a Results of absorbance from room pressure to 14.8 GPa. b Bandgap fitting by K-M equation (red) and calculated by DFT with HSE06 (blue). c Electronic structure of Sb2S3 with bandgap 1.55 eV at ambient pressure. d At 5.2 GPa, Sb2S3 is converted into a direct bandgap semiconductor with bandgap 1.35 eV. e Sb2S3 undergoes a 2D-3D phase transition, and the bandgap is compressed to 0.86 eV at 11 GPa.
Once we pressurized the sample to the previously observed isostructural transition point, we observed a kink of band-gap energies (Fig. 3b). It is worth noting that the isostructural phase transition does not alter the direct bandgap, but only stagger the change of bandgap energies. The kink was verified by our first-principles simulation, where the closing of band gap slightly accelerated in between 11 and 13 GPa. It is worth noting that the narrowed bandgap at above 11 GPa is specifically useful for thermoelectrical materials20. We stopped our experiment at ~15 GPa because the band gap energy becomes greatly lowered and evolves towards full metallization31. A previous work on Sb2S3 thin film reported a broad albeit weak photoluminescence peak from the states at ambient conditions14. We also closely monitored possible photoluminescence during the compression experiment through our optical window. However, throughout the pressure experiment, the photoluminescence has yet become visible and should keep weak due to the active self-trapping states.
Collapsed layers and the bandgap transition
On the basis of pioneering works, our results attempt to clarify two main points during the densification of Sb2S3 crystals. First, the previously observed turning of electrical conductivity at ~4 GPa31 is due to the shift of CBM to the Γ point of Brillouin zone. At the same pressure, Sb2S3 is still chained by Sb–S polyhedron and a well-defined layered structure. Also, our experiments demonstrate that compressed Sb2S3 maintains the same crystal space group up to 20.1 GPa under room-temperature compression. Although under high pressure, the Pnma phase might not be the most energetically favored phase34, large-scale atomic movement or reconstructive structural transition was not observed in our single-crystal experiment most likely due to the high energy barrier, the bulky single-crystal sample and relatively fast compression rate. Transition kinetics and sample crystallinity should be taken into consideration for polymorphism in similar layered structures46,47.
Loading strain is well-known to influence the electrical conductivity of materials, and may reversely response to the Seebeck coefficient. Our experiment demonstrated that hydrostatic compression of Sb2S3 single-crystals has greatly squeezed the interatomic spacing and reduced the bandgap to below 1.0 eV above 11 GPa, at which pressure normal strains of 5.89%, 6.11%, and 5.42% were applied along the x, y, and z axis, respectively. The improved electrical conductivity may partially offset the relatively low carrier concentration of Sb2S3, which was measured on the order of 1012 at ambient conditions and enhanced the overall thermoelectric performance. However, it is still necessary to directly calibrate the Seebeck effect under pressure for more accurate description under pressure, which will be systematically studied in the future.
An interesting issue is the electronic topological transition in antimony chalcogenides like Sb2S3 and Sb2Se3. Those chalcogenides have the same layered structure at ambient conditions. Both of them were reported to undergo electronic topological transitions at a few GPa30,32,38,48, at which the atomic vibration and lattice compressibility exhibit sharp anomaly. The transition occurs when a band extreme associated with a Van Hove singularity passes through the Fermi level and causes a strong redistribution of the density of electronic states near the Fermi surface. The density of states as a function of pressure over the entire range of pressure is provided in Supplementary Fig. 5. Our work not only verified previous results on the compressibility and vibrational modes, but also, observed the onset of band gap energy discontinuity at ~4 GPa, along with the indirect-direct type of band gap. This is probably caused by the charge density redistribution from the electronic topological transition. The indirect-direct bandgap transition of Sb2S3 was previous reported in Ibañez et al.33 and was verified by our hybrid function simulation. This bandgap transition was achieved by the opposite shifts of the conduction band minima at the Z and Γ points in the Brillion zone. While the d-electrons are deep in the valence state of Sb2S3 and the electronegativity of S atoms are stable in the pressure range of 0-11 GPa (Supplementary Fig. 6), the abnormal shifts in the conduction band is mainly a pressure effect, which reduces the interatomic distances and strengthens the atomic interactions, leading to the redistribution of energy bands. The critical transition pressure was then anchored to the formula used to calculate the band gap in our UV-Vis experiment.
We also conducted Bader charge analysis to confirm the transition at 11 GPa49. A sudden change of Sb and S charges was observed at the critical transition pressure. For example, charges of Sb(1) increased from 2.0 to 2.5 while that of S(1) dropped from 7.5 to 7.0. The transition came along with the disappearance of Sb3+ lone-electron pair and the formation of SbS7 polyhedra in the bulk structure. Pressure has been previously used to engineer the band gap energies of insulators and semiconductors, which also alters their electronic structures. For example, insulators like CsAuI3 perovskite can even reach a rate of 0.2 eV/GPa in closing its band gap. Our UV-Vis experiment showed a normalized 0.07(1) eV/GPa decrease of band gap energy, and this trend generally reflected the shortening of bond-length with more overlapped charge density between atoms (Fig. 3).
Conclusion
In summary, the band gap engineering in Sb2S3 is achieved through two-step transitions at 4 and 11 GPa. The first bandgap transition is mainly due to the redistribution of charge density near the CBM. The latter is controlled by an isostructural phase transition, which is the result of collapsing layers. The evolution of band gap energies in compressed Sb2S3 is covered by this hierarchical electronic phase transition mechanism. Although compression alone could not overcome self-trapping or yield strong photoluminescence, future opportunities may lie in combined doping and pressurization methods to eliminate the harmful self-trapping states and optimize band structures14,50,51.
Methods
Sb2S3 single crystals
We use natural antimony (III) sulfide (Sb2S3) single crystal collected from Xikuangshan mountain, Hunan province, China. The natural crystals were polished and the chemical composition was measured by electron probe micro-analysis coupled with a scanning electron microscope (SEM-EPMA) available at the Central South University (Supplementary Fig. 7 and Supplementary Table 1). By averaging 8 spots on the polished single-crystal facet, the natural single-crystal sample exceeds 99% purity and its deviated atomic ratio of δ (Sb: S) value is below 0.08%. Single-crystal sample was then crushed into small pieces with typical size of 50 × 20 × 10 μm3 and arbitrary orientation before loading into the diamond anvil cell (DAC).
X-ray diffraction experiments
Single-crystal x-ray diffraction experiments were performed at 13BM-C station of GeoSoilEarthCARS (GSECARS) of the Advanced Phonon Source, Argonne National Laboratory. The crushed natural stibnite (Sb2S3) single-crystal sample was loaded in between two diamond anvils of 400 μm culet size and was sealed with a T301 steel gasket. The sample chamber was a drilled hole of 200 μm diameter with neon gas as the pressure medium. Pressure was applied by increasing pressure in a gas memberane system that coupled with the DAC. The monochromatic beam wavelength used for data collection was 0.434 Å with a focus spot of 12 × 18 μm2. Single-crystal diffraction patterns were collected on a Pilatus detector at each x-ray incident angle (1o per image) from −30o to 30o for 10 s each. The orientation matrix, the diffraction data reduction, and crystal structure refinement were performed using the APEX3 program (Bruker). The lattice parameters from powder XRD patterns were intially reduced by the software Unitcell52. Then their atomic positions are refined by the program GSAS. Pressure is primarily determined by calibrating the ruby fluorescence line shift in an online Ruby system. The pressures are also compared to the equation of state of neon, from which measurement uncertainties <1 GPa are achieved throughout the experiment.
Low-frequency Raman spectroscopy
In situ high-pressure Raman measurements were conducted on a customized system available at Center for High Pressure Science and Technology Advanced Research (HPSTAR). Spectrums are taken for the back-scattering geometry using an Argon laser (532 nm and power <1 mW) in the range 0-500 cm−1 with a spectral resolution of 1.0 cm−1, and the resolution of the laser spot is ~10 μm. The acquiring time for each spectrum was 60 s and each collection was repeated for 10 times to attenuate the effects of fluorescence and cosmic rays. Raman spectra were fitted by a Lorenz-type function using Peakfit v4.12 software to determine the positions of each Raman mode.
In situ high-pressure photoluminescence measurement
In situ high-pressure photoluminescence measurements were conducted on a customized system available at the HPSTAR. To measure the high-pressure optical properties (e.g., UV-Vis absorption spectroscopy and photoluminescence) of Sb2S3 in an diamond anvil cells (DACs), we used low fluorescence type IIa diamonds with a culet size of 300 μm. Absorption spectra were collected using a Xeon light source between 320 and 1600 nm. The absorption spectra and optical images were measured in a home-designed spectroscopy system in a micro-region (Gora-UVN-FL, built by Ideaoptics, Shanghai, China). Silicone oil was used as the pressure transmitting medium.
First-principles calculation
First-principles calculations were performed under the framework of density functional theory through Vienna’s Ab Initio Package ver. 5.3.4. The generalized gradient approximation of Perdew, Burke, and Ernzerhof revised for solids was implemented to describe the exchange-correlation functions53,54. Pseudopotentials were used with eight valence electrons for Sb atoms (4s24p3) and six for S atoms (3s23p4). We employed a 2 × 7 × 2 k point mesh. The structures were allowed to relax for cell variables, cell volume, and atomic positions. We applied a simple D2 method of Grimme55 with a 50 Å cutoff radius to calculate the long-distance van der Waals correction. A plane-wave basis set with a kinetic energy cutoff of 350 eV was found sufficient to converge the force between atoms less than 0.01 eV/Å. After structural relaxation, the density of stateas and band structures are re-calcualted using the HSE06 hybrid functional56.
For simulated Raman spectroscopy, we first calculated the vibrational modes of Sb2S3 unit cell using a density functional perturbation theory. The Raman off-resonant activity of each vibrational mode was then computed the derivative of the polarizability through the program Raman-sc, and the source code for the algorism is available at https://raw.githubusercontent.com/raman-sc/.
Data availability
The authors declare that all data supporting the findings of this study are available within the paper and its supplementary files (Supplementary Information and Supplementary Data 1). The data supporting the findings of this study have been deposited at the 4TU Center for Research Data (https://doi.org/10.4121/15131655). Any additional data can be requested by e-mailing the corresponding author. Source data are provided with this paper.
References
De Castro, C., Mediavilla, M., Miguel, L. J. & Frechoso, F. Global solar electric potential: a review of their technical and sustainable limits. Renew. Sustain. Energy Rev. 28, 824–835 (2013).
Kong, L., Liu, G., Gong, J., Mao, L. & Mao, H. K. Highly tunable properties in pressure-treated two-dimensional Dion-Jacobson perovskites. Proc. Natil Acad. Sci. USA 117, 16121–16126 (2020).
Righini, G. C. & Enrichi, F. Solar cells’ evolution and perspectives: a short review. Solar Cells and Light Management 1–32 (Elsevier, 2020).
Sahu, A., Garg, A. & Dixit, A. A review on quantum dot sensitized solar cells: Past, present and future towards carrier multiplication with a possibility for higher efficiency. Sol. Energy 203, 210–239 (2020).
Yan, J. & Saunders, B. R. ChemInform abstract: third-generation solar cells: a review and comparison of polymer:fullerene, hybrid polymer and perovskite solar cells. ChemInform 45 (Wiely, 2014).
Kondrotas, R., Chen, C. & Tang, J. Sb2S3 solar cells. Joule 2, 857–878 (2018).
Ito, S., Tsujimoto, K., Nguyen, D. C., Manabe, K. & Nishino, H. Doping effects in Sb2S3 absorber for full-inorganic printed solar cells with 5.7% conversion efficiency. Int. J. Hydrog. Energy 38, 16749–16754 (2013).
Bansal, N., O’Mahony, F. T. F., Lutz, T. & Haque, S. A. Solution processed polymer–inorganic semiconductor solar cells employing Sb2S3 as a light harvesting and electron transporting material. Adv. Energy Mater. 3, 986–990 (2013).
Ishaq, M. et al. High open-circuit voltage in full-inorganic Sb2S3 solar cell via modified Zn-doped TiO2 electron transport layer. Sol. RRL 4, 2000551 (2020).
Janošević, V., Mitrić, M., Bundaleski, N., Rakočević, Z. & Validžić, I. L. High-efficiency Sb2S3-based hybrid solar cell at low light intensity: cell made of synthesized Cu and Se-doped Sb2S3. Prog. Photovolt. Res. Appl. 24, 704–715 (2016).
Ghosh, C. & Varma, B. P. Optical properties of amorphous and crystalline Sb2S3 thin films. Thin Solid Films 60, 61–65 (1979).
Vos, A. D. Detailed balance limit of the efficiency of tandem solar cells. J. Phys. D Appl. Phys. 13, 839–846 (1980).
Wang, Q. et al. Sb2S3 solar cells: functional layer preparation and device performance. Inorg. Chem. Front. 6, 3381–3397 (2019).
Yang, Z. et al. Ultrafast self-trapping of photoexcited carriers sets the upper limit on antimony trisulfide photovoltaic devices. Nat. Commun. 10, 4540 (2019).
Luo, J., Xiong, W., Liang, G., Liu, Y. & Chen, S. Fabrication of Sb2S3 thin films by magnetron sputtering and post-sulfurization/selenization for substrate structured solar cells. J. Alloy. Compd. 826, 154235 (2020).
Xu, Y. et al. Template deposition of Sb2S3 for solid-state sensitized solar cells. J. Alloy. Compd. 784, 947–953 (2019).
Liang, G.-X. et al. Sputtered and selenized Sb2Se3 thin-film solar cells with open-circuit voltage exceeding 500 mV. Nano Energy 73, 104806 (2020).
Yang, H., Boulet, P. & Record, M.-C. Thermoelectric properties of Sb-S system compounds from DFT calculations. Materials 13, 4707 (2020).
Shi, X.-L., Zou, J. & Chen, Z.-G. Advanced thermoelectric design: from materials and structures to devices. Chem. Rev. 120, 7399–7515 (2020).
Shi, X.-L., Chen, W.-Y., Zhang, T., Zou, J. & Chen, Z.-G. Fiber-based thermoelectrics for solid, portable, and wearable electronics. Energy Environ. Sci. 14, 729–764 (2021).
Wang, L. et al. Manipulating band convergence and resonant state in thermoelectric material SnTe by Mn–In codoping. ACS Energy Lett. 2, 1203–1207 (2017).
Tan, X. et al. Optimizing the thermoelectric performance of In–Cd codoped SnTe by introducing Sn vacancies. J. Mater. Chem. C 5, 7504–7509 (2017).
Tan, X. et al. Improving thermoelectric performance of α-MgAgSb by theoretical band engineering design. Adv. Energy Mater. 7, 1700076 (2017).
Zheng, Y. et al. A synergy of strain loading and laser radiation in determining the high-performing electrical transports in the single Cu-doped SnSe microbelt. Mater. Today Phys. 13, 100198 (2020).
Kong, L. et al. Simultaneous band-gap narrowing and carrier-lifetime prolongation of organic–inorganic trihalide perovskites. Proc. Natl Acad. Sci. USA 113, 8910–8915 (2016).
Guo, S. et al. Pressure‐suppressed carrier trapping leads to enhanced emission in two‐dimensional perovskite (HA)2(GA)Pb2I7. Angew. Chem. Int. Ed. 59, 17533–17539 (2020).
Guo, S., Bu, K., Li, J., Hu, Q. & Lü, X. Enhanced photocurrent of all-inorganic two-dimensional perovskite Cs2PbI2Cl2 via pressure-regulated excitonic features. J. Am. Chem. Soc. 143, 2545–2551 (2021).
Bayliss, P. & Nowacki, W. Refinement of the crystal structure of stibnite, Sb2S3. Z. Kristallogr. Cryst. Mater. 135, 308–315 (1972).
Bocquillon, G., Léger, J.-M. & Bogicevic, C. Large-volume device for pressures of 20 GPa. High Temp. High Press. 35/36, 355–370 (2003).
Sorb, Y. A. et al. Pressure induced electronic topological transition in Sb2S3. J. Phys. Condens. Matter 28, 015602 (2016).
Dai, L. et al. Pressure-induced irreversible metallization accompanying the phase transitions in Sb2S3. Phys. Rev. B 97, 024103 (2018).
Efthimiopoulos, I., Buchan, C. & Wang, Y. Structural properties of Sb2S3 under pressure: evidence of an electronic topological transition. Sci. Rep. 6, 24246 (2016).
Ibáñez, J. et al. Structural, vibrational, and electronic study of Sb2S3 at high pressure. J. Phys. Chem. C 120, 10547–10558 (2016).
Wang, Y. et al. Experimental observation of the high pressure induced substitutional solid solution and phase transformation in Sb2S3. Sci. Rep. 8, 14795 (2018).
Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 71, 809–824 (1947).
Kejun, B., Luo, H., Guo, S., Li, M. & Lu, X. Pressure-regulated dynamic stereochemical role of lone-pair electrons in layered Bi2O2S. J. Phys. Chem. Lett. 11, 9702–9707 (2020).
Matsuishi, K., Ishihara, T., Onari, S., Chang, Y. H. & Park, C. H. Optical properties and structural phase transitions of lead-halide based inorganic-organic 3D and 2D perovskite semiconductors under high pressure. Phys. Status Solidi 241, 3328–3333 (2010).
Xiao, G. et al. Pressure-induced reversible phase transformation in nanostructured Bi2Te3 with reduced transition pressure. J. Phys. Chem. C 119, 3843–3848 (2015).
Wang, P. et al. Pressure-induced structural and electronic transitions, metallization, and enhanced visible-light responsiveness in layered rhenium disulphide. Phys. Rev. B 97, 235202 (2018).
Park, S., Rittman, D. R., Tracy, C. L., Chapman, K. W. & Ewing, R. C. A2TiO5 (A = Dy, Gd, Er, Yb) at high pressure. Inorg. Chem. 57, 2269–2277 (2018).
Radescu, S. et al. Study of the orpiment and anorpiment phases of As2S3 under pressure. J. Phys. Conf. Ser. 950, 042018 (2017).
Guo, L. et al. Scalable and efficient Sb2S3 thin-film solar cells fabricated by close space sublimation. APL Mater. 7, 041105 (2019).
Kortüm, G., Braun, W. & Herzog, G. Principles and techniques of diffuse reflectance spectroscopy. Angew. Chem. Int. Ed. 2, 333–341 (1963).
Ellis, J. K., Lucero, M. J. & Scuseria, G. E. The indirect to direct band gap transition in multilayered MoS2 as predicted by screened hybrid density functional theory. Appl. Phys. Lett. 99, 8207 (2011).
Zhuang, Y. K. et al. Pressure-induced permanent metallization with reversible structural transition in molybdenum disulfide. Appl. Phys. Lett. 110, 122103 (2017).
Sheng-Cai, Z. et al. Structure-controlled oxygen concentration in Fe2O3 and FeO2. Inorg. Chem. 58, 5476–5482 (2018).
Guo, Y. et al. Probing the dynamics of the metallic-to-semiconducting structural phase transformation in MoS2 crystals. Nano Lett. 15, 5081–5088 (2015).
Efthimiopoulos, I., Kemichick, J., Zhou, X., Khare, S. V. & Wang, Y. High-pressure studies of Bi2S3. J. Phys. Chem. A 118, 1713–1720 (2014).
Zhao, K. et al. First principles study of isostructural phase transition in Sb2Te3 under high pressure. Phys. Status Solidi RRL 9, 379–383 (2015).
Lu, X. et al. Regulating off-centering distortion maximizes photoluminescence in halide perovskites. Natl. Rev. Sci. nwaa288 (2020).
Lee, C., Kim, S., Son, W.-J., Shim J.-H. & Whangbo. M.-H. Ternary selenides A2Sb4Se8 (A = K, Rb and Cs) as an n-type thermoelectric material with high power factor and low lattice thermal conductivity: importance of the conformationally flexible Sb–Se–Se–Sb bridges. RSC Adv. 10, 14415–14421 (2020).
Holland, T. J. B. & Redfern, S. A. T. Unit cell refinement from powder diffraction data; the use of regression diagnostics. Mineral. Mag. 61, 65–77 (1997).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Perdew, J. P. et al. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100, 246–249 (2008).
Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comp. Chem. 27, 1787–1799 (2006).
Krukau, A. V., Vydrov, O. A., Izmaylov, A. F. & Scuseria, G. E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 125, 3865 (2006).
Acknowledgements
We acknowledge the use of synchrotron X-ray diffraction at the 13BM-C of GSECARS, Advanced Photon Source, Argonne National Laboratory. GeoSoilEnviroCARS is supported by the National Science Foundation – Earth Sciences (EAR – 1634415) and Department of Energy- GeoSciences (DE-FG02-94ER14466). 13BM-C is partially supported by COMPRES under NSF Cooperative Agreement EAR -1606856. Y.Z. is supported by China Postdoctoral Science Foundation with grant 18NZ021-0213-216308. Q.H. is supported by the CAEP Research Project (CX20210048) and a Tencent Xplorer Prize. R.T.H. is supported by the National Science Foundation of China (Grant No. 11974034). Operations of Center for High Pressure Science and Technology Advanced Research (HPSTAR) is partially supported by NSAF (Grant No: U1530402).
Author information
Authors and Affiliations
Contributions
Z.C., K.B., Y.Z., M.-E.D., D.Z., P.D.-S., R.T.H., and J.Z. carried out the experiment. Z.C., D.Z., and Q.H. performed the experimental data analysis and interpretation. Q.H. performed the theoretical simulation. X.L. and Q.H. conceived and designed the project. Z.C. and Q.H. wrote the manuscript. All authors contributed to the discussion of the results and revision of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Chemistry thanks Zhi-Gang Chen, Shuo Chen and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cui, Z., Bu, K., Zhuang, Y. et al. Phase transition mechanism and bandgap engineering of Sb2S3 at gigapascal pressures. Commun Chem 4, 125 (2021). https://doi.org/10.1038/s42004-021-00565-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42004-021-00565-4
This article is cited by
-
Comparative analysis of substrate and superstrate configurations in Sb2S3 thin-film solar cells by numerical modelling
Journal of Materials Science (2024)
-
Improvement of the photoelectrical properties of chemical bath-deposited Sb2S3 thin films with low copper doping
Journal of Materials Science: Materials in Electronics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.