Abstract
The quantum anomalous Hall effect in magnetic topological insulators has potential for use in quantum resistance metrology applications. Electronic conductance is quantized to e2/h (where e is the elementary charge and h is the Planck constant) due to the effect, which persists down to zero external magnetic field and is compatible with the quantum standard of voltage. However, metrological applications of the quantum anomalous Hall effect are currently restricted by the need for low measurement currents and low temperatures. Here we report a measurement scheme that increases the robustness of a zero-magnetic-field quantum anomalous Hall resistor and extends its operating range to higher currents. In the scheme, we simultaneously inject current into two disconnected perimeters of a multi-terminal Corbino device, which is based on V0.1(Bi0.2Sb0.8)1.9Te3, to balance the electrochemical potential between the edges. This screens the electric field that drives backscattering through the bulk and thus improves the stability of the quantization at increased currents. Our approach could also be applied to existing quantum resistance standards that rely on the integer quantum Hall effect.
Similar content being viewed by others
Main
The interplay between topology and magnetism in topological insulators1,2,3 results in phenomena such as the quantum anomalous Hall effect (QAHE)4,5,6, which has various underlying magnetic and electrodynamic properties5,7,8,9,10,11,12,13,14,15. The effect is characterized by a universal electrical conductance that is quantized to e2/h, where e is the elementary charge and h is the Planck constant. This quantization persists even at zero external magnetic field and could be of use in quantum resistance metrology16,17,18,19,20.
One goal in quantum metrology is to combine the quantum voltage standard based on the a.c. Josephson effect21 with the quantum resistance standard based on the quantum Hall effect22 into a single reference instrument. This would provide simultaneous access to the von Klitzing and the Josephson constants (RK = h/e2 and KJ = 2e/h), from which e and h can be determined. Thus, this would be a universal quantum electrical standard, which is of particular relevance to the recent redefinition of the kilogram in terms of Planck’s constant23 and to related experiments aimed at tracing the kilogram, such as the elaboration of a Kibble balance24,25.
Compared to the ordinary quantum Hall effect, an advantage of the QAHE is that it eliminates the need for an external magnetic field. However, metrological applications of the QAHE are restricted because its perfect quantization is limited to low temperatures and small measurement currents. Metrology-grade measurements of the QAHE have, thus, been limited to dilution fridge temperatures16,17,18,19. There is, though, evidence that edge states survive to higher temperatures (up to the Curie temperature of a few tens of kelvin26,27,28), which suggests that liquid 4He temperatures commonly used for Josephson quantum voltage standards can potentially be reached through material optimization.
In regard to the low measurement currents, metrological measurements typically use a cryogenic current comparator29, which works optimally at currents of tens of microamps30. When the current is restricted to lower levels, the accuracy of the instrument is reduced16. Therefore, it would be beneficial if metrologically relevant devices could operate at currents approaching tens of microamps. Thus far, metrological-level quantization of the QAHE at zero external magnetic field has been limited to currents below some 100 nA, which restricts the quantization precision to the 10−6–10−7 range16,17,18. An operating current of 1 μA has been achieved with a field of around 200 mT produced by a permanent magnet19, which improved the precision to the 10−8 level. However, the use of a magnetic field hampers integration with the superconducting devices needed to determine the Josephson constant. Improved stability of the zero-magnetic-field QAHE at higher currents is needed to bring the quantization precision closer to the level of the primary quantum standards based on graphene and GaAs, which routinely achieve a level of 10−11 (ref. 30).
In this article, we report a measurement scheme that improves the robustness of the zero-magnetic-field QAHE at higher currents31. This is achieved through the simultaneous injection of current into two disconnected perimeters of a multi-terminal Corbino device. In this geometry, the electric field created between the edges of the sample is compensated, which suppresses backscattering through the bulk. The same measurement method can also be applied to integer quantum Hall devices.
Inter-perimeter electrochemical potential balancing
The basic idea of electrochemical potential balancing comes from realizing that, in macroscopic devices (devices where the separation between edge states is larger than all other relevant length scales, such as the effective width of the edge state, the magnetic length or the screening length), the breakdown mechanism for both the ordinary quantum Hall and quantum anomalous Hall edge state transport is driven by the electric field between opposite edges of the device17,32,33,34,35,36.
How this electric field is distributed between the edges37 depends on the exact nature of the reconstruction of the edge electrostatic potential into compressible and incompressible regions and the associated screening38 and can be quite rich. The essence nevertheless remains that when the electric field between edge states at different potentials exceeds a critical value, electrons are driven by this field to traverse the bulk and backscatter to the opposite edges of the device, thus causing a breakdown in the quantization of the Hall signal. For the purposes of this paper and in the limit of large devices, the single-electron picture of purely one-dimensional edge states with no special screening properties captures the essence of the relevant mechanism and is sufficient.
Figure 1a,b illustrates the basic advantage of our measurement scheme in this simple picture. In a Hall bar geometry in the edge state regime, the electrochemical potential along the edges of the device is distributed as presented schematically in Fig. 1a. A bias voltage is applied to the source contact, whereas the drain contact is grounded. The edge state equilibrates the electric potential along one edge to that of the source contact and the other edge to that of the drain. The edge state drawn in dark blue is at high electrochemical potential, whereas the one shown in light grey represents a low electrochemical potential (here grounded). As the measurement current is increased by applying a larger bias between source and drain, the electrochemical potential difference between the two edges of the sample increases. This increases the inter-edge backscattering probability and eventually leads to a breakdown of the perfect conductance quantization.
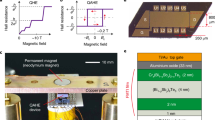
a, Schematic of a Hall bar device under an applied bias voltage. The dark blue line depicts the edge of the device with a high electrochemical potential (\({\mu }_{{{{\rm{e}}}}}^{{{{\rm{S}}}}}\)), and the grey line shows the edge state with a low electrochemical potential (\({\mu }_{{{{\rm{e}}}}}^{{{{\rm{D}}}}}\)). b, Schematic of an optimally double-sourced multi-terminal Corbino device. c, Top, Photograph of the bonded multi-terminal Corbino quantum anomalous Hall device. Bottom, Optical microscope image of the same device (before bonding). The letters A–D label contacts along the outer perimeter, and numbers 1–4 those along the inner perimeter. G denotes the gate contact. d,e, Basic characterization of the device, without any balancing. d, Four-terminal Hall resistance (VB–D/IA–C) measured along the outer perimeter as a function of a perpendicular-to-plane external magnetic field. e, The corresponding measured longitudinal resistance (VB–C/IA–D). The coloured arrows give the direction of the magnetic field sweep. Measurements in d and e were done at 21.21 Hz with a bias voltage of 100 μV at a sample temperature of 35 mK and with 4 V applied to the gate. The horizontal dashed lines represent the resistance values expected for a perfect QAHE: ±h/e2 for the Hall resistance in d, and 0 for the longitudinal resistance in e.
A multi-terminal Corbino geometry, first used in ref. 28, is pictured in Fig. 1c. In the limit of an insulating bulk, the inner and the outer perimeters can independently be used to measure the QAHE. On the outer (inner) perimeter, one can determine the Hall voltage by passing, for example, a current from A to C (1 to 3) and then measuring the resulting voltage between B and D (2 and 4).
Making use of both perimeters allows the measuring scheme sketched in Fig. 1b. The source and (grounded) drain contacts along each perimeter are chosen in such a way that for one part of the circumference, the edge states running along both edges are at high electrochemical potential, whereas for the remainder of the circumference, both the edges are at the grounded electrochemical potential. This biasing method prevents the build-up of an electric field between the inner and outer edges and, thus, suppresses breakdown mechanisms induced by an electric field.
Proof of concept
The device was patterned using standard optical lithography methods from a magnetic topological insulator V0.1(Bi0.2Sb0.8)1.9Te3 layer grown by molecular beam epitaxy (MBE) on a Si(111) substrate39. The outer diameter of the ring was 1 mm, the separation between the inner and outer perimeters was 100 μm and the constriction defining each contact was 50 μm wide. The magnetic topological insulator layer had a thickness of 8.2 nm and was capped with a 10-nm-thick protective layer of amorphous Te, which is insulating. The sample was fitted with a ring-shaped top gate, labelled G in Fig. 1c, which comprises a 15-nm-thick atomic-layer-deposition AlOx film and a 100-nm-thick layer of Au.
The material was optimized to have a fully insulating bulk (when properly gated and below 100 mK) and, thus, quantized anomalous Hall resistance8,16. The sample was mounted in a top-loader-type dilution refrigerator with a modest cooling power of 400 μW at 100 mK and a base temperature of about 30 mK. A gate voltage of 4 V was applied to tune the Fermi level and adjust the sample onto the QAHE plateau. In Fig. 1d,e, the Hall VB–D/IA–C and longitudinal VB–C/IA–D resistances are plotted as a function of the external perpendicular-to-plane magnetic field and show a perfect QAHE. All other measurements in this paper were done under a zero external magnetic field. Measurements collected at various gate voltages can be found in the Supplementary Fig. 3.
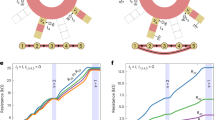
To test the effectiveness of the balancing method, we first performed a reference experiment without any balancing. Figure 2a shows a circuit schematic for a measurement in which the d.c. bias voltage was applied to the outer perimeter (between contacts A and C, which results in the d.c. IA–C). The inner perimeter was grounded through contact 1. With both contacts C and 1 grounded, for the half of the circumference that includes contacts B and 2, the electrochemical potential difference between the inner and outer edges was proportional to the bias applied at contact A and, thus, proportional to the measurement current. This situation is equivalent to that of a measurement on a Hall bar.
a, Circuit diagram for a reference measurement of the Hall resistance VB–D/IA–C without electrochemical potential balancing. The outer perimeter was electrically biased, which drove the d.c. IA–C in the outer perimeter, whereas the inner perimeter was grounded through contact 1. The dark blue colour indicates the high electrochemical potential part of the circuit, whereas light grey shows the low potential. b, A measurement of VB–D/IA–C for this configuration as a function of current IA–C. c,d, Same for the Hall resistance VB–D/IA–C measured with electrochemical potential balancing: circuit diagram (c) and measurements (d). An additional d.c. I3–1 (of the same magnitude as IA–C) was passed at the inner perimeter to balance the electrochemical potentials along the ring. e–h, Analogous, but for the longitudinal resistance VB–C/IA–D: circuit diagram (e) and measurements (f) without and circuit diagram (g) and measurements (h) with electrochemical potential balancing. The horizontal dashed lines in b, d, f and h show the expected values for ideal quantum anomalous Hall edge states. All data were collected at zero external magnetic field, a temperature of 30 mK and an applied gate voltage of 4 V to tune the Fermi level so that we could observe the quantization plateau.
Figure 2b shows the corresponding four-terminal Hall resistance VB–D/IA–C measurement along the outer perimeter as a function of the current IA–C. At low currents, this resistance was quantized to h/e2. At a current IA–C exceeding about 620 nA (with a relative deviation from quantization of about 1% observed at a current of about 680 nA), the critical electrochemical potential difference between the inner and outer edges was reached, and an abrupt breakdown of quantization was observed.
Figure 2c,d presents the balanced scheme. Figure 2c shows a circuit diagram schematic with an additional d.c. I3–1 (of nominally the same magnitude as IA–C; both currents were measured and found to be equal to within about 1%) flowing into the inner perimeter at contacts 3 and 1, whereas C and 1 were grounded. A 110 kΩ resistor was placed in series with each perimeter to minimize the effects of contact resistance variations along the device (contact resistances were of the order of a few hundred ohms in this device). In this scenario, as the edge states equilibrated the electrochemical potentials, contacts 4 and D adjusted to the electrochemical potential determined by the circuit ground, whereas contacts B and 2 were at the electrochemical potential determined by the source contacts, A and 3, respectively. As the two currents IA–C and I3–1 were equal in magnitude, the electrochemical potential at contacts A and 3 was equal, leading to an electrochemical potential balance between the inner and outer edges at all points around the circumference of the ring. This was, of course, independent of the amplitude of the measurement current. Alternative configurations producing an equivalent balanced setting (such as applying the electrical bias between contact pairs B and D and between 4 and 2) can, of course, also be used; see Supplementary information Fig. 2 for measurements of such configurations.
The Hall resistance VB–D/IA–C measured in the configuration in Fig. 2c is plotted in Fig. 2d as a function of the measurement current IA–C. It is clear that the breakdown induced by the electric field, as observed in Fig. 2b, was effectively suppressed, thus allowing a larger current to be injected into the sample before any deviation from quantization is observed (a relative deviation from quantization of 1% was observed at a current of about 2.85 μA). Importantly, the nature of the departure from quantization in Fig. 2d is very different from that in Fig. 2b. In Fig. 2b, an abrupt departure is observed, characteristic of the critical electrochemical potential difference having been reached. In contrast, in Fig. 2d, the Hall resistance moves away from quantization smoothly and gradually and at higher current values. We will show below that the breakdown of perfect quantization in this case can be attributed to thermal activation of bulk conductance caused by Joule heating.
Figure 2e–h presents an equivalent analysis for the four-terminal longitudinal resistance VB–C/IA–D. Pertinent reference measurements are shown in Fig. 2e–f, where the d.c. IA–D was flowing between contacts A and D, and contacts D and 1 were referenced to the ground. This resistance configuration shows the expected value of 0 at low currents, with a clear onset of dissipation observed when the measurement current IA–D exceeded 620 nA, consistent with the Hall resistance measurement from Fig. 2b. Remarkably, in Fig. 2g–h, under the balanced scheme (with an additional current of the same magnitude I4–1 flowing into the inner perimeter), we observe that the longitudinal resistance signal remained below some 0.00002h/e2 (limited by the measurement resolution) up to the measurement current of 3 μA.
To further support our interpretation that the slow drift away from the quantized value observed in Fig. 2d was caused by current-induced heating, we consider measurements done at various higher temperatures on the same device, as shown in Fig. 3. It is well established for Cr/V-doped (Bi,Sb)2Te317,28,36,40 that as the temperature is increased above some 100 mK, spurious conductance from the bulk of the material increases, the edge states become partially electrically shorted through the bulk and the observed Hall resistance decreases. The data nevertheless show that, as the sample temperature was increased, the change in Hall resistance as a function of applied bias was progressively suppressed, as one would expect if the effects of current-induced heating diminish.
Hall resistance VB–D/IA–C measured in the balanced scheme (Fig. 2c) at various temperatures as a function of IA–C. The coloured horizontal dashed lines are guides to the eye and indicate the resistance at each temperature in the low-current limit. Measurements are at zero external magnetic field and with 4 V applied to the gate.
Note that the current at which we observed a breakdown without balancing in Fig. 2b,f (some 620 nA) corresponds to ~16 mV of voltage difference between the perimeters VB-2. We found a clear breakdown of Hall resistance quantization whenever this voltage drop exceeded ±16 mV, regardless of the magnitude of the measurement current IA–C. In the multi-terminal Corbino geometry, this can be directly tested by connecting two independent voltage sources to the sample, one into each perimeter, and separately controlling the IA–C and I3–1 currents. This is analysed and discussed in detail in Supplementary Fig. 1, which further confirms that the electrochemical potential difference between the perimeters is the key parameter driving the breakdown of QAHE quantization.
Conclusions
There are two main obstacles to using the QAHE in mainstream metrology: the need for devices to support currents that are compatible with high-precision current comparators and the need for the devices to work at liquid helium temperatures. We have reported a measurement scheme that addresses the issues surrounding the measurement current. Our approach drives the measurement current through the inner and outer edges of a multi-terminal Corbino ring. Balancing the electrochemical potential between the two edges eliminates the breakdown of the quantization induced by the electric field.
By turning off this primary current-induced breakdown mechanism, we increased the allowed measurement current before a secondary current-induced effect (Joule heating) becomes relevant. The effects of Joule heating can be suppressed by using a dilution refrigerator with a higher cooling capacity, and we expect that the maximum current that the edge states can stably support will further increase by applying a higher cooling power. The effects of Joule heating could further be mitigated by optimizing the material, such as increasing the device operating temperature, whether based on Cr/V-doped (Bi,Sb)2Te3 or another material system.
Our wiring scheme is an extension of established Hall bar measurements, but it is fundamentally different in that it requires two current sources instead of one (as well as two grounding points on the device). Although the scheme was implemented in a research laboratory at the precision level offered by standard d.c. measurements, there is presently no instrument with metrologically relevant precision (namely, no cryogenic current comparator) that satisfies these requirements. The required modification to allow measurements with a cryogenic current comparator in this scheme are, though, clear and work has begun in this direction. Lastly, note that our balancing method is not limited to QAHE-based devices and could be used to increase the maximum current allowed in traditional quantum Hall based resistance devices, for applications where higher currents are useful.
Methods
Device preparation
The V0.1(Bi0.2Sb0.8)1.9Te3 layer was grown using MBE on an insulating, hydrogen, passivated, Si(111) substrate capped in situ with a 10-nm-thick layer of insulating Te (ref. 39). Using X-ray reflectivity, the epilayer thickness was measured to be approximately 8.2 nm. The Bi/Sb ratio of 1/4 and V doping of 2% (of all atoms) were determined by X-ray diffraction and energy dispersive X-ray spectroscopy measurements of the layer as well as thicker (about 50 nm thick) calibration samples.
After MBE growth, the devices were fabricated using standard optical lithography methods. First, a mesa was patterned using Ar milling. The ohmic contacts were patterned in a second step. For that, the sample was transferred into a dry-etching chamber, where the Te cap was removed using Ar milling. Afterwards, the sample was transferred into an electron beam evaporation chamber, without breaking the high vacuum conditions, where a stack comprising 50 nm of AuGe and 50 nm of Au was deposited. A top gate was fabricated in a third step. The sample was transferred into an atomic-layer-deposition chamber, where a 15-nm-thick layer of AlOx was deposited onto the entire surface of the sample. This was followed by electron beam evaporation of a 100-nm-thick Au top gate pad. In the final lithographic step, the AlOx layer was removed from the area of the ohmic contacts using hydrofluoric acid (HF) diluted 1:200 with water. After the patterning, the sample was glued to a chip carrier using GE varnish and mechanically wedge bonded using Au wires.
Transport measurements
All transport measurements were performed in a conventional top-loader-type dilution refrigerator with a base temperature of about 30 mK (with the exception of the 4.2 K curve in Fig. 3, which was measured in a conventional 4He cryostat) and equipped with a superconducting solenoid magnet that produced a field perpendicular to the plane of the sample.
Electrical transport measurements were performed using conventional d.c. techniques in a voltage-biased (limited) scheme. Each potential difference was measured using an ultra-high impedance operational amplifier (input impedance of about 1 TΩ). The output was read directly by a nanovoltmeter. Each current was determined by measuring the voltage drop across a calibrated reference resistor that was placed in series with the sample.
Data availability
Source data are provided with this paper. Other data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Kane, C. L. & Mele, E. J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
König, M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007).
Yu, R. et al. Quantized anomalous Hall effect in magnetic topological insulators. Science 329, 61–64 (2010).
Nomura, K. & Nagaosa, N. Surface-quantized anomalous Hall current and the magnetoelectric effect in magnetically disordered topological insulators. Phys. Rev. Lett. 106, 166802 (2011).
Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Lachman, E. O. et al. Visualization of superparamagnetic dynamics in magnetic topological insulators. Sci. Adv. 1, e1500740 (2015).
Grauer, S. et al. Coincidence of superparamagnetism and perfect quantization in the quantum anomalous Hall state. Phys. Rev. B 92, 201304(R) (2015).
Liu, M. et al. Large discrete jumps observed in the transition between Chern states in a ferromagnetic topological insulator. Sci. Adv. 2, e1600167 (2016).
Yasuda, K. et al. Geometric Hall effects in topological insulator heterostructures. Nat. Phys. 12, 555–559 (2016).
Mogi, M. et al. A magnetic heterostructure of topological insulators as a candidate for an axion insulator. Nat. Mater. 16, 516–521 (2017).
Grauer, S. et al. Scaling of the quantum anomalous Hall effect as an indicator of axion electrodynamics. Phys. Rev. Lett. 118, 246801 (2017).
Fijalkowski, K. M. et al. Coexistence of surface and bulk ferromagnetism mimics skyrmion Hall effect in a topological insulator. Phys. Rev. X 10, 011012 (2020).
Fijalkowski, K. M. et al. Any axion insulator must be a bulk three-dimensional topological insulator. Phys. Rev. B 103, 235111 (2021).
Fijalkowski, K. M. et al. Macroscopic quantum tunneling of a topological ferromagnet. Adv. Sci. 10, 203165 (2023).
Götz, M. et al. Precision measurement of the quantized anomalous Hall resistance at zero magnetic field. Appl. Phys. Lett. 112, 072102 (2018).
Fox, E. J. et al. Part-per-million quantization and current-induced breakdown of the quantum anomalous Hall effect. Phys. Rev. B 98, 075145 (2018).
Okazaki, Y. et al. Precise resistance measurement of quantum anomalous Hall effect in magnetic heterostructure film of topological insulator. Appl. Phys. Lett. 116, 143101 (2020).
Okazaki, Y. et al. Quantum anomalous Hall effect with a permanent magnet defines a quantum resistance standard. Nat. Phys. 18, 25–29 (2022).
Rodenbach, L. K. et al. Realization of the quantum ampere using the quantum anomalous Hall and Josephson effects. Preprint at https://doi.org/10.48550/arXiv.2308.00200 (2023).
Josephson, B. D. Possible new effects in the superconductive tunnelling. Phys. Lett. 1, 251 (1962).
von Klitzing, K., Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494 (1980).
BIPM The International System of Units, 9th edn (Bureau International des Poids et Mesures, 2019); www.bipm.org/documents/20126/41483022/SI-Brochure-9-EN.pdf
Kibble, B. P. in Atomic Masses and Fundamental Constants (eds Sanders, J. H. & Wapstra, A. H.) Ch. 5 (Springer, 1976).
Stock, M. Watt balance experiments for the determination of the Planck constant and the redefinition of the kilogram. Metrologia 50, R1 (2013).
Chang, C.-Z. et al. Zero-field dissipationless chiral edge transport and the nature of dissipation in the quantum anomalous Hall state. Phys. Rev. Lett. 115, 057206 (2015).
Yasuda, K. et al. Large non-reciprocal charge transport mediated by quantum anomalous Hall edge states. Nat. Nanotechnol. 15, 831–835 (2020).
Fijalkowski, K. M. et al. Quantum anomalous Hall edge channels survive up to the Curie temperature. Nat. Commun. 12, 5599 (2021).
Harvey, I. K. A precise low temperature dc ratio transformer. Rev. Sci. Instrum. 43, 1626–1629 (1972).
Ribeiro-Palau, R. et al. Quantum Hall resistance standard in graphene devices under relaxed experimental conditions. Nat. Nanotechnol. 10, 965–971 (2015).
Fijalkowski, K. M. & Gould, C. Quantization breakdown protection for semiconductors and in particular topological insulators. European patent EP23162996.5 (2023).
Komiyama, S., Takamasu, T., Hiyamizu, S. & Sasa, S. Breakdown of the quantum Hall effect due to electron heating. Solid State Commun. 54, 479–484 (1985).
Komiyama, S. & Kawaguchi, Y. Heat instability of quantum Hall conductors. Phys. Rev. B 61, 2014 (2000).
Kawamura, M. et al. Current-driven instability of the quantum anomalous Hall effect in ferromagnetic topological insulators. Phys. Rev. Lett. 119, 016803 (2017).
Rodenbach, L. K. et al. Bulk dissipation in the quantum anomalous Hall effect. APL Mater. 9, 081116 (2021).
Lippertz, G. et al. Current-induced breakdown of the quantum anomalous Hall effect. Phys. Rev. B 106, 045419 (2022).
McCormick, K. L. et al. Scanned potential microscopy of edge and bulk currents in the quantum Hall regime. Phys. Rev. B 59, 4654 (1999).
Chklovskii, D. B., Shklovskii, B. I. & Glazman, L. I. Electrostatics of edge channels. Phys. Rev. B 46, 4026 (1992).
Winnerlein, M. et al. Epitaxy and structural properties of (V,Bi,Sb)2Te3 layers exhibiting the quantum anomalous Hall effect. Phys. Rev. Mater. 1, 011201(R) (2017).
Bestwick, A. J. et al. Precise quantization of the anomalous Hall effect near zero magnetic field. Phys. Rev. Lett. 114, 187201 (2015).
Acknowledgements
We thank the team of H. Scherer (M. Kruskopf, M. Götz, D. Patel and E. Pesel) from Physikalisch-Technische Bundesanstalt, Braunschweig, for useful discussions about the metrological relevance of this work and gratefully acknowledge the financial support of the Free State of Bavaria through the Institute for Topological Insulators to L.W.M., the German Research Foundation (Grant No. SFB 1170 258499086 to C.G., K.B. and L.W.M.), the Würzburg-Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter (Grant No. EXC 2147 39085490 to L.W.M.) and the European Commission under Horizon 2020 programme FETPROACT (Grant No. TOCHA 824140 to C.G. and L.W.M.).
Funding
Open access funding provided by Julius-Maximilians-Universität Würzburg.
Author information
Authors and Affiliations
Contributions
K.M.F. and C.G. developed the electrochemical potential balancing method. K.M.F. designed and patterned the measured devices and performed the transport experiments. N.L. grew the MBE layer. M.K., S.S. and K.B. contributed to MBE material development. C.G. and L.W.M. supervised the work. All authors contributed to the analysis and interpretation of the results and the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Electronics thanks Shuji Nakamura and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–3 and Discussion.
Source data
Source Data for Fig. 1
Resistance values plotted in the figure.
Source Data for Fig. 2
Resistance values plotted in the figure.
Source Data for Fig. 3
Resistance values plotted in the figure.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fijalkowski, K.M., Liu, N., Klement, M. et al. A balanced quantum Hall resistor. Nat Electron 7, 438–443 (2024). https://doi.org/10.1038/s41928-024-01156-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41928-024-01156-6