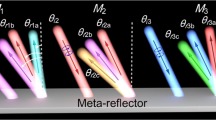
Abstract
Non-reciprocal metasurfaces can encode optical functions on forward- and backward-propagating waves, and could be used to create non-reciprocal antennas and radomes for full-duplex wireless communication and radar systems. However, such metasurfaces typically require external electric- or magnetic-field biasing or rely on non-linear effects, which makes practical implementation challenging. Here we report a self-biased non-reciprocal metasurface based on magnetic meta-atoms made from lanthanum-doped barium hexaferrite. The metasurface offers a transmittance of up to 77% and an operation angle of ±64°. We show that they can be used for on-demand bidirectional phase modulation, which provides non-reciprocal functionalities including microwave isolation, non-reciprocal beam steering, non-reciprocal focusing and non-reciprocal holography. The approach could also be potentially extended to megahertz and optical frequencies by using different self-biased magnetic materials.
Similar content being viewed by others
Main
Metasurfaces have a flat, low-profile form factor and can be used to control electromagnetic wave propagation. Their planar structure also facilitates scalable fabrication based on printed circuit boards or silicon photonic technologies. Developments in the field have led to functionalities such as polarization conversion1, perfect absorption2 and wavefront control3,4. However, most metasurfaces obey the Lorentz reciprocity and non-reciprocal metasurfaces (NRMs) have only recently emerged5,6,7,8,9. Unlike conventional metasurfaces whose characteristics are symmetric with respect to the wave propagation direction, NRMs perform direction-dependent functions. For instance, NRM-integrated radomes can act as non-reciprocal antennas, which can curtail antenna echoes10 and enable arbitrary emission and receiving characteristics of electromagnetic waves. NRMs can also be used to create full-duplex wireless communications by doubling the bandwidth of wireless communications11.
For practical applications, an NRM should ideally be able to produce arbitrary phase and amplitude combinations for on-demand wavefront modulation along both transmission directions. It should also be passive, linear and operate without active bias fields to reduce power consumption and improve scalability. Several mechanisms can be used to achieve non-reciprocity12. First, a transistor-loaded circuit can allow the unidirectional gain of electromagnetic waves because of its rectifying effect and thereby breaking Lorentz reciprocity13,14. NRMs based on this mechanism have been demonstrated at radio frequency15,16. These devices can exhibit a broad operational bandwidth and forward transmission gain. However, they suffer from low operation frequencies (which is limited by the transistor speed), low power-handling capability, high biasing power and poor signal-to-noise ratio17,18. Passive and linear properties are also hard to implement with this approach.
Second, non-linearity in metasurfaces with asymmetric structures can be used to generate non-reciprocity. These metasurfaces are sensitive to incident power and are limited by dynamic reciprocity to pulsed-wave applications19,20. Non-linear metasurfaces exhibiting non-reciprocal behaviour have been implemented in both theory and experiment5,21,22,23. Third, reciprocity can be lifted by spatiotemporal modulation. Such devices have been theoretically proposed24,25,26 and experimentally validated at both radio8,27,28 and optical frequencies7. However, these metasurfaces suffer from a large constant power consumption, a trade-off between modulation frequency and operation bandwidth, and undesired high-harmonic generation11,16.
Finally, magnetic materials can be used. Magnetic materials are non-reciprocal because of their asymmetric permittivity or permeability tensors. Such materials are widely used in commercial isolators or circulators, but their use in NRM applications is limited. This is probably because the local control of individual meta-atoms is challenging with bulky biasing magnets available. Non-reciprocal magnetic metasurfaces have been considered for one-way transmission using indium antimonide29,30, graphene31 and yttrium iron garnet32,33. However, creating a passive phase-gradient NRM using gyromagnetic effects remains a challenge.
In this article, we report all-dielectric NRMs that consist of self-biased magnetic meta-atoms fabricated from La-doped BaFe12O19 (La:BaM). Such M-type hexaferrites have a giant magnetic anisotropy of up to 17,500 Oe and a large magnetic coercivity34,35,36,37,38, and have been used to create radio-frequency isolators/circulators37,38,39,40,41,42. Their large coercivity and strong magnetic remanence supports magnetic bias-free operation of devices34,43. In our NRMs, the strong magnetic coercivity overcomes the shape anisotropy and magnetic static interaction between meta-atoms. Each meta-atom can be individually magnetized along arbitrary directions and we used this to create NRMs with bidirectional non-reciprocal phase-gradient profiles. Following a non-reciprocal digital coding metasurface design methodology, we show that the NRMs can offer a range of functionalities, including unidirectional transmission, non-reciprocal beam deflection, non-reciprocal beam focusing and non-reciprocal holography in the Ku band (~15 GHz, λ = 2 cm). Our all-dielectric NRMs could be of use in applications such as electromagnetic wave isolation, circulation, non-reciprocal antennas and radomes, and full-duplex transmission.
Device structure and operation principles
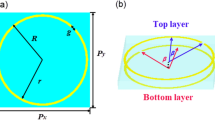
The meta-atom of the NRM is shown in Fig. 1a. We chose La:BaM as the magnetic material because of its large off-diagonal component of the permeability tensor (Supplementary Fig. 1) and the high remanent magnetization (Mr) resulting from its strong magnetocrystalline anisotropy field (Ha = 14,600 Oe). The meta-atom consists of a subwavelength La:BaM cuboid pillar on top of a Teflon substrate, with Mr along the surface normal (+z or z) direction (Fig. 1a). The magnetic hysteresis, permittivity and permeability tensor of La:BaM in the remanence state are measured and calculated in Supplementary Note 1. In this configuration, a circularly polarized electromagnetic wave ‘sees’ different refractive indices and extinction coefficients when the wavevector is parallel or antiparallel to the magnetization direction, which is attributed to magnetic circular birefringence and magnetic circular dichroism effects (for low-loss frequencies, magnetic circular birefringence dominates). Therefore, magnetic Mie resonators exhibit different resonance frequencies for forward- and backward-propagating waves, leading to an asymmetric transmission amplitude (Fig. 1b) and phase (Fig. 1c). Figure 1d shows a schematic of the non-reciprocal phase-gradient metasurface design, with the orange colour indicating Mr along the +z direction and purple colour indicating Mr along the −z direction. The arrangement of these cells can generate arbitrary direction-dependent phase and amplitude profiles by leveraging magnetic circular birefringence/magnetic circular dichroism effects.
a, Operation mechanism of a self-biased magnetic meta-atom. b, Non-reciprocal transmission near Mie resonance modes, leading to non-reciprocity in the transmission amplitude. c, Non-reciprocal transmission near Mie resonance modes, leading to non-reciprocity in the transmission phase. d, Schematic of the phase-gradient NRM design principle.
One-way-transmission NRMs
The concept of a one-way-transmission NRM is illustrated in Fig. 2a. This device was realized by detuning the Mie resonance wavelength through the magnetic circular birefringence effect. The metasurface consists of periodically arranged cuboid pillars of La:BaM, which were initially magnetized at a magnetic field of 24 kOe and then attached to a 18.0 cm × 18.0 cm × 0.5 cm Teflon substrate in their remanence state. The device was designed to operate in the Ku band (~15 GHz, λ = 2 cm). The width and height of each cuboid were 3 and 6 mm, respectively. The period of the meta-atoms was 1 cm. Figure 2b shows the fabricated sample.
a, Schematic of the one-way-transmission NRM. b, Image of the fabricated sample. c,d, Simulated (c) and experimental (d) transmission spectra for forward and backward right-circularly polarized incidence. e,f, Simulated (e) and experimental (f) transmission difference between the forward and backward right-circularly polarized incidence as a function of incident angle (θ) and frequency. PTFE, polytetrafluoroethylene; ED, electric dipole; MQ, magnetic quadrupole; MD, magnetic dipole.
We first simulated the transmission spectra of the metasurface under right-circularly polarized incidence for forward and backward transmissions (Fig. 2c). The forward transmission spectrum shows two resonance peaks at 13.2 GHz and 14.6 GHz. These two peaks shifted to higher frequencies at 13.6 GHz and 15.4 GHz, respectively, for backward transmission. Multipole decomposition indicates that the two resonances correspond to a magnetic dipole resonance mode at 13.2 GHz and a hybrid electric dipole–magnetic quadrupole mode at 14.6 GHz, respectively (Supplementary Fig. 2). Non-reciprocal one-way transmissions with an isolation ratio of 10.9 dB and insertion loss of 0.6 dB at 15.4 GHz, and an isolation ratio of 10.4 dB and insertion loss of 5 dB at 13.6 GHz were theoretically predicted. Figure 2d shows the experimental transmission spectra of the metasurface (Supplementary Fig. 3 shows the measurement setup details). An isolation ratio of 7.0 dB and insertion loss of 8.4 dB at 13.7 GHz, and an isolation ratio of 5.6 dB and insertion loss of 1.1 dB at 15.7 GHz were experimentally observed, consistent with the simulation results. The minor difference between the experiment and simulation could be potentially due to the imperfect circular polarization of the source antenna with an axis ratio of 2.5 dB.
We further simulated (Fig. 2e) and measured (Fig. 2f) the transmission contrasts at incident angles ranging from 0° to 64°. The results showed that the resonance frequencies (especially those of the hybrid electric dipole–magnetic quadrupole mode) were almost independent of the incident angle. The maximum angle was only limited by the finite size of the NRM and our experimental setup. The results would also be identical for 0° to −64° incidence because of symmetry considerations. This wide-angle tolerance suggests that such an NRM is compatible with integration on curved surfaces, such as on-antenna radomes.
Phase-gradient NRMs
Phase-gradient NRMs, whose phase profiles differ for forward and backward incidence, allow the full on-demand control of bidirectional electromagnetic wave propagation. The design of such metasurfaces is based on the concept of non-reciprocal digital coding metasurface: each element has both forward- and backward-propagation phases, which can be written as (ϕf(ω), ϕb(ω)), where ϕf(ω) and ϕb(ω) are the forward- and backward-transmission phases, respectively, at frequency ω. To construct a two-bit phase-gradient NRM for arbitrary forward- and backward-propagation phase profiles, 16 elements were required44 (Supplementary Fig. 4a). However, because the magnetic meta-atoms can be placed with either their magnetization pointing up or down, the phase of the forward and backward incidence can be switched by flipping the direction of Mr. This reduces the required elements to ten for arbitrary and non-reciprocal phase profiles (Supplementary Notes 4 and 5).
The optimal meta-atom design must minimize the phase error whereas maximize the transmission efficiency for both forward and backward waves. To balance the trade-off between phase error and transmission efficiency, we used a single figure of merit to evaluate the meta-atom designs45 (Supplementary Note 4). The ten elements were selected in a parameter space consisting of 9,192 parameter combinations (Supplementary Note 4). The transmission spectra of each of the ten fabricated elements were characterized. The transmittance and phase as a function of frequency were characterized by measuring the S21 and S12 parameters, which agreed well with the simulation results (Supplementary Note 5). The optimal ten-element configuration yielded an average transmittance of 42.4% and 38.5% and an average phase error of ±11.9° and ±12.0° for forward and backward incidence, respectively.
Non-reciprocal beam deflection
It is possible to construct NRMs with on-demand bidirectional phase profiles using the ten non-reciprocal elements in a ‘LEGO-like’ manner. We demonstrated this by first assembling a non-reciprocal beam deflector using meta-atoms (Fig. 3b). Figure 3a shows the concept of the device. At 14.6 GHz, the device allows forward normal transmittance of an incident right-circularly polarized plane wave, whereas it diffracts the incident wave away from the surface normal in case of a backward wave. The entire device area measured 17 cm × 10 cm. Four elements with (forward, backward) phase delays of (0, 0), (0, π/2), (0, π) and (0, 3π/2) constituted one period of 10 mm. Therefore, the metasurface exhibited an almost flat phase distribution for forward transmission and a sawtooth phase profile for backward transmission (Fig. 3c,d); the experimental phase map (stars) agrees with the target phase profile (dashed lines). Figure 3e,f shows the simulated electric-field profile at 14.6 GHz, confirming the proposed non-reciprocal diffraction functionality.
a, Schematic of the non-reciprocal beam deflector. b, Image of the fabricated non-reciprocal beam deflector. c, Target (dotted line) and measured (star) phase profiles for forward incidence. d, Target (dotted line) and measured (star) phase profiles for backward incidence. e,f, Simulated electric-field profiles of the supercell for forward incidence (e) and backward incidence (f). g,h, Measured and simulated far-field radiation patterns for forward incidence (g) and backward incidence (h).
The simulated diffraction angle reached 29°, with a diffraction efficiency of 17.7% for backward incidence. For forward incidence, the transmission efficiency reached 33.5%. The relatively low transmission efficiency can be attributed to the large impedance mismatch at the air/metasurface interface as well as the energy loss into different diffraction orders (<4%). These imperfections induce ~24% and ~34% reflected energy for forward and backward incidence, respectively (Supplementary Fig. 7). Experimentally, we demonstrate a 31.3% transmission efficiency for the zeroth-order diffraction in case of forward incidence and 13.8% transmission efficiency for the first-order diffraction at 30.0° ± 0.5° in case of backward incidence. As shown in Fig. 3g,h, the experimental radiation patterns are in agreement with the simulation (Supplementary Fig. 8 shows the experimental details). The slightly lower measured transmission efficiency compared with the simulation may be attributed to the lower transmittance of the experimental meta-atoms and the spherical wavefront of the incident wave (Supplementary Fig. 9). The non-reciprocal beam deflector can also be regarded as a free-space quasi-circulator by treating the forward and backward zeroth and first diffraction orders as ports 1–3, and it satisfies all the relevant requirements for full-duplex communication systems (Supplementary Note 9).
Non-reciprocal metalens
The non-reciprocal metalens exhibits different focal lengths for forward and backward transmission (Fig. 4a). Figure 4b shows a photograph of the fabricated non-reciprocal metalens sample. The sample area was 17 cm × 17 cm. The meta-atoms were arrayed with a 1 cm period. The hyperbolic phase profiles of the metalens are given by46
where r is the radial coordinate, λ is the designed wavelength, f1/2 is the designed focal length for forward and backward incidence and φf/b(r) is the phase profile at position r for forward and backward incidence.
a, Schematic of the non-reciprocal metalens. b, Image of the fabricated non-reciprocal metalens. c,d, Phase profiles of the metalens for forward incidence (c) and backward incidence (d). e,f, Simulated focal-spot profiles in the y–z plane for forward incidence (e) and backward incidence (f) at 15 GHz. g,h, Measured focal-spot profiles in the y–z plane for forward incidence (g) and backward incidence (h). i,j, Normalized focal-spot distributions along the x direction in the focal plane for forward incidence (i) and backward incidence (j).
In our prototype, focal lengths of f1 = 6 cm and f2 = 13 cm were implemented for forward and backward transmission, respectively. The ten elements with forward- and backward-transmission phases were mapped onto the targeted phase profiles of the metalens (Fig. 4c,d). Figure 4e displays the electric-field intensity profiles in the y–z plane for forward right-circularly polarized incidence at 15 GHz. The simulated focal length was 5.4 cm with a focusing efficiency of 46.9%. The discrepancy between the theoretical (6.0 cm) and simulated (5.4 cm) focal lengths stemmed from coupling between adjacent meta-atoms (Supplementary Fig. 12). For backward incidence, the focal length and focusing efficiency were 11 cm and 42.3%, respectively. Meanwhile, the full-width at half-maximum of the focal spot in the forward and backward directions were 1.6 cm and 2.2 cm, respectively. The focusing efficiency was defined as the ratio of the power on the focal plane within a radius of three times the full-width at half-maximum of the focal spot and total incident power. The electric-field intensity profiles (Fig. 4g,h) were measured using a near-field scanning setup via antenna scanning in the x–y plane at different z positions (Supplementary Fig. 13). The shadowed areas in both figures could not be probed because of the finite size of the scanning antenna. The intensity profiles showed clear focal spots with focal lengths of 55.0 ± 1.5 and 105.0 ± 1.5 mm for forward and backward transmission, respectively. The ripple patterns were caused by interference between the incident and reflected waves47.
The measured focusing efficiencies were 30.5% and 30.0% for forward and backward incidence, respectively. The lower focusing efficiency in the experiment compared with the simulation was attributed to the spherical instead of plane wavefront of the incident wave (~7% and ~3% focusing efficiency attenuation for forward and backward incidence, respectively; Supplementary Note 8), as well as the lower transmission of experimentally fabricated meta-atoms compared with the simulation (~9% lower transmittance on average; Supplementary Table 1). Figure 4i shows the linescans of the normalized intensity distributions at the focal plane. The insets in Fig. 4i show the simulated and measured focal-spot images; the dashed curve shows the focal-spot profile of an ideal aberration-free lens with the same aperture size and focal length. The Strehl ratio of the experiment reached 0.81, indicating the diffraction-limited focusing of our metalens. The focal-spot profiles of backward incidence are presented in Fig. 4j. In this case, the Strehl ratio reached 0.91. The evolution of the focal-spot profiles in the x–y plane along the z axis was also measured (Supplementary Fig. 14).
Non-reciprocal holography
Holography is a promising technology for three-dimensional displays48, beam shaping49 and artificial intelligence50. Here we utilize the NRM to achieve non-reciprocal holography, which displays different holograms for forward and backward propagation. To design phase-only computer-generated holograms, we selected two image planes 10 cm from the surface of each side of the sample. Handwritten Greek letters ε and μ were used as the holographic patterns (Fig. 5a). The Gerchberg–Saxton algorithm was used to retrieve the phase profiles of the hologram (Supplementary Fig. 15).
a, Schematic of the non-reciprocal phase-only hologram sample. b, Image of the fabricated non-reciprocal phase-only hologram sample. c,d, Phase profiles of the metasurface for forward incidence (c) and backward incidence (d). e,f, Simulated electric-field intensity profiles of the metasurface for forward incidence (e) and backward incidence (f). g,h, Measured holographic images for forward incidence (g) and backward incidence (h).
Figure 5c,d depicts the discrete phase profiles of the ε and μ patterns for forward and backward incidences at 15 GHz, respectively. Figure 5e,f shows the holographic images simulated with the phase profiles in Fig. 5c,b, showing clear ε and μ letters in the respective image planes. Using the same measurement setup used for metalens characterization, the intensity profiles of ε and μ letters (Fig. 5g,h) were mapped, confirming good agreement with the design. The diffraction efficiency51,52, defined as the power concentrated in the holographic image referenced to the total power transmitted by the hologram, reaches 84.1% and 76.4% for the two incident directions in our experiment. The transmission efficiencies51,53 (energy on the holographic plane normalized by the total incident energy) for the two incident directions were 27.0% and 26.8%, respectively. Compared with the simulated efficiencies of 44.0% and 42.4%, the difference was caused by the spherical wavefront (~5.3% and ~4.0% deviation from the plane wave), lower transmittance of the meta-atoms in the experiment (~9.0% lower than the simulation in average) and phase errors of the meta-atoms (~3.0% deviation from the simulation). The holographic efficiency could be improved by using magnetic materials with lower loss, an impedance-matching layer and meta-atoms with more phase-sampling levels (Supplementary Note 13).
Conclusions
We have reported a self-biased NRM for on-demand bidirectional phase modulation. Due to the strong gyromagnetic effect and strong magnetocrystalline anisotropy of La:BaM, we achieved non-reciprocal and arbitrary intensity and phase profiles for both forward and backward propagation with subwavelength-scale Mie resonators. Our intensity-modulated NRM demonstrated one-way transmission over a wide angular range of 0° to ±64° at 15.7 GHz frequency. Using phase-gradient NRMs, we demonstrated three functional devices: a non-reciprocal deflector, a non-reciprocal metalens and non-reciprocal holography in the Ku band.
Self-biased magnetic meta-atoms eliminate the need for an external field, thereby resolving a major roadblock in the deployment of magnetic metasurfaces. Our approach also circumvents the challenges encountered in other NRMs, such as the sensitivity to incident-wave intensity, large active power consumption, high-harmonic generation, low signal-to-noise ratio, poor power-handling capability and bandwidth limitations. Our metasurfaces are insensitive to incidence angles, and could be potentially used as omnidirectional antennas in, for example, wireless communications or integration on curved surfaces such as antenna radomes. The transmission efficiency of the metasurfaces reaches 30–77% in the Ku band, which compares well with other NRMs8,54, and uses no gain elements. Our experiments were carried out in the Ku band, but the non-trivial off-diagonal component at these frequencies (Supplementary Fig. 1d) indicate that the NRMs could also be constructed in the V band (40 GHz to 75 GHz) and W band (75 GHz to 110 GHz) using the same La:BaM material.
The operating frequency of such metasurfaces can be potentially extended to cover megahertz to optical frequencies by choosing different self-biased magnetic materials. For example, cobalt or nickel spinel ferrites could be used to reach the megahertz frequency range55,56; hexaferrites with tunable magnetic anisotropies could be used to reach the gigahertz to terahertz frequency range39; and self-biased garnet thin films with magnetoelastic effects could be used to reach the optical frequency range57,58.
There is also room to improve device performance. First, reflection at the air/metasurface interface, phase error and absorption in the meta-atoms, on average, account for 15%, 6% and 40% efficiency losses in the devices, respectively. Impedance-matching structures could be incorporated into the meta-atoms to reduce reflection loss. Optimized doping or growth protocols could reduce the imaginary parts of ε and μ in hexaferrite materials59. With suppressed material loss, phase error and reflection, we estimate that the average efficiency can be substantially improved. Moreover, the large off-diagonal µ element implies a ‘non-perturbative’ design scheme in which forward and backward waves yield different modal overlaps with meta-atoms, thereby suppressing the insertion loss to a level beyond the material’s figure-of-merit limit60. This effect is illustrated in Supplementary Fig. 2i,j, where the scattering cross-section is different for forward and backward propagation in the same meta-atom, leading to a one-way-transmission metasurface with a low insertion loss of only 1.1 dB.
Second, polarization-independent NRMs can be developed by using different magneto-optical effects, such as transverse magneto-optical Kerr effects for linearly polarized waves or the Faraday effect for circularly polarized waves (Supplementary Note 14). Third, the bandwidth of metasurfaces can be further extended because the gyromagnetic property of the magnetic material is broadband (Supplementary Fig. 1c). The dispersion engineering of both forward- and backward-propagating modes can be performed on the meta-atoms, analogous to the design of an achromatic metalens, except for the bidirectional nature. These approaches could lead to the development of high-efficiency NRMs that offer broadband and on-demand non-reciprocal control of electromagnetic radiation.
Methods
Metasurface fabrication
Metasurface fabrication involved the fabrication of La:BaM elements and their attachment onto a Teflon substrate. La:BaM bulk crystals were cut using an ultrahigh-precision computer numerical control machine to fabricate square nanopillars with a dimensional accuracy better than 0.05 mm. Subsequently, the nanopillars were placed in an electromagnet with a maximum magnetic field of 24 kOe. The magnetization easy axis was saturated by gradually applying the voltage and current of the electromagnet, and the external magnetic field was gradually removed to maintain the remanent magnetization of the ferrite. The Teflon substrates were 18.0 cm × 18.0 cm sheets with a thickness of 0.5 cm. A double-sided adhesive was applied and the acrylic plate was covered with an array of pockets to facilitate a meta-atom fixture. The magnetized meta-atoms were placed in predefined pockets and laminated with double-sided adhesive. After all the elements were arranged in the substrate, the acrylic plate and unused double-sided adhesive were removed.
Metasurface characterization
All the experimental results were measured using a vector network analyser (VNA; Agilent E8363C) to obtain the Ku-band complex scattering parameters S21 and S12 in a microwave darkroom. To obtain the transmittance spectra of the metasurfaces, two identical circularly polarized antennas were placed on each side of the sample and connected to the two ports of the VNA via cables. Each antenna could function either as a source or detector to obtain the S-parameters. A Teflon lens with a focal length of 30 cm was placed between the metasurface and antennas on both sides to better focus energy on the sample. Calibration was first performed by eliminating the path loss without the sample using a two-port-through calibration. The sample was then placed to obtain the complex S-parameters. For circularly polarized antennas, only microwaves with the same handedness as the antennas could be detected. Because the reflected microwave possesses opposite handedness to the incident wave, the S11 and S22 parameters vanish. Therefore, only two-port-through calibration was used instead of through-reflect-line calibration. To eliminate the multipath effect, the time-domain gate was activated in the VNA to smoothen the spectra.
During the transmittance spectra measurement under oblique incidence, the sample holder was replaced by a scaled rotatable platform (scale accuracy, 1°), and the scattering matrix under oblique incidence was obtained by rotating the sample. During the beam deflector measurement, the sample and transceiver antenna were fixed on the same rotating platform with the rotation axis located at the centre of the sample holder. The rotation angle was measured using an electronic angle ruler with 0.05° accuracy. The beam deflector sample was placed towards or opposite the transceiver antenna to obtain the intensity of the transmitted microwave. To fully characterize the radiation pattern, measurements were performed at angles ranging from 0° to 180°.
In case of the metalens and hologram measurements, only one Teflon lens was used in front of the source antenna to focus the incident microwave. The transceiver antenna (field resolution, 5 mm) was fixed on a linear translation stage driven by a stepper motor in the horizontal and vertical directions. The maximum moving range was 30 cm in both horizontal and vertical directions. In our measurements, the moving speed of the receiving antenna was 5 mm s−1. The custom-built motor-scanning program communicated with the VNA to execute point-by-point measurements, and the energy/phase distribution on a specific plane was obtained.
Metasurface simulation
Simulations were performed using the commercial COMSOL Multiphysics 4.4 software based on the finite element method. Periodic boundary conditions were employed in both transverse directions around each unit cell, whereas the polarization and incident angle of the microwave were defined in the incident port along the z (longitudinal) axis. A perfectly matched layer was imposed on the incident port to absorb scattered waves. The phase and transmission spectra were inferred from the S-parameters in COMSOL Multiphysics. Home-made Python codes (Python 3.10) based on the Kirchhoff diffraction integral and Gerchberg–Saxton algorithm were used to calculate the non-reciprocal focusing characteristics and holographic patterns, respectively.
Data availability
Source data are provided with this paper. All other data from this study are available from the corresponding authors upon reasonable request.
Code availability
The codes that support the fitting of La:BaFe12O19 electromagnetic parameters and design of NRMs are available from the corresponding authors upon reasonable request.
References
Wu, C. et al. Spectrally selective chiral silicon metasurfaces based on infrared Fano resonances. Nat. Commun. 5, 3892 (2014).
Arbabi, A., Horie, Y., Bagheri, M. & Faraon, A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat. Nanotechnol. 10, 937–943 (2015).
Yin, X., Ye, Z., Rho, J., Wang, Y. & Zhang, X. Photonic spin Hall effect at metasurfaces. Science 339, 1405–1407 (2013).
Pfeiffer, C. & Grbic, A. Controlling vector Bessel beams with metasurfaces. Phys. Rev. Applied 2, 044012 (2014).
Mahmoud, A. M., Davoyan, A. R. & Engheta, N. All-passive nonreciprocal metastructure. Nat. Commun. 6, 8359 (2015).
Shaltout, A. M., Shalaev, V. M. & Brongersma, M. L. Spatiotemporal light control with active metasurfaces. Science 364, eaat3100 (2019).
Guo, X., Ding, Y., Duan, Y. & Ni, X. Nonreciprocal metasurface with space-time phase modulation. Light Sci. Appl. 8, 123 (2019).
Zhang, L. et al. Breaking reciprocity with space-time-coding digital metasurfaces. Adv. Mater. 31, 1904069 (2019).
Mazor, Y. & Alù, A. Nonreciprocal hyperbolic propagation over moving metasurfaces. Phys. Rev. B 99, 045407 (2019).
Hadad, Y., Soric, J. C. & Alù, A. Breaking temporal symmetries for emission and absorption. Proc. Natl Acad. Sci. USA 113, 3471–3475 (2016).
Kord, A., Sounas, D. L. & Alù, A. Microwave nonreciprocity. Proc. IEEE 108, 1728–1758 (2020).
Jalas, D. et al. What is—and what is not—an optical isolator. Nat. Photon. 7, 579–582 (2013).
Tanaka, S., Shimomura, N. & Ohtake, K. Active circulators—the realization of circulators using transistors. Proc. IEEE 53, 260–267 (1965).
Kodera, T., Sounas, D. L. & Caloz, C. Artificial Faraday rotation using a ring metamaterial structure without static magnetic field. Appl. Phys. Lett. 99, 031114 (2011).
Ma, Q. et al. Controllable and programmable nonreciprocity based on detachable digital coding metasurface. Adv. Opt. Mater. 7, 1901285 (2019).
Taravati, S. & Eleftheriades, G. V. Full-duplex reflective beamsteering metasurface featuring magnetless nonreciprocal amplification. Nat. Commun. 12, 4414 (2021).
Carchon, G. & Nanwelaers, B. Power and noise limitations of active circulators. IEEE Trans. Microw. Theory Techn. 48, 316–319 (2000).
Dinc, T. et al. Synchronized conductivity modulation to realize broadband lossless magnetic-free non-reciprocity. Nat. Commun. 8, 795 (2017).
Shi, Y., Yu, Z. & Fan, S. Limitations of nonlinear optical isolators due to dynamic reciprocity. Nat. Photon. 9, 388–392 (2015).
Hofstrand, A., Cotrufo, M. & Alù, A. Nonreciprocal pulse shaping and chaotic modulation with asymmetric noninstantaneous nonlinear resonators. Phys. Rev. A 104, 053529 (2021).
Lawrence, M., Barton, D. R. & Dionne, J. A. Nonreciprocal flat optics with silicon metasurfaces. Nano Lett. 18, 1104–1109 (2018).
Luo, Z. et al. Digital nonlinear metasurface with customizable nonreciprocity. Adv. Funct. Mater. 29, 1906635 (2019).
Jin, B. & Argyropoulos, C. Self-induced passive nonreciprocal transmission by nonlinear bifacial dielectric metasurfaces. Phys. Rev. Applied 13, 054056 (2020).
Shaltout, A., Kildishev, A. & Shalaev, V. Time-varying metasurfaces and Lorentz non-reciprocity. Opt. Mater. Express 5, 2459–2467 (2015).
Hadad, Y., Sounas, D. & Alù, A. Space-time gradient metasurfaces. Phys. Rev. B 92, 100304 (2015).
Shi, Y. & Fan, S. Dynamic non-reciprocal meta-surfaces with arbitrary phase reconfigurability based on photonic transition in meta-atoms. Appl. Phys. Lett. 108, 021110 (2016).
Zhang, L. et al. Space-time-coding digital metasurfaces. Nat. Commun. 9, 4334 (2018).
Zang, J. W. et al. Nonreciprocal wavefront engineering with time-modulated gradient metasurfaces. Phys. Rev. Applied 11, 054054 (2019).
Ji, Y., Fan, F., Tan, Z. & Chang, S. Terahertz nonreciprocal isolator based on magneto-plasmon and destructive interference at room temperature. Front. Phys. 8, 334 (2020).
Tan, Z. et al. High-efficiency terahertz nonreciprocal one-way transmission and active asymmetric chiral manipulation based on magnetoplasmon/dielectric metasurface. Adv. Opt. Mater. 9, 2002216 (2021).
Correas-Serrano, D. & Gomez-Diaz, J. S. Nonreciprocal and collimated surface plasmons in drift-biased graphene metasurfaces. Phys. Rev. B 100, 081410 (2019).
Liu, N. et al. Giant nonreciprocal transmission in low-biased gyrotropic metasurfaces. Opt. Lett. 45, 5917–5920 (2020).
Wang, W., Yau, W. T., Cui, Y., Wang, J. & Fung, K. H. Maxwell’s demon-like nonreciprocity by non-Hermitian gyrotropic metasurfaces. Phys. Rev. Research 3, L022006 (2021).
Harris, V. G. et al. Recent advances in processing and applications of microwave ferrites. J. Magn. Magn. Mater. 321, 2035–2047 (2009).
Chen, Y. et al. Oriented barium hexaferrite thick films with narrow ferromagnetic resonance linewidth. Appl. Phys. Lett. 88, 062516 (2006).
Chen, Y., Nedoroscik, M. J., Geiler, A. L., Vittoria, C. & Harris, V. G. Perpendicularly oriented polycrystalline BaFe11.1Sc0.9O19 hexaferrite with narrow FMR linewidths. J. Am. Ceram. Soc. 91, 2952–2956 (2008).
Laur, V. et al. Self-biased Y-junction circulators using lanthanum- and cobalt-substituted strontium hexaferrites. IEEE Trans. Microw. Theory Techn. 63, 4376–4381 (2015).
Laur, V. et al. Application of molded interconnect device technology to the realization of a self-biased circulator. J. Magn. Magn. Mater. 404, 126–132 (2016).
Harris, V. G. & Sokolov, A. S. The self-biased circulator: ferrite materials design and process considerations. J. Supercond. Nov. Magn. 32, 97–108 (2019).
Wang, J. et al. Self biased Y-junction circulator at Ku band. IEEE Microw. Wireless Compon. Lett. 21, 292–294 (2011).
Neil, B. K. O. & Young, J. L. Experimental investigation of a self-biased microstrip circulator. IEEE Trans. Microw. Theory Techn. 57, 1669–1674 (2009).
Heidenreich, M. et al. Ga-, Y-, and Sc-substituted M-type ferrites for self-biasing circulators in LTCC microwave modules. AIP Adv. 10, 025315 (2020).
Harris, V. G. Modern microwave ferrites. IEEE Trans. Magn. 48, 1075–1104 (2012).
Shalaginov, M. Y. et al. Design for quality: reconfigurable flat optics based on active metasurfaces. Nanophotonics 9, 3505–3534 (2020).
Shalaginov, M. Y. et al. Reconfigurable all-dielectric metalens with diffraction-limited performance. Nat. Commun. 12, 1225 (2021).
Chen, W. T., Zhu, A. Y. & Capasso, F. Flat optics with dispersion-engineered metasurfaces. Nat. Rev. Mater. 5, 604–620 (2020).
Chen, K. et al. A reconfigurable active Huygens’ metalens. Adv. Mater. 29, 1606422 (2017).
Tay, S. et al. An updatable holographic three-dimensional display. Nature 451, 694–698 (2008).
Wang, Z. et al. Three-dimensional microwave holography based on broadband Huygens’ metasurface. Phys. Rev. Applied 13, 014033 (2020).
Lin, X. et al. All-optical machine learning using diffractive deep neural networks. Science 361, 1004–1008 (2018).
Ni, X., Kildishev, A. V. & Shalaev, V. M. Metasurface holograms for visible light. Nat. Commun. 4, 2807 (2013).
Wang, L. et al. Grayscale transparent metasurface holograms. Optica 3, 1504–1505 (2016).
Wu, J. W. et al. Anisotropic metasurface holography in 3-D space with high resolution and efficiency. IEEE Trans. Antennas Propag. 69, 302–316 (2021).
Cardin, A. E. et al. Surface-wave-assisted nonreciprocity in spatio-temporally modulated metasurfaces. Nat. Commun. 11, 1469 (2020).
Hannour, A. et al. Self-biased cobalt ferrite nanocomposites for microwave applications. J. Magn. Magn. Mater. 353, 29–33 (2014).
Zhang, J. et al. Self-biased magnetoelectric gyrators in composite of samarium substituted nickel zinc ferrites and piezoelectric ceramics. AIP Adv. 9, 035137 (2019).
Avci, C. O. et al. Current-induced switching in a magnetic insulator. Nat. Mater. 16, 309–314 (2017).
Zhang, Y. et al. Dysprosium substituted Ce:YIG thin films with perpendicular magnetic anisotropy for silicon integrated optical isolator applications. APL Mater. 7, 081119 (2019).
Joseph, S. D., Huang, Y., Schuchinsky, A., Lebourgeois, R. & Roussel, L. Self-biased CPW circulator with low insertion loss. In 2020 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP) 1–3 (IEEE, 2020).
Zhang, Q. et al. Broadband nonvolatile photonic switching based on optical phase change materials: beyond the classical figure-of-merit. Opt. Lett. 43, 94–97 (2018).
Acknowledgements
We are grateful to K. Sun, University of Electronic Science and Technology of China, for providing the La:BaM material. We are also grateful for support from the National Natural Science Foundation of China (NSFC) (grant nos. U22A2014 and 51972044 to L.B., no. 52021001 to L.D. and no. 52102357 to J.Q.), the Ministry of Science and Technology of the People’s Republic of China (MOST) (grant no. 2021YFB2801600 to J.Q.), Sichuan Provincial Science and Technology Department (grant nos. 2019YFH0154, 2021YFSY0016 and 99203070 to L.B.) and the Fundamental Research Funds for the Central Universities (grant no. ZYGX2020J005 to J.Q.).
Author information
Authors and Affiliations
Contributions
L.B. and J.Q. conceived the idea. W. Yang performed the device design, metasurface fabrication and characterization. J.L., W. Yan and Y.Y. conducted the device characterization. C.L., E.L., L.D. and J.H. analysed the data and drafted the manuscript. J.Q., L.D., Q.D., J.H. and L.B. supervised the study. All the authors contributed to the technical discussions and polishing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Electronics thanks Long Li and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–17, Table 1 and discussion.
Electric-field propagation of a non-reciprocal deflector under backward incidence.
Electric-field propagation of a non-reciprocal deflector under forward incidence.
Focusing process of a non-reciprocal metalens under backward incidence.
Focusing process of a non-reciprocal metalens under forward incidence.
Source data
Source Data Fig. 2
Statistical source data.
Source Data Fig. 3
Statistical source data.
Source Data Fig. 4
Statistical source data.
Source Data Fig. 5
Statistical source data.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yang, W., Qin, J., Long, J. et al. A self-biased non-reciprocal magnetic metasurface for bidirectional phase modulation. Nat Electron 6, 225–234 (2023). https://doi.org/10.1038/s41928-023-00936-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41928-023-00936-w