Abstract
Non-volatile computing-in-memory macros that are based on two-dimensional arrays of memristors are of use in the development of artificial intelligence edge devices. Scaling such systems to three-dimensional arrays could provide higher parallelism, capacity and density for the necessary vector–matrix multiplication operations. However, scaling to three dimensions is challenging due to manufacturing and device variability issues. Here we report a two-kilobit non-volatile computing-in-memory macro that is based on a three-dimensional vertical resistive random-access memory fabricated using a 55 nm complementary metal–oxide–semiconductor process. Our macro can perform 3D vector–matrix multiplication operations with an energy efficiency of 8.32 tera-operations per second per watt when the input, weight and output data are 8, 9 and 22 bits, respectively, and the bit density is 58.2 bit µm–2. We show that the macro offers more accurate brain MRI edge detection and improved inference accuracy on the CIFAR-10 dataset than conventional methods.
Similar content being viewed by others
Main
The use of convolutional neural networks (CNNs) has led to improvements in computer vision, natural language processing and speech recognition. These methods do, however, have tremendous computational and storage demands1,2,3. In particular, CNNs require a large parameter space for operation, especially the three-dimensional (3D) CNNs used in video recognition or medical applications such as brain magnetic resonance imaging (MRI)4,5,6. Artificial intelligence (AI) edge devices7,8,9 based on the von Neumann architecture limit performance and energy efficiency due to the large amount of data transfer between processing and memory units. The energy consumption of memory access alone can be more than 100 times greater than floating-point computation and the development of memory performance is, in general, far behind processor technologies10.
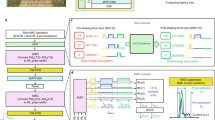
Non-volatile computing-in-memory (nvCIM) architectures based on memristor technologies could be used to break this memory-wall bottleneck. Previous nvCIM work has focused on resistive random-access memory (RRAM) systems that use a two-dimensional (2D) layout11,12,13,14,15,16,17,18,19. But the use of 2D RRAM nvCIMs to create large-scale 3D CNNs has a number of challenges (Fig. 1a,b). Increased number of weights, multibit weight representation and wider metal lines to carry the higher bit-line (BL) readout current (IBL) are needed when conventional parallel word-line (WL) input in situ vector–matrix multiplication (PWIVMM) schemes are used, making array areas large. In addition, when the number of RRAM cells involved in vector–matrix multiplication (VMM) operations is large, error accumulation caused by cell conductance drift can be difficult to distinguish. Here 3D RRAMs could provide higher parallelism, capacity and density for VMM operations. Their increased RRAM cell resistance can decrease the total IBL (and thus the power) during VMM operation. However, small IBL can also lead to latency (TAC), especially when the input vector or weight matrix is sparse and the more difficult manufacturing of 3D RRAM creates the potential for greater error accumulation. Previous work on 3D RRAM-based nvCIMs has been limited only to the memory array, and effective 3D computing systems that include peripheral circuits are lacking20,21,22,23,24,25,26,27,28,29,30,31.
a, Challenge of more area due to more weights, multibit weight representation and wider metal wire. b, Challenges of readout current IBL overlap and conflict between low power and low latency. c, Proposed high-precision nvCIM scheme based on MLSS 3D VRRAM. ADINWM scheme with the aid of CADS circuits can effectively alleviate IBL overlap caused by the conventional PWIVMM scheme and improve the inference accuracy. The implementation of the CIM macro based on the integrated 3D VRRAM chip elaborates a complete solution to execute CNN edge computing.
In this Article, we report a two-kilobit (kb) 3D vertical resistive random-access memory (VRRAM)-based nvCIM macro. We create this high-density computing scheme by combining a multilevel self-selective (MLSS) 3D VRRAM array (Supplementary Fig. 1) with an antidrift multibit analogue input-weight multiplication (ADINWM) scheme. A current-amplitude-discrete-shaping (CADS) scheme included in ADINWM is used to enlarge the IBL sensing margin (SM) and eliminate the distortion error typically observed in conventional PWIVMM schemes. Our 3D VRRAM operates at nanoampere current levels to reduce the system power; to minimize latency, we use an analogue multiplier (AM) with a gate precharge switch follower and a direct small-current converter (DSCC). The peripheral circuits of our nvCIM macro are fabricated using 55 nm complementary metal–oxide–semiconductor (CMOS) technology. Our 3D nvCIM macro achieves computing precision with a range of input-, weight- and output-bit levels, and offers improved inference accuracies compared with conventional approaches when tested using the Modified National Institute of Standards and Technology (MNIST) and Canadian Institute For Advanced Research (CIFAR-10) datasets.
System architecture
Figure 2a shows the architecture of our 3D VRRAM-based nvCIM macro used to implement 1-bit input to 2-bit weight (1bIN–2bW), 4-bit input to 5-bit weight (4bIN–5bW) and 8-bit input to 9-bit weight (8bIN–9bW) VMM operations. The whole structure includes several parts: MLSS 3D VRRAM array, CADS, DSCC and digital processor. Specific information about the eight-layer 3D VRRAM is shown in Supplementary Fig. 1 and Methods, including the writing scheme, schematic, interior image and distribution of readout current IBL. This array has 32 WLs and 8 × 8 BLs. The 3D VRRAM only contains WLs and BLs because of using a self-selective cell (SSC) to avoid the introduction of planar electrodes and select line (SL) in conventional 3D VRRAMs. The SSC is realized by using a bilayer HfO2/TaOx device. When adopting conventional 3D VRRAMs, using WL or SL as the input cannot guarantee that all the devices participate in VMM operations in one computing cycle27,29. When using a pillar electrode as the input and a planar electrode as the output, although all the devices participate in the calculation in one cycle, the number of neurons depending on the number of layers is limited29. Using WL as the input and BL as the neuron output, all the devices of our array engage in VMM operations in one cycle and the number of neurons is not limited. Therefore, this structure is better for highly parallel VMM computing in one cycle than the conventional structure of 3D VRRAMs. Compared with previous work28, this array is easy to manufacture. The array size can be increased to 10 Mb by future technology advancements32. Each VRRAM cell can be set to two or four conductance states corresponding to 1-bit or 2-bit weight, respectively. Multibit weights are composed of low-bit weights33 through the cooperation of peripheral circuits. In this work, the positive weights (PWs) and negative weights (NWs) are stored in two adjacent layers (positive-weight layer (PWL) and negative-weight layer (NWL), respectively) of 3D VRRAMs. Four-bit PWs are represented by four 1-bit weights stored in the PWL. Eight-bit PWs are represented by four 2-bit weights stored in the PWL. The NW case is similar to the PW case. The 5-bit weight of the 4bIN–5bW operation consists of a 4-bit weight in the PWL and NWL each. Similarly, the 9-bit weight of the 8bIN–9bW operation consists of an 8-bit weight in the PWL and NWL each.
a, Data flow and architecture of the conventional PWIVMM scheme for 1bIN–1bPW VMM operation (red lines) and the ADINWM scheme for 8bIN–8bPW VMM operation (blue lines). The dotted lines show the corresponding data flow of the 1bIN–1bNW and 8bIN–8bNW operations in the NWL. b, Implementation framework of the conventional PWIVMM scheme and proposed ADINWM scheme. The macro can be configured as the 1bIN–2bW, 4bIN–5bW and 8bIN–9bW operations based on the ADINWM scheme. As a comparison, it also realizes the 1bIN–2bW operation using the PWIVMM scheme. c, Formula and table of the 8bIN–8bPW operation in the PWL. The result takes the difference with the result of the 8bIN–8bNW operation in the NWL to get the result of the 8bIN–9bW operation. The 4bIN–5bW operation is similar to the 8bIN–9bW operation (Supplementary Fig. 2).
In previous works, the PWIVMM scheme is widely adopted11,12,13,14,16,17,18. The red lines in Fig. 2a represent the data flow of the conventional PWIVMM scheme when implementing the 1bIN–2bW operation. Figure 2b demonstrates the concrete work flow of the PWIVMM scheme in this work. The input voltages (INWL0–INWL31) enter the VRRAM in parallel through the WL switches. The difference in IBL processed by the DSCC in the PWL and NWL is the result of the VMM operation. However, as shown in Fig. 1b and the formula shown in Fig. 1a, when using multilevel RRAMs, the distributions of the final output results may overlap due to error accumulation caused by the conductance drift of multiple cells. When the number n of RRAM cells involved in VMM computing is large, the distribution overlap is more obvious. For 3D RRAMs, the difficulty in manufacturing makes the cell conductance fluctuate greatly. Therefore, the problem is more serious than that of the 2D RRAM array, which limits the number of cells involved in computing and further limits computing parallelism.
In this work, the ADINWM scheme is proposed and the data flow of the 8bIN–9bW VMM operation is depicted (Fig. 2a, blue lines). The following discussion mainly focuses on operations in the PWL for illustration; the situation is the same for the NWL. For all precision operations, VREAD is applied to the WL in series. For the 8bIN–9bW operation, the number of bits of four serial cells (Wn0–Wn3) on the same WL is set as 2 bits. The inputs are IN0–IN7 and each IBL represents 2-bit data. After IBL shaping by the CADS circuit, we obtain four discrete stable currents (IShaped0–IShaped3). Figure 2b shows that the 8bIN–9bW operation can be attained by the difference between the results of the 8bIN–8bPW and 8bIN–8bNW operations. For 8bIN–8bPW multiplication, according to the formula and table shown in Fig. 2c, it is divided into four 4-bit multiplications and the results correspond to four output currents (namely, IOUTLL, IOUTLH, IOUTHL and IOUTHH). These multiplications are realized by 4-bit AMs. The currents are converted into an 8-bit digital signal by the DSCC and then shifted (OUTHH shifts 8 bits to the left, and OUTHL and OUTLH shift 4 bits to the left) and combined to complete the 8-bit multiplication operation for the input and PW in PWL. All the multiplication results from 32 WLs are accumulated after 32 cycles in series by a digital processor. Finally, the difference with the result of the 8bIN–8bNW VMM operation in the NWL is used to obtain the final VMM result. For 4bIN–4bPW multiplication (Supplementary Fig. 2), the number of bits of four serial cells is set as 1 bit. After IBL shaping by the CADS circuit, the four currents (IShaped0–IShaped3) are combined with 4-bit inputs (IN0–IN3) by two 4–2-bit AMs (multiplying 2-bit input by 4-bit input). The outputs are the multiplication results IOUTL and IOUTH, which are later sampled by the DSCC and combined to get the 4-bit multiplication result. The result accumulates with the results from the remaining 31 rows in series by a digital processor. The complete result is obtained by subtracting the result of the 4bIN–4bNW operation in the NWL. The 1bIN–2bW operation is very similar to the 4bIN–5bW operation, except that only one IShaped from a 1-bit cell needs to be multiplied by the 1-bit input through the 1-bit AM.
The antidrift in the ADINWM scheme is to avoid the cumulative error caused by device conductance variation by reading the current through the WL in series, further stabilizing the current to be calculated through current shaping and completing the multiply–accumulate (MAC) computing by combining the near-memory multibit analogue multiplication with the digital processing unit. It overcomes the error accumulation problem caused by the conductance drift of multiple cells in the PWIVMM scheme.
CADS scheme for error mitigation
There are two challenges for IBL. First, due to fluctuations in IBL caused by the drift in the RRAM cell conductance, it will be difficult to distinguish IBL; consequently, the SM becomes smaller. In this work, the SM is defined as half the interval between two adjacent readout currents. Because a 3D VRRAM is much more difficult to manufacture, this downside will be more prominent. Second, when applying the conventional PWIVMM scheme, each weight must have one-to-one correspondence with the RRAM cell conductance to ensure accurate VMM operations. However, this puts forward high requirements for the write circuit and the device itself. To overcome these challenges, the CADS scheme is proposed.
Figure 3a illustrates the CADS circuit. CADS consists of one input current mirror, three current comparators and three output current mirrors. The circuit can convert fluctuating IBL into a discrete stable current and enlarge the SM for the next accurate operations (Fig. 3b). Besides, as long as IBL is within a certain range, it can be converted into a fixed value. Therefore, the VRRAM cell conductance corresponding to a specific weight can be within a certain range rather than a fixed value, which mitigates the requirement of the writing circuit. Figure 3c shows the operation of current shaping by the CADS circuit. Further, IBL is copied three times through the current mirror, which connects three current comparators with different threshold currents (ISn) controlled by three switches (namely, S1, S2 and S3). For the 8bIN–9bW operation (2-bit cell), S1, S2 and S3 are at a high level and three current comparators work simultaneously. If IBL is higher than ISn, the corresponding VSn is low and the switch of the output current mirror will be enabled to control the multiples of the benchmark current (IBM = 10 nA). Finally, IShaped can be selected from 0, 10, 20 and 30 nA depending on the range of IBL of the VRRAM cell. For the 4bIN–5bW operation, one of S1, S2 and S3 is at a high level. When IBL is higher than ISX, VSX is low and the corresponding switch of the output current mirror is turned on to obtain IBM, namely, IShaped. After IBL shaping by CADS, the SM of IBL is enlarged to 5 nA and a discrete, stable IShaped is suitable for the next accurate computing.
a, Schematic of the CADS circuit. Here N is the normalized width of the CMOS transistor. b, Initial readout current IBL distribution and the current distribution after shaping by the CADS circuit. The variation in IBL leads to a decrease in the inference accuracy on the dataset. This scheme enlarges the SM to 5 nA. Stable IBL after shaping can improve the inference accuracy. c, Operations and waveform of the CADS circuit. At the beginning of each cycle, the CADS circuit can convert IBL in a certain range to a fixed value.
DSCC and AM scheme for high speed and performance
Due to the nanoampere operation current of 3D VRRAMs, the power consumption of the overall nvCIM macro can be greatly reduced at the cost of system latency. For high energy efficiency, the high performance of peripheral circuits is required.
Figure 4a shows the operation of 1 million samples per second (MSPS) 8-bit DSCC. The DSCC mainly comprises an 8-bit current digital-to-analogue converter (DAC) consisting of current mirrors, a successive approximation register (SAR) logic circuit and a comparator composed of a differential amplifier. The DSCC can directly sample and convert small currents, eliminating the time required for a conventional analogue-to-digital converter (ADC) to convert from analogue current to analogue voltage and reducing the TAC. Besides, the power of the DSCC mainly depends on the input current (Supplementary Notes 2 and 3), which elucidates that it can save a lot of energy when implementing the VMM operations between sparse matrices (such as sparse weights)34 or the readout current of RRAM is small. Furthermore, we add in a structure that can set the initial voltage of 0.9 V to make the complementary current mirror in the saturation region to reduce the voltage swing, reducing the latency from 10.00 to 0.83 µs (Supplementary Note 2). Therefore, the DSCC is very suitable for the VMM operations in RRAM with current as the output. In all precision operations of our work, an 8-bit DSCC is adopted because the number of bits of the output can be adjusted as needed. Taking the 8bIN–9bW operation as an example, the inputs of the DSCC are the output currents IOUTLL, IOUTLH, IOUTHL and IOUTHH of the AM. The difference between the DAC current and input current drives the load capacitor to generate the corresponding response voltage. The voltage is converted into a logic signal by double-sampling amplification and transmitted to the SAR logic and current DAC. After eight double samplings, the final results (namely, OUTLL, OUTLH, OUTHL and OUTHH) are sent to a digital processor for the next computing. As the main power of the DSCC depends on the input currents, the nanoampere operation current significantly reduces the power consumption.
a, Structure of 1 MSPS 8-bit DSCC. The DSCC can directly sample and convert the analogue current to a digital signal. The structure dominated by complementary current mirrors makes the power of the DSCC highly dependent on the input current. These features are suitable for the current result of the VMM operation of CNN with sparse weights in the RRAM. b, Schematic of a 4-bit AM group with a gate precharge switch follower 4-bit AM group used for the 8bIN–9bW configuration. The input currents (IShaped0–IShaped3) are multiplied by inputs IN0–IN7 and the output results IOUTLL, IOUTLH, IOUTHL and IOUTHH are sent to the DSCC. Here N is the normalized width of the CMOS transistor. c, Simulated waveform of the output gate voltage of the AM and the structure of the gate precharge switch follower. The added gate precharge switch follower reduces the TAC by 54%.
Figure 4b illustrates the 4-bit AM comprising current doublers with gate precharge switch followers. For the 8bIN–9bW operation, four shaped currents (IShaped0–IShaped3) are input to the AM, and these currents are multiplied by inputs IN0–IN7 through current doublers to get the output currents IOUTLL, IOUTLH, IOUTHL and IOUTHH. Due to the large parasitic capacitance of the output gate of the current doubler, the gate precharge switch follower has been added to reduce TAC. As demonstrated in Fig. 4c, when the gate precharge mode is used, en and S2 are turned on at the beginning of the cycle; then, the follower controlling the output gate is started. The output (VWSF) quickly approaches the target value; then, the follower will be off and S1 will be on. The direct connection between the input gate and output gate of the current mirror can eliminate the follower error and accurate VWSF can be obtained. In this way, the TAC of AM can be reduced by 54%.
The combination of the two schemes reduces the total TAC from 10 to 1 µs due to the dominant role of the AM (Supplementary Note 5). Details of the AMs for the 1bIN–2bW and 4bIN–5bW operations are provided in Supplementary Note 4.
Evaluation of 3D VRRAM-based nvCIM macro
Figure 5a,b demonstrates the input 3D brain MRI and hardware automatic test platform with 3D VRRAM-based nvCIM macro as the computing core (Methods and Supplementary Fig. 6). This platform controlled by a field-programmable gate array (FPGA) implements the 1bIN–2bW, 4bIN–5bW and 8bIN–9bW VMM operations based on the ADINWM scheme and realizes the 1bIN–2bW VMM operation under the PWIVMM scheme for comparison. Figure 5c depicts the ideal results by software simulation and the experimental results using the ADINWM and PWIVMM schemes under the 1bIN–2bW VMM configuration for the edge detection of 3D brain MRI. The result with the ADINWM scheme is close to the ideal result, whereas the result of the PWIVMM scheme introduces more noise due to error accumulation caused by the drift in the conductance of the 3D VRRAM cell.
a, Three-dimensional brain MRI slices as the input data. b, Hardware automatic test platform with a 3D VRRAM-based nvCIM macro under FPGA control. The function of each module is described in Methods. c, Comparison between the results of 3D Prewitt kernels convolving on 3D brain MRI slices based on the ADINWM scheme, PWIVMM scheme and software simulation. The results of edge detection using the ADINWM scheme are closer to the ideal result by correcting the error in time. The difference between the PWIVMM scheme and ADINWM scheme is more obvious in the red box. Besides, for the 1bIN–2bW, 4bIN–5bW and 8bIN–9bW configurations, the inference accuracy on the MNIST dataset is shown in Supplementary Fig. 7 and Methods. d, Comparison of inference accuracy on the CIFAR-10 dataset for the VGG-8 model between the ADINWM scheme, PWIVMM scheme and ideal result at the 8bIN–9bW configuration. The implementation method is shown in Methods. Compared with the PWIVMM scheme, the ADINWM scheme improves the inference accuracy by 0.91% on the CIFAR-10 dataset. e, Energy efficiency of the 3D VRRAM-based nvCIM macro. Compared with previous works, the energy efficiency of the nvCIM macro is improved and 8bIN–9bW computing precision is achieved (Supplementary Table 1). f, Bit density of the nvCIM macro. With the MLSS 3D VRRAM, the bit density is greatly improved compared with a 2D RRAM.
For the 4bIN–5bW and 8bIN–9bW configurations, compared with pure software simulation, we only lose 0.81% and 0.84% inference accuracy on the MNIST dataset with a self-defined CNN. For the 1bIN–2bW configuration, the ADINWM scheme improves the inference accuracy under the PWIVMM scheme from 93.89% to 94.70% on the MNIST dataset (Supplementary Fig. 7 and Methods). Figure 5d presents a comparison of inference accuracy on the CIFAR-10 dataset for the VGG-8 model between the ADINWM scheme, PWIVMM scheme and ideal result without the drift of cell conductance at the 8bIN–9bW configuration. All the tests are completed on the software platform (Methods). Compared with the conventional method, the ADINWM scheme can effectively alleviate the accuracy drop caused by device fluctuations and achieve an inference accuracy of 90.54% on the CIFAR-10 dataset.
The power analysis of the 3D VRRAM-based nvCIM macro is provided in Supplementary Figs. 8 and 9 and Supplementary Note 6. The power of our chip is at the nanowatt level owing to the higher resistance of the 3D VRRAM cell, which is suitable for extremely low-power edge computation. In the 1bIN–2bW operation using the PWIVMM scheme, the main power is produced by the 3D VRRAM, whereas the DSCC consumes the most energy using the ADINWM scheme, especially for the 1bIN–2bW operation. Figure 5e,f demonstrates the energy efficiency and bit density of our work. This work achieves 62.11 tera-operations per second per watt (TOPS W–1) at the 1bIN–2bW operation, and 29.94 and 8.32 TOPS W–1 at the 4bIN–5bW and 8bIN–9bW operations, respectively. The 3D VRRAM cell density is 16.6 times or more—higher than previous 2D RRAM-based works. Therefore, this structure of nvCIM based on a multilayer 3D RRAM has important density and power consumption advantages for a large-capacity 2D/3D CNN calculation. A comparison between this work and previous nvCIM works is shown in Supplementary Table 1. The die photo and summary of our chip are depicted in Supplementary Fig. 10.
Conclusions
We have reported a 2-kb 3D VRRAM nvCIM macro that includes peripheral circuits and is fabricated using 55 nm CMOS technology. Our computing-in-memory (CIM) system achieves an energy efficiency of 62.11 TOPS W–1 in a 1bIN–2bW configuration, 29.94 TOPS W–1 in a 4bIN–5bW configuration and 8.32 TOPS W–1 when using an 8bIN–9bW configuration. The bit density is 58.2 bit µm–2, which is higher than previous 2D RRAM-based systems. The ADINWM scheme can improve the inference accuracy compared with more common PWIVMM schemes. The macro can be used for brain MRI edge detection and shows a 0.91% improvement in inference accuracy using the CIFAR-10 dataset compared with conventional approaches. Our scheme for AI edge computation is also potentially useful in the design of nvCIM macros based on other emerging 3D RRAM technologies that may suffer from device stability issues. Future work will focus on building a larger 3D VRRAM and the construction of a CIM system with the capacity to contain an entire CNN.
Methods
3D VRRAM-based hardware platform
The hardware platform consists of three main parts:
-
a power management system that supplies power to other modules,
-
a printed circuit board with 3D VRRAM-based nvCIM macro. A 2-kb 3D VRRAM and peripheral circuits including a CADS circuit, AM, DSCC and partial digital circuits are bonded and packaged in a stacked way and they communicate with the outside through the printed circuit board.
-
an FPGA board with an embedded processor is responsible for data management between the nvCIM macro and the host computer as well as the logic control of the nvCIM macro.
For the 1bIN–2bW configuration, we employ the developed platform for the edge detection of 3D brain MRI, which is one of the main effects of convolution kernels from the first several layers of the CNN. Specifically, 3D Prewitt kernels—the prevailing kernels for the edge detection of 3D images—are unrolled into 1 × 27 vectors and programmed into 3D VRRAM cells belonging to different BLs by the peripheral write circuits and used for convolving on 3D brain MRI.
When adopting the PWIVMM scheme, 27 pixels in the receptive field are parallelly input into the 3D VRRAM through the WL switches in the form of 27 1-bit input voltages each time. Since each pixel is 8-bit data, after eight consecutive cycles, the VMM operation in the receptive field is completed, and the edge detection image is obtained after multiple sliding window operations (the 1-bit input data flow is shown in Fig. 2). For the ADINWM scheme, the pixels converted into the corresponding 1-bit input voltage are serially input into the AM, and the VMM operation in the receptive field is completed after 8 × 27 cycles; the edge detection image is obtained after multiple sliding window operations (the 1-bit input data flow is shown in Supplementary Fig. 2).
Details of 3D VRRAM
The details of the 3D VRRAM are shown in Supplementary Fig. 1. The size of the eight-layer 3D VRRAM used in this work is 8 × 8 × 32 (corresponding to 64 BLs and 32 WLs; Fig. 2) limited to the current process. The detailed fabrication flow of the 3D VRRAM is given in Supplementary Note 1.
The Vw/2 writing scheme is applied to the 3D VRRAM. Here Vw refers to the write voltage. During the writing process, the WLs and BLs of the selected cells are biased at Vw and ground, respectively, whereas both WLs and BLs of the unselected cells are biased at Vw/2.
Evaluation of inference accuracy on MNIST and CIFAR-10 datasets
The detailed configuration of the self-defined CNN is depicted in Supplementary Fig. 7. The feature extraction layer contains six 5 × 5 convolution kernels and 2 × 2 max pooling layer. The classification layer is a 200 × 10 full connection layer. As a proof-of-concept demonstration, six 5 × 5 convolution kernels learned by the self-defined CNN on the MNIST dataset at the 1bIN–2bW, 4bIN–5bW and 8bIN–9bW configurations are unrolled into multiple 1 × 25 vectors and mapped on 3D VRRAM cells belonging to different BLs. Similar to the edge detection of 3D images, the learned convolution kernels are used to extract features of handwritten digits under the control of the FPGA platform. The results of the VMM operations on hardware are input to the next modules implemented by software including activation functions, max pooling layer and classification layer.
The quantized VGG-8 CNN model for inference on CIFAR-10 uses the ‘WAGE’ method for reference35. The CADS, AM and DSCC circuits are implemented by functions embedded in the inference process of VGG-8. Limited by current technology, although the inference accuracy can be obtained by repeatedly writing the weights of CNN to the 3D VRRAM, the device may be broken down due to too many write operations caused by a large CNN. However, larger 3D VRRAMs or multiple arrays in our future work will resolve this problem.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request. The MRI data in the paper are available at http://www.ia.unc.edu/MSseg.
Code availability
The code that supports the experimental platforms and proposed 3D VRRAM-based nvCIM test chip is available from the corresponding authors upon reasonable request.
References
Lecun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
Krizhevsky, A., Sutskever, I. & Hinton, G. ImageNet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 25, 1097–1105 (2017).
Sze, V., Chen, Y.-H., Yang, T.-J. & Emer, J. S. Efficient processing of deep neural networks: a tutorial and survey. Proc. IEEE 105, 2295–2329 (2017).
Xu, X. et al. Scaling for edge inference of deep neural networks. Nat. Electron. 1, 216–222 (2018).
Ji, S. et al. 3D convolutional neural networks for human action recognition. IEEE Trans. Pattern Anal. Mach. Intell. 35, 221–231 (2013).
Hegde, K., Agrawal, R., Yao, Y. & Fletcher, C. Morph: flexible acceleration for 3D CNN-based video understanding. In 2018 51st Annual IEEE/ACM International Symposium on Microarchitecture (MICRO) 933–946 (IEEE, 2018).
Liu, S. et al. Cambricon: an instruction set architecture for neural networks. In 2016 ACM/IEEE 43rd Annual International Symposium on Computer Architecture (ISCA) 393–405 (IEEE, 2016).
Shin, D. et al. DNPU: an 8.1TOPS/W reconfigurable CNN-RNN processor for general-purpose deep neural networks. In 2017 IEEE International Solid-State Circuits Conference (ISSCC) 240–241 (IEEE, 2017).
Chen, Y.-H., Krishna, T., Emer, J. S. & Sze, V. Eyeriss: an energy-efficient reconfigurable accelerator for deep convolutional neural networks. IEEE J. Solid State Circuits 52, 127–138 (2017).
Pandiyan, D. & Wu, C. Quantifying the energy cost of data movement for emerging smart phone workloads on mobile platforms. In 2014 IEEE International Symposium on Workload Characterization (IISWC) 171–180 (IEEE, 2014).
Chen, W. H. et al. CMOS-integrated memristive non-volatile computing-in-memory for AI edge processors. Nat. Electron. 2, 420–428 (2019).
Cai, F. et al. A fully integrated reprogrammable memristor–CMOS system for efficient multiply–accumulate operations. Nat. Electron. 2, 290–299 (2019).
Yao, P. et al. Fully hardware-implemented memristor convolutional neural network. Nature 577, 641–646 (2020).
Chi, P. et al. PRIME: a novel processing-in-memory architecture for neural network computation in ReRAM-based main memory. ACM SIGARCH Comput. Archit. News 44, 27–39 (2016).
Xue, C. et al. A 22nm 2Mb ReRAM compute-in-memory macro with 121-28TOPS/W for multibit MAC computing for tiny AI edge devices. In 2020 IEEE International Solid-State Circuits Conference—(ISSCC) 244–246 (IEEE, 2020).
Liu, Q. et al. A fully integrated analog ReRAM based 78.4TOPS/W compute-in-memory chip with fully parallel MAC computing. In 2020 IEEE International Solid-State Circuits Conference—(ISSCC) 500–502 (IEEE, 2020).
Xue, C. et al. A 1Mb multibit ReRAM computing-in-memory macro with 14.6ns parallel MAC computing time for CNN based AI edge processors. In 2019 IEEE International Solid-State Circuits Conference—(ISSCC) 388–390 (IEEE, 2019).
Chen, W.-H. et al. A 65 nm 1 Mb nonvolatile computing-in-memory ReRAM macro with sub-16 ns multiply-and-accumulate for binary DNN AI edge processor. In 2018 IEEE International Solid-State Circuits Conference—(ISSCC) 494–495 (IEEE, 2018).
Lee, M. et al. 2-stack 1D-1R cross-point structure with oxide diodes as switch elements for high density resistance RAM applications. In 2007 IEEE International Electron Devices Meeting 771–774 (IEEE, 2007).
Lee, M. et al. Stack friendly all-oxide 3D RRAM using GaInZnO peripheral TFT realized over glass substrates. In 2008 IEEE International Electron Devices Meeting 1–4 (IEEE, 2008).
Yoon, H. et al. Vertical cross-point resistance change memory for ultra high density non-volatile memory applications. In 2009 Symposium on VLSI Technology 26–27 (IEEE, 2009).
Chen, H. et al. HfOx based vertical resistive random access memory for cost-effective 3D cross-point architecture without cell selector. In 2012 International Electron Devices Meeting 20.7.1–20.7.4 (IEEE, 2012).
Yu, S. et al. 3D vertical RRAM—scaling limit analysis and demonstration of 3D array operation. In 2013 Symposium on VLSI Technology T158–T159 (IEEE, 2013).
Deng, Y. et al. Design and optimization methodology for 3D RRAM arrays. In 2013 IEEE International Electron Devices Meeting 25.7.1–25.7.4 (IEEE, 2013).
Shulaker, M. M. et al. Three-dimensional integration of nanotechnologies for computing and data storage on a single chip. Nature 547, 74–78 (2017).
Adam, G. C. et al. 3-D memristor crossbars for analog and neuromorphic computing applications. IEEE Trans. Electron Devices 64, 312–318 (2017).
Li, Z., Chen, P. Y., Xu, H. & Yu, S. Design of ternary neural network with 3-D vertical RRAM array. IEEE Trans. Electron Devices 64, 2721–2727 (2017).
Lin, P. et al. Three-dimensional memristor circuits as complex neural networks. Nat. Electron. 3, 225–232 (2020).
Li, H. et al. Four-layer 3D vertical RRAM integrated with FinFET as a versatile computing unit for brain-inspired cognitive information processing. In 2016 IEEE Symposium on VLSI Technology 1–2 (IEEE, 2016).
Luo, Q. et al. 8-layers 3D vertical RRAM with excellent scalability towards storage class memory applications. In 2017 IEEE International Electron Devices Meeting (IEDM) 2.7.1–2.7.4 (IEEE, 2017).
Huo, Q. et al. Demonstration of 3D convolution kernel function based on 8-layer 3D vertical resistive random access memory. IEEE Electron Device Lett. 47, 497–500 (2020).
Xu, X. et al. Fully CMOS compatible 3D vertical RRAM with self-aligned self-selective cell enabling sub-5nm scaling. In 2016 IEEE Symposium on VLSI Technology 1–2 (IEEE, 2016).
Irem, B. et al. Neuromorphic computing with multi-memristive synapses. Nat. Commun. 9, 2514 (2018).
Han, S. et al. EIE: efficient inference engine on compressed deep neural network. In 2016 ACM/IEEE 43rd Annual International Symposium on Computer Architecture (ISCA) 243–254 (ACM, 2016).
Wu, S. et al. Training and inference with integers in deep neural networks. In 2018 International Conference on Learning Representations (ICLR) (2018).
Acknowledgements
This work is supported by the National Key Research Plan of China (nos. 2018YFB0407500, 2019YFB2205100, 2021YFB3601300 and 2019Q1NRC001); Strategic Priority Research Program of the Chinese Academy of Sciences, China (grant no. XDB44000000); and the National Natural Science Foundation of China under grant nos. 61720106013, 61888102, 61922083, 61834009 and 62025406.
Author information
Authors and Affiliations
Contributions
Q.H., Y. Yang and F.Z. conceived the concept of this work and designed the CIM chip and experiments. X.X., Q. Luo and D.L. contributed to the 3D VRRAM design, measurements and device optimizations. Y. Yang, D.L. and Q.H. built the test platform. Q.H. conceived the CNN algorithm and simulation design. Q.H., X.F. and Q.R. wrote the manuscript. F.Z. and M.L. supervised this work. All the authors contributed to the results and discussion and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Electronics thanks Lu Lu, Jae-sun Seo and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–10, Table 1 and Notes 1–6.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Huo, Q., Yang, Y., Wang, Y. et al. A computing-in-memory macro based on three-dimensional resistive random-access memory. Nat Electron 5, 469–477 (2022). https://doi.org/10.1038/s41928-022-00795-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41928-022-00795-x
This article is cited by
-
Multidimensional vision sensors for information processing
Nature Nanotechnology (2024)
-
Memristor-based hardware accelerators for artificial intelligence
Nature Reviews Electrical Engineering (2024)
-
Bioinspired sensing-memory-computing integrated vision systems: biomimetic mechanisms, design principles, and applications
Science China Information Sciences (2024)
-
First demonstration of in-memory computing crossbar using multi-level Cell FeFET
Nature Communications (2023)
-
A full spectrum of computing-in-memory technologies
Nature Electronics (2023)