Main

The idea of exploiting quantum mechanics to build computers with computational powers beyond any classical device has gathered momentum since the 1980s1. However, in order for full-fledged quantum computers to become a reality, they need to be fault tolerant: that is, errors from unavoidable decoherence must be reversed faster than they occur2. The most promising architectures also require a system that is scalable to millions of individually addressable qubits with a gate fidelity over 99% and tuneable nearest-neighbour couplings3,4.

Spin qubits in gate-defined quantum dots (QDs) offer great potential for quantum computation due to their small size and relatively long coherence times5,6,7. Single-qubit gate fidelities over 99.9% (refs. 8,9) and two-qubit gate fidelities over 99% (refs. 10,11,12) have already been demonstrated, as well as algorithms13, conditional teleportation14, three-qubit entanglement15 and four-qubit universal control16. Moreover, silicon spin qubits have been operated at relatively high temperatures of 1–4 K (refs. 17,18), where the higher cooling power enables scaling strategies with the integration of control electronics19,20,21,22,23.

A major advantage of silicon spin qubits is that they could leverage decades of technology development in the semiconductor industry. Today, industrial manufacturing conditions allow the fabrication of uniform transistors with gate lengths of several tens of nanometres and spaced apart by 34 nm (fins) to 54 nm (gates)—feature sizes that are well below the 193 nm wavelength of the light used in the lithography process24. This engineering feat, as well as the high yield that allows integrated circuits containing billions of transistors to function, is enabled by adhering to strict design rules and by using advanced semiconductor manufacturing techniques such as multiple patterning for pitch doubling, subtractive processing, chemically selective plasma etches and chemical mechanical polishing25. These processing conditions are more intrusive than those in electron-beam lithography8,13,18,26,27,28,29,30,31,32,33,34,35,36,37 and metal lift-off8,13,18,26,28,30,31,32,33 typically used for QD fabrication, but they will be key to achieving the extremely high yield necessary for the fabrication of thousands or millions of qubits in a functional array.

A QD device is similar to a transistor, taken to the limit where the gate above the channel controls the flow of electrons one at a time38. In linear qubit arrays, the transistor gate is replaced by multiple gates, which are used to shape the potential landscape of the channel into multiple potential minima (QDs), to control the occupation of each dot down to the last electron, and to precisely tune the wavefunction overlap (tunnel coupling) of the electrons in neighbouring dots39. In addition, qubit devices commonly rely on nearby integrated charge sensors to provide single-shot spin readout and high-fidelity initialization7,40.

A key question is then whether the reliable but strict design rules of industrial patterning can produce suitable qubit device layouts. A separate consideration is that qubit coherence is easily affected by microscopic charge fluctuations from the interface, surface and bulk defects. Therefore, another key question is whether the coherence properties of the qubits survive the processing conditions needed to achieve high yield and uniformity. QDs and qubits fabricated on the wafer scale in industrial foundries have been reported27,34,35,36,37, but they rely on electron-beam lithography and avoid chemical mechanical polishing for the active device area. Chemical mechanical polishing requires a uniform metal density across the wafer, which introduces its own complexities for QD devices due to the large amount of floating metal and added capacitance. In this Article, we report fully optically patterned QDs and qubits that are made in a state-of-the-art 300 mm wafer process line, similar to those used for commercial advanced integrated circuits.

Device architecture and fabrication

A dedicated mask set based on 193 nm immersion lithography is created for patterning QD arrays of various lengths, as well as a number of test structures, such as transistors of various sizes and Hall bars. These test structures allow us to directly extract important metrics at both room temperature and low temperature, including mobility, threshold voltage, subthreshold slope and interface trap density. Analysed together, these metrics give us an understanding of the gate oxide and contact quality along with the electrostatics to help troubleshoot process targeting41. Once the test structure metrics are satisfactory, we then characterize the QD arrays.

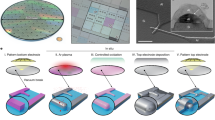
As in current complementary metal–oxide–semiconductor transistors, the active region of these QD devices consists of a fin, varying in width between 20 and 70 nm, etched out of the silicon substrate24. Nested top gates with a pitch of 50 nm, separated from the fin by a composite SiO2/high-k dielectric (with k the dielectric constant), are used to form and manipulate QDs. Figure 1a shows a high-angle annular dark-field scanning transmission electron microscopy image of the active device area. A cross-section transmission electron microscopy (TEM) image along a fin with QD gates is shown in Fig. 1b. Phosphorus ion implants on both ends of the fin, well separated from the active region, serve as ohmic contacts to the fins. We pattern two such linear QD arrays, separated by 120–150 nm (Fig. 1c shows a TEM image across both fins). In our experiments, we use a QD in one array as a charge sensor for the qubit dots in the other array. A schematic of the device is shown in Fig. 1d.

Fig. 1: Industrially fabricated QD devices.
figure 1

a, High-angle annular dark-field scanning transmission electron microscopy image of a typical device. The active region consists of two parallel silicon fins: one hosts the qubits and the other hosts the sensing dot. The fan-out of the gates is clearly visible, as well as the many additional metallic structures (called dummification) needed to maintain a roughly constant density of metal on the surface, which ensures homogeneous polishing on the wafer scale. b, TEM image along a Si fin, showing seven metallic finger gates to define the QD array and two accumulation gates (ACL and ACR) to induce reservoirs connecting to the phosphorus n-type implants that serve as ohmic contacts (outside the image). The gates are isolated from the fin by a composite SiO2 and high-k dielectric layer. A SiO2 ILD is located between the gates for isolation. c, False-coloured TEM image perpendicular to the Si fins, showing the silicon fins and SiO2 STI fill in between the fins. d, Schematic of the active region of the device. e, Schematic of the process steps used to fabricate the devices: Si fin formation (i); STI planarization (ii); poly-silicon dummy-gate patterning and n+ implants for source/drain formation (iii); ILD deposition for gate-spacer formation, planarization, dummy-gate removal and first gate-layer formation (iv); ILD etch to open a window for the second gate layer and second gate-layer formation (v); ILD deposition, trench formation and metal fill for contacting the gates and implants and ESR line formation (vi).

Full size image

The process flow starts from a conventional transistor flow but is adapted to fabricate two sets of gates in successive steps using a combination of 300 mm optical lithography, thin-film deposition, plasma etch and chemical mechanical polishing. The main steps are illustrated in Fig. 1e. First, the fins are defined in a Si substrate. The space between the fins is filled in with a SiO2 shallow-trench-isolation (STI) dielectric material and polished. Then, a composite SiO2 and high-k dielectric layer is formed to isolate the gates from the substrate. The first gate layer (with even numbers) is defined using an industry-standard replacement metal gate process42,43,44 and consists of a workfunction metal with tungsten fill. Ohmic regions are formed by means of phosphorus n+ implantation at the end of both fins. The area between the gates of the first layer is filled with a SiO2 interlayer dielectric (ILD) and patterned to selectively remove the oxide in the qubit device region, allowing the second gate layer to be formed. The second gate layer (with odd numbers) is then formed adjacent to the first gate layer. Finally, a tungsten or copper contact layer is patterned to enable routing to bond pads, as well as ohmic and gate contacts. For the devices intended for coherent experiments (Fig. 4), alternate masking steps are run to integrate an electron-spin-resonance (ESR) line within the existing contact routing layer. The ESR line consists of a copper wire that shunts a coplanar stripline (connected to an on-chip coplanar waveguide45), placed parallel to the fins (Extended Data Fig. 1).

Fig. 2: Tuneable single and double QDs.
figure 2

a, Room-temperature yield map for wafer 20, which contains devices with ESR striplines. The yield is defined in the main text. b, Histogram of room-temperature threshold voltages for all the gates of the second gate layer (G1, G3, G5 and G7) from yielding devices of wafers 11–14 (2,288 gates from 286 devices in total). The standard deviation of all these gates across the four wafers is 70 mV. c, Correlation map for threshold voltages at room temperature and low temperatures for all the gates from all the samples from wafers 11–14 that have been cooled. d, Charge stability diagram for a single QD measured via electron transport. e–h, Charge stability diagrams of a double QD formed under gates G3 and G5. The gate voltage on G4 is gradually increased (G4 is 1,245 mV, 1,308 mV, 1,353 mV and 1,398 mV from e to h, respectively), showing good control over the interdot tunnel coupling.

Full size image
Fig. 3: Charge sensing and single-shot spin readout.
figure 3

a, Charge stability diagram of the last-electron regime of a QD, measured with a sensing dot in the other fin. The points ‘w’, ‘r’ and ‘e’ refer to the wait, readout and empty stages of the gate voltage pulse, respectively. b, Real-time current through the sensing dot indicating a spin-up (purple line) and spin-down (orange line) electron, recorded with a measurement bandwidth of 3 kHz set by an external low-pass filter. c, Spin-up probability as a function of load time at a magnetic field of 1 T. The exponential fit yields T1 of 1.6 ± 0.6 s. d, Relaxation rate (1/T1) as a function of the applied magnetic field (purple dots). The relaxation rate is fitted by a model (orange line) that includes the effect of Johnson noise and phonon coupling to the spin via spin–orbit interaction. From this fit, we extract a valley splitting of Ev = 260 ± 2 µeV.

Full size image
Fig. 4: An industrial silicon spin qubit.
figure 4

a, Rabi oscillations of the measured spin-up probability as a function of the microwave burst duration. b, CPMG experiment: the measured spin-up probability as a function of the free evolution time separating 50 π-pulses, with an artificial phase detuning on the last pulse. The data are fitted with A(cos(ωt + φ) + B)exp(−(t/T2CPMG)2) + C. The fitted CPMG coherence time T2CPMG is 3.7 ± 0.2 ms. c, Demodulated and normalized CPMG amplitude as a function of the total evolution time for different numbers n of π-pulses. d, Measured coherence time T2CPMG for different numbers of CPMG π-pulses. The orange line represents a fit through the data (excluding n = 1) following T2CPMG ∝ nexp(γ/(γ + 1)). We extract γ = 1.1 ± 0.2.

Full size image

The samples used only for QD formation are fabricated on natural silicon substrates, whereas the samples used for qubit readout and manipulation are fabricated on an isotopically enriched 28Si epilayer with a residual 29Si concentration of 800 ppm (refs. 46,47). This reduces the hyperfine interaction of the qubits with nuclear spins in the host material and thus increases the qubit coherence6.

A single 300 mm wafer contains 82 unit cells (die) with a total of more than 10,000 QD arrays of various lengths, with up to 55 finger gates per fin. Figure 1b shows a TEM image of a typical device with seven finger gates on top of each fin.

High-volume device characterization

To analyse the device yield and sample uniformity—both within the wafer and across different wafers, automated probing at room temperature is used to measure one seven-gate device per die and determine the threshold voltage per gate. Devices are considered yielding if the channel in both fins turns on, all the individual gates on both fins can switch off the current flow through the respective channel, and the ohmic contacts and gates are not leaking. Figure 2a shows a map that indicates the device yield of wafer 20, containing devices with an ESR line. The device yield is about 98%, with only two devices at the edge of the wafer not fully functioning. Extended Data Fig. 2 shows additional yield maps for four almost-identical wafers without a stripline (wafers 11–14), which differ from each other only by the etching and polishing parameters, to illustrate how the process parameters are targeted. Repeatedly, for optimized process parameters, we find only a few samples at the edge of the wafer to be not fully yielding.

Process uniformity is studied by comparing the room-temperature threshold voltage of individual gates. Figure 2b shows a histogram of the threshold voltage for the gates in the second gate layer of all the devices over wafers 11–14, with a standard deviation in the threshold voltage of 70 mV. The standard deviation in the first gate layer is higher, as we consistently find the samples at the edge of the wafers to have lower threshold voltages (Supplementary Fig. 4). Further analysis of the threshold voltages (Supplementary Figs. 1–6) reveals that the variation in threshold voltage within a device is similar to that across a wafer and between wafers. Additionally, we find that the threshold-voltage variation for the (wide) accumulation gates is smaller than that for the finger gates made in the same layer. These observations are consistent with known sources of variability in transistor manufacturing48. Unlike scaled transistors, our qubit devices are not optimized for short-channel effects; as we go from accumulation gates to gate layer 2 to gate layer 1, this reduction in short-channel control causes the threshold voltage to have a very strong dependence on gate dimensions, which augments variability.

Next, we study the relation between the threshold voltages measured at room temperature versus those measured at low temperature (5 K and below) for all the gates. Figure 2c shows the data from wafers 11–14, and Extended Data Fig. 3a includes data for over 600 gates on 20 different wafers for which the low-temperature data were obtained. Interestingly, the threshold voltage measured at room temperature shows a linear correlation with that measured at low temperature. Due to different processing parameters for the different wafers, both slope and offset of the linear correlation can shift slightly. When examining the low-temperature threshold voltages, we again find that the spread in gate layer 1 is larger than the spread in gate layer 2 (Extended Data Fig. 4).

From the 79 samples that we cooled across 20 wafers, four samples were not working due to human errors in wire bonding. Out of the other 75 samples, we find that only 21 out of the 1,050 gates were not working, indicating that room-temperature measurements can be used to preselect samples to cool down for QD analysis. Published data rarely present device-yield analysis like we are presenting here16. However, it is our experience that with conventional electron-beam lithography and lift-off processing, only a small percentage of the devices with similar complexity functions fully.

QD measurements

All QD and qubit measurements are carried out in a dilution refrigerator operated at base temperature. The measurements have been performed on a plethora of different devices from different process flow generations, measured in three different dilution refrigerators in different laboratories.

We form QDs by individually tuning the gates to define a suitable potential landscape (dots can be controllably formed below any of the inner five gates). Figure 2d shows a typical result, where we measure the current through a QD while sweeping three gate voltages (Fig. 1b), one of which (G3) mostly controls the electrochemical potential of the QD and the others (G2 and G4) mostly control the tunnel barriers. In the range of 1.0 < VG3 < 3.9 V, we count more than 80 lines (known as Coulomb peaks) separating regions with a stable number of electrons on the QD. As the voltage on G3 is made more negative, exactly one electron is removed from the QD after crossing each Coulomb peak. Although the Coulomb peaks are parallel and evenly spaced at a high G3 voltage (>3 V), they become irregular and also further separated towards the few-electron regime (around 1.5 V on G3). Such irregular behaviour is characteristic of Si metal–oxide–semiconductor (MOS) devices, due to their close proximity to the dielectric interface18,26,27,28,29,35,49,50. More importantly, the measured samples from anywhere across wafers 11–14 consistently show regular Coulomb oscillations in the many-electron regime (Supplementary Figs. 8–12), allowing to reach a similarly looking few-electron regime whenever we tried.

Analysing these first-generation dots through so-called Coulomb diamonds40 gives an average charging energy of 8.9 ± 0.2 meV (all the error bars are 1σ from the mean) per dot in the multi-electron regime (Supplementary Fig. 13). Charge noise measurements in the multi-electron regime give a power spectral density (PSD) with approximately a 1/f slope and a charge noise amplitude in the range of 1–10 µeV Hz–1/2 at 1 Hz (Extended Data Fig. 5). These are common charge noise values in Si-MOS-based QD samples28. The variations between the data points are not unexpected, as different gate voltages typically activate different charge fluctuators in the stack.

Figure 2e shows the transport through a double QD as a function of the gate voltages that (mostly) control the electrochemical potential of each dot, namely, G3 and G5. Characteristic points of conductance are measured, the so-called triple points. At these points, the electrochemical potentials of the reservoirs are aligned with the electrochemical potentials of the left and right dots, such that electrons can sequentially tunnel through the two dots39. Increasing the voltage applied to intermediate gate G4 is expected to lower the tunnel barrier between the dots, eventually reaching the point where one large dot is formed. This behaviour is shown in Fig. 2e–h, as the gradual transition from triple points to single, parallel and evenly spaced Coulomb peaks. This shows the tuneability of the interdot tunnel coupling in this double dot, which is advantageous for two-qubit control in such a system15,18,23,31.

In the next step, we use a QD in one fin as a charge sensor for the charge occupation of the QDs in the other fin. This allows us to unambiguously map the charge states of the qubit dots down to the last electron40. A characteristic charge stability diagram showing the last electron transition is shown in Fig. 3a. The current through the sensor is measured as a function of the voltage on two of the gates controlling the qubit dot. In the few-electron regime, we can usually distinguish lines with several different slopes, indicating the formation of additional, spurious dots next to the intended dot. However, we are consistently able to find a clean region in the charge stability diagram with an isolated addition line corresponding to the last electron. In this regime, we observe a 500 pA difference in the sensing dot current between the occupied and unoccupied QD states for a source–drain voltage of 500 µV.

Industrially manufactured qubits

To define a qubit via the electron spin states, we apply a magnetic field in the [100] direction, parallel to the fins, separating the spin-up and spin-down levels in energy. We perform single-shot readout of the spin of a single electron by means of spin-dependent tunnelling and real-time charge detection (Fig. 3b). Here and below, we did not optimize the state preparation and measurement conditions. We measure the spin relaxation time T1 using a three-stage pulse to gate G6 (ref. 51) and find T1 exceeding 1 s at a magnetic field of 1 T (Fig. 3c). This T1 is among the longest relaxation times previously reported for silicon QDs18,28,37,52 and indicates that the advanced semiconductor processing conditions do not degrade the spin relaxation time. On measuring T1 as a function of the magnetic field, we find a striking, non-monotonic dependence, which is well described in the literature and the result of the valley structure in the conduction band of silicon. Following other studies28,52, we fit the magnetic-field dependence of the spin relaxation rate (1/T1) with a model including the effect of Johnson noise and phonons inducing spin transitions mediated by spin–orbit coupling, and taking into account the lowest four valley states (Fig. 3d). The peak in the relaxation rate around 2.25 T corresponds to the situation where the Zeeman energy equals the valley splitting energy, from which we extract a valley splitting of 260 ± 2 µeV, well above the thermal energy and qubit splitting in this system.

To coherently control the spin states, we apply an a.c. current to the stripline to generate an oscillating magnetic field at the QD53. ESR occurs when the driving frequency matches the spin Larmor frequency of f = 17.1 GHz, which is set by the static magnetic field at the dot. By selectively pulsing only the spin-down level below the Fermi reservoir, we load the QD with a spin-down electron. We then pulse deep in the Coulomb blockade regime to manipulate the spin with microwave bursts. Finally, we pulse to the readout point. The spin-up probability as a function of the microwave burst duration shows clear Rabi oscillations (Fig. 4a). We have studied coherent control in three different qubits (this comparably small number does not reflect a decrease in the device yield from electrically functional devices to operational qubits (Methods)). Figure 4 shows the data for qubit 1 (Q1); Extended Data Figs. 6 and 7 show the data for qubit 2 (Q2) (formed on the same device (Extended Data Fig. 8)) and qubit 3, respectively. As expected, the Rabi frequency is linear in the driving amplitude, reaching up to about 900 kHz for Q2.

The spin dephasing time \(T_2^ \ast\) is measured through a Ramsey interference measurement (Supplementary Fig. 14). Fitting this Ramsey pattern with a Gaussian-damped oscillation yields a decay time of \(T_2^ \ast\) = 24 ± 6 µs when averaging data over 100 s (the error bar here refers to the statistical variation between 41 post-selected repetitions of 100 s segments). As we repeat such Ramsey measurements, we observe slow jumps in the qubit frequency. Averaging the free induction decay over 160 min still gives a \(T_2^ \ast\) of 11 ± 2 µs (Methods).

To analyse the single-qubit gate fidelity, we employ randomized benchmarking54 (Supplementary Fig. 15). A number m of random Clifford gates is applied to the qubit, followed by a gate that ideally returns the spin to either the spin-up or spin-down state. In reality, the probability to reach the target state decays with m due to imperfections. The standard analysis gives a single-qubit gate fidelity of 99.0% for Q1 and 99.1% for Q2. With the Rabi decay being dominated by low-frequency noise, the present combination of \(T_2^ \ast\) and Rabi frequency should allow an even higher fidelity17,18,49. We suspect the single-qubit gate fidelity to be limited by improper calibration.

Finally, we study the limits of spin coherence by performing dynamical decoupling using Carr–Purcell–Meiboom–Gill (CPMG) sequences (Fig. 4b shows the coherence decay using 50 pulses). These sequences eliminate the effect from quasi-static noise sources. Figure 4c shows the normalized amplitude of the CPMG decay as a function of evolution time for different numbers of π-pulses, n. By fitting these curves, we extract T2CPMG(n). We use a Gaussian decay envelope that yields distinctly better agreement than an exponential decay. The T2CPMG times are plotted as a function of n (Fig. 4d). We obtain a T2CPMG value of over 3.5 ms for n = 50 CPMG pulses, more than 100 times larger than \(T_2^ \ast\), with room for further increases through additional decoupling pulses. The CPMG data for Q1 are consistent with the charge noise as the limiting mechanism (Methods). For Q2, an additional noise mechanism is probably present.

Conclusions

We have shown that QD samples fabricated using industrial processing conditions exhibit exceptionally good yield, as well as key performance indicators—charge noise, charge sensing signal, T1, \(T_2^ \ast\) and T2CPMG—that are comparable to commonly observed values (Supplementary Table 1). The formation of easily tuneable double dots bodes well for the implementation of two-qubit gates in this system. Several further improvements are possible. The current ESR stripline has a finite resistance of the order of 50 Ω, which causes device heating. This effect can be minimized by making the ESR wire wider and using materials with lower resistivity. Spurious dots in the few-electron regime and two-level systems can also be removed by reducing the presence of material charge defects55,56.

Although the growth conditions for high-quality Si/dielectric interfaces have been identified, we have indications that performance-limiting defects are formed through downstream processing. Further work is ongoing to optimize the process flow and recipes (temperature budget, plasma conditions, chemical exposure and annealing conditions) to reduce defects at the end of the line. Although there are significant challenges to overcome to engineer out these defects and improve the qubit performance and scalability, the full 300 mm device-integration line established by us will allow us to run a high volume of experiments to accelerate this development over that achievable by conventional fabrication methods.

These advanced manufacturing methods can also be adapted to allow for two-dimensional QD arrays. Moreover, the processing steps are, by default, integratable with any other complementary metal–oxide–semiconductor technology, which opens up the potential to integrate classical circuits next to the qubit chip. Eventually, industrial processing will have the potential to achieve the very high QD uniformity that would enable cross-bar addressing schemes21. The compatibility of silicon spin qubits with fully industrial processing demonstrated here highlights their potential for scaling and for creating a fault-tolerant full-stack quantum computer.

Methods

Setup and instrumentation

The measurements were performed on two different setups, namely, setup 1 (S1, Delft) and setup 2 (S2, Hillsboro). The samples were cooled in a dilution refrigerator, operated at the base temperature of around 10 mK (S1, Oxford Triton dry dilution refrigerator; S2, Bluefors XLD dry dilution refrigerator). Further, d.c. voltages were applied via Delft’s in-house built, battery-powered voltage sources (S1 and S2). The printed circuit board onto which the sample was mounted contained bias tees with a cut-off frequency of 3 Hz to allow for the application of gate voltage pulses (S1 and S2). The pulses were generated by an arbitrary waveform generator (S1, Tektronix AWG5014; S2, Zurich Instruments HDAWG). The baseband current through the sensing dot was converted to a voltage by means of a home-built amplifier, filtered through a room-temperature low-pass filter (S1, 3.0 kHz; S2, 1.5 kHz) and sampled by a digitizer (S1, M4i spectrum; S2, Zurich Instruments MFLI). Microwave bursts for driving ESR were generated by a vector source with an internal I/Q mixer (S1 and S2: Keysight PSG8267D), with the in-phase (I) and quadrature (Q) channels controlled by two output channels of the arbitrary waveform generator.

Charge noise measurements

Each charge-noise data point in Extended Data Fig. 5 is obtained by recording a 140 s time trace (at 28 Hz sampling rate) of the current through the QD with the plunger gate voltage fixed at the steepest point of the Coulomb peak flank. To convert the current signal to energy, we proceed as follows. First, we convert the current to gate voltage by multiplying the data by the slope of the Coulomb peak at the operating point. Then, we multiply with the lever arm to convert from the plunger gate voltage to energy. To obtain the PSD, we divide the data into ten equally long segments, take the single-sided fast Fourier transform of the segments and average the values. Fitting the PSD to A/fα, we extract the energy fluctuations at 1 Hz (A–1/2) for each Coulomb peak. We extract a mean value of α = 1.1 ± 0.3.

Spin readout

To read the spin eigenstate, we use energy-selective tunnelling to the electron reservoir51. The spin levels are aligned with respect to the Fermi reservoir, such that a spin-up electron can tunnel out of the QD, whereas a spin-down electron is energetically forbidden to leave the QD. Thus, depending on the spin state, the charge occupation in the QD will change. To monitor the charge state, we apply a fixed voltage bias across the sensing dot and measure the baseband current signal through the sensing dot, filtered with a low-pass filter and sampled via the digitizer. In the post-analysis, we threshold the sensing dot signal and accordingly assign a spin-up or spin-down value to every single-shot experiment. After readout, we empty the QD to repeat the sequence.

As commonly seen in spin-dependent tunnelling, the readout errors are not symmetric, which is reflected in the range of oscillations (Fig. 4a,b).

Qubit operations

When addressing the qubit, we phenomenologically observe that the qubit resonance frequency shifts depending on the burst duration. The precise origin of this resonance shift is unclear so far, but appears to be caused by heating. Similar observations have been made in recent spin qubit experiments8,13,23 that used electric-dipole spin resonance via micromagnets as the driving mechanism. To ensure a reproducible qubit frequency in the experiments, we apply an off-resonant microwave burst before the intended manipulation phase to saturate this frequency shift. We further investigate this frequency shift in Extended Data Figs. 9 and 10.

Ramsey oscillation

We observe that the qubit resonance frequency in the devices exhibits jumps of several hundreds of kilohertz on a timescale of 5–10 min. To extract meaningful results, we monitor this frequency shift throughout the experiments and accordingly discard certain data traces such that we only take into account data acquired with the qubit in a narrow frequency window. To illustrate the frequency shift, we show the fast Fourier transform of 100 repetitions of a Ramsey interference measurement of qubit 1 (measurement time, ~160 min; Supplementary Fig. 14a), which tracks the qubit frequency over time. To estimate the \(T_2^ \ast\) value of qubit 1, we fit each of the 100 repetitions of the Ramsey measurement (measurement time per repetition, ~100 s) and extract a \(T_2^ \ast\) value. Evidently, some of the data quality is rather poor due to the previously described frequency jumps in which case the extracted \(T_2^ \ast\) value is meaningless. We calculate the mean square error of each fit and disregard all the measurements with a high error. The average \(T_2^ \ast\) of the 41 remaining traces is 24 ± 6 µs (Supplementary Fig. 14b). Averaging the data traces of all the 41 traces and then fitting a decay curve yields a dephasing time of 16 ± 2 µs (Supplementary Fig. 14c); averaging the data of all the 100 traces still gives a dephasing time of 11 ± 2 µs (Supplementary Fig. 14d).

CPMG coherence measurements and PSD

To ensure robust fitting, the CPMG sequences are applied with a phase detuning on the last pulse. We fit the resulting curves with a Gaussian-damped cosine function: A(cos(ωt + φ) + B)exp(−(t/T2CPMG)2) + C, where A, C, ω and φ are fitting parameters. Instead of using a Gaussian decay, if we leave the exponent of the decay open as a fitting parameter, we obtain values for the exponent between 2.3 and 2.6, but the use of the additional parameter results in less robust fits. The offset B is included to compensate for the loss of readout visibility for long microwave burst duration. We attribute this to heating generated while driving the spin rotations. The measurement is divided into segments, each consisting of 200 single shots. Each segment includes a simple calibration part, based on which we post-select repetitions for which the spin-up probability after applying a π-pulse is above 25%. In this way, we can exclude repetitions where the qubit resonance frequency has drastically shifted. The remaining repetitions are averaged to obtain the characteristic decay curves for each choice of n, one of which is shown in Fig. 4b. From fitting the decay curves, we extract the T2CPMG times as a function of n (Fig. 4d). To extract the CPMG amplitude as a function of evolution time from the data, we demodulate the measured values with the parameters extracted from the fit, according to ACPMG = (x − C)/(A(cos(ωt + φ) + B)), where x is the measured data. Due to experimental noise, points where the denominator is small do not yield meaningful results. Hence, we exclude the data points for which the absolute value of the expected denominator is smaller than 0.4. The extracted CPMG amplitudes are plotted in Fig. 4c. In a commonly used simplified framework57,58, we can relate the data shown in Fig. 4d to a noise PSD of the form S(ω) ∝ 1/ωγ. Specifically, fitting the data to T2CPMG(n) ∝ nγ/(γ+1) gives γ = 1.1 ± 0.2. Alternatively, we can estimate γ by fitting the noise PSD extracted from the individual data points in the CPMG decays58 (Supplementary Fig. 16a). This analysis gives γ = 1.2 ± 0.1. Either way, the extracted PSD is close to the 1/f dependence that is characteristic of charge noise. Charge noise can affect spin coherence since the spin resonance frequency is sensitive to the gate voltage, as also reported before for Si-MOS-based spin qubits26. We next estimate how large the charge noise needs to be to dominate spin decoherence. To do so, we extrapolate the extracted spectral density in the range between 103 and 104 Hz to an amplitude at 1 Hz, which, after conversion to units of charge noise, gives 29 ± 27 µeV Hz–1/2. With the caveat that this extrapolation is not very precise, we note that this value is only slightly larger than the charge noise amplitude in the multi-electron regime of 2−10 µeV Hz–1/2. Considering that charge noise values are typically higher in the few-electron regime, this suggests that the coherence of Q1 may be limited by charge noise58. For Q2, which is another qubit in the same sample, the same procedure gives an extrapolated noise at 1 Hz that is an order of magnitude larger. Possibly, a two-level fluctuator is active in the vicinity of this qubit in the regime where the qubit data were taken.

Down-selection of qubit samples

To select devices for coherent measurements, we use an automated probe station for room-temperature tests of QD arrays on wafer 20. Across the 82 die on the wafer, we test the turn on for both fins of a single device and find that 80/82 samples (162/164 fins) conduct. Furthermore, each of the gates (G1–G7) for these 160 fins can control the current. The device yield as far as can be established by room-temperature testing is thus 98%. From this wafer, we selected seven samples for low-temperature testing, for which the threshold voltages looked clean and the spread in threshold voltages was below 125 mV. For these samples, 13 of the 14 fins conducted at low temperature. The failure mode of the other one is not known. The gate response was hysteretic for one of the seven gates on one of the 13 fins, and was fine for the other gates on this fin and all the gates on the other fins. With all the six samples, we reached the single-electron regime. With three samples, we had confirmed technical issues outside the sample (filter board limitations and human errors); with the fourth sample, we had a suspected issue with the transmission line outside the sample. These issues could most probably have been resolved, but we did not pursue them; this is because on the other two samples (out of the six samples), we had taken the qubit data, realizing three different qubits. Evidently, the room-temperature automated prober allows high-volume characterization. By comparison, sequential cool downs of individual samples to cryogenic temperatures and the subsequent experiments for qubit control and measurement are much more time consuming, hence the much lower number of samples for which we characterized the qubit performance.