Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Review Article
  • Published:

Scaling silicon-based quantum computing using CMOS technology

Nature Electronics volume 4, pages 872–884 (2021)Cite this article

Subjects

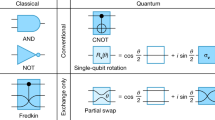
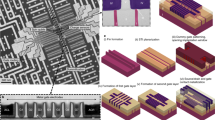
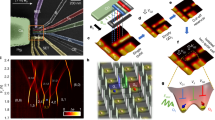
Abstract

As quantum processors grow in complexity, attention is moving to the scaling prospects of the entire quantum computing system, including the classical support hardware. Recent results in high-fidelity control of individual spins in silicon, combined with demonstrations that these qubits can be manufactured in a similar fashion to field-effect transistors, create an opportunity to leverage the know-how of the complementary metal–oxide–semiconductor (CMOS) industry to address the scaling challenge at a system level. Here we review the prospects of scaling silicon-based quantum computing using CMOS technology. We consider the concept of a quantum computing system, which we decompose into three distinct layers—the quantum layer, the quantum–classical interface and the classical layer—and explore the challenges involved in their development, as well their assembly into an architecture. Silicon offers the enticing possibility that all layers can, in principle, be manufactured using CMOS technology, creating an opportunity to move from distributed quantum–classical systems to integrated quantum computing solutions.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Silicon QD devices.
Fig. 2: A QCS.
Fig. 3: 2D arrays.
Fig. 4: Challenges.

Similar content being viewed by others

References

  1. Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).

    Article  Google Scholar 

  2. Zhong, H.-S. et al. Quantum computational advantage using photons. Nature 370, 1460–1463 (2020).

    Google Scholar 

  3. Sarma, S. D., Freedman, M. & Nayak, C. Majorana zero modes and topological quantum computation. npj Quantum Inf. 1, 15001 (2015).

    Article  Google Scholar 

  4. Karzig, T. et al. Scalable designs for quasiparticle-poisoning-protected topological quantum computation with Majorana zero modes. Phys. Rev. B 95, 235305 (2017).

    Article  Google Scholar 

  5. Lidar, D. & Brun, T. Quantum Error Correction (Cambridge Univ. Press, 2013).

  6. Devitt, S. J., Munro, W. J. & Nemoto, K. Quantum error correction for beginners. Rep. Prog. Phys. 76, 76001 (2013).

    Article  Google Scholar 

  7. Campbell, E. T., Terhal, B. M. & Vuillot, C. Roads towards fault-tolerant universal quantum computation. Nature 549, 172–179 (2017).

    Article  Google Scholar 

  8. Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 32324 (2012).

    Article  Google Scholar 

  9. Bauer, B., Wecker, D., Millis, A. J., Hastings, M. B. & Troyer, M. Hybrid quantum–classical approach to correlated materials. Phys. Rev. X 6, 31045 (2016).

    Google Scholar 

  10. Reiher, M., Wiebe, N., Svore, K. M., Wecker, D. & Troyer, M. Elucidating reaction mechanisms on quantum computers. Proc. Natl Acad. Sci. USA 114, 7555–7560 (2017).

    Article  Google Scholar 

  11. Shor, P. W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 26, 1484–1509 (1997).

    Article  MathSciNet  MATH  Google Scholar 

  12. Monroe, C. & Kim, J. Scaling the ion trap quantum processor. Science 339, 1164–1169 (2013).

    Article  Google Scholar 

  13. Devoret, M. H. & Schoelkopf, R. J. Superconducting circuits for quantum information: an outlook. Science 339, 1169–1174 (2013).

    Article  Google Scholar 

  14. Awschalom, D. D., Bassett, L. C., Dzurak, A. S., Hu, E. L. & Petta, J. R. Quantum spintronics: engineering and manipulating atom-like spins in semiconductors. Science 339, 1174–1179 (2013).

    Article  Google Scholar 

  15. Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).

    Article  Google Scholar 

  16. Maurand, R. et al. A CMOS silicon spin qubit. Nat. Commun. 7, 13575 (2016).

    Article  Google Scholar 

  17. Zwerver, A. M. J. et al. Qubits made by advanced semiconductor manufacturing. Preprint at https://arxiv.org/abs/2101.12650 (2021).

  18. Camenzind, L. C. et al. A spin qubit in a fin field-effect transistor. Preprint at https://arxiv.org/abs/2103.07369 (2021).

  19. Veldhorst, M., Eenink, H. G. J., Yang, C. H. & Dzurak, A. S. Silicon CMOS architecture for a spin-based quantum computer. Nat. Commun. 8, 1766 (2017).

    Article  Google Scholar 

  20. Lekitsch, B. et al. Blueprint for a microwave trapped ion quantum computer. Sci. Adv. 3, e1601540 (2017).

    Article  Google Scholar 

  21. Cai, Z. Resource estimation for quantum variational simulations of the Hubbard model. Phys. Rev. Appl. 14, 014059 (2020).

    Article  Google Scholar 

  22. Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213 (2014).

    Article  Google Scholar 

  23. Farhi, E., Goldstone, J. & Gutmann, S. A quantum approximate optimization algorithm. Preprint at https://arxiv.org/abs/1411.4028 (2014).

  24. Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120–126 (1998).

    Article  Google Scholar 

  25. Kane, B. E. A silicon-based nuclear spin quantum computer. Nature 393, 133–137 (1998).

    Article  Google Scholar 

  26. Veldhorst, M. et al. An addressable quantum dot qubit with fault-tolerant control-fidelity. Nat. Nanotechnol. 9, 981–985 (2014).

    Article  Google Scholar 

  27. Kawakami, E. et al. Electrical control of a long-lived spin qubit in a Si/SiGe quantum dot. Nat. Nanotechnol. 9, 666–670 (2014).

    Article  Google Scholar 

  28. Yang, C. H. et al. Operation of a silicon quantum processor unit cell above one kelvin. Nature 580, 350–354 (2020).

    Article  Google Scholar 

  29. Petit, L. et al. Universal quantum logic in hot silicon qubits. Nature 580, 355–359 (2020).

    Article  Google Scholar 

  30. Zhao, R. et al. Single-spin qubits in isotopically enriched silicon at low magnetic field. Nat. Commun. 10, 5500 (2019).

    Article  Google Scholar 

  31. Elzerman, J. M. et al. Single-shot read-out of an individual electron spin in a quantum dot. Nature 430, 431–435 (2004).

    Article  Google Scholar 

  32. Johnson, A. C., Petta, J. R., Marcus, C. M., Hanson, M. P. & Gossard, A. C. Singlet–triplet spin blockade and charge sensing in a few-electron double quantum dot. Phys. Rev. B 72, 165308 (2005).

    Article  Google Scholar 

  33. Morello, A. et al. Single-shot readout of an electron spin in silicon. Nature 467, 687–691 (2010).

    Article  Google Scholar 

  34. Maune, B. M. et al. Coherent singlet–triplet oscillations in a silicon-based double quantum dot. Nature 481, 344–347 (2012).

    Article  Google Scholar 

  35. Fogarty, M. A. et al. Integrated silicon qubit platform with single-spin addressability, exchange control and single-shot singlet–triplet readout. Nat. Commun. 9, 4370 (2018).

    Article  Google Scholar 

  36. Pioro-Ladriére, M. et al. Electrically driven single-electron spin resonance in a slanting Zeeman field. Nat. Phys. 4, 776–779 (2008).

    Article  Google Scholar 

  37. Pla, J. J. et al. A single-atom electron spin qubit in silicon. Nature 489, 541–545 (2012).

    Article  Google Scholar 

  38. Veldhorst, M. et al. A two-qubit logic gate in silicon. Nature 526, 410–414 (2015).

    Article  Google Scholar 

  39. Xue, X. et al. Computing with spin qubits at the surface code error threshold. Preprint at https://arxiv.org/abs/2107.00628 (2021).

  40. Noiri, A. et al. Fast universal quantum control above the fault-tolerance threshold in silicon. Preprint at https://arxiv.org/abs/2108.02626 (2021).

  41. Zajac, D. M. et al. Resonantly driven CNOT gate for electron spins. Science 359, 439–442 (2018).

    Article  MathSciNet  MATH  Google Scholar 

  42. Watson, T. F. et al. A programmable two-qubit quantum processor in silicon. Nature 555, 633–637 (2018).

    Article  Google Scholar 

  43. Huang, W. et al. Fidelity benchmarks for two-qubit gates in silicon. Nature 569, 532–536 (2019).

    Article  Google Scholar 

  44. Vandersypen, L. M. K. Scaling up semiconductor spin qubits. In APS March Meeting V35.00002 (American Physical Society, 2021).

  45. Jones, N. C. et al. Layered architecture for quantum computing. Phys. Rev. X 2, 31007 (2012).

    Google Scholar 

  46. Vandersypen, L. M. K. et al. Interfacing spin qubits in quantum dots and donors—hot, dense, and coherent. npj Quantum Inf. 3, 34 (2017).

    Article  Google Scholar 

  47. Li, R. et al. A crossbar network for silicon quantum dot qubits. Sci. Adv. 4, eaar3960 (2018).

    Article  Google Scholar 

  48. Boter, J. M. et al. A sparse spin qubit array with integrated control electronics. In 2019 IEEE International Electron Devices Meeting (IEDM) 31.4.1–31.4.4 (IEEE, 2019).

  49. Vinet, M. et al. Towards scalable silicon quantum computing. In 2018 IEEE International Electron Devices Meeting (IEDM) 6.5.1–6.5.4 (IEEE, 2018).

  50. Reilly, D. J. Engineering the quantum–classical interface of solid-state qubits. npj Quantum Inf. 1, 15011 (2015).

    Article  Google Scholar 

  51. Cressler, J. D. Silicon Earth: Introduction to the Microelectronics and Nanotechnology Revolution (Cambridge Univ. Press, 2009).

  52. Corna, A. et al. Electrically driven electron spin resonance mediated by spin–valley–orbit coupling in a silicon quantum dot. npj Quantum Inf. 4, 6 (2018).

    Article  Google Scholar 

  53. Crippa, A. et al. Electrical spin driving by g-matrix modulation in spin–orbit qubits. Phys. Rev. Lett. 120, 137702 (2018).

    Article  Google Scholar 

  54. Ansaloni, F. et al. Single-electron control in a foundry-fabricated two-dimensional qubit array. Nat. Commun. 11, 6399 (2020).

    Article  Google Scholar 

  55. Zajac, D. M., Hazard, T. M., Mi, X., Nielsen, E. & Petta, J. R. Scalable gate architecture for a one-dimensional array of semiconductor spin qubits. Phys. Rev. Appl. 6, 54013 (2016).

    Article  Google Scholar 

  56. Geyer, S. et al. Self-aligned gates for scalable silicon quantum computing. Appl. Phys. Lett. 118, 104004 (2021).

    Article  Google Scholar 

  57. Hutin, L. et al. Gate reflectometry for probing charge and spin states in linear Si MOS split-gate arrays. In 2019 IEEE International Electron Devices Meeting (IEDM) 37.7.1–37.7.4 (IEEE, 2019).

  58. Chanrion, E. et al. Charge detection in an array of CMOS quantum dots. Phys. Rev. Appl. 14, 024066 (2020).

    Article  Google Scholar 

  59. Gilbert, W. et al. Single-electron operation of a silicon-CMOS 2 × 2 quantum dot array with integrated charge sensing. Nano Lett. 11, 7882–7888 (2020).

    Article  Google Scholar 

  60. Duan, J. et al. Remote capacitive sensing in two dimension quantum dot arrays. Nano Lett. 10, 7123 (2020).

    Article  Google Scholar 

  61. Jones, C. et al. Logical qubit in a linear array of semiconductor quantum dots. Phys. Rev. X 8, 021058 (2018).

    Google Scholar 

  62. Malinowski, F. K. et al. Fast spin exchange across a multielectron mediator. Nat. Commun. 10, 1196 (2019).

    Article  Google Scholar 

  63. Burkard, G., Gullans, M. J., Mi, X. & Petta, J. R. Superconductor–semiconductor hybrid-circuit quantum electrodynamics. Nat. Rev. Phys. 2, 129–140 (2020).

    Article  Google Scholar 

  64. Yoneda, J. et al. Coherent spin qubit transport in silicon. Nat. Commun. 12, 4114 (2021).

    Article  Google Scholar 

  65. Yoneda, J. et al. A quantum-dot spin qubit with coherence limited by charge noise and fidelity higher than 99.9%. Nat. Nanotechnol. 13, 102–106 (2018).

    Article  Google Scholar 

  66. Dehollain, J. P. et al. Nanoscale broadband transmission lines for spin qubit control. Nanotechnology 24, 15202 (2012).

    Article  Google Scholar 

  67. Laucht, A. et al. Electrically controlling single-spin qubits in a continuous microwave field. Sci. Adv. 1, e1500022 (2015).

    Article  Google Scholar 

  68. Kong, W.-C. et al. Introduction of dc line structures into a superconducting microwave 3D cavity. Rev. Sci. Instrum. 86, 023108 (2015).

    Article  Google Scholar 

  69. Vahapoglu, E. et al. Single-electron spin resonance in a nanoelectronic device using a global field. Sci. Adv. 7, eabg9158 (2021).

    Article  Google Scholar 

  70. Vahapoglu, E. et al. Coherent control of electron spin qubits in silicon using a global field. Preprint at https://arxiv.org/abs/2107.14622 (2021).

  71. Kawakami, E. et al. Gate fidelity and coherence of an electron spin in an Si/SiGe quantum dot with micromagnet. Proc. Natl Acad. Sci. USA 113, 11738–11743 (2016).

    Article  Google Scholar 

  72. Struck, T. et al. Low-frequency spin qubit energy splitting noise in highly purified 28Si/SiGe. npj Quantum Inf. 6, 40 (2020).

    Article  Google Scholar 

  73. Borjans, F., Zajac, D. M., Hazard, T. M. & Petta, J. R. Single-spin relaxation in a synthetic spin–orbit field. Phys. Rev. Appl. 11, 44063 (2019).

    Article  Google Scholar 

  74. Simion, G. et al. A scalable one dimensional silicon qubit array with nanomagnets. In 2020 IEEE International Electron Devices Meeting (IEDM) 30.2.1–30.2.4 (IEEE, 2020).

  75. Singh, K., Clarke, J. S., Veldhorst, M. & Vandersypen, L. M. K. Quantum dot devices. US patent 2,020,135,864-A1 (2017).

  76. Crippa, A. et al. Gate-reflectometry dispersive readout and coherent control of a spin qubit in silicon. Nat. Commun. 10, 2776 (2019).

    Article  Google Scholar 

  77. Bosco, S., Hetényi, B. & Loss, D. Hole spin qubits in Si finFETs with fully tunable spin–orbit coupling and sweet spots for charge noise. PRX Quantum 2, 010348 (2021).

    Article  Google Scholar 

  78. Martins, F. et al. Noise suppression using symmetric exchange gates in spin qubits. Phys. Rev. Lett. 116, 116801 (2016).

    Article  MathSciNet  Google Scholar 

  79. Reed, M. D. et al. Reduced sensitivity to charge noise in semiconductor spin qubits via symmetric operation. Phys. Rev. Lett. 116, 110402 (2016).

    Article  Google Scholar 

  80. Shim, Y.-P. & Tahan, C. Barrier versus tilt exchange gate operations in spin-based quantum computing. Phys. Rev. B 97, 155402 (2018).

    Article  Google Scholar 

  81. He, Y. et al. A two-qubit gate between phosphorus donor electrons in silicon. Nature 571, 371–375 (2019).

    Article  Google Scholar 

  82. Malinowski, F. K. et al. Spin of a multielectron quantum dot and its interaction with a neighboring electron. Phys. Rev. X 8, 011045 (2018).

    Google Scholar 

  83. Shulman, M. D. et al. Demonstration of entanglement of electrostatically coupled singlet–triplet qubits. Science 336, 202–205 (2012).

    Article  Google Scholar 

  84. Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).

    Article  Google Scholar 

  85. Laucht, A. et al. Roadmap on quantum nanotechnologies. Nanotechnology 32, 162003 (2021).

    Article  Google Scholar 

  86. Ono, K., Austing, D. G., Tokura, Y. & Tarucha, S. Current rectification by Pauli exclusion in a weakly coupled double quantum dot system. Science 297, 1313–1317 (2002).

    Article  Google Scholar 

  87. Kastner, M. A. The single-electron transistor. Rev. Mod. Phys. 64, 849–858 (1992).

    Article  Google Scholar 

  88. Le Guevel, L. Low-power transimpedance amplifier for cryogenic integration with quantum devices. Appl. Phys. Rev. 7, 041407 (2020).

    Article  Google Scholar 

  89. Schoelkopf, R. J., Wahlgren, P., Kozhevnikov, A. A., Delsing, P. & Prober, D. E. The radio-frequency single-electron transistor (rf-SET): a fast and ultrasensitive electrometer. Science 280, 1238–1242 (1998).

    Article  Google Scholar 

  90. Angus, S. J., Ferguson, A. J., Dzurak, A. S. & Clark, R. G. A silicon radio-frequency single electron transistor. Appl. Phys. Lett. 92, 112103 (2008).

    Article  Google Scholar 

  91. Curry, M. J. et al. Single-shot readout performance of two heterojunction-bipolar-transistor amplification circuits at millikelvin temperatures. Sci. Rep. 9, 16976 (2019).

    Article  Google Scholar 

  92. Connors, E. J., Nelson, J. & Nichol, J. M. Rapid high-fidelity spin-state readout in Si/Si–Ge quantum dots via rf reflectometry. Phys. Rev. Appl. 13, 024019 (2020).

    Article  Google Scholar 

  93. House, M. et al. High-sensitivity charge detection with a single-lead quantum dot for scalable quantum computation. Phys. Rev. Appl. 6, 044016 (2016).

    Article  Google Scholar 

  94. Ciriano-Tejel, V. N. et al. Spin readout of a CMOS quantum dot by gate reflectometry and spin-dependent tunneling. PRX Quantum 2, 010353 (2021).

    Article  Google Scholar 

  95. Urdampilleta, M. et al. Gate-based high fidelity spin readout in a CMOS device. Nat. Nanotechnol. 14, 737–741 (2019).

    Article  Google Scholar 

  96. Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004).

    Article  Google Scholar 

  97. Colless, J. I. et al. Dispersive readout of a few-electron double quantum dot with fast rf gate sensors. Phys. Rev. Lett. 110, 46805 (2013).

    Article  Google Scholar 

  98. Gonzalez-Zalba, M. F., Barraud, S., Ferguson, A. J. & Betz, A. C. Probing the limits of gate-based charge sensing. Nat. Commun. 6, 6084 (2015).

    Article  Google Scholar 

  99. Mi, X. et al. A coherent spin-photon interface in silicon. Nature 555, 599–603 (2018).

    Article  Google Scholar 

  100. Pakkiam, P. et al. Single-shot single-gate rf spin readout in silicon. Phys. Rev. X 8, 41032 (2018).

    Google Scholar 

  101. West, A. et al. Gate-based single-shot readout of spins in silicon. Nat. Nanotechnol. 14, 437–441 (2019).

    Article  Google Scholar 

  102. Ibberson, D. J. et al. Large dispersive interaction between a CMOS double quantum dot and microwave photons. PRX Quantum 2, 020315 (2021).

    Article  Google Scholar 

  103. Mizuta, R., Otxoa, R., Betz, A. & Gonzalez-Zalba, M. Quantum and tunneling capacitance in charge and spin qubits. Phys. Rev. B 95, 045414 (2017).

    Article  Google Scholar 

  104. Zheng, G. et al. Rapid gate-based spin read-out in silicon using an on-chip resonator. Nat. Nanotechnol. 14, 742–746 (2019).

    Article  Google Scholar 

  105. Hornibrook, J. M. et al. Frequency multiplexing for readout of spin qubits. Appl. Phys. Lett. 104, 103108 (2014).

    Article  Google Scholar 

  106. Schaal, S. et al. A CMOS dynamic random access architecture for radio-frequency readout of quantum devices. Nat. Electron. 2, 236–242 (2019).

    Article  Google Scholar 

  107. Schaal, S. et al. Fast gate-based readout of silicon quantum dots using Josephson parametric amplification. Phys. Rev. Lett. 124, 067701 (2020).

    Article  Google Scholar 

  108. Stockklauser, A. et al. Strong coupling cavity QED with gate-defined double quantum dots enabled by a high impedance resonator. Phys. Rev. X 7, 11030 (2017).

    Google Scholar 

  109. Samkharadze, N. et al. High-kinetic-inductance superconducting nanowire resonators for circuit QED in a magnetic field. Phys. Rev. Appl. 5, 44004 (2016).

    Article  Google Scholar 

  110. Mazin, B. A. Microwave Kinetic Inductance Detectors. PhD thesis, California Institute of Technology (2004).

  111. Vissers, M. R. et al. Low loss superconducting titanium nitride coplanar waveguide resonators. Appl. Phys. Lett. 97, 232509 (2010).

    Article  Google Scholar 

  112. Shearrow, A. et al. Atomic layer deposition of titanium nitride for quantum circuits. Appl. Phys. Lett. 113, 212601 (2018).

    Article  Google Scholar 

  113. Grünhaupt, L. et al. Loss mechanisms and quasiparticle dynamics in superconducting microwave resonators made of thin-film granular aluminum. Phys. Rev. Lett. 121, 117001 (2018).

    Article  Google Scholar 

  114. Grünhaupt, L. et al. Granular aluminium as a superconducting material for high-impedance quantum circuits. Nat. Mater. 18, 816–819 (2019).

    Article  Google Scholar 

  115. Esterli, M., Otxoa, R. & Gonzalez-Zalba, M. Small-signal equivalent circuit for double quantum dots at low-frequencies. Appl. Phys. Lett. 114, 253505 (2019).

    Article  Google Scholar 

  116. Maman, V. D., Gonzalez-Zalba, M. & Pályi, A. Charge noise and overdrive errors in dispersive readout of charge, spin, and Majorana qubits. Phys. Rev. Appl. 14, 064024 (2020).

    Article  Google Scholar 

  117. Culcer, D., Hu, X. & Sarma, S. D. Interface roughness, valley–orbit coupling, and valley manipulation in quantum dots. Phys. Rev. B 82, 205315 (2010).

    Article  Google Scholar 

  118. Rahman, R. et al. Engineered valley–orbit splittings in quantum-confined nanostructures in silicon. Phys. Rev. B 83, 195323 (2011).

    Article  Google Scholar 

  119. Ferdous, R. et al. Valley dependent anisotropic spin splitting in silicon quantum dots. npj Quantum Inf. 4, 26 (2018).

    Article  Google Scholar 

  120. Mazzocchi, V. et al. 99.992% 28Si CVD-grown epilayer on 300 mm substrates for large scale integration of silicon spin qubits. J. Cryst. Growth 509, 1–7 (2019).

    Article  MathSciNet  Google Scholar 

  121. Lo, C. et al. Hybrid optical–electrical detection of donor electron spins with bound excitons in silicon. Nat. Mater. 14, 490–494 (2015).

    Article  Google Scholar 

  122. Thorbeck, T. & Zimmerman, N. M. Formation of strain-induced quantum dots in gated semiconductor nanostructures. AIP Adv. 5, 87107 (2015).

    Article  Google Scholar 

  123. Zhang, Q. et al. Experimental study of gate-first finFET threshold-voltage mismatch. IEEE Trans. Electron Devices 61, 643–646 (2014).

    Article  Google Scholar 

  124. Zeng, Z., Triozon, F. & Niquet, Y.-M. Carrier scattering in high-k/metal gate stacks. J. Appl. Phys. 121, 114503 (2017).

    Article  Google Scholar 

  125. Brauns, M., Amitonov, S. V., Spruijtenburg, P.-C. & Zwanenburg, F. A. Palladium gates for reproducible quantum dots in silicon. Sci. Rep. 8, 5690 (2018).

    Article  Google Scholar 

  126. Huang, W., Veldhorst, M., Zimmerman, N. M., Dzurak, A. S. & Culcer, D. Electrically driven spin qubit based on valley mixing. Phys. Rev. B 95, 75403 (2017).

    Article  Google Scholar 

  127. Veldhorst, M. et al. Spin–orbit coupling and operation of multivalley spin qubits. Phys. Rev. B 92, 201401 (2015).

    Article  Google Scholar 

  128. Tanttu, T. et al. Controlling spin–orbit interactions in silicon quantum dots using magnetic field direction. Phys. Rev. X 9, 21028 (2019).

    Google Scholar 

  129. Khaneja, N., Reiss, T., Kehlet, C., Schulte-Herbrüggen, T. & Glaser, S. J. Optimal control of coupled spin dynamics: design of NMR pulse sequences by gradient ascent algorithms. J. Magn. Reson. 172, 296–305 (2005).

    Article  Google Scholar 

  130. Puddy, R. K. et al. Multiplexed charge-locking device for large arrays of quantum devices. Appl. Phys. Lett. 107, 143501 (2015).

    Article  Google Scholar 

  131. Pauka, S. et al. Characterizing quantum devices at scale with custom cryo-CMOS. Phys. Rev. Appl. 13, 054072 (2020).

    Article  Google Scholar 

  132. Wuetz, B. P. et al. Multiplexed quantum transport using commercial off-the-shelf CMOS at sub-kelvin temperatures. npj Quantum Inf. 6, 43 (2020).

    Article  Google Scholar 

  133. Baart, T. A., Eendebak, P. T., Reichl, C., Wegscheider, W. & Vandersypen, L. M. K. Computer-automated tuning of semiconductor double quantum dots into the single-electron regime. Appl. Phys. Lett. 108, 213104 (2016).

    Article  Google Scholar 

  134. Moon, H. et al. Machine learning enables completely automatic tuning of a quantum device faster than human experts. Nat. Commun. 11, 4161 (2020).

    Article  Google Scholar 

  135. Venitucci, B., Li, J., Bourdet, L. & Niquet, Y. Modeling silicon CMOS devices for quantum computing. In 2019 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD) 1–4 (IEEE, 2019).

  136. Mohiyaddin, F. A. et al. Multiphysics simulation and design of silicon quantum dot qubit devices. In 2019 IEEE International Electron Devices Meeting (IEDM) 39.5.1–39.5.4 (IEEE, 2019).

  137. Gamble, J. K. et al. Valley splitting of single-electron Si MOS quantum dots. Appl. Phys. Lett. 109, 253101 (2016).

    Article  Google Scholar 

  138. Ibberson, D. J. et al. Electric-field tuning of the valley splitting in silicon corner dots. Appl. Phys. Lett. 113, 53104 (2018).

    Article  Google Scholar 

  139. Bourdet, L. et al. All-electrical control of a hybrid electron spin/valley quantum bit in SOI CMOS technology. IEEE Trans. Electron Devices 65, 5151–5156 (2018).

    Article  Google Scholar 

  140. Bourdet, L. & Niquet, Y.-M. All-electrical manipulation of silicon spin qubits with tunable spin–valley mixing. Phys. Rev. B 97, 155433 (2018).

    Article  Google Scholar 

  141. Venitucci, B. & Niquet, Y.-M. Simple model for electrical hole spin manipulation in semiconductor quantum dots: impact of dot material and orientation. Phys. Rev. B 99, 115317 (2019).

    Article  Google Scholar 

  142. Kamgar, A. Subthreshold behavior of silicon MOSFETs at 4.2 K. Solid State Electron. 25, 537–539 (1982).

    Article  Google Scholar 

  143. Hanamura, H. et al. Operation of bulk CMOS devices at very low temperatures. IEEE J. Solid State Circuits 21, 484–490 (1986).

    Article  Google Scholar 

  144. Balestra, F., Audaire, L. & Lucas, C. Influence of substrate freeze-out on the characteristics of MOS transistors at very low temperatures. Solid State Electron. 30, 321–327 (1987).

    Article  Google Scholar 

  145. Broadbent, S. B. CMOS operation below freezeout. In Proc. Workshop on Low Temperature Semiconductor Electronics 43–47 (IEEE, 1989).

  146. Balestra, F. & Ghibaudo, G. Brief review of the MOS device physics for low temperature electronics. Solid State Electron. 37, 1967–1975 (1994).

    Article  Google Scholar 

  147. Simoen, E. & Claeys, C. Impact of CMOS processing steps on the drain current kink of nMOSFETs at liquid helium temperature. IEEE Trans. Electron Devices 48, 1207–1215 (2001).

    Article  Google Scholar 

  148. Yoshikawa, N. et al. Characterization of 4 K CMOS devices and circuits for hybrid Josephson–CMOS systems. IEEE Trans. Appl. Supercond. 15, 267–271 (2005).

    Article  Google Scholar 

  149. Hong, S. et al. Low-temperature performance of nanoscale MOSFET for deep-space rf applications. IEEE Electron Device Lett. 29, 775–777 (2008).

    Article  Google Scholar 

  150. Coskun, A. H. & Bardin, J. C. Cryogenic small-signal and noise performance of 32nm SOI CMOS. In 2014 IEEE MTT-S International Microwave Symposium (IMS2014) 1–4 (IEEE, 2014).

  151. Homulle, H. A. R. Cryogenic Electronics for the Read-Out of Quantum Processors. PhD thesis, Technical Univ. Delft (2019).

  152. Beckers, A., Jazaeri, F. & Enz, C. Cryogenic MOSFET threshold voltage model. In ESSDERC 2019 - 49th European Solid-State Device Research Conference (ESSDERC) 94–97 (IEEE, 2019).

  153. Yang, T. et al. Quantum transport in 40-nm MOSFETs at deep-cryogenic temperatures. IEEE Electron Device Lett. 41, 981–984 (2020).

    Google Scholar 

  154. Bohuslavskyi, H. et al. Cryogenic subthreshold swing saturation in FD-SOI MOSFETs described with band broadening. IEEE Electron Device Lett. 40, 784–787 (2019).

    Article  Google Scholar 

  155. Beckers, A., Jazaeri, F. & Enz, C. Theoretical limit of low temperature subthreshold swing in field-effect transistors. IEEE Electron Device Lett. 41, 276–279 (2019).

    Article  Google Scholar 

  156. Patra, B. et al. Characterization and analysis of on-chip microwave passive components at cryogenic temperatures. IEEE J. Electron Devices Soc. 8, 448–456 (2020).

    Article  Google Scholar 

  157. Patra, B. et al. Cryo-CMOS circuits and systems for quantum computing applications. IEEE J. Solid State Circuits 53, 309–321 (2018).

    Article  Google Scholar 

  158. Incandela, R. M. et al. Characterization and compact modeling of nanometer CMOS transistors at deep-cryogenic temperatures. IEEE J. Electron Devices Soc. 6, 996–1006 (2018).

    Article  Google Scholar 

  159. Hart, P. A. T., Babaie, M., Charbon, E., Vladimirescu, A. & Sebastiano, F. Subthreshold mismatch in nanometer CMOS at cryogenic temperatures. IEEE J. Electron Devices Soc. 8, 797–806 (2020).

    Article  Google Scholar 

  160. Galy, P. et al. Cryogenic temperature characterization of a 28-nm FD-SOI dedicated structure for advanced CMOS and quantum technologies cointegration. IEEE J. Electron Devices Soc. 6, 594–600 (2018).

    Article  Google Scholar 

  161. Beckers, A. et al. Characterization and modeling of 28-nm FDSOI CMOS technology down to cryogenic temperatures. Solid State Electron. 159, 106–115 (2019).

    Article  Google Scholar 

  162. Petit, L. et al. Spin lifetime and charge noise in hot silicon quantum dot qubits. Phys. Rev. Lett. 121, 76801 (2018).

    Article  Google Scholar 

  163. Likharev, K. K. & Semenov, V. K. RSFQ logic/memory family: a new Josephson-junction technology for sub-terahertz-clock-frequency digital systems. IEEE Trans. Appl. Supercond. 1, 3–28 (1991).

    Article  Google Scholar 

  164. McCaughan, A. N. & Berggren, K. K. A superconducting-nanowire three-terminal electrothermal device. Nano Lett. 14, 5748–5753 (2014).

    Article  Google Scholar 

  165. Franke, D., Clarke, J., Vandersypen, L. & Veldhorst, M. Rent’s rule and extensibility in quantum computing. Microprocess. Microsyst. 67, 1–7 (2019).

    Article  Google Scholar 

  166. Reilly, D. J. Challenges in scaling-up the control interface of a quantum computer. In 2019 IEEE International Electron Devices Meeting (IEDM) 31.7.1–31.7.6 (IEEE, 2019),

  167. Pauka, S. J. et al. A cryogenic CMOS chip for generating control signals for multiple qubits. Nat. Electron. 4, 64–70 (2021).

    Article  Google Scholar 

  168. Xu, Y. et al. On-chip integration of Si/SiGe-based quantum dots and switched-capacitor circuits. Appl. Phys. Lett. 117, 144002 (2020).

    Article  Google Scholar 

  169. Hasler, J. et al. Cryogenic floating-gate CMOS circuits for quantum control. IEEE Trans. Quantum Eng. 2, 5501510 (2021).

    Article  Google Scholar 

  170. Ruffino, A. et al. A cryo-CMOS chip that integrates silicon quantum dots and multiplexed dispersive readout electronics. Nat. Electron. https://doi.org/10.1038/s41928-021-00687-6 (2021).

  171. Charbon, E. et al. Cryo-CMOS for quantum computing. In 2016 IEEE International Electron Devices Meeting (IEDM) 13.5.1–13.5.4 (IEEE, 2016).

  172. Weinreb, S., Bardin, J. C. & Mani, H. Design of cryogenic SiGe low-noise amplifiers. IEEE Trans. Microw. Theory Tech. 55, 2306–2312 (2007).

    Article  Google Scholar 

  173. Prabowo, B. et al. 13.3 A 6-to-8GHz 0.17mW/qubit cryo-CMOS receiver for multiple spin qubit readout in 40nm CMOS technology. In 2021 IEEE International Solid-State Circuits Conference (ISSCC) 212–214 (IEEE, 2021).

  174. Ruffino, A. et al. 13.2 A fully-integrated 40-nm 5-6.5 GHz cryo-CMOS system-on-chip with I/Q receiver and frequency synthesizer for scalable multiplexed readout of quantum dots. In 2021 IEEE International Solid-State Circuits Conference (ISSCC) 210–212 (IEEE, 2021).

  175. Cochrane L. et al. Quantum dot-based parametric amplifiers. Preprint at https://arxiv.org/abs/2111.11825 (2021).

  176. Bardin, J. C. et al. 29.1 A 28nm bulk-CMOS 4-to-8GHz ¡2mW cryogenic pulse modulator for scalable quantum computing. In 2019 IEEE International Solid- State Circuits Conference - (ISSCC) 456–458 (IEEE, 2019).

  177. Patra, B. et al. 19.1 A scalable cryo-CMOS 2-to-20GHz digitally intensive controller for 4×32 frequency multiplexed spin qubits/transmons in 22nm FinFET technology for quantum computers. In 2020 IEEE International Solid- State Circuits Conference - (ISSCC) 304–306 (IEEE, 2020).

  178. Van Dijk, J. P. G. et al. A scalable cryo-CMOS controller for the wideband frequency-multiplexed control of spin qubits and transmons. IEEE J. Solid State Circ. 55, 2930–2946 (2020).

    Article  Google Scholar 

  179. Xue, X. et al. CMOS-based cryogenic control of silicon quantum circuits. Nature 593, 205–210 (2021).

    Article  Google Scholar 

  180. Park, J.-S. et al. 13.1 A fully integrated cryo-CMOS SoC for qubit control in quantum computers capable of state manipulation, readout and high-speed gate pulsing of spin qubits in intel 22nm FFL FinFET technology. In 2021 IEEE International Solid- State Circuits Conference (ISSCC) 208–210 (IEEE, 2021).

  181. van Dijk, J. P. G. et al. Impact of classical control electronics on qubit fidelity. Phys. Rev. Appl. 12, 44054 (2019).

    Article  Google Scholar 

  182. Lamb, I. D. C. et al. An FPGA-based instrumentation platform for use at deep cryogenic temperatures. Rev. Sci. Instrum. 87, 14701 (2016).

    Article  Google Scholar 

  183. Homulle, H. et al. A reconfigurable cryogenic platform for the classical control of quantum processors. Rev. Sci. Instrum. 88, 45103 (2017).

    Article  Google Scholar 

  184. Fu, X. et al. A microarchitecture for a superconducting quantum processor. IEEE Micro 38, 40–47 (2018).

    Article  Google Scholar 

  185. Varsamopoulos, S., Bertels, K. & Almudever, C. G. Decoding surface code with a distributed neural network-based decoder. Quantum Mach. Intell. 2, 3 (2020).

    Article  MATH  Google Scholar 

  186. Flentje, H. et al. Coherent long-distance displacement of individual electron spins. Nat. Commun. 8, 501 (2017).

    Article  Google Scholar 

  187. Hermelin, S. et al. Electrons surfing on a sound wave as a platform for quantum optics with flying electrons. Nature 477, 435–438 (2011).

    Article  Google Scholar 

  188. Borjans, F., Croot, X. G., Mi, X., Gullans, M. J. & Petta, J. R. Resonant microwave-mediated interactions between distant electron spins. Nature 577, 195–198 (2020).

    Article  Google Scholar 

  189. Bertrand, B. et al. Fast spin information transfer between distant quantum dots using individual electrons. Nat. Nanotechnol. 11, 672–676 (2016).

    Article  Google Scholar 

  190. Fujita, T., Baart, T. A., Reichl, C., Wegscheider, W. & Vandersypen, L. M. K. Coherent shuttle of electron-spin states. npj Quantum Inf. 3, 22 (2017).

    Article  Google Scholar 

  191. Mills, A. R. et al. Shuttling a single charge across a one-dimensional array of silicon quantum dots. Nat. Commun. 10, 1063 (2019).

    Article  Google Scholar 

  192. Mortemousque, P.-A. et al. Enhanced spin coherence while displacing electron in a 2D array of quantum dots. PRX Quantum 2, 030331 (2021).

    Article  Google Scholar 

  193. Jadot, J. et al. Distant spin entanglement via fast and coherent electron shuttling. Nat. Nanotechnol. 16, 570–575 (2021).

    Article  Google Scholar 

Download references

Acknowledgements

We thank D. J. Reilly, A. J. Ferguson, A. Laucht, A. Saraiva, S. Benjamin and L. A. Ibberson for providing useful comments. This research has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreements 951852, 688539 and 810504. M.F.G.-Z. acknowledges support from UKRI Future Leaders Fellowship (grant number MR/V023284/1), the Royal Society and the Winton Programme for the Physics of Sustainability. S.d.F., T.M. and M.V. acknowledge support from the Agence Nationale de la Recherche through the CMOSQSPIN project (ANR-17-CE24-0009). A.S.D. acknowledges support from an Australian Research Council Laureate Fellowship (FL190100167).

Author information

Authors and Affiliations

  1. Quantum Motion Technologies, Harrogate, UK

    M. F. Gonzalez-Zalba

  2. Université Grenoble Alpes and CEA, IRIG/PHELIQS, Grenoble, France

    S. de Franceschi

  3. École Polytechnique Fédérale de Lausanne, Neuchâtel, Switzerland

    E. Charbon

  4. CNRS, Grenoble INP, Institut Neel, Université Grenoble Alpes, Grenoble, France

    T. Meunier

  5. CEA/LETI-MINATEC, CEA-Grenoble, Grenoble, France

    M. Vinet

  6. School of Electrical Engineering and Telecommunications, The University of New South Wales, Sydney, NSW, Australia

    A. S. Dzurak

Authors
  1. M. F. Gonzalez-Zalba
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. de Franceschi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. E. Charbon
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. T. Meunier
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. M. Vinet
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. A. S. Dzurak
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed to the writing of the manuscript.

Corresponding author

Correspondence to M. F. Gonzalez-Zalba.

Ethics declarations

Competing interests

M.F.G.-Z is employed by Quantum Motion Technologies, a start-up focusing on building a silicon-based quantum computer. E.C. holds the position of Chief Scientific Officer of Fastree3D, a company making LiDARs for the automotive market, and he is co-founder of Pi Imaging Technology, a maker of sensors for microscopy. Neither company has been involved with the drafting of this Review. M.V., S.d.F., T.M. and A.S.D. declare no competing interests.

Additional information

Peer review information Nature Electronics thanks Guo-Ping Guo and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gonzalez-Zalba, M.F., de Franceschi, S., Charbon, E. et al. Scaling silicon-based quantum computing using CMOS technology. Nat Electron 4, 872–884 (2021). https://doi.org/10.1038/s41928-021-00681-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41928-021-00681-y

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing