Abstract
Future devices for the Internet of Things will require communication systems that can deliver higher data rates at low power. Backscatter radio—in which wireless communication is achieved via reflection rather than radiation—is a low-complexity approach that requires a minimal number of active elements. However, it is typically limited to data rates of hundreds of megabits per second because of the low frequency bands used and the modulation techniques involved. Here we report a millimetre-wave modulator and antenna array for backscatter communications at gigabit data rates. This radiofrequency front-end consists of a microstrip patch antenna array and a single pseudomorphic high-electron-mobility transistor that supports a range of modulation formats including binary phase shift keying, quadrature phase shift keying and quadrature amplitude modulation. The circuit is additively manufactured with inkjet printing using silver nanoparticle inks on a flexible liquid-crystal polymer substrate. A millimetre-wave transceiver is also designed to capture and downconvert the backscattered signals and route them for digital signal processing. With the system, we demonstrate a bit rate of two gigabits per second of backscatter transmission at millimetre-wave frequencies of 24–28 GHz, and with a front-end energy consumption of 0.17 pJ per bit.
Similar content being viewed by others
Main
The continuing development of the Internet of Things (IoT) requires the development of more scalable and robust communication systems that can deliver higher data rates and lower power consumption per device. Backscatter radios will be key here due to their low cost, low complexity and battery-free operation1,2,3,4. However, novel wireless communication techniques are still required to achieve the necessary combination of high data rates5,6,7 and minimized energy consumption.
Millimetre-wave (mmWave) communications have traditionally been considered as the ‘the last mile’, providing broadband, directive point-to-point and point-to-multipoint wireless links with applications such as local multipoint distribution systems. The advantages of this technology include the wide available bandwidth (on the order of gigahertz), which enables very large communication rates, and the ability to implement electrically large antenna arrays, which enables beam-forming capabilities. However, such mmWave systems are high cost in terms of components and system fabrication due to the need for low-loss materials and small-footprint assembly processes.
mmWave systems also dissipate more power than their corresponding counterparts operating in the ultra-high frequency (UHF) or low-microwave frequency range (such as the 1–5 GHz electronics that are commonly available in commercial devices). This is due primarily to limitations in device technologies leading to imperfect switching operation (diodes and transistors), but is also a result of layout parasitics resulting from fabrication and packaging tolerances effectively deteriorating the obtained efficiency, and due to losses in dielectric and conducting materials in the operating frequencies. Lower-frequency electronics are, however, limited in terms of data rate due to the drastically smaller fractional bandwidth they can support.
Backscatter radio has been extensively used in commercial radiofrequency identification (RFID) applications in sub-gigahertz bands to wirelessly transmit static identification codes with kilobits per second (kbps)-level data rates. mmWave identification systems have been proposed to leverage the advantages of directional antennas with the beam-scanning capabilities used in readers, permitting localization and ranging functionality8. Another advantage of mmWave operation is the direct integration of the antennas on integrated circuits (ICs)9, and various reader architectures and tag systems have been reported. These include pure complementary metal–oxide–semiconductor (CMOS)9,10,11,12,13,14 technologies, combinations of CMOS and low-temperature co-fired ceramic (LTCC)15, bipolar CMOS16, silicon micromachining9 and tag circuits consisting of off-the-shelf Schottky diodes placed on liquid-crystal polymer substrates17. However, backscatter rates are typically limited to hundreds of megabits per second at a frequency of 2.4 GHz (refs. 15,18,19).
In this Article, we show that backscatter radio can be used for gigabit-data-rate mmWave communications, while minimizing the front-end complexity to a single high-frequency transistor. We also show that a single mmWave transistor can support a range of modulation formats, including binary phase shift keying (BPSK), quadrature phase shift keying (QPSK) and quadrature amplitude modulation (16-QAM). Analogue modulation of the backscatter signal has previously been proposed20,21, but here we explore such modulation by introducing an analogue control signal in the gate of a commercial off-the-shelf transistor.
We have previously reported preliminary work on 4 Gbps binary modulation backscatter transmission at mmWave frequencies (and with a front-end with energy consumption of <0.15 pJ per bit)15. Using the same single transistor hardware, we now demonstrate transmission of a gigabits-per-second higher-order complex modulation and provide the received signal constellation in real time using commercial test equipment. We also show that the transmitted waveform provides a signal-to-noise and distortion level that are sufficient to implement complex modulation formats with high spectral efficiency (demonstrating a received gigabits-per-second 16-QAM signal constellation).
The low complexity of the front-end of our gigabit-data-rate backscatter means that it can be created with additive manufacturing using inkjet-printing techniques. Inkjet printing, which has been used to rapidly fabricate mmWave antennas22 and packaging solutions23, inherently requires a minimal amount of material and can achieve micrometre-level fabrication accuracy. The approach drastically reduces the fabrication cost and lead time typically associated with mmWave communication systems.
Single-transistor high-order modulation
The concept of single-transistor gigabit backscatter communications at mmWave frequencies is summarized in Fig. 1. A backscatter communicator consists of an antenna array with input impedance Za and a single radiofrequency (RF) transistor that is used for modulation with impedance Z. By controlling the RF transistor’s gate bias with a voltage Vb(t), the transistor impedance can be modified easily, yielding a variation of the reflection coefficient over time. The complex reflection coefficient between the antenna array input impedance and the voltage-controlled transistor impedance is
and denotes the relationship between the RF voltage \({V}_{\,\text{RF}}^{\text{refl}\,}\) that is reflected when an incident RF voltage \({V}_{\,\text{RF}}^{\text{inc}\,}\) is induced at the antenna’s terminal, as is evident from \({V}_{\,\text{RF}}^{\text{refl}\,}={{\varGamma }}{V}_{\,\text{RF}}^{\text{inc}\,}\). The complex function Γ can carry digital information (for example, a bitstream) in a similar way that a complex baseband communication signal digitally encodes information in a conventional transmitter. For example, binary data in typical RFIDs are encoded by transitioning between two Γ0 and Γ1 values when voltages V0 and V1, respectively, are applied to the transistor gate.
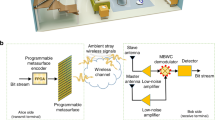
a, A mmWave backscatter system with gigabit-per-second data rate, with a 24–28 GHz transceiver and single-transistor backscatter communicator. The single-transistor communicator acts as a wireless mixer that is illuminated with an unmodulated continuous-wave signal by the transceiver and mixes high-speed data by controlling the transistor’s impedance. The transceiver receives the modulated backscattered signals and demodulates them for digital baseband processing. b, Heterodyne modulation and demodulation of gigabit-per-second-data-rate mmWave backscatter. Grey lobes correspond to spectra of complex-valued signals.
This Article introduces an exceptional difference compared with previous backscatter modulators that enables a high-order constellation (non-binary) with the use of a single transistor. Conceptually, multiple transistors or cascaded RF multiplexers could be used in different topologies to generate multiple reflection coefficient values, as has been showcased for UHF QAM backscatter in ref. 1 and refs. 16,24, respectively. However, increasing the number of transistors in a mmWave implementation may decrease the performance due to multiple device parasitics16, increase the cost and increase the complexity for higher constellation sizes, as seen in ref. 1, which limits scalability, whereas using switching-mode devices results in unwanted, increased spectrum occupancy, as argued in ref. 25. An important result of this work is that it applies the principles of continuously modulating the backscattered signal, as shown in analogue backscattering publications such as ref. 20 and our previous work related to pulse shaping of the backscattered signal25.
Modern communication devices push the signal processing complexity toward the digital baseband IC instead of, for example, employing multiple mixer stages in the RF front-end hardware. Radios tend to be more software-defined, leaving room for communication protocol upgrades and modulation scheme reconfiguration, while reutilizing unchanged, generic RF front-ends and antennas. The same philosophy is followed here, by keeping one single antenna array and one modulation transistor operating in mmWave bands, while pushing the complexity to lower-frequency digital operations.
The complex baseband signal x(t) in this implementation is a wide-band (main lobe width of 500 MHz to 1 GHz) BPSK, QPSK or 16-QAM modulation, which is digitally upconverted to an fsub = 2 GHz subcarrier, yielding a real-valued intermediate-frequency (IF) signal
which is used to bias the transistor’s gate. Because the baseband signal is digitally mixed with a subcarrier, and the IF signal is real-valued, only one transistor will always need to be excited, regardless of the baseband signal’s number of dimensions, which guarantees a feature that enables easy scalability.
When the backscatter communicator is illuminated with a 24.5 GHz unmodulated continuous wave, it reflects a wave that relies on the amplitude and phase of Γ, effectively mixing the IF signal around the 24.5 GHz carrier. This wireless mixing process enables mmWave transmissions, completely eliminating the need for mmWave oscillators and mixers on the communicator. The result is a passband mmWave signal with upper and lower sidebands that is captured by a 24.5 GHz receiver and directly downconverted to d.c. with a mixer that is coherent with the 24.5 GHz transmitter that emits the carrier continuous wave. The in-phase (I) and quadrature (Q) components of the mixer output are routed to a digital receiver that digitally removes the 2 GHz IF and demodulates the received complex baseband constellation. Employing a zero-IF downconverter in the mmWave hardware offers the flexibility of selecting any bias signal IF, without the need for additional mixing stages either in the backscatter communicator or the mmWave transceiver. The advantage of this heterodyne backscatter is that, within the bandwidth capability of the hardware, any baud rate, IF, constellation size and modulation format can be supported.
Printed mmWave backscatter communication array
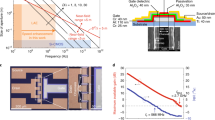
In principle, any antenna array can be used for mmWave backscattering, as long as it has a single feed that can be attached to a transistor’s terminal. For demonstration purposes, a microstrip 5 × 1 series-fed patch antenna array was designed with five patch elements separated by transmission line sections of approximate length λguided/2, where λguided is the effective wavelength in the microstrip, leading to in-phase excitation of the patches and a resonance frequency of 24.5 GHz. The antenna array is circularly polarized and circular polarization is achieved by appropriately truncating two corners of the patch radiators26. The simulated and vector network analyser (VNA)-measured return losses of the array are shown in Fig. 2a, where the principal resonance can be seen around 24.5 GHz and a secondary resonance around 26.5 GHz. The multiple-resonance frequency response is due to the fact that the series-fed antenna array has a structure of a bandpass microstrip stepped-impedance filter27,28. Owing to the Bode–Fano limits, a broadband-response antenna array will feature multiple local minima in the return loss response.
The directivity (Fig. 2b) of the array remains approximately constant over the whole 23–28 GHz band, with a value of ~13 dBi. The realized gain of the array (which includes the effect of the return loss, as well as conductor losses) is shown in Fig. 2c. The gain at the centre frequency (24.5 GHz) is 10 dBi and the gain between 25.5 and 28 GHz is flat at 8 dBi. The realized gain defines the frequency regions for the mmWave backscatter operation: the carrier continuous wave that illuminates the communicator will be centred at 24.5 GHz, while the backscatter response (subcarrier) will be centred 2 GHz further, at 26.5 GHz. An extra observation has to be made for the region at 22.5 GHz, where the realized gain is as low as 2 dBi. This frequency region inherently acts as a filter, which reduces the power of the lower modulated sideband that would otherwise act as a self-interfering image at the receiver. This ‘filtering effect’ is illustrated in Fig. 1b, where the 22.5 GHz lobe is shown as attenuated.
The antenna array layout and the backscatter modulator front-end are shown in Fig. 3. The antenna feed is connected through a 50 Ω microstrip line to an enhancement-mode high-electron mobility transistor (E-pHEMT; Avago VMMK-122529) drain. The transistor’s source has to be connected to an RF-short to achieve an ideal reflection of Γ = −1 when biased and Γ = +1 when non-biased. At the same time, a d.c. short is required to achieve the bias signal return through the gate–source path and effectively create a bias voltage of VGS > 0. Although a straightforward choice would be to place a grounded via as close as possible to the source pad, the physical dimension of the via would exceed the pad size, effectively shorting the gate and the drain. This layout issue is alleviated by connecting the transistor’s source to a grounded via through two approximately λ/4 lines in series and in a gamma configuration, guaranteeing an unchanged impedance (RF-short). The exact lengths of the lines were optimized to achieve a λ/2 total electrical length. The transistor’s gate is connected to a bias feed (RF choke) implemented with λ/4 transformers instead of parasitics-heavy lumped inductors. The utilized distributed RF choke features a rejection better than 25 dB at 24.5 GHz, which is the front end’s principal frequency of operation. This guarantees minimal carrier signal leakage to the gate and in turn to the bias gigabits-per-second source.
The integrated backscatter communicator was implemented on a 0.1778-mm-thick flexible liquid-crystal polymer (LCP) substrate with one copper-clad side used as the ground plane, while the other side (exposed LCP) was used for inkjet-printing the antenna array with silver nanoparticle (SNP) ink. The printing process is described in detail in the Methods, and includes preparation of the LCP substrate, inkjet-printing of the array and modulator circuit traces, followed by attachment of the surface mount 0402 E-pHEMT. Because of the good adhesion of the SNP ink on the thin LCP substrate, the entire structure is flexible, which can make it appealing for integration with wearable devices (such as smart wristbands), robots, autonomous cars and unmanned aerial vehicles (UAVs), space platforms and smart skins. For a printed SNP conductivity value of σ = 5 × 106 S m−1, the skin depth at 24 GHz is 1.45 μm, which can be guaranteed by printing four layers of silver22. The microphotographs in Fig. 4 show the high level of accuracy that is achieved with inkjet printing and four-layer stacking of SNPs. The accuracy of the fine feature sizes as well as metal-to-metal clearance gaps were achieved by modifying the surface energy of the LCP with UV–ozone exposure, as described in the Methods.
Custom mmWave backscatter transceiver
The test set-up of Fig. 5 was used to conduct the mmWave backscatter experiments. As shown in Fig. 1a, a mmWave transceiver was used to capture and downconvert the backscattered signals and route them for digital processing. For the testing in this work, a custom transceiver with off-the-shelf modules was set up, with a transmitter set up to emit a 24.5 GHz continuous wave. The spectrum of the receiver covered the whole 24–28 GHz band while discarding the 22.5 GHz frequency region, further attenuating the lower modulated sideband, as illustrated in Fig. 1b.
A voltage-controlled oscillator (VCO; Hittite HMC73930) was set up as a 24.5 GHz synthesizer and its output was amplified by a power amplifier (PA; Hittite HMC86331) before being sent to a wide-band horn antenna (A-info LB-180400-20-C-KF) for continuous-wave illumination of the backscatter array. The horn gain was 20 dB and the PA provided 24 dB of gain, +28.5 dBm of saturated output power or 27 dBm of output power for 1-dB compression, with a supply of +5.5 V. An identical horn antenna was used for the receive chain, connected to a mmWave low-noise amplifier (LNA; RF-Lambda RLNA26G40GB32). The output of the LNA was connected to a zero-IF mixer (Hittite HMC97733) with I/Q outputs.
To demonstrate the proof of concept of the proposed disruptive ultrabroadband backscatter communications, the mmWave communicator was connected to a Keysight M8190 arbitrary waveform generator (AWG) that provided the real-valued modulated bias signal. The transceiver’s I and Q outputs were directed to a Keysight Infiniium S-series digital storage oscilloscope (DSO) running vector signal analysis (VSA) digital demodulation software and performing constellation analysis (Fig. 5). The VSA receiver algorithm34 performed carrier and symbol synchronization and d.c. offset removal and rotation to generate a reference constellation. However, I/Q imbalance was not compensated.
The distance between the horn antennas and the backscatter RF front-end was fixed at 0.5 m. The linearly polarized transmit horn and received horn antennas were placed next to each other and rotated 90° with respect to each other to receive linearly polarized signals orthogonally polarized with respect to the transmitted linearly polarized continuous-wave signal. This cross-polarized arrangement improved the isolation between the transmitter (TX) and the receiver (RX) and permitted the system to reject structural scattering from the backscatter tag’s ground plane22.
Gigabit-per-second data rates for backscatter radio
The AWG was first set up to output BPSK pseudorandom data with a data rate of 1 Gbps and a subcarrier of 2 GHz, that is, the main lobe of the modulation bias covering the band from ~1.5 GHz to 2.5 GHz. Instead of performing binary-level switching between 0 V and 1 V, which results in excessive-bandwidth signals, the pulse-shaping principles of ref. 25 were applied to backscatter smooth, band-limited waveforms with most of the energy present in the main lobe. The front-end was biased with a BPSK waveform that was pulse-shaped with square-root raised cosine (SRRC) pulses and a rolloff factor of α = 0.35 to limit the signal bandwidth. The demodulated signal is shown in Fig. 6a, where the captured BPSK constellation and main-lobe spectrum can be seen, with a root mean square (r.m.s.) error vector magnitude (EVM) of 24.76%. This value corresponds to a bit error rate (BER) of 0.2%35 and has been achieved without any signal pre-distortion or forward error coding (FEC) at the AWG, and without equalization at the DSO/VSA. Considering a leakage gate–source current of IGS = 200 nA and maximum bias voltage of Vmax = 1 V, the maximum transistor static power consumption
is Pstatic = 200 nW. The maximum dynamic power consumption is36
where the gate capacitance is CGS = 0.3 pF and the maximum switching speed fmax = Fsub + W is related to the subcarrier fsub = 2 GHz and the baseband bandwidth W of the SRRC pulse used37:
where α = 0.35 is the SRRC rolloff factor and Tsym is the symbol period. In the case of 1 Gbps BPSK, fmax = 2.675 GHz and Pdyn = 401.25 μW. The energy per bit is
where Tbit is the bit period. This is then Eb = 0.4 pJ per bit.
To demonstrate the backscattering of high-order modulation with a single transistor, the AWG was set up to generate a QPSK waveform, digitally upconverted to a 2 GHz IF subcarrier, and the real-valued analogue signal output was used to drive the mmWave communicator. In Fig. 6b, the demodulated QPSK constellation is shown, with an EVM of 14.75%, or BER of 0.6%. The baud rate is 500 Msymbols s−1, with an effective bit rate of 1 Gbps. The energy per bit in this case is Eb = 0.35 pJ per bit. In Fig. 6c, the bit rate is increased even more, with a baud rate of 500 Msymbols s−1, but with a 16-QAM constellation, boosting the bit rate to 2 Gbps, with an EVM of 12.37%, a BER of 8% and maximum Eb of 0.17 pJ per bit. The 0.17 pJ per bit refers to the front-end only and the overall consumption of the tag should include the power dissipated in generating the gigabit-per-second modulation signal; however, this presents a challenge in all such gigabit-per-second systems due to the high power consumption of the AWG (digital-to-analogue converters and field programmable gate array logic). This work clearly demonstrates gigabit-per-second-level data rates for backscatter radio, accompanied by extremely low-energy front-end consumptions, as shown in Table 1. The fact that this performance can be achieved with all-printed antenna arrays of a small size (5 × 1) shows the great potential of using mmWave backscatter for low-complexity Gbit communication, without directly utilizing high-complexity mmWave modules (VCOs, mixers and amplifiers) on mobile devices, sensors or IoT nodes.
Backscatter range in mmWaves
Although mmWave propagation corresponds to an increased free-space path loss compared to propagation using signals at lower frequencies in the UHF or low gigahertz frequency bands due to a smaller wavelength, the overall system path loss is offset by the substantially larger antenna gains. Furthermore, recent works38 have supported the fact that rain attenuation and atmospheric absorption at mmWave frequencies would not present an important degradation of performance, especially when selecting specific low-absorption frequency ranges, such as the one around 28 GHz, for transmission. The range of backscatter communication systems such as RFID systems assuming free-space propagation is estimated as39
where Gt is the transmit reader/interrogator antenna gain, Gr is the receive tag antenna gain and λ is the free-space operating wavelength. The proportionality factor depends on the transmitted power, the sensitivity of the reader interrogator or the receive tag sensitivity, the polarization mismatch between the transmit and receive antennas and the impedance mismatch between the tag antenna and the tag transistor circuit. Therefore, assuming a fixed proportionality constant, scaling down the operating wavelength can be offset by scaling up by the square of the amount of the product of the transmit and receive antenna gains. For example, increasing the operating frequency by an order of magnitude (that is, 10 dB, for example from 2.4 GHz to 24 GHz) would require an increase of the combined transmit and receive antenna gains by two orders of magnitude (that is, 20 dB). The system prototype that we have implemented comprises a transmit antenna with 20 dB of gain and a receive antenna with 10 dB of gain. A typical UHF reader antenna has 7 dB of gain and a typical UHF RFID tag 0 dB of gain. Compared to a typical UHF RFID scenario, our prototype introduces an increase in the combined transmit and receive gain of 200 or 23 dB. The frequency scaling from 915 MHz to 24.5 GHz is 26.8 or 14.3 dB. This translates to an ~3-dB reduction in the achievable range. The range reduction can be minimized by employing a larger tag antenna array. However, a more accurate comparison should consider the sensitivity of the tag, as well as the operating bit rate. The use of an active tag or exploring forms of energy harvesting, for example, by integrating solar cells together with the tag antenna40, may further assist the implementation of the system.
Conclusions
We have reported a multi-gigabit-per-second backscatter with a printed mmWave modulator and antenna, which has a front-end power consumption of 0.17 pJ per bit. The potential of pJ-per-bit communication at those frequencies is considerable, given that commonly used active RF modules for mmWave communication consume several orders of magnitude more power. For example, an off-the-shelf mmWave mixer, HMC977, has a power consumption of 600–700 mW, whereas the power consumption of our single-transistor backscatter front-end is on the order of 0.5 mW. Viewing backscatter communication as ‘remote’ mixing could lead to drastically reduced complexity in commercial devices that require high-data-rate communication.
To benefit from the upcoming 5G standards and reach gigabit data-transfer speeds, cell phones will have to upgrade to full 28 GHz radios. However, the 2.4 GHz electronics that are already present in most cell phones could act as an IF bridge between baseband and mmWave frequencies with the addition of a single mmWave transistor for over-the-air mixing. Backscattering at mmWave frequencies has the potential to bring 5G network compatibility to devices without actually incorporating additional highly complex and costly 28 GHz Tx/Rx chains. Scenarios such as cell-phone data offloading (for example, sending photographs/videos to cloud storage) at hotspots in cafes or other public places are in line with the concept of wireless-charging hotspots that appear in similar locations.
Using single-transistor front-ends for backscatter mixing instead of active mmWave mixers has a direct effect on the communication radio’s cost, which drops by one to two orders of magnitude (from tens of dollars for an active mixer down to less than a dollar for a single transistor). These cost savings, combined with the notably smaller footprint of a minimal backscatter front-end, could reduce the total production cost of mobile devices, making wireless technology capable of rapid data transfer more accessible.
Moreover, by further optimization of reader sensitivity and the backscatter communicator’s antenna gain, higher-order constellations can be supported, which in turn would reduce the required symbol rate (and thus bandwidth) for a given bit rate. This would relax the bandwidth requirements of antennas and devices, and would reduce the device’s power consumption further due to the lower switching speeds. Finally, the implementation of wearable systems and small mobile devices creates additional challenges due to multipath and antenna bending, as well as antenna misalignments. Such implementations will require further evaluation of the approach.
Methods
Inkjet-printing fabrication of the backscatter communicator
The substrate used for the printed array fabrication was double-side copper-clad, 0.1778-mm-thick Ultralam 3850HT LCP from Rogers Corporation (ϵr = 3.14, \(\tan \delta =0.002\)), with one side of the copper cladding chemically etched off. Before printing, the LCP-exposed side of the substrate was cleaned by adhering and removing Kapton tape, which abrasively removed dust. The substrate was then exposed in a UV–ozone cleaner for 10 s to break down surface contaminants such as grease and modify the substrate’s surface energy for improved ink adhesion.
All printing was performed with a Dimatix DMP-2831 material deposition inkjet printer using Suntronic EMD5730 inkjet ink, with a 40% nanosilver content in water-based solvent. Four layers of SNP ink were printed at a 20-μm drop-to-drop spacing and with a 600-s inter-layer delay. The printer’s print table was heated to a maximum of 60 °C to promote solvent evaporation between layers. The resulting printed traces featured sharp edges, as shown in Fig. 4.
The LCP substrate with the printed array was annealed in a mechanical convection oven at 180 °C for 60 min to evaporate the remaining solvent and sinter the SNPs to form continuous conductive traces.
Vias were formed manually with a Dremel rotary tool driving a 0.5 mm drill bit. Metallization of vias was performed by deposition of MG Chemicals 8330S conductive epoxy (0.0007 Ω cm resistivity). The same epoxy was used for adhesion of the surface-mounted pHEMT transistor (Avago VMMK-1225) on the printed silver traces.
For the bias signal excitation port, a screw-on end-launch SMA connector was used (Southwest 292-06A-6); this provided a coaxial-to-microstrip transition.
Simulations
For the simulations, the Keysight Advanced Design System (ADS) solver was used to optimize the backscatter modulator and 5 × 1-antenna array and export the results shown in Fig. 2b,c. A full electromagnetic analysis with the method of moments was applied to the backscatter modulator and 5 × 1-antenna array to estimate the losses from the LCP substrate and SNP, the fringing fields and the electromagnetic coupling between ports. Next, harmonic-balance and large-signal analysis was applied, taking into account the nonlinear behaviour of the E-pHEMT.
In the simulations, the PHEMT was biased through a microstrip-stub RF choke (rejection better than 25 dB at 24 GHz) and for a bias voltage of 0 V and 1 V, respectively, the reflection coefficient values Γ0 and Γ1 were exported up to 40 GHz. The reflection coefficient difference amplitude ΔΓ = ∣Γ0 − Γ0∣ was then calculated; this is known as the modulation factor, which needs to be maximized to optimize backscatter communication performance41.
Backscatter signal modelling
A detailed analysis and derivation of the backscatter signal model can be found in ref. 42, where binary modulation is performed with a single transistor that alternates between two discrete states (‘on’–‘off’ switching when the transistor’s gate bias is high or low). Moreover, analysis of backscatter modulation with pulse-shaped signals instead of hard level switching is provided in ref. 25, where a single transistor is used to generate arbitrary, smooth waveforms, by continuous variation of the transistor’s gate bias over time. The following analysis shows how a single transistor can still be used to to backscatter signals corresponding to complex constellations, for example QPSK or 16-QAM.
A complex baseband QAM signal has the form
where I(t) and Q(t) correspond to the in-phase and quadrature signal components, respectively, gT(t) is the transmit filter pulse (for example, an SRRC with baseband bandwidth W), T is the symbol period, and an,I and an,Q are the nth in-phase and quadrature symbols to be transmitted. For QPSK/QAM, an,I, an,Q ∈ {−1, +1}, while in 16-QAM, an,I, an,Q ∈ {±1, ±3}, and so on.
The bias signal applied to the communicator’s transistor gate corresponds to an IF signal and can be represented as
where fsub is the IF (subcarrier) frequency. Assuming that the bias signal level is normalized, that is, xbias(t) ∈ [−1, +1], and the voltage applied to the transistor gate is unipolar, that is Vb ∈ [0, +1] V, the relationship between the bias voltage and the IF signal is
Applying a bias voltage to the transistor’s gate will modify the voltage-controlled impedance Z(Vb(t)) of the transistor, which, in the following, will modify the reflection coefficient Γ at the transistor’s source terminal (which is connected to the antenna). The reflection coefficient function over time is
In a simplified scenario, applying a low bias voltage (Vb = 0 V) to the transistor’s gate will turn the transistor ‘off’, creating an RF-open, which yields a reflection coefficient value Γ(0) = +1, whereas a high bias voltage (Vb = 1 V) will create an RF-short, which corresponds to a reflection coefficient of Γ(1) = −1. Furthermore, we will assume a linear relationship between the bias voltage and the reflection coefficient:
In other words, the IF signal is directly translated to reflection coefficient values. The above assumptions deviate from reality in practical systems, because perfect RF-short and RF-open are difficult to achieve with mmWave transistors due to parasitics and device insertion loss, which constrain Γ to an interval other than [−1, +1]. However, with proper signal normalization, as described in ref. 25, the reflected signals can be mapped to the [−1, +1] region. Also, the relationship between bias voltage and reflection coefficient is not exactly linear, which causes signal distortion. The exact Γ(Vb) function has to be characterized with the methods described in ref. 25, and any nonlinearities have to be taken into account with appropriate signal pre-distortion at the communicator, or equalization at the receiver.
Nevertheless, the aforementioned assumptions simplify the analysis of the heterodyne backscatter system. The backscattered signal that is received by a base station/access point and directly downconverted (zero-IF) is
where adc, amod and ϕdc, ϕmod are the amplitude scaling and phase rotation terms of the d.c. and the modulated signal component, respectively. The r(t) signal can be seen as
and is a complex signal that contains the real-valued IF bias signal. To remove the IF subcarrier, a frequency shifting operation followed by a low-pass filter operation is needed. The output signal is
where LPF∣f∣ ≤ W{ ⋅ } denotes an LPF with cutoff frequency W, that is, enough to preserve the frequency content of the band-limited signal of equation (8). Then, the resulting baseband signal is
which allows recovery of the original baseband QAM signal x(t), regardless of the constellation size.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Thomas, S. J. & Reynolds, M. S. A 96 Mbit/sec, 15.5 pJ/bit 16-QAM modulator for UHF backscatter communication. In Proc. 2012 IEEE International Conference on RFID 185–190 (IEEE, 2012); https://doi.org/10.1109/RFID.2012.6193049
Iyer, V., Talla, V., Kellogg, B., Gollakota, S. & Smith, J. Inter-technology backscatter: towards internet connectivity for implanted devices. In Proc. 2016 ACM SIGCOMM Conference 356–369 (ACM, 2016); https://doi.org/10.1145/2934872.2934894
Talla, V. et al. LoRa backscatter: enabling the vision of ubiquitous connectivity. Proc. ACM on Interactive, Mobile, Wearable and Ubiquitous Connectivity 105 (ACM, 2017).
Belo, D. et al. IQ impedance modulator front-end for low-power LoRa backscattering devices. IEEE Trans. Microw. Theory Tech. 67, 5307–5314 (2019).
Griffin, J. D. & Durgin, G. D. Multipath fading measurements for multi-antenna backscatter RFID at 5.8 GHz. In 2009 IEEE International Conference on RFID 322–329 (IEEE, 2009); https://doi.org/10.1109/RFID.2009.4911197
Bharadia, D., Joshi, K. R., Kotaru, M. & Katti, S. Backfi: high throughput WiFi backscatter. ACM SIGCOMM Computer Comm. Rev. 45, 283–296 (2015).
Tang, A., Kim, Y. & Chang, M.-C. F. A 65-nm CMOS 330-Mb/s microwave backscatter link at 2.4 to 2.9 GHz with ambient blocker cancellation. IEEE Microw. Wirel. Compon. Lett. 26, 61–63 (2015).
Pursula, P. et al. Millimeter-wave identification—a new short-range radio system for low-power high data-rate applications. IEEE Trans. Microw. Theory Tech. 56, 2221–2228 (2008).
Yoo, T.-W. & Chang, K. Theoretical and experimental development of 10 and 35-GHz rectennas. IEEE Trans. Microw. Theory Tech. 40, 1259–1266 (1992).
Shinohara, N., Nishikawa, K., Seki, T. & Hiraga, K. Development of 24-GHz rectennas for fixed wireless access. In Proc. 2011 XXXth URSI General Assembly and Science Symposium 1–4 (IEEE, 2011); https://doi.org/10.1109/URSIGASS.2011.6050505
Okba, A., Takacs, A., Aubert, H., Charlot, S. & Calmon, P.-F. Multiband rectenna for microwave applications. C. R. Phys. 18, 107–117 (2017).
Takacs, A., Aubert, H., Fredon, S., Despoisse, L. & Blondeaux, H. Microwave power harvesting for satellite health monitoring. IEEE Trans. Microw. Theory Tech. 62, 1090–1098 (2014).
Schmid, C. M., Feger, R. & Stelzer, A. Millimeter-wave phase-modulated backscatter transponder for FMCW radar applications. In Proc. 2011 IEEE MTT-S International Microwave Symposium 1–4 (IEEE, 2011); https://doi.org/10.1109/MWSYM.2011.5972773
Meyer, J., Dao, Q. H. & Geck, B. Design of a 24-GHz analog frontend for an optically powered RFID transponder for the integration into metallic components. In Proc. 2013 European Microwave Conference 1531–1534 (IEEE, 2013); https://doi.org/10.23919/EuMC.2013.6686961
Kimionis, J., Georgiadis, A. & Tentzeris, M. M. Millimeter-wave backscatter: a quantum leap for gigabit communication, RF sensing and wearables. In Proc. 2017 IEEE MTT-S International Microwave Symposium 812–815 (2017); https://doi.org/10.1109/MWSYM.2017.8058702
Matos, D., Jordao, M., Correia, R. & Carvalho, N. B. Millimeter-wave BiCMOS backscatter modulator for 5G-IoT applications. IEEE Microw. Wirel. Compon. Lett. 31, 173–176 (2020).
Ladan, S., Guntupalli, A. B. & Wu, K. A high-efficiency 24-GHz rectenna development towards millimeter-wave energy harvesting and wireless power transmission. IEEE Trans. Circuits Syst. I 61, 3358–3366 (2014).
Correia, R., Boaventura, A. & Carvalho, N. B. Quadrature amplitude backscatter modulator for passive wireless sensors in IoT applications. IEEE Trans. Microw. Theory Tech. 65, 1103–1110 (2017).
Correia, R. & Carvalho, N. B. Ultrafast backscatter modulator with low-power consumption and wireless power transmission capabilities. IEEE Microw. Wirel. Compon. Lett. 27, 1152–1154 (2017).
Talla, V., Buettner, M., Wetherall, D. & Smith, J. R. Hybrid analog–digital backscatter platform for high data rate, battery-free sensing. In Proc. 2013 IEEE Topical Conference on Wireless Sensors and Sensor Networks (WiSNet) 1–3 (IEEE, 2013).
Daskalakis, S.-N., Assimonis, S. D., Kampianakis, E. & Bletsas, A. Soil moisture scatter radio networking with low power. IEEE Trans. Microw. Theory Tech. 64, 2338–2346 (2016).
Cook, B. S., Tehrani, B., Cooper, J. R. & Tentzeris, M. M. Multilayer inkjet printing of millimeter-wave proximity-fed patch arrays on flexible substrates. IEEE Antennas Wirel. Propag. Lett. 12, 1351–1354 (2013).
Tehrani, B. K., Cook, B. S. & Tentzeris, M. M. Inkjet-printed 3D interconnects for millimeter-wave system-on-package solutions. In Proc. 2016 IEEE MTT-S International Microwave Symposium 1–4 (IEEE, 2016); https://doi.org/10.1109/MWSYM.2016.7540084
Correia, R. & Carvalho, N. B. Design of high order modulation backscatter wireless sensor for passive IoT solutions. In Proc. 2016 IEEE Wireless Power Transfer Conference 1–3 (IEEE, 2016); https://doi.org/10.1109/WPT.2016.7498833
Kimionis, J. & Tentzeris, M. M. Pulse shaping: the missing piece of backscatter radio and RFID. IEEE Trans. Microw. Theory Tech. 64, 4774–4788 (2016).
Pozar, D. M. & Schaubert, D. H. Microstrip Antennas: The Analysis and Design of Microstrip Antennas and Arrays (Wiley-IEEE Press, 1995).
Pozar, D. Considerations for millimeter wave printed antennas. IEEE Trans. Antennas Propag. 31, 740–747 (1983).
Pozar, D. M. Microwave Engineering 4th edn (Wiley, 2012).
0.5 to 26-GHz Low Noise E-PHEMT in a Wafer Scale Package (Avago Technologies, 2014); https://docs.broadcom.com/doc/AV02-1082EN
MMIC VCO with Half Frequency Output & Divide-by-16, 23.8–26.8 GHz V03.0309 (Analog Devices, 2009); https://www.analog.com/media/en/technical-documentation/data-sheets/hmc739.pdf
GaAs pHEMT MMIC 1/2 Watt Power Amplifier, 24–29.5 GHz V02.0118 (Analog Devices, 2018); https://www.analog.com/media/en/technical-documentation/data-sheets/hmc863alc4.pdf
Ultra Wide Band Low Noise Amplifier 20–40 GHz (RF-Lambda, 2018); https://www.rflambda.com/pdf/lownoiseamplifier/RLNA26G40GB.pdf
GaAs, MMIC, I/Q, Downconverter, 20 GHz to 28 GHz rev. D (Analog Devices, 2019); https://www.analog.com/media/en/technical-documentation/data-sheets/HMC977.pdf
Vector Signal Analysis Basics Application Note (Keysight Technologies, 2014); https://www.keysight.com/gb/en/assets/7018-01220/application-notes/5989-1121.pdf
Shafik, R. A., Rahman, M. S. & Islam, A. R. On the extended relationships among EVM, BER and SNR as performance metrics. In Proc. 2006 International Conference on Electrical and Computer Engineering 408–411 (IEEE, 2006); https://doi.org/10.1109/ICECE.2006.355657
Liu, D. & Svensson, C. Power consumption estimation in CMOS VLSI chips. IEEE J. Solid State Circuits 29, 663–670 (1994).
Proakis, J. G. Digital Communications 4th edn (McGraw-Hill, 1998).
Hong, W., Baek, K.-H., Lee, Y., Kim, Y. & Ko, S.-T. Study and prototyping of practically large-scale mmwave antenna systems for 5G cellular devices. IEEE Commun. Mag. 52, 63–69 (2014).
Occhiuzzi, C., Paggi, C. & Marrocco, G. Passive RFID strain-sensor based on meander-line antennas. IEEE Trans. Antennas Propag. 59, 4836–4840 (2011).
Niotaki, K., Collado, A., Georgiadis, A., Kim, S. & Tentzeris, M. M. Solar/electromagnetic energy harvesting and wireless power transmission. Proc. IEEE 102, 1712–1722 (2014).
Griffin, J. D. & Durgin, G. D. Complete link budgets for backscatter-radio and RFID systems. IEEE Antennas Propag. Mag. 51, 11–25 (2009).
Kimionis, J., Bletsas, A. & Sahalos, J. N. Increased range bistatic scatter radio. IEEE Trans. Commun. 62, 1091–1104 (2014).
Thomas, S. J., Wheeler, E., Teizer, J. & Reynolds, M. S. Quadrature amplitude modulated backscatter in passive and semipassive UHF RFID systems. IEEE Trans. Microw. Theory Tech. 60, 1175–1182 (2012).
Acknowledgements
The work of J.K. and M.M.T. was supported by the National Science Foundation-EFRI and the Defense Threat Reduction Agency (DTRA). The work of A.G. has been supported by the European Union Horizon 2020 Research and Innovation Programme under the Marie Skłodowska-Curie grant agreement no. 661621.
Author information
Authors and Affiliations
Contributions
J.K. and A.G. conceived the idea. J.K. designed and simulated the backscatter system, performed the measurements, interpreted the results and wrote the initial version of the manuscript. A.G. and M.M.T. supervised the research and contributed to the general concept and interpretation of the results. S.N.D. performed simulations, and revised and edited the final version of the manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Electronics thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kimionis, J., Georgiadis, A., Daskalakis, S.N. et al. A printed millimetre-wave modulator and antenna array for backscatter communications at gigabit data rates. Nat Electron 4, 439–446 (2021). https://doi.org/10.1038/s41928-021-00588-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41928-021-00588-8
This article is cited by
-
Flexible and wearable battery-free backscatter wireless communication system for colour imaging
npj Flexible Electronics (2024)
-
Free-standing printed electronics with direct ink writing
Nature Electronics (2024)
-
High gain quasi-omnidirectional dipole array fed by radial power divider for millimeter-wave IoT sensing
Scientific Reports (2024)
-
Battery-less long-range wireless fluidic sensing system using flexible additive manufacturing ambient energy harvester and microfluidics
Scientific Reports (2024)
-
Additively manufactured magic cube platforms for fully integrated wireless sensing nodes for Internet of Things applications
Scientific Reports (2023)