Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

In situ learning using intrinsic memristor variability via Markov chain Monte Carlo sampling

Nature Electronics volume 4, pages 151–161 (2021)Cite this article

Subjects

Abstract

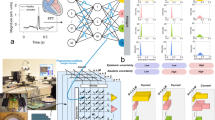
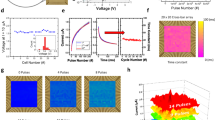
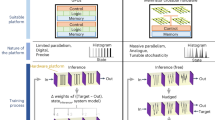
Resistive memory technologies could be used to create intelligent systems that learn locally at the edge. However, current approaches typically use learning algorithms that cannot be reconciled with the intrinsic non-idealities of resistive memory, particularly cycle-to-cycle variability. Here, we report a machine learning scheme that exploits memristor variability to implement Markov chain Monte Carlo sampling in a fabricated array of 16,384 devices configured as a Bayesian machine learning model. We apply the approach experimentally to carry out malignant tissue recognition and heart arrhythmia detection tasks, and, using a calibrated simulator, address the cartpole reinforcement learning task. Our approach demonstrates robustness to device degradation at ten million endurance cycles, and, based on circuit and system-level simulations, the total energy required to train the models is estimated to be on the order of microjoules, which is notably lower than in complementary metal–oxide–semiconductor (CMOS)-based approaches.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Strategies for training RRAM-based models.
Fig. 2: Electrical characterization of OxRAM cycle-to-cycle and device-to-device variability.
Fig. 3: Implementation of Metropolis–Hastings MCMC sampling on a fabricated RRAM array.
Fig. 4: Experimental results on the illustrative two-dimensional dataset.
Fig. 5: Experimental results on the supervised classification tasks.
Fig. 6: Behavioural simulation results on the cartpole reinforcement learning task.

Data availability

The Wisconsin breast cancer dataset41, the MIT-BIH ECG dataset42 and the reinforcement learning simulation environment are publicly available. All other measured data are freely available upon request.

Code availability

All software programs used in the presentation of the Article are freely available upon request.

References

  1. Shi, W., Cao, J., Zhang, Q., Li, Y. & Xu, L. Edge computing: vision and challenges. IEEE Internet Things J. 3, 637–646 (2016).

    Article  Google Scholar 

  2. Edge AI Chipsets: Technology Outlook and Use Cases. Technical Report (ABI Research, 2019).

  3. von Neumann, J. First draft of a report on the EDVAC. IEEE Ann. Hist. Comput. 15, 27–75 (1993).

    Article  MathSciNet  Google Scholar 

  4. LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).

    Article  Google Scholar 

  5. Rumelhart, D. E., Hinton, G. E. & Williams, R. J. Learning representations by back-propagating errors. Nature 323, 533–536 (1986).

    Article  Google Scholar 

  6. Strubell, E., Ganesh, A. & Mccallum, A. Energy and policy considerations for deep learning in NLP. In Proc. 57th Annual Meeting of the Association for Computational Linguistics (ACL) 3645–3650 (ACL, 2019).

  7. Li, D., Chen, X., Becchi, M. & Zong, Z. Evaluating the energy efficiency of deep convolutional neural networks on CPUs and GPUs. In 2016 IEEE International Conferences on Big Data and Cloud Computing (BDCloud), Social Computing and Networking (SocialCom), Sustainable Computing and Communications (SustainCom) (BDCloud-SocialCom-SustainCom) 477–484 (IEEE, 2016).

  8. Chua, L. Memristor—the missing circuit element. IEEE Trans. Circuit Theory 18, 507–519 (1971).

    Article  Google Scholar 

  9. Prezioso, M. et al. Training and operation of an integrated neuromorphic network based on metal-oxide memristors. Nature 521, 61–64 (2014).

    Article  Google Scholar 

  10. Wong, H. P. et al. Phase change memory. Proc. IEEE 98, 2201–2227 (2010).

    Article  Google Scholar 

  11. Chappert, C., Fert, A. & Dau, F. The emergence of spin electronics in data storage. Nat. Mater. 6, 813–823 (2007).

    Article  Google Scholar 

  12. Liu, Q. et al. Resistive switching: real-time observation on dynamic growth/dissolution of conductive filaments in oxide-electrolyte-based ReRAM. Adv. Mater. 24, 1774–1774 (2012).

    Article  Google Scholar 

  13. Beck, A., Bednorz, J. G., Gerber, C., Rossel, C. & Widmer, D. Reproducible switching effect in thin oxide films for memory applications. Appl. Phys. Lett. 77, 139–141 (2000).

    Article  Google Scholar 

  14. Garbin, D. et al. HfO2-based OxRAM devices as synapses for convolutional neural networks. IEEE Trans. Electron Dev. 62, 2494–2501 (2015).

    Article  Google Scholar 

  15. Gokmen, T., Onen, M. & Haensch, W. Training deep convolutional neural networks with resistive cross-point devices. Front. Neurosci. 11, 538 (2017).

    Article  Google Scholar 

  16. Boybat, I. et al. Neuromorphic computing with multi-memristive synapses. Nat. Commun. 9, 2514 (2017).

    Article  Google Scholar 

  17. Ambrogio, S. et al. Equivalent-accuracy accelerated neural-network training using analogue memory. Nature 558, 60–67 (2018).

    Article  Google Scholar 

  18. Nandakumar, S. R. et al. Mixed-precision architecture based on computational memory for training deep neural networks. In Proc. 2018 IEEE International Symposium on Circuits and Systems (ISCAS) 1–5 (IEEE, 2018).

  19. Li, C. et al. Efficient and self-adaptive in-situ learning in multilayer memristor neural networks. Nat. Commun. 9, 2385 (2018).

    Article  Google Scholar 

  20. Wang, Z. et al. Reinforcement learning with analogue memristor arrays. Nat. Electron. 2, 115–124 (2019).

    Article  Google Scholar 

  21. Yao, P. et al. Fully hardware-implemented memristor convolutional neural network. Nature 577, 641–646 (2020).

    Article  Google Scholar 

  22. Burr, G. W. et al. Experimental demonstration and tolerancing of a large-scale neural network (165,000 synapses) using phase-change memory as the synaptic weight element. IEEE Trans. Electron Dev. 62, 3498–3507 (2015).

    Article  Google Scholar 

  23. Sebastian, A., Krebs, D., Gallo, M. L., Pozidis, H. & Eleftheriou, E. A collective relaxation model for resistance drift in phase change memory cells. In Proc. 2015 IEEE International Reliability Physics Symposium MY.5.1–MY.5.6 (IEEE, 2015).

  24. Ambrogio, S. et al. Statistical fluctuations in HfOx resistive-switching memory: Part 1—set/reset variability. IEEE Trans. Electron Dev. 61, 2912–2919 (2014).

    Article  Google Scholar 

  25. Sidler, S. et al. Large-scale neural networks implemented with non-volatile memory as the synaptic weight element: impact of conductance response. In Proc. 2016 46th European Solid-State Device Research Conference (ESSDERC) 440–443 (IEEE, 2016).

  26. Agarwal, S. et al. Resistive memory device requirements for a neural algorithm accelerator. In Proc. 2016 International Joint Conference on Neural Networks (IJCNN) 929–938 (IEEE, 2016).

  27. Querlioz, D., Bichler, O., Dollfus, P. & Gamrat, C. Immunity to device variations in a spiking neural network with memristive nanodevices. IEEE Trans. Nanotechnol. 12, 288–295 (2013).

    Article  Google Scholar 

  28. Serb, A. et al. Unsupervised learning in probabilistic neural networks with multi-state metal–oxide memristive synapses. Nat. Commun. 7, 12611 (2016).

    Article  Google Scholar 

  29. Dalgaty, T. et al. Hybrid neuromorphic circuits exploiting non-conventional properties of RRAM for massively parallel local plasticity mechanisms. APL Mater. 7, 081125 (2019).

    Article  Google Scholar 

  30. Balatti, S., Ambrogio, S., Wang, Z. & Ielmini, D. True random number generation by variability of resistive switching in oxide-based devices. IEEE J. Emerg. Select. Top. Circuits Syst. 5, 214–221 (2015).

    Article  Google Scholar 

  31. Vodenicarevic, D. et al. Low-energy truly random number generation with superparamagnetic tunnel junctions for unconventional computing. Phys. Rev. Appl. 8, 054045 (2017).

    Article  Google Scholar 

  32. Faria, R., Camsari, K. Y. & Datta, S. Implementing Bayesian networks with embedded stochastic MRAM. AIP Adv. 8, 045101 (2018).

    Article  Google Scholar 

  33. Mizrahi, A. et al. Neural-like computing with populations of superparamagnetic basis functions. Nat. Commun. 9, 1533 (2018).

    Article  Google Scholar 

  34. Camsari, K. Y., Faria, R., Sutton, B. M. & Datta, S. Stochastic p-bits for invertible logic. Phys. Rev. X 7, 031014 (2017).

    Google Scholar 

  35. Borders, W. A. et al. Integer factorization using stochastic magnetic tunnel junctions. Nature 573, 390–393 (2019).

    Article  Google Scholar 

  36. Hastings, W. K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57, 97–109 (1970).

    Article  MathSciNet  Google Scholar 

  37. Ghahramani, Z. Probabilistic machine learning and artificial intelligence. Nature 521, 452–459 (2015).

    Article  Google Scholar 

  38. Neal, R. M. Bayesian Learning for Neural Networks Vol. 118 (Springer Science & Business Media, 2012).

  39. Grossi, A. et al. Resistive RAM endurance: array-level characterization and correction techniques targeting deep learning applications. IEEE Trans. Electron Dev. 66, 1281–1288 (2019).

    Article  Google Scholar 

  40. Ielmini, D. Modeling the universal set/reset characteristics of bipolar RRAM by field- and temperature-driven filament growth. IEEE Trans. Electron Dev. 58, 4309–4317 (2011).

    Article  Google Scholar 

  41. Wolberg, W. H. & Mangasarian, O. L. Multisurface method of pattern separation for medical diagnosis applied to breast cytology. Proc. Natl Acad. Sci. USA 87, 9193–9196 (1990).

    Article  Google Scholar 

  42. Moody, G. B. & Mark, R. G. The impact of the MIT-BIH arrhythmia database. IEEE Eng. Med. Biol. Mag. 20, 45–50 (2001).

    Article  Google Scholar 

  43. Sutton, R. S. & Barto, A. G. Introduction to Reinforcement Learning (MIT Press, 1998).

  44. Hoffman, M., Doucet, A., Freitas, N. D. & Jasra, A. Trans-dimensional MCMC for Bayesian policy learning. In Proc. 20th International Conference on Neural Information Processing Systems, NIPS’07 665–672 (Curran Associates, 2007).

  45. Barto, A. G., Sutton, R. S. & Anderson, C. W. Neuronlike adaptive elements that can solve difficult learning control problems. IEEE Trans. Syst. Man Cybern. SMC-13, 834–846 (1983).

    Article  Google Scholar 

  46. Berdan, R. et al. In-memory reinforcement learning with moderately-stochastic conductance switching of ferroelectric tunnel junctions. In Proc. 2019 Symposium on VLSI Technology T22–T23 (IEEE, 2019).

  47. Mnih, V. et al. Human-level control through deep reinforcement learning. Nature 518, 529–533 (2015).

    Article  Google Scholar 

  48. Pourret, O., Naïm, P. & Marcot, B. Bayesian Networks: A Practical Guide to Applications (Wiley, 2008).

  49. Maclaurin, D. & Adams, R. P. Firefly Monte Carlo: exact MCMC with subsets of data. In Proc. Thirtieth Conference on Uncertainty in Artificial Intelligence, UAI’14 543–552 (AUAI Press, 2014).

  50. Korattikara, A., Chen, Y. & Welling, M. Austerity in MCMC land: cutting the Metropolis–Hastings budget. In Proc. 31st International Conference on Machine Learning 181–189 (PMLR, 2014).

  51. Hoffman, M. D. & Gelman, A. The no-U-turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 15, 1593–1623 (2014).

    MathSciNet  MATH  Google Scholar 

  52. Liu, H. & Setiono, R. Chi2: feature selection and discretization of numeric attributes. In Proc. 7th IEEE International Conference on Tools with Artificial Intelligence 388–391 (IEEE, 1995).

Download references

Acknowledgements

We acknowledge funding support from the French ANR via Carnot funding as well as the H2020 MeM-Scales project (871371) and the European Research Council (grant NANOINFER, no. 715872). In addition, we thank E. Esmanhotto, J. Sandrini and C. Cagli (CEA-Leti) for help with the measurement set-up, J. F. Nodin (CEA-Leti) for providing the images in Fig. 3d and to S. Mitra (Stanford University), M. Payvand (ETH Zurich), A. Valentian, M. Solinas-Angel, E. Nowak (CEA-Leti), J. Diard (CNRS, Université Grenoble Alpes), P. Bessiére and J. Droulez (CNRS, Sorbonne Université), J. Grollier (CNRS, Thales) and J.-M. Portal (Aix-Marseille Université) for discussing various aspects of the Article.

Author information

Authors and Affiliations

  1. CEA, LETI, Université Grenoble Alpes, Grenoble, France

    Thomas Dalgaty, Niccolo Castellani & Elisa Vianello

  2. Université Paris-Saclay, CNRS, Centre de Nanosciences et de Nanotechnologies, Palaiseau, France

    Clément Turck, Kamel-Eddine Harabi & Damien Querlioz

Authors
  1. Thomas Dalgaty
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Niccolo Castellani
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Clément Turck
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Kamel-Eddine Harabi
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Damien Querlioz
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Elisa Vianello
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

T.D. developed the concept of RRAM-based MCMC sampling. N.C. built the computer-in-the-loop test set-up with the resistive memory array. T.D. and N.C. performed the computer-in-the-loop experiments with the resistive memory array. T.D. implemented the behavioural simulator, performed measurements on the array, which were used to calibrate the simulation and performed the benchmarking. K.-E.H., C.T. and D.Q. performed the design and energy analysis of the full system implementation. T.D., D.Q. and E.V. developed ideas and wrote the Article together.

Corresponding authors

Correspondence to Thomas Dalgaty, Damien Querlioz or Elisa Vianello.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1–17, Table 1 and Note 1.

Supplementary Video 1

Video of the cartpole task during one iteration of training through RRAM-based MCMC.

Supplementary Video 2

Video of the cartpole task during one iteration of testing using the trained model.

Rights and permissions

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Dalgaty, T., Castellani, N., Turck, C. et al. In situ learning using intrinsic memristor variability via Markov chain Monte Carlo sampling. Nat Electron 4, 151–161 (2021). https://doi.org/10.1038/s41928-020-00523-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41928-020-00523-3

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing