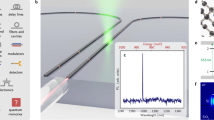
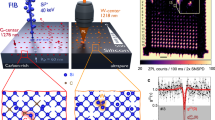
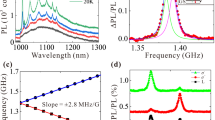
Abstract
Given its potential for integration and scalability, silicon is likely to be a key platform for large-scale quantum technologies. Individual electron-encoded artificial atoms, formed by either impurities or quantum dots, have emerged as a promising solution for silicon-based integrated quantum circuits. However, single qubits featuring an optical interface, which is needed for long-distance exchange of information, have not yet been isolated in silicon. Here we report the isolation of single optically active point defects in a commercial silicon-on-insulator wafer implanted with carbon atoms. These artificial atoms exhibit a bright, linearly polarized single-photon emission with a quantum efficiency of the order of unity. This single-photon emission occurs at telecom wavelengths suitable for long-distance propagation in optical fibres. Our results show that silicon can accommodate single isolated optical point defects like in wide-bandgap semiconductors, despite a small bandgap (1.1 eV) that is unfavourable for such observations.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
Source data are provided with this paper. All other results are available from the corresponding author upon reasonable request.
References
He, Y. et al. A two-qubit gate between phosphorus donor electrons in silicon. Nature 571, 371–375 (2019).
Watson, T. et al. A programmable two-qubit quantum processor in silicon. Nature 555, 633–637 (2018).
Maurand, R. et al. A CMOS silicon spin qubit. Nat. Commun. 7, 13575 (2016).
Qiang, X. et al. Large-scale silicon quantum photonics implementing arbitrary two-qubit processing. Nat. Photon. 12, 534–539 (2018).
Silverstone, J., Bonneau, D., O’Brien, J. & Thompson, M. Silicon quantum photonics. IEEE J. Sel. Top. Quantum Electron. 22, 390–402 (2016).
Awschalom, D., Hanson, R., Wrachtrup, J. & Zhou, B. Quantum technologies with optically interfaced solid-state spins. Nat. Photon. 12, 516–527 (2018).
Aharonovich, I., Englund, D. & Toth, M. Solid-state single-photon emitters. Nat. Photon. 10, 631–641 (2016).
Gruber, A. et al. Scanning confocal optical microscopy and magnetic resonance on single defect centers. Science 276, 2012–2014 (1997).
Beveratos, A. et al. Single photon quantum cryptography. Phys. Rev. Lett. 89, 187901 (2002).
Hensen, B. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
Gross, I. et al. Real-space imaging of non-collinear antiferromagnetic order with a single-spin magnetometer. Nature 549, 252–256 (2017).
Weber, J. et al. Quantum computing with defects. Proc. Natl Acad. Sci. USA 107, 8513–8518 (2010).
Davies, G. The optical properties of luminescence centres in silicon. Phys. Rep. 176, 83–188 (1989).
Beaufils, C. et al. Optical properties of an ensemble of G-centers in silicon. Phys. Rev. B 97, 035303 (2018).
Beveratos, A. et al. Room temperature stable single-photon source. Eur. Phys. J. D 18, 191–196 (2002).
Chartrand, C. et al. Highly enriched 28Si reveals remarkable optical linewidths and fine structure for well-known damage centers. Phys. Rev. B 98, 195201 (2018).
Docaj, A. & Estreicher, S. Three carbon pairs in Si. Physica B 407, 2981–2984 (2012).
Wang, H., Chroneos, A., Londos, C., Sgourou, E. & Schwingenschlegl, U. G-centers in irradiated silicon revisited: a screened hybrid density functional theory approach. J. Appl. Phys. 115, 183509 (2014).
Timerkaeva, D., Attaccalite, C., Brenet, G., Caliste, D. & Pochet, P. Structural, electronic, and optical properties of the C–C complex in bulk silicon from first principles. J. Appl. Phys. 123, 161421 (2018).
Song, L., Zhan, X., Benson, B. & Watkins, G. Bistable defect in silicon: the interstitial-carbon–substitutional-carbon pair. Phys. Rev. Lett. 60, 460–463 (1988).
Capaz, R., Dal Pino, A. & Joannopoulos, J. Theory of carbon–carbon pairs in silicon. Phys. Rev. B 58, 9845–9850 (1998).
Tkachev, V. & Mudryi, A. Piezospectroscopic effect on zero-phonon luminescence lines of silicon. J. Appl. Spectrosc. 29, 1485–1491 (1978).
Schmitt, S., Sarau, G. & Christiansen, S. Observation of strongly enhanced photoluminescence from inverted cone-shaped silicon nanostructures. Sci. Rep. 5, 17089 (2015).
Cueff, S. et al. Tailoring the local density of optical states and directionality of light emission by symmetry breaking. IEEE J. Sel. Top. Quantum Electron. 25, 4700807 (2019).
Gérard, J. et al. Enhanced spontaneous emission by quantum boxes in a monolithic optical microcavity. Phys. Rev. Lett. 81, 1110–1113 (1998).
Lee, K., O’Donnell, K., Weber, J., Cavenett, B. & Watkins, G. Optical detection of magnetic resonance for a deep-level defect in silicon. Phys. Rev. Lett. 48, 37–40 (1982).
Manson, N. et al. NV−–N+ pair centre in 1b diamond. New J. Phys. 20, 113037 (2018).
Lohrmann, A. et al. Diamond based light-emitting diode for visible single-photon emission at room temperature. Appl. Phys. Lett. 99, 251106 (2011).
Anderson, C. et al. Electrical and optical control of single spins integrated in scalable semiconductor devices. Science 366, 1225–1230 (2019).
Bernien, H. et al. Two-photon quantum interference from separate nitrogen vacancy centers in diamond. Phys. Rev. Lett. 108, 043604 (2012).
Riedinger, R. et al. Remote quantum entanglement between two micromechanical oscillators. Nature 556, 473–477 (2018).
Lee, S.-Y. et al. Readout and control of a single nuclear spin with a metastable electron spin ancilla. Nat. Nanotechnol. 8, 487–492 (2013).
Wehner, S., Elkouss, D. & Hanson, R. Quantum internet: a vision for the road ahead. Science 362, eaam9288 (2018).
Tait, A. et al. Microring resonator-coupled photoluminescence from silicon W centers. J. Phys. Photonics 2, 045001 (2020).
Ziegler, J. F. SRIM-2003. Nucl. Instrum. Methods Phys. Res. B 219/220, 1027–1036 (2004).
Binder, J. et al. Qudi: a modular Python suite for experiment control and data processing. SoftwareX 6, 85–90 (2017).
Martínez, L. et al. Efficient single photon emission from a high-purity hexagonal boron nitride crystal. Phys. Rev. B 94, 121405 (2016).
Kitson, S. C., Jonsson, P., Rarity, J. & Tapster, P. Intensity fluctuation spectroscopy of small numbers of dye molecules in a microcavity. Phys. Rev. A 58, 620–627 (1998).
Beveratos, A., Brouri, R., Poizat, J.-P. & Grangier, P. in Quantum Communication, Computing, and Measurement 3 (eds Tombesi, P. & Hirota, O.) 261–267 (Springer, 2002).
Benisty, H., Stanley, R. & Mayer, M. Method of source terms for dipole emission modification in modes of arbitrary planar structures. J. Opt. Soc. Am. A 15, 1192–1201 (1998).
Genovese, L. et al. Daubechies wavelets as a basis set for density functional pseudopotential calculations. J. Chem. Phys. 129, 014109 (2008).
Acknowledgements
We thank P. Valvin for his technical support and fruitful discussions, and C. L’Henoret for his technical support at the mechanics workshop. We acknowledge support from the French National Research Agency (ANR) through the PRCI projects ULYSSES (no. ANR-15-CE24-0027-01) and OCTOPUS (no. ANR-18-CE47-0013-01), the German Research Foundation (DFG) through the ULYSSES project and the European Union’s Horizon 2020 research and innovation programme through the FET-OPEN project NARCISO (no. 828890). P.P. and D.C. acknowledge GENCI for the use of French computational resources in CCRT and IDRIS supercomputer centres (grant no. 6107). A. Durand acknowledges support from the French DGA.
Author information
Authors and Affiliations
Contributions
A. Durand, I.R.-P., V.J., A. Dréau and G.C. designed the experimental set-up. T.H., A.B., S.P., J.M. and A.Y.K. prepared the samples. W.R., A. Durand and A. Dréau carried out the experiments. J.-M.G., D.C. and P.P. performed numerical simulations. W.R., A. Durand, J.-M.G., I.R.-P., B.G., M.A., V.J., A. Dréau and G.C. analysed the data. A. Dréau prepared the manuscript with contributions from I.R.-P., V.J. and G.C. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Analysis of the photodynamics of the G-center.
a, Simplified three-level model of the G-center under optical excitation. b, Second-order autocorrelation function \({g}_{{\rm{cor}}}^{(2)}(\tau )\) with increasing laser excitation power (from bottom to top). Data are corrected from background counts (see Eq. (1)) and fitted with equation (3). c, Evolution of the rates Λ0 and Λ1 with increasing optical power. The dashed lines correspond to data fitting excluding the last point at 30 μW. d, The bunching amplitude decreases with increasing optical power. The dotted line is a guide to the eye. Error bars represent the standard error resulting from data fitting of b with Python lmfit package.
Extended Data Fig. 2 Time-resolved PL counts recorded under pulsed laser excitation.
Histogram of the PL counts measured on a single defect under a 50-ps pulse laser excitation at 532 nm, with a periodicity of 270 ns. The measurement sequence was repeated 2.8 billion times. Counts are integrated in the window [0, 150] ns (shaded area), subtracted from noise counts (gray shaded area), and finally divided by the number of sweeps to get the probability to detect a photon per optical excitation Pphoton ≃ 4.1 ⋅ 10−4.
Extended Data Fig. 3 Calculations of the photon collection efficiency by a NA=0.85 objective.
a, Scheme of the simulated structure. The emitter dipole is assumed to be lying in the plane perpendicular to the surface, as this configuration maximizes photon collection. b, Evolution of the collection efficiency ηcoll as a function of the depth d of the embedded emitter.
Source data
Source Data Fig. 1
Source data of the plots in Fig. 1.
Source Data Fig. 2
Source data of the plots in Fig. 2.
Source Data Fig. 3
Source data of the plots in Fig. 3.
Source Data Extended Data Fig. 1
Source data of the plots in Extended Data Fig. 1.
Source Data Extended Data Fig. 2
Source data of the plots in Extended Data Fig. 2.
Source Data Extended Data Fig. 3
Source data of the plots in Extended Data Fig. 3.
Rights and permissions
About this article
Cite this article
Redjem, W., Durand, A., Herzig, T. et al. Single artificial atoms in silicon emitting at telecom wavelengths. Nat Electron 3, 738–743 (2020). https://doi.org/10.1038/s41928-020-00499-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41928-020-00499-0
This article is cited by
-
Cavity-coupled telecom atomic source in silicon
Nature Communications (2024)
-
Activation of telecom emitters in silicon upon ion implantation and ns pulsed laser annealing
Communications Materials (2024)
-
The kinetics of carbon pair formation in silicon prohibits reaching thermal equilibrium
Nature Communications (2023)
-
Individually addressable and spectrally programmable artificial atoms in silicon photonics
Nature Communications (2023)
-
All-silicon quantum light source by embedding an atomic emissive center in a nanophotonic cavity
Nature Communications (2023)