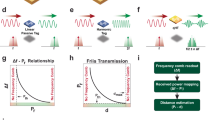
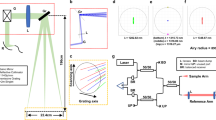
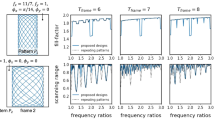
Abstract
The accurate sensing of the location of specific objects in an indoor setting is critical for applications including robotic feedback control and non-intrusive structural integrity monitoring. Current optical and ultrasound approaches often suffer from insufficient accuracy, obstruction by other objects, and ambiguous identification. Alternatively, conventional radar-like radio-frequency (RF) methods can suffer from problems such as multipath ambiguity, small time of flight, and limited item recognition. Attachment of a passive RF identification (RFID) tag can provide a unique marker by modulating the backscattering signal, but current systems struggle with high interference and noise, and thus have poor ranging accuracy. Here we show that a 1 GHz harmonic RFID system can provide a ranging resolution of less than 50 micrometres with a sampling rate of greater than 1 kHz. The fundamental limits on ranging precision in our system are traced to the phase noise of the RF source and the aperture jitter of the data converter. The small passive tag required for the approach can be embedded in indoor or underwater objects, as well as within building structures.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Ni, L. et al. LANDMARC: indoor location sensing using active RFID. Wirel. Netw. 10, 701–710 (2004).
Nikitin, P. V. et al. Phase based spatial identification of UHF RFID tags. Proc. IEEE Int. Conf. on RFID 102–109 (IEEE, 2010).
Hekimian-Williams, B. et al. Accurate localization of RFID tags using phase difference. Proc. IEEE Int. Conf. on RFID 89–96 (IEEE, 2010).
Arnitz, D., Witrisal, K. & Muehlmann, U. Multifrequency continuous-wave radar approach to ranging in passive UHF RFID. IEEE Trans. Microw. Theory Tech. 57, 1398–1405 (2010).
Wang, J. et al. RF-compass: robot object manipulation using RFIDs. Proc. 19th Annual Intl. Conf. on Mobile Comput. 3–14 (ACM, 2013).
Lesthaeghe, T. J. et al. RFID tags for detecting concrete degradation in bridge decks. http://lib.dr.iastate.edu/intrans_reports/70/ (Iowa State University, 2017).
Kulkarni, P. et al. SensEye: A multi-tier camera sensor network. Proc. 13th Annual Intl. Conf. on Multimedia 229–238 (ACM, 2005).
Davison, A. J. et al. MonoSLAM: Real-time single camera SLAM. IEEE Trans. Pattern Anal. Mach. Intell. 29, 1052–1067 (2007).
Foix, S., Alenyà, F. & Torras, C. Lock-in time-of-flight (ToF) cameras: a survey. IEEE Sens. J. 11, 1917–1926 (2011).
Rusinkiewicz, S., Hall-Holt, O. & Levoy, M. Real-time 3D model acquisition. ACM Trans. Graph. 21, 438–446 (2002).
Lingemann, K. et al. High-speed laser localization for mobile robots. Robot. Auton. Syst. 51, 275–296 (2005).
Muhammad, H. et al. Development of a bioinspired MEMS based capacitive tactile sensor for a roboticfinger. Sens. Actuat. A 165, 221–229 (2011).
Hui, X., Ma, Y. & Kan, E. C. Real-time 3D robotic arm tracking in indoor environment by RF nonlinear backscattering. Proc. ACM S3 Workshop 3–5 (ACM, 2016).
Hawkes, E. et al. A soft robot that navigates its environment through growth. Sci. Robot. 2, eaan3028 (2017).
Xu, B. et al. Improving RF-based device-free passive localization in cluttered indoor environments through probabilistic classification methods. Proc. 11th Intl. Conf. on IPSN 209–220 (ACM, 2012).
Wang, J., Vasisht, D. & Katabi, D. RF-IDraw: virtual touch screen in the air using RF signals. Proc. Conf. on SIGCOMM 235–246 (ACM, 2014).
Wang, J. & Katabi, D. Dude, where’s my card?: RFID positioning that works with multipath and non-line of sight. Proc. Conf. on SIGCOMM 51–62 (ACM, 2013).
Yang, L. et al. Tagoram: real-time tracking of mobile RFID tags to high precision using cots devices. Proc. 20th Annual Intl. Conf. on Mobile Comput. 237–248 (ACM, 2014).
Ma, Y. & Kan, E. C. Accurate indoor ranging by broadband harmonic generation in passive NLTL backscatter tags. IEEE Trans. Microw. Theory Techn. 62, 1249–1261 (2014).
Stove, A. G. Linear FMCW radar techniques. IEE Proc. F 139, 343–350 (1992).
Yang, T., Cao, J. & Guo, Y. Placement selection of millimeter wave FMCW radar for indoor fall detection. IEEE MTT-S Int. Wireless Symp. 1–3 (IEEE, 2018).
Huang, N. E. Hilbert-Huang Transform and its Applications (World Scientific, Singapore, 2014).
Huang, N. E. et al. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis. Proc. R. Soc. A 459, 2317–2345 (2003).
Chang, N. F. et al. On-line empirical mode decomposition biomedical microprocessor for Hilbert Huang transform. Proc. Biomedical Ciruits and Systems Conf. (BioCAS). 420–423 (IEEE, 2011).
Hong, Y. & Bao, Y. FPGA implementation for real-time empirical mode decomposition. IEEE Trans. Instrum. Meas. 61, 3175–3184 (2012).
Currie, N. C. & Brown, C. E. Principles and Applications of Millimeter-wave Radar (Artech House, Norwood, 1987).
TI mmWave Sensors: The world’s most precise millimeter wave sensor available today on a single chip; http://www.ti.com/sensors/mmwave/overview.html.
IMPINJ RAIN RFID Connectivity Devices; https://www.impinj.com/platform/connectivity/.
Mayordomo, I. et al. Design and implementation of a long-range RFID reader for passive transponders. IEEE Trans. Microw. Theory Techn. 57, 1283–1290 (2009).
Fletcher, R., Marti, U. P. & Redemske, R. Study of UHF RFID signal propagation through complex media. Proc. Anten. Propag. Soc. Int. Symp. 747–750 (IEEE, 2005).
Capdevila, S. et al. Water infiltration detection in civil engineering structures using RFID. Proc. 2016 6th Eur. Conf. on Antenna and Propagation (EUCAP) 2505–2509 (IEEE, 2012).
Benelli, G. et al. An RFID-based toolbox for the study of under-and outside-water movement of pebbles on coarse-grained beaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 5, 1474–1482 (2012).
Ma, Y., Hui, X. & Kan, E. C. 3D real-time indoor localization via broadband nonlinear backscatter in passive devices with centimeter precision. Proc. 22nd Ann. Int. Conf. on Mobile Comput. Network. 216–229 (ACM, 2016).
EPC radio-frequency identity protocols generation-2 UHF RFID; http://www.gs1.org/.
Bolic, M., Simplot-Ryl, D. & Stojmenovic, I. RFID Systems: Research Trends and Challenges (John Wiley & Sons, Chichester, 2010).
Nan, T. et al. Acoustically actuated ultra-compact NEMS magnetoelectric antennas. Nat. Commun. 8, 296 (2017).
Hui, X. & Kan, E. C. Monitoring vital signs over multiplexed radio by near-field coherent sensing. Nat. Electron. 1, 74 (2018).
Ma, Y., Hui, X. & Kan, E. C. Harmonic-WISP: a passive broadband harmonic RFID platform. Proc. IEEE MTT-S Int. Microw. Symp. 1–4 (IEEE, 2016).
Hui, X., Ma, Y. & Kan, E. C. Code division multiple access in centimeter accuracy harmonic RFID locating system. IEEE J. Radio Freq. Identif. 1, 51–58 (2017).
Yu, F., Lyon, K. & Kan, E. C. A novel passive RFID transponder using harmonic generation of nonlinear transmission lines. IEEE Trans. Microw. Theory Techn. 58, 4121–4127 (2010).
Li, W., Bao, X., Li, Y. & Chen, L. Differential pulse-width pair BOTDA for high spatial resolution sensing. Opt. Exp. 16, 21616–21625 (2008).
Ma, Y., Rong, H. & Kan, E. C. Millimeter accuracy passive tag ranging via second harmonics RF backscattering against body movement interference. Proc. IEEE Glob. Com. 448–454 (IEEE, 2014).
Ma, Y. & Kan, E. C. Passive ranging by low-directivity antennas with quality estimate. Proc. IEEE MTT-S Int. Microw. Symp. 1–4 (IEEE, 2015).
Yeager, D. J., Sample, A. P. & Smith, J. R. in RFID Handbook: Applications, Technology, Security, and Privacy (eds Ahson, S. & Ilyas, M.) 261–278 (CRC Press, Boca Raton, 2008).
Rasilainen, K. et al. On design and evaluation of harmonic transponders. IEEE Trans. Antennas Propag. 63, 15–23 (2015).
Prete, M. D. et al. Exploitation of multi-sine intermodulation for passive backscattering UWB localization. Proc. IEEE MTT-S Int. Microw. Symp. 262–265 (IEEE, 2018).
Andia Vera, G. et al. Exploitation of harmonic signals generated by the UHF RFID chips: new promises for the radio frequency identification technology. Proc. 2017 XXXIInd General Assembly Sci. Symp. of the International Union of Radio Science 1–4 (IEEE, 2017).
Ken, T., Hanssmon, H. & Wellings, A. J. Analysing real-time communications: controller area network (CAN). Proc. Real-Time Syst. Symp. 259–263 (IEEE, 1994).
Acknowledgements
This project is supported by Department of Energy (DoE) of the United States under the Advanced Research Projects Agency – Energy (ARPA-E) project numbers: DE-AR0000528 and DE-AR0000946. The authors thank G. C. McLaskey and A. Lal for discussions.
Author information
Authors and Affiliations
Contributions
X.H. and E.C.K. perceived the fundamental concepts and brainstormed the design of experiments together. X.H. conducted all the experiments, data processing and manuscript preparation. E.C.K. supervised the project direction and helped with revisions of design and writing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figures 1–10
Supplementary Video 1
Real-time experiment with 25 μm step size in water.
Supplementary Video 2
Real-time experiment with 5 cm round trip in water.
Rights and permissions
About this article
Cite this article
Hui, X., Kan, E.C. Radio ranging with ultrahigh resolution using a harmonic radio-frequency identification system. Nat Electron 2, 125–131 (2019). https://doi.org/10.1038/s41928-019-0219-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41928-019-0219-0
This article is cited by
-
Wide-range soft anisotropic thermistor with a direct wireless radio frequency interface
Nature Communications (2024)
-
Passive frequency comb generation at radiofrequency for ranging applications
Nature Communications (2024)
-
Quantum enhanced radio detection and ranging with solid spins
Nature Communications (2023)