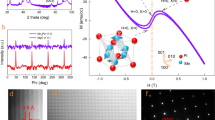
Abstract
The anomalous Hall effect is allowed by symmetry in some non-collinear antiferromagnets and is associated with Bloch-band topological features. This topological anomalous Hall effect is of interest in the development of low-power electronic devices, but such devices are likely to demand electrical control over the effect. Here we report the observation of the anomalous Hall effect in high-quality thin films of the cubic non-collinear antiferromagnet Mn3Pt epitaxially grown on ferroelectric BaTiO3 substrates. We demonstrate that epitaxial strain can alter the anomalous Hall conductivity of the Mn3Pt films by more than an order of magnitude. Furthermore, we show that the anomalous Hall effect can be turned on and off by applying a small electric field to the BaTiO3 substrate when the heterostructure is at a temperature of around 360 K and the Mn3Pt is close to the phase transition between a low-temperature non-collinear antiferromagnetic state and a high-temperature collinear antiferromagnetic state. The switching effect is due to piezoelectric strain transferred from the BaTiO3 substrate to the Mn3Pt film by interfacial strain mediation.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Hall, E. H. On a new action of the magnet on electric currents. Am. J. Math. 2, 287–292 (1879).
Hall, E. H. On the ‘rotational coefficient’ in nickel and cobalt. Philos. Mag. 12, 157–172 (1881).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Karplus, P. & Luttinger, J. M. Hall effect in ferromagnetics. Phys. Rev. 95, 1154–1160 (1954).
Berry, M. V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 392, 45–57 (1984).
Jungwirth, T., Niu, Q. & MacDonald, A. H. Anomalous Hall effect in ferromagnetic semiconductors. Phys. Rev. Lett. 88, 207208 (2002).
Onoda, M. & Nagaosa, N. Topological nature of anomalous Hall effect in ferromagnets. J. Phys. Soc. Jpn 71, 19–22 (2002).
Fang, Z. et al. The anomalous Hall effect and magnetic monopoles in momentum space. Science 302, 92–95 (2003).
Chen, H., Niu, Q. & MacDonald, A. H. Anomalous Hall effect arising from noncollinear antiferromagnetism. Phys. Rev. Lett. 112, 017205 (2014).
Kübler, J. & Felser, C. Non-collinear antiferromagnetism and the anomalous Hall effect. Europhys. Lett. 108, 67001 (2014).
Nakatsuji, S., Kiyohara, N. & Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 527, 212–215 (2015).
Kiyohara, N., Tomita, T. & Nakatsuji, S. Giant anomalous Hall effect in the chiral antiferromagnet Mn3Ge. Phys. Rev. Appl. 5, 064009 (2016).
Nayak, A. K. et al. Large anomalous Hall effect driven by a nonvanishing Berry curvature in the noncollinear antiferromagnet Mn3Ge. Sci. Adv. 2, e1501870 (2016).
Suzuki, T. et al. Large anomalous Hall effect in a half-Heusler antiferromagnet. Nat. Phys. 12, 1119–1123 (2016).
Jungwirth, T., Marti, X., Wadley, P. & Wunderlich, J. Antiferromagnetic spintronics. Nat. Nanotech. 11, 231–241 (2016).
Ramesh, R. & Spaldin, N. A. Multiferroics: progress and prospects in thin films. Nat. Mater. 6, 21–29 (2007).
Matsukura, F., Tokura, Y. & Ohno, H. Control of magnetism by electric fields. Nat. Nanotech. 10, 209–220 (2015).
Krén, E., Kádár, G., Pál, L., Sólyom, J. & Szabó, P. Magnetic structures and magnetic transformations in ordered Mn3(Rh,Pt) alloys. Phys. Lett. 20, 331–332 (1966).
Krén, E., Kádár, G., Pál, L. & Szabó, P. Investigation of the first-order magnetic transformation in Mn3Pt. J. Appl. Phys. 38, 1265–1266 (1967).
Krén, E. et al. Magnetic structures and exchange interactions in the Mn-Pt system. Phys. Rev. 171, 574–585 (1968).
Cherifi, R. O. et al. Electric-field control of magnetic order above room temperature. Nat. Mater. 13, 345–351 (2014).
Liu, Z. Q. et al. Full electroresistance modulation in a mixed-phase metallic alloy. Phys. Rev. Lett. 116, 097203 (2016).
Song, C., Cui, B., Li, F., Zhou, X. J. & Pan, F. Recent progress in voltage control of magnetism: materials, mechanisms, and performance. Prog. Mater. Sci. 87, 33–82 (2017).
Yasui, H. et al. Pressure dependence of magnetic transition temperatures and lattice parameter in an antiferromagnetic ordered alloy Mn3Pt. J. Phys. Soc. Jpn 56, 4532–4539 (1987).
Gao, R. et al. Electric control of the Hall effect in Pt/Bi0.9La0.1FeO3 bilayers. Sci. Rep. 6, 20330 (2016).
Tomiyasu, K., Yasui, H. & Yamaguchi, Y. Observation of partial-disorder-type spin fluctuations in frustrated Mn3Pt. J. Phys. Soc. Jpn 81, 114724 (2012).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Mostofi, A. A. et al. An updated version ofwannier90: a tool for obtaining maximally-localized Wannier functions. Comput. Phys. Commun. 185, 2309 (2014).
Acknowledgements
Z.Q.L. acknowledges financial support from the National Natural Science Foundation of China (NSFC grant no. 51771009) and a startup grant from Beihang University. H.C. and A.H.M. are supported by SHINES, an Energy Frontier Research Center funded by the US Department of Energy, Office of Science, Basic Energy Sciences, under award #SC0012670, and Welch Foundation grant TBF1473. H.C. and A.H.M acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing high-performance computer resources for performing the electronic structure calculations. J.M.D.C. acknowledges support from Science Foundation Ireland contract no. 12/RC/2278. X.R.W. acknowledges supports from a Nanyang Assistant Professorship grant from Nanyang Technological University and Academic Research Fund Tier 1 (RG108/17S) from the Singapore Ministry of Education.
Author information
Authors and Affiliations
Contributions
Z.Q.L. performed sample growth and electrical and magnetic measurements, with assistance from J.M.W., J.H.L., K.W., Z.X.F., H.Y., X.R.W. and C.B.J. Structural measurements were performed by Z.Q.L. and K.W. Theoretical calculations were performed by H.C. and A.H.M. All authors contributed to the discussion of results. Z.Q.L., H.C., J.M.D.C and A.H.M wrote the manuscript. Z.Q.L. led the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figure 1 and Supplementary Note 1
Rights and permissions
About this article
Cite this article
Liu, Z.Q., Chen, H., Wang, J.M. et al. Electrical switching of the topological anomalous Hall effect in a non-collinear antiferromagnet above room temperature. Nat Electron 1, 172–177 (2018). https://doi.org/10.1038/s41928-018-0040-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41928-018-0040-1
This article is cited by
-
Discrete degeneracies distinguished by the anomalous Hall effect in a metallic kagome ice compound
Nature Physics (2024)
-
Universal scaling law for chiral antiferromagnetism
Nature Communications (2024)
-
Chiral mesostructured hematite with temperature-independent magnetism due to spin confinement
Nano Research (2024)
-
Room-temperature magnetoresistance in an all-antiferromagnetic tunnel junction
Nature (2023)
-
Octupole-driven magnetoresistance in an antiferromagnetic tunnel junction
Nature (2023)