Abstract
Increasing the speed limits of conventional electronics requires innovative approaches to manipulate other quantum properties of electrons besides their charge. An alternative approach utilizes the valley degree of freedom in low-dimensional semiconductors. Here we demonstrate that the valley degeneracy of exciton energies in transition metal dichalcogenide monolayers may be lifted by coherent optical interactions on timescales corresponding to few tens of femtoseconds. The optical Stark and Bloch-Siegert effects generated by strong nonresonant circularly-polarized light induce valley-selective blue shifts of exciton quantum levels by more than 30 meV. We show these phenomena by studying the two most intensive exciton resonances in transiton metal dichalcogenide monolayers and compare the results to a theoretical model, which properly includes the Coulomb interaction and exciton dispersion. These results open the door for ultrafast valleytronics working at multiterahertz frequencies.
Similar content being viewed by others
Introduction
Valleytronics aims at information processing and storage by utilizing the valley degree of freedom of electrons instead of their charge. This new quantum number is associated with the inequivalent groups of energy degenerate valleys of the conduction or valence bands, which are occupied by an electron or a hole. Principles allowing to generate, control and read imbalanced valley populations of charge carriers have been demonstrated and studied in several dielectric and semiconductor materials such as diamond1,2, silicon3, or AlAs4, in semimetallic bismuth5 and in two-dimensional materials including graphene6 and transition metal dichalcogenides monolayers (TMDs)7,8.
Among the other materials, two-dimensional TMDs have exceptional properties, which make them attractive for valleytronic applications. Two typical examples of TMDs are WSe2 and MoS2. These materials belong to the direct band gap 2D semiconductors with band gap minima in the K± points (valleys) of the Brillouin zone9,10,11. Due to the spatial and time-reversal symmetries of the electronic wave functions in the K+ and K− points determined by the symmetry point group of the crystal D3h, these materials exhibit valley-dependent optical selection rules. Resonant light with right- (σ+) or left-handed (σ−) circular polarization induces optical transitions only in K+ or K− valley, respectively. The optically allowed transitions lead to the generation of so-called intravalley bright excitons, the electron–hole pairs tightly bound by the Coulomb interaction that strongly interact with photons.
The exciton states in opposite valleys have the same energies, i.e., they are doubly degenerate by valley. They form a basis for a two-level system and superpositions of these states belong to the valley pseudospin space12,13,14. The controllable probing and manipulation of such states are necessary prerequisites for valleytronic devices7,8,15,16. One of the crucial elements of the pseudospin operations is the control of the energies of the two-level system, i.e., the energies of the exciton states in each valley.
Lifting the energy degeneracy of the excitons in K+ and K− valleys may be reached by Zeeman-type splitting in static magnetic field17,18,19,20 or by DC Stark effect due to electric field21 applied perpendicularly to the sample plane. However, these two effects are not practical for several reasons: (i) the fields required to observe significant shifts are extremely high, e.g., magnetic field of 10 T generates Zeeman splitting of the exciton states of only 2 meV, (ii) the application of static fields allows neither ultrafast operation nor high spatial resolution, (iii) the experiments are typically limited to low-temperatures due to the small splitting.
An alternative approach, which simultaneously solves all the aforementioned problems, is to use the strong coupling of the excitons to light fields and to lift the energy degeneracy of the exciton states by coherent optical phenomena. The corresponding coupling is different in the K+ and K− points (valleys) of the monolayer for the light fields of a fixed circular polarization due to optical selection rules in TMDs. Such a difference can be observed in the change of the optical response of the TMD monolayer irradiated with off-resonant circularly polarized light. Namely, the off-resonant σ± circularly-polarized light applied to TMDs generates large optical Stark (OS) and weaker Bloch-Siegert (BS) shifts in K± and \(\rm{K}^{\rm{mp}}\) valleys of the monolayer, respectively22,23,24.
Since the OS and BS shifts appear in different corners of the Brillouin zone of the TMD monolayer, they can be independently detected using the resonant probe pulse of fixed circular polarization. Let us consider for example the case of the off-resonant pump pulse of \({\sigma }_{{{{\rm{pump}}}}}^{+}\) polarization. It induces the OS shift in the K+ valley and the BS shift in the K− valley. Therefore, to probe the OS and BS shifts in the monolayer one needs to apply the resonant \({\sigma }_{{{{\rm{probe}}}}}^{+}\) and \({\sigma }_{{{{\rm{probe}}}}}^{-}\) probe pulses, respectively. In other words, one can measure the OS and BS shifts in the \({\sigma }_{{{{\rm{pump}}}}}^{+}/{\sigma }_{{{{\rm{probe}}}}}^{+}\) and \({\sigma }_{{{{\rm{pump}}}}}^{+}/{\sigma }_{{{{\rm{probe}}}}}^{-}\) geometries of the experiment.
The OS and BS shifts can be described qualitatively in the framework of a two-level system driven by light with photon energy ℏωpump detuned from the energy of the transition E0. In the case of small detuning E0 − ℏωpump ≪ E0 the OS shift dominates25,26. The magnitude of the shift of the resonance energy can be expressed as \(\Delta {E}_{{{{\rm{OS}}}}}\propto {{{{\mathcal{E}}}}}_{{{{\rm{pump}}}}}^{2}/({E}_{0}-\hslash {\omega }_{{{{\rm{pump}}}}})\), where \({{{{\mathcal{E}}}}}_{{{{\rm{pump}}}}}\) is the amplitude of the electric field of the pump pulse. When the pump photon energy is small, E0 − ℏωpump ~ E0, then the contribution to the energy shift due to the Bloch-Siegert effect27\(\Delta {E}_{{{{\rm{BS}}}}}\propto {{{{\mathcal{E}}}}}_{{{{\rm{pump}}}}}^{2}/({E}_{0}+\hslash {\omega }_{{{{\rm{pump}}}}})\) becomes similar to the OS. However, the simple two-level model, which was applied for the description of coherent optical phenomena in TMDs in the past22,23,24, completely neglects the effects of the Coulomb interaction, which bring significant corrections to the OS and BS effects28. Moreover, these coherent phenomena were observed so far i) only for the lowest resonance in system (1sA-exciton line); ii) in a limited number of materials22,23,24,29; and iii) at large time scales (several hundreds of femtoseconds), where the coherent nature of observed OS and BS shifts becomes disputable.
In this study we report on an ultrafast valley-selective control of the blue spectral shifts of 1sA as well as 1sB exciton resonances in WSe2 and MoS2 monolayers via the interaction with off-resonant circularly-polarized laser pulses with sub-50 femtosecond durations. Furthermore, we present a theoretical approach for the description of the observed effects, which is based on the semiconductor Bloch equations (SBE) and goes beyond the simple two-level approximation used in the previous works22,23,24,30. This description takes into account i) the excitonic (many-body) nature of the observed shifts, and ii) the Rytova-Keldysh potential, i.e., the Coulomb potential in TMD monolayers, modified due to inhomogeneity of the system31,32,33.
Results and discussion
Characterization of MoS2 and WSe2 monolayers
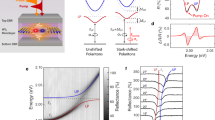
The studied TMDs are fabricated by exfoliation from bulk crystals. The monolayers are transferred to a Si/SiO2 substrate and are covered by multilayer of hBN to preserve their optical properties in ambient air. In our experiments we measure the spectrum of transient change of reflectivity of monolayers WSe2 and MoS2 as a function of the time delay between a femtosecond infrared pump pulse (central photon energy 0.62 eV, FWHM pulse duration of τpump = 38 fs) and a broadband supercontinuum probe pulse (photon energy 1.3–2.25 V), see Supplementary Note 1 for the details. The layout of the experimental setup is shown in Fig. 1a (detailed scheme can be found in Supplementary Fig. 1). During the experiments, the samples are imaged in situ using an optical microscope setup to ensure the spatial overlap of the pump and probe pulses and their position at the monolayer (each sample is about 20–30 μm in size, see Fig. 1b and c). The polarization state of both pump and probe beams is controlled using broadband quarter-wave plates, which generate circular polarizations. The experiments are carried out at room temperature with laser repetition rate of 50 kHz.
a Layout of the experimental setup used for transient reflection spectroscopy of TMDs. The monolayer is pumped with an infrared circularly polarized pump pulse and probed by a broadband circularly polarized pulse, whose spectrum is measured. b, c Optical microscope images of the studied samples of TMDs. White polygons mark the monolayers. The size of the white scale bar is 10 μm. Differential reflectivity spectra of WSe2 (d) and MoS2 (e) monolayers. f Sketch of the monolayer reflectivities without (R0(ℏω)) and with the pump pulse at zero delay time δt = 0 between the pump and probe pulses R(ℏω, δt = 0). The distance ΔE between the two extrema of the reflectivities manifests the shift of exciton energy due to pump pulse. g Sketch of the transient reflectance contrast [R(ℏω, δt = 0) − R0(ℏω)]/R0(ℏω). Its peak-and-dip shape explains the experimental data presented in Figs. 2c and 3c.
Because the samples are prepared on an absorptive substrate, an increase of absorption in the monolayer corresponds to a decrease of reflectivity of the sample34. This was verified both by measuring the differential reflectivity [R0(ℏω) − Rsub(ℏω)]/Rsub(ℏω) of the monolayers, where R0(ℏω) (Rsub(ℏω)) is the reflectivity of the sample (substrate), and by using finite-difference time-domain method simulations (for details see ref. 28). The energies of the 1sA and 1sB exciton transitions obtained from our differential reflectivity measurements in the WSe2 monolayer (Fig. 1d) are \({E}_{{{{\rm{1sA}}}}}^{{{{{\rm{WSe}}}}}_{{{{\rm{2}}}}}}=1.639\,{{{\rm{eV}}}}\) and \({E}_{{{{\rm{1sB}}}}}^{{{{{\rm{WSe}}}}}_{{{{\rm{2}}}}}}=2.083\,{{{\rm{eV}}}}\). In the MoS2 monolayer (Fig. 1e), the excitonic transitions are shifted to \({E}_{{{{\rm{1sA}}}}}^{{{{{\rm{MoS}}}}}_{{{{\rm{2}}}}}}=1.886\,{{{\rm{eV}}}}\) and \({E}_{{{{\rm{1sB}}}}}^{{{{{\rm{MoS}}}}}_{{{{\rm{2}}}}}}=2.032\,{{{\rm{eV}}}}\). These values are in a good agreement with the previously measured values35 and with the theoretical calculations of the spin-orbit splitting energy11.
Optical Stark and Bloch-Siegert shifts
When the sample is illuminated by the non-resonant pump pulse, the excitonic transitions move to higher energies leading to a blue shift ΔE of the resonances in the reflectivity spectra. The information about this shift is encoded in the reflectivity of the sample R(ℏω, δt) measured after time δt of the pulse application (see Fig. 1f). We consider the difference ΔR(ℏω, δt) = R(ℏω, δt) − R0(ℏω) to eliminate the contribution of the optical response of the Si/SiO2 substrate. Hence, ΔR(ℏω, δt) contains only the contribution from the excitons in the monolayer. In the following we consider the experimentally measurable ratio ΔR(ℏω, δt = 0)/R0(ℏω), sketched in Fig. 1g.
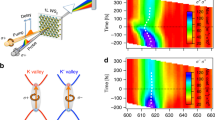
In Figs. 2a and 3a, we show the delay time dependence of the transient reflectivity spectra ΔR(ℏω, δt)/R0(ℏω) in monolayers WSe2 and MoS2. In Figs. 2b and 3b the temporal profile of the signal at the energy of 1sA exciton ℏω = E1sA is presented for WSe2 and MoS2, respectively. In both materials we identify two features corresponding to the shifts of 1sA and 1sB excitons. The spectra at the zero time delay are plotted in Figs. 2c and 3c for different combinations of circular polarization handedness of the pump and probe pulses, namely for \({\sigma }_{{{{\rm{pump}}}}}^{+}/{\sigma }_{{{{\rm{probe}}}}}^{+}\) and \({\sigma }_{{{{\rm{pump}}}}}^{+}/{\sigma }_{{{{\rm{probe}}}}}^{-}\). The measurements with opposite combinations of the polarizations, i.e., \({\sigma }_{{{{\rm{pump}}}}}^{-}/{\sigma }_{{{{\rm{probe}}}}}^{-}\) and \({\sigma }_{{{{\rm{pump}}}}}^{-}/{\sigma }_{{{{\rm{probe}}}}}^{+}\), provide the same shifts in accordance with the time-reversal symmetry of TMDs (see details in Supplementary Note 2 and Supplementary Fig. 2).
a Transient reflectivity spectra of WSe2 monolayer ΔR(ℏω, δt)/R0(ℏω) as a function of the time delay between pump (photon energy of 0.62 eV) and broadband probe pulses both of the same circular polarization handedness. b Profile of the signal in time-domain for the same (black curve) and opposite (red curve) circular polarization handedness of the pump and probe pulses. c Transient reflectivity spectrum at zero time delay for peak intensity of the pump pulse of 30 GW/cm2. d Maximum energy shift obtained from the measured spectra at zero time delay as a function of the peak intensity of the pump pulse for 1sA and 1sB excitonic resonances. Black/red dashed and dotted curves represent the linear fitting of the OS/BS shifts of 1sA and 1sB excitons, respectively.
a Transient reflectivity spectra of MoS2 monolayer ΔR(ℏω, δt)/R0(ℏω) as a function of the time delay between the pump (photon energy of 0.62 eV) and broadband probe pulses both of the same circular polarization handedness. b Profile of the signal in time-domain for the same (black curve) and opposite (red curve) circular polarization handedness of the pump and probe pulses. c Transient reflectivity spectrum at zero time delay for peak intensity of the pump pulse of 36 GW/cm2. d Maximum energy shifts obtained from the measured spectra at zero time delay as a function of the peak intensity of the pump pulse for 1sA and 1sB excitonic resonances. Black/red dashed and dotted curves represent the linear fitting of the OS/BS shifts of 1sA and 1sB excitons, respectively.
In Figs. 2d and 3d, we show the measured energy shifts of the exciton lines for the two combinations of circular polarization handedness of the pump and probe pulses as functions of the peak intensity of the pump pulse. In all cases, we observed that OS and BS shifts for 1sA and 1sB excitonic transitions scale linearly with the pump pulse intensity. Using the linear fitting procedure of the experimental data we obtained the ratios between the shifts caused by OS and BS effects. We summarized the obtained results in Table 1 and compared them to the theoretical values. The observed deviations of the experimental and theoretical results can be explained by an inaccuracy of the determination of the parameters of the monolayer used for the theoretical estimation as well as 2D crystal’s imperfections which reduce its valley-dependent optical response.
The maximum observed energy shift of 1sA exciton in both materials is about 30 meV, which is a much larger value compared to the previously published results. Such a large transient shift is reached due to high peak intensities of the pump pulse of 30–50 GW/cm2. Thanks to the short pump pulse duration (τpump = 38 fs), the transient signal is not accompanied by a long signal component corresponding to the real carrier population generated by nonlinear absorption of the pump pulse. The maximum relative transient change of the sample reflectivity of about 20% is promising for applications of this effect in valleytronic devices working on femtosecond time scales. Note that this reflectivity change is reached at room temperature and without an enhancement by an optical cavity, which could further increase the transient signal36.
Theoretical model
The theoretical description of the observed blue shifts of the exciton resonances is based on a perturbative solution of the SBE. Since the 1sA and 1sB exciton transitions couple the valence and conduction bands with the same spin, i.e., the fixed pair of the bands, we restrict our consideration to an effective two band model11. The interaction between σ± polarized light, characterized by electric field \({{{{\bf{E}}}}}_{\pm }={{{\mathcal{E}}}}(\cos (\omega t),\pm \sin (\omega t))\), with carriers in the K±(τ = ±) valleys of TMDs is defined by the Hamiltonian \({H}^{\tau }={H}_{0}^{\tau }+{H}_{{{{\rm{int}}}}}^{\tau }\). Here
is the two-band Hamiltonian with included Coulomb interaction. The first term defines a spectrum of electrons Ee,k = ℏ2k2/2me + Eg and holes Eh,k = ℏ2k2/2mh in TMDs, where k = ∥k∥ is an absolute value of the vector k. me, mh > 0 are the electron and hole effective masses, Eg is the bandgap in the system, \({\alpha }_{{{{\bf{k}}}}}^{\tau }\) and \({\beta }_{{{{\bf{k}}}}}^{\tau }\) are the annihilation operators for electrons and holes, with momentum k in τ valley. The remaining terms describe the Coulomb interaction in the system. Here Vq is the Fourier transform of the Rytova-Keldysh potential. The light-matter interaction term reads
where Pτ and \({d}_{{{{\rm{cv}}}}}^{\tau }\equiv \tau {d}_{{{{\rm{cv}}}}}\) are the polarization operator of the system and the transition dipole moment between the valence and conduction bands in τ = ± 1 valley respectively, and \({{{{\mathcal{E}}}}}_{\pm }^{\tau }(t)\equiv {{{\mathcal{E}}}}\exp (\mp i\tau \omega t)\). Note that \({H}_{{{{\rm{int}}}}}^{\tau }\) has a similar form as the light-matter interaction for a two-level system in the rotating-wave approximation. However, \({H}_{{{{\rm{int}}}}}^{\tau }\) is exact and its form originates from the specific structure of the interband transition dipole moments in the K± points of TMDs. To describe the energy shift of the exciton transitions we introduce the quantum average of polarization \({P}_{{{{\bf{k}}}}}^{\tau }(t)\equiv \langle {\beta }_{-{{{\bf{k}}}}}^{\tau }{\alpha }_{{{{\bf{k}}}}}^{\tau }\rangle\) and the electron and hole population \({n}_{{{{\bf{k}}}}}^{\tau }(t)\equiv \langle {\alpha }_{{{{\bf{k}}}}}^{\tau {\dagger} }{\alpha }_{{{{\bf{k}}}}}^{\tau }\rangle =\langle {\beta }_{-{{{\bf{k}}}}}^{\tau {\dagger} }{\beta }_{-{{{\bf{k}}}}}^{\tau }\rangle\). For the latter equality we omit the damping and collision terms in the monolayer (see details of this approximation in ref. 28). Then the SBE read
where we have introduced the parameter \(\hslash {e}_{k}^{\tau }(t)={E}_{{{{\rm{g}}}}}+{\hslash }^{2}{k}^{2}/2m-{\sum }_{{{{\bf{q}}}}}{V}_{{{{\bf{k}}}}-{{{\bf{q}}}}}{n}_{{{{\bf{q}}}}}^{\tau }\), with the exciton reduced mass m ≡ memh/(me + mh), and Rabi energy \(\hslash {\omega }_{R,{{{\bf{k}}}}}^{\tau }(t)={d}_{{{{\rm{cv}}}}}^{\tau }{{{{\mathcal{E}}}}}_{\pm }^{\tau }(t)+{\sum }_{{{{\bf{q}}}}\ne {{{\bf{k}}}}}{V}_{{{{\bf{k}}}}-{{{\bf{q}}}}}{P}_{{{{\bf{q}}}}}^{\tau }\). We solve this set of equations for the electric field given by a superposition of the pump and probe fields (the algorithm of the derivation is discussed in the “Methods” section). The solution of the equations for this case contains a resonant term \(\delta {P}_{{{{\bf{k}}}}}^{\tau }\approx 1/({E}_{{{{\rm{ex}}}}}+\Delta {E}_{{{{\rm{ex}}}}}^{\tau }-\hslash {\omega }_{{{{\rm{probe}}}}})\) near the 1sA(1sB) exciton energy Eex=A(B), which identifies the energy shift of the 1sA (1sB) exciton resonance,
Here \(\Delta {E}_{{{{\rm{ex}}}}}^{\pm }\) correspond to the OS and BS shifts in the K± points, respectively. The first term in the multiplier \({C}_{{{{\rm{ex}}}}}^{\pm }={\rho }_{1s}+2{\eta }_{1s}/({E}_{{{{\rm{ex}}}}}\mp \hslash {\omega }_{{{{\rm{pump}}}}})\) of Eq. (5) corresponds to the exciton-pump-field interaction, while the second term provides a correction due to exciton–exciton interaction in the system37. To evaluate ρ1s and η1s we use the hydrogen-like 1s wavefunction, which is a remarkably good approximation for the ground-state excitons38. In this case ρ1s = 16/7, while the exciton-exciton correction is material dependent and reaches ~ 10−20% of ρ1s for the studied monolayers. Hence, our predicted energy shift is ~2–3 times larger than the two-level approximation result24. It demonstrates the importance of the Coulomb interaction and many-body effects in the evaluation of the OS and BS shifts.
Note the following properties of \({C}_{{{{\rm{ex}}}}}^{\pm }\) coefficients. First, \({C}_{{{{\rm{ex}}}}}^{+}\, > \,{C}_{{{{\rm{ex}}}}}^{-}\), for the same (ex = A or B) exciton transitions. Second, \({C}_{{{{\rm{A}}}}}^{\pm }\, > \,{C}_{{{{\rm{B}}}}}^{\pm }\) for the studied WSe2 and MoS2 monolayers. And finally, ∥dcv(A)∥ for 1sA exciton transition is always larger than ∥dcv(B)∥ for the 1sB exciton transitions in the same material (see ref. 28 for details). Based on these observations and Eq. (5) we conclude that i) the OS shift is always larger than the BS shift in the same material for the same optical transition \(\Delta {E}_{{{{\rm{ex}}}}}^{+}\, > \,\Delta {E}_{{{{\rm{ex}}}}}^{-}\), and ii) the absolute value of the OS (BS) shift for 1sA excitons is larger than for 1sB excitons in the studied materials \(\Delta {E}_{{{{\rm{A}}}}}^{\pm }\, > \,\Delta {E}_{{{{\rm{B}}}}}^{\pm }\). These theoretical conclusions are consistent with the experimental observations.
Using the presented theory we have numerically calculated the expected energy shifts for the parameters used in our experiments28. The results in form of coefficient \(\kappa \equiv \Delta {E}_{{{{\rm{ex}}}}}^{\pm }/{{{{\mathcal{E}}}}}_{{{{\rm{pump}}}}}^{2}\) are presented in Table 2. Almost all experimental results are close to the theoretical estimates. The observed deviations of both results, in particular for 1sB excitons in WSe2, can be explained either by the peculiarities of 2D crystals used in the experiment or by an inaccuracy of the parameters of the monolayer used for the theoretical study. For example, the inaccuracy of transition dipole matrix element dcv ∝ v/Eg (see ref. 28 for details) come from the inaccuracy of the numerical estimation of the Fermi velocity v and the band energy Eg11,39,40,41 for WSe2 monolayer. Since \(\Delta {E}_{{{{\rm{ex}}}}}^{\pm }\propto {\left\Vert {d}_{{{{\rm{cv}}}}}\right\Vert }^{2}\), the underestimation of dcv can lead to significant underestimation of the value of the shift \(\Delta {E}_{{{{\rm{ex}}}}}^{\pm }\).
The observed valley-specific energy shifts of excitonic resonances in 2D TMDs WSe2 and MoS2 allow to lift the valley degeneracy in these materials at extremely short time scales of several tens of femtoseconds. The observed maximum relative transient change of the reflectivity of the WSe2 monolayer at the 1sA exciton resonance reaches 20%. Together with the large circular dichroism of \({\xi }_{\max }=(\Delta {R}_{{\sigma }^{+}/{\sigma }^{+}}-\Delta {R}_{{\sigma }^{+}/{\sigma }^{-}})/\Delta {R}_{{\sigma }^{+}/{\sigma }^{+}}\approx 38 \%\) (\(\Delta {R}_{{\sigma }^{+}/{\sigma }^{+}}\) and \(\Delta {R}_{{\sigma }^{+}/{\sigma }^{-}}\) are reflectivity changes of the probe pulse for the co- and counter-rotating circularly polarized pump and probe fields) and the nonresonant ultrafast operation without a significant population of real excitons, this effect is promising for ultrafast valleytronic applications. Furthermore, by applying circularly polarized pump pulses with low photon energy and high intensity, strong-field nonlinear coherent phenomena may lead to generation of valley-polarized currents observable in transport42,43 or optical44 measurements.
Methods
Sample preparation and characterization
The samples are prepared by gel-film assisted mechanical exfoliation from bulk crystals. The monolayers are then transferred to a Si substrate with 90 nm thick layer of SiO2 at the surface. Samples are covered by multilayer of hBN to protect them from degradation at ambient atmosphere. The samples were characterized by differential reflectivity measurements by measuring the spectrum of the probe pulse reflected from the sample and the spectrum reflected from the bare substrate (differential reflectivity spectra are shown in Fig. 1d, e) by shifting the sample in the direction perpendicular to the probe beam.
The samples used in our experiments consist of a monolayer, which is placed on the Si/SiO2 substrate (90 nm thick layer of SiO2) and covered from top by a thin layer of hBN, which is also prepared by exfoliation. The presence of the SiO2 layer on the substrate decreases the peak intensity of the pump pulse in the monolayer due to destructive interference. To determine the electric field amplitude of the pump pulse in the monolayer we perform 1D finite-difference time domain (FDTD) simulations of light propagation in this multilayer structure using commercial software Lumerical FDTD. To describe the structure with sufficient spatial resolution we use spatial step of 0.25 nm in the simulation. The monolayer is considered as 1 nm thick layer of material with the real and imaginary parts of the dielectric function ε1 = 12.3 and ε2 = 0.2 in case of WSe245 and ε1 = 8.5 and ε2 = 0 for MoS246. The hBN layer is simulated as 10 nm thick layer of bulk hBN with dielectric constant ε1 = 4.3 (extrapolated for the wavelength of 2 μm from47. The silicon substrate and the SiO2 layer are simulated with real dielectric constants of ε1 = 11.89 and ε1 = 2.07, respectively (imaginary parts of both are zero in this wavelength region). In the simulation we propagate a short pulse with center wavelength of 2 μm from air through the multilayer and evaluate the square of absolute value of the frequency domain field amplitude at the central frequency inside the monolayer \({\left\Vert {E}_{{{{\rm{mono}}}}}\right\Vert }^{2}\). The resulting \({\left\Vert {E}_{{{{\rm{mono}}}}}\right\Vert }^{2}=0.35{\left\Vert {E}_{0}\right\Vert }^{2}\), where E0 is the amplitude of the incident pump pulse. We find that this value does practically not depend on the material of the monolayer and it is solely determined by the surrounding multilayered structure consisting of much thicker materials.
Pump and probe experiment
The pump and probe experiment is carried out in the reflection geometry with mid-infrared pump pulses (central photon energy of 0.62 eV, duration of τpump = 38 fs) and broadband supercontinuum pulses covering the visible and near-infrared spectral region of 1.3–2.25 eV. The pump pulses are generated in a setup based on a noncollinear optical parametric amplifier and subsequent difference-frequency generation pumped by Yb:KGW femtosecond laser (Pharos SP 6W, Light Conversion).
The output pulse parameters are the central wavelength of 1030 nm, the pulse duration of 170 fs, the pulse energy of 120 μJ and the pulse repetition rate of 50 kHz. The output is split to two beams for generation of pump and probe pulses. The mid-infrared pump pulse is generated in a noncolinear optical parametric amplifier (NOPA) seeded with femtosecond supercontinuum with subsequent difference frequency generation (DFG) between the amplified NOPA output and the fundamental pulse at 1030 nm. The seed supercontinuum is generated by focusing a fraction of fundamental laser output to 3 mm long yttrium aluminum garnet, which provides higher spectral power density of the generated supercontinuum in the required spectral range 620–750 nm and higher power stability than sapphire. Broadband part of the supercontinuum is subsequently amplified in the NOPA pumped by the second harmonic of the fundamental output at 515 nm. The NOPA is based on 2 mm thick BBO crystal cut under 23.4∘. The amplified beam is sent to a prism compressor (fused silica prisms with apex angles of 67∘) for dispersion compensation.
Subsequently, DFG of the NOPA output and the fundamental laser output is performed in a 1 mm thick BBO crystal cut under 23∘ using type-I phase matching. The generated pulses have pulse energy of 100 nJ, spectrum covering the range 1500–2500 nm and passively stabilized carrier-envelope phase. An additional OPA stage pumped with the fundamental laser output allows to increase the mid-infrared pulse energy to 2 μJ with only a small limitation of the spectral bandwidth. Visible and near-infrared light is filtered from the beam at the output of the setup using interference long-pass filter with transmission window of 1350–5000 nm. In the experiments, the pump pulses with the FWHM duration of 38 fs are used. The details of this laser source can be found in ref. 48.
The broadband supercontinuum probe pulse is generated by focusing the fundamental laser output in a 2 mm thick sapphire crystal. The supercontinuum is then partially compressed by 8 bounces at a pair of chirped mirrors DCM-9 (Venteon). The time delay between the pulses is controlled using optical delay line. The arrival time of each spectral component of the broadband probe pulse with respect to the compressed pump pulse is measured using nonresonant nonlinearity in a thin glass. Time delays of different spectral components are then shifted accordingly in the presented transient reflectivity data. The probe spectrum is detected using grating spectrograph (Shamrock 163, Andor) and cryo-cooled CCD camera (iDus 420, Andor).
To increase the signal/noise ratio, the probe beam is split to two replicas. One of them propagates through the excited region on the sample, while the second replica serves as reference spectrum. By dividing the two spectra we significantly suppress the noise of the supercontinuum probe. The circular polarizations of pump and probe pulses are generated and controlled by two independent broadband quarter-wave plates. The pump and probe pulses are intersected on the sample under an angle of about 10∘. An optical microscope setup is used to ensure the optimal focusing of the probe beam at the monolayers and to align the spatial overlap of the pump and probe beams.
Theoretical background
We solve the system of Eqs. (3) and (4) for the case of the superposition of σ+-polarized pump and σ±-polarized probe pulses for each valley τ = ± 1 separately. To this end we make a substitution \({{{{\mathcal{E}}}}}_{\pm }^{\tau }(t)\to {{{{\mathcal{E}}}}}_{{{{\rm{pump}}}}}{e}^{-i\tau {\omega }_{{{{\rm{pump}}}}}t}+{{{{\mathcal{E}}}}}_{{{{\rm{probe}}}}}{e}^{\mp i\tau {\omega }_{{{{\rm{probe}}}}}t}\) in the expression for ωR,k of the corresponding equations. Here ωpump and ωprobe are the frequencies of the pump and probe pulses, respectively. Since the electric field of the probe pulse \({{{{\mathcal{E}}}}}_{{{{\rm{probe}}}}}\) is much smaller than the electric field of the pump pulse \({{{{\mathcal{E}}}}}_{{{{\rm{pump}}}}}\) the polarization \(\delta {P}_{{{{\bf{k}}}}}^{\tau }\) generated by the probe field is much smaller than the polarization \({P}_{{{{\bf{k}}}}}^{\tau }\) induced by the pump field, \(\parallel \delta {P}_{{{{\bf{k}}}}}^{\tau }\parallel \ll \parallel {P}_{{{{\bf{k}}}}}^{\tau }\parallel\). The same arguments provide the relations between the occupation numbers of the quasiparticles \(\delta {n}_{{{{\bf{k}}}}}^{\tau }\) and \({n}_{{{{\bf{k}}}}}^{\tau }\) induced by the probe and pump pulses, i.e., \(\parallel \delta {n}_{{{{\bf{k}}}}}^{\tau }\parallel \ll \parallel {n}_{{{{\bf{k}}}}}^{\tau }\parallel\). It allows us to solve the system of differential equations perturbatively using the terms \(\delta {P}_{{{{\bf{k}}}}}^{\tau }\) and \(\delta {n}_{{{{\bf{k}}}}}^{\tau }\) as small parameters.
Substituting \({P}_{{{{\bf{k}}}}}^{\tau }+\delta {P}_{{{{\bf{k}}}}}^{\tau }\) and \({n}_{{{{\bf{k}}}}}^{\tau }+\delta {n}_{{{{\bf{k}}}}}^{\tau }\) into Eq. (3), then applying the relation \(\delta {n}_{{{{\bf{k}}}}}^{\tau }=[{P}_{{{{\bf{k}}}}}^{\tau }{\left(\delta {P}_{{{{\bf{k}}}}}^{\tau }\right)}^{* }+{\left({P}_{{{{\bf{k}}}}}^{\tau }\right)}^{* }\delta {P}_{{{{\bf{k}}}}}^{\tau }]/(1-2{n}_{{{{\bf{k}}}}}^{\tau })\) (see ref. 28 for details) we obtain an equation for \(\delta {P}_{{{{\bf{k}}}}}^{\tau }\) in the presence of \({P}_{{{{\bf{k}}}}}^{\tau }\). After the linearization of this equation and introducing the new variables \({P}_{{{{\bf{k}}}}}^{\tau }={p}_{{{{\bf{k}}}}}^{\tau }{e}^{-i\tau {\omega }_{{{{\rm{pump}}}}}t}\), \(\delta {P}_{{{{\bf{k}}}}}^{\tau }=({a}_{{{{\bf{k}}}}}^{\tau }{e}^{i\tau {\Delta }_{\pm }t}+{b}_{{{{\bf{k}}}}}^{\tau }{e}^{-i\tau {\Delta }_{\pm }t}){e}^{-i\tau {\omega }_{{{{\rm{pump}}}}}t}\), with Δ± = ωpump ∓ ωprobe, one obtains the system of inhomogeneous equations for the parameters \({a}_{{{{\bf{k}}}}}^{\tau }\) and \({b}_{{{{\bf{k}}}}}^{\tau }\). Solving this system of equations, and returning back to the original notations we observe that \(\delta {P}_{{{{\bf{k}}}}}^{\tau }\) in energy domain has a resonance structure at the energies close to the 1s exciton energy Eex
Hence the parameter \({E}_{\rm{ex}}^{\tau }\) given by Eq. (5) defines the shift of the 1s exciton energy in the presence of the σ+-polarized pump pulse in τ = ± 1 valley.
The parameters ρ1s and η1s in \(\Delta {E}_{{{{\rm{ex}}}}}^{\pm }\) read
Here ψ1s(r) is the 1s excitonic wave-function, φ1s(k) = ∫d2r ψ1s(r)e−ikr is its Fourier transform, ε is the dielectric constant of the medium surrounding the TMD monolayer, and r0 is an in-plane screening parameter of the Rytova-Keldysh potential31,32,33
The technical details of calculation of the numerical values of the parameters ρ1s and η1s are presented in ref. 28 and for the hydrogen like excitonic wave-functions they lead to the results mentioned in the “Results and discussion” section.
Data avialability
The data that support the plots in this study are available from the corresponding author upon reasonable request.
Code avialability
The code used in the experimental data analysis is available from the corresponding author upon reasonable request.
References
Isberg, I. et al. Generation, transport and detection of valley-polarized electrons in diamond. Nat. Mater. 12, 760 - 764 (2013).
Suntornwipat, N. et al. A valleytronic diamond transistor: electrostatic control of valley currents and charge-state manipulation of NV centers. Nano Lett. 21, 868 - 874 (2021).
Takashina, K. et al. Valley polarization in Si(100) at zero magnetic field. Phys. Rev. Lett. 96, 236801 (2006).
Gunawan, O. et al. Valley susceptibility of an interacting two-dimensional electron system. Phys. Rev. Lett. 97, 186404 (2006).
Zhu, Z. et al. Field-induced polarization of Dirac valleys in bismuth. Nat. Phys. 8, 89 - 94 (2012).
Xiao, D., Yao, W. & Niu, Q. Valley-contrasting physics in graphene: magnetic moment and topological transport. Phys. Rev. Lett. 99, 236809 (2007).
Xiao, D. et al. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012).
Cao, T. et al. Valley-selective circular dichroism of monolayer molybdenum disulphide. Nat. Comm. 3, 887 (2012).
Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2. Nano Lett. 10, 1271 - 1275 (2010).
Mak, K. F. et al. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Kormányos, A. et al. k⋅p theory for two-dimensional transition metal dichalcogenide semiconductors. 2D Mater. 2, 22001 (2015).
Jones, A. M. et al. Optical generation of excitonic valley coherence in monolayer WSe2. Nat. Nanotechnol. 8, 634 - 638 (2013).
Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 10, 343 - 350 (2014).
Ye, Z., Sun, D. & Heinz, T. F. Optical manipulation of valley pseudospin. Nat. Phys. 13, 26–27 (2017).
Mak, K. F., He, K., Shan, J. & Heinz, T. F. Control of valley polarization in monolayer MoS2 by optical helicity. Nat. Nanotechnol. 7, 494 - 498 (2012).
Molas, M. R. et al. Probing and manipulating valley coherence of dark excitons in monolayer WSe2. Phys. Rev. Lett. 123, 096803 (2019).
Srivastava, A. et al. Valley Zeeman effect in elementary optical excitations of monolayer WSe2. Nat. Phys. 11, 141 - 147 (2015).
Aivazian, G. et al. Magnetic control of valley pseudospin in monolayer WSe2. Nat. Phys. 11, 148 - 152 (2015).
Wang, G. et al. Control of exciton valley coherence in transition metal dichalcogenide monolayers. Phys. Rev. Lett. 117, 187401 (2016).
Smoleński, T. et al. Tuning valley polarization in a WSe2 monolayer with a tiny magnetic field. Phys. Rev. X 6, 021024 (2016).
Kormányos, A., Zólyomi, V., Drummond, N. D. & Burkard, G. Spin-orbit coupling, quantum dots, and qubits in monolayer transition metal dichalcogenides. Phys. Rev. X 4, 011034 (2014).
Kim, J. et al. Ultrafast generation of pseudo-magnetic field for valley excitons in WSe2 monolayers. Science 346, 1205 - 1208 (2014).
Sie, E. J. et al. Valley-selective optical Stark effect in monolayer WS2. Nat. Mater. 14, 290 - 294 (2015).
Sie, E. J. et al. Large, valley-exclusive Bloch-Siegert shift in monolayer WS2. Science 355, 1066 - 1069 (2017).
Autler, S. H. & Townes, C. H. Stark effect in rapidly varying fields. Phys. Rev. 100, 703 - 722 (1955).
Delone, N. B. & Krainov, V. P. AC Stark shift of atomic energy levels. Physics-Uspekhi 42, 669 (1999).
Bloch, F. & Siegert, A. Magnetic resonance for nonrotating fields. Phys. Rev. 57, 522 (1940).
Slobodeniuk, A. O. et al. Semiconductor Bloch equation analysis of optical Stark and Bloch-Siegert shifts in monolayer WSe2 and MoS2. Phys. Rev. B. 106, 235304 (2022).
Cunningham, P. D. et al. Resonant optical Stark effect in monolayer WS2. Nat. Commun. 10, 5539 (2019).
LaMountain, T. et al. Valley-selective optical Stark effect probed by Kerr rotation. Phys. Rev. B 97, 045307 (2018).
Rytova, N. S. Screened potential of a point charge in a thin film. Moscow University Physics Bulletin 3, 30 https://arxiv.org/abs/1806.00976 (1967).
Keldysh, L. V. Coulomb interaction in thin semiconductor and semimetal films. JETP Lett. 29, 658 (1979).
Cudazzo, P., Tokatly, I. V. & Rubio, A. Dielectric screening in two-dimensional insulators: Implications for excitonic and impurity states in graphane. Phys. Rev. B 84, 085406 (2011).
McIntyre, J. D. E. & Aspnes, D. E. Differential reflection spectroscopy of very thin surface films. Surface Science 24, 417 (1971).
Niu, Y. et al. Thickness-dependent differential reflectance spectra of monolayer and few-layer MoS2, MoSe2, WS2 and WSe2. Nanomater. 8, 725 (2018).
LaMountain, T. Valley-selective optical Stark effect of exciton-polaritons in a monolayer semiconductor. Nat. Commun. 12, 4530 (2021).
Ell, C., Müller, J. F., Sayed, K. E. & Haug, H. Influence of many-body interactions on the excitonic optical Stark effect. Phys. Rev. Lett. 62, 304 (1989).
Molas, M. R. et al. Energy spectrum of two-dimensional excitons in a nonuniform dielectric medium. Phys. Rev. Lett. 123, 136801 (2019).
Fang, S., Carr, S., Cazalilla, M. A. & Kaxiras, E. Electronic structure theory of strained two-dimensional materials with hexagonal symmetry. Phys. Rev. B 98, 075106 (2018).
Kapuściński, P. et al. Rydberg series of dark excitons and the conduction band spin-orbit splitting in monolayer WSe2. Commun. Physics 4, 186 (2021).
Wang, G. et al. Colloquium: excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 90, 021001 (2018).
Kundu, A., Fertig, H. A. & Seradjeh, B. Floquet-engineered valleytronics in dirac systems. Phys. Rev. Lett. 116, 016802 (2016).
Jiménez-Galán, A., Silva, R. E. F., Smirnova, O. & Ivanov, M. Lightwave control of topological properties in 2D materials for sub-cycle and non-resonant valley manipulation. Nat. Photon. 14, 728 - 732 (2020).
Langer, F. et al. Lightwave valleytronics in a monolayer of tungsten diselenide. Nature 557, 76 - 80 (2018).
Ermolaev, G. A. et al. Spectroscopic ellipsometry of large area monolayer WS2 and WSe2 films. AIP Conf. Proc. 2359, 020005 (2021).
Islam, K. M. In-plane and out-of-plane optical properties of monolayer, few-layer, and thin-film MoS2 from 190 to 1700 nm and their application in photonic device design. Adv. Photonics Res. 2, 2000180 (2021).
Lee, S. Y., Jeong, T. Y., Jung, S. & Yee, K. J. Refractive index dispersion of hexagonal boron nitride in the visible and near-infrared. Phys. Status Solidi B 256, 1800417 (2018).
Kozák, M. et al. Generation of few-cycle laser pulses at 2 μm with passively stabilized carrier-envelope phase characterized by f-3f interferometry. Optics Laser Technol. 144, 107394 (2021).
Acknowledgements
We thank B. Velický for his comments to the manuscript. The authors would like to acknowledge the support by Czech Science Foundation (project GA23-06369S) and Charles University (UNCE/SCI/010, SVV-2020-260590, PRIMUS/19/SCI/05). M. Bartoš acknowledges the support by the ESF under the project CZ.02.2.69/0.0/0.0/20_079/0017436.
Author information
Authors and Affiliations
Contributions
M.B. prepared the samples. P.K. and M.K. carried out the reflectance contrast and transient reflectivity measurements, analyzed and interpreted the experimental data. A.O.S. and T.N. did the theoretical calculation and analysis for interpreting the experimental results. M.K., P.M., and T.N. initiated and supervised the work. M.K., T.N., and A.O.S. wrote the paper. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Slobodeniuk, A.O., Koutenský, P., Bartoš, M. et al. Ultrafast valley-selective coherent optical manipulation with excitons in WSe2 and MoS2 monolayers. npj 2D Mater Appl 7, 17 (2023). https://doi.org/10.1038/s41699-023-00385-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-023-00385-1