Abstract
Two-dimensional magnetic materials with strong magnetostriction are attractive systems for realizing strain-tuning of the magnetization in spintronic and nanomagnetic devices. This requires an understanding of the magneto-mechanical coupling in these materials. In this work, we suspend thin Cr2Ge2Te6 layers and their heterostructures, creating ferromagnetic nanomechanical membrane resonators. We probe their mechanical and magnetic properties as a function of temperature and strain by observing magneto-elastic signatures in the temperature-dependent resonance frequency near the Curie temperature, TC. We compensate for the negative thermal expansion coefficient of Cr2Ge2Te6 by fabricating heterostructures with thin layers of WSe2 and antiferromagnetic FePS3, which have positive thermal expansion coefficients. Thus we demonstrate the possibility of probing multiple magnetic phase transitions in a single heterostructure. Finally, we demonstrate a strain-induced enhancement of TC in a suspended Cr2Ge2Te6-based heterostructure by 2.5 ± 0.6 K by applying a strain of 0.026% via electrostatic force.
Similar content being viewed by others
The recent discovery of long range order in two-dimensional (2D) (anti)ferromagnets1,2,3 has triggered extensive studies of 2D materials to experimentally probe magnetism of reduced dimensionality4. One material of particular interest is Cr2Ge2Te6 (CGT)—a semiconducting ferromagnet with a bulk Curie temperature, TC, ~ 60–66 K2,5 with inter- and intra-layer ferromagnetic coupling for any number of layers2. Recent progress has been made in manipulating the magnetic order of CGT using electrostatic gating6,7, magnetic field2,8, pressure9,10, ion intercalation11, and via spin-orbit torque12,13. Mechanical strain offers another degree of freedom for such manipulation as bulk CGT was recently shown to exhibit strong spin-lattice coupling9,14 and a negative thermal expansion coefficient near TC5, which is common amongst bulk chromium-based magnetic van der Waals crystals, like CrI3, CrCl3, CrBr3 and Cr2Si2Te615,16,17,18. However, the coupling between magnetic order and strain in thin CGT has not been studied experimentally, as strain is a difficult parameter to control in substrate-supported ultrathin layers19,20.
Emerging nanomechanical methods allow for high-precision strain manipulation and control when 2D materials are suspended forming ultrathin membrane resonators21,22. Due to the combination of low mass, high strength23 and high frequency tunability21,24, these membranes find potential use in a wide range of sensor applications25 as well as in high-performance nanoelectromechanical systems, where these are used as probes for nonlinear dynamics and condensed matter effects in the materials they are made of26. The resonance frequency of these membranes can be tuned over a large range by strain21, which can be controlled both statically23 and dynamically21,22. Moreover, the difference between the thermal expansion coefficient of suspended 2D material layers and the substrate27,28 or other materials in a heterostructure29,30 provides additional routes for strain engineering, leading to either stretching or compressing ultrathin layers. Nanomechanical strain can also be used to probe magnetic states of membrane material27 and switch between these states30,31. The relation between strain, a material’s thermal expansion coefficient, and its magnetic properties result in the coupling between mechanical and magnetic degrees of freedom, which allows the investigation of magnetic phase transitions in 2D layered material membranes27,30.
Here, we demonstrate that the magnetic phase transition of suspended thin CGT membranes can be probed mechanically via the temperature-dependent resonance frequency. CGT is known to exhibit high magnetostriction, i.e., a strong magneto-elastic coupling between magnetic order and the lattice5,9,14, that deforms the crystal near TC5. Thus, to control the strain in thin CGT flakes and deterministically probe the transition temperature, we choose other 2D material layers, WSe2 and FePS3, with positive thermal expansion coefficient and integrate them to form heterostructure membranes with CGT29,32,33,34, which are important to compensate CGT’s negative thermal expansion5. We then use these heterostructure membranes to probe and analyze the effect of the mutual interaction between the different 2D materials and CGT, and study the effect of electrostatically induced strain on the ferromagnetic order near TC.
Results
Mechanical properties of CGT membranes
The force-deflection curve of suspended membranes contains information about mechanical properties of the material. Thus, we first study thin layers of CGT by a static deflection method23,35. We fabricate a freestanding membrane by suspending a mechanically exfoliated thin CGT flake over a circular hole (Fig. 1a). We then apply the atomic force microscopy (AFM) force nanoindentation method23,35 to indent the centre of the membrane with the tip of an AFM cantilever to cause a deflection of the membrane δ, as shown in Fig. 1b. The force applied to the centre of the membrane, F, is proportional to the stiffness kc of the cantilever used and its deflection, Δzc. Using cantilevers with calibrated stiffnesses, we record the force versus membrane deflection curves of this membrane, as depicted in Fig. 1c with filled blue circles. The observed trend can be described by the point-force deflection model for a circular membrane, assuming negligible tip radius compared to the membrane diameter23,35:
where E is the Young’s modulus of the membrane, r the membrane radius, h the membrane thickness, ν = 0.22 the Poisson ratio of CGT36, n0 the pre-tension, and q = 1/(1.05 − 0.15ν − 0.16ν2) is a dimensionless geometrical parameter. To our knowledge, the Young’s modulus of CGT has not been experimentally studied. We, therefore, extract its Young’s modulus ECGT from the experimental data using Eq. (1), as shown in Fig. 1c by the solid magenta line. To obtain a more reliable estimate of ECGT, we measure 18 different membranes of varying thicknesses (h = 9.5–30.1 nm) and radii (r = 1–2.5 μm). We find a mean value, ECGT = 56.2 ± 8.2 GPa, as shown in the inset of Fig. 1c. The obtained value of ECGT is consistent with the calculated37 2D Young’s modulus of CGT, E2D = 41.8 N m−1, which yields to E = E2D/h2D = 61.0 GPa, in which h2D is the single-layer thickness, taken as a third of that of the unit cell of CGT5: h2D = 2.056 nm/3 ≈ 0.685 nm. The standard deviation for our measurements is comparable to that reported in similar experiments on other 2D material membranes23,35. We also found no layer number dependence for the studied range of thicknesses38 (see Supplementary Note 1).
a An optical image of a 9.5 ± 0.3 nm thin CGT membrane with a radius r = 2 μm. Scale bar: 12 μm. b A schematic of the membrane deflection by a cantilever tip. Δzc is the cantilever deflection, g0 = 285 nm the separation between the membrane and the bottom Si substrate, d the membrane diameter, and δ the membrane deflection. c A force versus membrane deflection plot of the membrane shown in (a). Experimental data (filled blue circles) are fit by the point-force deflection of a circular membrane model of Eq. (1) (solid magenta line). The inset shows a histogram of the Young's moduli extracted from 18 CGT membranes of 9.5–30.1 nm thicknesses (see Supplementary Note 1), which were used to obtain the mean value of the Young's modulus E and corresponding standard deviation σ.
Resonating membranes
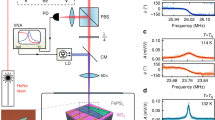
In order to study the coupling between the magnetic phase and the mechanical motion, we further investigate the dynamic nanomechanical properties of these membranes as a function of temperature. The temperature dependence of the mechanical resonances of the magnetic membranes is sensitive to changes in the magnetization of the 2D layers30 and the magnetic phase, via a mechanism that couples the specific heat to the membrane tension via the thermal expansion coefficient27. Thus, by observing changes in motion of the membrane at TC it is possible to probe the ferromagnetic to paramagnetic transition via the mechanical resonance frequency27. To do this, we use a laser interferometry technique27,39 (Fig. 2a and “Methods”). A CGT membrane (see the inset of Fig. 2b) is placed in the chamber of an optical cryostation. We use a power-modulated blue laser to opto-thermally excite a fundamental resonance mode of the membrane, and a red laser to measure the change in the reflected signal due to the subsequent displacement of the membrane.
a Schematic diagram of the laser interferometry setup. b Filled blue circles—measured amplitude of the fundamental resonance peak at T = 4 K. Solid magenta line—fit to a damped harmonic oscillator model. The inset shows an optical image of a 17.4 ± 0.3 nm thin CGT membrane of 2 μm radius. Scale bar: 8 μm. c The comparison of the measured resonance frequency f0 of the thin film shown in (b) (see also Supplementary Note 2) and the lattice constant of bulk CGT as a function of temperature. The filled and open blue circles represent the measured data during heating and cooling cycles respectively. The connected magenta circles represent the lattice constant a of bulk CGT as measured by Carteaux et al.5. The dashed black horizontal line represents a at T = 300 K. The insets show schematics of membrane stretching or buckling at tensile or compressive strain, on the right and left respectively. The pink region indicates the temperature range where compressive strain is dominant and is a guide to an eye.
We first measure the resonance peak of the fundamental membrane mode at T = 4 K (blue circles in Fig. 2b). We fit the experimental data to a damped harmonic oscillator model (solid magenta line in Fig. 2b) to determine the frequency of the fundamental membrane mode, f0. Subsequently, while recording f0(T) we heat the sample to T = 78 K, above the expected TC of 66 K2,5, and cool it down to T = 4 K. We plot the experimental data for the heating (filled blue circles) and the cooling (open blue circles) cycle in Fig. 2c. As the CGT membrane is cooled through the TC, its resonance frequency f0 reduces from 19.3 MHz at 78 K to 6.3 MHz at 4 K. To describe the f0(T) behaviour of CGT, we model the resonance frequency of a circular membrane as:
where f0(T0) is the resonance frequency at a reference temperature T0 (e.g., room temperature) due to the contribution of the pre-tension and the bending rigidity, ρ the mass density, \({n}_{{{{\rm{th}}}}}(T)=\frac{Eh}{(1-\nu )}{\epsilon }_{{{{\rm{th}}}}}\) the thermally accumulated tension, \({\epsilon }_{{{{\rm{th}}}}}=-\int\nolimits_{{T}_{0}}^{{T}_{{{{\rm{i}}}}}}\left({\alpha }_{{{{\rm{CGT}}}}}(T)-{\alpha }_{{{{\rm{Si}}}}}(T)\right)\,{{{\rm{d}}}}T\) the thermal strain at an arbitrary temperature Ti27,28, αSi(T) the literature values for thermal expansion coefficient of Si substrate40, and αCGT(T) the temperature-dependent thermal expansion coefficient of CGT. Thus, we attribute the observed f0(T) trend to a large change in the in-plane lattice constants of the unit cell and the resulting negative αCGT(T) near the phase transition, which was also previously reported for bulk CGT5. This anomalous lattice expansion, when cooling down from the paramagnetic to the ferromagnetic state, is related to the strong magnetostriction effect at the ferromagnetic ordering temperature TC in CGT5,14 that causes a substantial drop in strain ϵth(T) and a corresponding reduction of the membrane tension near TC.
In Fig. 2c we also plot the change of the in-plane lattice constant, a, of bulk CGT, experimentally obtained by Carteaux et al.5, as a function of temperature and compare it with the observed resonance frequency. The lattice constant a is shown to be smaller at room temperature (indicated by the black horizontal dashed line) in comparison to temperatures below the paramagnetic to ferromagnetic phase transition (~66 K). Since the lattice constant increases, the suspended part of the flake effectively has a larger volume at T < TC than at room temperature, indicating a switch from tensile to compressive strain, as indicated by the pink region in Fig. 2c. In this temperature range, the compressively strained suspended flake is likely to sag, wrinkle, or buckle, which possibly explains a different warming and cooling trend for the resonance frequency f0(T). Buckling of thicker magnetic CGT layers itself is interesting for the future development of reprogrammable mechanical memory devices at nano- and micro-scale41, utilizing the bi-stable states of a buckled thick flake42,43. However, in the case of thin membranes, due to the changing resonance mode shape in the compressive strain regime and the potential wrinkling, a comprehensive analysis of f0(T) using Eq. (2)27 is not reliable for T < TC and thus cannot be applied directly to resonators made of bare CGT.
Tensile strain in heterostructure membranes
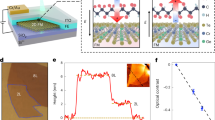
To prevent the compressive strain that can lead to wrinkling in CGT membranes, and controllably probe f0(T) near and below its phase transition temperature, we fabricate a suspended membrane heterostructure composed of CGT and WSe2 flakes, shown in Fig. 3. WSe2 is a material with well-known mechanical properties28,44,45 that does not undergo a phase transition from 4 to 300 K45. In the heterostructure, its positive thermal expansion coefficient \({\alpha }_{{{{\rm{WS{e}}}_{2}}}}(T)\) counteracts the negative αCGT(T) near TC of CGT, such that the total membrane stress remains tensile and f0 can be used to probe α(T) even below TC.
a Top panel: Schematic cross-section of the sample consisting of the suspended CGT/WSe2 heterostructure membrane and the reference WSe2 membrane of the same flake. Bottom panel: Optical image of the sample with specific membranes indicated. Scale bar: 16 μm. b Measured resonance frequencies f0 of the membranes in (a). Solid green line—the fitted model of the resonance frequency of the CGT/WSe2 heterostructure (Eq. (4)). Light green region—the allowed higher and lower boundary of the model due to the uncertainties in h1,2, E1,2 and \({f}_{0}^{2}({T}_{0})\). Insets: Schematic of a CGT/WSe2 structure with the collinear and random magnetic spin arrangement in a bilayer of CGT in the ferromagnetic (FM) and the paramagnetic (PM) phases respectively. c Dissipation factor Q−1 as a function temperature. The origin of a broad feature at ~20 K remains unclear and is a subject of future studies. d Filled blue circles—\(\, \frac{{{{\rm{d}}}}\left({f}_{0}^{2}\right)}{{{{\rm{d}}}}T}\) of the CGT/WSe2 heterostructure as a function of temperature. Connected magenta circles—the thermal expansion coefficient of bulk CGT5. The black vertical dashed lines in (b–d) indicate the measured \({T}_{{{{\rm{C}}}}}^{* }=58\pm 0.5\) K as determined from the peak position of \(\frac{{{{\rm{d}}}}\left({f}_{0}^{2}\right)}{{{{\rm{d}}}}T}\).
We measure f0(T) of the suspended CGT/WSe2 heterostructure together with a reference drum of the same WSe2 flake (Fig. 3b). The \({f}_{0,{{{\rm{WSe}}}}_{2}}(T)\) follows a monotonous increase trend with decreasing temperature (filled orange circles), as expected from its positive \({\alpha }_{{{{\rm{WS{e}}}_{2}}}}(T)\)28,45. In contrast, \({f}_{0,{{{\rm{CGT}}}}/{\rm{WSe}}_{2}}(T)\) has a downturn with decreasing temperature near the transition temperature (filled blue circles). This behaviour is distinct from the bare CGT resonator (Fig. 2c) due to the positive thermal expansion coefficient of the WSe2 layer, which maintains a tensile total strain of the heterostructure and produces corresponding smaller tuning range of \({f}_{0,{{{\rm{CGT}}}}/{\rm{WSe}}_{2}}(T)\) near TC.
We also plot the mechanical dissipation, the inverse of a quality factor Q−1(T), of both the WSe2 and CGT/WSe2 resonators in Fig. 3c. A notable peak in \({Q}_{{{{\rm{CGT/WS{e}}}_{2}}}}(T)\) is visible at T = 58 K. We attribute this observation to an increase of the thermoelastic damping46,47 expected near TC in magnetic resonators27. This observation is supported by the measured maximum in \(\frac{{{{\rm{d}}}}\left({f}_{0}^{2}\right)}{{{{\rm{d}}}}T}\) (filled blue circles)27 at 58 ± 0.5 K, the temperature which we define as \({T}_{{{{\rm{C}}}}}^{* }\) and indicated by the black vertical dashed lines in Fig. 3d. The observed maximum at \({T}_{{{{\rm{C}}}}}^{* }\) relates to the peak in the thermal expansion coefficient of CGT at TC (filled magenta circles) that is shifted to lower temperatures in comparison to its bulk values of 60–66 K2,5.
We model the resonance frequency of a heterostructure f0,h(T) by modifying Eq. (2) to describe the observations in Fig. 3b. We describe the total thermally accumulated tension of the CGT/WSe2 heterostructure as a sum of individual tensions in each layer29,33:
We assume that the slippage between the layers is negligible. Therefore, we obtain the final equation for the resonance frequency of the heterostructure as:
where nth is given by Eq. (3). We plot the model of Eq. (4) for the CGT/WSe2 heterostructure in Fig. 3b (solid green line). In doing so, we use the bulk αCGT(T) values5, ρCGT = 6091 kg m−3 5, νCGT = 0.2236, and ECGT = 56.2 ± 8.2 GPa for CGT; \({\epsilon }_{{{{\rm{th,WS{e}}}_{2}}}}(T)\) extracted from the measured \({f}_{0,{{{\rm{WSe}}}}_{2}}(T)\) of the reference drum using equation (2), \({\rho }_{{{{\rm{WS{e}}}_{2}}}}=9320\) kg m−3 44,48, \({\nu }_{{{{\rm{WS{e}}}_{2}}}}=0.19\)44,49 and \({E}_{{{{\rm{WS{e}}}_{2}}}}=167.1\pm 0.7\) GPa (measured for this membrane using the nanoindentation method described above, which is consistent which previous studies44) for WSe2; and f0(94 K) = 27.2 ± 0.4 MHz. The resulting model reproduces the experiment qualitatively, yet lacks quantitative agreement above TC, most likely due to the overestimation of αCGT(T) for thin layers of CGT in contrast to its bulk value5.
Magnetic heterostructures
The presented methodology is not limited exclusively to the use of WSe2, given that the thermal expansion coefficient of the added material is large and positive. To explore the possibility of detecting two magnetic phase transitions in the same membrane and also the possibility of having emergent properties arising from a coupling between the two flakes, we fabricate a heterostructure membrane made of a ferromagnetic CGT covered by an antiferromagnetic FePS3 layer, which exhibits positive \({\alpha }_{{{{\rm{FeP{S}}}_{3}}}}(T)\)27, as shown in Fig. 4a. Using the methods described above, we measure the resonance frequency of this suspended structure as a function of temperature. In Fig. 4b, we plot experimental f0(T) (filled blue circles) together with its \(\frac{{{{\rm{d}}}}\left({f}_{0}^{2}(T)\right)}{{{{\rm{d}}}}T}\) (filled grey circles). The temperature derivative of \({f}_{0}^{2}\) shows two clear extrema, indicated by black vertical dashed lines: the first one at \({T}_{{{{\rm{C}}}}}^{* }=62\pm 1\) K we attribute to the TC of CGT2,5; the second one at \({T}_{{{{\rm{N}}}}}^{* }=113\pm 1\) K corresponds to the Néel temperature, TN, of FePS33,27. The temperatures at which these peaks appear correspond to the peaks in the specific heat of CGT and FePS3, as a consequence of its relation to the thermal expansion coefficient α(T)27,50.
a Top panel: A schematic cross-section of the suspended heterostructure membrane. Bottom panel: The optical image of the sample with the CGT/FePS3 heterostructure. Scale bar: 10 μm. b Filled blue circles—the measured resonance frequency as a function of temperature. Filled grey circles—the temperature derivative of \({f}_{0}^{2}\). Solid green line—the heterostructure resonance frequency model as described by Eq. (4). The light green region indicates the higher and lower boundary of the model allowed due to the uncertainties in h1,2, ECGT and \({f}_{0}^{2}({T}_{0})\). The insets: Schematic pictures of a magnetic spin configuration in FePS3 and CGT layers in corresponding combinations of antiferromagnetic (AFM), ferromagnetic (FM), and paramagnetic (PM) phases. c The dissipation factor Q−1 as a function temperature, in which the filled orange circles represent the measured data of the CGT/FePS3 heterostructure. The black vertical dashed lines in (b) and (c) represent the measured \({T}_{{{{\rm{C}}}}}^{* }=62\pm 1\) K of CGT and \({T}_{{{{\rm{N}}}}}^{* }=113\pm 1\) K of FePS3 as determined from positions of extrema in \(\frac{{{{\rm{d}}}}\left({f}_{0}^{2}\right)}{{{{\rm{d}}}}T}\) in (b).
We now analyze the measured f0(T) curve by plotting the model of Eq. (4) in Fig. 4b (solid green line) for the CGT/FePS3 heterostructure using material parameters, such as α(T), of CGT and FePS3 obtained from literature5,27,36 and ECGT as determined from Fig. 1. We use \({E}_{{{{\rm{FeP{S}}}_{3}}}}=103\) GPa, \({\rho }_{{{{\rm{FeP{S}}}_{3}}}}=3375\) kg m−3, \({\nu }_{{{{\rm{FeP{S}}}_{3}}}}=0.304\)27,51 for FePS3, and f0(150 K) = 30.9 ± 0.7 MHz. The model describes the experiment well with some deviations at low temperatures similar to the ones described above in Fig. 3c. In addition, we observe two peaks in Q−1(T), displayed in Fig. 4c, that we attribute to an increased thermoelastic damping near the phase transition27,46,47. The temperatures of these peaks coincide with the extrema from Fig. 4b, confirming the phase transitions in CGT and FePS3.
Electrostatic strain tuning of T C
Since strong magnetostriction is responsible for the large anomalies in the mechanical response of CGT membranes at TC5,14 (Fig. 1), we expect that the inverse effect should also be present allowing us to tune the TC via strain27,30. To study this effect, we fabricate another CGT/WSe2 heterostructure membrane contacted to Pd electrodes, as shown in Fig. 5a–c. We apply a gate voltage Vg between the heterostructure membrane and the bottom Si substrate electrode to induce an electrostatic force, Fel, that pulls the membrane down and thus strains the CGT/WSe2 stack. In Fig. 5d, we show the measured f0 of the heterostructure membrane as a function of temperature for six different values of Vg. A notable increase of f0 as a function of Vg is evident which is attributed to the electrostatic strain introduced. To describe the gate dependence of the resonance frequency, we show the f0(Vg) relationship near the phase transition temperature at T0 = 60 K in Fig. 5e. We fit the measurement data to a continuum mechanics model of a circular membrane resonator52,53 (see “Methods”), which describes the experiment well. We thus estimate the electrostatically added strain in CGT layer as:
where ϵel is the strain due to electrostatic pulling30,53, ϵb the strain due to bending54,55, Δz = zneut − zCGT the distance from the neutral plane of the heterostructure zneut to the central axis of CGT layer zCGT (see Supplementary Note 3), ε0 the dielectric permittivity of vacuum, and n(T0) = 2.538 ± 0.003 N m−1 the total tension in the suspended heterostructure at T0 = 60 K (extracted from the fit in Fig. 5e).
a The schematic cross-section of the suspended CGT/WSe2 heterostructure membrane. b The optical image of the heterostructure with materials indicated. Membrane radius: r = 2 μm. Scale bar: 12 μm. c The schematics of the electrostatic strain-tuning principle. d Measured resonance frequencies f0 of the heterostructure membrane as a function of temperature for different gate voltages Vg. e Filled blue circles—the measured resonance frequency as a function of Vg at 60 K. Solid magenta line—the continuum mechanics model fit52,53. f The temperature derivative of \({f}_{0}^{2}\) as a function of temperature for different Vg. The black vertical dashed lines in (d) and (e) show the peak position in \(\frac{{{{\rm{d}}}}\left({f}_{0}^{2}\right)}{{{{\rm{d}}}}T}\) at Vg = 0 V. g Filled blue circles—the shift in measured \({T}_{{{{\rm{C}}}}}^{* }\) as a function of Vg extracted from the peak position in (e). Solid magenta line—the estimate of electrostatically induced strain Δϵ as a function of Vg (see Supplementary Note 3). The shaded magenta region shows the uncertainty in Δϵ. The inset shows \({{\Delta }}{T}_{{{{\rm{C}}}}}={T}_{{{{\rm{C}}}}}^{* }({V}_{{{{\rm{g}}}}})-{T}_{{{{\rm{C}}}}}^{* }(0\,{{{\rm{V}}}})\) as a function of added voltage induced strain Δϵ in addition to calculations from Li and Yang37 (solid green line) and from Dong et al.56 (solid orange line). The vertical error bars in \({T}_{{{{\rm{C}}}}}^{* }\) were estimated from determining the peak position in (e) within 2% accuracy in the measured maximum.
Apart from the effect of electrostatically induced strain on f0(Vg) in Fig. 5d, the characteristic feature in the f0(T) curve, that we attribute to the Curie temperature of CGT27, shifts to higher temperatures. This trend becomes even more apparent in Fig. 5f, where we plot \(\frac{{{{\rm{d}}}}({f}_{0}^{2})}{{{{\rm{d}}}}T}\) for six different Vg. We extract \({T}_{{{{\rm{C}}}}}^{* }\) from the peak positions in \(\frac{{{{\rm{d}}}}({f}_{0}^{2})}{{{{\rm{d}}}}T}\) for multiple Vg and plot it against the gate-induced strain, Δϵ, in Fig. 5g. The observed enhancement in \({T}_{{{{\rm{C}}}}}^{* }\) qualitatively agrees with the added tensile strain dependence symmetrically both for positive and negative Vg as shown in Fig. 5g. This indicates that the gate-induced strain has a dominant contribution to the change in the \({T}_{{{{\rm{C}}}}}^{* }({V}_{{{{\rm{g}}}}})\) instead of a field effect6,7. In the inset of Fig. 5g, we plot the experimental \({{\Delta }}{T}_{{{{\rm{C}}}}}={T}_{{{{\rm{C}}}}}^{* }({V}_{{{{\rm{g}}}}})-{T}_{{{{\rm{C}}}}}^{* }(0\,{{{\rm{V}}}})\) versus the estimated strain Δϵ, together with predictions from density-functional theory calculations for 2D CGT by Li and Yang37, considering the direct exchange interaction (solid green line), and by Dong et al.56, attributing the enhancement of TC to the super-exchange interaction via Cr–Te–Cr bonds (solid orange line). The closer experimental agreement with the results of Dong et al.56 suggests that it is the decreasing energy difference between 3d orbitals of Cr and 5p orbitals of Te in nearly ~90∘ Cr–Te–Cr bonds of CGT that is likely to contribute to the enhancement of \({T}_{{{{\rm{C}}}}}^{* }\) as a function of strain56. Interestingly, we observed that the maximal \({T}_{{{{\rm{C}}}}}^{* }\) increase by mechanical strain was as much as 2.5 ± 0.6 K at Δϵ ≈ 0.026%. This is comparable to what was previously achieved in bulk CGT by applying an out-of-plane magnetic field of 0.7–1 T2,8, proving that strain-based nanomechanical methods provide a compelling route for controlling and probing magneto-elastic coupling in ferromagnetic 2D layers and heterostructures.
Discussion
In conclusion, we have probed the mechanical properties of CGT membranes by both static and dynamic nanomechanical means. We demonstrated that due to CGT’s strong magnetostriction5,14 and large negative thermal expansion near TC, bare CGT membranes experience strong resonance frequency reductions near their ferromagnetic Curie temperature and an accumulation of compressive strain. The compressive strain can produce buckling, wrinkling, or sagging of the CGT layers, which significantly complicates the analysis for nanomechanical measurements of TC27. We showed that this challenge can be solved by integrating CGT in heterostructures with other materials with positive thermal expansion coefficients. This methodology can also be applied using materials that have phase transitions themselves, which we demonstrate by probing both TN of FePS3 and TC of CGT within a single measurement of a CGT/FePS3 heterostructure. The presented measurements and methodologies for nanomechanical characterization of magnetic heterostructures open up possibilities to investigate the magnetic properties that are the result of interfacial interactions in 2D magnetic heterostructures membranes57,58, allowing also for novel magnetic properties to be discovered near the monolayer limit while excluding substrate interactions. In addition, we expect that focused studies of the mechanical dissipation in such heterostructures as a function of temperature and strain could in the future provide more insights to thermodynamics and heat transport in the 2D materials involved27,59,60. Finally, we showed that TC of CGT can be enhanced by gate-induced electrostatic straining, demonstrating control of magnetic order in these ferromagnetic heterostructures using strain. We anticipate that future studies will lead to the development of membrane devices with gate-controlled magnetic actuation61 for low-power spintronic applications.
Methods
Device fabrication and characterization
We first pattern a diced Si/SiO2 wafer and define circular holes with a radius of r = 1–2.5 μm and cavity depth of g0 = 285 nm using an e-beam lithography and reactive ion etching. SiO2 provides an electrical insulation between subsequently transferred 2D material membranes and the bottom Si electrode. To realize electrical contact to some samples for electrostatic experiments, Pd electrodes are pre-patterned on top of Si/SiO2 chips by a lift-off technique. To create suspended membranes, thin flakes of CGT, FePS3, and WSe2 crystals are mechanically exfoliated and transferred on a pre-patterned chip by the all-dry viscoelastic stamping method62 directly after exfoliation. Flakes of van der Waals crystals are exfoliated from high quality synthetically grown crystals with known stoichiometry. Using the same method, flakes are deterministically stacked on top of each other forming heterostructures. We stack FePS3 and WSe2 flakes on top of CGT to minimize the exposure time of the suspended CGT layers to air. Subsequently, samples are kept in an oxygen-free or vacuum environment to avoid degradation. The total time an average membrane is exposed to air during the fabrication and characterisation is in order of a few tens of minutes. No signs of degradation, such as change in optical contrast of the flakes, its thickness, or apparent disintegration of studied layers, was found during routine characterization of all samples.
Atomic force microscopy characterisation
AFM height profile scans and inspection are performed in tapping mode on a Bruker Dimension FastScan AFM. We use cantilevers with spring constants of kc = 30–40 N m−1 for inspection. Error bars on reported thickness values are determined by measuring multiple profile scans of the same flake. For force nanoindentation experiments, we use two different cantilevers with spring constants of kc = 8.87 ± 0.08 N m−1 and kc = 18.90 ± 0.11 N m−1. kc for each cantilever was calibrated using thermal and solid surface deflection. We use cantilever tips with a tip radius of ~7–10 nm, as confirmed by scanning electron microscope imaging.
Laser interferometry measurements
The sample is mounted on a xy piezopositioning stage inside a dry optical 4 K cryostat Montana Instruments Cryostation s50. A local sample heater is used to perform temperature sweeps at a rate of ~3 K min−1, keeping the pressure in the chamber below 10−6 mbar. A power modulated blue diode laser of λ = 405 nm is used to optothermally excite the motion of the membrane. Membrane displacement is then measured using a laser interferometer with a He–Ne laser beam of λ = 632 nm focused on the suspended membrane. In doing so, the interfering reflections from the membrane and the Si electrode underneath are recorded using a photodiode and processed by a vector network analyzer. All measurements were performed at incident laser powers of Pred ≤ 8 μW and Pblue ≤ 1 μW. Laser spot size is on the order of ~1 μm. During the data acquisition it is checked for all membranes that resonance frequency changes due to laser heating are insignificant. During data acquisition temperature is kept constant with ~10 mK stability by the local heater and a closed feedback loop controller. The uncertainty in measured transition temperatures is estimated from determining the peak position in \(\frac{{{{\rm{d}}}}({f}_{0}^{2})}{{{{\rm{d}}}}T}\) within 2% accuracy in the measured maximum.
Continuum mechanics model of electrostatically strained circular membrane
A membrane suspended over a circular cavity forms a capacitor with a bottom gate electrode underneath. The change in gate voltage causes the membrane to deflect, tuning the tension and producing a shift in the resonance frequency. The resonance frequency of the fundamental vibration mode of the drum as a function of gate voltage is described as52:
where \({\delta }_{{{{\rm{g}}}}}\approx \frac{{\varepsilon }_{0}{r}^{2}}{8{g}_{0}^{2}n({T}_{0})}{V}_{{{{\rm{g}}}}}^{2}\) is the maximal deflection at the membrane centre53, \(\frac{{\partial }^{2}{C}_{{{{\rm{g}}}}}}{\partial {z}^{2}}\approx \frac{0.542{\varepsilon }_{0}\pi {r}^{2}}{{g}_{0}^{3}}\) the second derivative of capacitance53,63, and meff = 0.27ρhπr2 the effective mass. In the case of a heterostructure membrane, material parameters are substituted for the heterostructure analogues29: \(E=\frac{{E}_{1}{h}_{1}+{E}_{2}{h}_{2}}{{h}_{1}+{h}_{2}}\), \(\rho =\frac{{\rho }_{1}{h}_{1}+{\rho }_{2}{h}_{2}}{{h}_{1}+{h}_{2}}\), \(\nu =\frac{{\nu }_{1}{h}_{1}+{\nu }_{2}{h}_{2}}{{h}_{1}+{h}_{2}}\), and h = h1 + h2. For the CGT/WSe2 heterostructure (19.7 ± 0.1 nm/8.5 ± 0.2 nm) in Fig. 5 we use the following material parameters: E = 89.6 GPa, h = 28.2 nm, ν = 0.21, ρ = 7064 kg m−3. We extract ϵ = 0.079 ± 0.004%, \(\frac{{\partial }^{2}{C}_{{{{\rm{g}}}}}}{\partial {z}^{2}}=3.46\pm 0.11\) mFm−2 and meff = 996.45 fg from the fit in Fig. 5e, that are close to the expected values53,63 of \(\frac{{\partial }^{2}{C}_{{{{\rm{g}}}}}}{\partial {z}^{2}}=2.61\) mFm−2 and meff = 675.9 fg.
Data availability
The numerical data that support the findings of this study are available from the data repository. The experimental data shown in figures of the manuscript can be downloaded from the Zenodo online repository at https://doi.org/10.5281/zenodo.6501917
References
Huang, B. et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 546, 270 (2017).
Gong, C. et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546, 265 (2017).
Lee, J.-U. et al. Ising-type magnetic ordering in atomically thin FePS3. Nano Lett. 16, 7433 (2016).
Gibertini, M., Koperski, M., Morpurgo, A. F. & Novoselov, K. S. Magnetic 2D materials and heterostructures. Nat. Nanotechnol. 14, 408 (2019).
Carteaux, V., Brunet, D., Ouvrard, G. & Andre, G. Crystallographic, magnetic and electronic structures of a new layered ferromagnetic compound Cr2Ge2Te6. J. Phys. Condens. Matter. 7, 69 (1995).
Verzhbitskiy, I. A. et al. Controlling the magnetic anisotropy in Cr2Ge2Te6 by electrostatic gating. Nat. Electron. 3, 460 (2020).
Wang, Z. et al. Electric-field control of magnetism in a few-layered van der Waals ferromagnetic semiconductor. Nat. Nanotechnol. 13, 554 (2018).
Selter, S., Bastien, G., Wolter, A. U. B., Aswartham, S. & Büchner, B. Magnetic anisotropy and low-field magnetic phase diagram of the quasi-two-dimensional ferromagnet Cr2Ge2Te6. Phys. Rev. B 101, 014440 (2020).
Sun, Y. et al. Effects of hydrostatic pressure on spin-lattice coupling in two-dimensional ferromagnetic Cr2Ge2Te6. Appl. Phys. Lett. 112, 072409 (2018).
Sakurai, T. et al. Pressure control of the magnetic anisotropy of the quasi-two-dimensional van der Waals ferromagnet Cr2Ge2Te6. Phys. Rev. B 103, 024404 (2021).
Wang, N. et al. Transition from ferromagnetic semiconductor to ferromagnetic metal with enhanced Curie temperature in Cr2Ge2Te6 via organic ion intercalation. J. Am. Chem. Soc. 141, 17166 (2019).
Gupta, V. et al. Manipulation of the van der Waals magnet Cr2Ge2Te6 by spin–orbit torques. Nano Lett. 20, 7482 (2020).
Ostwal, V., Shen, T. & Appenzeller, J. Efficient spin-orbit torque switching of the semiconducting van der Waals ferromagnet Cr2Ge2Te6. Adv. Mater. 32, 1906021 (2020).
Tian, Y., Gray, M. J., Ji, H., Cava, R. J. & Burch, K. S. Magneto-elastic coupling in a potential ferromagnetic 2D atomic crystal. 2D Mater. 3, 025035 (2016).
Kozlenko, D. P. et al. Spin-induced negative thermal expansion and spin–phonon coupling in van der Waals material CrBr3. npj Quantum Mater. 6, 19 (2021).
Casto, L. D. et al. Strong spin-lattice coupling in CrSiTe3. APL Mater. 3, 041515 (2015).
McGuire, M. A., Dixit, H., Cooper, V. R. & Sales, B. C. Coupling of crystal structure and magnetism in the layered, ferromagnetic insulator CrI3. Chem. Mater. 27, 612–620 (2015).
Schneeloch, J. A. et al. Gapless Dirac magnons in CrCl3. Preprint at https://arxiv.org/abs/2110.10771v1 (2021).
Miao, F., Liang, S.-J. & Cheng, B. Straintronics with van der Waals materials. npj Quantum Mater. 6, 59 (2021).
Yang, S., Chen, Y. & Jiang, C. Strain engineering of two-dimensional materials: Methods, properties, and applications. InfoMat 3, 397–420 (2021).
Chen, C. et al. Performance of monolayer graphene nanomechanical resonators with electrical readout. Nat. Nanotechnol. 4, 861 (2009).
Zhang, X. et al. Dynamically-enhanced strain in atomically thin resonators. Nat. Commun. 11, 5526 (2020).
Lee, C., Wei, X., Kysar, J. W. & Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 321, 5887 (2008).
Chen, C. et al. Graphene mechanical oscillators with tunable frequency. Nat. Nanotechnol. 8, 923 (2013).
Lemme, M. C. et al. Nanoelectromechanical sensors based on suspended 2D materials. Research 2020, 8748602 (2020).
Steeneken, P. G., Dolleman, R. J., Davidovikj, D., Alijani, F. & van der Zant, H. S. J. Dynamics of 2D material membranes. 2D Mater. 8, 042001 (2021).
Šiškins, M. et al. Magnetic and electronic phase transitions probed by nanomechanical resonators. Nat. Commun. 11, 2698 (2020).
Morell, N. et al. High quality factor mechanical resonators based on WSe2 monolayers. Nano Lett. 16, 5102 (2016).
Ye, F., Lee, J. & Feng, P. X.-L. Atomic layer MoS2-graphene van der Waals heterostructure nanomechanical resonators. Nanoscale 9, 18208 (2017).
Jiang, S., Xie, H., Shan, J. & Mak, K. F. Exchange magnetostriction in two-dimensional antiferromagnets. Nat. Mater. 19, 1295 (2020).
Ni, Z. et al. Imaging the Néel vector switching in the monolayer antiferromagnet MnPSe3 with strain-controlled Ising order. Nat. Nanotechnol. 16, 782–787 (2021).
Liu, K. et al. Elastic properties of chemical-vapor-deposited monolayer MoS2, WS2, and their bilayer heterostructures. Nano Lett. 14, 5097 (2014).
Kim, S., Yu, J. & van der Zande, A. M. Nano-electromechanical drumhead resonators from two-dimensional material bimorphs. Nano Lett. 18, 6686 (2018).
Novoselov, K. S., Mishchenko, A., Carvalho, A. & Neto, A. H. C. 2D materials and van der Waals heterostructures. Science 353, aac9439 (2016).
Castellanos-Gomez, A. et al. Elastic properties of freely suspended MoS2 nanosheets. Adv. Mater. 24, 772 (2012).
de Jong, M. et al. Charting the complete elastic properties of inorganic crystalline compounds. Sci. Data 2, 150009 (2015).
Li, X. & Yang, J. CrXTe3 (X = Si, Ge) nanosheets: Two dimensional intrinsic ferromagnetic semiconductors. J. Mater. Chem. C 2, 7071 (2014).
Cantos-Prieto, F. et al. Layer-dependent mechanical properties and enhanced plasticity in the van der Waals chromium trihalide magnets. Nano Lett. 21, 3379–3385 (2021).
Castellanos-Gomez, A. et al. Single-layer MoS2 mechanical resonators. Adv. Mater. 25, 6719 (2013).
Lyon, K. G., Salinger, G. L., Swenson, C. A. & White, G. K. Linear thermal expansion measurements on silicon from 6 to 340 K. J. Appl. Phys. 48, 865 (1977).
Chen, T., Pauly, M. & Reis, P. M. A reprogrammable mechanical metamaterial with stable memory. Nature 589, 386 (2021).
Mahboob, I. & Yamaguchi, H. Bit storage and bit flip operations in an electromechanical oscillator. Nat. Nanotechnol. 3, 275 (2008).
Roodenburg, D., Spronck, J. W., van der Zant, H. S. J. & Venstra, W. J. Buckling beam micromechanical memory with on-chip readout. Appl. Phys. Lett. 94, 183501 (2009).
Zhang, R., Koutsos, V. & Cheung, R. Elastic properties of suspended multilayer WSe2. Appl. Phys. Lett. 108, 042104 (2016).
Çakír, D., Peeters, F. M. & Sevik, C. Mechanical and thermal properties of h-MX2 (M = Cr, Mo, W; X = O, S, Se, Te) monolayers: A comparative study. Appl. Phys. Lett. 104, 203110 (2014).
Lifshitz, R. & Roukes, M. L. Thermoelastic damping in micro- and nanomechanical systems. Phys. Rev. B 61, 5600 (2000).
Sun, Y., Fang, D. & Soh, A. K. Thermoelastic damping in micro-beam resonators. Int. J. Solids. Struct. 43, 3213 (2006).
Agarwal, M. & Wani, P. Growth conditions and crystal structure parameters of layer compounds in the series Mo1−xWxSe2. Mater. Res. Bull. 14, 825 (1979).
Zeng, F., Zhang, W.-B. & Tang, B.-Y. Electronic structures and elastic properties of monolayer and bilayer transition metal dichalcogenides MX2 (M = Mo, W; X = O, S, Se, Te): A comparative first-principles study. Chinese Phys. B 24, 097103 (2015).
Khan, S. et al. Spin dynamics study in layered van der Waals single-crystal Cr2Ge2Te6. Phys. Rev. B 100, 134437 (2019).
Hashemi, A., Komsa, H.-P., Puska, M. & Krasheninnikov, A. V. Vibrational properties of metal phosphorus trichalcogenides from first-principles calculations. J. Phys. Chem. C 121, 27207 (2017).
Chen, C. Graphene nanoelectromechanical resonators and oscillators (PhD thesis, Columbia University, 2013).
Weber, P., Güttinger, J., Tsioutsios, I., Chang, D. E. & Bachtold, A. Coupling graphene mechanical resonators to superconducting microwave cavities. Nano Lett. 14, 2854 (2014).
Wunnicke, O. Analytical model of the quasistatic mechanical behavior of galvanic piezoelectric microelectromechanical system switches. J. Appl. Phys. 106, 104502 (2009).
Roldán, R., Castellanos-Gomez, A., Cappelluti, E. & Guinea, F. Strain engineering in semiconducting two-dimensional crystals. J. Phys.: Condens. Matter 27, 313201 (2015).
Dong, X.-J., You, J.-Y., Zhang, Z., Gu, B. & Su, G. Great enhancement of Curie temperature and magnetic anisotropy in two-dimensional van der Waals magnetic semiconductor heterostructures. Phys. Rev. B 102, 144443 (2020).
Zhang, L. et al. Proximity-coupling-induced significant enhancement of coercive field and Curie temperature in 2D van der Waals heterostructures. Adv. Mater. 32, 2002032 (2020).
Wang, Y. et al. Modulation doping via a two-dimensional atomic crystalline acceptor. Nano Lett. 20, 8446–8452 (2020).
Dolleman, R. J. et al. Optomechanics for thermal characterization of suspended graphene. Phys. Rev. B 96, 165421 (2017).
Morell, N. et al. Optomechanical measurement of thermal transport in two-dimensional MoSe2 lattices. Nano Lett. 19, 3143 (2019).
Ben-Shimon, Y. & Ya’akobovitz, A. Magnetic excitation and dissipation of multilayer two-dimensional resonators. Appl. Phys. Lett. 118, 063103 (2021).
Castellanos-Gomez, A. et al. Deterministic transfer of two-dimensional materials by all-dry viscoelastic stamping. 2D Mater. 1, 011002 (2014).
Will, M. et al. High quality factor graphene-based two-dimensional heterostructure mechanical resonator. Nano Lett. 17, 5950 (2017).
Acknowledgements
The authors thank B. Simon for continuous support and feedback on the manuscript. M.Š., M.L., H.S.J.v.d.Z., and P.G.S. acknowledge funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement number 881603. H.S.J.v.d.Z., E.C., and S.M.-V. thank COST Action MOLSPIN CA15128; E.C. and S.M.-V. acknowledge the financial support from the European Union (ERC AdG Mol-2D 788222), the Spanish MICINN (MAT2017-89993-R co-financed by FEDER and Excellence Unit “María de Maeztu", CEX2019-000919-M) and the Generalitat Valenciana (Prometeo programme and PO FEDER Programme, ref. IDIFEDER/2018/061 and IDIFEDER/2020/063). W.X., S.J., and W.H. thank National Natural Science Foundation of China (11974025). S.K. and T.v.d.S. acknowledge financial support by the Dutch Research Council (NWO Projectruimte grant 680.91.115).
Author information
Authors and Affiliations
Contributions
M.Š., S.K., E.C., H.S.J.v.d.Z., T.v.d.S., and P.G.S. conceived the experiments. M.Š. performed the laser interferometry measurements. M.Š. and M.L. fabricated and inspected the samples. S.M.-V. and E.C. synthesized and characterized the FePS3 crystals. W.X., S.J., and W.H. synthesized and characterized the Cr2Ge2Te6 crystals. M.Š., S.K., and B.J.M.S. analyzed and modelled the experimental data. H.S.J.v.d.Z., T.v.d.S., and P.G.S. supervised the project. The paper was jointly written by all authors with a main contribution from M.Š. All authors discussed the results and commented on the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
41699_2022_315_MOESM1_ESM.pdf
SUPPLEMENTARY INFORMATION: Nanomechanical probing and strain tuning of the Curie temperature in suspended Cr2Ge2Te6-based heterostructures
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Šiškins, M., Kurdi, S., Lee, M. et al. Nanomechanical probing and strain tuning of the Curie temperature in suspended Cr2Ge2Te6-based heterostructures. npj 2D Mater Appl 6, 41 (2022). https://doi.org/10.1038/s41699-022-00315-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-022-00315-7
This article is cited by
-
Visualizing thickness-dependent magnetic textures in few-layer Cr2Ge2Te6
Communications Materials (2024)
-
Extreme mechanical tunability in suspended MoS2 resonator controlled by Joule heating
npj 2D Materials and Applications (2023)
-
Magnetic order in 2D antiferromagnets revealed by spontaneous anisotropic magnetostriction
Nature Communications (2023)
-
A monolithically sculpted van der Waals nano-opto-electro-mechanical coupler
Light: Science & Applications (2022)