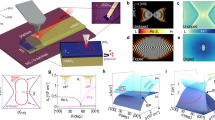
Abstract
This work presents a new substrate platform, which provides tunability of the group velocity and spontaneous emission of a dipolar scatterer graphene–ferroelectric slab hybrid system in the terahertz ranges. We use analytical models to determine the hybridization of graphene surface plasmon and ferroelectric LiNbO3 type I and type II reststrahlen hyperbolic phonon–polariton. The variation of the chemical potential of graphene and the thickness of the ferroelectric layer results in several distinct features. Flipping the group velocity, strongly coupled hybrid hyperbolic surface plasmon–polaritons, and surface plasmon–polariton mode exists for the same momentum at different frequencies. The group velocity sign reversal for both a single-graphene- and double-graphene-integrated system depends on the thickness of the hyperbolic layer and the chemical potential of graphene. Comparative analysis of Purcell radiation is presented for a quantum emitter positioned at different locations between ferroelectric and graphene-integrated ferroelectric layers, revealing that this system can support strong spontaneous emission that can be modulated with the graphene chemical potential. Changing the chemical potential through selective voltage biasing demonstrates a substantial increase or decrease in the decay rate for spontaneous emission. Further analysis of the emission phenomenon shows a dependence on factors, such as the relative radiating source position and the thickness of the ferroelectric film. These characteristics make graphene–ferroelectric materials promising candidates to modify the light–matter interaction at the low terahertz ranges.
Similar content being viewed by others
Introduction
The discovery of two-dimensional (2D) materials, such as graphene,1,2 has drawn immense scientific attention, both experimentally and theoretically for advanced electrical and optoelectronic applications.3,4 Light, an external time-varying electric field, can interact with graphene’s conduction electrons, causing collective charge oscillations known as surface plasmon–polaritons (SPPs).5,6 In graphene, the oscillating surface electrons are extremely well confined with a relatively low level of losses, offering much-better-quality plasmonic properties than traditional noble metals, which primarily operate in the optical spectrum.7,8 Conventional metals used for plasmonics, such as Au, Ag, and Al, behave as nearly perfect electrical conductors mainly at longer wavelengths, while around near-infrared wavelengths, they suffer losses.9 For wavelengths of light above the infrared range, phononic materials, such as SiC and the III nitrides, are widely used since they are capable of supporting both propagating surface phonon–polaritons and localized surface phonon–polaritons in this range.10 However, these materials are often limited to operation over a very narrow band, typically bounded between the longitudinal and transverse phonon modes; they lack flexibility over the full infrared spectral range. Graphene plasmon resonances, on the other hand, are unbounded by the phonon limits and can be controlled through several mechanisms, such as optimization of geometry,11 number of layers,11 mechanical strain,12 magnetic bias,13 or dynamic tuning by chemical doping or gate voltage from the infrared to the THz range.11
With this insight, high-quality heterostructures that support propagating phonon modes or hyperbolic phonon–polaritons (HPPs), especially material comprising graphene, are regarded as having great potential for plasmonic applications. Both theoretical predictions and extensive experimental investigations of graphene plasmons and surface phonon–polaritons are widely available for many mid-IR polar dielectric optical materials,14,15,16 thin III–V group semiconductors,17 and piezoelectrics.18 These offer better understanding of hybridization mechanisms that leads to the formation of localized surface plasmon–phonon–polaritons. In addition, materials with type I and type II hyperbolicity of the reststrahlen (RS) bands, which support propagating HPPs,19 show strong coupling with graphene surface plasmons. For example, hybridization with graphene SPPs and the two RS bands in hexagonal boron nitride (hBN) exhibits low loss, long-lived, and highly confined three-dimensional modes of hybridized HPPs in the mid-infrared.19,20 The coupled hybrid modes can be highly confined three-dimensional modes19,20,21 and are highly tunable by gate modulation.
Also, recent success in fabrication of graphene on LiNbO322,23 and other ferroelectric material substrates24,25 has drawn considerable attention for several applications: electrically programmable nonvolatile memory, field-effect transistors,26,27 thermal-phase transitions, and a number of other THz applications.28,29 Studies of graphene plasmon hybridization with LiNbO3 surface phonon–polaritons lead to waveguide modes with extreme confinement, compared with conventional dielectric materials.30 Graphene–LiNbO3 hybrid systems show absorption spectra that depend on the number of graphene layers,31 planar-tunable waveguides with ultra-low loss and high attenuation in the THz region.32 The propagation of transverse magnetic graphene SPPs in the visible to mid-infrared range can be controlled by different polarization levels and the polarization direction of the LiNbO3 ferroelectric domains.33 Beside these reports, studies of the interaction of graphene plasmon using hyperbolic material are seldom reported in the low-terahertz regime (<20 THz), since most naturally hyperbolic materials only exhibit this property in the infrared and near the optical frequency range.
In this work, we theoretically demonstrate that combining the optical parameters of graphene and the optical phonon resonance response of a submicron layer of LiNbO3 introduces several bands with rich features of hybridized surface plasmon–phonon–polariton (HSPP) modes in the rarely explored low-terahertz regime (0–15 THz). The strong hybridization of graphene SPPs and HPPs shows the gate-tunable group velocity sign reversal. Usually, the group velocity reversal has been realized by other mechanisms, such as an external laser source34 or artificially engineered multilayer 2D metamaterials.35,36 However, these methods are limited due to lack of active gate tunability and challenges in fabricating multilayer hyperbolic 2D material devices. As a special case, we conducted detailed analysis of spontaneous emission (SE) rate or Purcell factor21,37 from a single quantum emitter of the proposed device. The THz emission rate associated with an increase in optical energy density demonstrates dependence on graphene chemical potential and the size of the ferroelectric layer. This is particularly important to couple light efficiently to quantum emitters, and our results reveal a new design of materials operating in extreme regimes of the light–matter interactions. In addition, we propose an active tuning technique for generating efficient sources of single-photon emission.
Figure 1 depicts the schematics of three-structure configurations to study HPPs of ferroelectric and SE rates: (a) graphene on the surface of a ferroelectric slab and (b) ferroelectric sandwiched between two graphene layers. The graphene layers are connected in such a way that an external voltage source can be used to modulate its optical properties.
Schematics of two-structure configurations: a single-graphene structure with air/graphene/LiNbO3/substrate and b double-graphene structure with air/graphene/LiNbO3/graphene/substrate. The incident light is normal to the surface with the electric field shown (E). The circuit configurations are shown in c, d, and have DC voltage sources
Results and discussion
HSPP modes in graphene–LiNbO3
For the purpose of our investigation of the hybridization of SPPs of graphene HPPs of a ferroelectric, we computed the dispersion of the air/graphene/LiNbO3/Si heterostructure, shown in Fig. 1a, using computations outlined in the “Methods” section. As background, one can compare these results to freestanding graphene, which are plotted in Supplementary Fig. 1 and a ferroelectric (LiNbO3) on a substrate, plotted in Supplementary Fig. 2a–e. The dispersion properties are calculated from Eq. (3) for three chemical potentials, μ = 0.1, 0.3, and 0.6 eV and two ferroelectric-layer thicknesses, t = 50 and 200 nm. The results shown in Fig. 2 are compared with those in Supplementary Fig. 2a–e to demonstrate the effects of adding graphene into the system. The first observation is the presence of strong dispersion above the type I, between the two bands, and below the type II energy range of the ferroelectric for both t = 50 and t = 200 nm. These dispersion modes are not purely SPP nor HPP modes but rather a combination effect regarded as HSPP modes. HSPP modes in the region above the upper limit of type I shift toward the light line, as the chemical potential increases, forming weakly confined modes, and follows different from \(\omega \propto \sqrt {k_x}\), exhibiting nearly linear dispersion, Fig. 2a, b. Increasing ferroelectric thickness for the same chemical potential, HSPP modes above the type I band region stay the same, further illustrating the graphene-dominated hybridization. The HPP modes inside the type I band, for low chemical potential, the HPP modes are pushed further reaching a flat kx. Increasing the chemical potential for small thickness, the HPP coupling mode inside type I bands disappears. However, most of the HPPs appear for larger ferroelectric thicknesses (t = 200 nm) and lower chemical potential. Their gradual dominant appearance is also noticeable in Supplementary Fig. 2f–j, as the ferroelectric thickness increases. The hyperbolic dominated confining modes can be realized in a ferroelectric–graphene–ferroelectric system30; here the HPPs are exited first. This has also been demonstrated in a hBN–graphene–silicon system.38
Evolution of HSPPs strength color map from the imaginary part of the reflection coefficient for three selected chemical potential (µ = 0.1, 0.3, and 0.6 eV) for air/graphene/LiNbO3/Si under TM-polarized illumination. The thickness of the ferroelectric is t = 50 nm for (a–c), t = 200 nm for (d–f). The green arrow indicates the light line \(\left( {c = \omega /k_0} \right)\) for vacuum dispersion. 2D schematics of the structure and the TM incident field polarization direction are shown in g and h. Note that b is the same as the result presented in Supplementary Fig. 2g, e is the same as Supplementary Fig. 2f
Above the lower limit of the type II band, HPP modes become strongly dependent on the hybridization of graphene SPPs. Near smaller kx the HSPPs have \(v_g > \,0\); as kx increases, HSPPs cross above the type II band reverse inside the type II energy, \(v_g < 0\), Fig. 2b, c, f. The change in kx is due to the rise of mismatching momentum between the HPPs and the SPPs at lower frequency for small kx. The shift and sign change of the HSPPs’ νg above the type II bands weakens for large t, even for highly biased graphene, as shown in Fig. 2d–f. The local density of states in and above the type II band significant decreases as μ increases, Fig. 2b, c, e, f. Below the lower limit of the type II region, additional dispersion modes are observed for μ = 0.1 eV at lower kx and frequencies, independent of size of the ferroelectric. These weak nonlinear dispersion curves attain flat values for higher kx. Since none of these modes were observed in the ferroelectric/substrate system, and the graphene SPPs lead to their formation. This is further illustrated by the rise of the chemical potential. A higher chemical potential pushes these modes toward lower kx, merging with the light line for μ = 0.6 eV, as in Fig. 2f.
HSPP modes in graphene–LiNbO3–graphene
An additional system we considered for the hybridization process of HSPPs was the placement of a surface plasmon source on either side of the ferroelectric LiNbO3, the structure shown in Fig. 1b. Figure 3a–i displays the results determined for a thin LiNbO3 layer sandwiched between two graphene layers for equal chemical potential; we consider them as symmetric sources.
Color maps of the imaginary part of the reflection coefficient for three selected Fermi-energies of air/graphene/LiNbO3/graphene/Si under TM-polarized illumination, representing the surface plasmon dispersion strength. The thickness of the ferroelectric is t = 50 nm for a–c as shown in the schematic (g), and t = 200 nm for d, e as shown in h. In each case, μ1 = μ2
For μ1 = μ2 = 0.1 eV, the hybridized modes both appear outside the two RS bands with longer wavevectors (Fig. 4a, d). The HPP modes in the type II band are pushed outside of the upper limit for a thin ferroelectric slab, extending into the type I band. When the ferroelectric film thickness increases, the number of HPP modes moves toward the type II band region, as shown in Fig. 3d. To efficiently excite the HSPPs to higher frequency, the chemical potential of the two graphene layers was increased to μ1 = μ2 = 0.3 eV and μ1 = μ2 = 0.6 eV, as shown in Fig. 3b, c, e, f. The effect of the chemical potential becomes prominent above the type II band. As it increases to 0.3 eV, and for 0.6 eV, the wavevectors are pushed to longer wavelengths, close to the light line, gaining a large positive νg, see Supplementary Discussion and Supplementary Fig. 2f. For a ferroelectric below 50 nm, the hybrid modes can be dominated by the graphene surface plasmon, Supplementary Fig. 2f, k, p. For small thickness the dispersion from the hyperbolic band is flat acting like a pure dielectric covering very narrow frequency range. Therefore, the number of available modes to couple with graphene are less, hence tuning effect is actively dominated by graphene. It is important to note that for 0.6 eV, separate weak and strong HSPP modes are obtained, contrary to the case of two-layer graphene separated by a vacuum or dielectric, where the graphene surface plasmon modes merge together at higher energies.39,40 However, such claims can be achieved for equal chemical potential with careful inspection of the hyperbolic layer thickness between 50 and 100 nm (see Supplementary Fig. 2); this is shown in Fig. 3 for t = 50 nm. Compared with a single-layer graphene system and above the type I band, nonlinear dispersion is exhibited for small t and large μ, as shown in Fig. 4. In the intermediate condition, graphene-like, nonlinear HSPPs dispersion can exist. This analysis indicates that linear and nonlinear frequency and momentum-dependent excited HSPPs can be controlled through the applied voltage. The size and dielectric function of the hyperbolic material both strongly affect the dispersion modes below the upper limit of the type I region. Unlike single-layer graphene, double-layer graphene systems show strong hybridization effects. This represents a significant advantage over air/graphene/ferroelectric/Si systems, where the hybridization process needs a large chemical potential. The above analysis also shows the possibility to cause mixed modes of the reversible group velocity, as seen in the case of a large gate voltage in Fig. 4b, f and in Supplementary Fig. 2p–t.
Color map of the imaginary part of the reflection coefficient for different Fermi energies for the top and lower parts of a graphene-free air/graphene/LiNbO3/graphene/Si under TM-polarized illumination, representing surface plasmon dispersion strength. The thicknesses of the ferroelectric are a, b t = 50 nm and c, d t = 100 nm. e, f 2D schematics of a ferroelectric layer sandwiched between dissimilar graphene (μ1 ≠ μ2)
Next, in order to obtain highly modified HSPP modes, we set the double-graphene hybrid system to dissimilar chemical potentials, μ1 ≠ μ2, Fig. 4a–d. To control the hybridization process in these systems, we focus on tuning the chemical potential of the top graphene while keeping the other fixed. First, we consider a chemical potential μ1 = 0.1 eV for the graphene at the top of the ferroelectric and μ2 = 0.6 eV for the bottom graphene layer with a constant thickness, t = 50 nm, Fig. 5a, b. In the region above the type I hyperbolic band there exist two distinct HSPPs dispersion bands because higher chemical potential difference leads to different kx. The first HSPPs curve, close to the light line, comes from the bottom graphene layer while the second curve, with higher momentum, is from the graphene atop the ferroelectric. Increasing the chemical potential of the top graphene layer to μ1 = 0.3 eV pushes the second dispersion mode closer to the light line, as shown in Fig. 4b. Gate modulation of hybrid modes between two dissimilar graphene layers shows that the formation of symmetric and antisymmetric electric fields for different systems between two graphene sheets separated by a vacuum,40 inside a dielectric between the two graphene sheets,41 and in a hyperbolic slab21 is a result of phase difference. When the two graphene sheets are gated with identical chemical potentials, the dispersion modes merge together as shown in Fig. 4c.
SE rate of different dipole distances modulated with different Fermi energy. The results show the Purcell factor versus frequency and as a function of the distance between the dipole emitter d, located in air, and the air/graphene/LiNbO3/graphene/Si for μ1 = μ2: a d = 10 nm, t = 50 nm; b d = 100 nm, t = 50 nm; c d = 10 nm, t = 200 nm; and d d = 100 nm, t = 200 nm. e, f show the sandwiched ferroelectric with thickness labeled in a 2D schematic
At higher frequencies, through a selective asymmetric chemical potential, it is also possible to obtain single HSPPs, as shown in Fig. 4c, d, for large kx as reported by Kumar and Hanson.21,30,42 In addition, for ferroelectric thickness t = 100 nm, the HSPP modes converge, creating weak momentum coupling. The larger the separation of the two graphene sheets, the weaker the interaction and hence the identical graphene response even with different chemical potentials. The effect of the dispersion for large wave vectors comes from the top graphene as evidenced in Figs 3 and 4 when the chemical potential is 0.3 eV. In the region below the upper limit of the type I hyperbolicity, μ1 = 0.1 eV for t = 50 and 100 nm, strong HSPP modes are found for high frequencies and low kx and shift to lower frequency as kx increases. The HSPP modes here cross into the type I range for lower kx, and return for larger kx towards the lower limit of the type II band and then stay flat. It is also noticeable that, at lower frequencies, additional surface modes are below the minimum wavenumber of the type II band. These dispersion modes do not cross the lower-frequency range of the type II and stay flat for higher kx when μ1 = 0.6 eV for t = 50 and 100 nm from Fig. 4. As in a symmetric graphene system, above the type I hyperbolic region one can find several HSPP modes for the same momentum, kx, for t = 50 nm, exhibiting the mixed group velocities (\(v_{\rm{g}} \,> \, 0\) and \(v_{\rm{g}} \,< \,0\)). Such cases are less frequently observed for t = 100 nm and larger t values. As the thickness increases above 100 nm in the hybrid system, the HSPPs highest confinement gradually splits to SPPs and HPPs, moving away from the group velocity sign reversal transition point, see Supplementary Fig. 3s, t. Additional effects are observed when there are two graphene sheets; the linear dispersion behavior observed over a specific energy range is not seen as in the case of single graphene. The variation of the top graphene and bottom graphene chemical potentials offers a great means to break the symmetric nature of the hybridization behavior for thin ferroelectric films. This is opposed to the thick case, where the total effect appears as if the chemical potential was symmetric. Moreover, the degree of confinement of the hybrid mode group velocity sign reversal depends on the thickness and more importantly the value of the chemical potential. Specifically, for double-graphene hyperbolic slabs with asymmetric graphene optical properties, there is a wider potential for regulation of the direction of power flow. This is different from methods implemented previously which feature graphene sheets that are arranged tightly with a period smaller than a critical value43 or a patterned graphene sheet on a substrate, a graphene/photonic crystal hybrid systems.44
Spontaneous emission rate
In this section, we extend the studies of SE rate for our proposed device. The strength of the SE rate is related to the available hybrid modes and the local density of states. Modulation of the local density of states of hyperbolic materials leads to variation of near- and far-field emission of radiation. We numerically validated the modulation of the SE rate by an impressed dipole via Eq. (9), comparing the results from a thin ferroelectric layer and a graphene-gated ferroelectric layer.
SE rate for graphene–LiNbO3–graphene
In order to investigate the effect of the graphene on the SE rate, in the Supplementary Discussion with Supplementary Fig. 4 we show the computational results obtained from Eq. (9) for an emitter above the top graphene at a distance d pointing in z direction. We explore the SE rate effects in a double-graphene-integrated system and compared these results with a substrate without graphene and with a single-graphene system, when μ1 = μ2 (see Fig. 5). For μ1 = μ2 = 0.1 eV the peaks show a similar trend for single-layer graphene and without graphene when d = 10 nm for t = 50 nm and t = 200 nm, as shown in Fig. 5a, b. Small peaks are observed in the type II band, and the peaks in type I band vanish. The nature of this peak is from HSPPs than HPPs since a weak hybrid mode exists in this band, as shown in Figs 3 and 4.
As the chemical potential of both graphene layers is increased to 0.6 eV, the contributions of HSPP modes dominate by flattening the SE rate in the type II band. Distinct SE peak shifts in the type I band are more noticeable in the double-layer graphene system, Fig. 5c, d, than in the single-layer graphene system, presented in Supplementary Fig. 4b, d, when the dipole is located far from the top graphene layer, d = 100 nm. In general, above the type I band there is a trend of SE increasing with μ. For both the single and double-graphene systems, the variation in the SE rate level did not show any significant changes below the type II band. In both single- or double-layer graphene-modulated ferroelectric systems, the SE rate below the type II band is dominated by the properties of graphene. Furthermore, HSPP modes play opposite roles from those of SPPs for SE, i.e., suppressing the SE in the hyperbolic regions and enhancing them outside the hyperbolic region.
In the calculation of the SE rate from in Eq. (9), we have not specified the radiating channeling source. The expression of the SE rate indicates the total decay rate, which is the sum of the radiative decay rate and the nonradiative decay rate. For graphene and other 2D material systems, the total radiation scales as 1/d4,45,46 and for thin film photonic modes it scales as 1/d3.47 At a small distance, both the plasmonic material (graphene) and the hyperbolic ferroelectric material environment can increase both the radiative and nonradiative SE rates. However, predominant spontaneous decay channels, for an emitter that is placed at a small separation distance, are nonradiative modes due to considerable Ohmic loss, coupling to absorption losses in the graphene sheet48 and the hyperbolic layer.49 Therefore, for the total SE rate the two processes are in competition with each other. The complete nonradiative process due to the Joule losses in the hyperbolic slab, caused by the near field, can be calculated using the integral part of Eq. (9) in narrow regions around the poles corresponding to hybrid modes resonances.21,50 The effect of the dielectric loss of the hyperbolic ferroelectric in the SE rate, and its corresponding energy at different point dipole and thickness, is further detailed in the Supplementary Discussion with Supplementary Figs 5 and 6.
In this study, systematic analysis of hybrid heterostructure consisting of graphene and ferroelectric film has been conducted in the THz range. The surface plasmon waves formed in graphene affect the local density of states of the bounded hyperbolic band. HPPs can be supported out beyond the two RS band, bounded inside the ferroelectric. Lower-frequency and large-wavevector SPP modes of graphene couple with the lower-band HPP modes, causing the crossing of the LiNbO3 lower-bound band and increasing the group velocity. These HSPP modes formed in the lower-frequency region do not extend to large wave vectors for high chemical potential. In addition to actively changing the graphene chemical potential, the HSPP modes can also be modulated through the number of graphene layers in the hyperbolic medium. Increasing the number of graphene layers from single to double layers allows more HSPPs inside the effective hyperbolic regions. Moreover, the strong coupling between graphene SPPs and HPPs provides a feasible way to achieve group velocity sign reversal via an ultrathin hyperbolic slab with its thickness down to few hundred nanometers and a finely tuned gate voltage. Such results have been recently reported in graphene–hBN system for mid-infrared spectra.51,52 Numerically calculated SE rate of the hyperbolic band contribution of LiNbO3 compared with that of the graphene-integrated hyperbolic material demonstrates that both enhancement and reduction are achieved. The HSPP modes provide a strong enhancement of SE compared with outside the hyperbolic band of the pure ferroelectric layer and are effective for a radiation source at a small distance. Doubling the graphene layer results in a higher SE rate. In addition, there is a ferroelectric film thickness that can maximize hybridization of HSPPs, and thus the SE rate. Therefore, modulation of radiative near-field and far-field emission via electrostatics can control propagation lengths and hybrid HSPP mode confinement in ultrathin hyperbolic ferroelectric materials; this is advantageous for applications, such as near-field thermophotovoltaic devices and waveguides.
Methods
Optical properties of graphene and ferroelectric LiNbO3
The local limit of the 2D complex conductivity of a graphene sheet, within the random phase approximation, is given as53
Here, the first and second terms are the intraband and interband contributions, respectively, ω is the angular frequency, kB is Boltzmann constant, T is the temperature, e is the electron charge, τ is a finite relaxation time, and μc is the chemical potential. The chemical potential can be modulated by external voltage biasing,54 and the relation between the gate voltage (vg) and the chemical potential is \(\mu _{\rm{c}} = \hbar v_{\rm{F}}\sqrt {\pi \left| {\alpha _{\rm{0}}\left( {v_{\rm{g}} - v_{\rm{0}}} \right)} \right|}\), where ν0 is the voltage from natural doping at the Fermi level and α0 ≈ 9 × 1016 m−2 V −1, estimated from a parallel-plate capacitor model.54 We assume constant temperature, T = 300 K, and constant relaxation time, τ = 10−13 s, which are also within the range of experimentally attained values.7
We choose LiNbO3 as the ferroelectric layer because it has uniaxial anisotropic properties over the low THz range. The dielectric tensor is uniaxial and have opposite signs, which are essential for several applications.26,27 The dispersion relations for optical iso-frequency surfaces for the momentum vector and permittivity are \(k_x^2/\varepsilon _{zz} + k_y^2/\varepsilon _{zz} + k_z^2/\varepsilon _{xx} = \omega ^2/c^2\) and \(k_x^2/\varepsilon _{xx} + k_y^2/\varepsilon _{xx} + k_z^2/\varepsilon _{xx} = \omega ^2/c^2\) for TM (p)- and TE (s)-polarized waves, respectively, where \(\varepsilon _{xx} = \varepsilon _{yy} = \varepsilon _{||} \,\ne \,\varepsilon _{zz} = \varepsilon _ \bot\). Here, kx, ky, and kz are the x, y, and z components of the wavevector, respectively, ω is the wave frequency, and c is the speed of light. LiNbO3 supports spherical or elliptic iso-frequency in the TE polarization, and it shows hyperbolicity in the TM case. Using in-plane (\(\omega _{{\rm{T0}}, \bot }\) and \(\omega _{{\rm{L0}}, \bot }\)) and out-of-plane (\(\omega _{{\rm{T0}},||}\) and \(\omega _{{\rm{L0}},||}\)) transversal and longitudinal phonon vibrations, the dielectric constant of LiNbO3 in the THz range can be described by a Lorentz oscillator model as,30,55
where u stands for either ⊥ or ||. At room temperature, the dielectric parameters are \(\varepsilon _{\infty ,||}\) = 19.5, \(\varepsilon _{0,||}\) = 41.5, \(\gamma _{||}\) = 17.0 cm−1, \(\omega _{{\rm{T0}},||}\) = 153.5 cm−1, \(\varepsilon _{\infty , \bot }\) = 10.0, \(\varepsilon _{0, \bot }\) = 26.0, \(\gamma _ \bot\) = 28.0 cm−1, and \(\omega _{{\rm{T0}}, \bot }\) = 253.5 cm−1. The Lyddane–Sachs–Teller relation, \(\omega _{{\rm{L0,u}}} = \omega _{{\rm{T0,u}}}\sqrt {\varepsilon _{{\rm{0,u}}}/\varepsilon _{\infty ,{\rm{u}}}}\), is applied here for values \(\omega _{{\rm{L0}},||}\) = 224.2 cm−1 and \(\omega _{{\rm{L0}}, \bot }\) = 408.8 cm−1. Depending on the sign of the real part of the relative permittivity in a given direction, LiNbO3 can have one of the two terahertz hyperbolicity bands.30 For the type I hyperbolic bands, \(\omega _{{\rm{T0}},||}\) = 253.5 cm−1 and \(\omega _{{\rm{L0}},||}\) = 408.8 cm−1; for the type II hyperbolic bands, \(\omega _{{\rm{T0}},||}\) = 153.5 cm−1 and \(\omega _{{\rm{L0}},||}\) = 224.2 cm−1.
Plasmon–phonon–polariton dispersion
The first objective of this work was to numerically identify phononic, plasmonic, and combined effects on the dispersion modes due to the two hyperbolic bands and graphene in the THz range. The dispersion modes for graphene-integrated, layered material can be determined from the Fresnel total reflection coefficient. The reflection coefficient of TE-polarized and TM-polarized waves propagating in the normal direction from the air side in each layered structure (as differentiated in Fig. 1) can be generally expressed as56
and
where the subscripts 1, 2, and 3 correspond to the air, ferroelectric material, and substrate, respectively. Graphene is treated as a 2D conducting sheet in the reflection coefficient calculation while solving Maxwell’s equation with appropriate boundary conditions,57 the reflection coefficients \(r_{12}^{s,p}\) and \(r_{23}^{s,p}\) are given by
and
where \(k_{1z}^p = \sqrt {\varepsilon _1k_0^2 - k_x^2}\), \(k_{2z}^p = \sqrt {\varepsilon _ \bot k_0^2 - \frac{{\varepsilon _{2, \bot }}}{{\varepsilon _{2,||}}}k_x^2}\), \(k_{3z}^p = \sqrt {\varepsilon _3k_0^2 - k_x^2}\), \(k_{1z}^s = k_{1z}^p\), \(k_{3z}^s = \sqrt {\varepsilon _3k_0^2 - k_x^2}\), and \(k_{3z}^s = k_{3z}^p\) correspond to propagation in perpendicular directions at each medium, kx, is the tangential component of the wavevector along the propagation direction (x-direction) that gives general dispersion modes; μ0 and ε0 are permeability and permittivity in vacuum, respectively. The usual Fresnel coefficients without graphene can be obtained at σ = 0.
Emission rate
The surface plasmon–phonon-modulated interaction of light with graphene/hyperbolic material has significant effects on the lifetime of SE processes of quantum emitters in the THz range. The competing SE rate (Purcell spectra) is58,59,60
in the presence of a dipole emitter oriented in the z direction (perpendicular, \({\boldsymbol{P}} = p_z\hat z\)), where we choose pz = 1C-m above a semi-infinite plane (the three schematics in Fig. 1) normalized by the emission of dipoles in free space. Here, \(\Gamma _0 = \frac{{\omega _0^3\left| {p_z} \right|^2}}{{3\pi \varepsilon _0\hbar c^3}}\) is the SE rate of a dipole in free space, \(k_{z1} = \sqrt {\varepsilon _1k_0^2 - k_x^2}\), and \(r_{123}^p\) is the TM-polarized total reflection coefficient of a given layered medium. The choice of perpendicular orientation in this work is mainly due to the fact that parallel-oriented dipoles lead to SE rates of half the corresponding value for the same perpendicular emitter direction when considering SPs of a single emitter.60,61
Data availability
All the data derived from the computational method, computational codes, and calculations of this study are available from the corresponding author upon reasonable request.
References
Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004).
Novoselov, K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005).
Geim, A. K. & Novoselov, K. S. The rise of graphene. Nat. Mater. 6, 183–191 (2007).
Berger, C. et al. Electronic confinement and coherence in patterned epitaxial graphene. Science 312, 1191–1196 (2006).
Wunsch, B., Stauber, T., Sols, F. & Guinea, F. Dynamical polarization of graphene at finite doping. N. J. Phys. 8, 318 (2006).
Hwang, E. H. & Das Sarma, S. Dielectric function, screening, and plasmons in two-dimensional graphene. Phys. Rev. B 75, 205418 (2007).
Koppens, F. H. L., Chang, D. E. & Javier García de Abajo, F. Graphene plasmonics: a platform for strong light–matter interactions. Nano Lett. 11, 3370–3377 (2011).
Vakil, A. & Engheta, N. Transformation optics using graphene. Science 332, 1291–1294 (2011).
Law, S., Podolskiy, V. & Wasserman, D. Towards nano-scale photonics with micro-scale photons: the opportunities and challenges of midinfrared plasmonics. Nanophotonics 2, 103–130 (2013).
Streyer, W., Feng, K., Zhong, Y., Hoffman, A. J. & Wasserman, D. Engineering the reststrahlen band with hybrid plasmon/phonon excitations. MRS Commun. 6, 1 (2016).
Luo, X., Qiu, T., Lu, W. & Ni, Z. Plasmons in graphene: recent progress and applications. Mater. Sci. Eng. R. Rep. 74, 351–376 (2013).
Pellegrino, F. M. D., Angilella, G. G. N. & Pucci, R. Dynamical polarization of graphene under strain. Phys. Rev. B 82, 115434 (2010).
Gómez-Díaz, J. S. & Perruisseau-Carrier, J. Propagation of hybrid transverse magnetic-transverse electric plasmons on magnetically biased graphene sheets. J. Appl. Phys. 112, 124906 (2012).
Liu, Y. & Willis, R. F. Plasmon-phonon strongly coupled mode in epitaxial graphene. Phys. Rev. B 81, 081406(R) (2010).
Koch, R. J., Seyller, T. & Schaefer, J. A. Strong phonon‐plasmon coupled modes in the graphene/silicon carbide heterosystem. Phys. Rev. B 82, 201413 (2010).
Duo, Q. et al. Electrothermal control of graphene plasmon-phonon polaritons. Adv. Mater. 29, 1700566 (2017).
Liu, P. Q., Reno, J. & Brener, I. Quenching of infrared-active optical phonons in nanolayers of crystalline materials by graphene surface plasmons. ACS Photonics 5, 2706–2711 (2018).
Schiefele, J., Pedrós, J., Sols, F., Calle, F. & Guinea, F. Coupling light into graphene plasmons through surface acoustic waves. Phys. Rev. Lett. 111, 237405 (2013).
Dai, S. et al. Graphene on hexagonal boron nitride as a tunable hyperbolic metamaterial. Nat. Nanotechnol. 10, 682–686 (2015).
Brar, V. W. et al. Hybrid surface-phonon-plasmon polariton modes in graphene/monolayer h-BN heterostructures. Nano Lett. 14, 3876–3880 (2014).
Kumar, A., Low, T., Fung, K. H., Avouris, P. & Fang, N. X. Tunable light–matter interaction and the role of hyperbolicity in graphene-hBN system. Nano Lett. 15, 3172–3180 (2015).
Baeumer, C. et al. Ferroelectrically driven spatial carrier density modulation in graphene. Nat. Commun. 6, 6136 (2015).
Gopalan, K. K. et al. Mid-infrared pyroresistive graphene detector on LiNbO3. Adv. Opt. Mater. 5, (2017), (in press).
Hong, X., Posadas, A., Zou, K., Ahn, C. H. & Zhu, J. High-mobility few-layer graphene field effect transistors fabricated on epitaxial ferroelectric gate oxides. Phys. Rev. Lett. 102, 136808 (2009).
Rajapitamahuni, A., Hoffman, J., Ahn, C. H. & Hong, X. Examining graphene field effect sensors for ferroelectric thin film studies. Nano Lett. 13, 4374–4379 (2013).
Zheng, Y. et al. Gate-controlled nonvolatile graphene-ferroelectric memory. Appl. Phys. Lett. 94, 3119215 (2009).
Zheng, Y. et al. Wafer-scale graphene/ferroelectric hybrid devices for low-voltage electronics. Europhys. Lett. 93, 17002 (2011).
Hebling, J., Yeh, K.-L., Hoffmann, M. C., Bartal, B. & Nelson, K. A. Generation of high-power terahertz pulses by tilted-pulse-front excitation and their application possibilities. J. Opt. Soc. Am. B 25, B6–B19 (2008).
Stepanov, A., Hebling, J. & Kuhl, J. Generation, tuning, and shaping of narrow-band, picosecond THz pulses by two-beam excitation. Opt. Express 12, 4650–4658 (2004).
Jin, D., Kumar, A., Hung Fung, K., Xu, J. & Fang, N. X. Terahertz plasmonics in ferroelectric-gated graphene. Appl. Phys. Lett. 102, 201118 (2013).
Gu, X. Q. & Yin, W. Y. Terahertz wave responses of dispersive few-layer graphene (FLG) and ferroelectric film composite. Opt. Commun. 319, 70–74 (2014).
Gu, X. Q., Yin, W. Y. & Zheng, T. Attenuation characteristics of the guided THz wave in parallel-plate ferroelectric-graphene waveguides. Opt. Commun. 330, 19–23 (2014).
Wang, H. et al. Graphene based surface plasmon polariton modulator controlled by ferroelectric domains in lithium niobate. Sci. Rep. 5, 18258 (2015).
Harutyunyan, H., Beams, R. & Novotny, L. Controllable optical negative refraction and phase conjugation in graphite thin films. Nat. Phys. 9, 423–425 (2013).
Sreekanth, K. V., De Luca, A. & Strangi, G. Negative refraction in graphene-based hyperbolic metamaterials. Appl. Phys. Lett. 103, 023107 (2013).
Huang, H., Wang, B., Long, H., Wang, K. & Lu, P. Plasmon-negative refraction at the heterointerface of graphene sheet arrays. Opt. Lett. 39, 5957–5960 (2014).
Koppens, F. H. L., Chang, D. E. & García de Abajo, F. J. Graphene plasmonics: a platform for strong light–matter interactions. Nano. Lett. 11, 3370–3377 (2011).
Qu, S. et al. Graphene-hexagonal boron nitride heterostructure as a tunable phonon–plasmon coupling system. Crystals 7, 49 (2017).
Wang, B., Zhang, X., Yuan, X. & Teng, J. Optical coupling of surface plasmons between graphene sheets. Appl. Phys. Lett. 100, 131111 (2012).
Ilic, O. et al. Near-field thermal radiation transfer controlled by plasmons in graphene. Phys. Rev. B 85, 155422 (2012).
Gan, C. H., Chu, H. S. & Li, E. P. Synthesis of highly confined surface plasmon modes with doped graphene sheets in the midinfrared and terahertz frequencies. Phys. Rev. B 85, 125431 (2012).
de Vega, S. & García de Abajo, F. J. Plasmon generation through electron tunneling in graphene. ACS Photonics 4, 2367–2375 (2017).
Wang, B., Zhang, X., García-Vidal, F. J., Yuan, X. & Teng, J. Strong coupling of surface plasmon polaritons in monolayer graphene sheet arrays. Phys. Rev. Lett. 109, 073901 (2012).
Zhong, S. et al. Tunable plasmon lensing in graphene-based structure exhibiting negative refraction. Sci. Rep. 7, 41788 (2017).
Swathi, R. S. & Sebastian, K. L. Resonance energy transfer from a dye molecule to graphene. J. Chem. Phys. 129, 054703 (2008).
Gómez-Santos, G. & Stauber, T. Fluorescence quenching in graphene: a fundamental ruler and evidence for transverse plasmons. Phys. Rev. B 84, 165438 (2011).
Barnes, W. L. Fluorescence near interfaces: the role of photonic mode density. J. Mod. Opt. 45, 661 (1998).
Huidobro, P. A., Nikitin, A. Y., González-Ballestero, C., Martín-Moreno, L. & García-Vidal, F. J. Superradiance mediated by graphene surface plasmons. Phys. Rev. B 85, 155438 (2012).
Agranovich, V. M., Gartstein, Y. N. & Litinskaya, M. Hybrid resonant organic inorganic nanostructures for opto-electronic, applications. Chem. Rev. 111, 5179–5124 (2011).
Nguyen, H. M. et al. Efficient radiative and nonradiative energy transfer from proximal cdse/zns nanocrystals into silicon nanomembranes. ACS Nano 6, 5574–5582 (2012).
Jiang, Y., Lin, X., Low, T., Zhang, B. & Chen, H. Group-velocity-controlled and gate-tunable directional excitation of polaritons in graphene-boron nitride heterostructures. Laser Photonics Rev. 12, 1800049 (2018).
Lin, X. et al. All-angle negative refraction of highly squeezed plasmon and phonon polaritons in grapheneboron nitride heterostructures. PNAS 114, 6717–6721 (2017).
Chen, P. Y. & Alu, A. Atomically thin surface cloak using graphene monolayers. ACS Nano 5, 5855 (2011).
Liu, M. et al. Graphene-based broadband optical modulator. Nature 474, 64–67 (2011).
Feurer, T. et al. Terahertz polaritonics. Annu. Rev. Mater. Res. 37, 317–350 (2007).
Born, M, & Wolf, E. Principles of Optics. (Pergamon Press: Oxford, 1980).
Falkovsky, L. A. Optical properties of graphene. J. Phys. 129, 012004 (2008).
Koppens, F. H. L., Chang, D. E. & García de Abajo, F. J. Graphene plasmonics: a platform for strong light–matter interactions. Nano Lett. 11, 3370–3377 (2011).
Haroche, S. Cavity Quantum Electrodynamics in Fundamental Systems in Quantum Optics, les Houches session LIII. (eds Dalibard, J., Raimond, J. M. & J. Zinn Justin, J.) (Elsevier Science Publishers, Oxford, United Kingdom, 1992).
Cuevas, M. Surface plasmon enhancement of spontaneous emission in graphene waveguides. J. Opt. 18, 105003 (2016).
Vos, W. L., Koenderink, A. F. & Nikolaev, I. S. Orientation-dependent spontaneous emission rates of a two-level quantum emitter in any nanophotonic environment. Phys. Rev. A 80, 053802 (2009).
Acknowledgements
For all of their support, the authors would like to acknowledge the administrative staff in the Physics and in the Microelectronics-Photonics Graduate Program at the University of Arkansas; and Lisa Battiato in the R.B. Annis School of Engineering at the University of Indianapolis. Funding and support was provided by the University of Arkansas through the Department of Physics, the Fulbright College of Arts and Sciences, and the Office of Research & Innovation.
Author information
Authors and Affiliations
Contributions
D.T.D. formulated the research goals, devised the study, developed the method, performed theoretical calculations and analysis, created visualizations, and wrote the original draft. J.B.H. modified the visualizations and performed supervision and resource acquisition. F.T.L., D.F., S.J.B., and J.B.H. discussed the results, provided valuable insight, and reviewed and edited the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Debu, D.T., Ladani, F.T., French, D. et al. Hyperbolic plasmon–phonon dispersion on group velocity reversal and tunable spontaneous emission in graphene–ferroelectric substrate. npj 2D Mater Appl 3, 30 (2019). https://doi.org/10.1038/s41699-019-0112-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-019-0112-8