Abstract
Monolayer transition metal dichalcogenides/metal (MX2/metal) based transistors have been widely studied. However, further development is hindered by the large contact resistance between MX2 and metal contact. In this paper, we demonstrated that interfacial charge transfer between MX2 and metal is the key for tuning contact resistance. With the lattice misfit criterion applied to screen combination of MX2s and metals, it has been found out that both phase stability of MX2 and contact nature between MX2 and metal will be sensitively affected by interfacial charge transfer. Additionally, we have identified seven MX2/metal systems that can potentially form zero Schottky barrier contacts utilizing phase engineering. On base of interfacial charge calculations and contact resistance analysis, we have presented three types of MX2/metal contacts that can be formed with distinguished contact resistance. Our theoretical results not only demonstrate various choice of MX2/metal designs in order to achieve different amounts of interfacial charge transfer as well as manipulate contact resistance, but also shed light on designing ohmic contacts in MX2/metal systems.
Similar content being viewed by others
Introduction
The difficulty of extending Moore’s law on classic silicon devices largely limits the further development of logic transistors. Successful fabrication of 2D materials opens the gate of extending the scaling limit of nanoelectronic devices. Compared with the conventional metal oxide semiconductor based on Si, GaAs et al., the lack of trapping states at interface and surface, atomic thin thickness and controllable electronic structure of 2D materials, making them as promising candidates for devices with high performance. However, for some of the 2D materials, such as graphene, h-BN, the band gaps are inappropriate for channel materials. Even though the value of band gap can be tuned with defects,1,2,3,4,5 doping4,6 or strain engineering,1,6 the precise control is always challenging both experimentally and theoretically. Among all the 2D materials identified to date, monolayer transition metal dichalcogenides (MX2s) offer wide space of tunable band gaps,7,8,9 therefore have been widely investigated in field effect transistors (FET) based nanodevices.10,11,12
However, the large contact resistance between MX2s and metal substrate hinders the direct application of MX2s as high-performance FET devices.11,13 As a result, reducing the contact resistance between MX2s and the metal substrate has become one of the critical problems to be solved.14,15,16,17,18,19 As can be inferred from several previous studies, interfacial orbital overlapping will facilitate electron tunneling through the interface.11,13,20,21 However, systematic investigation on the influence of interfacial charge transfer on MX2/metal design is still absent. More specifically, the amount of charge transfer will be affected by interfacial lattice coherency, work function of metals as well as how MX2 is stacked on top of metals. Meanwhile, with the electron polarization from metal into MX2 layer, the phase stability of MX2 membrane may also be altered,22,23 which lead to drastic change of contact nature. There have already been several experimental reports6,24 on applying phase engineering techniques to improve the performance of MX2 based transistors. Nevertheless, studies about how metal substrate can affect the phase stability is still missing. With adequate investigation of those topics above, a design strategy can be proposed for manipulating contact resistance of MX2/metal system.
In this work, a computational framework based on the density functional theory (DFT), bader charge analysis25,26,27 and contact nature evaluation have been presented to screen potential metal candidates with 3d or 4d orbitals and their contacts with five types of MX2, i.e., MoS2, MoSe2, WS2, WSe2, and MoTe2. The potential stacking sequence and 2H→T (1T, 1T’ and 1T”) phase transformation are considered in the structure screening process. It has been found that several MX2/metal systems would be energetically more stable with T phases in MX2. This phase transition will consequently lead to ohmic contact behavior at the interface. Meanwhile, large variations of band alignment are observed as a result of interfacial charge transfer, which are supported by the simulated ARPES images. This study not only offers a systematic consideration of the contact nature at MX2/metal systems, but also predicts new types of MX2/metal interfaces with low interfacial electrical resistance.
Results and discussion
Phase stability and energetics
The potential of phase stability transition from 2H phase to T phases on different metal substrate (1T, 1T’ or 1T”) has been investigated by DFT calculated energetics. Our calculations indicate that the 1T phase will always have much higher energy compared with other phases. Therefore, the interfacial charge will not likely to induce the 2H→1T phase transition, which is also consistent with previous studies.7,22,23,44 As a result, we construct the phase stability profile as presented in Fig. 1(a) with the description of competition between 2H with either 1T’ or 1T” phases. To compare the energetics of MX2 on top of different substrates, the reference energy \({\mathrm{E}}_{2{\mathrm{H}}(1{\mathrm{T}},1{\mathrm{T}}^\prime ,1{\mathrm{T}}^\prime\prime )}\) is defined as \({\mathrm{E}}_{2{\mathrm{H}}(1{\mathrm{T}},1{\mathrm{T}}^\prime ,1{\mathrm{T}}^\prime\prime )} = {\mathrm{E}}_{{\mathrm{MX}}_2{\mathrm{/metal}}} - {\mathrm{E}}_{{\mathrm{metal}}}\). While both \({\mathrm{E}}_{{\mathrm{MX}}_2{\mathrm{/metal}}}\) and Emetal are the total energies calculated from DFT.
(Color online): a Energetic diagram showing the phase stability transition, only the T phase (1T’ or 1T”) with lower energetics are demonstrated in the diagram; Colors are used to distinguish different MX2 as black for MoS2, red for MoSe2, green for WS2, blue for WSe2 and purple for MoTe2; b Atomic configurations of selected MX2/metal contact
Several features can be identified from the energetic diagrams as shown in Fig. 1a. In all the examined MX2/metal contacts, the most energetically favorable T phase can be either 1T’ or 1T”. Meanwhile, for each type of MX2 monolayer, the energetics differ quite a bit depending on the type of metal with which to form the interfaces. Moreover, for several MX2/metal contacts, i.e., MoSe2-Sc, WS2-Zr, WS2-V, WSe2-Ti, WSe2-Sc, Nb-MoTe2, and Cr-MoTe2 systems, 1T’(1T”) phases turned out to be more energetically favorable compared with the original 2H phase.
All those phenomena can be explained with the significant charge transfer at MX2/metal contacts. For all the interfaces examined, they all have relatively small lattice mismatch compared with those not selected. Small lattice mismatch allows for more orbital overlapping between the bottom layers of X (S or Se) atoms and the topmost metal atoms, which is in accordance with the phenomenon that the energetics of 2H phase is significantly depending on the interface type as shown in Fig. 1a. For those MX/metal systems with phase stability transition, more charge is transferred from metal into MX2 monolayer compared to those without phase transition. As being pointed out by our previous study and various experimental reports, enough amount of charge injection into MX2 will trigger the structural transition into T phases.44,45,46,47 To support this explanation, we visualize the charge transfer at the interface and the corresponding lattice distortion within two selected systems as demonstrated in Fig. 1b. Meanwhile, the quantitative analysis of charge transfer is illustrated by the bader charge calculations as presented in Fig. 2.
(Color online): a–e: The average Bader charge amount of all X atoms that are adjacent to the metal surface for five types of MX2: a MoS2; b WS2; c MoSe2; d WSe2; e MoTe2. The error bars illustrate the fluctuation of bader charges with respect to stacking sequences. f: Calculated work function for certain metal surfaces
The charge transfer can be directly visualized by the isosurface of deformation charge density. Figure 1b illustrates the deformation charge density isosurface in MoS2 (MoS2-Cu) and WS2 (WS2-V), which correspond to the smallest and largest charger transfer amount that can happen between metal and adjacent S layer, respectively. By comparing the two extreme cases, one can get that T phases generally obtain more electrons from the metal surface, which makes the interlayer distance in 1T”/metal contact smaller. By analyzing the bader charge in all systems as shown in Figs. 2a, we found that for MoS2, MoSe2, WS2 and WSe2 contact with metals, the charge will always polarized from the metal side to the MS2 or MSe2 layer, which lead to the bader charges in MS2 or MSe2 layer higher than the one of free standing case (black line). However, two exceptions for MoTe2/Ru and MoTe2/Rh systems can be observed for MoTe2/metal systems. In both cases, electrons would transfer from the Te atom to Ru and Rh surface.
The variation of charge transfer conditions at MX2/metal interfaces is dependent on the different work functions of metal surfaces as well as the interface coherency of MX2/metal. By comparing the work functions of the substrate metals (Fig. 2f), we can obtain that generally the higher the work function is, the more difficult to make it lose electrons. Consistently, for those systems with more charge transferred to MX2s, the work functions of the corresponding metal surface are generally lower. Meanwhile, it is worthy to mention that among those metal surfaces with similar calculated surface work function, lower work function does not always mean more interfacial charge transfer. For instance, although the work function of Ti (001) surface (4.37 eV) is slightly larger than that of W (001) surface (4.26 eV), larger amount of charge transfer from metal to MX2 is observed in MSe2/Ti systems rather than in the MSe2/W system. This phenomenon mainly originates from the discrepancies in interface coherency. To minimize the misfit strain, for MSe2/Ti system, we designed a \(2\sqrt 3 \times 2\sqrt 3\) supercell of MSe2 aligning with a 4 × 4 supercell of Ti (001) surface (Table 1), in this case, in each periodic unit of the interface model, 12 Se atoms will interact with 16 Ti atoms at interfaces. When comes to MSe2/W system, a 4 × 4 supercell of MSe2 is put on top of a 33 supercell of W (001) surface to minimize the misfit strain, in which 16 atoms interact with 9 W atoms at interfaces in each periodic unit of the interface model. As a result, less charge transfer would happen in MSe2/W systems as presented in Figs. 2, c. One other thing worth mentioning is that for those cases with large charge transfer so that phase transition could occur, the fluctuation of charge transfer is generally more significant as demonstrated by the error bar, which also illustrate that the interfacial atomic orientation plays a significant role. To sum up, with all the MX2/metal system identified, there would be a wide tunable space for interfacial charge transfer as well as structural phase transition of MX2 with the selection of various metal and design of interface orientation.
Electronic structure of MX2/metal contacts
Due to the metallization at the MX2/metal interface, the electronic structure of MX2 will be largely modified due to (transition from orbital overlap) the chemical bond formation. Moreover, for those MX2/metal interface with phase transition, the modification of electronic structure would be more significant due to the strong charge transfer. DFT calculations on superlattice models are always applied to analyze such systems with interfaces, however, unfolded band structure would be more useful and convenient to illustrate the interfacial charge transfer behavior.48,49 Therefore, the unfolded band structures, which can be measured using the angle-resolved photoemission spectroscopy (ARPES) in experiment, have been calculated and demonstrated in Fig. 3. Meanwhile, a more zoomed in version can be found in Fig. S1 in supplementary information.
As illustrated in Fig. 3, when compared to 2H-MoS2 phase with the same metal substrate, more impurity states appear in the band structure of 1T” phase, which is also reflected by the density of states. Those are consistent with the bader analysis results shown in Fig. 2. Besides, for 2H-MoS2 on top of Cu, the impurity states appear mostly from −4 to −2 eV below the fermi level. However, when 2H-WS2 is placed on top of V, the impurity states appear on both valence and conduction bands. This phenomenon illustrates more significant charge transfer from metal into monolayer WS2 so that both bonding and anti-bonding states are rearranged as a result. This observation is supported by the corresponding PDOS in Figs. 3a, b. The enhanced electronic structure evolution in 2H-WS2/V is also in consistent with the larger geometry distortion and more transferred charge demonstrated in Figs. 1b and 2.
Contact properties of MX2/metal
Because of controllable charge transfer in MX2/metal interface, the electron injection efficiency would be tuned with the selection of MX2 and metal candidate. As a consequence of metallization, the electron tunnel barrier from metal into MX2 membrane will vanish13,20,21 (see Fig. S2 in Supplementary information). The efficiency of electron injection will thus be determined by Schottky barriers at MX2/metal interface, which can be calculated as the energy difference between the fermi level of the MX2/metal contact (EF) and the band edges of free standing MX2s. To be more specific, the energy difference between the fermi energy of the hybrid system and conduction band minimum (EC–EF) of free standing MX2s yields the Schottky barrier of electrons while the energy difference between the corresponding fermi energy and valence band maximum (EF–EV) indicates the Schottky barrier of holes. To give a direct schematic view of this method, the \({\mathrm{\Phi }}_{SB}^{electron}\) and \({\mathrm{\Phi }}_{SB}^{hole}\) of 2H-MoS2/Cu are indicated in the band structure plot in Fig. 4a as one example. The fermi level of this contact is set as 0 eV, while the band structure of free standing MoS2 is plot on top of the contact band structure to show the band alignment. Based on this strategy, the Schottky barrier of all the MX2/metal contact has been calculated. Due to the variation of phase stability, we only show the Schottky barriers for the contacts with the structure of the lowest energy as a representative of the equilibrium contact status. That is to say, 1T’-MX2/metal contact or 1T”-MX2/metal contact will be demonstrated for those systems with potential structural phase transition in MX2 monolayer as shown in Fig. 1.
As being demonstrated in Figs. 4a, b all the contacts can be divided into two categories. For those metal contact with 2H MoS2 and MoSe2, low resistance interfaces are formed when MoS2 or MoSe2 possess n-type doping. For example, V/MoS2 and Mo/MoSe2 are expected to have the lowest Schottky barrier under N doping. For WS2 and WSe2 contacts with the studied metals, the hole barrier is always lower than the electron barrier (Figs. 4c, e). For MoTe2/metal contacts, the Schottky hole barriers of MoTe2/Ru and MoTe2/Rh turn out to be 0 eV, meanwhile the Schottky electron barrier is the same as the bandgap of monolayer MoTe2. This can be understood by the fact that electrons in MoTe2 will be polarized into Ru or Rh once the contacts are formed (shown by Fig. 2e), which shift the fermi level of the contact system below the original valance band maximum.
Moreover, for those MX2/metal contacts with structural phase transition, 1T’(1T”)-MX2/metal contact will be formed at equilibrium state. In those contacts, i.e., 1T”-MoSe2/Sc, 1T”-WS2/Zr, 1T”-WS2/V, 1T”-WSe2/Sc, 1T”-WSe2/Ti 1T”-MoTe2/Cr and 1T’-MoTe2/Nb, both \({\mathrm{\Phi }}_{SB}^{electron}\) and \({\mathrm{\Phi }}_{SB}^{hole}\) will vanish. The reason is mainly due to the fact that significant charge transfer will finally shift the fermi energy of the MX2/metal system above the conduction band minimum of 2H-MX2, in this case no energy barrier is needed to overcome for electron transport from MX2/metal to the channel.
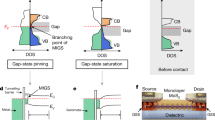
With the information obtained from contact analysis, we suggest that three types of MX2/metal contacts can be formed depending on the amount of interfacial orbital overlapping and charge transfer. As illustrated by Fig. 5a, the first type would induce the largest interfacial resistance for MX2/metal contact, this mostly applies to all the MX2/metal contacts that possess very large lattice misfit, some of them are reported in literature13,20,21 but were screened out using the lattice misfit criterion we described above. Typically, there would be significant interfacial lattice incoherency in such MX2/metal system, which inhibit effective orbital overlapping as being shown in Fig. 3. As a consequence, a sizable tunnel barrier as well as Schottky barrier should be overcome when electrons travel from metal to MX2 channel. This is also the main problem that occurs in previous investigated MX2/metal contacts13,20,21. As suggested by our study, if we can increase the orbital overlapping to some degree, the metallization of MX2 would occur at interface, which can vanish the tunnel barrier between MX2 and metal (Fig. 5b). Because of lattice coherency and orbital overlapping, the metal systems studied in this study generally have very small or zero tunneling barrier. Therefore, the Schottky barrier would be the main factor to limit the contact resistance. Among all the identified candidates, those with smallest \({\mathrm{\Phi }}_{SB}^{electron}\) or \({\mathrm{\Phi }}_{SB}^{hole}\) would be optimal contacts since small size of Schottky can be easily reduced with adequate gating. Additionally, for those 7 systems, we would expect the formation of third types of contact as shown in Fig. 5c if 1T’(1T”)-MX2 is the energetically stable structure. In this case, structural phase transition would happen in MX2 domain that is contacted with metal. Meanwhile, since the fermi level of 1T’(1T”)-MX2/metal is higher than the conduction band minimum of 2H-MX2, the Schottky barrier would vanish as a consequence. Meanwhile, utilizing the states of art phase engineering techniques, the contact nature of such systems can be flexibly engineered. To give one example, MX2 monolayer can be first deposited on top of metal to form 2H-MX2 contact. Due to the finite activation barrier required for 2H→1T’(1T”), contact type as shown in Fig. 5b would be formed. Furthermore, as already been reported in experiments, thermal fluctuation,45,50 plasmonic hot electrons51 or electron beam47 can be effective options to trigger the 2H→1T’(1T”) structure transformation. Accompanied by the phase transition, direct injection of electrons without Schottky barriers would be achieved while the contact type transforms from type 2 (Fig. 5b) to type 3 (Fig. 4c).
(Color online): Illustration of three types of MX2/metal contact, the tunnel barrier and Schottky barrier are demonstrated with \({\mathbf{\Phi }}_{{\boldsymbol{SB}}}^{{\boldsymbol{electron}}}\) and \({\mathbf{\Phi }}_{{\boldsymbol{SB}}}^{{\boldsymbol{hole}}}\) a MX2/metal contact with little orbital overlapping, thus both sizable \({\mathbf{\Phi }}_{{\boldsymbol{TB}}}\) and \({\mathbf{\Phi }}_{{\boldsymbol{SB}}}\) would appear; b MX2/metal contact with strong orbital overlapping, the metallization would eliminate \({\mathbf{\Phi }}_{{\boldsymbol{TB}}}\) but sizable \({\mathbf{\Phi }}_{{\boldsymbol{SB}}}\) still exist; c MX2/metal contact with phase transformation, the new structure would possess higher fermi level than conduction band minimum of the 2H-MX2
To conclude, we have systematically investigated the influences of interface interaction on phase stability of MX2s. With the lattice misfit criterion, 28 MX2/metal systems with strong interface interaction have been identified. Based on interfacial charge calculations and contact resistance analysis, all MX2/metal contacts can be categorized into three groups. The first type of contact would possess zero tunnel barrier between MX2 and metal, while the Schottky barrier can be tuned with injection of electron or holes. In the second contact type, there is a significant charge transfer between the MX2 layer and metal substrate, which induces the structure transformation of MX2 layer from 2H to 1T’(1T”). In this case, both the tunnel barrier and the Schottky barrier vanish. Finally, we presented several schematic designs for applying our theoretical findings, among which the techniques are already reported in experiments. Our research not only provide realistic theoretical reference for the contact behavior for all MX2/metal systems, but also shed lights on potential solutions for conquering the bottleneck of concurrent 2D transistors.
Methods
Atomistic modeling of MX2/metal interface
All the 3d and 4d transition metal are visited for evaluating the performance in metal-MX2 contact. Meanwhile, as being reported in experiments, non-transition metals such as Al,28,29 Ga,30,31 In24,32 are also considered. The smallest lattice misfit strain that can exist between MX2 and metal is used to screen metal contacts with MX2 since large lattice misfit could not provide enough orbital overlapping11,13,20,21 so that charge transfer between MX2 and transition metals are relatively weak. A threshold value of 2% lattice misfit is used to screen MX2/metal systems as a result. Meanwhile, it is worth noting that with such a small lattice misfit strain, very small artificial strain will be enforced for DFT simulation so that the results will be more reasonable.
During the screening process, we first construct low index surfaces of metals, i.e., (001) (110) and (111), due to relatively low surface free energies and better thermodynamic stability.33,34 After then we considered three types of orientations which correspond to –30, 0, and 30 degrees of rotation between the [100] orientation of MX2 and metal substrate. Other interfacial rotations, which might exist in experiments and lead to certain moiré patterns, cannot guarantee enough orbital overlapping due to the small lattice coherency. Besides, other rotations require supercells with more than thousands of atoms, thus it is very challenge or impossible for DFT calculations. Therefore, we do not consider other rotation angles in this investigation. For each orientation considered, the charge transfer amount for all the possible stacking sequences are calculated.
Employing this criterion, we have identified 11 metal and 28 MX2/metal contacts from the periodic table (Fig. 6e). Examples of the selected MX2/metal contact atomic model are demonstrated in Figs. 6a–c. Those models can be applied to study the properties of contact nature in MX2/metal based transistor as shown in Fig. 6d. All the selected metals are summarized in Fig. 6e, in each box, the name of the metal is put on top followed by the lattice type and facet selected to form the MX2/metal interface. Meanwhile, the lattice misfit at interface has also been indicated in Fig. 6e. For visual convenience, different colors are filled in the box to illustrate the amount of interfacial strain. The green color indicates the metal can form MX2/metal interface with misfit less than 1%, while orange means the misfit strain is about 1–2%. For some of the metals, they can form small misfit interface with two types of MX2s but with different level of misfit strain, mixing of corresponding colors has been adopted for those situations. Meanwhile, the supercell of both MX2 and metal used to construct the smallest periodic unit for MX2/metal interface have been given in Table 1.
(Color online): Examples of atomic models for computing contact properties: a Side view of 1T’-MoS2 on (111) surface of FCC-Cu; b Side view of 2H-WSe2 on top of (001) surface of HCP-Ti; c Top view of 1T-MoTe2 on top of (111) surface of BCC-Cr; d Illustration of the use of MX2/metal contact in a field effect transistor (FET); e Illustration of metal selection procedures and selected metals. In the periodic table, the location of selected metals is highlighted with red color. For each selected metal, the crystal structure, the interfacial misfit strain, and the surface orientation are demonstrated. Color is used to illustrate the misfit strain in certain MX2/metal systems, green indicates the interface with misfit strain < 0.1% while yellow indicates the interface misfit strain from 0.1 to 0.2%. A mixture of both colors indicates that interface with both types of misfit strain can exist
DFT calculations
First-principles DFT calculations employing the Perdew-Burke-Ernzerhof functional35 and projector augmented-wave36 method were performed using the Vienna ab initio simulation package for structure optimization and energetic calculations. The dispersive van der Waals interactions between the MoS2 and metals were included using the DFT-D2 method of Grimme.37,38,39 In each calculation, k-point grids are benchmarked to be sufficient for accurate calculation. The energy cutoff has been set as 400 eV for all the MX2/metal interface models and it has been tested to be large enough for energy convergence. A vacuum space of 20 Å perpendicular to each slab model is used to eliminate image interactions. When performing the structure optimizations, the system is regarded as converged when the force per atom is less than 0.01 eV/Å. Being ware of the fact that traditional GGA method failed to provide accurate estimation of band edges,40 we have implemented the consideration of spin orbital coupling (soc) in our calculations. As being demonstrated in previous studies, both the band gaps and the soc induced energy splitting can be well captured with such calculation setup.7,41,42,43
Meanwhile, it should be noted that small lattice misfit still exists in the MX2/metal systems (see Fig. 6e). Since we are mainly interested in how electron transfer from metal to MX2 can influence the phase stability, it would be better not to deform the MX2 lattice as in this case the phase stability will be affected by both strain and charge transfer, making it difficult to decouple the two effects. As a result, for all systems, we deform slightly the metal lattice to fit into the MX2 monolayer.
Data availability
The data related to the findings of this work are available from the corresponding author subject to reasonable request.
References
Ouyang, B. & Song, J. Strain engineering of magnetic states of vacancy-decorated hexagonal boron nitride. Appl. Phys. Lett. 103, 102401 (2013).
Ouyang, B. & Song, J. Covalent pathways in engineering h-BN supported graphene. Carbon 98, 449–456 (2016).
Song, J., Ouyang, B. & Medhekar, N. V. Energetics and kinetics of Li intercalation in irradiated graphene scaffolds. ACS Appl. Mater. Interfaces 5, 12968–12974 (2013).
Ouyang, B., Meng, F. & Song, J. Energetics and kinetics of vacancies in monolayer graphene boron nitride heterostructures. 2D Mater. 1, 035007 (2014).
Ouyang, B., Chen, C. & Song, J. Conjugated π electron engineering of generalized stacking fault in graphene and h -BN. Nanotechnology 29, 09LT01 (2018).
Ouyang, B. & Song, J. Tuning magnetic states of planar graphene/h-BN monolayer heterostructures via interface transition metal-vacancy complexes. J. Phys. Chem. C. 120, 23529–23535 (2016).
Ouyang, B., Mi, Z. & Song, J. Bandgap transition of 2H transition metal dichalcogenides: predictive tuning via inherent interface coupling and strain. J. Phys. Chem. C. 120, 8927–8935 (2016).
Lu, N. et al. MoS2/MX2 heterobilayers: bandgap engineering via tensile strain or external electrical field. Nanoscale 6, 2879–2886 (2014).
Mak, K. F., Lee, C., Hone, J., Shan, J. & Heinz, T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Desai, S. B. et al. MoS2 transistors with 1-nanometer gate lengths. Science 354, 99–102 (2016).
Allain, A., Kang, J., Banerjee, K. & Kis, A. Electrical contacts to two-dimensional semiconductors. Nat. Mater. 14, 1195–1205 (2015).
Radisavljevic, B., Radenovic, A., Brivio, J., Giacometti, V. & Kis, A. Single-layer MoS2 transistors. Nat. Nano. 6, 147–150 (2011).
Kang, J.., Liu, W.., Sarkar, D.., Jena, D.., & Banerjee, K.. Computational study of metal contacts to monolayer transition-metal dichalcogenidesemiconductors. Phys. Rev. X4, 031005 (2014).
Gong, C. et al. Metal contacts on physical vapor deposited monolayer MoS2. ACS Nano 7, 11350–11357 (2013).
Smyth, C. M., Addou, R., McDonnell, S., Hinkle, C. L. & Wallace, R. M. Contact metal–MoS2 interfacial reactions and potential implications on MoS2-based device performance. J. Phys. Chem. C. 120, 14719–14729 (2016).
Leong, W. S. et al. Low resistance metal contacts to MoS2 devices with nickel-etched-graphene electrodes. ACS Nano 9, 869–877 (2015).
Bruix, A. et al. Single-layer MoS2 on Au(111): band gap renormalization and substrate interaction. Phys. Rev. B 93, 165422 (2016).
Cook, M. et al. Influence of interface coupling on the electronic properties of the Au/MoS2 junction. Phys. Rev. B 92, 201302 (2015).
Zhou, Y. et al. Compliant substrate epitaxy: Au on MoS2. Phys. Rev. B 93, 054106 (2016).
Popov, I., Seifert, G. & Tománek, D. Designing electrical contacts to MoS2 monolayers: a computational study. Phys. Rev. Lett. 108, 156802 (2012).
Wang, Y. et al. Does p-type ohmic contact exist in WSe2-metal interfaces? Nanoscale 8, 1179–1191 (2016).
Ouyang, B., Ou, P., Wang, Y., Mi, Z. & Song, J. Phase engineering of MoS2 through GaN/AlN substrate coupling and electron doping. Phys. Chem. Chem. Phys. 18, 33351–33356 (2016).
Ouyang, B., Xiong, S., Yang, Z., Jing, Y. & Wang, Y. MoS2 heterostructure with tunable phase stability: strain induced interlayer covalent bond formation. Nanoscale 9, 8126–8132 (2017).
Srivastava, S. K. & Avasthi, B. N. Synthesis and characterization of indium intercalation compounds of molybdenum diselenide, In x MoSe2 (0 ≤ x ≤ 1). J. Mater. Sci. 24, 1919–1924 (1989).
Tang, W., Sanville, E. & Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 21, 084204 (2009).
Yu, M. & Trinkle, D. R. Accurate and efficient algorithm for Bader charge integration. J. Chem. Phys. 134, 064111 (2011).
Henkelman, G., Arnaldsson, A. & Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comp. Mater. Sci. 36, 354–360 (2006).
Kanthavel, K., Sumesh, K. R. & Saravanakumar, P. Study of tribological properties on Al/Al2O3/MoS2 hybrid composite processed by powder metallurgy. Alex. Eng. J. 55, 13–17 (2016).
Li, N., Feng, L.-p., Su, J., Zeng, W., & Liu, Z.-t. Optical and electrical properties of Al:WS2 films prepared by atomic layer deposition and vulcanization. RSC Adv. 6, 64879–64884 (2016).
Ye, Y. et al. Electrical generation and control of the valley carriers in a monolayer transition metal dichalcogenide. Nat. Nano. 11, 598 (2016).
Gardos, M. N. An Analysis of the Ga/In/WSe2 Lubricant Compact. ASLE Trans. 28, 231–238 (1985).
Deshpande, M. P., Patel, P. D., Vashi, M. N. & Agarwal, M. K. Effect of intercalating indium in WSe2 single crystals. J. Cryst. Growth 197, 833–840 (1999).
Xiong, S. et al. Size and shape dependent surface free energy of metallic nanoparticles. J. Comput. Theor. Nanosci. 8, 2477–2481 (2011).
Xiong, S. et al. Modeling size effects on the surface free energy of metallic nanoparticles and nanocavities. Phys. Chem. Chem. Phys. 13, 10648–10651 (2011).
Perdew, J., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Grimme, S., Ehrlich, S. & Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 32, 1456–1465 (2011).
Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 27, 1787–1799 (2006).
Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104 (2010).
Zhong, H. et al. Interfacial properties of monolayer and bilayer MoS2 contacts with metals: beyond the energy band calculations. Sci. Rep. 6, 21786 (2016).
Kormányos, A., Zólyomi, V., Drummond, N. D. & Burkard, G. Spin-orbit coupling, quantum dots, and qubits in monolayer transition metal dichalcogenides. Phys. Rev. X 4, 011034 (2014).
Kuc, A. & Heine, T. The electronic structure calculations of two-dimensional transition-metal dichalcogenides in the presence of external electric and magnetic fields. Chem. Soc. Rev. 44, 2603–2614 (2015).
Kormányos, A. et al. Monolayer MoS2: trigonal warping, the valley, and spin-orbit coupling effects. Phys. Rev. B 88, 045416 (2013).
Ouyang, B., Lan, G., Guo, Y., Mi, Z. & Song, J. Phase engineering of monolayer transition-metal dichalcogenide through coupled electron doping and lattice deformation. Appl. Phys. Lett. 107, 191903 (2015).
Guo, Y. et al. Probing the dynamics of the metallic-to-semiconducting structural phase transformation in MoS2 crystals. Nano Lett. 15, 5081–5088 (2015).
Kappera, R. et al. Phase-engineered low-resistance contacts for ultrathin MoS2 transistors. Nat. Mater. 13, 1128–1134 (2014).
Lin, Y.-C., Dumcenco, D. O., Huang, Y.-S. & Suenaga, K. Atomic mechanism of the semiconducting-to-metallic phase transition in single-layered MoS2. Nat. Nano. 9, 391–396 (2014).
Medeiros, P. V. C., Tsirkin, S. S., Stafström, S. & Björk, J. Unfolding spinor wave functions and expectation values of general operators: Introducing the unfolding-density operator. Phys. Rev. B 91, 041116 (2015).
Medeiros, P. V. C., Stafström, S. & Björk, J. Effects of extrinsic and intrinsic perturbations on the electronic structure of graphene: Retaining an effective primitive cell band structure by band unfolding. Phys. Rev. B 89, 041407 (2014).
Voiry, D., Mohite, A. & Chhowalla, M. Phase engineering of transition metal dichalcogenides. Chem. Soc. Rev. 44, 2702–2712 (2015).
Kang, Y. et al. Plasmonic hot electron induced structural phase transition in a MoS2 monolayer. Adv. Mater. 26, 6467–6471 (2014).
Acknowledgements
This work is supported by the Jiangsu provincial natural science funding Project No. BK20160308, NSF of China under Grants No. 11304059, the NSF of Heilongjiang Province of China under Grants No. QC2015001 and the International Postdoctoral Exchange Fellowship Program No. 20140016.
Author information
Authors and Affiliations
Contributions
B.O. designed this research; B.O. and Y.J. performed calculations and data analysis; B.O., S.X., and Y.J. wrote this paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ouyang, B., Xiong, S. & Jing, Y. Tunable phase stability and contact resistance of monolayer transition metal dichalcogenides contacts with metal. npj 2D Mater Appl 2, 13 (2018). https://doi.org/10.1038/s41699-018-0059-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-018-0059-1
This article is cited by
-
Efficient Ohmic contacts and built-in atomic sublayer protection in MoSi2N4 and WSi2N4 monolayers
npj 2D Materials and Applications (2021)
-
The effect of metallic substrates on the optical properties of monolayer MoSe2
Scientific Reports (2020)
-
Stable InSe transistors with high-field effect mobility for reliable nerve signal sensing
npj 2D Materials and Applications (2019)