Abstract
Conventional field-effect transistors (FETs) are not expected to satisfy the requirements of future large integrated nanoelectronic circuits because of these circuits’ ultra-high power dissipation and because the conventional FETs cannot overcome the subthreshold swing (SS) limit of 60 mV/decade. In this work, the ordinary oxide of the FET is replaced only by a ferroelectric (Fe) polymer, poly(vinylidene difluoride-trifluoroethylene) (P(VDF-TrFE)). Additionally, we employ a two-dimensional (2D) semiconductor, such as MoS2 and MoSe2, as the channel. This 2D Fe-FET achieves an ultralow SS of 24.2 mV/dec over four orders of magnitude in drain current at room temperature; this sub-60 mV/dec switching is derived from the Fe negative capacitance (NC) effect during the polarization of ferroelectric domain switching. Such 2D NC-FETs, realized by integrating of 2D semiconductors and organic ferroelectrics, provide a new approach to satisfy the requirements of next-generation low-energy-consumption integrated nanoelectronic circuits as well as the requirements of future flexible electronics.
Similar content being viewed by others
Introduction
The development of integrated nanoelectronic devices together with the scaling down of field-effect transistors (FETs), has rendered energy consumption a nonnegligible factor for future electronics applications. Metal–oxide–semiconductor FETs (MOSFETs), an elementary unit of integrated circuits, must be constantly improved to satisfy nanoelectronics requirements.1,2 A key factor in this regard is the subthreshold swing (SS), which is derived from the transfer characteristics of the FET and calculated as follows,3
where V GS is the gate voltage, I DS the drain current, ψ s the surface potential of the semiconducting channel, C s the semiconductor capacitance, C ins the gate insulator capacitance, k the Boltzmann constant, T the temperature, and q the electron unit charge. Conventional MOSFETs have a fundamental barrier due to Boltzmann statistics, which necessitate a minimum voltage of 60 mV to change the current by one order of magnitude at room temperature.4 In recent years, numerous studies have examined various approaches to overcome this limit of 60 mV/dec.4,5,6,7,8 Of these, two approaches are considered the most promising. One is the use of tunneling FET, an ambipolar device in principle that exhibits a p-type behavior with dominant hole conduction and an n-type behavior with dominant electron conduction.4 The second is the negative capacitance FET (NC-FET), which utilizes the negative capacitance (NC) effect of ferroelectric (FE) materials,7,8 a phenomenon wherein negative differential capacitance achieves an energy gain by changing the polarization; its physical origin has been discussed by A. K. Jonscher.9 Especially recently, the NC effect has been increasingly investigated as it is considered one of the most promising mechanisms for overcoming the limitations of transistors.10,11,12,13,14 In 2008, S. Salahuddin and S. Datta theorized a low-power nanoscale device that utilizes the ferroelectric NC effect to amplify gate voltage.7 Continuing experiments on NC-FETs over the past 10 years have improved this device. For example, in 2008, G. A. Salvatore et al. utilized a metal–ferroelectric–insulator–semiconductor (MFIS) structure to realize a P(VDF-TrFE)-based NC-FET.10 In 2016, J. Jo et al. achieved a P(VDF-TrFE)-based NC-FET but using a metal–ferroelectric–metal–insulator–semiconductor (MFMIS) structure.14 In summary, to achieve an NC-FET with an SS lower than 60 mV/dec, a composite gate dielectric is the most suitable mechanism for its structural design.
Furthermore, the semiconducting channel should be composed of a traditional semiconductor, such as silicon (Si) or germanium (Ge).10,15 However, two-dimensional (2D) materials have been widely used in the past 10 years because of their unique physical, chemical, photoelectrical, and electrical properties.16,17,18,19 These materials, especially 2D semiconductors, have been widely applied in FETs to substantially reduce device size and power consumption.20,21,22,23 Thus, 2D materials are the most promising candidates for future nanoelectronic devices. For 2D FETs, however, ordinary dielectric materials, such as SiO2, Al2O3, and HfO2, are usually selected as the gate dielectric; therefore, the working principle of such 2D FETs is the same as that of a conventional FET;21,22,23 accordingly, the SS limit (60 mV/dec) persists, hindering further reduction in power consumption. Therefore, the objective of this study was to incorporate ferroelectric materials possessing the NC effect in 2D materials in order to achieve a ferroelectric/2D FET (Fe2DFET) with ultralow SS and power consumption (hereafter referred to as a 2D NC-FET). Several earlier studies have reported on the combination of ferroelectrics and 2D materials, but most applications have been in memory devices and photodetectors.18,24,25,26,27,28 In addition, F. A. McGuire et al. achieved an Fe2DFET with a sub-60 mV/dec SS, but their device was based on the MFMIS structure.29 In addition to poly(vinylidene difluoride-trifluoroethylene) (P(VDF-TrFE)), hafnium zirconium oxide (HZO) has recently emerged as an environmentally friendly ferroelectric material. M. Si et al. and F. A. McGuire et al. combined HZO and molybdenum disulfide (MoS2) to obtain the 2D NC-FETs that provide the advantages of low voltage and power consumption.30,31 Although they selected the same materials, they obtained 2D NC-FETs with different structures, namely MFIS and MFMIS. The standard structure of NC-FETs, especially 2D NC-FETs, is not clear yet. Moreover, the interaction between ferroelectrics and 2D materials has not been adequately investigated theoretically or experimentally. These are topics that warrant comprehensive investigation.
In this work, we realize a 2D NC-FET based on the metal–ferroelectric–semiconductor (MFS) structure, in which the ordinary oxide of the FET is replaced only by a FE polymer, P(VDF-TrFE). We employ a 2D semiconductor, such as MoS2 and molybdenum diselenide (MoSe2), as the channel. This 2D NC-FET achieved an ultralow SS of 24.2 mV/dec over four orders of magnitude in drain current at ultralow drain voltage (0.1 V) and room temperature. Moreover, we comprehensively investigated the thickness of ferroelectrics in these 2D NC-FETs, and an SS of 51.2 mV/dec over one decade was obtained even when the P(VDF-TrFE) thickness was reduced to 50 nm. Furthermore, we clarify the NC effect in the developed 2D NC-FETs on the basis of the Landau theory. For comparison, we prepared MFMIS- and MFIS-based Fe2DFETs. The experimental results showed that none of the MFMIS and MFIS devices could obtain a sub-60 mV/dec SS, meaning that these two types of devices cannot fully exploit the NC effect of P(VDF-TrFE) in 2D NC-FETs. Therefore, this work presents a stable 2D NC-FET gated only by a ferroelectric polymer layer; the MFS-based 2D NC-FET not only maximizes the NC effect of P(VDF-TrFE) but also has a simplified device structure. The developed device has potential for applications in future nanoelectronic devices requiring ultralow power consumption and fast switching.
Results and discussion
NC effect is a transient and unstable phenomenon; nevertheless, its occurrence in ferroelectric materials has been verified.7,9 The NC effect was first observed in 2014 by A. I. Khan et al. in a ferroelectric Pb(Zr0.2Ti0.8)O3 capacitor based on the voltage pulse method.32 The NC effect of ferroelectric materials employed as the gate dielectric in FETs should improve device performance, for example, by reducing the operating voltage and accelerating the switching rate.7,12,33 The switching rate and power consumption of FETs depend completely on the scale of the SS used to measure the gate voltage increment required to change the drain current by one order of magnitude. SS can be calculated using equation (1), in which the term 1 + C s/C ins is referred to as the m factor:
In equation (1), (kT/q) × ln10 is a constant equaling 60 mV/dec at 300 K. Thus, in a conventional FET, the SS limit is 60 mV/dec because C S and C ins are always positive, that is m > 1, a phenomenon known as the Boltzmann tyranny. However, when a ferroelectric material is used as the gate dielectric in FETs, C ins can become negative because of its NC characteristic. Accordingly, if C ins < 0 in equation (2), then m < 1, and the SS will likely be less than 60 mV/dec at room temperature.
Numerous studies have focused on optimizing the performance of NC-FETs. These studies have mostly used one of the following three device structures: (1) MFMIS, (2) MFIS, and (3) MFS.10,12,34,35 The NC effect is a dynamic state that occurs when the polarized electric field switches from one stable state to another,7,12,32 which renders difficult the direct measurement of the NC in a ferroelectric capacitor. Therefore, researchers usually connect a dielectric capacitor in series with a ferroelectric capacitor to neutralize this instability. In this composite configuration, the total capacitance is stable and positive and larger than the capacitance of an ordinary capacitor. Therefore, in both MFMIS and MFIS devices, the insulation layer can act as an ordinary capacitor stabilizing the NC effect of the ferroelectric layer. Specifically, in an MFMIS device, the role of the interlayer metal between the ferroelectric and insulation is mainly to eliminate the leakage current between the ferroelectric and substrate.12 Furthermore, the interlayer metal provides an equipotential surface as a floating gate, thus enabling the treatment of the ferroelectric and the underlying MOSFET as two separate circuit entities connected by a wire.36 Without this interlayer metal, an MFIS device can be achieved only if a ferroelectric and an insulation composite film are used as the gate dielectric. However, without the interlayer metal, the insulation in an MFIS device also serves to stabilize the NC effect of the ferroelectric material and shield against gate leakage current.37 G. Pahwa et al. compared MFMIS-based and MFIS-based devices with theoretical models and reported that the MFIS device exhibits a higher ON current and a steeper SS than does the MFMIS device.36
To modulate the semiconductor channel in a conventional MFS FET, we could replace the gate dielectric with only a ferroelectric layer. As argued by S. Salahuddin and S. Datta, who first proposed the concept of NC-FET in 2008, if a ferroelectric replaced the ordinary insulator in a MOSFET, the electrostatic potential ψ s at the ferroelectric–semiconductor interface would exceed the external gate voltage (V GS) because of the NC effect of the ferroelectric;7 in this approach, the device structure (MFS) does not change. Although diverse materials are used for the ferroelectric and channel semiconductors in NC-FETs, the devices based on these three structures, namely MFMIS, MFIS, and MFS, all have high potential to facilitate the NC effect of ferroelectric materials, effectively improving FET performance. The NC effect has been confirmed in ferroelectric materials, but the device structure of NC-FETs remains to be standardized for different materials, especially in the case of integration with 2D materials, which is a recent and growing trend. Therefore, in this study, we prepared, tested, and comprehensively investigated a large number of devices with the aforementioned three structures. The experimental results indicated that only the MFS-based device fully utilizes the NC effect of the ferroelectric materials.
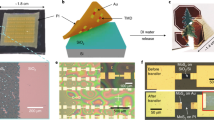
Fig. 1a is a schematic of the MFS-based 2D NC-FET, in which MoS2 is used as the semiconducting channel and P(VDF-TrFE) thin film with a molar ratio of 70%/30% is used as the ferroelectric gate dielectric. Figure 1b shows optical microscope images captured at three stages in the fabrication process. The configuration of the MFS structure was confirmed through transmission electron microscopy (TEM) (Fig. 1c). In this study, all MoS2 films selected for fabricating the semiconducting channel were a few (approximately four) layers thick; this was confirmed through Raman spectroscopy (Fig. 1d) and atomic force microscopy (AFM) (Fig. 1e). The technological and experimental details are summarized in the “methods” section. The present section details and discusses the experimental results for the MFS-based 2D NC-FET and examines the working principle of the device and the mechanism of the NC effect on the basis of the Landau theory. We carefully studied the effect of ferroelectric thickness on device performance when using MoS2 as the semiconducting channel and MoSe2 as the auxiliary. For comparison, MFMIS and MFIS Fe2DFETs were prepared. All measurements were conducted in an atmospheric environment and at room temperature, and all drain biases (V SD) were set to 0.1 V to ensure ultralow power consumption.
a 2D structure schematic of a 2D NC-FET based on the MFS structure, with P(VDF-TrFE) employed as the ferroelectric layer and MoS2 as the 2D semiconductor channel. b Optical microscope images of a 2D NC-FET at different process stages; all scale bars (blue) are 20 µm. c Cross-sectional TEM image of a 2D NC-FET showing layered MoS2 (≈4 layers). d Raman spectra of MoS2 used in this device; the two peaks at E2g 1 = 383.84 cm−1 and A1g = 407.79 cm−1 indicate the four layers. e AFM height image of the MoS2. The cross-section along the black line shows a height of 3.5 nm, reflecting the four MoS2 layers
For the MFS-based 2D NC-FET, we investigated the device with an MoS2 channel, which featured strong semiconducting properties.21 In this case, the P(VDF-TrFE) thickness was varied from 50 to 300 nm; the corresponding transfer curves are plotted in Fig. 2a, where all transfer curves are counterclockwise; an SS of 24.2 mV/dec over four orders of magnitude was achieved at the left side of the transfer curve for the 300-nm P(VDF-TrFE). Because of the direct contact between P(VDF-TrFE) and MoS2, the carriers and the band of the MoS2 channel can be fully controlled by the polarized electric field. Moreover, the coercive voltage is strongly correlated to and thus increases with P(VDF-TrFE) thickness.38 Hence, the threshold voltage of the 2D NC-FET is heavily dependent on the coercive voltage of P(VDF-TrFE), and the counterclockwise hysteresis window in the transfer curves widen with increase in P(VDF-TrFE) thickness (Fig. 2a). For improved image clarity and for analysis of the SS characteristics, the left subthreshold regions of these four transfer curves are extracted and presented in Fig. 2b. Clearly, the 2D NC-FET with the 300-nm P(VDF-TrFE) achieved the lowest SS of 24.2 mV/dec over 4 decades. As the thickness of P(VDF-TrFE) decreased, its SS deteriorated; nevertheless, SS = 29.6 mV/dec over 3 decades for the 200-nm P(VDF-TrFE), SS = 33.1 mV/dec over 2 decades for the 100-nm P(VDF-TrFE), and SS = 51.2 mV/dec over 1 decade for the 50-nm P(VDF-TrFE), all of which exceeded the limit of 60 mV/dec.
a Transfer curves of 2D NC-FETs based on the MFS structure with MoS2 channel and P(VDF-TrFE) of different thicknesses (50, 100, 200, and 300 nm). All transfer curves are counterclockwise, and the hysteresis window reduces with decrease in P(VDF-TrFE) thickness. In these measurements, all V SD was set to 0.1 V. b Extracted curves of the left side of each transfer curve in a. The dotted green line is a datum line of the limit of SS = 60 mV/dec for a conventional MOSFET. The lowest SS = 24.2 mV/dec over 4 decades was achieved at a P(VDF-TrFE) thickness of 300 nm. For a P(VDF-TrFE) thickness of 50 nm, SS = 51.2 mV/dec over 1 decade, which is lower than 60 mV/dec. c Schematic of the 2D NC-FET with P(VDF-TrFE) as the gate dielectric and MoS2 as the channel. The right panel shows the equivalent capacitive divider of the gate voltage. d Simplified diagram of the 2D NC-FET work processes showing cyclical switching form one state to another. P(VDF-TrFE) polarization reverses from downward to upward abruptly, but the converse change in polarization is gradual
The schematic of the 2D NC-FET and the corresponding voltage divider are shown in Fig. 2c. Per the Landau theory, for BaTiO3, the surface potential of the semiconducting channel (ψ s) can be amplified by the NC effect of the ferroelectric, which is larger than the external gate voltage (V GS); moreover, the ψ s/V GS ratio increases with ferroelectric thickness.7 Therefore, these sub-60 mV/dec SSs of the 2D NC-FETs can be completely attributed to the NC effect of P(VDF-TrFE). As explained earlier, the NC effect occurs when the polarization reverses, which is driven by the external gate voltage. Because the MoS2 used in this study is an n-type semiconductor, sub-60 mV/dec SSs can be achieved on only one side (always the left side) of the transfer curves. This phenomenon can be explained on the basis of band theory.39,40 When the P(VDF-TrFE) is polarized downward (left panel, Fig. 2d), the electrons in the MoS2 are engaged to compensate for the polarization charges. Because the Fermi level of MoS2 is increased to reduce the difference in the work function levels of source and drain electrodes (ψ D), and electrons are the majority carriers in MoS2, which maintain the drain current at a high level, MoS2 can fully compensate the downward polarization field. In addition, the top-gate aluminum (Al) is a metal and can compensate completely for the polarization charges; this enables a steady state before reversing polarization orientation. As long as the external gate voltage does not exceed its negative coercive field, the drain current remains at a high level because the electrons in MoS2 are bounded by the internal electric field (i.e., poling field). When the external gate voltage slightly exceeds the negative coercive voltage, the polarization direction suddenly changes from downward to upward; simultaneously, the compensation charges in the MoS2 are instantly converted from electrons to holes. In other words, the Fermi level of MoS2 is rapidly decreased as the polarization orientation shifts from downward to upward; in addition, and ψ D increases, hindering the movement of electrodes, at which time the drain current abruptly alters from the ON state to the OFF state, resulting in an ultrasteep SS.
Holes, the minority carriers in MoS2, cannot completely compensate for the upward polarized electric field (right panel, Fig. 2d). When the external gate voltage is swept from negative to positive (to less than the positive coercive voltage), the carrier concentration in the MoS2 channel is simultaneously modulated by the external and internal electric fields, which have opposing effects: the upward internal field bounds the holes and tends to maintain the low Fermi level of MoS2; by contrast, although the negative external gate voltage also induces holes and lowers the Fermi level of MoS2, the hole concentration declines and the Fermi level increases as the external gate voltage changes from a negative value to zero. When the external gate voltage exceeds zero, electrons are induced in the MoS2, and the Fermi level increases more easily, which increases the drain current; this phenomenon is completely opposite to that of the internal field. Because the hole concentration in MoS2 is insufficient to compensate for the upward internal field, especially in the positive external gate voltage range, the drain current increases slowly as the external gate voltage is swept from zero to positive; consequently, the SS is considerably higher than 60 mV/dec. In sum, over the entire work process, the 2D NC-FET switches from the ON state to the OFF state and then back to the ON state cyclically (Fig. 2d), wherein the ON–OFF switching is abrupt and the OFF–ON switching is gradual.
For comparison, the experimental results of the MFMIS-based and MFIS-based Fe2DFETs are presented in Supplementary Information Part 1. None of the MFMIS and MFIS Fe2DFETs could obtain a sub-60 mV/dec SS. This is due to the interlayer metal and the insulator layer in these devices partly shield the polarization effect of P(VDF-TrFE) on the MoS2 channel, and without the constraint of polarized charge on the carriers in the MoS2 channel, the voltage amplified by the NC effect of P(VDF-TrFE) cannot act on the MoS2 channel. Therefore, devices based on these two structures cannot be used to fabricate FETs with ultralow power consumption. Accordingly, we conclude that MFMIS and MFIS structures are unsuitable for fabricating 2D NC-FETs.
The key operating principle of 2D NC-FETs is determined by the nonlinear polarization (P)–electric field (E) relationship of the ferroelectric insulator.41 Therefore, it is necessary to affirm whether the P(VDF-TrFE) used in the 2D NC-FET experiences the NC effect. To this end, a series of Al-P(VDF-TrFE)-Au capacitors with different P(VDF-TrFE) thicknesses were prepared and their P–V and P–E relationships were measured. The P–V curves (Fig. 3a) clarify that the coercive voltage is strongly correlated to and increases with the P(VDF-TrFE) thickness. Then, by converting the voltage into the electric field by using E = V/t, where t is the P(VDF-TrFE) thickness, the P–E curves can be derived (solid lines, Fig. 3b). From these experimental P–E curves, we carefully derived the P–E relationship for P(VDF-TrFE) by using the Landau–Khalatnikov (LK) equation to confirm its NC characteristic. The LK equation is the most advanced approach for modeling the dynamic characteristics of ferroelectric materials7 and can be expressed as follows:
where G is Gibbs free energy, P the polarization of the ferroelectric insulator, t the thickness of the ferroelectric layer, and δ a temperature independent parameter.42 G can be calculated as
where α is a temperature dependent parameter, β and γ are assumed to be independent of the temperature42 and E is the electric field applied on the ferroelectric capacitor. The P–E relationship can be derived from equations (3) and (4):
a, Hysteresis loops of a series of Al-P(VDF-TrFE)-Au capacitors with 50, 100, 200, and 300-nm P(VDF-TrFE). The coercive voltage of P(VDF-TrFE) significantly reduces with P(VDF-TrFE) thickness, but its polarization intensity is almost constant. b, Polarization vs. electric filed for P(VDF-TrFE) of thickness 300, 200, 100, and 50 nm. The solid lines are experimental data and the dotted lines are calculated using the LK equation
From the experimental P−E curves, the material parameter α, β, and γ for P(VDF-TrFE) with different thicknesses were extracted through fitting with equation (5) (dotted line, Fig. 3b). We assumed that dP/dt = 0. The Landau coefficients for P(VDF-TrFE) with different thicknesses are displayed in Table 1. Figure 3b shows that there is a negative differential capacitance in each curve, meaning that P(VDF-TrFE) does have the NC effect. However, in the case of the Al-P(VDF-TrFE)-Au capacitor, the NC effect weakened with reduction in P(VDF-TrFE) thickness. This characteristic is consistent with the electrical results obtained for the proposed 2D NC-FETs. Hence, electrode material is a crucial parameter that must be considered in the further development of 2D NC-FETs.
The SS for all devices in all experiments were extracted and analyzed. The result show that none of the MFMIS and MFIS devices achieved a sub-60 mV/dec SS, whereas most of the MFS devices achieved an ultralow SS much lower than 60 mV/dec. Furthermore, the 2D NC-FETs based on the MFS structure with an MoSe2 channel exhibited the lowest SS of 24.3 mV/dec over 4 decades (Supplementary Information Part 2). Therefore, the NC effect of P(VDF-TrFE) manifests in MFS-based devices with a transition metal dichalcogenide channel. However, the NC effect is generally unstable unless an ordinary capacitor is connected in series.7,32 To understand why the proposed MFS-based device can be used to fabricate a 2D NC-FET, we measured the capacitance of a series of Al-P(VDF-TrFE)-Au–based capacitors of area 1 × 104 µm2 with different P(VDF-TrFE) thicknesses. According to the capacitance series model, the total capacitance can be expressed as
where C is the total capacitance of the entire capacitor, C i is the interface capacitance, and C f is the ferroelectric capacitance. The reciprocal of capacitance (C −1) varies linearly with P(VDF-TrFE) thickness.43 After linear fitting using equation (6), we found that a fixed capacitance of approximately 5.5 nF persists even when the P(VDF-TrFE) thickness is reduced to zero (Fig. 4a). Therefore, we hypothesized that a dead layer exists at the interface between Al and P(VDF-TrFE);44,45,46 TEM (inset, Fig. 4a) confirmed this hypothesis: specifically, AlF3 was found directly between Al and P(VDF-TrFE), but no contact was observed between P(VDF-TrFE) and other metals such as silver (Ag), gold (Au), and cooper (Cu).45,47 In this case, the AlF3 layer served as an ordinary capacitor, resulting in a stable MFS-based 2D NC-FET.
a Linearity of the reciprocal capacitance vs. the P(VDF-TrFE) thickness. Semisolid circles show the experimental data, and the red line is the fitted curve. Inset shows a cross-sectional TEM image of the interface between Al and P(VDF-TrFE); a dead layer can be seen at the interface. Scale bar = 50 nm. b SS statistics for 2D NC-FET based on the MFS structure with different P(VDF-TrFE) thicknesses
The SSs of most 2D NC-FETs based on the MFS structure were less than 60 mV/dec (Fig. 4b). Each point in Fig. 4b originates from the transfer curves shown in Supplementary Information Part 3. Moreover, Fig. 4b clarifies that the SS significantly declines as the thickness of P(VDF-TrFE) is rduced to 50 nm, because polarization intensity is independent of P(VDF-TrFE) thickness but depends on film crystallinity, which in turn is dependent on the preparation method.38 Therefore, this reduction in SS is mainly due to technological limitations as well as the choice of the top-gate metal, which strongly influences the capacitance of the dead layer. Our group has been able to maturely prepare ultrathin P(VDF-TrFE) films with excellent ferroelectricity by using the Langmuir–Blodgett method,48 but its integration with 2D NC-FETs requires further study. Because both the coercive voltage of P(VDF-TrFE) (Fig. 2a) and threshold voltage of 2D NC-FET (Fig. 3a) are strongly dependent on the P(VDF-TrFE) thickness. Therefore, further scaling the P(VDF-TrFE) thickness can narrow the hysteresis window and reduce the sweeping range of the gate voltage, which in turn reduces the power consumption.
In conclusion, we demonstrated an n-type NC-FET with a 2D channel whose gate dielectric is only a ferroelectric polymer film without any other complex structure. This 2D NC-FET exhibits an ultralow SS of 24.2 mV/dec over four orders of magnitude in drain current at room temperature. Sub-60 mV/dec switching was achieved for ferroelectric P(VDF-TrFE) layers of various thicknesses. Additionally, the mechanism of the NC effect of P(VDF-TrFE) was clarified using the Landau theory. This study provides a new methodology to adapt to the demands of next-generation low-energy-consumption integrated nano/flexible electronic applications.
Methods
High-quality MoS2 or MoSe2 nanosheets were fabricated through mechanical exfoliation using bulk crystals (2D semiconductor, Inc.) and transferred to a substrate composed of heavily doped p-type Si and 280 nm SiO2. The few-layer MoS2 or MoSe2 was screened under a microscope and its coordinates marked for electron beam exposure (EBL). Design CAD was used to draw the desired electrodes in the exposure range. Next, methyl methacrylate and poly(methyl methacrylate) were sequentially spin-coated onto the substrate. The source and drain electrodes were thus prepared using the EBL method followed by thermal evaporation and lift off. Here, Cr/Au (10 nm/50 nm) was deposited through thermal evaporation with a vacuum degree of less than 1 × 10−3 Pa to form the source and drain metal electrodes to ensure good Ohmic contact between the electrodes and the MoS2 or MoSe2 channel. Subsequently, the devices were annealed at 200 °C for 2 h in a vacuum chamber with 100 sccm argon (Ar) to remove the residual and to improve the Ohmic contact between source/drain and the MoS2 or MoSe2 channel. For MFMIS and MFIS devices, HfO2 (10 and 15 nm) was prepared through atomic layer deposition in a vacuum chamber at 95 °C. The interlayer metal Cr/Au (8 nm/16 nm) in MFMIS devices was also fabricated through the EBL method. P(VDF-TrFE) thin film with a molar ratio of 70%/30% was dissolved in 2.5%wt diethyl carbonate. Then, P(VDF-TrFE) films were prepared through spin-coating of the substrates under atmospheric conditions. Per our experience, in the spin-coating of P(VDF-TrFE), a thickness of 50 nm per layer can be obtained at 3000 rpm in 20 s. Cyclic spin-coating yielded a P(VDF-TrFE) film with the target thickness, which was annealed at 115 °C for 10 min per layer to evaporate the solvent in an annealing furnace under atmospheric conditions. After the final layer was spin-coated, the P(VDF-TrFE) films were annealed at 135 °C for 4 h to enhance their crystallinity. Top-gate electrode aluminum film (Al; 35 nm) was fabricated through thermal evaporation with a vacuum degree of less than 1 × 10−4 Pa, and then patterned through negative photoresist ultraviolet photolithography and argon ion etching. Finally, the residual negative photoresist on the top gate was removed through oxygen (O2) plasma etching.
In this work, all electric measurements were performed under ambient conditions and at room temperature. Electrical characterizations were performed using the Lake Shore probe station and an Agilent B2902A Semiconductor parameter analyzer. The hysteresis loops were measured using a Radiant Precision LC materials analyzer, and the capacitance of the Al-P(VDF-TrFE)-Au capacitor was measured using an Agilent E4980A precision LCR meter. TEM data was obtained at Dongguan Xinke Technology Research and Development Co., Ltd. Materials Science Laboratory.
Data availability
The data that support the findings of this study are available upon the request from the Corresponding Author.
References
Sakurai, T. Perspectives of low-power VLSI’s. IEICE Trans. Electron. 87, 429–436 (2004).
Waldrop, M. M. More than moore. Nature. 530, 144 (2016).
Van Overstraeten, R. J., Declerck, G. J. & Muls, P. A. Theory of the MOS transistor in weak inversion-new method to determine the number of surface states. IEEE Trans. Electron Devices 22, 282–288 (1975).
Ionescu, A. M. & Riel, H. Tunnel field-effect transistors as energy-efficient electronic switches. Nature 479, 329–337 (2011).
Gopalakrishnan, K., Griffin, P. B. & Plummer, J. D. I-MOS: a novel semiconductor device with a subthreshold slope lower than kT/q. In Electron Devices Meeting, 2002. IEDM'02. International (ed. Shuji, I.) 289–292 (IEEE, San Francisco, CA, 2002).
Padilla, A., Yeung, C. W., Shin, C., Hu, C. & Liu, T.-J. K. Feedback FET: a novel transistor exhibiting steep switching behavior at low bias voltages. In Electron Devices Meeting, 2008. IEDM 2008. IEEE International (ed. Ralf, B.) 1–4 (IEEE, San Francisco, CA, 2008).
Salahuddin, S. & Datta, S. Use of negative capacitance to provide voltage amplification for low power nanoscale devices. Nano Lett. 8, 405–410 (2008).
Zhirnov, V. V. & Cavin, R. K. Nanoelectronics: Negative capacitance to the rescue? Nat. Nanotechnol. 3, 77–78 (2008).
Jonscher, A. K. The physical origin of negative capacitance. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 82, 75–81 (1986).
Salvatore, G. A., Bouvet, D. & Ionescu, A. M. Demonstration of subthrehold swing smaller than 60mV/decade in Fe-FET with P(VDF-TrFE)/SiO2 gate stack. In Electron Devices Meeting, IEDM 2008. IEEE International (ed. Ralf, B.) 1–4 (IEEE, San Francisco, CA, 2008).
Rusu, A., Salvatore, G. A., Jimenez, D. & Ionescu, A. M. Metal-ferroelectric-meta-oxide-semiconductor field effect transistor with sub-60 mV/decade subthreshold swing and internal voltage amplification. In Electron Devices Meeting (IEDM), 2010 IEEE International (ed. Meikei, I.) 11–16 (IEEE, San Francisco, CA, 2010).
Jo, J. et al. Negative capacitance in organic/ferroelectric capacitor to implement steep switching MOS devices. Nano Lett. 15, 4553–4556 (2015).
Park, J. H. et al. Sub-kT/q subthreshold-slope using negative capacitance in low-temperature polycrystalline-silicon thin-film transistor. Sci. Rep. 6, 24734 (2016).
Jo, J. & Shin, C. Negative capacitance field effect transistor with hysteresis-free sub-60-mV/decade switching. IEEE Electron Device Lett. 37, 245–248 (2016).
Liao, Y.-H., Fan, S.-T. & Liu, C. Modeling and simulation of negative capacitance gate on Ge FETs. ECS Trans. 75, 461–467 (2016).
Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004).
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Wang, X. et al. Ultrasensitive and broadband MoS2 photodetector driven by ferroelectrics. Adv. Mater. 27, 6575–6581 (2015).
Mas-Balleste, R., Gomez-Navarro, C., Gomez-Herrero, J. & Zamora, F. 2D materials: to graphene and beyond. Nanoscale 3, 20–30 (2011).
Desai, S. B. et al. MoS2 transistors with 1-nanometer gate lengths. Science 354, 99–102 (2016).
Radisavljevic, B., Radenovic, A., Brivio, J., Giacometti, iV. & Kis, A. Single-layer MoS2 transistors. Nat. Nanotechnol. 6, 147–150 (2011).
Li, L. et al. Black phosphorus field-effect transistors. Nat. Nanotechnol. 9, 372–377 (2014).
Liu, W. et al. Role of metal contacts in designing high-performance monolayer n-type WSe2 field effect transistors. Nano Lett. 13, 1983–1990 (2013).
Wang, X. et al. Ferroelectric FET for nonvolatile memory application with two-dimensional MoSe2 channels. 2D Mater. 4, 025036 (2017).
Chen, Y. et al. Optoelectronic properties of few-layer MoS2 FET gated by ferroelectric relaxor polymer. ACS Appl. Mater. Interfaces 8, 32083–32088 (2016).
Zheng, Y. et al. Graphene field-effect transistors with ferroelectric gating. Phys. Rev. Lett. 105, 166602 (2010).
Lee, Y. T. et al. Nonvolatile ferroelectric memory circuit using black phosphorus nanosheet-based field-effect transistors with P(VDF-TrFE) polymer. ACS Nano 9, 10394–10401 (2015).
Ko, C. et al. Ferroelectrically gated atomically thin transition‐metal dichalcogenides as nonvolatile memory. Adv. Mater. 28, 2923–2930 (2016).
McGuire, F. A., Cheng, Z., Price, K. & Franklin, A. D. Sub-60 mV/decade switching in 2D negative capacitance field-effect transistors with integrated ferroelectric polymer. Appl. Phys. Lett. 109, 093101 (2016).
Si, M. et al. Steep slope MoS2 2D transistors: negative capacitance and negative differential resistance. arXiv preprint arXiv:1704.06865 (2017).
McGuire, F. A. et al. Sustained sub-60 mV/decade switching via the negative capacitance effect in MoS2 transistors. Nano Lett. 17, 4801–4806 (2017).
Khan, A. I. et al. Negative capacitance in a ferroelectric capacitor. Nat. Mater. 14, 182–186 (2015).
Catalan, G., Jiménez, D. & Gruverman, A. Ferroelectrics: negative capacitance detected. Nat. Mater. 14, 137–139 (2015).
Xiao, Y. et al. An improved model for the surface potential and drain current in negative capacitance field effect transistors. RSC Adv. 6, 103210–103214 (2016).
Rollo, T. & Esseni, D. Supersteep retrograde doping in ferroelectric MOSFETs for sub-60mV/dec subthreshold swing. Solid-State Device Research Conference (ESSDERC), 2016 46th European (ed. Thomas, E.) 360–363 (IEEE, Lausanne, Switzerland, 2016)
Pahwa, G., Dutta, T., Agarwal, A. & Chauhan, Y. S. Compact model for ferroelectric negative capacitance transistor with MFIS structure. IEEE Trans. Electron Devices 64, 1366–1374 (2017).
Dasgupta, S. et al. Sub-kT/q switching in strong inversion in PbZr0.52Ti0.48O3 gated negative capacitance FETs. IEEE J. Explor. Solid-State Comput. Devices Circuits 1, 43–48 (2015).
Wang, J. et al. Transition of the polarization switching from extrinsic to intrinsic in the ultrathin polyvinylidene fluoride homopolymer films. Appl. Phys. Lett. 104, 182907 (2014).
Lopez-Sanchez, O., Lembke, D., Kayci, M., Radenovic, A. & Kis, A. Ultrasensitive photodetectors based on monolayer MoS2. Nat. Nanotechnol. 8, 497–501 (2013).
Li, H.-M. et al. Metal-semiconductor barrier modulation for high photoresponse in transition metal dichalcogenide field effect transistors. Sci. Rep. 4, 4041 (2014).
Majumdar, K., Datta, S. & Rao, S. P. Revisiting the theory of ferroelectric negative capacitance. IEEE Trans. Electron Devices 63, 2043–2049 (2016).
Rabe, K. M., Ahn, C. H. & Triscone, J.-M. Physics of ferroelectrics: a modern perspective, Vol. 105 (Springer-Verlag, Berlin, Heidelberg, 2007).
Wang, J. et al. High electric tunability of relaxor ferroelectric Langmuir–Blodgett terpolymer films. Appl. Phys. Lett. 93, 192905 (2008).
Takahashi, Y., Kitahama, A. & Furukawa, T. Dielectric properties of the surface layer in ultra-thin films of a VDF/TrFE copolymer. IEEE Trans. Dielectr. Electr. Insul. 11, 227–231 (2004).
Liu, B. et al. Asymmetric capacitance-voltage curves induced by pinned interface dipoles in poly (vinylidene fluoride/trifluoroethylene) capacitor. J. Infrared Millim. Waves 35, 143–146 (2016).
Kitahama, A., Takahashi, Y. & Furukawa, T. Characterization of surface dead layer in VCF/TrFE nano films by means of broadband dielectric spectroscopy. In Electrets, 2002. ISE 11. Proceedings. 11th International Symposium (ed. Fleming, R. J.) 99–101 (IEEE, Melbourne, Victoria, Australia, 2002).
Wu, P., Yang, G. R., Ma, X. & Lu, T. M. Interaction of amorphous fluoropolymer with metal. Appl. Phys. Lett. 65, 508–510 (1994).
Tian, B. et al. Tunnel electroresistance through organic ferroelectrics. Nat. Commun. 7, 11502 (2016).
Acknowledgements
This work was partially supported by the Major State Basic Research Development Program (Grant Nos. 2013CB922302 and 2016YFA0203900), National Natural Science Foundation of China (Grant Nos. 51472210, 61274107, 61474131, 61574152, 61622401, 61674158 and 61404113), Key Research Project of Frontier Sciences of Chinese Academy of Sciences (QYZDB-SSWJSC016), Science and Technology Support Program of Jiangsu province (BE2014147-1), and Postgraduate Innovation Project of Hunan Province (CX2016B259). We acknowledge Wallace Academic Editing for editing this manuscript.
Author information
Authors and Affiliations
Contributions
J.W., P.Z. and M.T. conceived and supervised the research. X.W. and Y.C. fabricated the devices and carried out the measurements. X.W., J.W., W.H., S.S., H.S., T.L., J.S. and X.M. performed the data analysis. X.W., J.W. and T.L. carried out the calculation of negative effect of P(VDF-TrFE). X.W. and J.W. co-wrote the paper. All authors discussed the results and revised the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, X., Chen, Y., Wu, G. et al. Two-dimensional negative capacitance transistor with polyvinylidene fluoride-based ferroelectric polymer gating. npj 2D Mater Appl 1, 38 (2017). https://doi.org/10.1038/s41699-017-0040-4
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-017-0040-4
This article is cited by
-
Large-area synthesis of high electrical performance MoS2 by a commercially scalable atomic layer deposition process
npj 2D Materials and Applications (2023)
-
Domain wall enabled steep slope switching in MoS2 transistors towards hysteresis-free operation
npj 2D Materials and Applications (2022)
-
Charge carrier modulation in graphene on ferroelectric single-crystal substrates
NPG Asia Materials (2022)
-
Ferroelectric order in van der Waals layered materials
Nature Reviews Materials (2022)
-
Van der Waals engineering of ferroelectric heterostructures for long-retention memory
Nature Communications (2021)