Abstract
DNA methylation is an epigenetic modification involving the addition of a methyl group to DNA, which is heavily involved in gene expression and regulation, thereby critical to the progression of diseases such as cancer. In this work we show that detection and localization of DNA methylation can be achieved with nanopore sensors made of two-dimensional materials such as graphene and molybdenum di-sulfide. We label each DNA methylation site with a methyl-CpG binding domain protein (MBD1), and combine molecular dynamics simulations with electronic transport calculations to investigate the translocation of the methylated DNA–MBD1 complex through two-dimensional material nanopores under external voltage biases. The passage of the MBD1-labeled methylation site through the pore is identified by dips in the current blockade induced by the DNA strand, as well as by peaks in the transverse electronic sheet current across the two-dimensional layer. The position of the methylation sites can be clearly recognized by the relative positions of the dips in the recorded ionic current blockade with an estimated error ranging from 0 to 16%. Finally, we define the spatial resolution of the two-dimensional material nanopore device as the minimal distance between two methylation sites identified within a single measurement, which is 15 base pairs by ionic current recognition, but as low as 10 base pairs by transverse electronic conductance detection, indicating better resolution with this latter technique. The present approach opens a new route for precise and efficient profiling of DNA methylation.
Similar content being viewed by others
Introduction
DNA methylation is one the most common epigenetic modifications in eukaryotic genome, occurring primarily through the addition of methyl groups at the 5th-carbon of a cytosine ring. Methylation plays a crucial role in the expression of genes in mammalian cells and is therefore related to cell development, aging and development of diseases such as cancer. In vertebrates, methylation typically occurs in DNA sequences with a relatively high content of CpG dinucleotides (namely, 5’-CG-3’), known as CpG islands.1, 2 Owing to its relevance in gene expression, CpG island methylation can serve as a biomarker that can be used in risk assessment and early diagnosis of methylation-relevant diseases such as cancer. Since both hypo and hyper CpG methylation occur in the oncogene promoters and tumor suppressing genes respectively, detecting and mapping of both unmethylated and methylated CpGs across the genome is of crucial importance.3,4,5
The most widely used approach for mapping methylation sites in DNA currently involves bisulfite treatment of methylated DNA (mDNA),6,7,8,9 in which sodium bisulfite is used to convert unmethylated cytosine into deoxyuridine while leaving methylated cytosine unchanged. However, these bisulfite conversion-based techniques always involve time-consuming and expensive procedures such as sample preparation and subsequent DNA sequencing. Recently, new alternatives for methylation detection, without the need for bisulfite conversion, have emerged based on single-molecule techniques. For instance, a single-molecule real-time sequencing approach, developed by Pacific Biosciences, can recognize methylated nucleotides by monitoring the change in fluorescence pulse as a DNA polymerase catalyzes the incorporation of fluorescenently labeled nucleotides into a DNA strand.10, 11
Since mapping of DNA methylation involves differentiation between methylated and un-methylated nucleotides, it could be in principle benefit from the development of fast and low-cost DNA sequencing techniques that are used to recognize nucleotide types. Among these techniques is nanopore-based sequencing that involves the transport of DNA through a tiny hole in a membrane driven by voltage biases.12,13,14,15,16 The recorded ionic current blockade across the nanopore during such a translocation event can be used to characterize the dynamics and structure of translocating DNA molecule, and in turn, its sequence. Two dominating types of nanopores have been proposed for making the sensors: biological nanopores such as α-Hemolysin and MspA,17,18,19,20,21,22,23 and solid-state nanopores such as Si3N4 and SiO2.24,25,26,27,28,29 In contrast to conventional solid-state materials, graphene30 and other two-dimensional (2D) materials promise better resolution in nanopore sensing applications due to their atomically thin layer. Despite evident progresses in this field, a few technological obstacles, such as high translocation velocity of DNA, randomness in DNA conformations residing within the pore and high noise levels have to be overcome before these 2D material nanopore-based devices can be used for high-throughput DNA sequencing.16 In this context, bio-sensing approaches based on 2D materials will certainly benefit from subtle innovations in semiconductor nano-electronics, as well as rapid advances in signal processing and machine learning techniques.31
Aside from DNA sequencing, biological nanopores were also used to detect and map DNA methylation as a mDNA molecule was moved in single-nucleotide steps by a phi29 DNA polymerase.32 In solid state nanopores, the methylation sites in a mDNA, labeled by methyl-binding proteins (MBDs), can be detected indirectly through ionic current blockade induced by the protein.33, 34 The MBD protein serves as a marker for the methylation sites, facilitating their detection. In cells, such MBD proteins are believed to convert the information represented by DNA methylation into the appropriate functional state.35 Recently, an electro-optical sensing method utilizing solid state nanopores was adopted to detect un-methylated CpG dinucleotides.4 However, a limitation in utilizing conventional solid state materials arises from their thickness usually on the order of tens or hundreds of nanometers, which restricts the resolution of nanopore-based detection and quantification, especially in the case of detecting MBD protein-marked CpG sites. This restriction could be overcome by utilizing novel 2D solid-state materials such as graphene and molybdenum di-sulfide (MoS2), 36,37,38,39,40,41 with a thickness of single or a few atoms. Another advantage of electrically active 2D materials as nanopore membranes is the capability to measure in-plane transverse electronic sheet current, 42,43,44 in addition to the ionic current.36,37,38, 45 In our prior studies, we showed that a graphene layer with a nanopore in the center of an electric constriction is capable of detecting the conformational transition of a helical double-stranded DNA to a zipper DNA46 as well as counting nucleotides in a single stranded DNA.47, 48
In the present study, we investigate the detection and mapping of DNA methylation by 2D material nanopores, when a mDNA with its methylation sites labeled by MBD1 proteins is translocated through the pore under external voltage biases. The vertical ionic current across the nanopore was obtained directly from molecular dynamics (MD) simulations, while the transverse sheet current/conductance in a MoS2 layer was calculated using a semi-classical thermionic emission based transport model within the Poisson Boltzmann approximation.49 The results show that a 2D material nanopore is capable of detecting one or multiple MBD1-bound methylation sites by means of either ionic current or MoS2 electronic sheet current, while the later promises higher resolution than the former. Furthermore, the position of each methylation site can also be determined from the position of dip in the ionic current blockade trace, demonstrating the capability of 2D material nanopores to map DNA methylation.
Results and discussion
In the following sections, we present our findings related to detection and mapping of labeled methylation sites in mDNA using graphene-based or MoS2-based nanopore sensors. We consider mDNA strands with one or multiple methylated CpG sites (MBDs) at different positions, as well as different pore diameters.
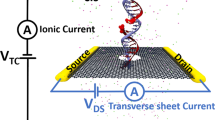
Figure 1a shows the schematic of a single CpG site in a mDNA molecule in complex with a MBD1 protein (left), along with chemical structures of cytosine and methylated cytosine (right). The mDNA-MBD1 complex has a cross-sectional diameter of about 5 nm, significantly larger than the 2.4 nm diameter for the mDNA itself. The complex is then threaded through a nanopore device, as shown in Fig. 1b. This device can be made from a nanoribbon in electrically active 2D materials such as graphene or transition metal di-chalcogenide (e.g., MoS2 and WSe2), connected to source and drain electrodes and embedded in an ionic water solution. A voltage bias along the vertical direction, V TC, is applied across the membrane to induce the transport of the mDNA-MBD1 complex through the pore and generate the ionic current. Meanwhile, another voltage bias along the transverse direction, V DS, is applied between the source and drain electrodes, inducing the flow of electronic sheet current in the membrane. Similar setup has been employed in experiments to successfully detect permeation of DNA through graphene nanopores, also by means of either ionic current or transverse current signals.50
Simulation system of DNA methylation detection with 2D material nanopores. a Schematic showing a CpG dinucleotide site in a mDNA molecule in complex with a MBD1 protein. The right panel shows the chemical structures of a cytosine (top) and a methylated cytosine (bottom) b Schematic of the simulated nanopore device. A mDNA-MBD1 complex is being threaded through a nanopore in a 2D material membrane (e.g., graphene or MoS2) embedded in an electrolyte solution. A voltage, V TC, was applied across the membrane to move the mDNA–MBD1 complex, and meanwhile, to induce an ionic current through the pore. Another voltage, V DS, was applied between a source electrode and a drain electrode connecting the 2D material, inducing the flow of a electronic sheet current in the membrane
We first investigate the detection and localization of DNA methylation via ionic current measurement through a 5 nm-diameter nanopore in graphene, the most widely-studied 2D material. For this purpose, we consider a 120 base pairs (bps)-long DNA strand, with each bp numbered 1 to 120 from the left end to the right end, as shown in insets of Fig. 2.
Mapping DNA methylation with graphene nanopores. Recorded ionic current traces through a 5 nm graphene nanopore for mDNA-MBD1 complexes with a single MBD protein/methylation site present in three different positions: a 20th, b 60th, and c 100th bp in a 120 bps mDNA (shown schematically on the right panel). The thick lines represent the moving average with a window of 1 ns. The yellow rectangles highlight the time duration when the MB1 protein resides in the pore and the arrows denote the time instant when the complex leaves the pore
Three 120 bps-long DNA molecules with each consisting of a MBD1 protein complexed to a CpG site at the 20th, 60th, and 100th bp were built, referred to as DNA-m20, DNA-m60, and DNA-m100, respectively. Shown in Fig. 2 are the recorded ionic current traces as the mDNA-MBD1 complexes are translocated through the graphene nanopore under an applied bias of 0.5 V. An evident dip can be seen in each ionic current signal, indicating a successful detection of the MBD1-labeled methylation site. The fact that the dip appears at different times in the current trace correlates to the location of the methylation site along the DNA. To further analyze such a correlation, we summarize in Table 1 the location of the methylation site in each mDNA, as well as the total translocation duration of each complex and time interval when the methylation site is detected. We assume here that the complex moves through the graphene pore at a constant velocity, which is reasonable as the translocation velocity of DNA and protein in all the simulations is found to fluctuate slightly around a constant value of ~1 Å/ns (Fig. S1 in Supporting Information). As a result, a linear relationship arises between the length of DNA portion that is translocated through the pore and the associated elapsed translocation time. Finally, the relative position of a methylation site, namely the ratio between the methylation site position with respect to the full DNA length, is derived through the relative position of the current dip, namely the ratio between the elapsed time before methylation site is detected to the total translocation time duration of the complex through the pore. We find that the detected relative positions in the system of mDNA-20, mDNA-60, and mDNA-100, are 0.185, 0.58, and 0.83, respectively, which are approximately consistent with the actual relative methylation site position of 0.167, 0.5, and 0.83, with error rates ranging from 0 to 16%. The error rate can be considerably reduced by statistical averaging over a large amount of events as one translocates a number of identical mDNA–MBD1 complexes through the pore.
While the methylated CpG site in mDNA needs to be marked by the MBD1 protein prior to nanopore translocation experiments, the binding procedure could be completed by adding purified mDNA and MBD1 protein to binding buffer and incubate for about half an hour at room temperature.33 This sample preparation procedure may exhibit significantly lower complexity, required time, and cost compared with the standard methylation map-ping approach of bisulfite treatment. Also in a previous study, it was suggested that DNA methylation enhances the MBD-mDNA binding by increasing in the hydrophobic interfacial area and strengthening the mDNA-MBD interaction.51 Therefore, our simulations did not consider such binding reaction. Instead, they were performed on experimentally-resolved NMR structures of the MBD1-mDNA complex.52
In addition to graphene, other 2D materials, such as MoS2 and hexagonal boron nitride, are also used as alternative nanopore membranes. MoS2 is of particular interest because it is a semiconductor with a direct band gap well suited as nanodevices for electronic detection.41, 53 Meanwhile, its weaker hydrophobicity reduces undesirable adsorption of biomolecules on MoS2.
In Fig. 3, we compare directly the adsorption process of a ssDNA molecule containing 20 adenine nucleotides (A20) onto a graphene and MoS2 surface. The simulation setup involves initially placing an ssDNA molecule 1 A above a graphene and MoS2 surface, respectively (see Fig. S2), and monitoring the number of DNA bases adsorbed onto the surface as a function of time. In the case of graphene, the number of adsorbed base rises immediately in the beginning of simulations, and within 15 ns, reaches a constant value of 13 bases (Fig. 3a). The adsorption starts from the two terminals of the ssDNA, and ends up with an aggregation of a few bases in the center of the DNA strand, which stops further DNA adsorption onto the graphene surface (Fig. 3a inset). In contrast, the number of adsorbed bases onto a MoS2 surface increases more slowly compared to graphene and display a lower steady value (~ 8) (Fig. 3b), indicating the significantly reduced hydrophobic interaction between the ssDNA and MoS2. In the case of a dsDNA molecule containing 20 A-T bps (AT20), we also find a quick adsorption process onto the graphene surface, with about 13 bases sticking to the surface after a 350 ns simulation (Fig. 3c). In sharp contrast, a dsDNA fails to adsorb onto a MoS2 surface, but rather, tends to detach from the surface and diffuse into the bulk solution. In order to constrain the DNA to the proximity of the membrane and prevent it from drifting too far away, we apply a fictive boundary plane located 2.6 nm above the MoS2 membrane. The distance between the membrane and the fictive boundary plane is a trade off between imposing too strong external forces to the molecule, and reducing time required to initiate its adsorption. We find that the dsDNA adsorbs again more slowly and ends up with fewer adsorbed bases on MoS2 than those on graphene (Fig. 3d), validating the weaker DNA–MoS2 hydrophobic interaction.40 These results suggest that MoS2 might be more suitable for methylation detection. This conclusion, valid for both single and double strand DNA in contact with the membrane is qualitatively similar to a previous study,54 for which the simulation set up consists of a nanopore in an electric field, where the interaction between the DNA and the 2D materials is a combination of the material hydrophobic properties and the DNA dynamics in the presence of the driving force, as well as the initial conditions of the DNA trajectories.
Comparison of DNA adsorption on graphene and MoS2 membranes. Top: Number of DNA bases adsorbed on a graphene a and MoS2 b membrane in simulations where an ssDNA A20 was initially placed 1 Å above the membrane. Bottom: same as top but for a dsDNA AT20. In the case of the dsDNA on a MoS2 membrane, a fictive mathematical boundary mimicking a wall parallel to the MoS2 layer and locating 2.6 nm above the membrane was applied in the simulation; without such a wall, the complex may diffuse quickly into the bulk once the simulation is initiated
In Fig. 4a, we show a representative ionic current trace during the translocation of a mDNA–MBD1 complex through a 5.2 nm-diameter MoS2 nanopore, along with the number of protein and DNA atoms residing in the pore (defined as atoms with z coordinates of −1.56 < z < 1.56 Å). In order to reduce computational cost of MD simulations, and particularly the subsequent electronic transport calculations, we consider here a mDNA containing 40 bps with a single methylation site. Initially (i), the ionic current fluctuates slightly around ~ 13 nA, because the pore is occupied solely by atoms from the DNA as indicated by the almost constant atom number of ~ 80 in the pore (see also panel (i) in Fig. 4c). After the protein enters the pore (ii), a sudden reduction in ionic current yields an evident dip with a minimum of ~ 9.3 nA. Meanwhile, the DNA/protein atom number increases gradually to a peak value of ~ 265, suggesting that the reduction in ionic current is induced by the blockade from presence of the MBD1 protein in the pore (see panel (ii) in Fig. 4c). When the protein leaves the pore (iii), the pore is again occupied solely by DNA, and both the ionic current and DNA/protein atom number recover the initial level comparable to (i), as expected. As the complex further moves downward (iv), the ionic current increases considerably to the open pore level at ~ 15.1 nA, due to the vanishing DNA/protein atom number in the pore.
Detection of DNA methylation with MoS2 nanopores by either ionic current or transverse electronic sheet current measurement. a A typical ionic current trace together with the number of DNA/protein atoms residing in a MoS2 pore when a mDNA-MBD complex translocates through the pore. b Calculated differential conductance in the MoS2 layer during the same translocation event as in a. c Successive snapshots from MD trajectory showing the translocation of the mDBA-MBD1 complex
A MoS2 nanopore with a larger diameter of 8 nm was also considered in our simulations, however no evident current dip associated with the methylation site was observed (Fig. S3 in Supporting Information). This observation agrees well with a previous theoretical study suggesting that increase in pore size or thickness could significantly reduce the signal, making it difficult to distinguish from the noise.55 In addition to the pore size, the ionic current through nanopores may be affected by the electro-osmotic flow (EOF) through the pore. The EOF is the consequence of the electrostatic interaction between an applied electric field and a charged nanopore. Though in our simulations the 2D material nanopore does not contain any surface charge, it may be different in realistic experiments. The induced EOF can influence the ion distribution and transport in the nanopore, which may eventually alter the magnitude of the ionic current. We can therefore expect that the disturbance caused by the methylated DNA in the pore may be enhanced with respect to the bare pore, which tends to confirm the main conclusion of our study.
After successfully detecting the MBD1 protein/DNA methylation by ionic current measurement, we now turn to the methylation detection involving transverse electronic sheet current/conductance measured in the MoS2 layer. Figure 4b displays the differential conductance (hereafter, abbreviated as conductance), defined as the difference in MoS2 conductance with and without DNA/protein, together with the number of DNA/protein atoms residing in the pore, as a mDNA-MBD1 complex translocates through the pore. In general, the MoS2 conductance profile (blue) reproduces well the shape of the profile of DNA/protein atom number (red). The sheet conductance fluctuates slightly around ~ 0.02 μS when the pore is occupied by the DNA only (i and iii). In contrast, with the MBD1 protein present in the pore (ii), a prominent peak emerges in the MoS2 conductance profile, coinciding with the maximum at the DNA/protein atom number profile. It was previously shown that, due to the screening effect by ions and water near the monolayer membrane, the electrostatic potential on the membrane is influenced predominantly by the atoms directly inside the pore, and within a thin slice co-planar with the 2D membrane.43, 56 Hence, during the protein translocation, the number and charge distribution of protein atoms in the membrane plane changes rapidly, inducing large variations in the electric potential in and around the pore, which results in the prominent peak in the sheet conductance. As this peak is caused by the inhomogeneous charge distribution of the MBD1, such protein serves as an excellent marker for transverse electronic current-based methylation detection.
For practical applications, the detection of multiple methylation sites within a mDNA by a single measurement is desirable. In this context the resolution of the nanopore device, defined as the minimal distance between two methylation sites in a single measurement, becomes a critical issue. By using a similar setup as above, we performed MD simulations of electric field-driven translocation of a mDNA-MBD1 complex containing two methylation sites separated by 20, 15, and 10 bps, respectively. In Fig. 5a, two clear dips are seen in the ionic current profile, when the two methylation sites and the bound MBD1 proteins are separated by 20 bps, indicating a successful detection to the two methylation sites. The two discrete dips in the current profile persist when the protein separation is reduced to 15 bps, suggesting both the proteins can still be detected (Fig. 5b). However, when the distance between the two proteins is shortened to 10 bps, the two ionic current dips merge with each other, forming a larger dip and making the two proteins indistinguishable in the ionic current trace (Fig. 5c). Therefore, we can conclude that the resolution of the MoS2 nanopore membrane in methylation detection using ionic current is ~ 15 bps.
The resolution for the ionic current measurement is determined not only by the 2D nature of the membrane but also the size of MBD1 protein that binds to each methylation site. The bound protein has a footprint of about 10 bps along the mDNA strand, and the minimal distance allowed between two MBD1 proteins is therefore estimated to be 10 bps. In such an extreme case, the two proteins are too close to one another and thus are indistinguishable in the ionic current signal. When the distance between the two methylation sites increases to 15–20 bps, a gap between the two MBD1 proteins emerges, thereby enabling their individual detection in the ionic current signal. As a consequence, ionic current detection might not be suited to resolve dense CpG islands unless using other bio-markers such as in electro-optic sensing.4 Another technique based on the transverse electronic sheet current in the membrane that senses only a slice of the protein, has potentially a higher resolution than the ionic current approach. To address this issue, we simulated the transverse electronic conductance in response to the translocation of the mDNA-MBD1 with a protein-protein separation of 10 bps that are indistinguishable by ionic current detection. Figure 6 shows a clear dip acting as the boundary of two distinguishable peaks in the conductance profile, indicating the presence of the two MBD proteins and suggesting a better resolution in methylation detection by the transverse electronic current than by the ionic current.
Higher resolution of methylation detection using transverse electronic current in MoS2. The differential conductance is shown together with the number of protein/DNA atoms occupying the pore as a mDNA-MBD1 complex containing two methylation sites separated by 10 bps is translocated through a MoS2 nanopore (same as Fig. 5c). The arrow marks a dip between two peaks, each corresponding to the permeation of a MBD1 protein bound to a methylation site
The transverse current inside the MoS2 membrane is sensitive only to the atoms within a thin slice co-planer with the membrane, due to the screening effect from ions and water. This ultrahigh sensitivity ensures the accurate capture of the narrow gap between two MBD1 proteins even in the case of the 10 bp-separation, leading to the successful detection of the two methylation sites from a single nanopore translocation event.
In summary, we show the ability of 2D material nanopores to detect DNA methylation sites labeled by MBD1 proteins through monitoring either dips in the ionic current blockade or peaks in transverse electronic sheet conductance, by combined molecular dynamics simulations and semi-classical transport calculations. Methylation site at difference positions on a DNA strand can be located through the relative position of the observed dip in the current signal, demonstrating the possibility to efficiently map DNA methylation with 2D material nanopores. Further results show that multiple methylation sites are distinguishable in a single ionic current measurement, provided that they are separated by at least 15 bps. A lower critical separation of 10 bps is determined in the case of electronic detection, indicating a higher resolution in this case. The superior performance of electronic detection is due to its ability to capture local protein charge variation within the thin slice of the membrane, unlike the ionic current approach where protein contributes as a whole. In addition to the detection of DNA methylation sites, we expect that the presented methodology may have broader applications in bio-molecular sensing such as detection of DNA barcoding.57
Methods
The approaches outlined below include MD simulations of molecular transport of mDNA–MBD1 complexes through graphene or MoS2 nanopores, calculation of electrostatic potential arising from translocating molecules by solving Poisson-Boltzmann equation, and determination of transverse electronic current in MoS2 by semi-classical transport calculations.
Molecular dynamics simulations
System setup
Figure 1b shows a nanopore sensor simulated in the present study for detection of DNA methylation. The nanosensor device consists of a graphene or MoS2 nanopore device, biased at a source and drain voltage (V SD) and solvated in a water box. A dsDNA molecule with a methylated CpG site (highlighted in red) in complex with a MBD protein is being threaded through the 2D material nanopore. The atomic structure of the complex was constructed by linking double-stranded DNA fragments, built with the X3DNA program,58 to the ends of the DNA molecule in the NMR structure of a mDNA-MBD1 complex (pdb code:1IG4).52
Initially, the complex was placed with two bps at the bottom end of the DNA below the MoS2 membrane, in order to avoid the time-consuming simulation of DNA capture by the pore, which is beyond the scope of the present study. K+ and Cl− ions were added to the solution to achieve a neutral system at a concentration of 1 M.
All MD simulations were carried out with the program NAMD,59 and visualized and analyzed with visual molecular dynamics (VMD).60 Protein and DNA were described by the CHARMM22 force field with CMAP corrections and the CHMARMM27 force field,61 respectively. Carbon atoms in graphene were treated as type CA atoms in the CHARMM27 force field. The Lennard–Jones parameters for MoS2 are σ Mo−Mo = 4.4 Å, ε Mo−Mo = 0.0135 kcal/mol and σ S−S = 3.13 Å, ε S−S = 0.3196 kcal/mol, taken from Ref. 62. All MoS2 and graphene atoms were fixed to their initial positions. In realistic experiments, only atoms at the boundary of the membrane could be fixed, while the remaining are free to move. In that case, the noise may be higher than in the present simulations due to the conformational fluctuation of the membrane, but as long as its amplitude is confined within a few nA, the signal will remain detectable. Water was modeled by TIP3P water model.63 A time step of 2 fs was used. Periodic boundary conditions were employed in all directions. van der Waals energies were calculated using a 12 Å cutoff. A particle-mesh Ewald method was used to treat long-range electrostatics.64 A Langevin thermostat was employed to maintain a constant temperature at 300 K. Each system was minimized for 5,000 step, followed by a 2 ns equilibration simulation as a NPT ensemble, where the pressure was maintained at 1 atm by a Langevin piston65 for pressure control and Langevin dynamics for temperature control. Subsequently, the system was further equilibrated as a NVT ensemble for 4 ns. An external electric field E = V TC/L z was then applied to the system along the +z direction to drive the molecular transport through graphene nanopores, where V TC is the voltage bias and L z is the length of the box in the z direction. Unless specified explicitly, a voltage V TC = 0.5 V was adopted in all simulations. In some of the translocation simulations, especially for graphene nanopores with higher hydrophobicity, the MBD1 protein may stick to the pore rim, slowing down the bimolecular translocation. To prevent such sticking effects, we consider a mathematical boundary mimicking a 5.2 nm diameter fictive cylindrical nanopore perpendicular to the 2D layer. The consequences of this fictive nanopore is to make the 2D membrane, especially graphene, less sticky than in reality. At the same time increasing the thickness of the membrane may reduce the resolution in methylation detection. The reduced membrane effective hydrophobicity could be observed experimentally through the application of a protective coating layer. However in such a scenario, the detection resolution via transverse sheet currents would remain unchanged since the presence of DNA on the surface of the graphene membrane would not influence the transverse sheet current due to the protective coating layer, except near the pore.
Ionic current calculation
The instantaneous ionic current I(t) through nanopores was calculated through66
where q i and z i are the charge and z coordinate of ion i, respectively. N represents the number of ions and L z is the length of simulation system along the owing direction of ions, namely the z-axis. t is the interval between trajectory frames, namely 10 ps.
Electric transport calculations
Once the translocation trajectories of mDNA–MBD1 complex through graphene nanopores were obtained in MD simulations, we then calculated the electrostatic potential for each frame at intervals of 50 ps using a non-linear Poisson–Boltzmann formulation and determined the effect of the resulting potential on the MoS2 conductance by semi-classical thermionic emission based transport calculations.43
Electric potential calculations
For each frame of the translocation trajectory, the electric potential φ(r) was calculated using the Poisson–Boltzmann equation
where \({\rho }_{DNA}({\boldsymbol{r}})\) and \({\rho }_{protein}({\boldsymbol{r}})\) are charge densities of DNA and protein, respectively. The concentrations of the solute ions, \({C}_{{K}^{+}}({\boldsymbol{r}})\) and \({C}_{C{l}^{-}}({\boldsymbol{r}})\), are described assuming Boltzmann equilibrium, namely by
Here C 0 is the molar concentration in the solution, chosen to be 1 M. The process to solve Eqs (2–4) was described in detail in our earlier studies.43, 67
Transverse electronic conductance
The electronic transport in MoS2 membranes with a constriction as a quantum point contact is formulated as a self-consistent model based on semi-classical thermionic Poisson–Boltzmann technique.49
The constriction in the MoS2 membrane forces the electrons in the MoS2 to flow around the pore, increasing the sensitivity of the device to the bio-molecules within the pore. An alternative way is the use of a hybrid MoS2 monolayer composed of a metallic strip embedded in a semiconducting MoS2 phase.68
As the conduction band of MoS2 has two minima at K and Q (located along the Γ-K axis) with an energy difference of 0.07 eV, the effective masses at K and Q are taken as 0.5 m 0 and 0.78 m 0 , respectively, where m 0 is the mass of an electron. The width of the MoS2 membrane at the constriction is 19.2 nm. The conductance calculated from the thermionic current at a given energy mode is given by49
Here, the quasi-Fermi level \({E}_{F}^{L}\) is set up depending on the carrier concentration, chosen as 1012 cm−2 in our calculation. n 1,2 represents the energy modes at the two electronic conductance channels on the membrane above and below the pore, denoted as subscripts 1 and 2, respectively, and \({E}_{{n}_{1,2}}^{K}\) and \({E}_{{n}_{1,2}}^{Q}\) are the energy modes at these channels due to the effective masses at K and Q, respectively. The total conductance is the sum of conductances through all energy modes in the channels.
The linear response of the electronic conductance at a given energy mode n 1, 2 in the presence of an external potential near the pore is given by
where \(\langle e{\varphi }_{{\rm{DNA}}}\rangle_{{n}_{1,2}}\) represents the spatially averaged value of external potential due to the DNA \(({\varphi }_{{\rm{DNA}}})\) across each channel of the MoS2 membrane. The total conductance variation (δG) with respect to the open pore conductance was obtained by summing individual variations due to each energy mode in each channel.49
References
Bird, A. The essentials of DNA methylation. Cell 70, 5–8 (1992).
Craig, J. M. & Bickmore, W. A. The distribution of CpG islands in mammalian chromosomes. Nat. Genet. 7, 376–382 (1994).
Robertson, K. DNA methylation and human disease. Nat. Rev. Genet. 6, 597–610 (2005).
Gilboa, T. et al. Single-molecule DNA methylation quantification using electro-optical sensing in solid-state nanopores. ACS Nano 10, 8861–8870 (2016).
Baker, M. Epigenome: mapping in motion. Nat. Methods 7, 181–186 (2010).
Frommer, M. et al. A genomic sequencing protocol that yields a positive display of 5-methylcytosine residues in individual DNA strands. Proc. Natl. Acad. Sci. 89, 1827–1831 (1992).
Lister, R. et al. Human DNA methylomes at base resolution show widespread epigenomic differences. Nature 462, 315–322 (2009).
Laird, P. Principles and challenges of genome-wide DNA methylation analysis. Nat. Rev. Genet. 11, 191 (2010).
Bock, C. et al. Quantitative comparison of genome-wide DNA methylation mapping technologies. Nat. Biotechnol. 28, 1106–1114 (2010).
Eid, J. et al. Real-time DNA sequencing from single polymerase molecules. Science 323, 133–138 (2009).
Flusberg, B. et al. Direct detection of DNA methylation during single-molecule, real-time sequencing. Nat. Methods. 7, 461–465 (2010).
Branton, D. et al. The potential and challenges of nanopore sequencing. Nat. Biotechnol. 26, 1146–1153 (2008).
Venkatesan, B. & Bashir, R. Nanopore sensors for nucleic acid analysis. Nat. Nanotechnol. 6, 615–624 (2011).
Lindsay, S. The promises and challenges of solid-state sequencing. Nat. Nanotechnol. 11, 109–111 (2016).
Di Ventra, M. & Taniguchi, M. Decoding DNA, RNA and peptides with quantum tunnelling. Nat. Nanotechnol. 11, 117–126 (2016).
Heerema, S. J. & Dekker, C. Graphene nanodevices for DNA sequencing. Nat. Nanotechnol. 11, 127–136 (2016).
Bezrukov, S., Vodyanoy, I., Brutyan, R. & Kasianowicz, J. Dynamics and free energy of polymers partitioning into a nanoscale pore. Macromolecules 29, 8517–8522 (1996).
Kasianowicz, J., Brandin, E., Branton, D. & Deamer, D. Characterization of individual polynucleotide molecules using a membrane channel. Proc. Natl. Acad. Sci. 93, 13770–13773 (1996).
Akeson, M., Branton, D., Kasianowicz, J., Brandin, E. & Deamer, D. Microsecond time-scale discrimination among polycytidylic acid, polyadenylic acid, and polyuridylic acid as homopolymers or as segments within single RNA molecules. Biophys. J. 77, 3227–3233 (1999).
Hornblower, B. et al. Single-molecule analysis of DNA-protein complexes using nanopores. Nat. Methods. 4, 315–317 (2007).
Kumar, S. et al. PEG-labeled nucleotides and nanopore detection for single molecule DNA sequencing by synthesis. Sci. Rep. 2, 684 (2012).
Butler, T., Pavlenok, M., Derrington, I., Niederweis, M. & Gundlach, J. Single-molecule DNA detection with an engineered MspA protein nanopore. Proc. Natl. Acad. Sci. 105, 20647–20652 (2008).
Derrington, I. et al. Nanopore DNA sequencing with MspA. Proc. Natl. Acad. Sci. 107, 16060–16065 (2010).
Skinner, G., van den Hout, M., Broekmans, O., Dekker, C. & Dekker, N. Distinguishing single- and double-stranded nucleic acid molecules using solid-state nanopores. Nano. Lett. 9, 2953–2960 (2009).
Dekker, C. Solid-state nanopores. Nat. Nanotechnol. 2, 209–215 (2007).
Wanunu, M., Sutin, J., McNally, B., Chow, A. & Meller, A. DNA translocation governed by interactions with solid-state nanopores. Biophys. J. 95, 4716–4725 (2008).
McNally, B., Wanunu, M. & Meller, A. Electromechanical unzipping of individual DNA molecules using synthetic sub-2 nm pores. Nano. Lett. 8, 3418–3422 (2008).
Qiu, H., Girdhar, A., Schulten, K. & Leburton, J. Electrically tunable quenching of DNA fluctuations in biased solid-state nanopores. ACS Nano 10, 4482–4488 (2016).
Gracheva, M., Vidal, J. & Leburton, J. p−n Semiconductor membrane for electrically tunable ion current rectification and filtering. Nano. Lett. 7, 1717–1722 (2007).
Sathe, C., Zou, X., Leburton, J. & Schulten, K. Computational investigation of DNA detection using graphene nanopores. ACS Nano 5, 8842–8851 (2011).
Schreiber, J. et al. Error rates for nanopore discrimination among cytosine, methylcytosine, and hydroxymethylcytosine along individual DNA strands. Proc. Natl. Acad. Sci. 110, 18910–18915 (2013).
Laszlo, A. et al. Detection and mapping of 5-methylcytosine and 5-hydroxymethylcytosine with nanopore MspA. Proc. Natl. Acad. Sci. 110, 18904–18909 (2013).
Shim, J. et al. Detection and quantification of methylation in DNA using solid-state nanopores. Sci. Rep. 3, 1389 (2013).
Shim, J. et al. Nanopore-based assay for detection of methylation in double-stranded DNA fragments. ACS Nano. 9, 290–300 (2015).
Fatemi, M. MBD family proteins: reading the epigenetic code. J. Cell. Sci. 119, 3033–3037 (2006).
Schneider, G. et al. DNA translocation through graphene nanopores. Nano. Lett. 10, 3163–3167 (2010).
Merchant, C. et al. DNA translocation through graphene nanopores. Nano. Lett. 10, 2915–2921 (2010).
Garaj, S. et al. Graphene as a subnanometre trans-electrode membrane. Nature 467, 190–193 (2010).
Qiu, H. & Guo, W. Detecting ssDNA at single-nucleotide resolution by sub-2-nanometer pore in monoatomic graphene: A molecular dynamics study. Appl. Phys. Lett. 100, 083106 (2012).
Liu, K., Feng, J., Kis, A. & Radenovic, A. Atomically thin molybdenum disulfide nanopores with high sensitivity for DNA translocation. ACS Nano 8, 2504–2511 (2014).
Feng, J. et al. Identification of single nucleotides in MoS2 nanopores. Nat. Nanotechnol. 10, 1070–1076 (2015).
Nelson, T., Zhang, B. & Prezhdo, O. Detection of nucleic acids with graphene nanopores: Ab initio characterization of a novel sequencing device. Nano. Lett. 10, 3237–3242 (2010).
Girdhar, A., Sathe, C., Schulten, K. & Leburton, J. Graphene quantum point contact transistor for DNA sensing. Proc. Natl. Acad. Sci. 110, 16748–16753 (2013).
Ahmed, T., Haraldsen, J., Zhu, J. & Balatsky, A. Next-generation epigenetic detection technique: identifying methylated cytosine using graphene nanopore. J. Phys. Chem. Lett. 5, 2601–2607 (2014).
Lv, W., Liu, S., Li, X. & Wu, R. Spatial blockage of ionic current for electrophoretic translocation of DNA through a graphene nanopore. Electrophoresis 35, 1144–1151 (2014).
Sathe, C., Girdhar, A., Leburton, J. & Schulten, K. Electronic detection of dsDNA transition from helical to zipper conformation using graphene nanopores. Nanotechnology 25, 445105 (2014).
Girdhar, A., Sathe, C., Schulten, K. & Leburton, J. Tunable graphene quantum point contact transistor for DNA detection and characterization. Nanotechnology 26, 134005 (2015).
Qiu, H., Sarathy, A., Leburton, J. & Schulten, K. Intrinsic stepwise translocation of stretched ssDNA in graphene nanopores. Nano. Lett. 15, 8322–8330 (2015).
Sarathy, A. & Leburton, J. Electronic conductance model in constricted MoS2 with nanopores. Appl. Phys. Lett. 108, 053701 (2016).
Traversi, F. et al. Detecting the translocation of DNA through a nanopore using graphene nanoribbons. Nat. Nanotechnol. 8, 939–945 (2013).
Zou, X., Ma, W., Solov’yov, I., Chipot, C. & Schulten, K. Recognition of methylated DNA through methyl-CpG binding domain proteins. Nucleic Acids Res. 40, 2747–2758 (2011).
Ohki, I. et al. Solution structure of the methyl-CpG binding domain of human MBD1 in complex with methylated DNA. Cell 105, 487–497 (2001).
Feng, J. et al. Electrochemical reaction in single layer MoS2: nanopores opened atom by atom. Nano. Lett. 15, 3431–3438 (2015).
Farimani, A., Min, K. & Aluru, N. DNA base detection using a single-layer MoS2. ACS Nano 8, 7914–7922 (2014).
Wen, C. et al. On nanopore DNA sequencing by signal and noise analysis of ionic current. Nanotechnology 27, 215502 (2016).
Feliciano, G. et al. Capacitive DNA detection driven by electronic charge fluctuations in a graphene nanopore. Phys. Rev. Appl. 3, 034003 (2015).
Singer, A. et al. Nanopore based sequence specific detection of duplex DNA for genomic profiling. Nano. Lett. 10, 738–742 (2010).
Lu, X. & Olson, W. 3DNA: a software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Res. 31, 5108–5121 (2003).
Phillips, J. et al. Scalable molecular dynamics with NAMD. J. Comput. Chem. 26, 1781–1802 (2005).
Humphrey, W., Dalke, A. & Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 14, 33–38 (1996).
MacKerell, A. et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 102, 3586–3616 (1998).
Stewart, J. & Spearot, D. Atomistic simulations of nanoindentation on the basal plane of crystalline molybdenum disulfide (MoS2). Model. Simul. Mat. Sci. Eng. 21, 045003 (2013).
Jorgensen, W., Chandrasekhar, J., Madura, J., Impey, R. & Klein, M. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79, 926–935 (1983).
Essmann, U. et al. A smooth particle mesh Ewald method. J. Chem. Phys. 103, 8577–8593 (1995).
Feller, S., Zhang, Y., Pastor, R. & Brooks, B. Constant pressure molecular dynamics simulation: The langevin piston method. J. Chem. Phys. 103, 4613–4621 (1995).
Aksimentiev, A., Heng, J., Timp, G. & Schulten, K. Microscopic kinetics of DNA translocation through synthetic nanopores. Biophys. J. 87, 2086–2097 (2004).
Girdhar, A., Sathe, C., Schulten, K. & Leburton, J. Gate-modulated graphene quantum point contact device for DNA sensing. J. Comput. Electron. 13, 839–846 (2014).
Sivaraman, G. et al. Electronic transport along hybrid MoS2 monolayers. J. Phys. Chem. C 120, 23389–23396 (2016).
Acknowledgements
This article is dedicated to the memory of Prof. Klaus Schulten, who was one of our closest collaborators and an inspiring colleague for many years. This work was supported by grants from Oxford Nanopore Technology, the Seeding Novel Interdisciplinary Research Program of the Beckman Institute, National Institutes of Health Grant 9P41GM104601 and National Science Foundation Grants PHY0822613 and PHY1430124. The authors gratefully acknowledge also supercomputer time provided through the Extreme Science and Engineering Discovery Environment (XSEDE) Grant MCA93S028 and by the University of Illinois at Urbana-Champaign on the TAUB cluster.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Qiu, H., Sarathy, A., Schulten, K. et al. Detection and mapping of DNA methylation with 2D material nanopores. npj 2D Mater Appl 1, 3 (2017). https://doi.org/10.1038/s41699-017-0005-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-017-0005-7
This article is cited by
-
Epigenetic tumor heterogeneity in the era of single-cell profiling with nanopore sequencing
Clinical Epigenetics (2022)
-
Detecting topological variations of DNA at single-molecule level
Nature Communications (2019)
-
Selective detections of single-viruses using solid-state nanopores
Scientific Reports (2018)
-
Your new travel guide to the flatlands
npj 2D Materials and Applications (2017)