Abstract
A heatwave in June 2021 exposed Pacific Northwest (PNW) snowpack to record temperatures, allowing us to probe seasonal snowpack response to short-term heat extremes. Using high-resolution contiguous snowpack and temperature datasets (daily 1 km2 SNODAS, 4 km2 PRISM), we examined daily snowmelt in cooler, higher-elevation zones during this event, contrasted with the prior 18 years (2004–2021). We found that multiple early season (spring) heatwaves, concluding with the 2021 heat dome itself, resulted in dramatic early season melt including the most persistent fraction of PNW snowpack. Using longer-term station records (1940–2021), we show that springtime +5 °C daily anomalies were historically rare but since the mid-1990s have doubled in frequency and/or intensity, now potentially affecting typically cool La Niña periods (2021). Collectively, these results indicate that successive heat extremes drive rapid snowmelt, and these extremes may increasingly threaten previously resilient fractions of seasonal snowpack.
Similar content being viewed by others
Introduction
In late June 2021, an extreme heatwave associated with a “heat dome” atmospheric pressure system exposed snowpack across the Pacific Northwest (PNW) to record temperatures. Air temperatures nearing 50 °C broke local records by several degrees and caused a range of destructive social1,2,3,4,5,6 and ecological impacts4,7,8,9,10,11,12. In British Columbia, this included severe floods in multiple snow- and glacier-fed watersheds and a large rock avalanche4,13,14. Snowpack loss during the heat dome was likely substantial across the entire PNW4,13,15. While both direct and indirect (stream discharge) measures of snowmelt have been extensively studied in relation to seasonal temperature effects and long-term climate trends16, impacts due to heatwaves are less well-understood, particularly for the shortest extremes.
Previous studies on snowpack and heatwaves have tended to focus on longer, more sustained events17,18,19,20. Season-length back-to-back austral summer heatwaves drove early, rapid snowmelt in New Zealand, for example, in 2017–2018 and 2018–201918. A 2-week cooler heatwave + rain-on-snow period warmed permafrost down to 5 m and caused slush avalanches during the 2012 high-arctic winter in Svalbard, with temperatures not much above 3 °C (notwithstanding this was ~18 °C above normal)17. For glaciers, shorter-term heatwaves have been more studied. In Europe and Canada, would-be streamflow deficiencies from low rainfall and high evaporation during warm and dry 7+ day periods are partially- to over-compensated for by increased glacial melt, but this pattern is heavily dependent on antecedent conditions such as accumulated snowpack and groundwater storage21. In the PNW, days- and weeks-long late-summer heatwaves increase glacial ablation and stream discharge4,22.
The increased melting during short-term heatwaves is consistent with and potentially a sub-seasonal expression of well-established decadal-scale trends of reduced snowpack levels in a gradually warming climate. Over the last century, warming has caused broad decline in western US peak annual snowpack levels23,24. Spring seasonal warming is modest in magnitude (+0.3–1.75 °C since pre-industrial times in the PNW25) compared to shorter-term temperature anomalies during heatwaves, but over seasonal scales it has substantial impact24. This general negative trend shows little to no impact at higher elevations, however. There, more modest declines or even increases are observed26. Warming in these cooler areas may have been insufficient, so far, to change snowpack accumulation and melting patterns, especially if increasing PNW precipitation compensates23,24,25,26,27,28. Although its influence on PNW precipitation may be declining as westerly wind strength trends weaker29, orographic lift’s combined impacts (colder temperatures, increased relative humidity, increased precipitation) somewhat buffer annual snowpack levels at higher elevations against decline from incremental warming. Extreme short-term heatwaves might overwhelm this buffer, but, in part because short-term events and impacts are effectively obscured in annual snowpack metrics analyzed over decadal scales, this is unclear.
In this study, we sought to better understand higher-elevation snowpack and sub-seasonal heatwave impacts by probing how the PNW’s higher-elevation snow responded to the 2021 heat dome. To address the comparative shortage of observations stations at higher altitudes, we used high-resolution (daily, 1 km2) SNOw Data Assimilation System (SNODAS) data, which we validated using an independent 9-year observational dataset of snow depth at higher-elevations (1544 ± 422 m; n = 28 stations; see Methods “SNODAS validation”) and coupled with independent gridded temperature data (PRISM)30,31. Our analysis centered on the contiguous US between 41.88–49.065°N and 124.80–119.60°W, which is the wetter, western half of the PNW and still held snow in late June 2021. A persistent snow zone was defined functionally as areas with ≥39 mm (1.5”) of snow water equivalent (SWE) on all April 1st’s in SNODAS’s record (2004–2022), excepting 2004, 2005, and 2015 (n = 16; see “Methods”). We and others use April 1st to reflect when, approximately, net SWE accumulation transitions to net melting26,32. This defined a 51,235 km2 persistent snow zone over the mid-high elevations of the Oregon and Washington Cascade and Olympic Mountains (1555 ± 349 m; mean ± s.d.). Using this zone, we set out to probe the response of higher-elevation snowmelt to the 2021 heat dome.
The 2021 heatwave was the PNW’s most extreme temperature event in recorded history. It was characterized by a “heat dome” atmospheric phenomenon, wherein an exceptionally high-pressure blocking system in the upper troposphere trapped lower troposphere air in place over the PNW for several days beginning June 26th, arresting typical circulation patterns33. An anomalously strong cyclone-anticyclone system in the NE Pacific, associated with an atmospheric river and large sensible and latent heat flux convergence, led to the event34,35. Under the heat dome, temperatures climbed as solar energy inputs accrued over several days of near-peak annual insolation. All-time temperature records were broken by several degrees in the region’s population centers (Portland, OR; Seattle, WA), with temperatures peaking on June 28th. Peak temperatures were slightly later in the Cascades, reflecting the slow eastward migration of the heat dome as large-scale westerly circulation with cooler marine air gradually displaced it36. Lower-elevation areas west of the Cascades cooled first, then higher-elevation areas including the coast-adjacent Olympic mountains by July 1st. Reflecting the heat dome’s onset over the PNW on June 26th and large temperature anomalies over the persistent snow zone extending to June 30th, we defined the heat dome as June 26th–30th and first examined snowpack behavior over these dates. While our motivation was initially to focus on the impacts of this single event, our analysis found that a longer-term dynamic was in play, of which the heat dome was simply an extreme example.
Results
Scale of warming during the 2021 heat dome
Mean daily temperature anomalies for the persistent snow zone were greatest from June 27th–30th, when daily anomalies were >11 °C above normal (average: +13.4 °C ± 1.6 °C). Absolute temperatures were greatest (>25 °C) from June 28th–30th, bookended with slightly cooler >20 °C days on June 27th and July 1st. The single hottest day in the persistent snow zone was June 29th, when the mean temperature was 26.5 °C, a +14.3 °C ± 1.6 °C anomaly relative to a 30-year normal for this date (1991–2020) (Fig. 1). Minimum temperatures were similarly greatest from June 28th–30th and reached a peak on June 29th (19.5 °C ± 3.3 °C; average anomaly +13.2 °C ± 2.6 °C). Maximum temperatures also peaked from June 28th–30th, with the absolute maximum reached on June 30th (34.5 °C ± 2.4 °C; average anomaly +16.5 °C ± 1.9 °C).
The warm temperature anomalies during the heat dome affected the persistent snow zone relatively homogenously (Fig. 1). What modest variation there was largely consisted of Washington having slightly greater warm anomalies than Oregon. Variation in anomalies primarily reflected variation in 30-year normal reference temperatures, with greater anomalies near the dependably cold heights of Mts. Olympus and Baker in Washington and smaller anomalies in Oregon, where baseline temperatures are generally warmer. This assessment is limited to PRISM’s accuracy, which is well-supported for regional-scale analyses37,38 but may not capture all local-scale temperature anomalies from small-scale positive feedbacks39.
Snowpack response to the heat dome
The heat dome event rapidly melted most of 2021’s remaining snowpack, all of which was contained in the higher-elevation persistent snow zone (Fig. 2). This shifted a late-melting trajectory characteristic of PNW La Niña periods (cooler, wetter) to an early conclusion more typical for El Niño (warmer, dryer). From June 26th–30th, 5.47 km3 of snow water storage (9.7% of 2021’s maximum SWE accumulation) was lost as SWE loss progressed from 180 to 74 mm (83.7% to 93.3% melted), averaged over the persistent snow zone. By contrast, over the prior 18 SNODAS years, this ~10% of SWE (between each year’s 84th–94th percentile) melted 2–5 times slower, irrespective of El Niño, La Niña, or total snowpack (Supplementary Fig. 1). The typically slower melt of this fraction may be explained by the preferential persistence of colder, more environmentally buffered (generally higher-elevation) snowpack. The heat dome undercut this persistence via a large, relatively spatially uniform temperature anomaly, averaging +12.3 °C from June 26th–30th. We found similar patterns in time series of snow-covered area (at the SWE ≥ 5 mm threshold) and SWE loss rates (Supplementary Figs. 2–4). Snow-covered area in the persistent snow zone fell from 27.5 to 11.8% during June 26th–30th, after which only the highest and wettest peaks in Washington held any snow (Fig. 2b–d). On its face, absolute SWE loss was unremarkable, reflecting the modest SWE volume present in late June. Adjusted to snow-covered area, however (rather than averaged over the entire persistent snow zone), SWE loss during the heat dome was 470 mm from June 26th–30th, the greatest 5-day SWE loss total in SNODAS to date (daily melt rates average −19.5 ± 14.9 mm day−1 over the main spring and summer melting periods in the persistent snow zone from 2004–2021; Fig. 3).
a Time series of daily SWE, averaged over the 51,235 km2 persistent snow zone, in 2004–2021 melt periods. SWE melt curves are colored by the predominant ENSO pattern of each spring and its preceding winter. This zone’s 2021 daily mean air temperatures are in solid red, over a 30-year climatological mean temperature (dashed). Periods in 2021 where daily temperature anomalies exceeded +3, +5, or +10 °C are shaded in grey. SWE during 2021’s heat dome fell from an average of 180 mm (16.3%) to 74 mm (6.7%) over 5 days, a loss of 5.47 km3 of water storage, melting faster than other years to prematurely end the melt season. Successive prior heatwaves enabled this by episodically accelerating snowmelt, which stalled in their absence. 2021 was different than previous La Niña years in: starting melt early, rapid melting episodes, and ending melt early. (b–d) SWE in the study region and persistent snow zone (black outline) in 2021: b April 1st, when net SWE melting began for the persistent snow zone in 2021; c June 25th, just before the heat dome; and d June 30th, the end of the heat dome. The heat dome melted most remaining snow, though its impacts were dwarfed by the cumulative impacts of successive prior springtime heatwaves. Persistent snow zone April 1st SWE was 35% above-average, but snow-covered area (SWE ≥ 5 mm) fell to 31.2% (15,997 km2) of the persistent snow zone on June 25th and 11.8% (6022 km2) by June 30th. The SWE scale in (b–d) is scaled to optimize contrast, however values at the peak of Mt Rainier (46.85°N, 121.8°W) exceed the maximum.
a Daily mean temperatures and SWE change in mm for days from the annual maximum SWE date (2004–2021) to when SWE fell below 2% of that value, adjusted to snow-covered area (Methods “Snowpack analysis”). Plotted trendlines reflect a linear model (slope: −2.5 mm day−1 per °C, p < 0.0001, R2 = 0.794) and generalized additive model (p < 0.0001, R2 = 0.813). The GAM is applied to reflect a non-linear intensification in melt rates at the most extreme high-temperatures. See Supplementary Fig. 4 for a time series. b Daily temperature anomalies and SWE percent change in April, May, and June from 2004–2021 (Slope: −0.17% day−1 per °C anomaly; p < 0.01, R2 = 0.364). Days with temperature anomalies ≥+5 °C are classified as heatwave days. ENSO classification is based on the dominant pattern of the preceding winter. Melt rates and temperature are plotted with 3-day moving averages, instead of daily data, to highlight sustained anomalies and accommodate the mismatch in the time of day when SWE and temperature are recorded.
As exceptional as the heat dome’s snowmelt impacts were, in the context of 2021’s entire melting season, we found that they were dwarfed by cumulative prior snowmelt. This was unexpected given the strength of 2021’s La Niña, which was the strongest since 2011, when nearly half (47.5%) of the year’s SWE persisted on June 26th. Moreover, persistent snow zone April 1st SWE was 135% of normal for our 18-year SNODAS record (2nd, after 2012). This led us to probe what led to the unusually early melt of 2021’s La Niña snowpack.
Temperature controls on snowpack loss
By comparing daily changes in SWE against daily temperatures, we found that most of 2021’s snowmelt occurred during warm periods prior to the heat dome. These periods ranged from +3.8 °C (May 14th–17th) to +7.1 °C (June 1st–4th) and accounted for an average of ~11–22 mm of SWE lost per day over 3–6 day periods, generally melting ~94 mm of the year’s SWE (~5–10% in 2021) each episode (Figs. 2 and 3 and Supplementary Figs. 2–4). The first occurred over 6 days in mid-April, as a +5.1 °C anomaly melted 57.6 mm SWE (2.95 km3, or 5.2% of the year’s SWE) to begin Spring melting in earnest. May 14th–17th’s +3.7 °C anomaly melted 87 mm SWE (4.45 km3, 7.9%), followed by June 1st–4th’s +7.0 °C anomaly which melted 126 mm SWE (6.43 km3, 11.4%). Two weeks later, a +6.1 °C anomaly over the 5 days prior to the heat dome melted 105 mm SWE (5.38 km3, 9.5%). Outside of these warm anomalies, however, melting slowed or stalled. This is most apparent during June’s cold anomaly, but also multiple times in May and once in late April. This suggests that warm anomalies drove most melting. The warmest days do account for the greatest SWE loss (Fig. 3). In 2021, the 32 days with warm anomalies ≥+2.55 °C between April 1st and June 30th (91 days, with April 1st being the first day of net melting in 2021) account for >50% of 2021’s melting. Daily SWE loss rates averaged −36.6 ± 29.5 mm in the snow-covered areas of the persistent snow zone on these 32 days (or −1.57 ± 0.71% annual SWE day–1). Over the 2021 snowmelt period, four +3–+5 °C heatwave events occurred prior to the heat dome. Cumulatively, this succession of anomalies melted much of 2021’s snow, leaving relatively little to melt during the heat dome.
Long-term increase in spring heatwaves
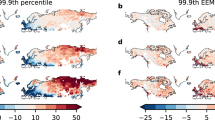
While the heat dome was extraordinary in magnitude and impact, our results point to the amplifying effect of successive springtime heat anomalies. To see how commonly these heatwaves occur, we examined total daily mean temperature anomalies ≥+5 °C during April, May, and June (AMJ) in the historical record. The PRISM record shows that the combined sum of these daily anomalies over the persistent snow zone has increased since the mid-1990s at a rate of ~1.93 °C year−1 (from 1993, Fig. 4a). This rate of increase translates into 1 additional +5 °C AMJ day every 3 years, or 11 additional days over the 29-year trend. El Niño was historically associated with the largest positive anomalies until the 2021 La Niña approached the extremes of 2015 and 2016. A positive trend for this period is widespread over the PNW study region and shows comparable trends in stations with longer records (Fig. 4b and Supplementary Figs. 5–7; see Methods “Historical record analysis” for further detail). While these heatwaves historically occurred nearly every spring, rarely, our results indicate their potential influence on melt dynamics has grown.
a PRISM record averaged over the persistent snow zone. Since 1993 there has been a positive trend of 1.93 °C per year (p = 0.048, n = 29, R2 = 0.105, 95% CI shown). b Portland Int’l Airport, where this metric has increased by 1.91 °C per year since 1993 (p < 0.01, n = 29, R2 = 0.293, 95% CI shown; see Methods “Historical record analysis” for a sensitivity analysis). From 1938–1991, these anomalies occurred nearly every year, but infrequently. However, minimum exposure in recent years (after 2015) now effectively matches the maximums of earlier decades. Moreover, the recent extremes of 2016 and 2021 are the greatest observed at this station, and 2021 is the first moderate La Niña year to show the high extremes that were previously reserved for El Niño periods. See Supplementary Figs. 5 and 6 for additional analysis.
The influence of these heatwaves on snowmelt may be quantified using a multiple linear regression. In 2021, they melted substantial snow, with only the fraction at the highest elevations persisting past the heat dome. In the western US, the timing of snow disappearance is also correlated with peak annual SWE, with greater masses of snow disappearing later40. Perennial snow patches in the persistent snow zone preclude complete snow disappearance, so an analogous response variable might be the Julian day when snow has disappeared from 95% (SD95) of the persistent snow zone. To evaluate how well snow disappearance is predicted by peak SWE and heatwaves, a multiple linear regression is applied:
where Peak SWE is the average maximum SWE of the persistent snow zone (mm), HW is the sum of daily mean temperature anomalies ≥+5 °C during AMJ (the cumulative heatwave metric used in Fig. 4), and the intercept at Julian day 178 is June 27th in non-leap years. The model and all terms are significant (p = 0.00012, R2 = 0.659; Supplementary Table 2). In 2021, the model suggests that multiple heatwaves advanced SD95 by 20.5 ± 6.6 days, from July 28th to July 8th, with the heat dome alone accounting for 9 of those days. If the +1.93 °C year−1 trend in the heatwave metric (Fig. 4) continued, the model suggests AMJ heatwaves would advance SD95 by ~1 day every 4 years, barring a ~15 mm increase in peak SWE.
Discussion
We found substantial melting of higher-elevation snowpack in our study due, in part, to an intense heat dome coupled with multiple earlier short-term (sub-weekly) spring heatwaves (Fig. 2). This complements prior work on snowpack trends that focused on snowpack loss in response to incremental annual or seasonal temperature increases over multi-decadal periods. Typically drawing on long-term station data and spatially contiguous hydrologic models, these studies find warming caused the greatest decline in western US snowpack at lower elevations23,24,26,28,41,42, with some also finding steeper declines in warmer months23,24,43. While much work has gone into attributing these long-term trends to climate warming23,24,28,41,44, daily-scale drivers of snow loss have been less considered. On different time-scales, however, the warming magnitudes differ substantially. In our study, daily anomalies were +3–5 °C or +5–10 °C during the 3 heatwaves preceding the heat dome (Fig. 2a), but 30-day moving average (i.e., monthly) anomalies centered on those periods were within ±1 °C (Table 1). A loss of temporal granularity is likely unimportant in more marginal snowpack environments (lower, warmer elevations), as more heatwaves or incrementally warmer baseline climates both translate to increased snowmelt. In areas buffered by cooler temperatures and greater precipitation, however, changes in SWE dynamics may only emerge when events, like short-term heatwaves, overwhelm that buffer. Importantly, those high-elevation sites generally receive the greatest amounts of precipitation and are the areas where meltwater contributions toward summer streamflows occur latest in the year, when water supply deficits are greatest.
The body of research focused on short-duration heatwave impacts to snowpack loss is limited. This is partially explained by our results (Fig. 4), which show spring heatwaves were less frequent in the historical record. So, until recently, their impacts to snow ablation were materially smaller and less detectable. Smaller heatwave anomalies even below the 0 °C threshold would still diminish accumulated snowpack cold content, modifying subsequent snowmelt timing and rate, but, especially in colder high-elevation areas where cold content presents a several times larger threshold to melting than at lower elevations, these impacts are relatively subtle45,46. Heatwave and snowpack research have each also prioritized different seasonal periods. Snowpack trends over decadal scales are typically derived over metrics that integrate cool-season physical processes (e.g., maximum annual SWE, April 1st SWE, date of maximum SWE) to which spring heatwaves are partially to completely invisible. Similarly, heatwave research typically centers summer events, either by design or through definitions based on exceeding absolute dry- or wet-bulb temperature thresholds. While this is effective for capturing historical trends and human impacts, it is less useful for capturing impacts to snowmelt, which largely happens prior to extreme summer temperatures. This might partially explain why the most rigorous studies to date of heatwave cryosphere impacts have focused on glaciers21,22. The recency of these studies (2021, 2022) also suggests the growing recognition (and frequency) of alpine heatwaves.
The El Niño–Southern Oscillation (ENSO) provides important context for western US snowpack, but its relationship to snowmelt is unclear. Depending on phase, strength, and interactions with other teleconnections and climate change, it influences atmospheric circulation and climate patterns globally47,48,49,50,51,52. In the PNW, this manifests as a negative correlation between annual snowpack accumulation and ENSO indices, with less snow during warmer, dryer, positive-phase (El Niño) years, and more during cooler, wetter, negative-phase (La Niña) periods53,54,55,56,57. The ENSO dipole is strongest in winter, when it influences mid-latitude jet stream strength and, thus, PNW precipitation. Over the cold months, this influence integrates into a single metric, maximum SWE, which exerts a physical control on snowmelt vis-à-vis minimum energy requirements for spring melting. After this inflection point, ENSO contributions to snowmelt are less clear. In 2021, multiple heatwaves accelerated snowmelt and led to earlier and more rapid seasonal melting, following a strong La Niña winter with high snowpack (ENSO in the 2020–2021 winter was its most negative since 2010–201158). However, La Niña is only weakly associated with PNW summer heat extremes47,51 and had arguably largely decayed by late spring, (La Niña persisted through summer 2021 in the NOAA PSL’s Multivariate ENSO Index59, but decayed in the NOAA NWS’s Oceanic Niño Index58). La Niña, though, is broadly consistent with the heat dome’s atmospheric dynamics, namely an unusually strong atmospheric river landfall in Alaska and omega block over the PNW33,34,35,60, and some have suggested it contributed to the heat dome61,62. Summers prior to La Niña also have more extreme heat summer days in certain northern mid-latitude regions, including the western US prior to double La Niña periods63 (2021 preceded a double La Niña from 2021–202358). We find little suggestion, however, that El Niño influences spring snowmelt beyond its typical influence on maximum SWE. Within our study, 2005 and 2015 (mild El Niño periods) had the slowest rates of absolute snowmelt (mm day−1; Fig. 2a), despite high cumulative heatwave exposure in 2015 (Fig. 4). This is consistent with prior work finding warmer winter temperatures lead to less SWE and earlier timing of maximum SWE, which, because available energy inputs are smaller in winter/early spring, leads to reductions in snowmelt rates and stream discharge53,64,65.
Net energy inputs control the rate of snowpack loss. We did not study energy balance directly here, but previous work on snowmelt controls (sensible and latent heat flux, net shortwave and longwave radiation, ground heat flux, and advected heat of precipitation), generally find that radiation and turbulent fluxes (sensible and latent heat) dominate, including in the western US and PNW66,67,68,69,70. Sensible heat flux likely plays a role via advection of warm air from adjacent snow-free sites70,71. This would be enhanced under heatwave temperatures, especially later in the season as snow cover becomes increasingly patchy and concentrated in high-relief topography. In late spring and summer heatwaves, net shortwave radiation would also be greater due to lower-albedo wet snowpack and the clear skies of the high-pressure conditions associated with these heatwaves. Occurring within days of the summer solstice, the heat dome maximized this effect. The lack of clouds somewhat mitigates net longwave radiation, although a water vapor anomaly trapped under the dry heat dome may have contributed to a greenhouse effect34, increasing longwave radiation input in the absence of clouds, on top of its inherent increase with air temperature. The remaining energy balance factors warrant further study but are less likely to play a major role in snowmelt during spring and summer heatwaves. Sublimation could play a role, depending on wind strength during high pressure ridging and the persistence of katabatic winds, but it is more associated with low pressure, freezing temperatures, and high wind speed66, which were not characteristic of the heatwaves examined in this study. So, it would seem unlikely that sublimation played a major role in either snowpack mass or energy balance during these heatwaves. This raises a question that future research might address: how do the mechanics (e.g., high-pressure ridging, wind strength and speed) and seasonal timing of heatwaves alter snowmelt energy balance? In the persistent snow zone, melt rates are generally highest in July and August (Supplementary Fig. 4), a generally hot, dry period in the western US when seasonal energy controls resemble those of extreme heatwaves, including higher sensible heat flux and radiative inputs. That the heat dome caused record rapid melting somewhat earlier than normal may be owed to: sensible heat flux of extreme high temperatures, maximized shortwave radiation near the solstice, and an amplifying effect of prior heatwaves that shifted snowpack factors (e.g., albedo, smoothness, patchiness) in the direction of enhanced energy absorption. By contrast, when those factors are less present, such as during early spring or winter, heatwaves would likely have less impact on snowpack loss.
Our results join others in finding increasing heat extremes in recent decades, which are consistent with projections of increased heat extreme frequency and severity in the future72,73,74,75. Our work highlights the role of heatwaves as an increasingly important driver of high-elevation snowpack loss. By focusing on these more granular events that are the proximal causes of accelerated snowmelt, rather than the incremental temperature increases captured at seasonal or annual scales, our study uncovered a positive heatwave trend undermining snowpack in the most reliably seasonally snow-covered zones of the study region. Particularly when these events occur at scale (e.g., 2003 European, 2010 Russian75, or 2020 Siberian heatwaves76), or with increasing frequency (in the Alps, daily maximum temperature anomalies ≥+10 °C during winter have increased more than twenty-fold between 1970–200077,78), and in succession (2021, concluding with the heat dome), they may impact higher-altitude and -latitude seasonal snowpack well before average climate warming might suggest.
In 2021, a record-breaking heat dome amplified this pattern and motivated our study, but we ultimately found that a larger pattern of successive heatwaves dwarfed the impacts of this extreme event. Subsequent research has suggested the heat dome’s probability was miniscule79, and so insight drawn from solely this event might be of limited use. The broader trend of increasing heatwaves that we uncovered in the process of probing the heat dome, however, is robust and in keeping with more established warming trends25,73,75. In the coming decades, record-breaking heat domes may continue to be rare, but the progression of a heatwave trend and its interactions with normal interannual and interdecadal variabilitys43,80,81 (e.g., ENSO, PNA, etc.) may serve similarly well to accelerate high-elevation snowpack loss.
Methods
Snowpack analysis
Snowpack was evaluated using SNODAS data in ArcMap (10.7.1) and R (4.0.5). SNODAS data from October 2003–April 2022 (n = 18 complete water years, each from October–September of the following calendar year), masked to the contiguous US with some extension into southern Canada, was downloaded via ftp per landing page guidance (https://nsidc.org/data/g02158). SWE rasters were extracted from daily .tar files, imported into ArcMap, and clipped to a PNW region within 41.88–49.065°N and 124.80–119.60°W. The Spatial Analyst extension was used to process the imported rasters. Using all the April 1st rasters from 2004–2022, excluding 2004, 2005 and 2015 (leaving n = 16 April 1st rasters), the “persistent snow zone” was defined as all gridcells within the region where at least 39 mm (1.5”) of SWE was present on April 1st for all these 16 years. April 1st, 2004 was excluded for excessive missing and discontinuous values, while April 1st’s in 2005 and 2015 both had record low SWE for unusual climatology and (in 2015) record season-length warmth26,44, and thus were considered less representative for classification criteria. This process identified and classified the “persistent snow zone” which was subsequently analyzed in this study over the SNODAS period of record through 2021 (n = 18 water years; 2004–2021, including 2004, 2005, and 2015). Zonal statistics were calculated for the persistent snow zone for each day, including mean SWE. These zonal statistics were tabulated and exported into a .csv form for analysis in R.
Daily zonal statistics for the persistent snow zone over these 18 water years, alongside values from the attribute tables of the daily rasters in ArcMap, are the basis for all reported descriptive statistics and snowpack values in this study, including SWE and snow-covered area. Mean SWE for the persistent snow zone is plotted in Fig. 2a for all days following each year’s peak SWE date, i.e., each year’s melting season. Normalized mean SWE was also derived for each water year by dividing daily SWE within a year by each water year’s maximum SWE value. These normalized SWE values are plotted in Supplementary Fig. 2 and Fig. 3b, and reported as percentages throughout this study to provide an additional basis for comparison across years, though it integrates a parameter not physically tied to heatwave-driven snowmelt: peak SWE. Despite this caveat, we include it for several reasons. First, it can help limit the influence of terrain heterogeneity when comparing regional SWE, with given SWE quartiles sharing at least some characteristics across years, as snowmelt first draws from predominantly warmer, lower elevation snowpack before progressively shifting to the highest alpine elevations. Additionally, it offers relative ease of use in estimating daily snow water volume loss (Fig. 3b) in needing only the annually fixed values of peak SWE and watershed area as conversion factors. Finally, it may be of potential interest to the hydrology and phenology communities due to factors including the relationship between relative snowmelt and runoff centers of volume82,83. Area-adjusted melt rate was derived by finding the change in total SWE between two consecutive days and dividing this value by the snow-covered area of the earlier day. Snow-covered area was defined as gridcells with ≥5 mm of SWE on a given day. The 5 mm minimum threshold was implemented to minimize the potential of inaccurately classifying snow-free cells as snow-covered. This follows approaches used in other snow cover assessments84,85,86, which also note no meaningful difference in snow-covered area by specific minimum threshold <15 mm. This lack of difference would be doubly true in this study, as daily SWE melt rates averaged nearly 4-times the 5 mm threshold (−19.5 mm day−1) during spring melting periods, meaning any inaccuracies should not persist more than ±1 day. These daily melt rates are plotted for the melting period from each year’s date of maximum SWE through either August (Supplementary Fig. 4, as a time-series), or until the date when SWE fell below 2% of its maximum annual value (Fig. 3a, as a scatterplot). Linear models and plotted fitted lines thereof (e.g., Figs. 3 and 4) were calculated using base R. The GAM fitted line in Fig. 3a was derived using mgcv::gam() in R.
El Niño and La Niña years were defined using NOAA’s Oceanic Niño Index (ONI)58. Five consecutive 3-month running means above or below the ±0.5 °C threshold of sea surface temperature anomalies in the Niño 3.4 region defines an El Niño (+) or La Niña (−) period. The most extreme values held for 3 consecutive periods within an El Niño or La Niña period were used to assign the strength of the ENSO period (extremes of ±0.5–1 = weak; ±1–1.5 = moderate; ±1.5–2 = strong; ±2+ = very strong). NOAA’s Extended Multivariate ENSO Index (MEI) (https://psl.noaa.gov/enso/mei.ext/) was used identically to calculate ENSO status and strength for years prior to 1950, as ONI does not extend earlier than 1950. MEI and ONI are qualitatively similar despite small deviations due to how the values are derived (bi-monthly empirical orthogonal function of 5 variables versus 3-monthly sea surface temperature anomalies). Additionally, the extended MEI is normalized for each bi-monthly period over its 1871–2005 record, instead of being centered on more recent reference periods. Characterizing years or melting seasons as El Niño or La Niña, when both modes occurred over the window from July–August–September of the preceding year until June–July–August of each year, was done on the basis of which pattern dominated during the 6 months prior to each year’s spring, when ENSO effects on snow accumulation and the subsequent spring’s snowmelt patterns would be most expressed. So, for example, 2010 was termed a moderate El Niño year in our analysis due to values of +0.6–1.6 between June–July–August 2009–February–March–April 2010 period, despite strong La Niña conditions emerging in the second half of the 2010 calendar year (July–December 2010). In this example, however, the strong La Niña characteristics over the last 6 months of 2010 were considered immaterial to snowmelt during 2010’s AMJ spring period. The ENSO paradigm for this spring, as in all PNW springs, was predominantly established by snowfall between the preceding October and April/May of each year, which is also when most of each year’s precipitation falls in the Mediterranean climate of the PNW.
SNODAS validation
An effort was made to validate the SNODAS dataset used in this study using an independent observational dataset of snow depth from 28 PNW stations over 9 years from October 2003–September 2012. This dataset consists of Northwest Weather and Avalanche Center (NWAC) weather stations prior to 2011, in addition to a small number of Western Regional Climate Center stations in California. SNOTEL observations were not used here, as, along with CADWR and NWS Co-op stations, they form the principal ground data sources ingested into SNODAS as part of its assimilation routines87. Thus, SNOTEL is not sufficiently independent for the validation effort. Snow depth at the analyzed stations is monitored using ultrasonic or laser depth sensors with either hourly or daily datalogging. The distribution of elevations for these stations (1544 ± 422 m, mean ± s.d.) closely aligned with the elevation distribution in the persistent snow zone overall (1555 ± 349 m; range 400–4307 m), with a reduced upper range (n = 4 stations >2000 m, overall range 605–2178 m). Stations were also checked for and found to be approximately representative of terrain, with similar size subgroups of windward (36%), leeward (46%), and neutral (18%) aspect, which has previously been a factor in local-scale SNODAS accuracy due to unaccounted-for wind redistribution of snow88. Most stations are located in the Washington Cascades, where most of the SWE in the persistent snow zone is located, with another ~1/3rd of stations in the Olympics, Oregon Cascades, and California Sierra Nevada (Supplementary Fig. 9).
Station observations of snow depth were compared with snow depth as modeled in SNODAS. From SNODAS snow depth rasters, daily values were extracted for cells where the observation stations were located. Values underwent basic post-processing correction to resolve missing or discontinuous/outlier values. Where possible with hourly datalogger records (the majority of cases) corrections consisted of replacing the 4 AM hourly data used for daily data with that of a different AM hourly observation. Infrequently, missing values were interpolated between adjacent dates. Stations were omitted from analysis when the corrections risked influencing the calculation of maximum annual SWE, the date thereof, or included April 1st. Observed (stations) and modeled (SNODAS) values were compared via linear regression using annual-scale metrics of maximum snow depth (using a 15-day moving average) and the date of that snow depth maximum. Snow depth on April 1st was also selected for comparison between modeled and observed values, by way of highlighting a daily scale comparison during the typical snowmelt transition period. Each of these annual metrics was pooled for all stations to generate regressions for each year evaluated across all stations.
The assumptions of linear regression were tested for the modeled versus observed regressions and found to generally hold (Supplementary Fig. 11). Heteroscedasticity was assessed using the Breusch-Pagan test (at the p < 0.05 level) and only found in the date of maximum snow depth metric in 2004–2005 and 2009–2010. Heteroscedasticity-consistent standard errors were thus implemented in those two instances (HC3, using estimatr::lm_robust() in R). Spatial autocorrelation was also evaluated and not found to play a major role in the strength of the correlations, with regression values with and without close neighbors not differing meaningfully (Supplementary Fig. 10 and Supplementary Tables 3 and 5). At similarly sited stations, spatial autocorrelation was expected to an extent (and the accuracy of interpolations in data assimilation systems such as SNODAS fundamentally rely on this pattern), but a review of observed snow depth curves did not show autocorrelation at a level precluding further analysis.
SNODAS was found to be in close agreement with observations, with some caveats. A full table of the regression results which includes the slopes, intercepts, and multiple-R2 of each set of regressions is included as Supplementary Tables 3 and 4 and discussed there. Overall, correlations for the 2003–2004 water year were weakest, though agreement was still robust. The relatively low correlations this year may reflect the same issue we identified while defining the persistent snow zone, namely that April 1st, 2004 had more discontinuous SWE and empty cells than other years, even when compared with exceptionally low-snow springs (2005, 2015). The 2003–2004 water year is the first in SNODAS’s operation, and SNODAS’ agreement with observations improves notably in all other years. So, issues with 2003–2004 are likely reflective of initial launch issues with the SNODAS model which are subsequently resolved. Outside of this year, agreement between SNODAS and station observations was quite high, especially where models with the intercept constrained to the origin were considered (Supplementary Table 4). In that formulation, R2 averaged 0.95 over all 27 year x metric combinations, and R2 > 0.87 in all years after 2003–2004. Maximum snow depth date had the strongest agreement across years (average R2 = 0.987), which lends some support to our use of SNODAS for determining the onset of the melt season each year in our study. Omitting 2003–2004, in the linear model formulation that left the intercept unconstrained, models contained an intercept of 0 and a slope of 1 in a 95% confidence ellipsoid (car::confidenceEllipse() in R 4.2.2) for all annual regressions except 2006–2007, 2008–2009, and 2009–2010 maximum snow depth date, indicating no significant statistical difference between observations and SNODAS in the majority of regressions (Supplementary Table 3). The data used for this analysis can be found with the data for supporting the findings of the overall study at https://doi.org/10.7910/DVN/BULLJL.
Temperature analysis
Gridded temperature data was obtained from the PRISM research group (https://prism.oregonstate.edu/) and processed in ArcMap and R. Daily mean temperatures at the 4 km2 resolution from March 1981–September 2021, in .bil raster format, were downloaded and extracted. This 1991–2021 period was chosen to align with the SNODAS record in this study (2003–2021), but also extending further back through 1991 to enable a calculation of daily normals using the same 30-year baseline as PRISM uses to derive its monthly normals. Records going further back through 1981, the earliest daily records available in PRISM, were also used to probe for longer term trends in the persistent snow zone. The rasters that were downloaded were then processed in R. Zonal statistics within the persistent snow zone were extracted using the raster package, using a shapefile of this zone converted from its original WGS 84 coordinate reference system (the SNODAS orientation) to the NAD 83 orientation system used by PRISM. Zonal statistics were calculated for all days from October 2003–September 2021, analogous to the snowpack analysis. Mean temperatures were tabulated and exported to a .csv form for further analysis in R. To calculate temperature anomalies, daily normal mean temperatures were derived using a 30-year period from 1991–2020. These daily normals were calculated by averaging for each day across this period from the raw PRISM data, and then further smoothed using a 7-day moving average. Using these derived normals, temperature anomalies were calculated by finding the difference between them and the mean temperatures in the persistent snow zone for each day. Daily normal NetCDF rasters were also written, using the ncdf4 package in R, for all days from April 1st–June 30th using the same 1991–2020 30-year reference period and 7-day moving average smoothing. This process was repeated for maximum and minimum temperature rasters from PRISM for the dates of the heat dome (June 26th–30th). These daily normal rasters, the zonal means extracted for the persistent snow zone for the heat dome dates, as well as the attribute tables of daily rasters when evaluated in ArcMap, were the basis for all temperatures reported.
The daily temperature anomalies in the persistent snow zone were modestly smoothed with a 3-day moving average in figures to account for potential misalignment between temperature and SWE observation times (daily SWE represents a snapshot at 06:00 UTC, while PRISM mean temperatures are the average of daily maximum and minimum temperatures, occurring at variable times each day). This potential misalignment appears to be minimal, however, as for any given year, we found only trivial improvement in the degree of correlation between a day’s temperature anomaly and the daily SWE change for that same day versus the day immediately prior. Three-day moving averaging SWE also allowed us to better highlight heatwaves, which are frequently defined as persisting for an at least 3-day period, and to improve signal-to-noise in our areal averaging, which on a 1-day scale may be more defined by heterogeneity in SWE and temperature over the persistent snow zone, but when smoothed over multiple days may be more likely to represent a larger region-wide anomaly.
Historical record analysis
To examine long-term trends, daily mean temperatures were compiled and analyzed for multiple stations as well as PRISM records. For stations, daily mean temperature values, as well as the normal values for each date (defined from 1991–2020) were exported into a .csv for analysis in R. Daily temperature anomalies during April, May and June (AMJ), which was used as an approximation for the snow melting season each year, were identified and used to estimate heat exposure ≥+5 °C for each station’s period of record. Daily temperature anomalies for all AMJ days where the anomaly was ≥+5 °C were summed for each year, producing a single metric, analogous to a seasonal heating or cooling degree-days sum referenced to a ±0 °C anomaly threshold, that captured both intensity (how much ≥+5 °C each day was) and frequency (how often ≥+5 °C days happened). Conceptually, this integrates the tailed events of the daily temperature distributions over each year’s AMJ period. Using the extracted daily average mean temperatures in the persistent snow zone and the daily normal temperatures derived in the above Methods “Temperature analysis” section, the analysis was repeated for the persistent snow zone over the PRISM period of record (1981–2021) (Fig. 4a). Lastly, using the daily normal temperature rasters we derived and the daily mean temperature rasters from PRISM, an analysis was done which calculated at each grid cell the temperature anomaly for every April–June day for years 1981–2021. Grid cells at each day where the anomaly was <+5 °C were filtered out, and the ≥+5 °C values retained and then pooled for the 91-day April–June window each year. From these pooled ≥+5 °C anomaly rasters for each year, the raster.kendall() function in the spatialEco package in R was used to calculate the trend for each cell from 1993–2021 using a Kendall’s tau test and Theil-Sen method for slope estimation. The Kendall tau statistic was used to better address the temporal and spatial auto-correlation concerns that would likely be an issue in an interpolated grid product like PRISM. The raster.kendall function includes in its output a raster of the tau statistic value for each grid cell in the study area, included here as Supplementary Fig. 6 to illustrate the level of positive correlation between the 1993–2021 time series and the more extreme temperature anomalies we studied.
Global Historical Climatology Network (GHCN) Stations were selected for analysis based on length and completeness of record (>90% coverage to 1950 or earlier) and proximity to areas of interest, generally either lower-elevation population centers in the PNW or higher-elevation stations in proximity to the persistent snow zone. Details on analyzed stations are included as Supplementary Table 1.
A sensitivity analysis was performed to test how different starting years affected the emergence of trends in the persistent snow zone, the Portland International Airport, and additional stations in the ≥+5 °C metric through 2021 (Fig. 4 and Supplementary Fig. 5). Trends were derived in R using the simple linear regression model: \(Y={\beta }_{0}+{\beta }_{1}X+\epsilon\), where \(Y\) is the value for the ≥+5 °C metric, \(X\) is the year of each AMJ period, and \({\beta }_{0}\), \({\beta }_{1}\), and \(\epsilon\) represent their traditional coefficient and error terms. Heteroscedasticity-consistent standard errors were implemented to address mild heteroscedasticity in the model (viz., recent extremes in 2016, 2021) using lm_robust() with se_type = ”HC3” (appropriate for smaller sample sizes) in the estimatr package. The slopes for all starting years from 1940–2010 are shown in Supplementary Fig. 7. For the six locations with trends calculated, except for a 1–4 year period in the mid-1980s in three of the locations, all years and locations show a positive trend in this metric for all starting years between 1940–2010. Across all long-term station records measured, for starting years 2010 and prior (see Supplementary Table 1 for record periods), 92% of trends are significant at the p < 0.1 level, and 81% at the p < 0.05 level, with most significance failures confined to a window from the late 1970s–early 1990s. The trend from 1993–2021 was chosen for emphasis and plotting in Fig. 4 due to the relative strength and significance of the trend from that year onwards, but similarly strong trends could be initiated at any point in the mid-1990s. Future research will be better equipped to ascertain this trend’s robustness more definitively. Trend emergence in the mid-1990s appeared relatively consistently, supporting the decision to fit a trend to this period and highlight it in our analysis. A positive trend in the intensity and/or frequency of extreme heat anomalies, insofar as they would emerge with greater regularity in a warm-shifted climate, is also better accounted for by the greater degree of warm-shifting that has manifested in more recent decades. Trend emergence in the mid-1990s is also more in agreement with natural modes of variability. The decade prior to then was unusually warm in spring due to what has been described as a Pacific-North American-like teleconnection81, but which oscillated in the mid-90s to its opposite phase that would typically contribute to cooler spring temperatures. Instead, a positive heatwave trend began in the opposite sign of this teleconnection influence, suggesting factors besides natural variability (e.g., an anthropogenic warming trend) emerged to dominate near this inflection point. This rationale was also applied to derive the trend in the PRISM record (Fig. 4b), although due in part to the greater variability in temperature anomalies at altitude, as well as the more limited time record (n = 40 years, 1981–2021), this trend is much more sensitive to starting year, only demonstrating significance at the p < 0.05 level in 1995, and at the p < 0.1 level for most of the 1990s and post-2004.
Multiple linear regression
A multiple linear regression was evaluated to predict snow-covered disappearance date as a function of peak annual SWE and AMJ heatwaves. Peak annual SWE was identified from the extracted SNODAS values for the persistent snow zone, for each spring in the study (2004–2021; Methods “Snowpack analysis”). Cumulative AMJ heatwaves were quantified using the same variable as in the historical record analysis, the sum of all daily mean temperature anomalies ≥+5 °C during April, May, and June (Fig. 4; Methods “Historical record analysis”). Because perennial snow patches in the persistent snow zone preclude complete snow disappearance, the model predicts the Julian day when 95% of the zone’s snow-covered area has disappeared (SD95), rather than a date of complete snow disappearance. The model was derived using lm() in base R. No outliers were found upon using Mahalanobis distance to screen for them. Diagnostic plots for the linear model were used to check for violations of the assumptions of normality, homoscedasticity, and linearity in the linear model, with no violations found. The model and its terms were all found to be significant, as detailed in Supplementary Table 2. It must be noted that extrapolating from the model gives nonsensical predictions at the lowest possible extremes of peak SWE. That is, the intercept of 177.9 implies that 95% of snow-covered area would persist until June 27th even with a complete absence of snowpack (peak SWE of 0 mm). However, the model performs normally to at least the two lowest observed extremes in the dataset (270 and 331 mm, 2005 and 2015, respectively), and the persistent snow zone, as defined, always holds substantial SWE on April 1st.
Data availability
Open raster, vector and tabular data are posted on the Harvard Dataverse under a CC0 Public Domain Dedication license that allows full and unrestricted global use of the data generated during this research while giving proper citation to the original author. These posted data allow for full replication, at the minimum mapping unit, of the results generated during this analysis. The data that support the findings of this study are available at https://doi.org/10.7910/DVN/BULLJL.
Code availability
Code used for the analysis is available at https://doi.org/10.7910/DVN/BULLJL.
References
Bratu, A. et al. The 2021 Western North American heat dome increased climate change anxiety among British Columbians: results from a natural experiment. J. Clim. Change Health 6, 100116 (2022).
Henderson, S. B., McLean, K. E., Lee, M. J. & Kosatsky, T. Analysis of community deaths during the catastrophic 2021 heat dome: early evidence to inform the public health response during subsequent events in greater Vancouver, Canada. Environ. Epidemiol. 6, e189 (2022).
Silberner, J. Heat wave causes hundreds of deaths and hospitalisations in Pacific north west. Br. Med. J. Online 374, n1696 (2021).
White, R. H. et al. The unprecedented Pacific Northwest heatwave of June 2021. Nat. Commun. 14, 727 (2023).
Gomez, M. B .C. heat wave ‘cooks’ fruit crops on the branch in sweltering Okanagan and Fraser valleys. CBC News (2021).
Taylor, A., Farzan, A. N. & Coletta, A. ‘Lytton is gone’: accounts of death, destruction in Canadian village that caught fire in record heat. Washington Post. https://www.washingtonpost.com/world/2021/07/01/lytton-canada-evacuated-wildfire-heatwave (2021).
Sloane, S. A., Gordon, A. & Connelly, I. D. Bushtit (Psaltriparus minimus) nestling mortality associated with unprecedented June 2021 heatwave in Portland, Oregon. Wilson J. Ornithol. 134, 155–162 (2022).
McElwee, P. Climate change and biodiversity loss: two sides of the same coin. Curr. Hist. 120, 295–300 (2021).
Tabrizian, A. AROUND OREGON: Northwest trees sapped by Oregon and Washington heat waves could be vulnerable to fire. Salem Reporter. https://www.salemreporter.com/2021/07/15/around-oregon-northwest-trees-sapped-by-oregon-and-washington-heat-waves-could-be-vulnerable-to-fire (2021).
Depinte, D. & Buhl, C. Detecting and mapping forest heat damage across the Pacific Northwest. in Mini-Symposium on June 2021 Heat Dome Foliage Scorch (College of Forestry, Oregon State University, 2021).
Klein, T., Torres-Ruiz, J. M. & Albers, J. J. Conifer desiccation in the 2021 NW heatwave confirms the role of hydraulic damage. Tree Physiol. 42, 722–726 (2022).
Raymond, W. W. et al. Assessment of the impacts of an unprecedented heatwave on intertidal shellfish of the Salish Sea. Ecology 103, e3798 (2022).
Menounos, B. et al. Cryospheric Response to the June, 2021 Heat Dome (AGU, 2021).
BC River Forecast Centre; Ministry of Forests, Lands, Natural Resource Operations and Rural Development. Flood Watch—Lillooet River. http://bcrfc.env.gov.bc.ca/warnings/advisories/FWT_2021_0626_1000_Lillooet_iss.pdf (2021).
Francovitch, E. Heat wave sends water pouring off Mount Rainier, exposing glaciers to summer heat sooner. The Spokesman-Review https://www.spokesman.com/stories/2021/jul/03/heat-wave-sends-water-pouring-off-mount-rainier-ex (2021).
McCabe, G. J. & Clark, M. P. Trends and variability in snowmelt runoff in the Western United States. J. Hydrometeorol. 6, 476–482 (2005).
Hansen, B. B. et al. Warmer and wetter winters: characteristics and implications of an extreme weather event in the High Arctic. Environ. Res. Lett. 9, 114021 (2014).
Salinger, M. J. et al. Unparalleled coupled ocean-atmosphere summer heatwaves in the New Zealand region: drivers, mechanisms and impacts. Clim. Change 162, 485–506 (2020).
Salinger, M. J. et al. The unprecedented coupled ocean-atmosphere summer heatwave in the New Zealand region 2017/18: drivers, mechanisms and impacts. Environ. Res. Lett. 14, 044023 (2019).
Ciavarella, A. et al. Prolonged Siberian heat of 2020 almost impossible without human influence. Clim. Change 166, 9 (2021).
Van Tiel, M., Van Loon, A. F., Seibert, J. & Stahl, K. Hydrological response to warm and dry weather: do glaciers compensate? Hydrol. Earth Syst. Sci. 25, 3245–3265 (2021).
Pelto, M. S., Dryak, M., Pelto, J., Matthews, T. & Perry, L. B. Contribution of glacier runoff during heat waves in the Nooksack River Basin USA. Water 14, 1145 (2022).
Mote, P. W., Li, S., Lettenmaier, D. P., Xiao, M. & Engel, R. Dramatic declines in snowpack in the western US. Npj Clim. Atmos. Sci. 1, 1–6 (2018).
Kapnick, S. & Hall, A. Causes of recent changes in western North American snowpack. Clim. Dyn. 38, 1885–1899 (2012).
Abatzoglou, J. T., Rupp, D. E. & Mote, P. W. Seasonal climate variability and change in the Pacific Northwest of the United States. J. Clim. 27, 2125–2142 (2014).
Mote, P., Hamlet, A. & Salathé, E. Has spring snowpack declined in the Washington cascades? Hydrol. Earth Syst. Sci. 12, 193–206 (2008).
Rupp, D. E., Abatzoglou, J. T. & Mote, P. W. Projections of 21st century climate of the Columbia River Basin. Clim. Dyn. 49, 1783–1799 (2017).
McCabe, G. J. & Wolock, D. M. Recent declines in Western U.S. snowpack in the context of twentieth-century climate variability. Earth Interact. 13, 1–15 (2009).
Luce, C. H., Abatzoglou, J. T. & Holden, Z. A. The missing mountain water: slower westerlies decrease orographic enhancement in the Pacific Northwest USA. Science 342, 1360–1364 (2013).
PRISM Climate Group, Oregon State University. Parameter-elevation Regressions on Independent Slopes Model (PRISM) Gridded Climate Data. https://prism.oregonstate.edu, https://www.nature.com/articles/s43247-022-00662-9#ref-CR19 (Accessed April 2022)
National Operational Hydrologic Remote Sensing Center. Snow Data Assimilation System (SNODAS) Data Products at NSIDC, Version 1 [SWE] (National Snow and Ice Data Center, 2004).
Montoya, E. L., Dozier, J. & Meiring, W. Biases of April 1 snow water equivalent records in the Sierra Nevada and their associations with large-scale climate indices. Geophys. Res. Lett. 41, 5912–5918 (2014).
Overland, J. E. Causes of the record-breaking Pacific Northwest heatwave, late June 2021. Atmosphere 12, 1434 (2021).
Mo, R., Lin, H. & Vitart, F. An anomalous warm-season trans-Pacific atmospheric river linked to the 2021 western North America heatwave. Commun. Earth Environ. 3, 1–12 (2022).
Neal, E., Huang, C. S. Y. & Nakamura, N. The 2021 Pacific Northwest heat wave and associated blocking: meteorology and the role of an upstream cyclone as a diabatic source of wave activity. Geophys. Res. Lett. 49, e2021GL097699 (2022).
Philip, S. Y. et al. Rapid attribution analysis of the extraordinary heat wave on the Pacific coast of the US and Canada in June 2021. Earth Syst. Dyn. 13, 1689–1713 (2022).
Daly, C., Gibson, W. P., Taylor, G. H., Johnson, G. L. & Pasteris, P. A knowledge-based approach to the statistical mapping of climate. Clim. Res. 22, 99–113 (2002).
Daly, C., Smith, J. W., Smith, J. I. & McKane, R. B. High-resolution spatial modeling of daily weather elements for a catchment in the Oregon Cascade Mountains, United States. J. Appl. Meteorol. Climatol. 46, 1565–1586 (2007).
Minder, J. R., Mote, P. W. & Lundquist, J. D. Surface temperature lapse rates over complex terrain: lessons from the Cascade Mountains. J. Geophys. Res. Atmospheres 115, D14122 (2010).
Heldmyer, A., Livneh, B., Molotch, N. & Rajagopalan, B. Investigating the relationship between peak snow-water equivalent and snow timing indices in the Western United States and Alaska. Water Resour. Res. 57, e2020WR029395 (2021).
Mote, P. W., Hamlet, A. F., Clark, M. P. & Lettenmaier, D. P. Declining Mountain Snowpack in Western North America*. Bull. Am. Meteorol. Soc. 86, 39–50 (2005).
Pierce, D. W. et al. Attribution of declining Western U.S. snowpack to human effects. J. Clim. 21, 6425–6444 (2008).
Siler, N., Proistosescu, C. & Po-Chedley, S. Natural variability has slowed the decline in Western U.S. snowpack Since the 1980s. Geophys. Res. Lett. 46, 346–355 (2019).
Mote, P. W. et al. Perspectives on the causes of exceptionally low 2015 snowpack in the western United States. Geophys. Res. Lett. 43, 10,980–10,988 (2016).
Jennings, K. S. & Molotch, N. P. Snowfall fraction, cold content, and energy balance changes drive differential response to simulated warming in an alpine and subalpine snowpack. Front. Earth Sci. 8, 186 (2020).
Jennings, K. S., Kittel, T. G. F. & Molotch, N. P. Observations and simulations of the seasonal evolution of snowpack cold content and its relation to snowmelt and the snowpack energy budget. Cryosphere 12, 1595–1614 (2018).
Loikith, P. C. & Broccoli, A. J. The influence of recurrent modes of climate variability on the occurrence of winter and summer extreme temperatures over North America. J. Clim. 27, 1600–1618 (2014).
Cayan, D. R., Redmond, K. T. & Riddle, L. G. ENSO and hydrologic extremes in the Western United States. J. Clim. 12, 2881–2893 (1999).
Higgins, R. W., Leetmaa, A. & Kousky, V. E. Relationships between climate variability and winter temperature extremes in the United States. J. Clim. 15, 1555–1572 (2002).
Kenyon, J. & Hegerl, G. C. Influence of modes of climate variability on global precipitation extremes. J. Clim. 23, 6248–6262 (2010).
Kenyon, J. & Hegerl, G. C. Influence of modes of climate variability on global temperature extremes. J. Clim. 21, 3872–3889 (2008).
Geng, T. et al. Emergence of changing Central-Pacific and Eastern-Pacific El Niño-Southern Oscillation in a warming climate. Nat. Commun. 13, 6616 (2022).
Beebee, R. A. & Manga, M. Variation in the relationship between snowmelt runoff in Oregon and ENSO and PDO. J. Am. Water Resour. Assoc. 40, 1011–1024 (2004).
Tamaddun, K. A., Kalra, A., Bernardez, M. & Ahmad, S. Multi-scale correlation between the Western U.S. snow water equivalent and ENSO/PDO using wavelet analyses. Water Resour. Manag. 31, 2745–2759 (2017).
Brown, D. P. & Comrie, A. C. A winter precipitation ‘dipole’ in the western United States associated with multidecadal ENSO variability. Geophys. Res. Lett. 31, L09203 (2004).
Thakur, B. et al. Linkage between ENSO phases and western US snow water equivalent. Atmos. Res. 236, 104827 (2020).
Patten, J. M., Smith, S. R. & O’Brien, J. J. Impacts of ENSO on snowfall frequencies in the United States. Weather Forecast. 18, 965–980 (2003).
NOAA/National Weather Service, Climate Prediction Center. Oceanic Niño Index. https://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php (2023).
NOAA Physical Sciences Laboratory. Multivariate ENSO index. https://www.psl.noaa.gov/enso/mei/ (2023).
Lin, H., Mo, R. & Vitart, F. The 2021 Western North American heatwave and its subseasonal predictions. Geophys. Res. Lett. 49, e2021GL097036 (2022).
NOAA. What is a heat dome? National Ocean Service website. https://oceanservice.noaa.gov/facts/heat-dome.html (2023).
Qian, Y. et al. Effects of subseasonal variation in the East Asian monsoon system on the summertime heat wave in Western North America in 2021. Geophys. Res. Lett. 49, e2021GL097659 (2022).
Luo, M. & Lau, N.-C. Summer heat extremes in northern continents linked to developing ENSO events. Environ. Res. Lett. 15, 074042 (2020).
Musselman, K. N., Clark, M. P., Liu, C., Ikeda, K. & Rasmussen, R. Slower snowmelt in a warmer world. Nat. Clim. Change 7, 214–219 (2017).
Barnhart, T. B. et al. Snowmelt rate dictates streamflow. Geophys. Res. Lett. 43, 8006–8016 (2016).
Jackson, S. I. & Prowse, T. D. Spatial variation of snowmelt and sublimation in a high-elevation semi-desert basin of western Canada. Hydrol. Process. 23, 2611–2627 (2009).
Marks, D. et al. Comparing simulated and measured sensible and latent heat fluxes over snow under a pine canopy to improve an energy balance snowmelt model. J. Hydrometeorol. 9, 1506–1522 (2008).
Mazurkiewicz, A. B., Callery, D. G. & McDonnell, J. J. Assessing the controls of the snow energy balance and water available for runoff in a rain-on-snow environment. J. Hydrol. 354, 1–14 (2008).
Male, D. H. & Granger, R. J. Snow surface energy exchange. Water Resour. Res. 17, 609–627 (1981).
Marks, D. & Dozier, J. Climate and energy exchange at the snow surface in the Alpine Region of the Sierra Nevada: 2. Snow cover energy balance. Water Resour. Res. 28, 3043–3054 (1992).
Marsh, P. Snowcover formation and melt: recent advances and future prospects. Hydrol. Process. 13, 2117–2134 (1999).
Perkins-Kirkpatrick, S. E. & Lewis, S. C. Increasing trends in regional heatwaves. Nat. Commun. 11, 3357 (2020).
Lopez, H. et al. Early emergence of anthropogenically forced heat waves in the western United States and Great Lakes. Nat. Clim. Change 8, 414–420 (2018).
García-Martínez, I. M. & Bollasina, M. A. Identifying the evolving human imprint on heat wave trends over the United States and Mexico. Environ. Res. Lett. 16, 094039 (2021).
Russo, S. et al. Magnitude of extreme heat waves in present climate and their projection in a warming world. J. Geophys. Res. Atmos. 119, 12,500–12,512 (2014).
Overland, J. E. & Wang, M. The 2020 Siberian heat wave. Int. J. Climatol. 41, E2341–E2346 (2021).
Beniston, M. Warm winter spells in the Swiss Alps: strong heat waves in a cold season? A study focusing on climate observations at the Saentis high mountain site. Geophys. Res. Lett. 32, 1–5 (2005).
Colucci, R. R., Giorgi, F. & Torma, C. Unprecedented heat wave in December 2015 and potential for winter glacier ablation in the eastern Alps. Sci. Rep. 7, 7090 (2017).
McKinnon, K. A. & Simpson, I. R. How unexpected was the 2021 Pacific Northwest Heatwave? Geophys. Res. Lett. 49, e2022GL100380 (2022).
Musselman, K. N. et al. Projected increases and shifts in rain-on-snow flood risk over western North America. Nat. Clim. Change 8, 808–812 (2018).
Abatzoglou, J. T. & Redmond, K. T. Asymmetry between trends in spring and autumn temperature and circulation regimes over western North America. Geophys. Res. Lett. 34, L18808 (2007).
Grogan, D. S., Burakowski, E. A. & Contosta, A. R. Snowmelt control on spring hydrology declines as the vernal window lengthens. Environ. Res. Lett. 15, 114040 (2020).
Stewart, I. T., Cayan, D. R. & Dettinger, M. D. Changes toward earlier streamflow timing across Western North America. J. Clim. 18, 1136–1155 (2005).
Dawson, N., Broxton, P. & Zeng, X. Evaluation of remotely sensed snow water equivalent and snow cover extent over the contiguous United States. J. Hydrometeorol. 19, 1777–1791 (2018).
Tong, J. & Velicogna, I. A comparison of AMSR-E/Aqua snow products with in situ observations and MODIS snow cover products in the Mackenzie River Basin, Canada. Remote Sens. 2, 2313–2322 (2010).
Di Marco, N. et al. Comparison of MODIS and model-derived snow-covered areas: impact of land use and solar illumination conditions. Geosciences 10, 134 (2020).
Carroll, T. et al. NOAA’s national snow analyses. in Proceedings of the 74th Annual Meeting of the Western Snow Conference, Vol. 74, 14 (2006).
Clow, D. W., Nanus, L., Verdin, K. L. & Schmidt, J. Evaluation of SNODAS snow depth and snow water equivalent estimates for the Colorado Rocky Mountains, USA. Hydrol. Process. 26, 2583–2591 (2012).
Acknowledgements
Observational snowpack station data used in the independent validation was provided by the US Forest Service in the Pacific Northwest. We would like to thank Dr. Andrew Fountain for reviewing and providing constructive feedback on earlier versions of this manuscript, and Brian Staab of the US Forest Service for reviewing earlier versions of the manuscript. This work was financially supported by National Research Initiative grant no. 2018-67020-2797 from the USDA National Institute of Food and Agriculture.
Author information
Authors and Affiliations
Contributions
L.R. and M.G.K. both conceived of and designed the study. SNODAS, PRISM and snow station and all temperature data were analyzed using a combination of coded scripts and R routines by L.R. L.R. wrote the manuscript, to which both authors contributed substantial interpretation, discussion, and text.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Reyes, L., Kramer, M.G. High-elevation snowpack loss during the 2021 Pacific Northwest heat dome amplified by successive spring heatwaves. npj Clim Atmos Sci 6, 208 (2023). https://doi.org/10.1038/s41612-023-00521-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-023-00521-0