Abstract
The East African region is highly susceptible to severe floods and persistent droughts, which greatly impact the livelihood of millions of people. Early warnings, at least a few seasons in advance, would help implement mitigation measures. However, most prediction systems using dynamical models perform poorly at long lead times. In this study, we propose a statistical deep learning approach based on a convolutional neural network (CNN) to predict extreme floods and droughts during the short rains season (October–December). The proposed CNN model captures the phase of extreme floods and droughts two to three seasons ahead, except for a few cases. By diagnosing the model’s skills using heatmaps, we find that predicted extreme floods and droughts are linked with the sea surface temperature anomalies of the Indian Ocean Dipole at shorter leads and with western and southern Indian Ocean, equatorial Pacific, and southern Atlantic Ocean at longer leads. Although there were a few poorly predicted exceptions, the superior skill of our CNN-based predictions at longer leads provides a significant advantage in developing mitigation measures.
Similar content being viewed by others
Introduction
East African countries rely on rain-fed agriculture, and their economies are highly dependent on the seasonal variability of rainfall. Extreme floods and droughts are therefore posing a serious threat to East African countries1,2. During extreme floods, millions of people are displaced due to loss of property and lack of safe drinking water. In addition, malaria and other water-borne diseases put a strain on poorly equipped health systems, often resulting in life-threatening situations1,3. In the most recent floods in 2019, an estimated 1.5 million people were affected1. Droughts are equally damaging, with child malnutrition, livestock deaths and lack of safe drinking water posing critical problems for millions of people4. These problems become even more dangerous during prolonged droughts, such as the recent one in 2021, which left 20 million people struggling to survive2. Accurate seasonal rainfall forecasting is therefore urgently needed in East Africa. This would greatly improve socio-economic activities by reducing disruption to the various sectors affected.
East Africa mainly receives rainfall during two seasons in a year, the first in March-April-May, known as the ‘long rains’, and the second in October-November-December (OND), known as the ‘short rains’. The amount of rainfall in the long rains season is relatively greater5. However, the interannual variability of the short rains is more intense6 due to the rapid southward movement of the inter-tropical convergence zone7, which is relatively slower during the long rains. Although both seasons pose considerable threats to the region3,4,5, the large-scale climate drivers of long rains variability are lesser known8,9 affecting its predictability skills and usefulness to society.
However, the interannual variability of the short rains is found to be strongly linked to SST variability over the Indian10,11,12,13,14, Pacific8,15,16,17, and partly over Atlantic Ocean18,19 and thus represent a major source of moisture variability. Among these teleconnections, the Indian Ocean is primarily responsible for above- or below-normal precipitation during short rains10,11,12 due to its independent phenomenon known as the Indian Ocean Dipole (IOD), in which the western part [50°E-70°E, 10°S-10°N] of the Indian Ocean is anomalously warmer (cooler) than the eastern part [90°E-110°E, 0°-10°N], creating a zonal positive (negative) SST gradient known as the Dipole Mode Index (DMI) (see “Methods”)10. The above-normal rainfall is due to the reversal of the usual westerlies in the Indian Ocean, which become easterlies11,20,21 during the strong positive IOD events (pIOD)11,20,21, as a result of the warmer western Indian Ocean compared to a much cooler eastern part, thus bringing more moisture to East Africa11,20,21. On the contrary, during negative IOD (nIOD), these westerlies become even stronger20,21 and sweep the equatorial Indian Ocean, diverting moisture away from East Africa20,21 and resulting in below-normal short rains. Additionally, the region of the southwestern Indian Ocean, west of Madagascar, is also strongly linked with above- and below-normal short rains via modulation of the south-easterlies22,23 during its high and low phases, respectively. Similarly, the equatorial Pacific Ocean has been shown in several previous studies to influence the variability of short rains by modifying the Walker circulation. During the warm (cold) phase of the El Niño/Southern Oscillation (ENSO), short rains are observed to be above (below) normal with a positive correlation8,13,15, whereas anomalies in the western Pacific are negatively correlated17. However, there is an arguable difference when such an effect is analyzed during pure ENSO events when the correlation is moderate but importantly negative11. Hence, the effect of ENSO on the short rains is suggested to be effectively mediated via the state of the Indian Ocean11,12,14, thus suggesting the preeminent role of the Indian Ocean. Additionally, the southwestern Atlantic Ocean also partly influences the variability of short rains by altering the south-easterlies18,19. These global teleconnections, therefore, imply the possibility of skillfully predicting short rains a few seasons in advance.
Various dynamical model-based seasonal prediction systems are quite good at predicting short rains, but only at short-lead times (when initialized from August/September)24,25,26. Moreover, their skill decreases rapidly at longer lead times26,27 (when initialized from April/May) and thus exhibits more false alarms25,26,28. Such an inability of the dynamical models to predict short rains at long lead times is supposedly associated with failure in simulating the mean state of the Indian Ocean24,29,30, which plays a vital role in controlling the variability of the short rains, and the spring predictability barrier phenomenon31, where the predictive skill of the forecasts declines rapidly when initialized during/before spring26,31. Similarly, seasonal predictions of short rains have also been studied in the past using the statistical models by training them on these various teleconnections32,33,34. Interestingly, a slightly superior skill was observed in them as compared to the dynamical models at longer lead times; however, several extreme floods and droughts events during the short rains season were largely missed25,32,34. Moreover, the predictive skill of these statistical models was considered to be biased due to the estimation of the teleconnections over the entire training-validation period, which should rather be estimated separately during each period, thus overestimating the predictive skill35.
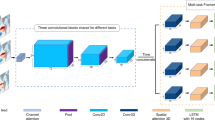
The strong teleconnections between short rains and SST variability in different oceanic regions, as well as the shortcomings in dynamical and statistical seasonal prediction models in predicting short rains at long leads, particularly extreme floods and droughts, to which East Africa is more prone, motivated us to investigate the predictability of short rains at both short and longer leads. To bridge this gap, we proposed a methodology based on the ‘convolutional neural network’ (CNN), a deep learning tool. In this study, we used SST anomalies (SSTA) and vertically averaged subsurface temperature anomalies (VATA) as predictors from September (short lead) and May/April (long lead) to develop an ensemble of CNNs to predict the East African short rain index during the OND season (hereafter EASRI). The predictability of various extreme floods and droughts that occurred over East Africa during a recent 39-year period (1983–2021) is discussed in the “Results” section, and the predictive skill is further diagnosed using CNN heatmap analysis to measure the self-sufficiency of these oceanic state-based predictors.
Results
EASRI predictability assessment
The EASRI is predicted using global monthly anomalies of SSTA and VATA as predictors from April, May, and September initializations for the 1983–2021 period, using the procedures discussed in “Methods”. As mentioned in “Methods”, the ensemble mean of CNN predicted (hereafter: CNN predicted) EASRI is evaluated using Global Precipitation Climatology Project (GPCP)36 estimated EASRI (hereafter: observed). For the September, May, and April initializations, the anomaly correlation coefficient (ACC) between CNN predicted and observed EASRI was 0.64, 0.64, and 0.61, respectively, significant at the 95% level (See Fig. 1). Such consistent ACC of the CNN predicted EASRI at different initializations is related to efficient extraction of precursors from oceanic predictors (discussed in more detail in subsequent sections). On the contrary, when evaluated over a similar time period, the leading seasonal dynamical prediction systems show a very poor to moderate ACC in predicting short rains. For example, the Scale Interaction Experiment-Frontier ver. 2 (SINTEX-F2) observes an ACC below 0.45 for September and June initialization25, the coupled forecast system model version 2 (CFSv2), the Global Environmental Multiscale Nucleus for European Modelling of the Ocean (GEM-NEMO), the Canadian Centre for Climate Modelling and Analysis Coupled Climate Model v.4 (CanCM4I), the Center for Ocean-Land-Atmosphere Community Climate System Model v.4 (COLA_CCSM4), the Geophysical Fluid Dynamics Laboratory (GFDL)-A, and the GFDL-B observed moderately poor ACC of 0.4, 0.4, 0.26, 0.24, −0.42, 0.06, and 0.40 (<0.4, 0.19, 0.24, −0.54, 0.04, 0.41, and 0.47)26, respectively, in May (April)-initialized predictions. Such poor predictive abilities of dynamical models to forecast EASRI from April/May initialization are reportedly linked to the spring predictability barrier26,31 and bias in simulating the Indian Ocean’s mean state24,29,30. However, it is possible to improve these poor skills by using a hybrid statistical-dynamical model approach. This approach has been shown to improve the correlation of May-initialized predictions for a few dynamical models25,26. Interestingly, we found that the CNN model performs even better than those dynamical and hybrid models in predicting EASRI from different initializations and is least affected by predictability barriers.
Comparison of observed EASRI (black-dashed) with CNN predicted using global SSTA and VATA as predictors from September (blue), May (orange), and April (blue) over a period from 1983 to 2021. Gray lines show the 90th and 10th percentile bounds. Ensemble mean ACC at different lead times is significant at the 95% significance level using a two-tailed t-test.
Given East Africa’s high vulnerability to extremes, we further examine CNN predictions during extreme floods and droughts. These extremes were classified using the 90th and 10th percentiles of the observed EASRI; if the EASRI exceeds either of these thresholds in a given year, it is referred to as an extreme flood/drought. During the validation period, 11 extreme events were observed, five of which were extreme floods: 1994, 1997, 2006, 2010, and 2019, while six were extreme droughts: 1996, 1998, 2005, 2010, 2016, and 2021. We also include the recent 2021 drought in the extremes, even though it was above the 10th percentile criteria because it was part of a series of recurrent droughts. Fig. 2 compares the CNN predictions of these various extreme floods and droughts from different initializations.
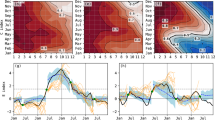
Comparison of CNN-predicted extreme floods and droughts initialized in September (blue), May (orange), and April (green) with observed GPCP precipitation anomalies (black). Extreme floods and droughts are sorted using the 90th and 10th percentile bounds (see Fig. 1) of EASRI. The standardized DMI (circle) and Niño3.4 (cross) indices calculated using OISSTv2 over September–November and November–January are overlaid.
Extreme floods
The CNN models generally predicted most of the extreme flood events, although with slight variations in the predicted amplitudes, for different lead times (Fig. 2). In particular, the phases of the two most severe floods of 1997 and 2019 are well predicted from different initialization months, due to the co-occurrence of pIOD and El Niño events. Similarly, the floods of 1994 were also predicted with high agreement with observations for all initializations. However, the prediction of the 2006 and 2011 floods was challenging for the CNN models during some initializations. The 2011 flood was predicted with very high agreement for the April initialization but was poorly predicted for the May and September initializations. The 2006 flood was predicted in phase with the April and May observations but failed the September initialization.
Investigating the cause of this high prediction skill during extreme floods using CNN heatmap analysis described in “Methods”, we observe a pIOD-like pattern in heatmaps as shown in Fig. 3. Such a pIOD pattern has been found to produce severe floods11,12 in East Africa due to the reversal of the usual westerlies to easterlies20,21 bringing with it abundant moisture; such a strong pIOD pattern is profoundly noted in the September initialization heatmaps (Fig. 3a–e), and these findings are consistent with previous analytical investigations11,12,14.
CNN gradient-based heatmaps observed during extreme flood prediction at different initializations of September (a–e), May (f–j) and April (k–o). Heatmaps are extracted from the first convolutional layer for the best ensemble member among ten others. The shading, red (blue), denotes the positive (negative) relationship with EASRI. The color bar at the bottom denotes the strength of the gradients from each region; higher strengths suggest a stronger influence on EASRI variability. The pIOD is highlighted with a solid black box in the western [50°E-70°E, 10°S-10°N] and eastern [90°E-110°E, 0°-10°N] Indian Ocean, and the Mascarene High in the southwestern Indian Ocean [60°E-90°E, 20°S-30°S] and while Niño3.4 is highlighted with a dotted black box.
Similar predictive skills are observed for May-initialized CNN predictions as in September, where all six extreme floods are predicted in phase with observations and with reasonable amplitude, while only one extreme (2011) is underestimated. The heatmap analysis for May-initialized CNN predictions (Fig. 3f–j) also reveals a pIOD-like pattern, though the intensity is slightly lower than in September heatmaps. Because of the early signals observed prior to the peak season, the pIOD-like pattern signals in May-initialized heatmaps (Supplementary Fig. 1: b1-c5). The pIOD-related prediction is aided by the anomalies in western, central, and eastern Pacific regions during a few of the extreme floods, as noted in previous studies15,16,17.
As the initialization month shifts to April, the intensity of the pIOD-like pattern for extreme flooding in the heatmap further decreases drastically, and a part of the southwestern Indian Ocean north of Madagascar, the Mascarene High (MH High), is seen to contribute significantly (Fig. 3k–o). The region above the MH high has a profound influence on the south-easterly winds, which intensify during its high phase and bring abundant moisture to East Africa, as do the unusual easterlies. Such a region is also investigated as a long-lead precursor of short rains in some important studies22,23. Also, we note a slightly greater contribution from the equatorial Pacific in April-initialized heatmaps, compared to the other initializations, as potential long-lead precursors of short rains13,15. In addition, a contribution from the southwestern Atlantic is also observed, which may be due to its effects on the southeastward flow18,19.
Despite the skillful prediction of various extreme floods, CNN did not predict the 2006 flood from September and underestimated the 2011 flood from September and May (Fig. 2). CNN’s poor September-initialized predictions in 2006 and 2011 could be attributed to strong MJO activity during those years37,38, whereas the 2011 May-initialized predictions could be attributed to a weak pIOD in the presence of a strong La Nina (see Supplementary Fig. 1: b4), both of which are known to affect short rains in opposite ways13,38. But CNN correctly predicted the phase of the 2011 flood because of the pIOD.
Extreme droughts
In a similar analysis for extreme droughts, we discovered that CNN predicted droughts in 1996, 1998, 2010, 2016, and the most recent 2021 with high agreement with the September initializations (Fig. 2) but with an underestimation for the 2005 droughts. Whereas four out of six extreme droughts were predicted in-phase in May, two (1996 and 2005) were incorrectly predicted (Fig. 2). However, when compared to May, April-initialized predictions show consistent underestimation, with predictions of two of the six extreme droughts out of phase (i.e., 2005 and 2021) and underestimating the droughts of 2010. Extreme droughts are subjected to the same heatmap analysis as extreme floods, as shown in Fig. 4.
Same as in Fig. 3, but observed during extreme droughts at different initialization from September (a–f), May (g–l) and April (m–r).
The high skill of September in predicting extreme droughts was found to be closely related to the nIOD-like pattern in the Indian Ocean (Fig. 4a–f), in contrast to the pIOD during extreme floods (Fig. 3a–e). Similar strong nIOD patterns were observed during the entire September initialization (Supplementary Fig. 2: a1–a6); such nIOD events further enhance the usual westerlies, diverting moisture away from East Africa and further leading to the droughts20,21, similar findings can be noted in many previous studies11,12,14. In addition to the Indian Ocean, the equatorial Pacific Ocean is also observed to contribute but with slightly less intensity.
During the May-initialized heatmaps (Fig. 4g–i), the nIOD-like pattern is slightly reduced in intensity compared to the September-initialized heatmaps (Fig. 4a–f). In addition, the contribution from the southwestern Indian Ocean, which has been studied as a potential cause of droughts22, is seen to increase in intensity, along with a slightly increased contribution from the equatorial Pacific.
Furthermore, in the April-initialized CNN heatmaps (Fig. 4m–r), this nIOD-like pattern further decreases compared to the May and September-initialized CNN heatmaps, along with an increase in intensities in the southwestern Indian Ocean and the equatorial Pacific Ocean. A contribution from the southern Atlantic is also detected, similar to the extreme flood heatmaps initialized in April.
Similar to extreme floods, there are a few cases where CNN has incorrectly predicted or underestimated droughts. These poor predictions of the 1996 and 2005 droughts from May may be related to the non-stationary relationship between the Indian Ocean and short rains in the former case, as in recent years39,40, and to the warmer Indian Ocean (Supplementary Fig. 2: b3) favoring floods in the latter case28. Similarly, the poor predictions during the April 2005 drought initialization were also related to the warmer Indian Ocean (Supplementary Fig. 2: b4), while the poor predictions for the 2010 and 2021 droughts could be due to the stronger MH high (Supplementary Fig. 2: c4, c6), which has been studied to favor floods22,23. In a further section, we discuss the results of the current study in terms of the comparative skill of the dynamical models and the differences in teleconnections observed for extreme flood and drought events.
Discussion
The prediction of extreme floods and droughts has been elaborated over the last 39 years (1983–2021) using deep learning-based CNN models trained with global monthly anomalies of SSTA and VATA. The ensemble means of the CNN models show excellent skill in predicting extreme flood and drought years in short rainy seasons from September initialization, compared to May and April (Fig. 1). The ACC of the CNN predictions from May and April are observed to be much higher than the various dynamical and hybrid models25,26 that have the potential to resolve the physical linkages and associated dynamics. Such improved long-lead prediction skills of CNN were related to its ability to capture early precursors of predictors (Figs. 3 and 4), including the obvious pattern of IOD, low and high phases of MH, anomalous warm and cold phases of the equatorial Pacific, and anomalies in the South Atlantic, in part. Interestingly, the short-lead precursors (Figs. 3a–e and 4a–f) were observed mainly in the Indian Ocean, especially in the western and eastern tropical Indian Ocean, with weak signals in the northern Indian Ocean and the equatorial Pacific Ocean. On the other hand, these precursors with long leads (Figs. 3f–o and 4g–r) show a slight shift toward the southern Indian, equatorial Pacific and southern Atlantic Oceans. Such precursors detected by CNN models are consistent with several studies investigating large-scale drivers of short rains. Moreover, the efficient extraction of these precursors also helped CNN to reduce the effect of the spring predictability barrier; however, dynamical models experience a rapid reduction in predictive skill25,26 due to such a barrier, leading to false predictions. For example, CFSv2 predicted the drought of 2016 as a flood from April, perhaps due to the lasting memory of the earlier 2015 El Niño26. However, CNN models trained on long-observed datasets correctly predicted the extreme floods of 1997 and 2019, and the withering droughts of 2010, 2016, and the most recent 2021 from May (Fig. 2). Nevertheless, there were a few cases of poor predictions for both extreme floods (2006 and 2011) and droughts (1996, 2005, 2010, and 2021). Such poor predictions can be partly attributed to the non-stationarity relation between the Indian Ocean and the short rains, the unfavorable warming of the western and southwestern Indian Ocean, and the co-occurrence of opposite states of IOD and ENSO. In addition, high-frequency weather and climate variations such as the MJO, which are not resolved by the monthly data used here, may also play a role in these poor predictions. Nevertheless, further study using dynamical models or heatmap-driven machine learning models with high-frequency data may help to understand such exceptional extreme cases.
In summary, the CNN-based models show a high degree of predictability for both extreme floods and droughts over East Africa at different lead times over the recent 39 years (1983–2021), especially for September initialization. This consistency is also evident for May and April initializations barring a few exceptions. The IOD pattern emerges as a dominant precursor for extreme floods and droughts, with a particularly strong impact in September initializations. This is in addition to the South Indian, Atlantic, Western and Central Pacific regions with longer lead times. However, a few cases were poorly predicted at longer lead times. Those were strongly associated with a weak DMI at the time of initialization, allowing factors other than IOD to degrade the relationship. The skills shown by CNN models for predicting extreme floods and droughts two to three seasons ahead are promising and will greatly help in organizing mitigation efforts to manage extremes, especially in cases such as the prolonged droughts of 2021.
Methods
Estimation of EASRI
EASRI is estimated over the East African region [35°E-46°E, 5°S-5°N]. This study region (see Supplementary Fig. 3) includes most of Kenya, followed by southeastern Somalia, southern Ethiopia, and northern Tanzania. Rainfall anomalies over this region were calculated by subtracting the actual rainfall values from the long-term climatological mean calculated over the period 1981–2010. These anomalies were then averaged for the OND season. This procedure is repeated for the Global Precipitation Climatology Center (GPCC)41 and GPCP rainfall datasets to prepare EASRI for the training and validation of CNN models.
DMI
The DMI is calculated by taking the difference in spatially averaged SSTA between the western [50°E-70°E, 10°S-10°N] and eastern [90°E-110°E, 0°-10°N] Indian Ocean, as described by Saji et al.10. The SSTA were calculated by subtracting the SST from its long-term climatological mean from 1981 to 2010. The NOAA Optimum Interpolation (OI) SST V2 (OISSTv2)42 monthly data sets were used to calculate the DMI.
CNN
We have attempted to predict EASRI using SSTA and VATA as predictors from the months of September, April, and May in separate experiments using an ensemble of CNN43. Here we describe in detail the structure of the CNN used. The proposed CNN involves convolutional processes over the global monthly SSTA and VATA to extract useful patterns from them in relation to the EASRI. This process is briefly elaborated by Eq. 1. Several key constituent parameters of the CNN are listed in Supplementary Table 1, and these are optimized using a random search algorithm44 over a range of values for each hyperparameter in the specific domain as listed in Supplementary Table 1. In a random search algorithm, 300 trials with different combinations of different parameters are considered, and CNNs are trained and evaluated for each of these 300 trials. The selection of 300 different combinations of CNN was considered in relation to the number of hyperparameters of the CNN (i.e., 10, see Supplementary Table 1) and an arbitrary ratio of 30, which is sufficiently large for such analysis44. For validation, we retained the top ten CNNs out of 300 based on high ACC criteria to estimate the ensemble mean skill. The number of ensemble members is equal to the number of hyperparameters, as the performance of the CNN is highly sensitive to variations in each of them44. The “Results” section elaborates on the predictive skill of EASRI based on the ensemble mean of the top ten CNN models.
where;
Training procedure of CNN
The training input attributes of the CNN, namely monthly SSTA and VATA, were derived from the Centennial in situ Observation-Based Estimates ver. 2 (COBEv2)45 (sea surface temperature) and Simple Ocean Data Assimilation (SODA)46 (subsurface temperature) datasets. These training attributes cover the period 1871–1980 with a spatial resolution of 5° × 5°, regridded from the original grid size by bi-linear interpolation to reduce the number of CNN parameters. In addition, the data were preprocessed by standardization followed by normalization (range −1 to +1) at each grid point. The target EASRI for CNN is calculated using GPCC datasets. The prediction of EASRI is performed using lagged monthly SSTA and VATA with a corresponding central month of the short rainy season (i.e., November). Different initializations are considered starting from April, May, and September monthly SSTA and VATA, where the distance between the initialization month and the central month of the seasonal EASRI is termed the lag. April, May, and September initializations are considered to have a lead of 7, 6, and 2 months, respectively.
We validate our proposed CNN model using SSTA obtained from OISSTv2, VATA obtained from the Global Ocean Data Assimilation System (GODAS)47 and the target EASRI index estimated based on GPCP rainfall anomalies (see Supplementary Fig. 4). These datasets are different from those used in the CNN training process, as similar sources may produce biased and non-robust predictions48.
A threefold cross-validation procedure was used to train the CNN, where the training data (1871–1980) was divided into several parts, and the CNN was trained on each part to ensure robust learning over data periods (see Supplementary Fig. 4). The hyperparameters of the CNN (see Supplementary Table 1) are optimized over training and cross-validation data sets using a mean square error-based loss function between observed and predicted EASRI. Model validation was performed over the period from 1983 to 2021. The training of the CNN was performed in an open-source Python environment based on Keras49 as the front-end APIs and Tensor-flow50 at the back-end, using the Earth Simulator at the Japan Agency for Marine-Earth Science and Technology (JAMSTEC).
Measures against overfitting
To overcome the overfitting problem in the CNN, several other layers are added in addition to the convolutional layers before the pooling layers. These are the drop-out layer51, the batch normalization layer52, and the l2 regularization layer43. The respective role of each layer is to filter out unnecessary parts of the predictors, to normalize the output after each convolution process to the limits of the transfer function, and to penalize the large trained weights. Apart from these measures, the training and cross-validation losses are also monitored, and the trials with validation losses lower than the training losses are avoided when choosing an ensemble member.
CNN heatmaps
The gradients of the trained CNN models from the first convolutional layer are extracted as heat maps to assess the importance of a specific region in the global ocean in controlling the variability of EASRI. The larger the gradients from a particular region, the more control it has over variability53. These gradient heatmaps differ from those used in some recent past studies48,54 where activation values were multiplied by gradients to produce heatmaps; however, such heatmaps are prone to contamination by large predictor values and thus misrepresent the importance of specific regions53. Equation 3 details the gradient-based heatmap extraction from the first convolution layer of trained CNN models. The heatmaps shown in Figs. 3 and 4 are extracted from the first convolutional layer for the best ensemble member (i.e., the first with the highest ACC) among the top ten ensemble members.
where;
Data availability
The various reanalysis and ocean data assimilation data for the experiment used in this study are publicly available. The Centennial-scale sea surface temperature analysis version-2 (COBE-SST 2), NCEP Global Ocean Data Assimilation System (GODAS), NOAA Optimum Interpolation (OI) SST V2, Global Precipitation Climatology Project (GPCP) and Global Precipitation Climatology Centre (GPCC) Monthly Analysis Product is available through the NOAA PSL, Boulder, Colorado, USA, from their website at https://psl.noaa.gov. Simple Ocean Data Assimilation (SODA) v 2.2.4 is acquired from http://apdrc.soest.hawaii.edu/las/v6/constrain?var=4787.
Code availability
The deep learning experimental analysis in this study is performed on python environment with tensorflow (https://www.tensorflow.org/) and keras (https://keras.io/) package and code can be obtained upon request to the corresponding author. Figures for this study are plotted using python matplotlib (https://matplotlib.org/) library and Microsoft excel software.
References
Flooding hits six million people in East Africa. BBC News, https://www.bbc.com/news/world-africa-54433904 (6 October 2020).
Etutu, J. & Ostasiewicz, A. East Africa drought: ‘The suffering here has no equal’. BBC News, Turkana. https://www.bbc.com/news/world-africa-61437239 (14 May 2022).
Wainwright, C. M., Finney, D. L., Kilavi, M., Black, E. & Marsham, J. H. Extreme rainfall in East Africa, October 2019–January 2020 and context under future climate change. Weather 76, 26–31 (2020).
Gebremeskel Haile, G. et al. Droughts in East Africa: causes, impacts and resilience. Earth Sci. Rev. 193, 146–161 (2019).
Hastenrath, S., Nicklis, A. & Greischar, L. Atmospheric-hydrospheric mechanisms of climate anomalies in the western equatorial Indian Ocean. J. Geophys. Res. 98, 20219 (1993).
Hastenrath, S., Polzin, D. & Mutai, C. Diagnosing the 2005 drought in equatorial East Africa. J. Clim. 20, 4628–4637 (2007).
Black, E., Slingo, J. & Sperber, K. R. An observational study of the relationship between excessively strong short rains in coastal East Africa and Indian Ocean SST. Mon. Weather Rev. 131, 74–94 (2003).
Ogallo, L. J. Relationships between seasonal rainfall in East Africa and the Southern Oscillation. J. Climatol. 8, 31–43 (1988).
Liebmann, B. et al. Understanding recent eastern Horn of Africa rainfall variability and change. J. Clim. 27, 8630–8645 (2014).
Saji, N. H., Goswami, B. N., Vinayachandran, P. N. & Yamagata, T. A dipole mode in the tropical Indian Ocean. Nature 401, 360–363 (1999).
Behera, S. K. et al. Paramount impact of the Indian Ocean Dipole on the East African short rains: a CGCM study. J. Clim. 18, 4514–4530 (2005).
Black, E. The relationship between Indian Ocean sea–surface temperature and East African rainfall. Philos. Trans. Royal Soc. A. 363, 43–47 (2005).
Clark, C. O., Webster, P. J. & Cole, J. E. Interdecadal variability of the relationship between the Indian Ocean zonal mode and East African coastal rainfall anomalies. J. Clim. 16, 548–554 (2003).
Ummenhofer, C. C., Sen Gupta, A., England, M. H. & Reason, C. J. C. Contributions of Indian Ocean sea surface temperatures to enhanced East African rainfall. J. Clim. 22, 993–1013 (2009).
MacLeod, D., Graham, R., O’Reilly, C., Otieno, G. & Todd, M. Causal pathways linking different flavours of ENSO with the Greater Horn of Africa short rains. Atmos. Sci. Lett. 22, e1015 (2021).
Vashisht, A. & Zaitchik, B. Modulation of East African boreal fall rainfall: combined effects of the Madden Julian Oscillation (MJO) and El Niño Southern Oscillation (ENSO). J. Clim. 35, 1–42 (2021).
Funk, C. et al. Examining the role of unusually warm Indo‐Pacific sea‐surface temperatures in recent African droughts. Q. J. R. Meteorol. 144, 360–383 (2018).
Camberlin, P., Janicot, S. & Poccard, I. Seasonality and atmospheric dynamics of the teleconnection between African rainfall and tropical sea-surface temperature: Atlantic vs. ENSO. Int. J. Climatol. 21, 973–1005 (2001).
Mwale, D. & Gan, T. Y. Wavelet analysis of variability, teleconnectivity, and predictability of the September–November East African rainfall. J. Appl. Meteorol. Climatol. 44, 256–269 (2005).
Hastenrath, S., Polzin, D. & Camberlin, P. Exploring the predictability of the ‘Short Rains’ at the coast of East Africa. Int. J. Climatol. 24, 1333–1343 (2004).
Nicholson, S. E., Fink, A. H., Funk, C., Klotter, D. A. & Satheesh, A. R. Meteorological causes of the catastrophic rains of October/November 2019 in equatorial Africa. Glob. Planet Change 208, 103687 (2022).
Peng, X., Steinschneider, S. & Albertson, J. Investigating long-range seasonal predictability of East African short rains: influence of the Mascarene high on the Indian Ocean Walker cell. J. Appl. Meteorol. Climatol. 59, 1077–1090 (2020).
Manatsa, D., Morioka, Y., Behera, S. K., Matarira, C. H. & Yamagata, T. Impact of Mascarene high variability on the East African ‘short rains’. Clim. Dyn. 42, 1259–1274 (2013).
Walker, D. P. et al. Skill of dynamical and GHACOF consensus seasonal forecasts of East African rainfall. Clim. Dyn. 53, 4911–4935 (2019).
Doi, T., Behera, S. & Yamagata, T. On the predictability of the extreme drought in East Africa. Geophys. Res. Lett. 49, e2022GL100905 (2022).
Colman, A. Skilful long‐lead hybrid predictions of the East African short‐rains season. Int. J. Climatol. 42, 4097–4110 (2021).
Young, H. R. & Klingaman, N. P. Skill of seasonal rainfall and temperature forecasts for East Africa. Weather Forecast. 35, 1783–1800 (2020).
Bahaga, T. K., Kucharski, F., Tsidu, G. M. & Yang, H. Assessment of prediction and predictability of short rains over equatorial East Africa using a multi-model ensemble. Theor. Appl. Climatol. 123, 637–649 (2015).
Hirons, L. & Turner, A. The impact of Indian Ocean Mean-state biases in climate models on the representation of the East African short rains. J. Clim. 31, 6611–6631 (2018).
Fathrio, I. et al. Assessment of western Indian Ocean SST bias of CMIP5 models. J. Geophys. Res. Oceans 122, 3123–3140 (2017).
Torrence, C. & Webster, P. J. The annual cycle of persistence in the El Nño/Southern Oscillation. Q. J. R. Meteorol. 124, 1985–2004 (1998).
Nicholson, S. E. The predictability of rainfall over the Greater Horn of Africa. Part I: Prediction of seasonal rainfall. J. Hydrometeorol. 15, 1011–1027 (2014).
Nicholson, S. E. Climate and climatic variability of rainfall over eastern Africa. Rev. Geophys. 55, 590–635 (2017).
Philippon, N., Camberlin, P. & Fauchereau, N. Empirical predictability study of October–December East African rainfall. Q. J. R. Meteorol. 128, 2239–2256 (2002).
Deman, V. M. H. et al. Seasonal prediction of Horn of Africa long rains using machine learning: the pitfalls of preselecting correlated predictors. Front. Water 4, 1053020 (2022).
Adler, R. F. et al. The Version-2 Global Precipitation Climatology Project (GPCP) monthly precipitation analysis (1979–present). J. Hydrometeorol. 4, 1147–1167 (2003).
Maybee, B., Ward, N., Hirons, L. C. & Marsham, J. H. Importance of Madden–Julian oscillation phase to the interannual variability of East African rainfall. Atmos. Sci. Lett. 24, e1148 (2022).
de Andrade, F. M. et al. Subseasonal precipitation prediction for Africa: forecast evaluation and sources of predictability. Weather Forecast. 36, 265–284 (2021).
Manatsa, D. & Behera, S. K. On the epochal strengthening in the relationship between rainfall of East Africa and IOD. J. Clim. 26, 5655–5673 (2013).
Bahaga, T. K., Fink, A. H. & Knippertz, P. Revisiting interannual to decadal teleconnections influencing seasonal rainfall in the Greater Horn of Africa during the 20th century. Int. J. Climatol. 39, 2765–2785 (2019).
Schneider, U. et al. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 115, 15–40 (2013).
Reynolds, R. W., Rayner, N. A., Smith, T. M., Stokes, D. C. & Wang, W. An improved in situ and satellite SST analysis for climate. J. Clim. 15, 1609–1625 (2002).
Lecun, Y., Bottou, L., Bengio, Y. & Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 86, 2278–2324 (1998).
Bergstra, J. & Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 13, 281–305 (2012).
Hirahara, S., Ishii, M. & Fukuda, Y. Centennial-scale sea surface temperature analysis and its uncertainty. J. Clim. 27, 57–75 (2014).
Carton, J. A. & Giese, B. S. A reanalysis of ocean climate using Simple Ocean Data Assimilation (SODA). Mon. Weather Rev. 136, 2999–3017 (2008).
Behringer, D. W. & Xue, Y. Evaluation of the global ocean data assimilation system at NCEP: The Pacific Ocean. In Proc. Eighth Symposium on Integrated Observing and Assimilation System for Atmosphere, Ocean, and Land Surface, AMS 84th Annual Meeting (AMS, 2004).
Ham, Y.-G., Kim, J.-H. & Luo, J.-J. Deep learning for multi-year ENSO forecasts. Nature 573, 568–572 (2019).
keras-team. keras-team/keras. GitHub https://github.com/keras-team/keras (2019).
Abadi, M. TensorFlow: learning functions at scale. ACM SIGPLAN Notices 51, 1–1 (2016).
Srivastava, N., Hinton, G., Krizhevsky, A. & Salakhutdinov, R. Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 15, 1929–1958 (2014).
Ioffe, S. & Szegedy, C. Batch normalization: accelerating deep network training by reducing internal covariate shift. In Proc. 32nd International Conference on International Conference on Machine Learning (ICML’15), Vol. 2015, 448–456 (ICML, 2015).
Simonyan, K., Vedaldi, A. & Zisserman, A. Deep inside convolutional networks: visualising image classification models and saliency maps. Preprint at https://arxiv.org/pdf/1312.6034.pdf (2014).
Feng, M. et al. Predictability of sea surface temperature anomalies at the eastern pole of the Indian Ocean Dipole—using a convolutional neural network model. Front. Clim. 4, 925068 (2022).
Acknowledgements
K.R.P. is grateful for the financial support provided by the JAMSTEC young research grant and the computational support provided by Earth Simulator by JAMSTEC.
Author information
Authors and Affiliations
Contributions
All authors (K.R.P., T.D., S.K.B.) were involved in study conceptualization. K.R.P. carried out the CNN modelling, results analysis and wrote the first draft of the manuscript. T.D. and S.K.B. further improvised the manuscript. All authors contributed to the interpretation and discussion of the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Patil, K.R., Doi, T. & Behera, S.K. Predicting extreme floods and droughts in East Africa using a deep learning approach. npj Clim Atmos Sci 6, 108 (2023). https://doi.org/10.1038/s41612-023-00435-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-023-00435-x
This article is cited by
-
Rainfall variability and its teleconnection with atmospheric circulation anomalies over southern and southeastern region, Ethiopia
Theoretical and Applied Climatology (2024)