Abstract
The complete or partial collapse of the forests of Amazonia is consistently named as one of the top ten possible tipping points of Planet Earth in a changing climate. However, apart from a few observational studies that showed increased mortality after the severe droughts of 2005 and 2010, the evidence for such collapse depends primarily on modelling. Such studies are notoriously deficient at predicting the rainfall in the Amazon basin and how the vegetation interacts with the rainfall is poorly represented. Here, we use long-term surface-based observations of the air temperature and rainfall in Amazonia to provide a constraint on the modelled sensitivity of temperature to changes in precipitation. This emergent constraint also allows us to significantly constrain the likelihood of a forest collapse or dieback. We conclude that Amazon dieback under IPCC scenario RCP8.5 (crossing the tipping point) is not likely to occur in the twenty-first century.
Similar content being viewed by others
Introduction
Amazonia hosts the largest rainforest in the world: it holds 10–15% of global land biodiversity1,2 and generates 17–20% of global runoff to the oceans3,4. Future changes in Amazonia’s temperature and precipitation will play a key role in the global carbon, energy and water cycles5. Yet, Earth System models generally perform poorly in predicting Amazonian temperature and rainfall6; a shortcoming that generates considerable uncertainty in model predictions. Nevertheless, it has been suggested that within the next 50–100 years Amazonia might experience a large-scale dieback of the forest7,8 and cross a “tipping point”—moving irreversibly into a savanna-like ecosystem. IPCC AR5, has allocated a low confidence level to this dieback due to the uncertainty of the climate predictions9. Thus, a reduction in the uncertainty of Amazonian temperature–precipitation relations would also enhance the credibility of these models and provide more accurate information for planning climate change mitigation and adaptation10.
Reducing the uncertainty in the prediction of Amazonian climate by general circulation and Earth System models has generally been a great challenge11. Much of this uncertainty arises from scientific and observational gaps in our description of the climate system and our representation of key processes. In recent years, the “emergent constraints method” (see Methods) has been applied to assessing the sensitivities of model output to particular variables12. The method relies on a tight link between historical climate and future predictions across a range of Earth System models; it has been used to reduce the uncertainty in the climate predictions of sensitivities such as: equilibrium climate sensitivity13, low cloud sensitivity14 and tropical carbon sensitivity. Here we introduce a emergent constraint for reducing the uncertainty in the prediction of Amazonian temperature–precipitation relations.
Drought not only implies a shortage of precipitation, but it is also almost always associated with an increase in surface air temperature15. In Amazonia, such negative correlations between surface air temperature and precipitation have been established for the 2005 and 2010 drought16,17. Such droughts can severely affect the ecophysiological behaviour of the forest18,19, with the ultimate possibility of a runaway scenario of forest dieback. Such a scenario was predicted about 20 years ago by Cox et al.20.
Here, we first explore a plausible mechanism behind this land surface temperature–precipitation correlation by looking at in situ observational data. Next, we investigate if a similar relation is reproduced by Earth System models. We then analyse whether the observed relation can be used to constrain the modelled sensitivity of Amazonian future temperature to precipitation change (∆T/∆P). We thus provide a way to reduce the uncertainty in the temperature sensitivity. Importantly, using the newly established temperature sensitivity constraint, we estimate how much rainforest dieback is likely to occur.
Results
Physical mechanisms of emergent constraint
We first explore and verify a plausible physical mechanism to support the existence of a possible relationship between surface air temperature and precipitation. From first principles such a relation between the surface air temperature of the Earth and the amount of precipitation is described through the surface energy balance, which can be expressed in a simplified form as
with σ the Stefan-Boltzmann constant, β the surface Bowen ratio, λ the latent heat of vaporisation, E the evaporation, α the surface shortwave albedo, and \(R_{\mathrm{s}}^{{\mathrm{down}}}\)and \(R_{\mathrm{l}}^{{\mathrm{down}}}\) the downward shortwave and the longwave radiation, respectively. In the imaginary case of a closed system (i.e. no net lateral influx of moisture or convergence), λE is equal to the precipitation and there is full recycling. In the low, or zero evaporation limit, Eq. (1) shows the surface air temperature to be dependent solely on the balance of incoming solar and longwave radiation. In the high evaporation limit, more typical of moist humid areas, Eq. (1) suggests that the land surface air temperature would balance the increasing evaporation, assuming no change in radiative fluxes. Varying land surface properties, moisture convergence, convection onset and radiation will make this relation more complex, but at its heart is a mechanism at the land surface that generally yields high surface air temperature when precipitation is low due to the reduced evaporative cooling effects, and vice versa15. In models this relation is probably best viewed as an emergent property of the model, i.e. it comes out as a final property of the model, incorporating various physical, thermodynamic and dynamic feedbacks and processes. The relation also forms the basis of many modelling results where Amazonia is deforested and the resulting land surface shows a general increase in surface air temperature and a decrease in rainfall21, albeit it with considerable variability between the models.
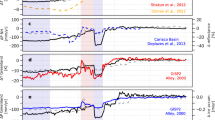
In Fig. 1a, we investigate whether such a relation exists in the observations by plotting the interannual variability of the surface air temperature and dry season precipitation from 1 May to 31 October22,23 for the sector of Amazonia bounded by 75°–45° W and 15°–0° S using the observational data from the HadCRUT4 data set. The observed temperature is near completely anti-correlated the dry season precipitation record; this relation (y = (−0.58 ± 0.16)x, p < 0.001, R = 0.45) is also significant in Fig. 1b for the linearly de-trended anomalies. Analysing four other observational data sets corroborates the negative correlation, although there is some relatively minor data set dependency (Supplementary Fig. 1 and Supplementary Table 1, p < 0.005). To investigate whether the dry season behaviour is reproduced by the Earth System models, the average land surface air temperature anomalies (1949–2002) from 29 different CMIP5 models, with one run per model (see Methods, Fig. 1c and Supplementary Table 2) and a 57-member physically perturbed HadCM3 model ensemble (Fig. 1d) are plotted against the precipitation anomalies. It is clear that such a relation is also reproduced by these model runs, albeit now one that is model dependent. The negative correlations are also significant at the annual-scale (y = (−0.32 ± 0.1)x, p < 0.001, R = 0.39, in Supplementary Fig. 2a), while during the wet season the correlation is not significant (y = (−0.33 ± 0.14)x, p = 0.021, R = 0.30, in Supplementary Fig. 2b). Apparently, and not unexpectedly, the feedback behaviour of precipitation on temperature at the annual-scale is mainly constrained by the response in the dry season rather than that in the wet season.
a The variation of the observed dry season average temperature and the observed dry season average of daily precipitation based on the observed data from the HadCRUT4 data set during 1949–2002. b The linear relationship between the observed dry season average temperature anomaly and the observed dry season average precipitation anomaly (y = (−0.58 ± 0.16)x, p < 0.001, R = 0.45). c, d The linear relationships between the simulated historical dry season temperature anomaly and the simulated historical dry season precipitation anomaly based on the mean outputs from the 29 CMIP5 models (y = (−2.17 ± 0.7)x, p < 0.005, R = 0.4, see the relation for each model in Supplementary Fig. 3a) and the 57 HadCM3 model runs (y = (−1.30 ± 0.56)x, p < 0.05 R = 0.31, see the relation for each model run in Supplementary Fig. 3b), respectively. e The uncertainties in the future annual temperature sensitivity to the precipitation (∆T/∆P) for the 86 Earth System model runs under RCP2.6 and RCP8.5 during 2006–2098. The grey shading represents the observed dry season sensitivity ± standard deviation (−0.58 ± 0.16 °C mm−1 day).
Based on the temperature–precipitation relation, we now define the sensitivity of Amazonian surface air temperature to a change in rainfall, ∆T/∆P, where T is the anomaly (°C) in the seasonal average temperature and P the precipitation anomaly (mm day−1). The future annual sensitivity here is calculated for 86 model runs (see Methods and caption to Fig. 1) using a similar procedure as for the observations in Fig. 1b; this procedure generates a set of 86 gradients for the future period. We find that the future annual temperature sensitivities show considerable variability ranging from −8.5 to 5.2 °C mm−1 day) (Fig. 1e). Few models are within the observed bounds (grey shading, −0.58 ± 0.16 °C mm−1 day) with most placed outside, even if we use the other observed data sets. Due to the observed strong control of the seasonal sensitivities on the annual sensitivities, we expect the seasonal cycle relations, in conjunction with the observations, to provide a meaningful constraint to the uncertainties in the future sensitivities—as long as we can establish a strong linear relation between historical seasonal and future annual sensitivities.
Emergent constraint on temperature sensitivity
Even with the large model-to-model variation in the future temperature sensitivity and the seasonal cycle of the dry season (Fig. 1e), the linear relationships for the 86 models are all significant, both for the 29 CMIP5 models as well as for the 57 HadCM3 model runs under the RCP2.6 and RCP8.5 scenarios (see Methods). The results for CMIP5 models are given in Fig. 2 and Supplementary Fig. 4, by the black circles and red fitting line. In contrast (Supplementary Fig. 5), the historical temperature sensitivity of the wet season exhibits extremely poor correlations with future climate. These tight relations in the dry season are in line with the observations where the observed annual temperature sensitivity is found to be highly dependent on the occurrence of precipitation in the dry season, rather than in the wet season. We now use these relations of the dry season with the observed seasonal sensitivity ± standard error (grey shading in Fig. 2 and Supplementary Fig. 4) to constrain the future annual temperature sensitivities. The associated probability density functions (PDF, see Methods and also see Cox et al.12) are also calculated for the inter-model spread in the future temperature sensitivity before (golden yellow lines) and after (blue lines) applying the observational constraint.
The outputs from the 29 models of the CMIP5 under RCP2.6 are used to derive the linear regression relationship between the future annual temperature sensitivity during 2006–2098 (see left y-axis) and the historical seasonal temperature (dry season) sensitivity during 1949–2002 (see bottom x-axis) (y = (0.81 ± 0.17)x-0.30, p < 0.001, R = 0.68); Each model output is shown by a black circle; the grey shading is the observational constraint from the HadCRUT4 (observed value ± 1 standard error, −0.58 ± 0.16 °C mm−1 day). The blue shading is the 90% prediction error of the linear fitting that has taken the fitting errors into consideration; the orange and blue probability density functions (PDFs) are for the future annual temperature sensitivities before and after applying the emergent constraint, respectively. We assumed all models obey a Gaussian distribution.
As shown in Fig. 2 and Supplementary Fig. 4a, the PDF for the constrained temperature sensitivities of the 29 CMIP5 models is considerably tightened when compared with the prior values. With 66% confidence limits, the observational constraint reduces the uncertainty of the future annual temperature sensitivities by a considerable amount, 20.3% and 14.1% for RCP2.6 and RCP 8.5 scenarios, respectively (Supplementary Table 3). We also find that the best estimates of the constrained temperature sensitivities at the peak of the PDF have been shifted towards the higher values with −0.78 °C mm−1 day and −1.49 °C mm−1 day for RCP 2.6 and RCP 8.5 scenarios, respectively. These values become less negative than the original results (Supplementary Table 3). These increased values of temperature sensitivities are a result of the strong relationship in the observed data, and suggest that the risks of a future increasing trend of the annual average temperature in response to decreasing precipitation might have been over-estimated in the CMIP5 ensemble for RCP2.6 and RCP8.5. The fact that this value is very close to the observed is fortuitous, a result of the particular value of the slope of the regression. For the other RCP scenarios and combinations with model sets there is a larger discrepancy. By multiplying the constrained future temperature sensitivity (∆T/∆P) and the future decreasing Amazonian precipitation (∆P, Supplementary Fig. 6), we find that the increase in annual temperature can be overestimated by up to 0.04 °C and 0.36 °C under RCP2.6 and RCP8.5, respectively, at the end of the twenty-first century (2089–2098), by comparing with the models’ original outputs.
When the same observational constraint is now also applied to the ensemble of 57 HadCM3 model runs (Supplementary Fig. 4b, c). We again find that the observed seasonal temperature sensitivities reduce the uncertainty of the future projections within a considerably tighter PDF at 23.0% and 15.1% for the RCP2.6 and RCP8.5 scenarios, respectively (Supplementary Table 3). Contrary to the CMIP5, the original outputs from the HadCM3 ensemble of model runs underestimated the risks of the future potential increase in annual temperature by 0.53 °C mm−1 day and 0.98 °C mm−1 day for the RCP2.6 and RCP8.5 scenarios, respectively. This result is due to a greater reduction in Amazonian precipitation in the HadCM3 ensemble than the CMIP5 models (Supplementary Fig. 6), with the best estimates shifting to more negative values. At the end of twenty-first century, the increased temperature can be underestimated by 0.03 °C and 0.22 °C under the RCP2.6 and RCP8.5 scenarios, respectively.
As shown in Fig. 2 and Supplementary Fig. 4, we also find that the best estimate of the temperature sensitivities under RCP2.6 and under RCP8.5 for the 57 HadCM3 model runs are higher than the sensitivities from the CMIP5 models, with the increased sensitivities up to 0.49 °C mm−1 day and 0.54 °C mm−1 day, respectively. The reason for these higher sensitivities is probably that the HadCM3 model runs explore a broader range of temperature, while the ensemble mean is also larger than that of the CMIP5 ensemble due to differences in physical climate feedbacks and carbon cycle responses between the two ensembles24.
Implications on Amazonian forest dieback
The realism of Earth System models is improving continuously as more physically based parameterisations of key processes are incorporated. Yet, the temperature sensitivity of Amazonian precipitation shows large variability among the predictions of the 86 model runs, even with values opposite in sign. We show that, based on strong emergent relationships between the current seasonal cycle and the future temperature sensitivity, the emergent constraint method can be used to reduce the models’ biases in temperature sensitivity. This holds for two nearly independent sets of models, and, importantly, we also identified a plausible physical mechanism for the relationships.
We find that the Earth System models from CMIP5 tended to overestimate the potential future increased temperature in response to the decreasing Amazonian precipitation. By comparing with the models’ original outputs, this temperature reduction was largely the result of feedbacks from the forest intensifying evaporative water recycling (evaporative cooling effects)25,26,27. The overestimated higher temperature can benefit modelled forest growth by reducing evaporative demand or by reducing respiration28,29. Thus, an overestimate of temperature increase also leads to a possible overestimated forest dieback based on the original outputs under RCP8.5 at the end of the twenty-first century.
To reveal the potential for forest dieback, the relationships between the future annual temperature sensitivity and the future forest losses for the CMIP5 models under RCP8.5 are shown in Fig. 3a and Supplementary Fig. 7a. We find a clear “tipping point” that might represent the limits of Amazonian forest drought tolerance (temperature sensitivity at −3.98 °C mm−1 day). A similar tipping point also occurs in the HadCM3 ensemble (Fig. 3b and Supplementary Fig. 7b, temperature sensitivity at −3.41 °C mm−1 day). Before this point, the rainforest appears to be able to access the water stored deep in soils for combating severe, seasonal droughts, even as the surface soil moisture stores are depleted30,31. Thus, in this range, the relation between sensitivity and forest cover before the tipping point is weak and the forest-cover fraction remains almost stable. Possible mechanisms are that forests can resist drought through, for instance, investing more carbohydrates into root growth for higher soil water availability32, increase stomatal closure during the middle of the day for less transpiration, thus increasing water-use efficiency (WUE)33 and leading to a more stable forest cover even during drought events34. The assumption of stable vegetation cover under drought is also supported by satellite-observed dry-season green up in Amazonian forest.
The relationships between the future forest losses (difference in forest-cover fraction between the periods 2089–2098 and 2006–2015) and the future annual temperature sensitivity for the CMIP5 (a) and HadCM3 (b) model ensembles under RCP8.5. The light blue bar is the constrained temperature sensitivity ± standard deviation (−1.49 ± 2.18 °C mm−1 day). The light brown bar is the initial mean temperature sensitivity of the CMIP5 models ± standard deviation (−3.61 ± 4.69 °C mm−1 day). The red lines before the tipping point are the mean future forest losses. The red lines after the tipping points are the linear relationships between the future forest losses and the future annual temperature sensitivities for the CMIP5 models (y = (2.280 ± 0.58)x + 8.45, p < 0.001, R = 0.89, for (a)) and for the 57 HadCM3 model runs (y = (20.08 ± 6.3)x + 64.31, p < 0.001, R = 0.53, for (b)). Note: Among the 29 CMIP5 models, 12 models output the leaf area index (LAI). Among them, we ignored the outputs of the LAI from the MIROC-ESM, GFDL-C3 and GFDL-ESM2G models, because of the unexpected result that for these three models, the more negative temperature sensitivity is, the higher is the LAI. This is not realistic because more negative temperature sensitivity represents a higher land surface temperature (see Methods for calculating forest-cover fraction using the LAI data).
In contrast, once this tipping point is crossed, the forest-cover fraction reduces sharply with further decreasing (more negative) temperature sensitivity. This relationship is significant (p < 0.001) for both the CMIP5 and for the HadCM3 model runs. There is a large set of observation-based papers that discusses the physiological mechanisms whereby Amazonian forest cover is sharply reduced under continuous drought (warmer temperature and less precipitation). This literature is largely based on long-term and large-scale ecosystem manipulation experiments, and suggests that multi-year severe drought can substantially reduce Amazonian forest cover35. For instance, an experimental exclusion of 35–41% of annual precipitation did exceed the drought-enduring upper limit of the forest, resulting in a sharp reduction in wood production by 13–62% in the region of Amazonia where the experiment was located. Apart from the effects of the long-term droughts on forest dieback, extreme drought events could also push the rainforest over the tipping point.
In Fig. 3a, our best estimate of the constrained temperature sensitivity (−1.49 °C mm−1 day) is mostly far away from reaching the tipping point identified by the CMIP5 models, leading to a 0.69% probability of forest dieback at the end of the twenty-first century. In contrast, although the best estimate of the original outputs from the models (−3.62 °C mm−1 day) also did not cross the tipping point, a probability (4.7%) for exceeding this point still exists. The initial CMIP5 findings may have been overestimating the impact of the temperature increase on Amazonian rainforest, with the overestimated future forest losses up to 1.78%. For the HadCM3 model runs (Fig. 3b), neither the central estimates of the constrained temperature sensitivity (−3.35 °C mm−1 day), nor the prior models’ mean results (−3.08 °C mm−1 day) passed the tipping point, while the original outputs are more likely to cross this point. Thus, although the potential future increase in temperature is underestimated by the original outputs, the best estimate of the forest losses from the original HadCM3 model runs are still overestimated by 8.68%, rather than underestimating forest dieback.
To evaluate the reliability of the constrained potential forest losses, we calculated the PDF of the forest dieback in response to the constrained and the unconstrained temperature sensitivities. As shown in Supplementary Fig. 8, at 66% confidence limits, the initial forest changes ranged between −6.29% and 1.35% for the CMIP5 models. After using the constrained temperature sensitivity, the constrained forest changes range between −2.55% and 1.17%, reducing the uncertainty by up to 51.0%. Similarly, the uncertainty of the future forest losses for the HadCM3 model runs is reduced by 13.8% (Supplementary Fig. 7b). Based on the original findings of the CMIP5 and HadCM3 model runs, the potential for large-scale forest dieback exists, with the reduced cover fraction being higher than 7.0% and 57.0% among the models, respectively. The initial probabilities of these extreme scenarios are up to 12.9% and 1.3% (Supplementary Fig. 7)36,37,38. In contrast, the constrained results show that the probabilities for the occurrence of these two extreme phenomena are almost impossible to reach for both the CMIP5 and HadCM3 model ensembles.
Discussion
Different global precipitation and temperature data sets all have their own uncertainties39, suggesting a possible bias in our findings when using only the HadCRU climate data set. However, using four other data sets for the observational constraint (Supplementary Figs. 8 and Supplementary Table 4), we still come to the same conclusions. Also, the potential future Amazonian forest losses are overestimated significantly, by both the CMIP5 and by the HadCM3 model runs. Thus, our main findings are neither observational data set dependent nor model-set dependent.
El Niño is the main driver of the drought events in Amazonia because under those conditions convection is suppressed40,41, leading to extremely high temperatures and low precipitation. These abnormal values may non-linearly affect the actual trends in the climate of Amazonia and it could be possible to obtain spurious and wrong precipitation–temperature relations. After smoothing out extreme fluctuations, using moving averages, we still find strong negative relations between precipitation and surface air temperature in the observations. Furthermore, the temperature sensitivities remain nearly the same, with the changed percentage only up to 6.8% (Supplementary Fig. 10). These findings further support the plausibility of the physical mechanisms behind our emergent constraint.
The current results show that the ESMs from CMIP5 may have been overestimating the sensitivity of land surface temperature to Amazonian precipitation, and that those from the HadCM3 ensemble tend to underestimate this sensitivity. In the RCP2.6 scenario runs, most of the models do not generate substantial dieback (Supplementary Fig. 11). Only with the stronger increases under RCP8.5 do a substantial number of the runs show such large-scale dieback, especially at the end of the twenty-first century42 (Supplementary Figs. 10), which should be receiving more attention. While the RCP8.5 climate change scenario may be unrealistic for the longer-term future43, previous deforestation modelling experiments, where substantial deforestation is simulated in the Amazon basin, have generally shown an increase in surface temperature44. This opens up the possibility that increasing human-induced deforestation may well bring the Amazonian forest closer to the tipping point than we have identified here. It is this interaction of a changing climate with human-induced deforestation that presents the next challenge for our understanding.
Methods
Selection of Earth System models and observational data sets
We selected 29 models from the Coupled Model Intercomparison Project 5 (CMIP5) based on the criterion of “one ensemble member per model”. The models’ historical outputs (1949–2002) and their outputs for a future under two representative concentration pathways (RCP2.6 and RCP8.5, 2006–2098) were collected from https://esgf-node.llnl.gov/projects/cmip5/. To verify that our proposed emergent constraint is independent of the selection of model sets, we also used the historical and future outputs from the 57-member ensemble made with the HadCM3 model for the same two scenarios45,46.
After identifying an empirical relationship between the current dry season temperature sensitivity and the future annual temperature sensitivity, we used the observed dry season temperature sensitivity during the period 1949–2002 from the HadCRUT4 data set (http://data.ceda.ac.uk/badc/cru/data/cru_ts) to constrain the future annual temperature sensitivity. To further verify our main findings, we also collected the four other data sets from the Delaware, GHCN, the “GISS vs GPCC” and the “NOAA vs GPCC”. The GISS data set and the NOAA data set have only the observed temperature data available. We therefore used the observed precipitation data from the GPCC data set for building their precipitation–temperature relations,
Calculating the probability density function involving in emergent constraints method
First, we calculate the PDF for the unconstrained future annual temperature sensitivity (the original results from CMIP5 under RCP2.6 and RCP8.5) by putting the mean value and standard deviation of the original future annual temperature sensitivity into Eq. (2). In general, we follow Cox et al.12 for the calculation of the PDFs.
where PDF(y/x) is the probability density around the best-fit linear regression, which represents the probability density of y given x. The “prediction error” of the regression is σy, calculated by Eq. (3); f(x) is the linear regression Eq. (4);
where yi is the value given by xi; a and b are the slope and intercept, respectively; s is used for minimising the least-squares error, calculating by Eq. (5); and N is the number of data points. σx is the variance of xi, calculated by Eq. (6); \(\overline x\) is the mean value;
As shown in Eq. (7), where PDF(F/H) is the probability density for “future annual temperature sensitivity” given “historical dry season temperature sensitivity”; PDF(H) is the observation-based PDF for “historical dry season temperature sensitivity”; Thus, after the emergent constraint, the PDF for “future annual temperature sensitivity” (PDF(F)) is calculated by numerically integrating PDF(F/H) and PDF(H).
Method for estimating vegetation-cover fraction
Based on the LAI data, we estimated vegetation-cover fraction using Eq. (8).
Where CF is the annual average vegetation-cover fraction of each grid cell (%); and LAI is the leaf area index.
Data availability
All the results data produced by this study are available from the corresponding author on reasonable request.
Code availability
The code for this study is available by request, from the corresponding author.
References
Hubbell, S. P. et al. How many tree species are there in the Amazon and how many of them will go extinct? Proc. Natl Acad. Sci. USA 105, 11498–11504 (2008).
Nobre, C. A., Sellers, P. J. & Shukla, J. Amazonian deforestation and regional climate change. J. Clim. 4, 957–988 (1991).
Jahfer, S., Vinayachandran, P. N. & Nanjundiah, R. S. Long-term impact of Amazon river runoff on northern hemispheric climate. Sci. Rep. 7, 10989 (2017).
Dolman, A. J. & Janssen, T. A. J. The enigma of the Amazonian carbon balance. Environ. Res. Lett. 13, 061002 (2018).
Wright, J. S. et al. Rainforest-initiated wet season onset over the southern Amazon. Proc. Natl Acad. Sci. USA 114, 8481–8486 (2017).
Joetzjer, E., Douville, H., Delire, C. & Ciais, P. Present-day and future Amazonian precipitation in global climate models: CMIP5 versus CMIP3. Clim. Dyn. 41, 2921–2936 (2013).
Malhi, Y. et al. Exploring the likelihood and mechanism of a climate-change-induced dieback of the Amazon rainforest. Proc. Nat. Acad. Sci. USA 106, 20610–20615 (2009).
Poulter, B. et al. Robust dynamics of Amazon dieback to climate change with perturbed ecosystem model parameters. Glob. Change Biol. 16, 2476–2495 (2010).
IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC, 2013).
Hall, A., Cox, P., Huntingford, C. & Klein, S. Progressing emergent constraints on future climate change. Nat. Clim. Change 9, 269–278 (2019).
Boisier, J. P., Ciais, P., Ducharne, A. & Guimberteau, M. Projected strengthening of Amazonian dry season by constrained climate model simulations. Nat. Clim. Change 5, 656 (2015).
Cox, P. M., Huntingford, C. & Williamson, M. S. Emergent constraint on equilibrium climate sensitivity from global temperature variability. Nature 553, 319–322 (2018).
Fasullo, J. T. & Trenberth, K. E. A less cloudy future: the role of subtropical subsidence in climate sensitivity. Science 338, 792–794 (2012).
Clement, A. C., Burgman, R. & Norris, J. R. Observational and model evidence for positive low-level cloud feedback. Science 325, 460–464 (2009).
Miralles, D. G., Teuling, A. J., Van Heerwaarden, C. C. & De Arellano, J. V. G. Mega-heatwave temperatures due to combined soil desiccation and atmospheric heat accumulation. Nat. Geosci. 7, 345 (2014).
Bagley, J. E., Desai, A. R., Harding, K. J., Snyder, P. K. & Foley, J. A. Drought and deforestation: has land cover change influenced recent precipitation extremes in the Amazon? J. Clim. 27, 345–361 (2014).
Ruivo, H. M., Sampaio, G. & Ramos, F. M. Knowledge extraction from large climatological data sets using a genome-wide analysis approach: application to the 2005 and 2010 Amazon droughts. Clim. Change 124, 347–361 (2014).
Toomey, M., Roberts, D. A., Still, C., Goulden, M. L. & McFadden, J. P. Remotely sensed heat anomalies linked with Amazonian forest biomass declines. Geophys. Res. Lett. 38, L19704 (2011).
Janssen, T., Fleischer, K., Luyssaert, S., Naudts, K. & Dolman, H. Drought resistance increases from the individual to the ecosystem level in highly diverse neotropical rain forest: a meta-analysis of leaf, tree and ecosystem responses to drought. Biogeosciences 17, 2621–2645 (2020).
Cox, P. M. et al. Sensitivity of tropical carbon to climate change constrained by carbon dioxide variability. Nature 494, 341–344 (2013).
Marengo, J. A., Jones, R., Alves, L. M. & Valverde, M. C. Future change of temperature and precipitation extremes in South America as derived from the PRECIS regional climate modeling system. Int. J. Climatol. 29, 2241–2255 (2009).
Harris, P. P., Huntingford, C. & Cox, P. M. Amazon Basin climate under global warming: the role of the sea surface temperature. Philos. Trans. R. Soc. B 363, 1753–1759 (2008).
Chai, Y. F. et al. Homogenization and polarization of the seasonal water discharge of global rivers in response to climatic and anthropogenic effects. Sci. Total Environ. 709, 136062 (2020).
Booth, B. B. B. et al. Scenario and modelling uncertainty in global mean temperature change derived from emission driven global climate models. Earth Syst. Dynam. 4, 95–108 (2013).
Betts, R. A. et al. The role of ecosystem-atmosphere interactions in simulated Amazonian precipitation decrease and forest dieback under global climate warming. Theor. Appl. Climatol. 78, 157–175 (2004).
Zemp, D. C. et al. Self-amplified Amazon forest loss due to vegetation-atmosphere feedbacks. Nat. Commun. 8, 1–10 (2017).
Lean, J. & Warrilow, D. A. Simulation of the regional climatic impact of Amazon deforestation. Nature 342, 411–413 (1989).
Allen, C. D. et al. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. Forest Ecol. Manage. 259, 660–684 (2010).
Harper, A. B. Drought Tolerance and Implications for Vegetation–Climate Interactions in The Amazon Forest. PhD thesis, University of Exeter (2012).
Nepstad, D. C., Stickler, C. M., Soares-Filho, B. & Merry, F. Interactions among Amazon land use, forests and climate: prospects for a near-term forest tipping point. Philos. Trans. R. Soc. B 363, 1737–1746 (2008).
Nepstad, D. et al. Amazon drought and its implications for forest flammability and tree growth: a basin‐wide analysis. Global Change Biol. 10, 704–717 (2004).
Metcalfe, D. B. et al. Shifts in plant respiration and carbon use efficiency at a large-scale drought experiment in the eastern Amazon. New Phytol. 187, 608–621 (2010).
Santos, V. A. H. F. D. et al. Causes of reduced leaf‐level photosynthesis during strong El Niñn drought in a central Amazon forest. Global Change Biol. 24, 4266–4279 (2018).
Jourdan, M., Kunstler, G. & Morin, X. How neighbourhood interactions control the temporal stability and resilience to drought of trees in mountain forests. J. Ecol. 108, 666–677 (2020).
Brando, P. M., Nepstad, D. C., Davidson, E. A., Trumbore, S. E. & Camargo, P. Drought effects on litterfall, wood production and belowground carbon cycling in an amazon forest: results of a throughfall reduction experiment. Philos. Trans. R. Soc. B 363, 1839–1848 (2008).
Huntingford, C. et al. Towards quantifying uncertainty in predictions of Amazon ‘dieback’. Philos. Trans. R. Soc. B 363, 1857–1864 (2008).
Cox, P. M., Betts, R. A., Jones, C. D., Spall, S. A. & Totterdell, I. J. Acceleration of global warming due to carbon-cycle feedbacks in a coupled climate model. Nature 408, 184–187 (2000).
Cox, P. M. et al. Amazonian forest dieback under climate-carbon cycle projections for the 21st century. Theor. Appl. Climatol. 78, 137–156 (2004).
Sun, Q. et al. A review of global precipitation data sets: data sources, estimation, and intercomparisons. Rev. Geophys. 56, 79–107 (2018).
Malhi, Y. et al. Climate change, deforestation, and the fate of Amazon. Science 319, 169–172 (2008).
Saleska, S. R. et al. Carbon in Amazon forests: unexpected seasonal fluxes and disturbance-induced losses. Science 302, 1554–1557 (2003).
Boulton, C. A., Booth, B. B. & Good, P. Exploring uncertainty of Amazon dieback in a perturbed parameter Earth system ensemble. Global Change Biol. 23, 5032–5044 (2017).
Hausfather, Z. & Peters, G. P. Emissions–the ‘Business as Usual’ story is misleading. Nature 577, 618–620 (2020).
Marengo, J. A. et al. Development of regional future climate change scenarios in South America using the Eta CPTEC/HadCM3 climate change projections: climatology and regional analyses for the Amazon, São Francisco and the Paraná River basins. Clim. Dyn. 38, 1829–1848 (2012).
Lambert, F. H. et al. Interactions between perturbations to different Earth system components simulated by a fully-coupled climate model. Clim. Dyn. 41, 3055–3072 (2013).
Murphy, J. M. et al. Transient climate changes in a perturbed parameter ensemble of emissions-driven Earth system model simulations. Clim. Dyn. 43, 2855–2885 (2014).
Acknowledgements
We greatly appreciate the help of Gillian Kay in obtaining the data from the HadCM3 ensemble. Further details can be found in references 31 and 32. We are thankful to Peter Cox, for his helpful advice and comments on an earlier version of this paper. AJD was originally funded by a Science without borders grant to CN and acknowledges support from the Netherlands Earth System Science Centre Grant/Award Number: 024.002.001. YC acknowledges support from the China Scholarship Council. Original funding for this work was also provided by the Amazalert project funded by the European Commission.
Author information
Authors and Affiliations
Contributions
Y.C. and H.D. led the writing, designed the research and performed the data analysis. G.M., C.N., C.R. and T.C. provided valuable comments.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chai, Y., Martins, G., Nobre, C. et al. Constraining Amazonian land surface temperature sensitivity to precipitation and the probability of forest dieback. npj Clim Atmos Sci 4, 6 (2021). https://doi.org/10.1038/s41612-021-00162-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-021-00162-1
This article is cited by
-
A precipitation downscaling framework for regional warning of debris flows in mountainous areas
Natural Hazards (2024)
-
Critical transitions in the Amazon forest system
Nature (2024)
-
A potential collapse of the Atlantic Meridional Overturning Circulation may stabilise eastern Amazonian rainforests
Communications Earth & Environment (2023)
-
Constrained tropical land temperature-precipitation sensitivity reveals decreasing evapotranspiration and faster vegetation greening in CMIP6 projections
npj Climate and Atmospheric Science (2023)
-
Constrained CMIP6 projections indicate less warming and a slower increase in water availability across Asia
Nature Communications (2022)