Abstract
Quantitative simulation of an aerosol’s lifecycle by regional-scale and global-scale atmospheric models is mandatory for unbiased analysis and prediction of aerosol radiative forcing and climate change. Globally, aerosol deposition is dominated by the rainout process, which is mostly triggered by activation of aerosols to liquid droplets in supersaturated domains of precipitating clouds. However, the actual environmental supersaturation value that aerosols experience in precipitating clouds is difficult for models to predict, and it has never been constrained by observations; as a result, there is large uncertainty in atmospheric aerosol simulations. Here, by a particle-tracer analysis of 37 rainfall events in East Asia, near the largest source region of anthropogenic aerosols in the northern hemisphere, we observed that the environmental supersaturation actually experienced by the removed aerosols in precipitating clouds averaged 0.08 ± 0.03% and ranged from 0.03 to 0.2%. Simulations by a mixing-state-resolved global aerosol model showed that the simulated long-range transport efficiency and global atmospheric burden of black carbon aerosols can be changed by a factor of two or three as a result of a change in the environmental supersaturation in precipitating clouds within just 0.08 ± 0.03%. This result is attributable to the fact that the sensitivity of an aerosol’s rainout efficiency to environmental supersaturation is higher for the less-aged black carbon concentrated near source regions. Our results suggest that observational constraints of environmental supersaturation in precipitating clouds, particularly near source regions, are of fundamental importance for accurate simulation of the atmospheric burden of black carbon and other aerosols.
Similar content being viewed by others
Introduction
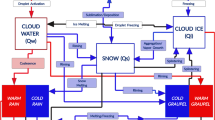
Atmospheric aerosols play an important role in Earth’s climate system through direct and indirect modification of the radiation budget.1,2 Most anthropogenic and biomass-burning aerosol particles of radiative significance belong to the accumulation mode, from ~0.1 to ~2 μm.3 Rainout during moist convection is the single most important atmospheric process limiting the vertical transport of accumulation-mode aerosols from the boundary layer to the free troposphere and, thus, their long-range transport and contribution to the global atmospheric burden.4,5 In a moist air parcel, rainout is usually triggered by activation of an aerosol to sub- or supercooled liquid cloud droplets;6,7,8 this process, called nucleation scavenging, occurs in localized supersaturated domains (LSDs) of a precipitating cloud system (Fig. 1). In each LSD, the aerosol’s critical supersaturation (SSc) value and the environmental supersaturation (SSlsd) value together determine the proportion of the aerosol particles susceptible to nucleation scavenging.
Conceptual diagram of the BC tracer method. The mass-equivalent diameter (Dtr) of each water-insoluble BC particle is an observable invariant during removal and transport processes. In a convective-type precipitating cloud system, the removal efficiency of aerosols in a moist air parcel uplifted from the boundary layer is determined mainly by the nucleation scavenging process within each localized supersaturated domain (LSD). The occurrence and activity of LSDs in a cloud system are complex functions of time and space. For simplicity, the figure illustrates a temporal snapshot of the spatial distribution of discrete LSDs (LSDk, k = 1, …, n). For each rainfall event, the average of SSlsd, weighted by the number of tracer particles scavenged in LSDk (k = 1, …, n), is estimated by comparing the Dtr-resolved number concentrations of initial tracer (in the surface air) and removed tracer (in rainwater) measured at a surface observation site. For each rainfall event, the rainwater sampling period was typically ~100−101 min (Table S1). The cloud system moves horizontally ~100−101 km during the rainwater sampling under the typical wind speed in the lower troposphere of ~10 ms–1. The number (n) of LSDs contributing to the scavenging of observed tracer depends on the sampling period as well as on the translational speed of the cloud system
The rainout amount of aerosols in a particular space-and-time (4D) domain comprising an ensemble of LSDs (e.g., a computational grid cell and the computational time interval in an atmospheric model) is determined primarily by two 4D-domain-averaged variables: condensed-water production and the SSlsd value maintained during droplet nucleation in each LSD. Atmospheric models that have been validated by precipitation observations may be reasonably able to predict the mean condensed-water production in a particular 4D domain, but it is difficult for current atmospheric models to predict the mean SSlsd value in a particular 4D domain with verified accuracy because in a non-adiabatic precipitating cloud, environmental supersaturation is highly sensitive to many physical processes at both macroscopic to microscopic scales.9,10 As a result, the prognostic environmental supersaturation value provided as an output variable by the aerosol activation parameterization scheme11,12,13 of an atmospheric model is not necessarily close to the 4D-domain-averaged SSlsd in the real atmosphere.
Recently developed global-scale atmospheric models coupled with aerosol microphysical modules explicitly14 or implicitly15,16 assume that only aerosol particles in clouds with SSc less than the modelled (or prescribed) SSlsd value are subject to nucleation scavenging and efficient rainout. In these models, the timescale for transforming fresh high-SSc hydrophobic particles (SSc > SSlsd) into low-SSc hydrophilic particles (SSc < SSlsd) can change drastically depending on the modelled (or prescribed) SSlsd value.17,18,19 Therefore, the model predictabilities of the atmospheric lifetime and spatial distribution of initially high-SSc aerosols such as black carbon (BC) and primary organic matter (POM) can be greatly reduced by a small bias in the modelled (or prescribed) SSlsd value in precipitating clouds.20 For these reasons, the current lack of any observational constraint on SSlsd in precipitating clouds is one of the largest sources of uncertainty in simulations of atmospheric aerosols, especially BC and POM.
Here, we propose an observational method for estimating SSlsd in convective-type precipitating clouds that uses water-insoluble BC as a particle tracer8 (Fig. 1, see Methods). Our method provides an estimate of the SSlsd value actually experienced by the removed aerosols at the time of their activation to droplets averaged over the LSDs distributed over a particular atmospheric 4D domain with dimensions similar to those of a discretized atmospheric 4D domain in regional-scale to global-scale atmospheric models. Thus, for the purpose of constraining simulations of aerosol rainout, SSlsd estimated by our observational method is physically more relevant than local instantaneous supersaturation in non-precipitating clouds estimated by in situ aircraft measurements.21,22,23,24 In this paper, we first present and discuss our observational results in East Asia, and then we demonstrate on the basis of sensitivity-test simulation results that SSlsd in precipitating clouds is an important parameter controlling the global BC distribution.
Results
Observational estimation of in-cloud supersaturation
We carried out observations at two different locations in Japan: Tokyo, which is dominated by fresh urban pollution25 in which BC-containing aerosols have higher SSc (i.e., they are more hydrophobic), and Okinawa, which is frequently influenced by aged Asian continent pollution26 in which BC-containing aerosols have lower SSc (i.e., more hydrophilic) (Supplementary Table 1).
For each rainfall event, we estimated the SSlsd value experienced by the removed aerosols from the results of a detailed comparison between the BC-containing aerosols in the surface air before the rainfall and the BC particles in the rainwater, under the assumption that the former had been transformed to the latter through localized moist convection (BC tracer method: Fig. 1). The BC tracer method utilizes the experimental finding that the mass-equivalent diameter of each water-insoluble BC particle core, denoted here as Dtr, is invariant during the rainout process.8 The assumption of localized moist convection by the method is plausible for convective-type precipitation but would be invalid for stratiform-type precipitation.27 We introduce the Convective Precipitation Index (CPI) as a measure of the relative contribution of lower tropospheric water vapor to vertically integrated condensed-water production near each observation site (see Methods). The assumption of localized moist convection is more plausible for rainfall events with higher CPI (Supplementary Table 1). Therefore, we pay particular attention to events with CPI > 0.5 (N = 23) among the observed rainfall events (N = 37) in the following analysis and discussion.
For each rainfall event, we calculated the ratio of the size-resolved tracer number concentration, dN/dlogDtr, in rainwater (i.e., the removed tracer) to dN/dlogDtr in the surface air before precipitation (i.e., the initial tracer) from in situ measurements (Fig. 2a, b). This rain-to-air number concentration ratio, the scavenged number fraction (SNF), is a function of Dtr and is denoted here as SNF(Dtr). Further, we define Relative SNF(Dtr) as SNF(Dtr) normalized by the SNF value at a particular Dtr = Dstd. In this study, Dstd was set to 900 ± 100 nm (Fig. 2a, b). We used Relative SNF in our analysis so that the results would be unaffected by the absolute tracer concentration in rainwater. We used κ-Köhler theory28 with measured input parameters (e.g., coating volume on BC core; Supplementary Fig. 1) to derive SSc-resolved number concentrations of the initial tracer-containing aerosols at each of four small-tracer Dtr values (D = 200 ± 10 nm, 220 ± 10 nm, 263 ± 15 nm, or 302 ± 20 nm) and at one large-tracer Dtr value (=Dstd, 900 ± 100 nm) (see Methods) (Fig. 2c–f).
Observational results of tracer particles used for estimating the SSlsd experienced by the removed tracers during each of the rainfall events (thin curves). Thick curves show averaged results over all rainfall events in each observation site. a Normalized size-resolved number concentrations (dN/dlogDtr) of the initial and removed tracer particles and the resulting Dtr-resolved relative scavenged number fraction (Relative SNF) in Tokyo. b Same as panel (a) but for Okinawa. c Normalized SSc-revolved number concentration (dN/dSSc) of the initial tracer evaluated at Dtr = 200 nm and at Dtr = Dstd (900 ± 100 nm) in Tokyo, where the SSc of tracer (BC)-containing particles was predicted by using κ-Köhler theory. d Same as panel (c) but for Okinawa. e, f Same as panels (c, d) but for Dtr = 302 nm instead of Dtr = 200 nm
Under our observational conditions, we estimated that the fractional contribution of nucleation scavenging to total scavenging is always greater than 0.8 for aerosols containing tracer particles in the size range 200 nm ≤ Dtr ≤ 1000 nm (see Methods). Thus, the following data analysis assumes that nucleation scavenging predominates over in-cloud and below-cloud impaction scavenging.
Under the assumption that both small (Dtr = D) and large (Dtr = Dstd) tracer particles in a collected rainwater sample are activated to droplets at environmental supersaturation SSlsd, we estimated SSlsd by numerically solving the following equation with respect to SSlsd:
where dN/dSSc denotes the probability density function of the observational SSc-resolved number concentration of tracer-containing aerosols at the indicated Dtr value normalized by
We estimated the systematic relative error of the derived SSlsd value resulting from the measurement uncertainties, and neglecting other scavenging mechanisms, to range between −10 and +20% (see Methods).
For each rainfall event, the SSlsd value determined by this procedure can be physically interpreted as the average of SSlsdk (k = 1,…, n) weighted by the number of measured tracer particles in rainwater that have been scavenged in LSDk (k = 1,…, n). For each rainfall event, the time duration of rainwater sampling ranged mostly from 5 to 30 min (Supplementary Table 1). For a cloud system moving horizontally with a constant speed of ~10 ms–1, which is a typical wind speed in the lower troposphere, the moving distance during the sampling time would thus be ~100−101 km. In this case, we can interpret the derived SSlsd value as the average over the LSDs distributed within a horizontal scale of ~100−101 km (Fig. 1). In the case of a cloud system that does not appreciably move during the sampling time, we can interpret the derived SSlsd value as the average over the LSDs above the observation site within a period of ~100−101 min. On the basis of these considerations, we interpret the derived SSlsd as the tracer-weighted average of SSlsdk (k = 1,…, n) in a particular space-and-time (4D) domain with a horizontal scale of ~100−101 km and a timescale of ~100−101 min.
The absolute scavenged number fraction of tracer particles at Dtr = D is defined here as
where SSlsd is determined by solving Eq. (1). Absolute SNF can be physically interpreted as the expected scavenged number fraction of initial tracer-containing aerosol particles with Dtr = D that have experienced environmental supersaturation SSlsd.
We compared scatter plots of Absolute SNF versus SSlsd for each of the four small-tracer Dtr values for all observed events (Fig. 3a) and for events with CPI > 0.5 (Fig. 3b). For the reason mentioned above, we assume the results for CPI > 0.5 events to be more reliable than those for all events. Consistent with our expectation, for CPI > 0.5 events, SSlsd did not depend on Dtr (Fig. 3b). For all events, we interpret the systematic dependence of SSlsd on Dtr (Fig. 3a) as an artifact resulting from the inclusion of low-CPI events that violate the assumption of localized moist convection.
Scatterplots between the absolute scavenged number fraction (Absolute SNF) and the SSlsd value estimated for a all rainfall events (N = 37) and b rainfall events with CPI > 0.5 (N = 23). Each open circle (triangle) indicates the results for a single rainfall event in Tokyo (Okinawa). The same analysis was performed using each of the four indicated distinct small-tracer Dtr values. The filled circles and error bars represent the median values and the 25th–75th percentile range
For CPI > 0.5 events, SSlsd ranged from 0.03 to 0.2% (average ± standard deviation, approximately 0.08 ± 0.03%; Supplementary Table 2), and, in contrast to the general trend predicted by a model using an aerosol activation parameterization scheme,29 SSlsd did not show a clear anti-correlation with the aerosol number concentration in the surface air before the rainfall. This result implies that the actual mechanism determining SSlsd in real precipitating clouds is complex. The SSlsd value of 0.08 ± 0.03% determined herein is substantially lower than the reported values of maximum supersaturation in non-precipitating marine stratocumulus clouds in East Asia (average ± standard deviation, 0.24 ± 0.06%).23 This systematic difference implies that for the majority of LSDs in a non-adiabatic precipitating cloud system, supersaturation is not maintained at as high a level as the maximum supersaturation realized in the updraft core of adiabatic non-precipitating clouds.
Sensitivity of the global BC distribution to in-cloud supersaturation
We performed a set of numerical experiments with the CAM5-chem/ATRAS2 global aerosol model14 to quantify changes in the simulated global aerosol fields due solely to differences in the model’s treatment of environmental supersaturation (SS) and the associated nucleation scavenging process in precipitating clouds. The base simulation was performed with the default CAM5-chem/ATRAS2 parameterization scheme, in which both the determination of the SS value and the nucleation scavenging process are treated differently between grid-scale and sub-grid-scale cloud types. In the case of grid-scale clouds, the scavenged number fraction of an aerosol is predicted from the dN/dSSc distribution for that aerosol, and the prognostic SS value is determined by using the aerosol’s activation parameterization.13 In the case of sub-grid-scale clouds, the scavenged number fractions of aerosols with SSc > 1.0, SSc > 0.5, and SSc ≤ 0.5% are assumed to be 0, 0.4, and 0.8, respectively, and the SS value is not computed. The categorization of clouds between grid-scale and sub-grid-scale types depends on the selected grid resolution of CAM5; thus, a physically meaningful categorization is not assured. In the sensitivity-test simulations, SS for both grid-scale and sub-grid-scale clouds was set to 0.05, 0.08, or 0.11%, corresponding to the average ± the standard deviation (about 0.03%) of the SSlsd values determined for CPI > 0.5 events (Supplementary Table 2). Only aerosol particles with SSc < SS were assumed to be scavenged by cloud water and removed by rainfall. We applied a single SS value globally to avoid the technical complexities of applying regional values in a global model.
The simulated global distributions of the BC column burden and wet deposition flux (Figs. 4 and 5, left panels) indicate that a substantially large portion of the total atmospheric BC mass in the northern hemisphere (NH) is deposited in the mid-latitudes, in particular around East Asia, the largest source region. Thus, our sensitivity-test simulations, in which a single SS value determined from observations around East Asia was applied globally, can provide useful insights, at least into BC fields in the NH.
a, c, e Global distributions of the 5-year mean column BC mass simulated by the CAM5-chem/ATRAS2 model with the supersaturation (SS) of precipitating clouds constrained to be 0.05%, 0.08%, and 0.11%, respectively. b, d, f Global distributions of the ratio of column BC mass obtained by the sensitivity-test simulations to that obtained by the base simulation. In the sensitivity-test simulations, the SS constraint was applied to both grid-scale and sub-grid-scale clouds
a, c, e Global distributions of the 5-year mean BC wet deposition flux simulated by the CAM5-chem/ATRAS2 model with the supersaturation (SS) of precipitating clouds constrained to be 0.05%, 0.08%, and 0.11%, respectively. b, d, f Global distributions of the ratio of the BC wet deposition flux obtained by the sensitivity-test simulations to that obtained by the base simulation. In the sensitivity-test simulations, the SS constraint was applied to both grid-scale and sub-grid-scale clouds
According to a recent detailed investigation of the aerosol mass deposition budget, nucleation scavenging may account for 94% of in-cloud scavenging of BC, with below-cloud scavenging contributing only 14% of total annual and global mean BC deposition.30 In our simulations, the contribution of below-cloud scavenging to total BC scavenging was negligibly small (~1% of the nucleation scavenging) on annual and global average. Thus, in the following discussion we assume that BC deposition is triggered predominantly by nucleation scavenging.
A global distribution map of annual mean maximum SS values in grid-scale clouds, derived from the base simulation, is shown in Supplementary Fig. 2. The major qualitative features of this map, higher SS in higher latitudes and lower SS in more polluted regions, are similar to the results obtained by another model in which a globally constant updraft velocity was assumed in grid-scale clouds.29 The simulated SS value of grid-scale clouds in our base simulation around our observation sites (Tokyo and Okinawa) was ~0.12%, which is slightly larger than our estimated SSlsd of 0.08 ± 0.03% for observed rainfall events.
The sensitivity-test simulations conducted using the three SS values all predicted substantially large BC mass concentrations (Fig. 4, right panels) and wet deposition values (Fig. 5, right panels), relative to the base simulation values, almost everywhere except near the major anthropogenic source regions in East Asia, India, Europe, and the United States. The large increase in the BC column burden in remote terrestrial and oceanic regions compared to the base simulation values is attributable to increased long-range transport of aerosols from the major BC source regions in the sensitivity-test simulations. This systematic increase in long-range BC transport in the sensitivity-test simulations relative to the base simulation can be explained by modest decreases of wet deposition and compensatory modest increases of vertical transport associated with less-efficient BC rainout during moist convection in the proximity of the major BC source regions (Fig. 5, right panels). In these regions, substantial proportions of BC-containing particles remain fresh and thus have relatively high SSc values; as a result, BC rainout efficiency tends to be more sensitive to the prescribed SS value.
The model was able to reproduce the aircraft-observed vertical profile of BC mass concentrations over East Asia (Supplementary Fig. 3a) reasonably well in both the base simulation and the sensitivity-test simulation with SS = 0.08%. In marked contrast, in the Arctic and other remote regions, the simulated vertical BC profile was up to an order of magnitude larger in the sensitivity-test simulation with SS = 0.08% compared with the base simulation (Supplementary Fig. 3b–h) because of a substantial increase in the long-range transport of BC to regions that are remote from the major source regions.
We estimated the fractional contribution of the BC emitted from the Asian region (60°E−160°E, 20°N−50°N) to the BC column burdens in Arctic (66°N−90°N) and NH mid-latitude (20°N−66°N) regions (Supplementary Table 3). The Asian source contribution to the Arctic BC column burden was ~2.5 times higher in the SS = 0.08% sensitivity-test simulation (32%) than in the base simulation (13%) as a result of the greater efficiency of long-range BC transport via moist convection. By contrast, the Asian source contribution to the NH mid-latitude BC column burden (~50% in the base simulation) did not change appreciably in the SS = 0.08% sensitivity-test simulation (~51%) because the majority of the NH mid-latitude BC column burden was attributable to the highly concentrated BC near the source regions before the moist convection processing.
Comparison of simulated and observed seasonal variations of surface BC mass concentrations at two observation sites in the Arctic (Fig. 6) shows that, except in summer, the base simulation severely underestimated, by an order of magnitude, the monthly BC mass concentration (See Sinha et al.31 for the details of these observation data). At both Arctic sites, the sensitivity-test simulation with SS = 0.08% for grid-scale + sub-grid-scale clouds reproduced the observed average and seasonal variations of surface BC concentrations better than the base simulation. This difference between the sensitivity-test and base simulation results for Arctic surface BC concentrations was due mostly to the difference in the simulated BC scavenging efficiency in grid-scale clouds. However, it should be noted that the relative contributions of grid-scale and sub-grid-scale clouds depend on the selected model grid size and the default scavenging scheme adopted in the base simulation.
Comparison of monthly surface BC mass concentrations between in situ observations and the CAM5-chem/ATRAS2 simulations for a Barrow, Alaska and b Ny-Ålesund, Norway. In the sensitivity-test simulations, the SS constraint was applied to both grid-scale and sub-grid-scale clouds. The black curves show base simulation results, and the light-blue dots show observation results. The period of observation data is August 2012−May 2015 for Barrow and March 2012−May 2015 for Ny-Ålesund
The essential conclusion that we deduce from the simulation results shown in Fig. 6 is that the Arctic surface BC concentration can shift by a factor of 2−3 solely as a result of a change in SSlsd within the quite narrow range of 0.05−0.11%, which is the average ± standard deviation range of our observational SSlsd value for convective-type precipitation in East Asia.
Finally, we examine the sensitivities of the global burdens of BC and other aerosols to the SSlsd value in light of our sensitivity-test simulation results for grid-scale + sub-grid-scale clouds (Supplementary Table 4). Our sensitivity-test simulations with SS = 0.05−0.11% predict a BC lifetime of 7−15 days, substantially longer than the current best estimate of less than ~5 days,32,33 which is constrained by global-scale atmospheric BC datasets. The overestimate of the BC lifetime is also implied by the overestimation of BC concentrations in the middle-to-upper troposphere relative to the lower troposphere (Supplementary Fig. 3b−g). Because of this issue, we focus our discussion on the relative change of each target variable depending on the assumed SS value, and we avoid any discussion directly related to the absolute accuracy of the target variables. The sensitivity-test simulation results (Supplementary Table 4) suggest that the absorption aerosol optical depth (AAOD), global burden, lifetime, and direct radiative forcing of BC can each be changed by a factor of 2 solely by a change of SSlsd within the range 0.05–0.11%. Total AAOD, which includes AAOD of both dust and BC, was slightly less sensitive to an SSlsd change than BC-AAOD, because dust rainout is almost unaffected by a change of the SSlsd value within the range 0.05–0.11%. In contrast, total AOD, which includes both absorbing and non-absorbing aerosols, is much less sensitive to an SSlsd change than total AAOD. This marked contrast in sensitivity reflects the fact that the major contributors to total AOD are hydrophilic particles with very low SSc (i.e., sulfate, sea salt, and moderately sized, water-soluble organic particles); thus, the dependence of their rainout on SSlsd values within 0.05–0.11% is small.
Discussion
The results of this pilot study suggest that observational constraint of rain-cloud supersaturation, particularly near aerosol source regions, is important for improving model predictability of lifecycle and climate effects of aerosols such as BC and POM, which are initially hydrophobic. The BC tracer method proposed herein provides estimates of SSlsd values actually experienced by removed aerosols in convective-type precipitating clouds averaged over the LSDs within a particular space-and-time domain with dimensions comparable to those of the currently smallest resolvable domain in global atmospheric models (i.e., horizontal scale ~100−101 km; timescale ~100−101 min),34,35 and thus it will contribute to the forthcoming researches for physically-based improvements of aerosol rainout simulations by cloud-resolving scale atmospheric models. In the future, controlling factors and mechanisms determining SSlsd values in various types of precipitating clouds should be investigated. In addition, an observational method for estimating SSlsd values applicable to stratiform-type precipitating clouds27 is also desirable.
Methods
Observation of rainfall events
Observations in Tokyo were conducted during July and August 2014 and June and July 2015 at the Hongo campus of the University of Tokyo, Japan. The experimental setup for collecting rainwater and sampling ambient air at this site has been described previously.8 Observations in Okinawa were conducted during March 2016 at the Cape Hedo Atmosphere and Aerosol Monitoring Station (CHAAMS), which is operated by the National Institute for Environmental Studies (NIES), Japan. At CHAAMS, rainwater samples are collected using a glass funnel and beaker installed on the station rooftop. The experimental setup for sampling ambient aerosols at this site is described by Yoshida et al.36
At both sites, initial tracer data for each rainfall event were acquired during the 1-h period just before the onset of precipitation. The rainwater sampling period during each rainfall event ranged from ~5 min to ~1 day (Supplementary Table 1) and was usually less than 30 min for CPI > 0.5 events. During each rainfall event, the observed size-resolved number concentration and the mixing state of BC-containing aerosols were almost unchanged during the 1-h period just before the onset of rainfall; this result implies that boundary layer aerosols around the observation sites were uniform on a horizontal scale of ~101 km. This observational fact supports an important assumption of our BC tracer method, which we designed for convective-type precipitation: BC-containing particles in surface air observed just before a rainfall are transformed into the BC particles in the collected rainwater through localized moist convection around the observation site.
Convective Precipitation Index
For each rainfall event, we evaluated the validity of the assumption of horizontal localization of moist convection in our BC tracer method by estimating the relative contribution of lower tropospheric water vapor convergence to the vertically integrated water vapor convergence in an atmospheric column above the observation site. For this purpose, we introduced the CPI, defined as follows:
where v, q, and \({\mathrm{\Sigma }}(P > 0)\) denote the horizontal wind velocity vector, specific humidity, and the precipitating area within a 1° × 1° rectangular domain around the observation site, respectively. For this analysis, we used atmospheric global spectral model reanalysis data for the Japan area with a horizontal resolution of 0.25° × 0.2° (longitude × latitude) provided by the Japan Meteorological Agency. Six-hourly meteorological datasets were time-interpolated to obtain the v and q fields at the time of each rainfall event. The precipitating area was defined as those subdomains in which the vertically integrated horizontal moisture convergence was positive. Rainfall events with higher positive CPI values are more likely to be convective-type precipitation, in which mass convergence in the lower troposphere is compensated by mass divergence in the upper troposphere.27 In contrast, rainfall events with near-zero or negative CPI might be stratiform-type precipitation, in which mass convergence in the middle troposphere level is compensated by mass divergence in both lower and upper tropospheric levels.27 Supplementary Table 1 lists the CPI value calculated for each observed rainfall event.
Measurement data for the BC tracer analysis
We used two distinct types of modified single-particle soot photometer (SP2, Droplet Measurement Technologies, Longmont, CO, USA) to measure BC particles: a wide-range SP237 and a standard SP2.38 The wide-range SP2 was used to measure dN/dlogDtr of BC particles in the 70 nm ≤ Dtr ≤ 2000 nm size range in both ambient air and rainwater, where the mass-equivalent diameter (Dtr) of BC core particles was derived from the BC mass quantified by using the incandescence signal and assuming a BC density of 1.8 g cm–3. We used the Marin-5 pneumatic nebulizer37 (Teledyne CETAC Technologies Inc.) for extracting the BC particles in rainwater into the air sampled by the wide-range SP2.
The standard SP2 was used for measuring the mixing state of individual BC-containing aerosols in the ambient air. The volume of coating materials on the BC core of known Dtr was derived from the measured time-dependent scattering cross section Cs(t) in the laser beam of the SP2 as follows. First, the Cs value before the onset of particle evaporation (Cs-be) and the Cs value at the onset of incandescence of the BC core (Cs-oi) were separately determined.39 Then, the unknown coating volume was determined to fit the theoretical Cs-be/Cs-oi ratio for the known Dtr value to the observed Cs-be/Cs-oi ratio. Theoretical Cs-be and Cs-oi values for BC-containing aerosols were computed by using original discrete-dipole approximation code (Block-DDA),40,41 along with the realistic assumption that each BC core was an aggregate of many BC spherules, each with a diameter of 40 nm, and that its fractal dimension Df was 2.8. Each BC spherule was approximated by a set of ~270 dipoles to suppress the discretization shape error. Dipoles were also assigned to approximate the coating material around each BC spherule, where the thickness of the coating depended on the prescribed total coating volume. When we assumed a refractive index (m) of 2.00 + 1.00i for the BC core, the theoretical Cs-oi value agreed reasonably with the measured Cs-oi value for BC-containing aerosols in both Tokyo and Okinawa (Supplementary Fig. 4). For this reason, we assumed m = 2.00 + 1.00i for the BC core, although m = 2.26 + 1.26i, as previously reported,42 could also explain the measured Cs-oi value in Okinawa. We assumed the coating materials to have m = 1.52 + 0.00i. This procedure was used to estimate the coating volume of ambient BC-containing particles with 185 nm ≤ Dtr ≤ 323 nm. The major source of uncertainty is the assumed Df value of the BC core, because Df can vary depending on the source and age of BC-containing aerosols. However, the coating volume derived by the above procedure differed by no more than 10% between an assumed value of Df = 2.5 and one of Df = 2.8. Therefore, we assumed the relative error bounds of the derived coating volume to be ±10%.
The mass-equivalent shell-to-core ratio (SCr) of BC-containing particles was defined as the ratio of the mass-equivalent diameter of each BC-containing particle to that of its BC core (=Dtr). The SCr-resolved number concentration dN/dSCr for BC-containing particles with 185 nm ≤ Dtr ≤ 323 nm was derived from the standard SP2 data (Supplementary Fig. 1). For particles with 323 nm ≤ Dtr ≤ 1000 nm, dN/dSCr was theoretically estimated by using an original box model that simulated the aerosol aging process on the basis of gas-to-particle condensation theory3 (Supplementary Fig. 1). In this simulation, the initial conditions and integration time were tuned so that at Dtr = 323 nm the simulated dN/dSCr agreed with the measured dN/dSCr.
In this study, we assumed the hygroscopicity parameter28 κ of coating materials on the BC core to be identical to that of non-BC aerosols in the submicrometre size range. An aerosol mass spectrometer43 (AMS: Aerodyne Research, USA) was used to measure the non-BC chemical composition of submicrometre aerosols in both Tokyo and Okinawa (Supplementary Fig. 5). In Okinawa, the hygroscopicity parameter κ of non-BC aerosols was derived by using the AMS data along with published parameter values28 (Supplementary Table 5). In Tokyo, κ for non-BC aerosols was estimated by using the hygroscopic growth factor of a 200-nm BC-free particle, measured with a humidified-SP225 (h-SP2), and this κ value was then assumed for the coating materials on the BC core. For each rainfall event, in situ data acquired during the 1-h period before the rainfall were used for estimating κ.
We used κ-Köhler theory28 to compute the critical supersaturation SSc of tracer-containing particles from the input parameters Dtr, SCr, and κ.
Relative contribution of each scavenging mechanism
We evaluated the plausibility of the assumption of the dominance of nucleation scavenging as the mechanism by which aerosols are incorporated into condensed water on the basis of numerical simulations of the aerosol scavenging process using a modified cloud parcel model. We extended the cloud parcel model developed by Feingold and Heymsfield44 to include aerosol-droplet impaction processes45 in our simulations. In the case of BC-containing particles, the aerodynamic effects of their nonspherical shape46 were considered in the impaction efficiency formula.45 To simulate the scavenging process during each rainfall event, the modified cloud parcel model was driven by in situ aerosol data and in situ meteorological data (temperature, moisture, rainfall intensity) acquired in each rainfall event. We tuned the updraft velocity w by finding the value that resulted in the best fit of the simulated Relative SNF(Dtr) to the observed Relative SNF(Dtr) in the size range 70 nm ≤ Dtr ≤ 1000 nm. The relative contributions of nucleation scavenging, in-cloud impaction scavenging, and below-cloud impaction scavenging derived from the simulations were averaged over all events and over CPI > 0.5 events (Supplementary Fig. 6). From these results, we inferred that the fractional contribution of nucleation scavenging was not less than 0.8 within the tracer size range of 200 nm ≤ Dtr ≤ 1000 nm that we used in our SSlsd estimation.
Estimating the error bounds of SSlsd
We estimated the uncertainty of SSlsd due to the uncertainties in the coating volume and fractional contribution of nucleation scavenging. Our calculations based on κ-Köhler theory showed that the ±10% relative error in the coating volume (∆v/v) causes a relative error of about ±9% in the estimated supersaturation (∆SSlsd/SSlsd).
We evaluated the systematic error of SSlsd due to ignoring the contributions of in- and below-cloud impaction scavenging to the observed Relative SNF as follows. To evaluate the error bounds, we considered a hypothetical worst case: a fractional contribution of nucleation scavenging of 0.8 for small-tracer particles (Dtr = D), and one of 1.0 for large-tracer particles (Dtr = Dstd). In this hypothetical case, we can estimate the supersaturation experienced by the removed tracers at the time of their activation to droplets (SSlsd′) by multiplying the left-hand side of Eq. (1) by 0.8 and then solving. We estimated the upper bound of systematic error by subtracting the derived SSlsd′ value from the original SSlsd value, ∆SSlsd = SSlsd – SSlsd′. The upper bound of relative systematic error of SSlsd averaged over the observed rainfall events was about +10%.
From these results, we estimated the relative error bounds of SSlsd to be −10% ≤ ∆SSlsd/SSlsd ≤ + 20%. This error range is substantially narrower than the relative standard deviation of the observed SSlsd for CPI > 0.5 events (~40%).
Model simulations
We conducted global model simulations using the Community Atmosphere Model version 5 (CAM5-chem)47 with the Aerosol Two-dimensional bin module for foRmation and Aging Simulation version 2 (CAM5-chem/ATRAS2),14,48 in which the nucleation scavenging scheme was modified as described below. The stand-alone version of CAM5 (FC5 compset) in Community Earth System Model version 1.2.0 was used with a horizontal resolution of 1.9° latitude × 2.5° longitude and 30 vertical layers from the surface to ~40 km. In addition to a base simulation, online sensitivity-test simulations were conducted for six (3 × 2) distinct cases: three SS values (0.05, 0.08, and 0.11%) and two different nucleation scheme implementations (sub-grid-scale clouds only and sub-grid-scale + grid-scale clouds). Each simulation was performed over six years, and averages of the last five years were used in the analysis. We used anthropogenic, biomass burning, and biogenic emissions of Lamarque et al.49 in the year 2000 for gas-phase and aerosol species. Nine aerosol species (sulfate, nitrate, ammonium, dust, sea salt, primary and secondary organic aerosol, BC, and water) were treated in the model. The model considered gas-phase chemistry,50 condensation/evaporation of inorganic and organic species,14 coagulation,51 nucleation,52 aerosol activation13 and evaporation53 from clouds, aerosol formation in clouds,54 dry and wet deposition,55 and aerosol optical properties.14 Aerosol particles were resolved with 12 size bins from 0.001 to 10 μm (dry diameter), as in the ATRAS-d model.48 Non-BC chemical compositions in each size bin were assumed to be internally mixed. Mixing states of BC-containing particles were resolved into seven BC mass fraction bins (1–0.99, 0.99–0.9, 0.9–0.8, 0.8–0.5, 0.5–0.2, 0.2–0.1, and 0.1–0.0001) for each of the five dry total diameter bins from 0.04 to 1.25 μm. This 2D bin representation was able to resolve the size and mixing-state dependences of the SSc value of BC-containing particles with sufficient accuracy for the purpose of this study.
Code availability
The computer codes that support the findings of this study are available from the corresponding author upon reasonable request.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Myhre, G. et al. Radiative forcing of the direct aerosol effect from AeroCom Phase II simulations. Atmos. Chem. Phys. 13, 1853–1877 (2013).
Rosenfeld, D., Sherwood, S., Wood, R. & Donner, L. Climate effects of aerosol-cloud interactions. Science 343, 379–380 (2014).
Seinfeld, J. H. & Pandis, S. N. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change. (John Wiley & Sons, Hoboken, New Jersey, 2016).
Schulz, M. et al. Radiative forcing by aerosols as derived from the AeroCom present-day and pre-industrial simulations. Atmos. Chem. Phys. 6, 5225–5246 (2006).
Kipling, Z. et al. What controls the vertical distribution of aerosol? Relationships between process sensitivity in HadGEM3-UKCA and inter-model variation from AeroCom Phase II. Atmos. Chem. Phys. 16, 2221–2241 (2016).
Flossmann, A. I., Hall, W. D. & Pruppacher, H. R. A Theoretical-study of the wet removal of atmospheric pollutants. 1. The redistribution of aerosol-particles captured through nucleation and impaction scavenging by growing cloud drops. J. Atmos. Sci. 42, 583–606 (1985).
Flossmann, A. I. & Wobrock, W. A review of our understanding of the aerosol-cloud interaction from the perspective of a bin resolved cloud scale modelling. Atmos. Res. 97, 478–497 (2010).
Ohata, S., Moteki, N., Mori, T., Koike, M. & Kondo, Y. A key process controlling the wet removal of aerosols: new observational evidence. Sci. Rep. 6, 34113 (2016).
Planche, C. et al. The influence of aerosol particle number and hygroscopicity on the evolution of convective cloud systems and their precipitation: a numerical study based on the COPS observations on 12 August 2007. Atmos. Res. 98, 40–56 (2010).
Hammer, E. et al. Sensitivity estimations for cloud droplet formation in the vicinity of the high-alpine research station Jungfraujoch (3580 m a.s.l.). Atmos. Chem. Phys. 15, 10309–10323 (2015).
Nenes, A. & Seinfeld, J. H. Parameterization of cloud droplet formation in global climate models. J. Geophys. Res. Atmos. 108, 4415 (2003).
Ghan, S. J. et al. Droplet nucleation: Physically-based parameterizations and comparative evaluation. J. Adv. Model. Earth Syst. 3, M10001 (2011).
Abdul-Razzak, H. & Ghan, S. J. A parameterization of aerosol activation 2. Multiple aerosol types. J. Geophys. Res. Atmos. 105, 6837–6844 (2000).
Matsui, H. Development of a global aerosol model using a two-dimensional sectional method: 1. Model design. J. Adv. Model. Earth Syst. 9, 1921–1947 (2017).
Lund, M. T., Berntsen, T. K. & Samset, B. H. Sensitivity of black carbon concentrations and climate impact to aging and scavenging in OsloCTM2-M7. Atmos. Chem. Phys. 17, 6003–6022 (2017).
He, C. L. et al. Microphysics-based black carbon aging in a global CTM: constraints from HIPPO observations and implications for global black carbon budget. Atmos. Chem. Phys. 16, 3077–3098 (2016).
Riemer, N., West, M., Zaveri, R. & Easter, R. Estimating black carbon aging time-scales with a particle-resolved aerosol model. J. Aerosol Sci. 41, 143–158 (2010).
Oshima, N. & Koike, M. Development of a parameterization of black carbon aging for use in general circulation models. Geosci. Model Dev. 6, 263–282 (2013).
Fierce, L., Riemer, N. & Bond, T. C. Explaining variance in black carbon’s aging timescale. Atmos. Chem. Phys. 15, 3173–3191 (2015).
Matsui, H. Black carbon simulations using a size- and mixing-state-resolved three-dimensional model: 2. Aging timescale and its impact over East Asia. J. Geophys. Res. Atmos. 121, 1808–1821 (2016).
Martin, G. M., Johnson, D. W. & Spice, A. The measurement and parameterization of effective radius of droplets in warm stratocumulus clouds. J. Atmos. Sci. 51, 1823–1842 (1994).
Politovich, M. K. & Cooper, W. A. Variability of the supersaturation in cumulus clouds. J. Atmos. Sci. 45, 1651–1664 (1988).
Koike, M. et al. Measurements of regional-scale aerosol impacts on cloud microphysics over the East China Sea: possible influences of warm sea surface temperature over the Kuroshio ocean current. J. Geophys. Res. Atmos. 117, D17205 (2012).
Hudson, J. G., Noble, S. & Tabor, S. Cloud supersaturations from CCN spectra Hoppel minima. J. Geophys. Res. Atmos. 120, 3436–3452 (2015).
Ohata, S. et al. Hygroscopicity of materials internally mixed with black carbon measured in Tokyo. J. Geophys. Res. Atmos. 121, 362–381 (2016).
Ueda, S., Osada, K. & Takami, A. Morphological features of soot-containing particles internally mixed with water-soluble materials in continental outflow observed at Cape Hedo, Okinawa, Japan. J. Geophys. Res. Atmos. 116, D17207 (2011).
Houze, R. A. Stratiform precipitation in regions of convection: a meteorological paradox? Bull. Am. Meteorol. Soc. 78, 2179–2196 (1997).
Petters, M. D. & Kreidenweis, S. M. A single parameter representation of hygroscopic growth and cloud condensation nucleus activity. Atmos. Chem. Phys. 7, 1961–1971 (2007).
Pringle, K. J., Carslaw, K. S., Spracklen, D. V., Mann, G. M. & Chipperfield, M. P. The relationship between aerosol and cloud drop number concentrations in a global aerosol microphysics model. Atmos. Chem. Phys. 9, 4131–4144 (2009).
Croft, B. et al. Influences of in-cloud aerosol scavenging parameterizations on aerosol concentrations and wet deposition in ECHAM5-HAM. Atmos. Chem. Phys. 10, 1511–1543 (2010).
Sinha, P. R. et al. Evaluation of ground-based black carbon measurements by filter-based photometers at two Arctic sites. J. Geophys. Res. Atmos. 122, 3544–3572 (2017).
Samset, B. H. et al. Modelled black carbon radiative forcing and atmospheric lifetime in AeroCom Phase II constrained by aircraft observations. Atmos. Chem. Phys. 14, 12465–12477 (2014).
Lund, M. T. et al. Short Black Carbon lifetime inferred from a global set of aircraft observations. npj Clim. Atmos. Sci. 1, 31 (2018).
Sato, Y. et al. Aerosol effects on cloud water amounts were successfully simulated by a global cloud-system resolving model. Nat. Commun. 9, 985 (2018).
Wang, M. et al. The multi-scale aerosol-climate model PNNL-MMF: model description and evaluation. Geosci. Model Dev. 4, 137–168 (2011).
Yoshida, A. et al. Abundance and emission flux of the anthropogenic iron oxide aerosols from the East Asian continental outflow. Aerosol Sci. Technol. 50, 242–254 (2016).
Mori, T. et al. Improved technique for measuring the size distribution of black carbon particles in liquid water. Aerosol Sci. Technol. 50, 242–254 (2016).
Moteki, N. & Kondo, Y. Dependence of laser-induced incandescence on physical properties of black carbon aerosols: Measurements and theoretical interpretation. Aerosol Sci. Technol. 44, 663–675 (2010).
Moteki, N., Kondo, Y. & Adachi, K. Identification by single-particle soot photometer of black carbon particles attached to other particles: Laboratory experiments and ground observations in Tokyo. J. Geophys. Res. Atmos. 119, 1031–1043 (2014).
Moteki, N. Discrete dipole approximation for black carbon-containing aerosols in arbitrary mixing state: A hybrid discretization scheme. J. Quant. Spectrosc. Radiat. Transf. 178, 306–314 (2016).
Moteki, N. et al. Anthropogenic iron oxide aerosols enhance atmospheric heating. Nat. Commun. 8, 15329 (2017).
Moteki, N., Kondo, Y. & Nakamura, S. Method to measure refractive indices of small nonspherical particles: application to black carbon particles. J. Aerosol Sci. 41, 513–521 (2010).
Jayne, J. T. et al. Development of an aerosol mass spectrometer for size and composition analysis of submicron particles. Aerosol Sci. Technol. 33, 49–70 (2000).
Feingold, G. & Heymsfield, A. J. Parameterizations of condensational growth of droplets for use in general-circulation models. J. Atmos. Sci. 49, 2325–2342 (1992).
Wang, X., Zhang, L. & Moran, M. D. Uncertainty assessment of current size-resolved parameterizations for below-cloud particle scavenging by rain. Atmos. Chem. Phys. 10, 5685–5705 (2010).
DeCarlo, P. F., Slowik, J. G., Worsnop, D. R., Davidovits, P. & Jimenez, J. L. Particle morphology and density characterization by combined mobility and aerodynamic diameter measurements. Part 1: Theory. Aerosol Sci. Technol. 38, 1185–1205 (2004).
Lamarque, J. F. et al. CAM-chem: description and evaluation of interactive atmospheric chemistry in the Community Earth System Model. Geosci. Model Dev. 5, 369–411 (2012).
Matsui, H. & Mahowald, N. Development of a global aerosol model using a two-dimensional sectional method: 2. Evaluation and sensitivity simulations. J. Adv. Model. Earth Syst. 9, 1887–1920 (2017).
Lamarque, J. F. et al. Historical (1850-2000) gridded anthropogenic and biomass burning emissions of reactive gases and aerosols: methodology and application. Atmos. Chem. Phys. 10, 7017–7039 (2010).
Emmons, L. K. et al. Impact of Mexico City emissions on regional air quality from MOZART-4 simulations. Atmos. Chem. Phys. 10, 6195–6212 (2010).
Matsui, H. et al. Development and validation of a black carbon mixing state resolved three-dimensional model: aging processes and radiative impact. J. Geophys. Res. Atmos. 118, 2304–2326 (2013).
Matsui, H. et al. Impact of new particle formation on the concentrations of aerosols and cloud condensation nuclei around Beijing. J. Geophys. Res. Atmos. 116, D19208 (2011).
Abdul-Razzak, H. & Ghan, S. J. A parameterization of aerosol activation - 3. Sectional representation. J. Geophys. Res. Atmos. 107, 4026 (2002).
Tie, X., Brasseur, G., Emmons, L., Horowitz, L. & Kinnison, D. Effects of aerosols on tropospheric oxidants: a global model study. J. Geophys. Res. Atmos. 106, 22931–22964 (2001).
Liu, X. et al. Toward a minimal representation of aerosols in climate models: description and evaluation in the Community Atmosphere Model CAM5. Geosci. Model Dev. 5, 709–739 (2012).
Acknowledgements
We thank K. Suzuki, M. Koike, and H. Miura for discussion. We are grateful to Y. Kondo (National Institute of Polar Research in Japan), M. Koike (University of Tokyo), and M. Irwin (Cambustion Ltd. in UK) for providing the BC data from Barrow and Ny-Ålesund. We also thank U.S. National Oceanic and Atmospheric Administration (NOAA) scientists for providing the BC data from the HIPPO campaign. We thank A. Takami and other NIES scientists for providing AMS data and supporting the observations in Okinawa. This research was supported by the Environment Research and Technology Development Fund (2-1403 and 2-1703) of Environmental Restoration and Conservation Agency, the Japan Society for the Promotion of Science (JSPS) KAKENHI program (15H05465, 16J04452, 16H01770, and 17H04709), and the Arctic Challenge for Sustainability (ArCS) project.
Author information
Authors and Affiliations
Contributions
N.M. designed the research and led the writing of manuscript in collaboration with T.M. and H.M. T.M. led the observation and data analysis in collaboration with S.O. H.M. designed and performed the simulations with the CAM5-Chem/ATRAS2 model, analyzed the simulation results, and performed the comparison with observation data. N.M. performed the light-scattering calculations for deriving the coating volume. N.M. performed the meteorological data analysis. T.M. performed the simulations for estimating the relative contribution of each scavenging mechanism. N.M., T.M., and H.M. contributed equally to the research.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Moteki, N., Mori, T., Matsui, H. et al. Observational constraint of in-cloud supersaturation for simulations of aerosol rainout in atmospheric models. npj Clim Atmos Sci 2, 6 (2019). https://doi.org/10.1038/s41612-019-0063-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-019-0063-y
This article is cited by
-
Climate-relevant properties of black carbon aerosols revealed by in situ measurements: a review
Progress in Earth and Planetary Science (2023)