Introduction

Construction is the pillar industry of national economy in many countries around the world and plays an indispensable role in the development of society (Onat and Kucukvar, 2020; Wang et al., 2021). With increasing demand for sustainable development, it is important to reduce the adverse impact of the construction industry on the environment, at this time, prefabrication construction, a sustainable construction way, has attracted interest from the government, investors and consumers (Balasubramanian and Shukla., 2017; Yu et al., 2021). Compared with the traditional onsite construction method, it is found that prefabricated construction has advantages of enhancing quality performance, reducing cost and time and shortening construction period (Jeong et al., 2017; Li et al., 2020; Tavares et al., 2021). In 2020, 630 million square meters of prefabricated construction started construction in China, accounting for about 20.5% of new construction area and an increase of 50% compared with that in 2019 (Ministry of Housing and Urban-Rural Development of People’s Republic of China, 2021). Therefore, prefabricated construction has become an inevitable trend of sustainable development in the construction industry (Jiang and Wu, 2021; Hussein et al., 2021).

The construction area of prefabricated construction in Europe, America and other advanced countries have been more than 60% (Chen et al., 2017). Compared with the rapid development of prefabricated construction in developed countries, prefabricated construction in China is still in its infant stage. The high construction cost and low technical level are critical factors that hinder its development (Wu et al., 2019a). In order to speed up the transformation of construction mode and promote the development of prefabricated construction, the government promulgates subsidy policies to reduce the cost and improve the technical level (Central People’s Government of People’s Republic of China, 2016). The government provides subsidies for enterprises according to the assembly rate level, such as Beijing city has provided fixed unit subsidy for enterprises and Chongqing city have provided per-unit production subsidy for enterprises based on different assembly rate levels (Beijing Municipal Commission of Housing and Urban-Rural Development, 2020; Chongqing Housing and Urban Rural Development Commission, 2022). The assembly rate refers to the comprehensive proportion of prefabricated components used in main structure, enclosure wall and internal partition wall, decoration and equipment pipeline above outdoor floor of single construction (Ministry of Housing and Urban-Rural Development of People’s Republic of China, 2017). It is the evaluation index of prefabricated construction industrialization degree and the main basis for the government to formulates supporting policies. The introduction of the subsidy policies complicate pricing strategies of the assembler and production decisions of the manufacturer. It remains obscure that how prefabricated construction enterprises determine the prices, the assembly rate and production strategies, which can not only attract consumers but also ensure their own profits. Therefore, the paper introduces the government subsidy and the assembly rate into prefabricated construction supply chain to discuss the impact of the subsidy policies on the assembly rate and pricing strategies.

In the decentralized model, supply chain members pursue their own profit maximization, which leads to double marginalization, while coordination is a strategic means to optimize supply chain and weaken or eliminate double marginalization (Edirisinghe et al., 2012). In this paper, the manufacturer determines the wholesale price for the purpose of ensuring its profit, and the assembler determines the reasonable order quantity while investing the assembly technology cost. They all focus on their own profits, which leads to profit loss of the whole supply chain. It is particularly important to choose the optimal coordination contract to reduce the loss of supply chain. This paper aims to establish coordination models in two subsidy scenarios to seek the optimal coordination mechanism of prefabricated construction supply chain and realizes supply chain optimization.

There are massive studies on prefabricated construction supply chain management (Luo et al., 2020; Liu et al., 2020a). Yet there are few studies on strategies and coordination of prefabricated construction supply chain considering subsidy policies. In order to fill this gap, this paper addresses the following three questions:

  1. (1)

    What are the optimal strategies of prefabricated construction supply chain when the government subsidy is taken into account?

  2. (2)

    What are the impacts of two subsidy modes on the optimal strategies of the manufacturer and the assembler?

  3. (3)

    How to coordinate prefabricated construction supply chain in two subsidy scenarios?

There are two aspects that this paper contributed to the literature. First, we solve strategies and coordination problems of prefabricated construction supply chain enterprises under different government subsidies. At present, the government has put forward diverse subsidy policies for prefabricated construction enterprises. However, the existing studies have focused on the incentive effect of single subsidy policy for prefabricated construction industry, while the impacts of different subsidy policies on decisions of prefabricated construction enterprises have not been discussed. It is an urgent problem that how different subsidy policies influence decisions and coordination of prefabricated construction supply chain. The second contribution is that we study the assembly rate optimization from the perspective of decisions of enterprises. The existing research mainly studies the assembly rate from the technical level and studies construction technology of prefabricated construction, which does not take the assembly rate as a decision variable to investigate the optimal strategies of supply chain. While we study the assembly rate optimization from the perspective of decisions of enterprises, which is more realistic and conducive for the government and enterprises to make decisions.

The rest of this paper is arranged as follows. In “Literature review”, a literature review is provided. We present model description and assumption in “Model description and assumption”. “Subsidy models” presents the optimal strategies in two subsidy models. “Coordination of prefabricated construction supply chain” designs the coordination mechanisms. A numerical analysis is conducted in “Numerical analysis”. In “Conclusions and future research”, we conclude the paper and highlight the future direction.

Literature review

There are three streams of literature generally related to this paper. Firstly, we have reviewed pricing strategies of supply chain with government subsidies and the subsidy incentives for prefabricated construction. Then we have illustrated coordination of supply chain with government subsidies.

Pricing strategies of supply chain with government subsidies

The government subsidies have been the hot issues of scholarly researches (Liu et al., 2020b). Some researchers focused on pricing strategies of different types supply chain under different subsidy modes. Wang et al. (2019) studied the impact of government subsidies with multiple subsidized parties (including one collector, one remanufacturer, and two retailers) on the optimal pricing strategies. The results showed that when the remanufacturing utilization rate of electronic waste is low, the government should give subsidy to collectors and retailers. Instead, the government should give the remanufacturer as much support as possible. He et al. (2019) analyzed pricing of the manufacturer in the presence of the government subsidy. The results indicated that subsidy level affects prices of remanufactured products and new products, and improves the performance of supply chain. Cao et al. (2020) gave the optimal production and pricing strategies of two enterprises under remanufacturing subsidy policy and carbon tax policy respectively. Meng et al. (2021) explored products collaborative pricing in dual-channel green supply chain and compared the optimal solutions in two cases of subsidies and subsidies. Chen et al. (2022) investigated the optimal production and subsidy strategies of three-layer supply chain consisting of a government, a manufacturer and a retailer, which the government provided unit-production subsidy to the manufacturer. Ling et al. (2022) considered the government proposes unit subsidy for two competitive manufacturers in terms of greenness level, so as to improve environmental quality and incentivize green production.

The subsidy incentives for prefabricated construction supply chain

Segerstedt and Olofsson (2010), Benton and McHenry (2010) and Papadopoulos et al. (2016) have considered construction supply chain structure and expounded supply chain management can improve the performance and competitiveness of construction enterprises. Eriksson (2010) conducted further empirical studies of construction supply chain. Following these studies, some scholars focused on researches of prefabricated construction supply chain. Wu et al. (2019a) depicted an empirical study with two cases in Chongqing to explore cost problems of prefabricated building supply chain. Han et al. (2022) proposed Hotelling model to investigate strategies of prefabricated construction developers with the consumer preference.

The studies showed that the subsidy also plays an important role in prefabricated construction supply chain. Arif and Egbu (2010) pointed out that the policy perception degree of construction enterprises is closely related to the promotion impact of prefabricated construction. Construction enterprises are ready to accept policy guidance and realize transformation and upgrading. Chen et al. (2017) proposed that the government can obtain social benefits by formulating subsidy policies, and construction enterprises can obtain greater economic benefits. Wu et al. (2019b) found the relative importance index of incentive policy accounts for 75.91%, which is an important factor to promote prefabricated construction in China. Gao and Tian (2020) investigated the impacts of prefabricated policies on the construction industries in China, which illustrated that only supportive policies with detailed incentive measures are beneficial for the development of prefabricated construction. However, the existing researches consider rarely how government subsidies stimulate prefabricated construction enterprises to optimize strategies. Du et al. (2022) considered prefabricated building supply chain consisting of a developer and a contractor, and studied the assembly rate strategies when developers encourage contractors to invest assembly technology under government subsidies. Han et al. (2023) established three-stage model to obtain the optimal price and optimal assembly rate with the government subsidy, and provided decisions suggestions for the developer, the contractor and the government. Yet these literature does not discuss the impacts of different subsidies on strategies of prefabricated construction supply chain.

Coordination of supply chain with government subsidies

Cachon (2003) discussed classical coordination contracts of supply chain. Then massive literature explored supply chain coordination issues. Li and Wang (2007), Arshinder and Deshmukh, (2008) and Bankvall et al. (2010) expounded the importance of coordination mechanisms based on supply chain decision structure and nature of demand. In terms of researches on carbon reduction issues, Yi and Li (2018) provided carbon-cost-sharing contract to coordinate supply chain to achieve greater energy conservation and emission reduction. Han et al. (2020) established the joint allocation contract of cost and profit considering government subsidies. Wang et al. (2022) investigated carbon emission reduction decisions of construction supply chain with the government subsidy, and designed cost-sharing contract improving the total profit of supply chain to achieve coordination. He et al. (2023) constructed the cost-sharing contract to attains a Pareto improvement and minimize carbon emissions. In green supply chains, Zhang and Yousaf (2020) designed a two-part tariff contract to reach green supply chain coordination with government subsidies, which optimizes supply chain performance and achieves green improvement. Li et al. (2021) an improved two-part tariff coordination model to improve the profit level of green supply chain.

In coordination issues of prefabricated construction supply chain. Zhai et al. (2018; 2020) focused on hedging coordination problem of prefabricated construction supply chain, Zeng et al. (2022) designed a side payment contract with a delivery-time dependent subsidy and two constant transfer terms to achieve win-win outcome for supply chain members. Jiang and Yuan (2022) investigated coordination of prefabricated construction supply chain with cap-and-trade policy, and found the two-part tariff contract obtain coordination improving performance. However, these studies lack the impact of government subsidies on coordination of prefabricated construction supply chain.

All the above literature shows that researches on pricing and coordination of other industries supply chain considering government subsidies have been mature. However, in prefabricated construction supply chain, there are few studies on pricing strategies and coordination with the government subsidy. Therefore, this paper incorporates the government subsidy into prefabricated construction supply chain, to study strategies optimization and coordination of prefabricated construction supply chain. It provides reference values for the government and favors prefabricated construction enterprises to make the optimal strategies.

Model description and assumption

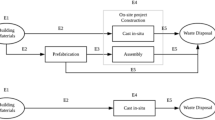
The paper considers the assembly rate as the subsidy standard, and subsidize the manufacturer or the assembler on the basis of unit product sold, which are divided two subsidy scenarios (subsidizing the manufacturer, subsidizing the assembler). In the context of subsidy policies, the paper investigates prefabricated construction supply chain consisting of a manufacturer \(M\) and an assembler \(A\). The manufacturer produces prefabricated components and transports them to the assembler, who sells prefabricated construction to consumers, without loss of generality, one prefabricated construction is assembled one-unit component. The paper considers the manufacturer is the leader who control the market and determines the wholesale price \(w\), while the assembler is the follower and determines the retail price \(p({p}\, > \,{w}\, > \,{c}\, > \,0)\) and the assembly rate \(g\). The manufacturer and the assembler aim to maximize their own profits. In order to facilitate the follow-up research, the notations in this paper are defined as Table 1.

Table 1 Notations of parameters and variables.
Full size table

In addition, we have made the following assumptions to develop the proposed models:

  1. (1)

    Following Swami and Shah (2013) to assume the market demand \(D(p,g)=\alpha -\beta p+\gamma g\) \((\alpha -\beta p \,>\, 0)\). The assumption indicates that market demand of prefabricated construction is affected by the retail price and the assembly rate.

  2. (2)

    Assume that producing prefabricated construction does not influence the traditional marginal costs of the manufacturer (Li et al., 2016). And the assembler bears the technical investment cost of design, assembly and management of prefabricated components. It is assumed that the cost is a quadratic function of the assembly rate (Hong et al., 2016). Therefore, the investment cost function is \(C\left(g\right)=k{g}^{2}/2\), where \(k > 0\) is the investment cost coefficient.

  3. (3)

    Combining Du et al. (2022); Han et al. (2023) with feature of subsidy policies in this paper, we derive the subsidy of unit product is \({\theta }_{i}g\).

  4. (4)

    In order to make the functions meaningful, we assume that \(2k\beta -{\gamma }^{2} > 0\), \(2k\beta -\gamma \left(\gamma +\beta {\theta }_{1}\right) > 0\), \(2k\beta -{\left(\gamma +\beta {\theta }_{2}\right)}^{2} > 0\).

We propose a base model without subsidies. According to above assumptions, the profit function of the manufacturer as:

$${\pi }_{M0}(w)=\left(w-c\right)\left(\alpha -\beta p+\gamma g\right)$$
(1)

\(\left(w-c\right)\) is the unit profit of the manufacturer, \(\left(\alpha -\beta p+\gamma g\right)\) is the market demand of prefabricated construction.

In the same way, the profit function of the assembler is:

$${\pi }_{A0}(p,g)=\left(p-w\right)\left(\alpha -\beta p+\gamma g\right)-k{g}^{2}/2$$
(2)

The first term \(\left(p-w\right)\) is the unit profit of the assembler, the second term \((k{g}^{2}/2)\) is the technology investment cost.

Proposition 1. The optimal price (\({p}_{0}\)), assembly rate (\({g}_{0}\)) and wholesale price (\({w}_{0}\)) are listed as follows:

$${p}_{0}=\frac{k\beta \left. (3\alpha +c\beta \right)-{\gamma }^{2}(\alpha +c\beta )}{2\beta (2k\beta -{\gamma }^{2})}$$
$${g}_{0}=\frac{\gamma \left(\alpha -c\beta \right)}{2(2k\beta -{\gamma }^{2})}$$
$${w}_{0}=\frac{\alpha +c\beta }{2\beta }$$

In base model, the optimal retail price, the optimal assembly rate and the optimal wholesale price are unique. We substitute them into profit functions of the manufacturer and the assembler respectively, \({\pi }_{A0}({p}_{0},{g}_{0})=\frac{k\left(\alpha -c\beta \right)^{2}}{8\left(2k\beta -{\gamma }^{2}\right)}\) and \({\pi }_{M0}({w}_{0})=\frac{k\left(\alpha -{\rm{c}}\beta \right)^{2}}{4\left(2k\beta -{\gamma }^{2}\right)}\) are obtained.

Subsidy models

We propose models of prefabricated construction supply chain in two cases of government subsidies to the manufacturer or the assembler (SM model SA model), then analyze the impacts of the subsidy rate and the consumer preference on the optimal strategies.

The model subsidizing the manufacturer (SM model)

We propose a game model when the government subsidizes the manufacturer, to examine the optimal retail price, the optimal assembly rate and the optimal wholesale price.

In SM model, the profit function of the manufacturer is:

$${\pi }_{M1}(w)=\left(w+{\theta }_{1}g-c\right)\left(\alpha -\beta p+\gamma g\right)$$
(3)

\(\left(w+{\theta }_{1}g-c\right)\) is the unit profit of the manufacturer, \(\left(\alpha -\beta p+\gamma g\right)\) is the market demand.

The profit function of the assembler is:

$${\pi }_{A1}(p,g)=\left(p-w\right)\left(\alpha -\beta p+\gamma g\right)-k{g}^{2}/2$$
(4)

The first term \(\left(p-w\right)\) is the unit profit of the assembler, \((k{g}^{2}/2)\) is the technology investment cost.

Proposition 2. The optimal price (\({p}_{1}\)), assembly rate (\({g}_{1}\)) and wholesale price (\({w}_{1}\)) are listed as follows:

$${p}_{1}=\frac{k\beta \left. (3\alpha +c\beta \right)-\alpha \gamma \left(\gamma +\beta {\theta }_{1}\right)-\beta \gamma (c\gamma +\alpha {\theta }_{1})}{2\beta [2k\beta -\gamma (\gamma +\beta {\theta }_{1})]}$$
$${g}_{1}=\frac{\gamma \left(\alpha -c\beta \right)}{2[2k\beta -\gamma (\gamma +\beta {\theta }_{1})]}$$
$${w}_{1}=\frac{2k\beta \left. (\alpha +{\rm{c}}\beta \right)-\alpha \gamma \left(\gamma +\beta {\theta }_{1}\right)-\beta \gamma (c\gamma +\alpha {\theta }_{1})}{2\beta [2k\beta -\gamma (\gamma +\beta {\theta }_{1})]}$$

The proof is given in appendix.

Proposition 2 shows that the optimal retail price, the optimal assembly rate and the optimal wholesale price uniquely exist in SM model.

Substitute \({p}_{1}\), \({g}_{1}\) and \({w}_{1}\) into profit functions of the manufacturer and the assembler. We have \({\pi }_{A1}({p}_{1},{g}_{1})=\frac{k(2k\beta -{\gamma }^{2})\left(\alpha -c\beta \right)^{2}}{8{\left[2k\beta -\gamma \left(\gamma +\beta {\theta }_{1}\right)\right]}^{2}}\) and \({\pi }_{M1}({w}_{1})=\frac{k{\left(\alpha -c\beta \right)}^{2}}{4\,[2k\beta -\gamma (\gamma +\beta {\theta }_{1})]}\).

In order to analyze the impacts of subsidies on prefabricated construction enterprises, we compare the optimal strategies of base model and SM model.

Proposition 3. \({g}_{1}\, > \,{g}_{0}\), \({w}_{1}\, < \,{w}_{0}\), \(\left\{\begin{array}{ll}{p}_{1}\, < \,{p}_{0},\,\gamma\, \le \,\beta {\theta }_{1},k \,> \,\frac{\gamma \left(\gamma +\beta {\theta }_{1}\right)}{2\beta }\,{\rm{and}}\,\gamma \,>\, \beta {\theta}_{1},k\, > \,\frac{{\gamma }^{2}}{\beta }\\ {p}_{1}\,\ge \,{p}_{0},\gamma\, > \,\beta {\theta }_{1},\frac{\gamma (\gamma +\beta {\theta }_{1})}{2\beta }\, < \,k\,\le\, \frac{{\gamma}^{2}}{\beta}\end{array}\right.\).

The proof is given in appendix.

Proposition 3 shows that the government subsidy to the manufacturer can increase the assembly rate and reduce the wholesale price, which has a favorable impact on the development of prefabricated construction. The impact of the government subsidy on the retail price is related to relationship between the investment cost coefficient \(k\), price sensitivity\(\,\beta\) and the consumer preference \(\gamma\). When \(0 \,< \,k\,\le \,\frac{\gamma (\gamma +\beta {\theta }_{1})}{2\beta }\), the retail price in SM model\(\,{p}_{1} < 0\), the assembler will exit the market because of unprofitable. The high investment cost coefficient (\(k > \frac{\gamma (\gamma +\beta {\theta }_{1})}{2\beta }\) or \(k > \frac{{\gamma }^{2}}{\beta }\)) indicates the low investment efficiency, at this time, the lower retail price in SM model can attract more consumers to purchase prefabricated construction. The market demand will increase, which is not only beneficial for prefabricated construction enterprises to increase profits, but also attracts more construction enterprises to join the prefabricated construction market. Compared to price sensitivity for the market demand, when the impact of the consumer preference is greater, with the middle investment cost efficiency, the retail price in SM model is higher. The purpose of the government subsidy is to promote the development of prefabricated construction and attract consumers to purchase prefabricated construction. Therefore, the government hopes to reduce the retail price, that is, to maintain a middle or low investment cost efficiency. Thus, the government and enterprises should pay attention to guide consumption consciousness of consumers, and improve consumers’ consumption preference for prefabricated construction.

Proposition 4.\(\,{\pi }_{M0}({w}_{0})\, < \,{\pi }_{M1}({w}_{1})\), \({\pi }_{A0}({p}_{0},{g}_{0})\, < \,{\pi }_{A1}({p}_{1},{g}_{1})\).

The proof is given in appendix.

Proposition 4 indicates that the government subsidy is an effective way to increase the profits of prefabricated construction supply chain members. When construction enterprises are profitable, they are willing to construct prefabricated buildings, thereby expanding the market scale of prefabricated construction. Therefore, subsidizing the manufacturer is favorable choice for the government.

Proposition 5. \(\frac{\partial {w}_{1}}{\partial {\theta }_{1}} < 0\), \(\frac{\partial {g}_{1}}{\partial {\theta }_{1}} > 0\). \(\left\{\begin{array}{c}\frac{\partial {p}_{1}}{\partial {\theta }_{1}} > 0,\beta < \frac{{\gamma }^{2}}{k}\\ \frac{\partial {p}_{1}}{\partial {\theta }_{1}}\le 0,\beta \ge \frac{{\gamma }^{2}}{k}\end{array}\right.\).

The proof is given in appendix.

Proposition 5 indicates that the higher subsidy rate will reduce the wholesale price and improve the assembly rate significantly. The impact of the subsidy rate \({\theta }_{1}\) on the retail price is related to relationship between the investment cost coefficient \(k\), price sensitivity\(\,\beta\) and the consumer preference \(\gamma\). The reason for this phenomenon is that when the government subsidizes the manufacturer, the manufacturer is willing to reduce the wholesale price which not only leads to the lower cost of the assembler, but also can increase the sales volume of prefabricated components and enhance its competitiveness. Due to the lower cost, the assembler has more market space to build prefabricated construction and the market demand will also increase. With the rising market demand of prefabricated construction, consumers have higher requirements for prefabricated construction, which stimulates the assembler to increase the assembly rate. In the meantime, the assembler adjusts the retail price to make sure the profit of itself.

Proposition 6.

  1. (1)

    \(\frac{\partial {g}_{1}}{\partial \gamma }\, > \,0\),

  2. (2)

    \(\left\{\begin{array}{ll}\frac{\partial {p}_{1}}{\partial \gamma }\, < \,0,\beta \,> \,\frac{{\gamma }^{2}}{k},\,\frac{2k\gamma }{k\beta +{\gamma }^{2}}\, < \,{\theta }_{1} \,< \,\frac{2k\beta -{\gamma }^{2}}{\beta \gamma }\\ \frac{\partial {p}_{1}}{\partial \gamma }\ge 0,\beta \,> \,\frac{{\gamma }^{2}}{k},\,{\theta }_{1}\,\le \,\frac{2k\gamma }{k\beta +{\gamma }^{2}}\,{\rm{or}}\,\beta \,\le \,\frac{{\gamma }^{2}}{k}\,{\theta }_{1}\,\le \,\frac{2k\beta -{\gamma }^{2}}{\beta \gamma }\end{array}\right.\).

The proof is given in appendix.

Proposition 6 indicates that the consumer preference for prefabricated construction can effectively improve the assembly rate in SM model. When the consumer preference increases, in order to occupy the market, prefabricated construction enterprises will improve the production scale of prefabricated construction and promote assembly technology innovation, so as to improve the assembly rate. The government can provide consumers with subsidies or welfare policies to improve consumers’ preference for prefabricated construction to improve the assembly rate. Compared to the consumer preference \(\gamma\), when the impact of price sensitivity \(\beta \,\) is greater \((\beta > \frac{{\gamma }^{2}}{k})\), with the middle subsidy rate (\(\,\frac{2k\gamma }{k\beta +{\gamma }^{2}} < {\theta }_{1} < \frac{2k\beta -{\gamma }^{2}}{\beta \gamma }\)), the retail price \({p}_{1}\) decreases with the increase of \(\gamma\). The increase of the consumer preference means that consumers’ acceptance of prefabricated construction increases, which effectively stimulates the prefabricated construction market. Only by reducing retail price can the assembler attract consumers and improve competitiveness. When the subsidy rate is low (\({\theta }_{1}\le \frac{2k\gamma }{k\beta +{\gamma }^{2}}\,{\rm{or}}\,{\theta }_{1}\le \frac{2k\beta -{\gamma }^{2}}{\beta \gamma }\)), \({p}_{1}\) increases with the increase of \(\gamma\). The assembler increases the retail price to balance the technology investment cost which ensure its profit.

The model subsidizing the assembler (SA model)

This section proposes a model when the government subsidizes the assembler, to examine the optimal retail price, the optimal assembly rate and the optimal wholesale price under the decentralized model.

The manufacturer ‘s profit function is:

$${\pi }_{M2}(w)=\left(w-c\right)\left(\alpha -\beta p+\gamma g\right)$$
(5)

\(\left(w-c\right)\) is the unit profit of the manufacturer, \(\left(\alpha -\beta p+\gamma g\right)\) is the market demand.

In SA model, the profit function of the assembler is:

$${\pi }_{A2}(p,g)=\left(p+{\theta }_{2}g-w\right)\left(\alpha -\beta p+\gamma g\right)-k{g}^{2}/2$$
(6)

\(\left(p+{\theta }_{2}g-w\right)\) is the unit profit of the assembler, \((k{g}^{2}/2)\) is the technology investment cost.

Proposition 7. The optimal price (\({p}_{2}\)), assembly rate (\({g}_{2}\)) and wholesale price (\({w}_{2}\)) are listed as follows:

$${p}_{2}=\frac{k\beta \left. (3\alpha +c\beta \right)-\left(\gamma +\beta {\theta }_{2}\right)(\alpha \gamma +c\beta \gamma +2\alpha {\beta \theta }_{2})}{2\beta [2k\beta -{(\gamma +\beta {\theta }_{2})}^{2}]}$$
$${g}_{2}=\frac{(\gamma +\beta {\theta }_{2})\left(\alpha -c\beta \right)}{2[2k\beta -{(\gamma +\beta {\theta }_{2})}^{2}]}$$
$${w}_{2}=\frac{{\rm{\alpha }}+c\beta }{2\beta }$$

The proof is given in appendix.

Proposition 7 shows that the optimal retail price, the optimal assembly rate and the optimal wholesale price uniquely exist in SA model.

Substitute \({p}_{2}\), \({g}_{2}\) and \({w}_{2}\) into profit functions of the manufacturer and the assembler, we obtain \({\pi }_{A2}({p}_{2},{g}_{2})=\frac{k\left(\alpha -c\beta \right)^{2}}{8[2k\beta -{(\gamma +\beta {\theta }_{2})}^{2}]}\) and \({\pi }_{M2}({w}_{2})=\frac{k\left(\alpha -c\beta \right)^{2}}{4[2k\beta -{(\gamma +\beta {\theta }_{2})}^{2}]}\).

Proposition 8.

  1. (1)

    \({g}_{2}\, > \,{g}_{0}\)

  2. (2)

    \({w}_{2}={w}_{0}\)

  3. (3)

    \(\left\{\begin{array}{ll}{p}_{2} \,< \,{p}_{0}, \gamma \,\le \,\beta {\theta }_{2},k \,>\, \frac{{\left(\gamma +\beta {\theta }_{2}\right)}^{2}}{2\beta }\,{\rm{and}}\; {{\gamma}}\, > \,\beta {\theta}_{2},k\, > \,\frac{{\gamma }^{2}}{\beta }+\frac{{\gamma }^{3}}{{\beta }^{2}{\theta }_{2}}\\ {p}_{2}\,\ge \,{p}_{0},\gamma\, >\, \beta {\theta }_{2},\frac{{(\gamma +\beta {\theta }_{2})}^{2}}{2\beta} \,< \,k\,\le\, \frac{{\gamma }^{2}}{\beta }+\frac{{\gamma }^{3}}{{\beta }^{2}{\theta }_{2}}\end{array}\right.\).

The proof is given in appendix.

Proposition 8 indicates that the subsidy to the assembler can increase the assembly rate, too. Furthermore, the wholesale price does not change. The impact of the subsidy rate \({\theta }_{2}\) on the retail price is related to relationship with the investment cost coefficient \(k\), price sensitivity\(\,\beta\) and the consumer preference \(\gamma\). When \(0 < k < \frac{{(\gamma +\beta {\theta }_{2})}^{2}}{2\beta }\), the retail price in SA model\(\,{p}_{2} < 0\), the assembler cannot guarantee profits and will exit the market. When the investment cost efficiency is low (\(k > \frac{{(\gamma +\beta {\theta }_{2})}^{2}}{2\beta }\) or \(k > \frac{{\gamma }^{2}}{\beta }+\frac{{\gamma }^{3}}{{\beta }^{2}{\theta }_{2}}\)), the retail price in SA model is lower than that in base model. It can increase the market demand to attract consumers, which balance the profit loss because of the reduction of the retail price. When the higher impact of the consumer preference for prefabricated construction (\(\gamma > \beta {\theta }_{2}\)), with the middle investment cost efficiency (\(\frac{{(\gamma +\beta {\theta }_{2})}^{2}}{2\beta } < k\le \frac{{\gamma }^{2}}{\beta }+\frac{{\gamma }^{3}}{{\beta }^{2}{\theta }_{2}}\)), the retail price in SA model is greater. The government and enterprises can increase comprehensive input to promote the consumer preference and regulate the investment cost efficiency, which aim to reduce the retail price.

Proposition 9. \({\pi }_{M0}({w}_{0}) < {\pi }_{M2}({w}_{2}),\,{\pi }_{A0}({p}_{0},{g}_{0}) < {\pi }_{A2}({p}_{2},{g}_{2})\).

The proof is given in appendix.

It can be seen from proposition 9 that profits of both the manufacturer and the assembler increase in SA model. The profit of supply chain in SA model is greater than that in base model. Therefore, the government subsidy is an effective way to improve profits of prefabricated construction enterprises. Prefabricated construction enterprises can obtain more profits, so that they have more enthusiasm to produce prefabricated construction.

Proposition 10.

  1. (1)

    \({w}_{2}\) has nothing to do with \({\theta }_{2}\),

  2. (2)

    \(\frac{\partial {g}_{2}}{\partial {\theta }_{2}}\, > \,0\),

  3. (3)

    \(\left\{\begin{array}{ll}\frac{\partial {p}_{2}}{\partial {\theta }_{2}}\,\ge \,0,\beta \,\le \,\frac{{2\gamma}^{2}}{k}\,{\rm{and}}\,\beta \,>\, \frac{{2\gamma }^{2}}{k},\,0 \,<\, {\theta }_{2}\le \frac{k\beta -{\gamma }^{2}-\sqrt{k\beta \left(k\beta -2{\gamma }^{2}\right)}}{\beta \gamma }\\ \frac{\partial {p}_{2}}{\partial {\theta }_{2}}\, < \,0,\beta \,>\, \frac{{2\gamma }^{2}}{k},\frac{k\beta -{\gamma }^{2}-\sqrt{k\beta \left(k\beta -2{\gamma }^{2}\right)}}{\beta \gamma } \,< \,{\theta }_{2} \,< \,\frac{\sqrt{2k\beta }-{\gamma }^{2}}{\beta }\end{array}\right.\)

The proof is given in appendix.

Proposition 10 indicates that in SA model, the wholesale price made by the manufacturer is not affected by the subsidy. Anyway, the government subsidy will stimulate the assembly rate and influence the retail price, while the impact for the retail price is also related to relationship between the investment cost coefficient \(k\), price sensitivity\(\,\beta\) and the consumer preference \(\gamma\). When the impact of the consumer preference on the prefabricated construction market is greater compared to the price sensitivity (\(\frac{{2\gamma }^{2}}{k}\ge \beta\)), the retail price increases with the subsidy rate. When the subsidy rate is at low level (\(0 < {\theta }_{2}\le \frac{k\beta -{\gamma }^{2}-\sqrt{k\beta \left(k\beta -2{\gamma }^{2}\right)}}{\beta \gamma }\)), regardless of the impact of the consumer preference and the price sensitivity on the prefabricated construction market, the retail price will increase with the subsidy rate. The growth of the assembly rate is relatively slow in low subsidy level, the investment costs still increase, the assembler has to raise the retail price to avoid the loss and ensure its profit; When the impact of the price sensitivity is greater compared to the consumer preference (\(\beta > \frac{{2\gamma }^{2}}{k}\)), with the middle subsidy rate (\(\frac{k\beta -{\gamma }^{2}-\sqrt{k\beta \left(k\beta -2{\gamma }^{2}\right)}}{\beta \gamma } < {\theta }_{2} < \frac{\sqrt{2k\beta }-{\gamma }^{2}}{\beta }\)), when the subsidies for the assembler increase, the assembler is willing to lower the retail price to promote the market demand which makes contributions to its profit promotion.

Proposition 11.

  1. (1)

    \(\frac{\partial {g}_{2}}{\partial \gamma }\, > \,0\)

  2. (2)

    \(\left\{\begin{array}{l}\frac{\partial {p}_{2}}{\partial \gamma }\,\le \,0,k\,\le \,2\beta {\theta }_{2}^{2}\,{\rm{and}}\,k \,> \,2\beta {\theta }_{2}^{2},\gamma \,\le \,\frac{(k-\beta {\theta }_{2})-\sqrt{{k}^{2}-2k\beta {\theta }_{2}^{2}}}{{\theta }_{2}}\left.\right)\,{\rm{or}}\,\gamma \,\ge \,\frac{\left(k-\beta {\theta }_{2}\right)+\sqrt{{k}^{2}-2k\beta {\theta }_{2}^{2}}}{{\theta }_{2}}\\ \frac{\partial {p}_{2}}{\partial \gamma }\, > \,0,k \,>\, 2\beta {\theta }_{2}^{2},\frac{(k-\beta {\theta }_{2})-\sqrt{{k}^{2}-2k\beta {\theta }_{2}^{2}}}{{\theta }_{2}}\, <\, \gamma \,<\, \frac{\left(k-\beta {\theta }_{2}\right)+\sqrt{{k}^{2}-2k\beta {\theta }_{2}^{2}}}{{\theta }_{2}}\end{array}\right.\)

The proof is given in appendix.

Proposition 11 indicates that the consumer preference can effectively improve the assembly rate in SA model, and the impact of the consumer preference \(\gamma\) on the retail price is related to relationship between the investment cost coefficient \(k\), price sensitivity\(\,\beta\) and the subsidy rate \({\theta }_{2}\). When \(k\) is small (\(k\le 2\beta {\theta }_{2}^{2}\)) and \(k\) is large (\(k > 2\beta {\theta }_{2}^{2}\)), \(\gamma\) is small (\(0 < \gamma \le \frac{(k-\beta {\theta }_{2})-\sqrt{{k}^{2}-2k\beta {\theta }_{2}^{2}}}{{\theta }_{2}}\)) or large (\(\gamma \ge \frac{\left(k-\beta {\theta }_{2}\right)+\sqrt{{k}^{2}-2k\beta {\theta }_{2}^{2}}}{{\theta }_{2}}\)), \({p}_{2}\) decreases with the increase of \(\gamma\). At this time, with the increasing consumer preference for prefabricated construction, the market demand will increase. The profit generated by the increase of market demand and the government subsidy can support technology investment cost so the assembler can lower the retail price to attract more consumers. When \(k\) is large (\(k > 2\beta {\theta }_{2}^{2}\)), \(\gamma\) is middle (\(\frac{(k-\beta {\theta }_{2})-\sqrt{{k}^{2}-2k\beta {\theta }_{2}^{2}}}{{\theta }_{2}} < \gamma < \frac{\left(k-\beta {\theta }_{2}\right)+\sqrt{{k}^{2}-2k\beta {\theta }_{2}^{2}}}{{\theta }_{2}}\)), \({p}_{2}\) increases with the increase of \(\gamma\). The assembly technology investment cost of the assembler is larger, and the income generated by the increase of market demand is not enough to compensate. The assembler will increase the retail price to ensure its own profit.

Comparative analysis

This subsection makes a comparative analysis of two subsidy models to observe the subsidy effects on the optimal strategies. Comparing the equilibrium outcomes of SM model and SA model, we obtain three propositions.

Proposition 12. If \({\theta }_{1}={\theta }_{2}\), \({w}_{1}\, < \,{w}_{2}\), \({{g}_{1}\, < \,g}_{2}.\) \(\left\{\begin{array}{l}{{p}_{1}\, < \,p}_{2}, \theta \,<\, \frac{\gamma }{\beta }\\ {{p}_{1}\,\ge \,p}_{2}, \theta \,\ge \,\frac{\gamma }{\beta }\end{array}\right.\).

The proof is given in appendix.

Proposition 12 indicates that when the government subsidizes different members of supply chain, the government subsidy makes different effects on the optimal strategies. The assembly rate in SA model is higher than that in SM model. Thus, in order to stimulate the assembly rate which makes contributions to promoting the development of prefabricated construction, it is better for the government to choose subsidizing the assembler.

Proposition 13. If \({\theta }_{1}={\theta }_{2}\), \({\pi }_{M1}({w}_{1}) < {\pi }_{M2}({w}_{2})\), \({\pi }_{A1}({p}_{1},{g}_{1}) < {\pi }_{A2}({p}_{2},{g}_{2})\).

The proof is given in appendix.

Proposition 13 indicates that the government subsidy makes different effects on profits under two subsidy model. The maximum profits of the manufacturer and the assembler in SA model is higher than that in SM model. In general, when the government has considerable government finances, in order to promote the profit of the manufacturer, the assembler and the whole supply chain, it’s a better choice to subsidize the assembler.

Proposition 14. If \({g}_{1}={g}_{2}\), \({\theta }_{1} > {\theta }_{2}\).

The proof is given in appendix.

Proposition 14 shows that when the assembly rate is equal under two subsidy scenarios, the government subsidy rate in SM model is greater. The two subsidy models achieve the same assembly rate, which means that the government has the same promotion effect on prefabricated construction, at this time, the subsidy cost in SM model is higher than that in SA model. Therefore, it is more beneficial for the government to choose the assembler as the subsidy object, which not only ensures the subsidy effect, but also reduces the subsidy expenditure of the government.

Coordination of prefabricated construction supply chain

In this section, we establish centralized decision models and design coordination mechanisms of prefabricated construction supply chain in two cases of subsidies to the manufacturer or the assembler.

Centralized models

In the centralized model, the manufacturer and the assembler constitute a community of interests, and determine the retail price and the assembly rate with the goal of maximizing the total profit of prefabricated construction supply chain.

The centralized model subsidizing the manufacturer

When the government subsidizes the manufacturer, the profit function of prefabricated construction supply chain is:

$${\pi }_{{SC}1}^{{\prime} }(p,g)=\left(p+{\theta }_{1}g-c\right)\left(\alpha -\beta p+\gamma g\right)-k{g}^{2}/2$$
(7)

\(\left(p+{\theta }_{1}g-c\right)\) is the unit profit of supply chain, \(\left(\alpha -\beta p+\gamma g\right)\) is the market demand and \(k{g}^{2}/2\) is the investment cost.

We obtain \({p}_{1}^{{\prime} }=\frac{k\left. (\alpha +c\beta \right)-(c\gamma +\alpha {\theta }_{1})(\gamma +{\beta \theta }_{1})}{2k\beta -(\gamma +\beta {\theta }_{1})^{2}}\) and \({g}_{1}^{{\prime} }=\frac{(\alpha -c\beta )(\gamma +\beta {\theta }_{1})}{2k\beta -(\gamma +\beta {\theta }_{1})^{2}}\), and substitute \({p}_{1}^{{\prime} }\) and \({g}_{1}^{{\prime} }\) into the overall profit function. The maximum profit is \({\pi }_{{SC}1}^{{\prime} }({p}_{1}^{{\prime} },{g}_{1}^{{\prime} })=\frac{k\left. (\alpha -c\beta \right)^{2}}{2[2k\beta -{\left(\gamma +\beta {\theta }_{1}\right)}^{2}]}\).

The centralized model subsidizing the assembler

The profit function of prefabricated construction supply chain is:

$${\pi }_{{SC}2}^{{\prime} }(p,g)=\left(p+{\theta }_{2}g-c\right)\left(\alpha -\beta p+\gamma g\right)-k{g}^{2}/2$$
(8)

\(\left(p+{\theta }_{2}g-c\right)\) is the unit profit of supply chain, \(\left(\alpha -\beta p+\gamma g\right)\) is the market demand and \(k{g}^{2}/2\) is the investment cost.

We obtain \({p}_{2}^{{\prime} }=\frac{k\left. (\alpha +c\beta \right)-(c\gamma +\alpha {\theta }_{2})(\gamma +{\beta \theta }_{2})}{2k\beta -(\gamma +\beta {\theta }_{2})^{2}}\) and \({g}_{2}^{{\prime} }=\frac{(\alpha -c\beta )(\gamma +\beta {\theta }_{2})}{2k\beta -(\gamma +\beta {\theta }_{2})^{2}}\). At this time, the maximum profit is \({\pi }_{{SC}2}^{{\prime} }({p}_{2}^{{\prime} },{g}_{2}^{{\prime} })=\,\frac{k\left. (\alpha -c\beta \right)^{2}}{2[2k\beta -{\left(\gamma +\beta {\theta }_{2}\right)}^{2}]}\). The profits of supply chain in two centralized models are higher than those in decentralized models.

Coordination models

This paper designs coordination mechanism based on revenue-cost sharing contract to optimize prefabricated construction supply chain. When supply chain can distribute the profit to the manufacturer and the assembler in any proportion, the decentralized decision achieves coordination (Cachon 2003). In this paper, the main idea of revenue-cost sharing contract is: after sells prefabricated construction to consumers, the assembler returns part of the revenue to the manufacturer. At the same time, the manufacturer shares part of the assembly technology investment cost of the assembler.

The coordination model subsidizing the manufacturer

We assume the revenue sharing ratio is \({\varphi }_{1}\,(0\le {\varphi }_{1}\le 1)\), the cost sharing ratio is \({\lambda }_{1}\,(0\le {\lambda }_{1}\le 1)\). The profit functions of the manufacturer and the assembler are as follows:

$${\pi }_{M1}^{s}\left(w\right)=\left(w+{\theta }_{1}g-c\right)\left(\alpha -\beta p+\gamma g\right)+(1-{\varphi }_{1})p\left(\alpha -\beta p+\gamma g\right)-\frac{(1-{\lambda }_{1})k{g}^{2}}{2}$$
(9)
$${\pi }_{A1}^{s}(p,g)=\left({\varphi }_{1}p-w\right)\left(\alpha -\beta p+\gamma g\right)-\frac{{\lambda }_{1}k{g}^{2}}{2}$$
(10)

\((1-{\varphi }_{1})p\left(\alpha -\beta p+\gamma g\right)\) is the partial revenue shared by the assembler to the manufacturer, \(\frac{(1-{\lambda }_{1})k{g}^{2}}{2}\) is partial investment cost of the assembler split by the manufacturer.

Proposition 15. For \({\delta }_{1}{\in}(\mathrm{0,1}]\), when \(\left\{\begin{array}{c}{\varphi }_{1}p-w={\delta }_{1}\left(p+{\theta }_{1}g-c\right)\\ {\lambda }_{1}={\delta }_{1}\end{array}\right.\) is satisfied, the revenue-cost sharing contract can realize supply chain coordination.

The proof is given in appendix.

When the government subsidizes the manufacturer, the prices, the assembly rate and cost satisfy the coordination condition \(\left\{\begin{array}{c}{\varphi }_{1}p-w={\delta }_{1}\left(p+{\theta }_{1}g-c\right)\\ {\lambda }_{1}={\delta }_{1}\end{array}\right.\), we can coordinate prefabricated construction supply chain. At this time, the profit of prefabricated construction supply chain can be distributed to the manufacturer and the assembler in any proportion, \({\delta }_{1}\) is profit distribution ratio of supply chain. Compared with the complex coordination parameters of supply chain based on revenue-cost sharing contract (Sane-Zerang et al., 2020), the coordination condition of this paper is simpler. When designing the coordination mechanism, we don’t need to consider the impacts of the investment cost efficiency, the price sensitivity of the market demand and other parameters. Therefore, strategies are easier to optimize and supply chain is more stable. When the government has determined the subsidy rate, the supply chain can determine its profit distribution proportion according to the optimal strategies. The manufacturer and the assembler coordinate and restrain each other, and work together to improve supply chain performance.

The coordination model subsidizing the assembler

When the government subsidizes the assembler, we assume that the revenue sharing ratio is \({\varphi }_{2}\,(0\le {\varphi }_{2}\le 1)\), the cost sharing ratio is \({\lambda }_{2}\,(0\le {\lambda }_{2}\le 1)\). The profit functions of the manufacturer and the assembler are:

$${\pi }_{M2}^{s}\left(w\right)=\left(w-c\right)\left(\alpha -\beta p+\gamma g\right)+(1-{\varphi }_{2})(p+{\theta }_{2}g)\left(\alpha -\beta p+\gamma g\right)-\frac{(1-{\lambda }_{2})k{g}^{2}}{2}$$
(11)
$${\pi }_{A2}^{s}\left(p,g\right)=[{\varphi }_{2}(p+{\theta }_{2}g)-w]\left(\alpha -\beta p+\gamma g\right)-\frac{{\lambda }_{2}k{g}^{2}}{2}$$
(12)

Due to subsidies for the assembler, the partial revenue shared to the manufacturer is \((1-{\varphi }_{2})(p+{\theta }_{2}g)\left(\alpha -\beta p+\gamma g\right)\), \(\frac{(1-{\lambda }_{2})k{g}^{2}}{2}\) is partial investment cost split by the manufacturer.

Proposition 16. Let \({\delta }_{2}{\in}(\mathrm{0,1}]\), when \(\left\{\begin{array}{c}{\varphi }_{2}(p+{\theta }_{2}g)-w={\delta }_{2}\left(p+{\theta }_{2}g-c\right)\\ {\lambda }_{2}={\delta }_{2}\end{array}\right.\), the decentralized decision model realizes coordination.

The proof is given in appendix.

In proposition 16, when \(\left\{\begin{array}{c}{\varphi }_{2}(p+{\theta }_{2}g)-w={\delta }_{2}\left(p+{\theta }_{2}g-c\right)\\ {\lambda }_{2}={\delta }_{2}\end{array}\right.\), the optimal strategies under decentralized decision can reach the level under centralized decision and realize supply chain coordination. The government subsidy will influence the wholesale price, the cost sharing ratio and the revenue sharing ratio. When the government subsidizes the assembler, the coordination condition is feasible and is not affected by the external parameters, which is conducive to the stable development of supply chain.

Numerical analysis

In this section, we conduct numerical examples to analyze the impacts of parameters on the retail price, the assembly rate, the wholesale price, and profits of the assembler and the manufacturer.

The impact of the subsidy rate on the optimal strategies

In order to observe changes of the optimal strategies, for simplifying model data, the paper refers the literature listed behind the data, assuming that price sensitivity \(\beta =1\), the consumer preference coefficient \(\gamma =0.5\) (Jiang et al., 2021), potential market demand \(\alpha =8000\), the investment cost coefficient\(\,k=4\) and the manufacturer’s initial cost \(c=4000\,\) and the subsidy rate \({\theta }_{i}{\in}\left[0,1\right]\) (Du et al., 2022).

The impact of the subsidy rate \(\theta\) on the retail price \(p\) is shown in Fig. 1.

Fig. 1
figure 1

The impact of \(\theta\) on p.

Full size image

From Fig. 1, we find that within the specific scope of the hypothesis, the government subsidy can reduce the retail price. Meanwhile, as the subsidy rate \(\theta\) increases, we can see that the retail prices in two subsidy scenarios decrease, the retail price in SA model (\({p}_{2}\)) changes more obvious. When \(\theta {\in}(0,0.5)\), the retail price in SM model (\({p}_{1}\)) is lower, which is more beneficial to consumers. \(\theta =0.5\), \({p}_{1}={p}_{2}\). When \(\theta {\in}(0.5,1)\), \({p}_{2} <\, {p}_{1}\). Subsidizing the assembler is better for consumers.

The impact of the subsidy rate \(\theta\) on the assembly rate \(g\) is analyzed in Fig. 2.

Fig. 2
figure 2

The impact of \(\theta\) on g.

Full size image

In Fig. 2, we observe that the subsidy can increase the assembly rate, as the subsidy rate \(\theta\) increases, the assembly rates in two subsidy scenarios increase. The change of the assembly rate in SA model is more significant. At this time, for the government, in order to improve the assembly rate, subsidizing the assembler is a better choice.

The impact of the subsidy rate \(\theta\) on the wholesale price \(w\) is analyzed in Fig. 3.

Fig. 3
figure 3

The impact of \(\theta\) on w.

Full size image

From Fig. 3, as the manufacturer is not subsidized, the wholesale price \({w}_{2}\) will not be affected by the subsidy rate, in order to ensure its the optimal profit. In SM model, as the subsidy rate \(\theta\) increases, the wholesale price \({w}_{1}\) decreases. At this time, for prefabricated construction enterprises, the wholesale price of SM model subsidizing the manufacturer is lower than that of SA model, so the cost of purchasing prefabricated components is also lower. The manufacturer and the assembler can negotiate pricing decisions, which are beneficial to achieving win-win cooperation.

The impacts of the subsidy rate \(\theta\) on profits of the assembler \({\pi }_{{Ai}}\) and the manufacturer \({\pi }_{{Mi}}\) are shown in Figs. 4 and 5.

Fig. 4
figure 4

The impact of \(\theta\) on profit of πAi.

Full size image
Fig. 5
figure 5

The impact of \(\theta\) on profit of πMi.

Full size image

Figures 4 and 5 indicates that the government subsidy can increase the profits of the assembler and the manufacturer. As \(\theta\) increases, the profits of both parties increase in two subsidy scenarios, the changing trend is more obvious in SA model. Figures 4 and 5 indicate subsidizing the assembler is a better choice when it is aimed to maximize the profit of supply chain. While \(\theta\) increases, the subsidy expenditure of the government will increase and social welfare will be affected, thus the government should cautiously formulate subsidy policies.

The impact of the investment cost efficiency and the consumer preference on the optimal strategies

We analyze the change of the retail price, the assembly rate, the wholesale price and profits under the joint action of the investment cost coefficient and the consumer preference. Set \(\theta =0.5\), and other parameters are same as “The impact of the subsidy rate on the optimal strategies”.

The impact of the investment cost coefficient \(k\) and the consumer preference \(\gamma\) on the retail price is shown in Fig. 6.

Fig. 6
figure 6

The impact of \(k\) and \(\gamma\) on p.

Full size image

It can be seen that the retail price generally increases with the increase of the consumer preference \(\gamma\) and the decrease of the investment cost coefficient \(k\), the retail price in SA model changes most obviously. When \(\gamma\) is small, the retail price in SA model is the lowest. When \(\gamma\) is large, the retail price in SM model is the lowest. The government can determine the subsidy object according to the consumer preference and the investment cost efficiency. The supply chain can adjust the retail price according to the consumer preference and the investment cost efficiency, which can maintain the stability of the market.

The impact of the investment cost coefficient \(k\) and the consumer preference \(\gamma\) on the assembly rate is shown in Fig. 7.

Fig. 7
figure 7

The impact of \(k\) and \(\gamma\) on g.

Full size image

In Fig. 7, no matter how the consumer preference \(\gamma\) and the investment cost coefficient \(k\) change, there is always \({g}_{2} >\, {g}_{1} >\, {g}_{0}\), meaning the assembly rate in SA model is the highest. \(g\) always increases with the increase of \(\gamma\) and the decrease of \(k\). It indicated that the higher consumers’ preference for prefabricated construction, the more conducive to improve the assembly rate. The government and enterprises can guide consumers to purchase prefabricated construction, which stimulate the increase of the assembly rate.

The impact of the investment cost coefficient \(k\) and the consumer preference \(\gamma\) on the wholesale price \(w\) is shown in Fig. 8.

Fig. 8
figure 8

The impact of \(k\) and \(\gamma\) on w.

Full size image

Figure 8 shows that the consumer preference \(\gamma\) and the investment cost coefficient \(k\) have no effect on the wholesale price of base model and SA model. The wholesale price of SM model is lower and decreases gradually with the increase of \(\gamma\) and the decrease of \(k\). When the consumer preference for prefabricated construction increases, the market demand will increase, and the demand of the assembler for prefabricated components increases, the manufacturer is willing to reduce the wholesale price to sell more prefabricated components.

The impact of the investment cost coefficient \(k\) and the consumer preference \(\gamma\) on profits of the assembler \({\pi }_{{Ai}}\) and the manufacturer \({\pi }_{{Mi}}\) are shown in Figs. 9 and 10.

Fig. 9
figure 9

The impact of \(k\) and \(\gamma\) on πAi.

Full size image
Fig. 10
figure 10

The impact of \(k\) and \(\gamma\) on πMi.

Full size image

In Figs. 9 and 10, no matter how the consumer preference \(\gamma\) and the investment cost coefficient \(k\) change, there is always \({\pi }_{A2} >\, {\pi }_{A1} >\, {\pi }_{A0}\), \({\pi }_{M2} >\, {\pi }_{M1} >\, {\pi }_{M0}\). The profits increase with the increase of \(\gamma\) and the decrease of \(k\). In order to obtain greater profits, the government can guide consumption consciousness of consumers, and enterprises can increase technology investment to adjust the investment coefficient appropriately.

Conclusions and future research

In this paper, in the context of subsidy policies, we have obtained the optimal strategies and maximum profits of prefabricated construction enterprises, then depicted coordination models of prefabricated construction supply chain. It shows that profits of the manufacturer and the assembler without the government subsidy is lower than those with government subsidies. The assembly rate will increase as the subsidy rate increases. The government subsidies prominently affect the determination of the retail price, a certain range of government subsidies can reduce the retail price, which is conducive to consumers purchasing prefabricated construction. The assembly rate and the whole profit of prefabricated construction supply chain in SA model are greater than those in SM model. The government subsidy can decrease the wholesale price in SM model. According to the conclusions, the paper puts forward the management insights for the government and prefabricated construction enterprises.

  1. (1)

    The government can give reasonable subsidies to the manufacturer or the assembler to support the produce of prefabricated construction. At present, most developing countries, such as China, has serious pollution and waste in the construction industry, so it is urgent to develop prefabricated construction for achieving energy conservation and emission reduction. The above results indicate that the government subsidy plays a positive role in strategies of prefabricated construction supply chain. When the government subsidizes prefabricated construction enterprises, the assembly rate has been significantly improved, and profits of prefabricated construction enterprises have been increased. When the government provides subsidies and other financial support, enterprises will actively produce prefabricated construction in pursuit of profits, expanding the scale of prefabricated construction.

  2. (2)

    The consumer preference for prefabricated construction can stimulate the assembly rate and influence the retail price. Therefore, we should manage to change the attitude of consumers towards prefabricated construction and improve their green consciousness. The greater consumer preference for prefabricated construction, the greater the market demand for prefabricated construction. The enterprise can obtain more profits, and will actively construct prefabricated buildings. The government can issue supporting policies to guide consumers to purchase prefabricated construction, such as tax reduction policies and consumption incentives. At the same time, enterprises should pay attention to the quality of components when manufacturing and assembling prefabricated components, so as to ensure structural safety and make consumers trust prefabricated construction more.

  3. (3)

    Revenue-cost sharing contract can optimize supply chain and increase the profit of supply chain. As the leader in the market, the manufacturer should actively coordinate the prefabricated construction market and provide coordination contracts for the assembler to strengthen cooperation. When the manufacturer and the assembler work together to maximize the profit of supply chain, not only can they increase the profit of supply chain, but also their respective profits, so as to achieve a win-win situation.

The conclusions and management suggestions can be applied in the prefabricated construction domains, construction enterprises (such as Changsha Broad Homes Industrial Group Co., Ltd., China State Construction Engineering Corporation Limited., Anchor Homes, Fleetwood Australia) can actively respond to the government’s call to increase the assembly rate and appropriately adjust retail price according to subsidy policies. The government (such as the Chinese government; the Australian government, the Turkey government) can choose the appropriate subsidy object according to the subsidy purpose. The government needs to gradually establish a complete and detailed subsidy policies and evaluation criteria for prefabricated buildings, so that construction enterprises have rules to follow, and products can be widely circulated, as well as the enthusiasm that enterprises adopt prefabricated construction will increase.

This paper considers pricing and the assembly rate strategies of prefabricated construction under subsidy polices, which enriches the research of construction supply chain. However, this paper only considers the impacts of subsidies on the manufacturer and the assembler, and only considers that the government encourages prefabricated construction enterprises in the form of financial subsidies. The conclusions have certain limitations. In fact, the subsidy policies also affect policy formulation of the government. Besides, the government can stimulate supply chain in other forms. Therefore, studying the impacts of subsidy policies on strategies of the government with taking the government as the decision object, and studying the impact of other government incentives on prefabricated construction supply chain will be the future research directions of this paper.