Abstract
Tonality is one of the most central theoretical concepts for the analysis of Western classical music. This study presents a novel approach for the study of its historical development, exploring in particular the concept of mode. Based on a large dataset of approximately 13,000 musical pieces in MIDI format, we present two models to infer both the number and characteristics of modes of different historical periods from first principles: a geometric model of modes as clusters of musical pieces in a non-Euclidean space, and a cognitively plausible Bayesian model of modes as Dirichlet distributions. We use the geometric model to determine the optimal number of modes for five historical epochs via unsupervised learning and apply the probabilistic model to infer the characteristics of the modes. Our results show that the inference of four modes is most plausible in the Renaissance, that two modes–corresponding to major and minor–are most appropriate in the Baroque and Classical eras, whereas no clear separation into distinct modes is found for the 19th century.
Similar content being viewed by others
Introduction
As a cultural, historical, cognitive, and formal system, music is subject to a number of forces that have shaped its evolution over time. In the Western tradition, music from the 17th, 18th, and 19th centuries sounds characteristically different. One main aspect of that difference, apart from the development of performance and instrumentation, is characterized by the music-theoretical system of tonality. Based on historical reasoning, music theorists have proposed accounts of the process by which Western tonality emerged, stabilized, extended, and eventually destabilized over the course of its history (Aldwell and Schachter, 2003; Dahlhaus, 1968; Fetis, 1844; Kostka and Payne, 2013; Rameau, 1722; Riemann, 1893; Schoenberg, 1969). For instance, Fetis (1844) describes the history of tonality as a succession of stages that are determined by significant changes in the relation of notes to each other. For example, he locates the transition from the tonalité ancienne to the tonalité moderne–roughly the transition from the Renaissance to the Baroque–in a specific bar in Claudio Monteverdi’s motet Cruda amarilli. There, Monteverdi writes an unprepared dominant seventh chord, which would have been regarded as false by Renaissance composers. Since then, Fétis’s claim and the particular musical example have been the subject of musicological debate (Chafe, 1992; Dahlhaus, 1968; Long, 2020; McClary, 1976).
In recent years, the emerging field of musical corpus studies has turned to these questions from a new angle. By analyzing large datasets of digital encodings of musical pieces with computational and statistical methods, researchers aim at bridging the gap between qualitative-historical and quantitative-empirical paradigms (Neuwirth and Rohrmeier, 2016) and develop novel ways to study the old questions mentioned above (see Section “Related empirical research”). This paper participates in this endeavor by using computational modeling for a data-driven analysis of historical changes in tonality and focuses on a particular aspect: the historical development of modes in Western classical music.
Related empirical research
Although definitions and models vary (Dahlhaus et al., 2001; Hyer, 2001; Lerdahl, 2001; Moss et al., 2019; Tymoczko, 2006), characterizations of tonality share (at least) some reference to the pitch level. For instance, a large number of previous empirical studies is based on a pitch-distribution model of tonality (e.g., Huron, 2006; Knopoff and Hutchinson, 1983; Krumhansl, 1990; Meyer, 1957; Snyder, 1990; Youngblood, 1958). Psychological and neuroscientific research often concentrates on the acquisition and mental representation of musical knowledge of pitch-class distributions (Bharucha and Krumhansl, 1983; Butler and Brown, 1994; Huron and Parncutt, 1993; Janata et al., 2002; Koelsch et al., 2013; Krumhansl, 1990; Krumhansl and Kessler, 1982; Large et al., 2016; Pearce and Rohrmeier, 2012; Tillmann et al., 2000, 2008; Zatorre and Salimpoor, 2013). Computational music-theoretical approaches aim at uncovering structures in the music itself by employing statistical methods to study distributions of pitch classes in musical corpora (Lieck et al., 2020; Moss, 2019; Parncutt, 2015; Savage et al., 2015; Temperley, 2009; White, 2013). The results of corpus-based research on tonality exhibit high similarities to the psychological findings (Huron, 2006; Krumhansl, 1990; Krumhansl and Cuddy, 2010): distributions of notes in musical corpora strongly resemble the patterns of mental representations and expectancy in behavioral experiments such as probe-tone studies (Krumhansl, 2004; Krumhansl and Kessler, 1982; Temperley and Marvin, 2008). Accordingly, it is assumed that implicit learning of statistical regularities in pitch distributions is a central factor for the cognition of tonality (Pearce, 2018; Rohrmeier and Cross, 2009; Rohrmeier and Rebuschat, 2012; Tillmann, 2005; Tillmann et al., 2000).
There are a number of previous empirical studies that investigate diachronic developments of tonality in Western classical music based on the statistics of pitch-class distributions. Rodrigues Zivic et al. (2013) study distributions of note bigrams (melodic intervals) in a large corpus of short melodies (Viro, 2011) and are able to distinguish four periods of music history based on the usage of these intervals in musical pieces. Several recent studies, as well as the present article use the music collection from the ClassicalArchives internet database (see Section “Data”). White and Quinn (2016) extracted a dataset of time slices of simultaneously sounding notes of approximately 13,800 pieces and report a diachronically increasing ratio of dominant-seventh chords to dominant triads. This finding is related to Dahlhaus’s (1968) assessment of the importance of dominant-seventh chords for the beginning of harmonic tonality, although the precise nature of this relation requires further investigation. A sub-sample of 33 composers from the time-slice dataset is used by Yust (2019) to study historical changes in pitch-class distributions using the discrete Fourier transform. His findings indicate that during the 18th and 19th centuries composers begin to explore modulations to more distantly-related keys, leading to a decrease in what he calls “diatonicity”. A similar finding is reported by Moss (2019) who shows that the tonal material used by Western classical composers expands historically, enabling them to write more chromatic and enharmonic compositions in the 18th and 19th centuries. Using approximately 24,000 pieces from ClassicalArchives, Huang et al. (2017) predict the composer of a musical piece based on the interval statistics of the pieces. Moreover, their clustering analysis shows that three groups of composers emerge which roughly correspond to three historical musical epochs. Weiß et al. (2019) use a dataset of 2000 audio recordings from which they computationally extract several features related to musical pitch in order to study a range of music historical questions. Their findings indicate a historical shift in the directionality of chord transitions (see also Moss et al., 2019; Rohrmeier and Cross, 2008), an increase in dissonant intervals, as well as an overall increase in tonal complexity.
Few studies focus exclusively on modes in Western classical music. A characterization of eight modes in medieval music is given by Huron and Veltman (2006), albeit only on the basis of a relatively small sample of 98 Gregorian chants. This work was recently enlarged by Cornelissen et al. (2020) who introduce and compare several mode classification methods, and apply them to this repertoire on the basis of more than 20,000 chants. The questions addressed by Albrecht et al. (2014) are particularly similar to the ones studied in this paper. Based on a dataset of 455 pieces sampled from various sources, they study the historical development of modes in Western classical music between 1400 and 1750, that is, in the transition between the Renaissance and Baroque periods. They acknowledge a particular difficulty: in order to classify musical pieces into different modes by calculating the similarity of their pitch-class distributions to pre-defined mode templates, one needs to know how many templates there are and what they look like. They propose to solve this problem by taking for granted that the major and minor modes were well-established in the Common-Practice period, and that they can be represented by the pitch-class distributions reported by Albrecht and Shanahan (2013). Their methodology can be summarized as follows: For the latest time period 1700–1750 they calculate the Euclidean distance of the given major and minor templates to all twelve transpositions of a piece and keep that transposed piece with minimal distance to either mode. These transposed pieces are then clustered together via a hierarchical clustering algorithm to determine the optimal number of modes for this time period. Subsequently, for each found cluster, the average pitch-class distribution is calculated and taken as new mode template for the earlier 50-year bin. By progressively moving backwards in time they find that the time period 1600–1650 suggest three rather than two modes. In the earliest period in their sample from 1400–1450 four modes emerge from this procedure. While their overall methodology bears resemblance to our proposed geometrical model (see Section “Geometric Model”), there is a crucial difference: our approach does not assume the existence and particular shapes of the major and minor modes a priori (see Section “Assumptions and contributions”) but demonstrates that both aspects can be inferred from data.
Assumptions and contributions
The aforementioned approaches rely on several specific music-theoretical assumptions, in particular that Western classical music is governed by exactly two modes, the major mode and the minor mode. With the notable exception of Albrecht et al. (2014), this underlying assumption is rarely discussed. The present approach explicitly and systematically addresses this fundamental assumption with data-driven methods. We do neither assume a fixed number of modes nor specific characteristics of these modes, but rather infer them in an unsupervised manner for different time periods.
Empirical music research commonly presupposes three further assumptions that are adopted in this study. The first assumption is octave equivalence, according to which notes group into pitch classes. For example, all Cs (e.g., C1, C2, C3, …) are grouped into the pitch class C. Second, musical keys are commonly assumed to be invariant under transposition. This means that the relative importances of a key’s scale degrees are independent of the root. The third assumption is that there are only twelve distinct pitch-classes that are commonly represented as integers {0, …, 11}. This, together with the assumption of two modes, implies that there are exactly 2 × 12 = 24 musical keys. While the assumption of octave equivalence is supported by empirical evidence (Wright et al., 2000), transpositional invariance is debatable, in particular with respect to the historical appropriateness of this concept (Gárdonyi and Nordhoff, 2002; Lieck et al., 2020; Moss, 2019). For instance, the findings of Quinn and White (2017) indicate that the pitch-class distributions of different keys might not generally be related by mere transposition. For a detailed account of the music theoretical concepts see the Appendix.
The contributions of this paper are summarized as follows: (1) We propose two novel models: a geometric model of modes as clusters of musical pieces in a non-Euclidean space, and a probabilistic Bayesian model of modes as Dirichlet distributions; (2) using the geometric model, we determine the relation between modes for five historical epochs and infer their cardinality via unsupervised learning, and (3) we apply the probabilistic model to infer the characteristics of major and minor from data and compare them to previous findings. Using recent computational methods, our approach provides a data-driven analysis of the historical changes of tonality.
Materials and models
Data
This study uses a dataset of files in Musical Instrument Digital Interface (MIDI) format from the internet platform ClassicalArchives, consisting of approximately 21,000 pieces of Western classical music.Footnote 1 The files were generated by users either transcribing musical scores or recording themselves playing the pieces. We use this dataset because it contains entire musical works as opposed to only segments or short melodic fragments. Moreover, it covers a broad historical range and links this study to previous research mentioned above. While the data does not conform to the high standards of scholarly editions, its quantity statistically outweighs potential errors caused by encoding, transcribing, or recording the pieces. In particular, minor errors in the encodings of musical pieces only marginally affect their pitch-class distributions and associated statistics that are the basis for this study. We inspected the dataset at random and did not find major errors such as incomplete or mislabeled pieces. In order to show chronological changes in tonality, we use the subset of 12,625 pieces (over 55 million notes) for which the year of composition is given.
Since the ClassicalArchives dataset is crowd-sourced, it is prone to certain biases. For instance, the prevalence of composers and pieces is likely to reflect contemporary rather than historical popularity. Moreover, piano compositions might be over-represented because many files have been entered by users via a MIDI keyboard. This also affects the historical balance of the data. In particular, we observe a lack of data from pre-Baroque periods in which music was predominantly vocal. Therefore, we additionally included 777 Renaissance pieces from several scholarly resources, namely from the Lost Voices project (Freedman, 2014),Footnote 2 the Citations: The Renaissance Imitation Mass project (CRIM; Freedman et al., 2017),Footnote 3 and the Electronic Locator of Vertical Interval Successions project (ELVIS; McKay and Fujinaga, 2015),Footnote 4 resulting in 12,625 + 777 = 13,402 pieces in total.
The data was subsequently converted into lists of notes from which pitch-class counts (e.g., Youngblood, 1958) were calculated for each piece, weighted by the total duration of each pitch-class. For example, if a piece contains 200 times the note F with a duration of 1/8 each, and 50 times the note C with a duration of 1/2, both would have a total duration of 25 in this weighted representation. Figure 1 shows the distribution of the pieces over time. Based on the minima of a Gaussian kernel density estimate (Bishop, 2006), shown as a smooth curve, boundaries between five time periods are determined, resulting in splits at the years 1649, 1758, 1817, and 1856. The earliest pieces have been grouped together into a single period before 1649 to reduce data sparsity. This division approximately reflects the succession of the Renaissance, Baroque, Classical, early Romantic, and late Romantic musical periods (Burkholder et al., 2014).
The data is split into periods according to the minima of a Gaussian kernel density estimate (Bishop, 2006). The boundaries are the years 1649, 1758, 1817, and 1856 (pieces prior to 1649 have been grouped into one epoch). The periods in between the boundaries correspond to the historical periods of Renaissance, Baroque, Classical, early Romantic, and late Romantic music.
A subset of 6655 pieces (49.7%) is annotated with a key label (e.g., C major or D minor) by the ClassicalArchive users. Albrecht and Shanahan (2013) estimate the accuracy of the labels to be 87.5%. We use these labels only for evaluating our model (see Section “Results and Discussion”) which operates on all 13,402 pieces (with or without key labels). In the following, we refer to key labels and years of composition as “metadata”, and to the musical pieces as “data”.
Geometric model
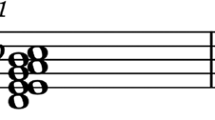
Similar to the bag-of-words model used in Natural Language Processing (Manning and Schütze, 2003), we model a musical piece as the vector of its pitch-class counts weighted by duration. Figure 2 shows the weighted pitch-class counts for an example piece in C major.
A pitch class is a set of notes which are related by multiplicities of octaves (0 represents C, 5 represents F, etc.). The diagram shows for each pitch class the sum of how often the pitches of this class appear in the piece. In this paper, musical pieces are represented by the vectors of their pitch-class counts weighted by duration. This abstraction from the order in which the notes appear in the piece is similar to the bag-of-words model used in Natural Language Processing.
This vector model is the basis of mathematical spaces in which pieces that have similar pitch-class counts are close to one another; different notions of similarity define different spaces. Mathematically, this representation allows for the application of geometrical approaches in \({{\mathbb{R}}}^{12}\) and its quotient spaces. The proposed geometric model formalizes tonality in two stages using the concepts key and mode. First, we define the key space in which pieces are close if they have similar keys and denote it by \({\mathbb{K}}\). Second, we define the mode space in which pieces are close if they have similar modes and denote it by \({\mathbb{M}}\). This approach enables a conceptualization of key and mode as related but distinct relations between pieces without assuming a specific number of keys or modes and their respective characteristics.
Since the key of a piece does not depend on the absolute frequencies of pitch classes (the length and the key of a piece are independent), the pitch-class vectors of all pieces are normalized such that each vector sums to one. This is expressed mathematically by dividing each pitch-class vector p by its sum ∑ipi (i.e., the L1 norm). We define the key-space distance of two pieces p and q as
where ∣∣ ⋅ ∣∣2 de notes the Euclidean norm, \(| | p| {| }_{2}=\sqrt{{\sum }_{i}{p}_{i}^{2}}\). Using this notion of distance, different keys emerge as clusters of pieces. Moreover, it is to be expected that keys which are close on the circle of fifths are also close in the key space because they share similar pitch-class statistics.
Under the assumption that the internal structure of a key is invariant under transposition (see Section “Assumptions and contributions”), modes correspond to invariance classes of keys. In the mode space \({\mathbb{M}}\), the distance of two pieces p and q is computed by choosing the minimum of the key distances from p to each of the twelve transpositions of q. If two pieces p and q are in the same mode, they are close with respect to the metric
where σi(p) denotes the transposition (circular shift) of p by i semitones, \({({\sigma }_{i}(p))}_{k}={p}_{(k-i\;\text{mod}\;12)}\) for \(k\in {{\mathbb{Z}}}_{12}\). Note that the mode-space distance \({d}_{{\mathbb{M}}}\) is symmetric. Analogously to the key space \({\mathbb{K}}\), modes emerge as clusters in the mode space \({\mathbb{M}}\). Note that two pieces that are far apart in the key space, such as pieces in C and F♯ major, are close in the mode space. A mathematical proof that \({\mathbb{M}}\) is a pseudometric space can be found in the Appendix.
Bayesian model
Since the size and structure of the clusters in \({\mathbb{M}}\) characterize the particular modes, we propose a generative Bayesian model for unsupervised mode learning and classification. Generally, Bayesian models are used in computational cognitive science to describe how the human mind acquires abstract symbolic knowledge inductively from the observation of examples (Chater et al., 2006; Griffiths et al., 2008; Tenenbaum et al., 2011). Bayesian statistics is expressive and powerful, because it provides a generic framework for the specification of scientific models and uses formalized plausible reasoning to implement them (Jaynes, 2003). In particular, this separation of modeling and inference facilitates the development of models tailored to the task at hand, instead of limiting scientific models to specific pre-existing algorithms (Bishop, 2013).
We propose and implement a Bayesian model that learns an abstract representation of modes from the observation of concrete musical pieces. Figure 3 shows the Bayesian network of the model that is briefly introduced in the following paragraphs; more detailed explanations can be found in the Appendix.
The Bayesian model analyzes the weighted pitch-class distributions of single pieces by re-generating them together with their roots and modes as latent variables. An inference algorithm (Gibbs sampling; described in the Appendix) is then used to infer the roots and modes of the pieces in the present dataset. In correspondence to the proposed geometric model (Section “Geometric Model”), all pieces are normalized to a common number of notes a priori. In contrast to the geometric model that represents key and mode as clusters of pieces, the Bayesian model operationalizes modes as probability distributions over pitch-class vectors. Keys are represented as pairs of a mode together with a root note, as it is also standard terminology in music theory, e.g., “A♭ major”, “B minor”. The number of different modes m, however, is not fixed but a parameter of the Bayesian model that is to be inferred.
For each time period T, the proportions of how often modes and roots are used in this period are generated first; they are denoted by θ(M) and θ(R), respectively. These proportions are later used to randomly generate modes and roots of pieces. For each mode M, a pitch-class distribution \({\theta }_{M}^{(P)}\) is generated. This distribution characterizes the internal structure of the mode (e.g., how much more or less likely a major third is than a minor third). For each piece P in the period, its mode M is sampled from θ(M) and its root R is sampled from θ(R). The pitch classes of the piece are generated by first drawing a pitch-class vector from \({\theta }_{M}^{(P)}\) and then transposing it according to the piece’s root R.
Given the present dataset D and a time period T, the posterior distribution p(R, M∣P, T, D) describes how plausible it is that a piece P has root R and mode M.Footnote 5 Since the Bayesian model represents keys as pairs of roots and modes, this distribution is called the posterior of the piece’s key. It is obtained using a Gibbs sampling method adopted from Johnson et al. (2007) and Sato (2011); see the Appendix for further explanation. The key (R*, M*) that maximizes the piece’s posterior is given by
It is called the maximum-a-posteriori estimate in the terminology of Bayesian statistics. A piece P from a time period T is then classified into the mode M* of this key.
Results and discussion
Classification results
A dimensionality reduction of the mode space \({\mathbb{M}}\) to the two-dimensional plane using t-distributed stochastic neighbor embedding (t-SNE, Van Der Maaten and Hinton, 2008) reveals a clear clustering of the pieces into several groups in the first three periods, namely four clusters in the Renaissance, two clusters in the Baroque and Classical periods, and a single large cluster in the later two periods (early and late Romantic). The columns of Fig. 4 show the different time periods, and the rows show different colorings that correspond to the classification into the modes according to different mode classification methods (metadata, Gaussian mixture model, Bayesian model) applied to the data. Each point corresponds to one piece in the dataset.Footnote 6
Each data point corresponds to a piece in the dataset. The columns represent the different time periods. The colors orange and blue correspond to major and minor, respectively. Gray corresponds to missing mode labels in the metadata. The coloring in the top row shows the key labels from the metadata. It approximately corresponds to the clusters in the reduced space. The middle row is colored according to the classification of a Gaussian mixture model (GMM) in the reduced space. The bottom row is colored according to the unsupervised Bayesian mode classifier which successfully learns the concepts of major and minor purely data-driven from the pitch-class counts of the pieces. In particular, the labeling of the Bayesian model corresponds to the geometrical positions of the pieces without using these distances for classification. This indicates that transpositional invariance is a characterizing property of the concept of mode.
Clustering according to metadata labels
The first row displays the key labels from the metadata for the five periods. Note that the earliest epoch, the Renaissance, contains almost no pieces with key labels in the metadata; most pieces are colored in gray. For the following two periods, Baroque and Classical, the coloring by the labels in the metadata and the clustering obtained by t-SNE are aligned: one cluster is largely orange and the other one is largely blue. This correspondence induced by the metadata indicates that the clusters in the Baroque and the Classical period represent the major and the minor mode (shown in orange and blue, respectively). This bipartition into two modes reflects a pillar of Common-Practice tonality. In contrast, no clear distinction into different modes exist in the Romantic periods; pieces with major and minor metadata labels are mixed together, along with a relatively large number of unlabeled pieces. Hence, the metadata labels suggest that the binary classification of pieces into “major” and “minor” is less adequate for the 19th century.
Gaussian mixture model
The second row of Fig. 4 displays clusterings by mixtures of two-dimensional Gaussian distributions, a so-called Gaussian Mixture Model (GMM, see e.g., MacKay, 2003), for each period. Such models explain data by optimally covering the data points using multidimensional bell curves. In our application, each mode corresponds to one bell curve, and a piece is classified into the mode whose bell curve it is covered with.Footnote 7 In order to obtain the optimal number of bell curves and thus the optimal number of modes for a given historical period, silhouette scores (Rousseeuw, 1987) were calculated for all possible numbers of modes between 2 and 6. Silhouette scores are a standard measure to quantify the visual impression of the appropriateness of different numbers of clusters mode generally.Footnote 8 Table 1 lists the silhouette scores for all five periods. These numbers largely confirm the visual impression of Fig. 4. For the Renaissance, a clustering of the data into four modes is most appropriate. The division into two clusters achieves the highest silhouette scores in the Baroque, Classical and early Romantic periods, while the optimal number of clusters is three in the last period. Furthermore, the separation between clusters is clearest in the Classical era, as expressed by the largest difference between the highest two silhouette scores for this time period (0.460 − 0.402 = 0.058), in which the corresponding silhouette score reaches the maximum over all periods and number of modes. The indication for two modes is thus strongest in the Classical and the Baroque periods, again confirming that the Common-Practice period is largely determined by the usage of the major and the minor modes. Three modes achieve the highest silhouette score in the late Romantic period, questioning this clear separation. These results suggest that the two modes shape the tonal structure of pieces only for the Baroque and Classical eras, at least from the global perspective of pitch-class distributions that abstracts from local keys and modulations.
The results of the geometric model exhibit a strong similarity to the classification based on the metadata in the first row which suggests the same interpretation: in the Baroque and Classical periods, the space is well separable into two modes which does not hold for the Renaissance and the Romantic periods. The mixture of Gaussian distributions moreover classifies one of the larger clusters in the Renaissance as minor (blue) and the second large, as well as the two smaller clusters as major (orange). Since there is no corresponding metadata for this period, we can not evaluate the mode classification on that basis but will inspect the modes in this period in more detail below (Section “Characteristics of modes”). While music-theoretical conceptions of Common-Practice tonality are largely corroborated by these mode classifications according to the metadata and the GMM, it is important to recall that the former is highly uncertain because the labeling in the metadata might be erratic. The latter classification by the GMM is uncertain because it has been performed in a dimensionality-reduced space, and this transformation might have affected the underlying similarities between the pitch-class distributions of musical pieces. In order to overcome this limitation and to derive a more appropriate mode classification for all periods, we introduce a Bayesian classifier that operates in the original, unreduced mode space \({\mathbb{M}}\).
Bayesian model
Based on the overall best silhouette scores for two modes (see Table 1), the mode predictions of the Bayesian model are shown by the coloring in the third row of Fig. 4; the appropriateness of major-minor classifications in the Renaissance will be considered below (Section “Characteristics of modes”). This classification into two modes closely resembles the partition by the GMM in all periods except in the Classical, where the Bayesian model is more exact. In other words, both the two-dimensional reduction via t-SNE (cluster shapes) and the unsupervised Bayesian mode classifier (coloring in the third row of Fig. 4) independently assign the musical pieces to one of the two modes in a similar manner. It is important to note that this agreement between the GMM and the Bayesian model is not trivial but a result of the close correspondence between the notion of distance in the mode space and the interaction of the Bayesian model’s distributions. The binary separation into major and minor is particularly strong in the Baroque and Classical periods for both methods, whereas the Renaissance and Romantic periods are somewhat more mixed for the Bayesian classifier.
Mode clarity
To quantify the visual impression that the binary separation into major and minor is particularly strong in the Baroque and Classical periods, we define the mode clarity of a time period as the proportion of correctly predicted modes according to the metadata. Figure 5 visualizes the estimated mode clarity for each period. The mode clarity of the Renaissance period is not well quantifiable due to the small amount of key labels in the metadata. Nonetheless, it is lowest among all periods. The mode clarity is highest in the Classical period and significantly higher for the Baroque and the Classical period than for the Romantic periods. This finding underpins again the evidence for two clusters of major and minor pieces in the Baroque and the Classical period. Furthermore, it validates that the binary distinction between major and minor pitch distributions are less adequate to characterize the tonality of Romantic music. In other words, the concepts “major” and “minor” as distinct global modes of musical pieces is much less appropriate in the Romantic eras.
The error bars show 95% bootstrap confidence intervals. The values confirm the clear distinction between major and minor in the Baroque and the Classical period. In the Romantic periods, this separation is still existent, but not as clear as before. The mode clarity of the Renaissance period is not quantifiable due to the small amount of pieces in this period.
Characteristics of modes
The Renaissance
As stated above, the mode clarity for the Renaissance is difficult to interpret because of lacking metadata. Moreover, the silhouette scores (see Table 1) clearly show that the pieces in this period group together in four and not only two clusters. We thus applied the Bayesian model to the pieces in this period separately, assuming the existence of four clusters. The result is shown in the coloring of Fig. 6, showing a large coherent cluster (red), a large mixed cluster (green and blue), as well as two small clusters (both violet). Recall that the clustering is a result of the dimensionality reduction and that the coloring expresses the similarity of pieces in the original mode space, in which the pieces of the two violet clusters are actually close to each other and the pieces in the green-blue cluster are actually separated. This provides further evidence that clustering the pieces in the reduced space with a GMM is not sufficient and again justifies the application of the Bayesian model for mode classification.
The clustering reveals one distinct mode (red), two very similar modes (blue, green), and another mode distinct from the others (violet). Note that the latter is separated into two subclusters after dimensionality reduction. In the original mode space, the pieces in the two violet clusters are all close to each other.
Since we cannot compare this clustering to the labels in the metadata, we inspect the pitch-class distributions of these four clusters separately and display them in so-called violin plots (see Fig. 7). Each of the violins depicts a kernel density estimation for the relative frequencies of the respective pitch classes in one of the four clusters. We manually added a threshold of 5% (dashed horizontal line) to distinguish between pitch classes belonging to our mode interpretations of the clusters and out-of-scale tones. The distributions of pitch classes within the respective clusters resemble music-theoretical descriptions of Renaissance modes (see Glareanus, 1547; Huron and Veltman, 2006; Judd, 2002). The first cluster (top row, violet) resembles the Mixolydian mode, the second cluster (second row, red) resembles the Ionian mode, the third cluster (third row, blue) resembles the Dorian mode, and the fourth cluster (bottom row, green) could be interpreted as a mode between the Aeolian and Dorian modes, lacking a clear expression of either pitch class 8 or 9 to distinguish them. Note, however, that our Bayesian classifier transposes all pieces to a common root, based on the assumption of transpositional invariance (see Section “Assumptions and contributions”). The results should therefore be interpreted with care since Renaissance composers did not transpose modes to arbitrary roots; rather the different modes were associated with specific absolute pitches as roots (Judd, 2002; Wiering, 2001).
The distribution of the first cluster (violet) resembles the Mixolydian mode, the second cluster (red) resembles the Ionian mode. The two remaining clusters (blue and green) exhibit relatively similar pitch-class distributions that resemble the Dorian mode. The fourth cluster (green) could also be interpreted as Aeolian.
The common-practice period
Both the silhouette scores (Table 1) and the mode clarities (Fig. 5) are clearest for the Common-Practice period, covering the Baroque and Classical periods. Figure 8 shows the distributions of each of the twelve pitch classes inferred via the Bayesian model for both modes (major and minor). The fact that the maxima of the distributions fall either above or below a threshold around five percent reflects the music-theoretical distinction between in-scale and out-of-scale notes (Lerdahl, 2001). The value of this threshold might be specific to the dataset we used. It is, however, interesting that there is a threshold separating in-scale from out-of-scale pitch classes so clearly. The variance of the distributions moreover differs across pitch classes and modes. Generally, it is smaller for of out-of-scale notes than for in-scale notes, expressing that out-of-scale notes are typically rarely used, while in-scale notes have a greater degree of freedom in their use in musical pieces.
The classification was performed by the Bayesian mode classifier. Each half violin shows a Gaussian kernel density estimate of the distribution over the respective pitch-class probabilities. For each pitch class, the areas of the two respective violin halves are equal. The maxima of all violins are scaled to a common size. The dotted line at the relative frequency of 5% was added post hoc to separate in-scale tones (density maximum above the line) from out-of-scale tones (density maximum below the line).
The characteristics of a mode can be summarized in its average pitch-class distribution (henceforth mode template). For example, drawing on traditional definitions of major and minor (e.g., Aldwell and Schachter, 2003) one would expect that both the major and the minor mode have similar characteristics for their roots and fifths (pitch classes 0 and 7), but contrasting characteristics for their thirds (pitch classes 3 and 4) and sixths (pitch classes 8 and 9). Commonly, such mode templates are reported as line or bar plots and show absolute or relative estimated or counted frequencies. Unfortunately, they rarely show an appropriate measure of the underlying variance of the distributions as in Fig. 8. In order to directly compare our results with previously published mode templates, we reduce the representation of the characteristics of the major and minor mode from the full distributions to only their maxima. Figure 9 compares the mode templates of the unsupervised Bayesian classification (Bayesian Model) to templates presented in previous research, in particular to templates based on data from psychological experiments (Krumhansl and Kessler, 1982 and Temperley, 2001), as well as to templates derived from corpus statistics (Metadata and Albrecht and Shanahan, 2013). In contrast to the earlier studies, we propose to use so-called radar plots that capture the circular structure of the pitch space (Harasim et al., 2016; Lerdahl, 2001) as opposed to the more common linear arrangement of mode templates. Moreover, pitch classes are not ordered chromatically ascending (see Fig. 8) but along the circle of fifths. This makes it possible to better reflect that in-scale and out-of-scale pitch classes form consecutive parts of the circular space, respectively (Carey and Clampitt, 1989).
The distance to the origin represents the probability of each pitch class. For each source, the pitch classes are ordered in the circle of fifths so that in-scale tones and out-of-scale tones are adjacent. The corpus-generated templates (Metadata, Byesian Model, and Albrecht and Shanahan, 2013) assign much less probability mass to out-of-scale notes than the experiment-based templates (Krumhansl and Kessler, 1982 and Temperley, 2001).
The corpus-driven templates assign less probability mass to out-of-scale notes than the experimental templates, supporting the music-theoretical concept of mode. Moreover, all corpus-driven templates further clearly exhibit the symmetry between major and minor mode. In all templates, the most distinctive pitch classes for the two modes are 3 and 4, the minor and major thirds, underpinning the music-theoretical definition of the two modes.
The close resemblance of the mode templates inferred by our Bayesian model to the other corpus-derived templates confirms that the two modes indeed correspond to the major and minor modes but establishes that neither their existence nor their particular shapes need to be assumed a priori; it is possible to infer them from a corpus of musical pieces in a data-driven, unsupervised fashion.
Conclusion
We investigated the evolution of tonality over time by inspecting a large dataset of MIDI-encoded pieces, covering a historical range of approximately 500 years. Unlike previous music-theoretical studies, which draw on complex analytical methods and a host of prior assumptions, we adopt simple statistical models of pitch-class distributions and propose a novel Bayesian generative model that only takes into account a “bag-of-notes” representation of the pitch classes in the pieces. We find that basic pitch statistics suffice to reveal, in an unsupervised way, the number of modes and their characteristic shapes for a given period of time. We did not assume the number and shape of the modes in advance in order to remove potential biases towards the major-minor tonality as described by music theory (Aldwell and Schachter, 2003; Kostka and Payne, 2013). The results therefore provide strong support for cognitive theories on mode inference via statistical learning (Huron, 2006; Rohrmeier and Rebuschat, 2012; Saffran, 2003; Tillmann, 2012), based on pitch-class frequencies in musical pieces.
Both the geometric and the probabilistic model reveal a similar pattern: modes can be predicted best for the Classical period, second best for the Baroque, and worst for the 19th century and the Renaissance. The two modes that emerge and stabilize over time in the Common-Practice period indeed correspond to the well-known major and minor modes. Applying the same methodology to the Renaissance separately shows that a larger number of independent modes is more appropriate. However, this needs to be studied in more detail in future research, since our fundamental assumption of transpositional invariance seems least appropriate for this era. The poor prediction for the 19th century can be interpreted to reflect the substantial changes in tonality that took place over the course of the 19th century (Meyer, 1989), such as the use of new types of scales, as well as of pitch and harmonic relations (Aldwell and Schachter, 2003; Cohn, 2012; Haas, 2004). It moreover suggests that the concept of a single global mode for 19th-century pieces is much less suitable for this time period, likely due to more frequent local modulations to more distantly-related keys.
Our approach provides an avenue for data-driven corpus research to become a foundation for the empirical study of the historical evolution of tonality. The outcomes of this study open up several directions for future research. Especially the application of hierarchical models and mixture models seems to be very promising in order to draw more fine-grained conclusions about the relative importance of modes and the development of tonality not only on the global but also on more local and intermediate levels of a composition (Lieck and Rohrmeier, 2020). While the dataset used in this study only allows the distinction between twelve pitch classes, Lieck et al. (2020) have recently shown that the incorporation of algebraic models of tonal spaces can be used for more structured representations of of pitch-class distributions of musical pieces. They provide initial evidence that this is also relevant for historical changes of tonality which suggests to further explore the implications of this approach. The expansion of the historical extent of the database used for this study—potentially increasing the range from medieval to contemporary popular music—will broaden the horizon of the empirical historiography of tonality. The models proposed in this article can generally be applied to any musical style for which the representation by pitch classes is adequate and are thus not strictly limited to the study of Western classical music. They might thus be adopted to compare pitch-class distributions not only within but also between musical cultures. This might, in turn, potentially contribute to ongoing debates between biological (e.g., Honing et al., 2015; Merker et al., 2014; Wiggins et al., 2015) and cultural (e.g., Mehr et al., 2019; Nettl, 2001; Savage, 2019) approaches to the evolution of music.
Data availability
The data for this article and the code to reproduce the results are published at https://github.com/DCMLab/HistoryModes_DataCode).
Notes
http://crimproject.org/. From this collection, we excluded six pieces between the 11th and 14th centuries because they had uncertain publication dates and were historically too remote from the rest of the Renaissance pieces (16th century).
Since keys are defined as pairs (R, M), this is effectively a key-finding method. In this study, however, we focus only on the modes.
Note that with this dimensionality reduction method the relative within-cluster and between-cluster distances are more interpretable than the absolute positions of data points in the plane.
Note a potential conflict of terminology: "mode” can be either understood as a system governing the relations between notes in musical pieces, or as the locally or globally most likely value of a probability distribution. Here, we only use mode in the former sense.
The optimal number of clusters K was determined in the reduced space by clustering the data with a Gaussian mixture model (GMM) for different values of K between 2 and 6 and calculating silhouette scores of these different clusterings, independently for each period. Silhouette scores quantify the visual impression of the appropriateness of different numbers of clusters. To explain their calculation, let x be a data point classified into the cluster C and denote the average distance from x to all other points in C of x by a(x). The value a(x) is minimal when x is in the center of C. The dissimilarity of x to any other cluster \(C^{\prime}\) is given by the average distance between x and all points in \(C^{\prime}\). Denote the smallest of these similarities by b(x). The silhouette score of the data point x is then given by
$$s(x)=\frac{b(x)-a(x)}{\max \{a(x),b(x)\}}.$$The silhouette score of a cluster is defined as the average silhouette score of all its points and the silhouette score of a clustering is defined as the average silhouette of all its clusters. The silhouette score of a clustering is therefore an indicator of how well the data points are assigned to the different clusters.
References
Albrecht JD, Shanahan D (2013) The use of large corpora to train a new type of key-finding algorithm: an improved treatment of the minor mode. Music Percept 31(1):59–67
Albrecht JD, Huron D (2014) A statistical approach to tracing the historical development of major and minor pitch distributions, 1400-1750. Music Percept 31(3):223–243
Aldwell E, Schachter C (2003) Harmony and voice leading, 3rd edn. Wadsworth Group/Thomson Learning, Belmont
Bharucha JJ, Krumhansl CL (1983) The representation of harmonic structure in music: hierarchies of stability as a function of context. Cognition 13(1):63–102
Bishop CM (2006) Pattern recognition and machine learning. Springer, London
Bishop CM (2013) Model-based machine learning. Phil Trans R Soc A 371. https://doi.org/10.1098/rsta.2012.0222
Burkholder PJ, Grout, DJ, Palisca CV (2014) A history of western music, 9th edn. Norton, New York and London
Butler D, Brown H (1994) Describing the mental representation of tonality in music. In: Aiello R, Sloboda JA (eds) Musical Perceptions. Oxford University Press, New York, pp. 191–212
Carey N, Clampitt D (1989) Aspects of well-formed scales. Music Theory Spectr 11(2):187–206
Chafe E (1992) Monteverdi’s tonal language. Schirmer books, New York
Chater N, Tenenbaum JB, Yuille A (2006) Probabilistic models of cognition: conceptual foundations. Trends Cogn. Sci. 10(7):287–291
Cohn R (2012) Audacious euphony: chromatic harmony and the triad’s second nature. Oxford University Press, Oxford
Cornelissen B, Zuidema W, Burgoyne JA (2020) Mode Classification and Natural Units in Plainchant. In: Proceedings of the 21st International Society for Music Information Retrieval Conference, Montréal, Canada
Dahlhaus, C (1968) Untersuchungen über die Entstehung der harmonischen Tonalität. Saarbrücker Studien zur Musikwissenschaft. Bärenreiter, Kassel
Dahlhaus C, Anderson J, Wilson C, Cohn R, Hyer B (2001) Harmony. In: Sadie S, Tyrrell J (eds) The New Grove Dictionary of Music and Musicians, 2nd edn. Macmillan Publishers, London, pp. 858–877
Freedman R (2014) The Renaissance chanson goes digital: digitalduchemin.org. Early Music 42(4):567–578
Freedman R, Viglianti R, Crandell A (2017) The collaborative musical text. Music Ref Serv Quart 20(3-4):151–167
Fétis F-J (1844) Traité complet de la theorie et de la pratique de l’harmonie, 2nd edn. Eugéne Duverger
Glareanus H (1547) Dodekachordon. Basel, Switzerland
Griffiths TL, Kemp C, Tenenbaum JB (2008) Bayesian models of cognition. In: Sun R (ed) The Cambridge Handbook of Computational Cognitive Modeling. Cambridge University Press, Cambridge
Gárdonyi Z, Nordhoff H (2002) Harmonik. Möseler Verlag, Wolfenbüttel
Haas B (2004) Die neue Tonalität von Schubert bis Webern: Hören und Analysieren nach Albert Simon. Noetzel F, Wilhelmshaven
Harasim D, Schmidt SE, Rohrmeier M (2016) Bridging scale theory and geometrical approaches to harmony: the voice-leading duality between complementary chords. J Math Music 10(3):193–209
Honing H, ten Cate C, Peretz I, Trehub SE (2015) Without it no music: cognition, biology and evolution of musicality. Phil Trans R Soc B 370. https://doi.org/10.1098/rstb.2014.0088
Huang P, Wilson M, Mayfield-Jones D, Coneva V, Frank M, Chitwood DH (2017) The evolution of Western tonality: a corpus analysis of 24,000 songs from 190 composers over six centuries. preprint, SocArXiv. https://doi.org/10.31235/osf.io/btshk
Huron D (2006) Sweet anticipation. Music and the psychology of expectation. MIT Press, Cambridge, pp. 33–35
Huron D, Parncutt R (1993) An improved model of tonality perception incorporating pitch salience and echoic memory. Psychomusicology 12(2):154–171
Huron D, Veltman J (2006) A cognitive approach to medieval mode: evidence for an historical antecedent to the major/minor system. Empirical Musicol Rev 1(1):33–55
Hyer B (2001) Tonality. In: Sadie S, Tyrrell J (eds) The new grove dictionary of music and musicians. 2nd edn. Macmillan Publishers, London, pp. 583–594
Janata P, Birk J, Horn JV, Leman M, Tillmann B, Bharucha JJ (2002) The cortical topography of tonal structures underlying Western music. Science 298(5601):2167–2170
Jaynes ET (2003) Probability theory: the logic of science. Cambridge University Press, Cambridge
Johnson M, Griffiths T, Goldwater S (2007) Bayesian inference for PCFGs via Markov chain Monte Carlo. In: Human Language Technologies 2007: The Conference of the North American Chapter of the Association for Computational Linguistics; Proceedings of the Main Conference, Rochester, New York, pp. 139–146
Judd CC (2002) Renaissance modal theory: theoretical, compositional, and editorial perspectives. In: Christensen T (ed) The Cambridge History of Western Music Theory. Cambridge University Press, Cambridge, pp. 364–406
Knopoff L, Hutchinson W (1983) Entropy as a measure of style: the influence of sample length. J Music Theory 27(1):75–97
Koelsch S, Rohrmeier M, R T, Jentschke S (2013) Processing of hierarchical syntactic structure in music. Proc Natl Acad Sci USA 110(38):15443–8
Kostka S, Payne D (2013) Tonal harmony. McGraw-Hill Higher Education, New York
Krumhansl CL (1990) Cognitive foundations of musical pitch. Oxford University Press, New York
Krumhansl CL (2004) The cognition of tonality—as we know it today. J New Music Res 33(3):253–268
Krumhansl CL, Cuddy LL (2010) A theory of tonal hierarchies in music. Music Percept 36:51–87
Krumhansl CL, Kessler EJ (1982) Tracing the dynamic changes in perceived tonal organization in a spatial representation of musical keys. Psychol Rev 89(4):334–368
Large EW, Kim JC, Flaig NK, Bharucha JJ, Krumhansl CL (2016) A neurodynamic account of musical tonality. Music Percept 33(3):319–331
Lerdahl F (2001) Tonal pitch space. Oxford University Press, Oxford
Lieck R, Moss FC, Rohrmeier M (2020) The Tonal Diffusion Model. Trans Intl Soc Music Info Retrv 3(1):153–164
Lieck R, Rohrmeier M (2020) Modelling hierarchical key structure with pitch scapes. In: Proceedings of the 21st International Society for Music Information Retrieval Conference, Montréal, Canada
Long MK (2020) Hearing homophony. Oxford University Press, Oxford
MacKay D (2003) Information theory, inference and learning algorithms. Cambridge University Press, Cambridge
Manning C, Schütze H (2003) Foundations of statistical natural language processing, 6th edn. MIT Press, Cambridge
McClary S (1976) The Transition from Modal to Tonal Organization in the Works of Monteverdi. Dissertation, Harvard University
McKay C, Fujinaga I (2015) Building an Infrastructure for a 21st-Century Global Music Library. In: Extended Abstracts for the Late-Breaking Demo Session of the 16th International Society for Music Information Retrieval Conference, Málaga, Spain
Mehr SA, Singh M, Knox D et al. (2019) Universality and diversity in human song. Science 366(6468). https://doi.org/10.1126/science.aax0868
Merker B, Morley I, Zuidema W (2014) Five fundamental constraints on theories of the origins of music. Phil Trans R Soc B 370. https://doi.org/10.1098/rstb.2014.0095
Meyer LB (1957) Meaning in music and information theory. J Aesthet Art Crit 15(4):412–424
Meyer LB (1989) Style and music. theory, history, and ideology. University of Chicago Press, Chicago
Moss FC (2019) Transitions of tonality: a model-based corpus study. Dissertation, École Polytechnique Fédérale de Lausanne, Switzerland
Moss FC, Neuwirth M, Harasim D, Rohrmeier M (2019) Statistical characteristics of tonal harmony: a corpus study of Beethoven’s string quartets. PLoS ONE 14(6):e0217242
Nettl B (2001) An ethnomusicologist contemplates universals in musical sound and musical culture. In: Wallin NL, Merker B, Brown S (eds) The origins of music. MIT Press, Boston
Neuwirth M, Rohrmeier M (2016) Wie wissenschaftlich muss Musiktheorie sein? Chancen und Herausforderungen musikalischer Korpusforschung. Zeitschrift der Gesellschaft für Musiktheorie [Journal of the German-Speaking Society of Music Theory] 13:171–193
Parncutt R (2015) Understanding major-minor tonality: humanities meet Sciences. In: Ginsborg J, Lamont A, Phillips M, Bramley S (eds) Proceedings of the 9th Triennial Conference of the European Society for the Cognitive Sciences of Music, Manchester
Pearce M, Rohrmeier M (2012) Music cognition and the cognitive sciences. Top Cogn Sci 4(4):468–484
Pearce MT (2018) Statistical learning and probabilistic prediction in music cognition: mechanisms of stylistic enculturation. Ann NY Acad Sci 1423:378–395
Quinn I, White CW (2017) Corpus-derived key profiles are not transpositionally equivalent. Music Percept 34(5):531–540
Rameau JP (1722) Traité de l’harmonie réduite à ses principes naturels. Imp de Ballard JBC
Riemann H (1893) Vereinfachte Harmonielehre oder Die Lehre von den Tonalen Funktionen der Akkorde. Augener, London
Rodrigues Zivic PH, Shifres F, Cecchi GA (2013) Perceptual basis of evolving Western musical styles. Proc Natl Acad Sci USA 110(24):10034–10038
Rohrmeier M, Cross I (2008) Statistical Properties of Tonal Harmony in Bach’s Chorales. In: Miyazaki K (ed) Proceedings of the 10th International Conference on Music Perception and Cognition, Sapporo, Japan, pp. 619–627
Rohrmeier M, Cross I (2009) Tacit tonality: Implicit learning of context-free harmonic structure. In: Louhivuori J, Eerola T, Saarikallio S et al. (eds) Proceedings of the 7th Triennial Conference of the European Society for the Cognitive Sciences of Music, Jyväskylä, Finland, pp. 443–452
Rohrmeier M, Rebuschat P (2012) Implicit learning and acquisition of music. Top Cogn Sci 4(4):525–53
Rousseeuw PJ (1987) Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J Comput Appl Math 20:53–65
Saffran JR (2003) Musical learning and language development. Ann NY Acad Sci 999(1):397–401
Sato T (2011) A general MCMC method for Bayesian inference in logic-based probabilistic modeling. In: Proceedings of the 22nd International Joint Conference on Artificial Intelligence. pp. 1472–1477
Savage PE (2019) Cultural evolution of music. Pal Commun 5(1):16
Savage PE, Brown S, Sakai E, Currie TE (2015) Statistical universals reveal the structures and functions of human music. Proc Natl Acad Sci USA 112(29):8987–8992
Schoenberg A (1969) Structural functions of harmony. Faber and Faber, London
Snyder JL (1990) Entropy as a measure of musical style: the influence of a priori assumptions. Music Theory Spectr 12(1):121–160
Temperley D (2001) The Cognition of Basic Musical Structures. MIT Press, Cambridge, MA
Temperley D (2009) A statistical analysis of tonal harmony. http://davidtemperley.com/kp-stats/. Accessed 3 Nov 2020
Temperley D, Marvin EW (2008) Pitch-class distribution and the identification of key. Music Percept 25(3):193–212
Tenenbaum JB, Kemp C, Griffiths TL, Goodman ND (2011) How to grow a mind: statistics, structure, and abstraction. Science 331(6022):1279–1285
Tillmann B (2005) Implicit investigations of tonal knowledge in nonmusician listeners. Ann NY Acad Sci 1060:100–10
Tillmann B (2012) Music and language perception: expectations, structural integration, and cognitive sequencing. Top Cogn Sci 4(4):568–84
Tillmann B, Bharucha JJ, Bigand E (2000) Implicit learning of tonality: a self-organizing approach. Psychol Rev 107(4):885–913
Tillmann B, Janata P, Birk J, Bharucha JJ (2008) Tonal centers and expectancy: facilitation or inhibition of chords at the top of the harmonic hierarchy? J Exp Psychol Hum Percept Perform 34(4):1031–43
Tymoczko D (2006) The geometry of musical chords. Science 313(5783):72–74
Van Der Maaten L, Hinton G (2008) Visualizing data using t-SNE. J Mach Learn Res 9:2579–2605
Viro V (2011) Peachnote: Music score search and analysis platform. In: Proceedings of the 12th International Society for Music Information Retrieval Conference. pp. 359–362
Weiß C, Mauch M, Dixon S, Müller M (2019) Investigating style evolution of Western classical music: a computational approach. Musicae Scientiae 23(4):486–507
White CW (2013) Some statistical properties of tonality, 1650–1900. Dissertation, Yale University
White CW, Quinn I (2016) The Yale-classical archives corpus. Empir Musicol Rev 11(1):50–58
Wiering F (2001) The language of the modes: studies in the history of polyphonic modality. Routledge, New York and London
Wiggins GA, Tyack P, Scharff C, Rohrmeier M (2015) The evolutionary roots of creativity: mechanisms and motivations. Phil Trans R Soc B 370(1664):20140099
Wright AA, Rivera JJ, Hulse SH, Shyan M, Neiworth JJ (2000) Music perception and octave generalization in Rhesus Monkeys music perception and octave generalization in Rhesus Monkeys. J Exp Psychol 129(3):291–307
Youngblood JE (1958) Style as information. J Music Theory 2(1):24–35
Yust J (2019) Stylistic information in pitch-class distributions. J New Music Res 48(3):217–231
Zatorre RJ, Salimpoor VN (2013) From perception to pleasure: music and its neural substrates. Proc Natl Acad Sci USA 110(2):10430–10437
Acknowledgements
This project has received partial funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program under grant agreement No 760081-PMSB. It was also partially funded through the Swiss National Science Foundation within the project “Distant Listening - The Development of Harmony over Three Centuries (1700–2000)”. We thank Claude Latour for supporting this research through the Latour Chair in Digital Musicology. We want to express our gratefulness towards the owners of ClassicalArchives, in particular Pierre R. Schwob, for making the data available for our research. We also thank the team of the Digital and Cognitive Musicology Lab (DCML), particularly Markus Neuwirth, for their helpful comments on earlier versions of this paper. Furthermore, we thank Timothy O’Donnell for fruitful discussions on the computational models developed in this paper.
Author information
Authors and Affiliations
Contributions
DH, FCM, and MRa designed research and analyzed data; DH preprocessed data and performed Bayesian computation; MRo supervised the research and all authors were involved in writing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
41599_2020_678_MOESM1_ESM.tex
Exploring the foundations of tonality: Statistical cognitive modeling of modes in the history of Western classical music (Appendix)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Harasim, D., Moss, F.C., Ramirez, M. et al. Exploring the foundations of tonality: statistical cognitive modeling of modes in the history of Western classical music. Humanit Soc Sci Commun 8, 5 (2021). https://doi.org/10.1057/s41599-020-00678-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1057/s41599-020-00678-6