Introduction

Hypoid gears are widely used to transfer power between two non-intersecting crossed axes, mostly found in the front and the rear axles of all-wheel-drive vehicles or in the rear axles of rear-wheel-drive ones1,3. Furthermore, most hypoid gears are manufactured by either the face-milling method or the face-hobbing method2,3,4. The face-milling method mainly depends on local syntheses5,6,7,8, which predetermine the contact characteristics of the pinion and the gear at a mean point, including the direction of the contact path. Besides determining the contact characteristics around the mean point, Wu et al.9 presented a theory for the function-oriented design of point contact tooth surfaces. The theory was applied to determine the contact path, major axial length of the instantaneous contact ellipse, and higher-order acceleration as required. Compared with the face-milling method, the face-hobbing method only considers the first-order parameters at the mean point in computing the machine tool settings, such as the position of the reference point, pressure angle, and spiral angle at the reference point; nevertheless, it does not consider the contact path10. To guarantee the quality of hypoid gears, various strategies, including higher-order modifications to correct the tooth flank form machining errors11,12, ease-off flank modifications for tooth correction and meshing performance improvement13,14,15, and multi-objective tooth optimization with modification-based loaded tooth contact analysis to improve the overall meshing quality16,17 have been proposed. However, most of them are based on Gleason’s hypoid generator.

There are three common face-hobbing systems for computing the machine tool settings for hypoid gears, including Klingelnberg’s CycloPalloid system, Oerlikon’s Spirac and Spiroflex systems, and Gleason’s Phoenix system4,18. In the Spiroflex system, the pinion and the gear are cut using the generated method; the contact paths on the concave and convex tooth surfaces of the gear are approximately symmetrical, and the instantaneous contact ellipses at the reference point are also symmetrical. However, in the Spirac system, the pinion is cut by the generated method, the gear is cut by the nongenerated method (which enhances production), and the symmetry of the contact paths cannot be guaranteed. Consequently, the contact paths must be modified artificially and repeatedly by correcting the machine tool settings during the tooth contact analysis. The Spirac system is applicable under two conditions for the hypoid gears: when the transmission ratio is greater than or equal to 3 and when the pitch angle of the gear is greater than or equal to 60°10. Generally, the hypoid gears cut by the Spirac system are called Spirac hypoid gears. For Spirac hypoid gears, few studies have been conducted to develop a universal hypoid generator mathematical model19, a flank-correction methodology from the six-axis Cartesian-type CNC hypoid generator18, anew analytical method for the basic machine tool settings to realize conjugated action20, an active tooth surface–design methodology based on coordinate measurements21, etc.

The contact path is one of the dominant factors governing the load behaviors of hypoid gears 10. In this paper, a new method is proposed to calculate the machine tool settings for Spirac hypoid gears. It controls the direction angles of the contact paths to be equated to achieve symmetrical contact paths on both tooth surfaces of the gear. Furthermore, the relation between the direction angles is formulated, the influence of the angular setting of the pinion head cutter on the contact paths is determined, and the equations to solve for the values of the machine tool settings are derived. The computation is tested using a numerical example.

Theoretical background

In the face-hobbing method, the cutting of tooth surfaces is a continuous indexing process. As shown in Fig. 1, the concave and convex tooth surfaces of a tooth slot are manufactured simultaneously using blade groups12. Each blade group contains an inside blade and an outside one, which are placed at the same reference circle on the pitch plane of the head cutter. In the face-hobbing method, the traces of the cutting edges of the head cutter blades form the teeth of virtual generating gear. The curve of the tooth trace of the generating gear forms an extended epicycloid.

Figure 1
figure 1

Face-hobbing method.

Full size image

In the generated method, two sets of related motions are defined: the relative rotation between the head cutter and the blank, and the rolling (or generating) motion, corresponding to the relative rotation between the virtual generating gear and the blank. In the nongenerated method, which is usually applied to the gear, only the indexing motion is considered.

Generation of the gear tooth surface

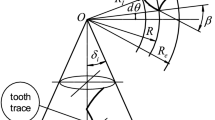
When the gear is cut by the nongenerated method, the trace of the blade on the blank is the tooth surface of the gear. Figure 2 shows the relative position between the head cutter and the gear with the right-hand teeth. The reference plane, T, is the basis of the relative position between the gear and the generating gear. P0 is the pitch point of the blades and its distance to the axis of the head cutter is the nominal cutter radius (r0). T0 is a plane parallel to plane T and that passes through point P0 with the addendum modification (hx2). T′ is a plane perpendicular to the axis of the head cutter and rotating about point P0 by tilt angle of the head cutter (χ2). M is the reference point of either the pinion or the gear. In order to accommodate the correct orientation with respect to the cutting motion vector, the effective cutting direction of the blades in the head cutter is not perpendicular to the cutter radius vector. δ02 is the angle between the cutting direction of the blade and the cutter radius vector. βm2 is the mean spiral angle of the gear at point M. Rm2 is the gear cone distance of point M. rm2 is the radius of the reference circle at point M. δM2 is the gear installment angle. When angle δM2 equals the gear pitch angle δ2, origin Op coincides with the gear pitch cone apex O′2.

Figure 2
figure 2

Relative position between the head cutter and the gear with the right-hand teeth.

Full size image

Coordinate system S(O; i, j, k) is rigidly connected to the head cutter, where origin O is at the intersection point of plane T′ and the axis of the head cutter, axis i directs to point P0, and axis k coincides with the axis of the head cutter. Coordinate system S0(O’0; i0, j0, k0) is an auxiliary coordinate system, where origin O’0 is at the intersection point of plane T0 and the axis of the head cutter, axis i0 directs to point P0, and axis k0 is perpendicular to plane T0. Origin O0 is at the intersection point of plane T and axis k0, initially located based on the radial setting (Ex2) and the angular setting (q2) in coordinate system Sp(Op; ip, jp, kp). Axis ip passes through point M, and axis kp coincides with axis k0. Coordinate system S2(O″2;i2, j2, k2) is rigidly connected to the gear, where origin O″2 is at the center of the reference circle of the gear; axis i2 passes through point M, axis j2 coincides with axis jp, and axis k2 coincides with the axis of the gear and points to the heel.

The trace of the cutting edge of the head cutter blade is presented in coordinate system S (rigidly connected to the head cutter) by the vector-parametric equation (fully described in Reference22):

$$\left({{\varvec{R}}}_{2}\right)={\varvec{O}}{{\varvec{P}}}_{0}+{{\varvec{P}}}_{0}{\varvec{Q}}={{\varvec{R}}}_{2}\left({u}_{2},{\psi }_{2},{\alpha }_{2}\right),$$
(1)

Where (R2) is a position vector of an arbitrary point of the trace of the cutting edge; u2 is the distance from the intersection point of the edge of the blade and plane T′ to an arbitrary point along the edge of the blade; ψ2 is the angle of rotation of the head cutter; α2 is the blade angle. The subscript inside the parentheses indicates the number of a body the considered quantity belongs to (index 1 indicates a pinion, index 2 indicates a gear, index 4 indicates a generating gear of pinion). The subscript outside the parentheses indicates a coordinate system in which the considered vector is defined.

The gear tooth surface (Σ2) produced by coordinate transformation from coordinate system S to coordinate system S2 (connected to the gear) is defined by the following equation (based on Fig. 2)22:

$$({{\varvec{r}}}_{2}^{*}{)}_{2}={{\varvec{M}}}_{22}\cdot {{\varvec{M}}}_{P2}\cdot {{\varvec{M}}}_{20P}\cdot {{\varvec{M}}}_{20}\cdot \left({{\varvec{R}}}_{2}\right),$$
(2)

The coordinate transformations between coordinate systems S, S0, Sp, S2 (Fig. 2), are performed as it follows:

$$({{\varvec{R}}}_{2}{)}_{0}={{\varvec{M}}}_{20}\cdot ({{\varvec{R}}}_{2})=\left[\begin{array}{cc}\begin{array}{c}\mathit{cos}{\chi }_{2}\\ 0\\ \begin{array}{c}-\mathit{sin}{\chi }_{2}\\ 0\end{array}\end{array}& \begin{array}{ccc}0& \mathit{sin}{\chi }_{2}& 0\\ 1& 0& 0\\ \begin{array}{c}0\\ 0\end{array}& \begin{array}{c}\mathit{cos}{\chi }_{2}\\ 0\end{array}& \begin{array}{c}{r}_{0}\cdot \mathit{tan}{\chi }_{2}\\ 1\end{array}\end{array}\end{array}\right]\cdot ({{\varvec{R}}}_{2}),$$
(3)
$$({{\varvec{r}}}_{2}{)}_{p}={{\varvec{M}}}_{20P}\cdot ({{\varvec{R}}}_{2}{)}_{0}=\left[\begin{array}{cc}\begin{array}{c}\mathit{cos}\left({\theta }_{p2}-{90}^{^\circ }\right)\\ \mathit{sin}\left({\theta }_{p2}-{90}^{^\circ }\right)\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{ccc}-\mathit{sin}\left({\theta }_{p2}-{90}^{^\circ }\right)& 0& {E}_{x2}\cdot \mathit{cos}{q}_{2}\\ \mathit{cos}\left({\theta }_{p2}-{90}^{^\circ }\right)& 0& {E}_{x2}\cdot \mathit{sin}{q}_{2}\\ \begin{array}{c}0\\ 0\end{array}& \begin{array}{c}1\\ 0\end{array}& \begin{array}{c}{h}_{x2}\\ 1\end{array}\end{array}\end{array}\right]\cdot ({{\varvec{R}}}_{2}{)}_{0},$$
(4)
$$({{\varvec{r}}}_{2}{)}_{2}={{\varvec{M}}}_{P2}\cdot ({{\varvec{r}}}_{2}{)}_{p}=\left[\begin{array}{cc}\begin{array}{c}\mathit{sin}{\delta }_{M2}\\ 0\\ \begin{array}{c}\mathit{cos}{\delta }_{M2}\\ 0\end{array}\end{array}& \begin{array}{ccc}0& -\mathit{cos}{\delta }_{M2}& {R}_{m2}-{r}_{m2}\cdot \mathit{sin}{\delta }_{M2}\\ 1& 0& 0\\ \begin{array}{c}0\\ 0\end{array}& \begin{array}{c}\mathit{sin}{\delta }_{M2}\\ 0\end{array}& \begin{array}{c}{r}_{m2}\cdot \mathit{cos}{\delta }_{M2}\\ 1\end{array}\end{array}\end{array}\right]\cdot ({{\varvec{r}}}_{2}{)}_{p},$$
(5)

Where

$${\theta }_{p2}={\beta }_{m2}-{\delta }_{02}.$$
(6)

To obtain surface Σ2 in the generating process, the head cutter is rolled with the work gear, and surface Σ2 are defined by the following:

$$({{\varvec{r}}}_{2}^{*}{)}_{2}={{\varvec{M}}}_{22}\cdot ({{\varvec{r}}}_{2}{)}_{2}=\left[\begin{array}{cc}\begin{array}{c}\mathit{cos}\left({i}_{20}\cdot {\psi }_{2}\right)\\ \mathit{sin}\left({i}_{20}\cdot {\psi }_{2}\right)\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{ccc}-\mathit{sin}\left({i}_{20}\cdot {\psi }_{2}\right)& 0& 0\\ \mathit{cos}\left({i}_{20}\cdot {\psi }_{2}\right)& 0& 0\\ \begin{array}{c}0\\ 0\end{array}& \begin{array}{c}1\\ 0\end{array}& \begin{array}{c}0\\ 1\end{array}\end{array}\end{array}\right]\cdot ({{\varvec{r}}}_{2}{)}_{2}=[{x}_{2}{y}_{2}{z}_{2}1{]}^{T},$$
(7)

Where the velocity ratio i20 in the kinematic scheme of the head cutter for the generation of gear tooth surfaces, based on the ratio of the numbers of blades (z0) and teeth (z2), is:

$${i}_{20}=\frac{{z}_{0}}{{z}_{2}}.$$
(8)

The unit normal vector to surface Σ2 at point M in coordinate system S2 is:

$$({{\varvec{n}}}_{2}^{*}{)}_{2}=\frac{{\left({{\varvec{r}}}_{{2}{\text{u}}}^{*}\right)}_{2}\times {\left({{\varvec{r}}}_{{2}\psi }^{*}\right)}_{2}}{\left|{\left({{\varvec{r}}}_{{2}{\text{u}}}^{*}\right)}_{2}\times {\left({{\varvec{r}}}_{{2}\psi }^{*}\right)}_{2}\right|}=\frac{\frac{\partial ({{\varvec{r}}}_{2}^{*}{)}_{2}}{\partial {u}_{2}}\times \frac{\partial ({{\varvec{r}}}_{2}^{*}{)}_{2}}{\partial {\psi }_{2}}}{\left|\frac{\partial ({{\varvec{r}}}_{2}^{*}{)}_{2}}{\partial {u}_{2}}\times \frac{\partial ({{\varvec{r}}}_{2}^{*}{)}_{2}}{\partial {\psi }_{2}}\right|}$$
(9)

Generation of the generating gear tooth surface of pinion

In the generated method, the generation of the pinion is based on the concept of the virtual generating gear, and the pinion tooth surface (Σ1) is generated as an envelope of the virtual generating gear (Σ4). Figure 3 shows the relative position between the head cutter, generating gear of pinion, and pinion with the left-hand teeth. The virtual generating gear is similar to the gear. hx1 is the addendum modification, and χ1 is the tilt angle of the head cutter. Coordinate systems S and S0 are established similar to the coordinate systems of the gear shown in Fig. 2. Coordinate system S4(O4; i4, j4, k4) is connected to the virtual generating gear, where origin O4 is at the center of the pitch circle of the generating gear, axis i4 passes through point M, axis j4 coincides with axis jp, and axis k4 coincides with the axis of the generating gear of pinion. Origin O0 is at the intersection point of plane T and axis k0, initially located based on the radial setting (Ex1) and the angular setting (q1) in coordinate system Sp(Op; ip, jp, kp). δ4 is the pitch angle of the generating gear. δ40 is the generating gear installment angle.

Figure 3
figure 3

Positions of the head cutter, generating gear, and pinion with the left-hand teeth.

Full size image

The movable coordinate system S4 is rigidly connected with the generating gear of pinion. It is constructed by analogy to system S4. The generating gear tooth surface of pinion (Σ4) and the unit normal to surface Σ4 at point M are 22

$$({{\varvec{r}}}_{4}^{*}{)}_{4}={{\varvec{M}}}_{44}\cdot {{\varvec{M}}}_{P4}\cdot {{\varvec{M}}}_{40P}\cdot {{\varvec{M}}}_{40}\cdot ({{\varvec{R}}}_{4})=[{x}_{4}{y}_{4}{z}_{4} 1{]}^{T},$$
(10)
$$({{\varvec{n}}}_{4}^{*}{)}_{4}=\frac{{\left({{\varvec{r}}}_{{4}{\text{u}}}^{*}\right)}_{4}\times {\left({{\varvec{r}}}_{{4}\psi }^{*}\right)}_{4}}{\left|{\left({{\varvec{r}}}_{{4}{\text{u}}}^{*}\right)}_{4}\times {\left({{\varvec{r}}}_{{4}\psi }^{*}\right)}_{4}\right|}=\frac{\frac{\partial ({{\varvec{r}}}_{4}^{*}{)}_{4}}{\partial {u}_{1}}\times \frac{\partial ({{\varvec{r}}}_{4}^{*}{)}_{4}}{\partial {\psi }_{1}}}{\left|\frac{\partial ({{\varvec{r}}}_{4}^{*}{)}_{4}}{\partial {u}_{1}}\times \frac{\partial ({{\varvec{r}}}_{4}^{*}{)}_{4}}{\partial {\psi }_{1}}\right|}.$$
(11)

Here, (R4) is a position vector of an arbitrary point of the trace of the cutting edge, presented in system S by the vector-parametric equation (fully described in Reference 22):

$$({{\varvec{R}}}_{4})={{\varvec{R}}}_{4}({u}_{1},{\psi }_{1},{\alpha }_{1}),$$
(12)

Where u1 is the distance from the intersection point of the edge of the blade and plane T′ to an arbitrary point along the edge of the blade, ψ1 is the angle of rotation of the head cutter, and α1 is the blade angle. Subscript 4 inside the parentheses indicates the parameter of the generating gear of the pinion. x4, y4, and z4 are Cartesian coordinates representing the position of (r*4)4.

Matrices Mi provide the coordinate transformations from coordinate systems S to S4, defined by equations:

$$({{\varvec{R}}}_{4}{)}_{0}={{\varvec{M}}}_{40}\cdot ({{\varvec{R}}}_{4})=\left[\begin{array}{cc}\begin{array}{c}\mathit{cos}{\chi }_{1}\\ 0\\ \begin{array}{c}-\mathit{sin}{\chi }_{1}\\ 0\end{array}\end{array}& \begin{array}{ccc}0& \mathit{sin}{\chi }_{1}& 0\\ 1& 0& 0\\ \begin{array}{c}0\\ 0\end{array}& \begin{array}{c}\mathit{cos}{\chi }_{1}\\ 0\end{array}& \begin{array}{c}{r}_{0}\cdot \mathit{tan}{\chi }_{1}\\ 1\end{array}\end{array}\end{array}\right]\cdot ({{\varvec{R}}}_{4}),$$
(13)
$$({{\varvec{r}}}_{4}{)}_{p}={{\varvec{M}}}_{40P}\cdot ({{\varvec{R}}}_{4}{)}_{0}=\left[\begin{array}{cc}\begin{array}{c}\mathit{cos}\left({\theta }_{p1}-{90}^{^\circ }\right)\\ \mathit{sin}\left({\theta }_{p1}-{90}^{^\circ }\right)\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{ccc}-\mathit{sin}\left({\theta }_{p1}-{90}^{^\circ }\right)& 0& {E}_{x1}\cdot \mathit{cos}{q}_{1}\\ \mathit{cos}\left({\theta }_{p1}-{90}^{^\circ }\right)& 0& {E}_{x1}\cdot \mathit{sin}{q}_{1}\\ \begin{array}{c}0\\ 0\end{array}& \begin{array}{c}1\\ 0\end{array}& \begin{array}{c}{h}_{x1}\\ 1\end{array}\end{array}\end{array}\right]\cdot ({{\varvec{R}}}_{4}{)}_{0},$$
(14)
$$({{\varvec{r}}}_{4}{)}_{4}={{\varvec{M}}}_{P4}\cdot ({{\varvec{r}}}_{4}{)}_{p}=\left[\begin{array}{cc}\begin{array}{c}\mathit{sin}{\delta }_{40}\\ 0\\ \begin{array}{c}-\mathit{cos}{\delta }_{40}\\ 0\end{array}\end{array}& \begin{array}{ccc}0& \mathit{cos}{\delta }_{40}& {R}_{m2}-{r}_{m2}\cdot \mathit{sin}{\delta }_{40}\\ 1& 0& 0\\ \begin{array}{c}0\\ 0\end{array}& \begin{array}{c}\mathit{sin}{\delta }_{40}\\ 0\end{array}& \begin{array}{c}{-r}_{m2}\cdot \mathit{cos}{\delta }_{40}\\ 1\end{array}\end{array}\end{array}\right]\cdot ({{\varvec{r}}}_{4}{)}_{p},$$
(15)

Where

$${\theta }_{p1}={\beta }_{m1}-{\delta }_{01},$$
(16)

Matrix M44 defines the relation between the pinion and its generating gear rotating through mesh, and it is described by the following equation (Fig. 3):

$$({{\varvec{r}}}_{4}^{*}{)}_{4}={{\varvec{M}}}_{44}\cdot ({{\varvec{r}}}_{4}{)}_{4}=\left[\begin{array}{cc}\begin{array}{c}\mathit{cos}\left({i}_{20}\cdot {\psi }_{1}\right)\\ \mathit{sin}\left({i}_{20}\cdot {\psi }_{1}\right)\\ \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{ccc}-\mathit{sin}\left({i}_{20}\cdot {\psi }_{1}\right)& 0& 0\\ \mathit{cos}\left({i}_{20}\cdot {\psi }_{1}\right)& 0& 0\\ \begin{array}{c}0\\ 0\end{array}& \begin{array}{c}1\\ 0\end{array}& \begin{array}{c}0\\ 1\end{array}\end{array}\end{array}\right]\cdot ({{\varvec{r}}}_{4}{)}_{4}.$$
(17)

Curvature parameters of the tooth surfaces in the tooth trace and tooth profile directions at the reference point

Each of the tooth surfaces described above covers two families of parameter curves, namely, the u-parameter curve and the ψ-parameter curve. For each point on surface Σ2, tangent vector α2u to the u-parameter curve and tangent vector α2ψ to the ψ-parameter curve are represented in coordinate system S2, as follows (based on Fig. 4):

Figure 4
figure 4

Positions of the tangent vectors to the parameter curves, tooth profile curve, and toothtrace curve at point M.

Full size image
$${\left({\boldsymbol{\alpha }}_{\text{2u}}\right)}_{2}=\frac{{\left({{\varvec{r}}}_{{2}{\text{u}}}^{*}\right)}_{2}}{\left|{\left({{\varvec{r}}}_{{2}{\text{u}}}^{*}\right)}_{2}\right|},$$
(18)
$${\left({\boldsymbol{\alpha }}_{2\psi }\right)}_{2}=\frac{{\left({{\varvec{r}}}_{{2}\psi }^{*}\right)}_{2}}{\left|{\left({{\varvec{r}}}_{{2}\psi }^{*}\right)}_{2}\right|}.$$
(19)

The angle between vector α2u and vector α2ψ is determined by

$${\gamma }_{2u\psi }=\mathit{arccos}\left[({\boldsymbol{\alpha }}_{\text{2u}}{)}_{2}\cdot ({\boldsymbol{\alpha }}_{2\psi }{)}_{2}\right].$$
(20)

The normal curvature and the geodesic torsion of surface Σ2 for the directions of the u-parameter curve and the ψ-parameter curve are determined and denoted by κ2u, τ2u, κ2ψ and τ2ψ, respectively:

$${\kappa }_{2u}=0,$$
(21)
$${\kappa }_{2\psi }=\frac{({{\varvec{n}}}_{2}^{*}{)}_{2}\cdot {\left({{\varvec{r}}}_{{2}\psi \psi }^{*}\right)}_{2}}{{\left[{\left({{\varvec{r}}}_{{2}\psi }^{*}\right)}_{2}\right]}^{2}}=\frac{({{\varvec{n}}}_{2}^{*}{)}_{2}\cdot \frac{{\partial }^{2}({{\varvec{r}}}_{2}^{*}{)}_{2}}{{\left(\partial {\psi }_{2}\right)}^{2}}}{{\left[\frac{\partial ({{\varvec{r}}}_{2}^{*}{)}_{2}}{\partial {\psi }_{2}}\right]}^{2}},$$
(22)
$${\tau }_{2u}=\frac{({{\varvec{n}}}_{2}^{*}{)}_{2}\cdot {\left({{\varvec{r}}}_{{2}{\text{u}}\psi }^{*}\right)}_{2}}{\sqrt{{\left[{\left({{\varvec{r}}}_{{2}{\text{u}}}^{*}\right)}_{2}\right]}^{2}{\left[{\left({{\varvec{r}}}_{{2}\psi }^{*}\right)}_{2}\right]}^{2}-{\left[{\left({{\varvec{r}}}_{{2}{\text{u}}}^{*}\right)}_{2}\cdot {\left({{\varvec{r}}}_{{2}\psi }^{*}\right)}_{2}\right]}^{2}}}=\frac{({{\varvec{n}}}_{2}^{*}{)}_{2}\cdot \frac{{\partial }^{2}({{\varvec{r}}}_{2}^{*}{)}_{2}}{\partial {\psi }_{2}\partial {u}_{2}}}{\sqrt{{\left[\frac{\partial ({{\varvec{r}}}_{2}^{*}{)}_{2}}{\partial {u}_{2}}\right]}^{2}{\left[\frac{\partial ({{\varvec{r}}}_{2}^{*}{)}_{2}}{\partial {\psi }_{2}}\right]}^{2}-{\left[{\left(\frac{\partial ({{\varvec{r}}}_{2}^{*}{)}_{2}}{\partial {u}_{2}}\right)}_{2}\cdot \frac{\partial ({{\varvec{r}}}_{2}^{*}{)}_{2}}{\partial {\psi }_{2}}\right]}^{2}}},$$
(23)
$${\tau }_{2\psi }=\frac{{\kappa }_{2\psi }\cdot {\left({{\varvec{r}}}_{{2}{\text{u}}}^{*}\right)}_{2}\cdot {\left({{\varvec{r}}}_{{2}\psi }^{*}\right)}_{2}}{\sqrt{{\left[{\left({{\varvec{r}}}_{{2}{\text{u}}}^{*}\right)}_{2}\right]}^{2}{\left[{\left({{\varvec{r}}}_{{2}\psi }^{*}\right)}_{2}\right]}^{2}-{\left[{\left({{\varvec{r}}}_{{2}{\text{u}}}^{*}\right)}_{2}\cdot {\left({{\varvec{r}}}_{{2}\psi }^{*}\right)}_{2}\right]}^{2}}}-{\tau }_{2u}$$
(24)

As shown in Figs. 4 and 5, an initial position of the gear is the position in which the reference point M, located in the gear pitch cone generatrix. Angle φM of the gear rotation about its axis k2 is measured from initial positions. Vector m2(φM, δ2) is the unit vector of the gear pitch cone generatrix and n2(φM, δ2) is the normal vector of the gear pitch cone surface at point M (Fig. 4). Parameter αn2 is the pressure angle of the gear tooth surface at point M. α2v is the unit vector for the direction of the tooth trace, and α2G is the unit vector for the direction of the tooth profile. α2v is perpendicular to α2G. α2v and α2G are in the tangent planes to surface Σ2 at point M, and α2v can be represented in coordinate system S2 as:

Figure 5
figure 5

Directions of the tangent vectors to the parameter curves, tooth profile curve, and tooth trace curve at M.

Full size image
$$({\boldsymbol{\alpha }}_{\text{2v}}{)}_{2}=\frac{{{\varvec{n}}}_{2}({\varphi }_{\text{M2}},{\delta }_{2})\times ({{\varvec{n}}}_{2}^{*}{)}_{2}}{\mathit{sin}(9{0}^{\circ }-{\alpha }_{n})},$$
(25)
$$({\boldsymbol{\alpha }}_{\text{2G}}{)}_{2}=({\boldsymbol{\alpha }}_{\text{2v}}{)}_{2}\times ({{\varvec{n}}}_{2}^{*}{)}_{2}.$$
(26)

Here,

$${{\varvec{n}}}_{2}({\varphi }_{M2},{\delta }_{2})=\left[\begin{array}{c}\mathit{cos}{\delta }_{2}\mathit{cos}{\varphi }_{M2}\\ \mathit{cos}{\delta }_{2}\mathit{sin}{\varphi }_{M2}\\ \begin{array}{c}-\mathit{sin}{\delta }_{2}\\ 1\end{array}\end{array}\right],$$
(27)
$${\varphi }_{\text{M2}}=\mathit{arctan}(\frac{{y}_{2}}{{x}_{2}}),$$
(28)
$${\alpha }_{n}=\mathit{arcsin}\left[{{\varvec{n}}}_{2}({\varphi }_{M2},{\delta }_{2})\cdot ({{\varvec{n}}}_{2}^{*}{)}_{2}\right].$$
(29)

The angle between vectors α2u and α2v is determined by

$${\gamma }_{2u\psi }=\mathit{arccos}\left[({\boldsymbol{\alpha }}_{\text{2u}}{)}_{2}\cdot ({\boldsymbol{\alpha }}_{\text{2v}}{)}_{2}\right].$$
(30)

The normal curvatures and the geodesic torsion for the directions of the tooth trace and the tooth profile can be represented respectively by.

$${\kappa }_{\text{2v}}=\left[{\kappa }_{{2}\psi }+({\tau }_{{2}\psi }-{\tau }_{\text{2u}})/{\mathit{tan}\gamma }_{{\text{2u}}\psi }\right]{{\mathit{sin}}^{2}\gamma }_{\text{2uv}}+{\tau }_{\text{2u}}\mathit{sin}2{\gamma }_{{\text{2u}}{\text{v}}}.$$
(31)
$${\kappa }_{\text{2G}}=\left[{\kappa }_{{2}\psi }+({\tau }_{{2}\psi }-{\tau }_{\text{2u}})/{\mathit{tan}\gamma }_{{\text{2u}}\psi }\right]{{\mathit{cos}}^{2}\gamma }_{\text{2uv}}-{\tau }_{\text{2u}}\mathit{sin}2{\gamma }_{\text{2uv}}.$$
(32)
$${\tau }_{\text{2v}}=0.5\left[{\kappa }_{{2}\psi }+({\tau }_{{2}\psi }-{\tau }_{\text{2u}})/{\mathit{tan}\gamma }_{{\text{2u}}\psi }\right]\mathit{sin}2{\gamma }_{\text{2uv}}+{\tau }_{\text{2u}}\mathit{cos}2{\gamma }_{\text{2uv}}.$$
(33)
$${\tau }_{\text{2G}}=-{\tau }_{\text{2v}}$$
(34)

The normal curvatures and the geodesic torsion of the generating gear tooth surface Σ4 of the pinion for the directions of the tooth trace and the tooth profile can be represented and denoted respectively by κ4v, τ4v, κ4G, τ4G, and γ4uv, γ4uψ. The detailed derivations, fully provided in Reference 22, are the same as Eqs. (18–34).

In the generation method, the pinion tooth surface Σ1 is the envelope of the family of generating surfaces Σ4. Based on the meshing theory, the normal curvatures and the geodesic torsion (κ1v, κ1G, and τ1v) of surface Σ1 for tangent vectors α1v and α1G of the tooth trace and the tooth profile at point M are determined with respect to the curvature relations between the mating surfaces and represented by the following equations:

$${\kappa }_{\text{1v}}={\kappa }_{\text{4v}}-{\kappa }_{\text{41v}}.$$
(35)
$${\kappa }_{\text{1G}}={\kappa }_{\text{4G}}-{\kappa }_{\text{41G}}.$$
(36)
$${\tau }_{\text{1v}}={\tau }_{\text{4v}}-{\tau }_{\text{41v}}.$$
(37)

Here, κ41v, κ41G, and τ41v are the induction normal curvatures and the induction geodesic torsion, respectively, and their detailed derivation is provided in Reference22.

Direction angle of the contact path at the reference point

Figure 6 shows the relative position of the pinion and gear when they are meshing at point M. Coordinate system S0i(Oi; i0i, j0i, k0i) (i = 1, 2) is rigidly connected to the machine frame. Origin Oi is the foot point of the common perpendicular of the axis of the pinion and the axis of the gear; axis k0i coincides with the axis of the blank, and axis j0i coincides with the common perpendicular. Origin O″2 is in the center of the pitch circle of the gear at point M. Parameter E is the offset, and parameter Σ is the shaft angle.

Figure 6
figure 6

Coordinate systems connected to the machine frame.

Full size image

By coordinate transformation, the gear tooth surface Σ2 is represented in system S02 as (based on Fig. 6):

$$({{\varvec{r}}}_{2}{)}_{02}={A}_{\text{m2}}{{\varvec{k}}}_{02}+{{\varvec{M}}}_{202}\cdot ({{\varvec{r}}}_{2}^{*}{)}_{2},$$
(38)

Where

$${{\varvec{M}}}_{202}=\left[\begin{array}{ccc}\mathit{cos}\left(18{0}^{\circ }-{\varphi }_{M2}+{\varepsilon }_{2}\right)& -\mathit{sin}\left(18{0}^{\circ }-{\varphi }_{M2}+{\varepsilon }_{2}\right)& \begin{array}{cc}0& 0\end{array}\\ \mathit{sin}\left(18{0}^{\circ }-{\varphi }_{M2}+{\varepsilon }_{2}\right)& \mathit{cos}\left(18{0}^{\circ }-{\varphi }_{M2}+{\varepsilon }_{2}\right)& \begin{array}{cc}0& 0\end{array}\\ \begin{array}{c}0\\ 0\end{array}& \begin{array}{c}0\\ 0\end{array}& \begin{array}{c}\begin{array}{cc}1& 0\end{array}\\ \begin{array}{cc}0& 1\end{array}\end{array}\end{array}\right],$$
(39)
$${\varepsilon }_{2}=\mathit{arcsin}(\mathit{sin}{\beta }_{\text{m12}}\mathit{cos}{\delta }_{1}/\mathit{sin}\Sigma ).$$
(40)

Am2 is the installment distance of the gear, βm12 is the difference between the spiral angles of the pinion and that of the gear, and δ1 is the pitch angle of the pinion.

The vectors of the axes of coordinate system SM(M, α2v, α2G, n2) are represented in system S02 as (based on Fig. 7):

Figure 7
figure 7

Relative positions of Σ2 and Σ1 and the coordinate system.

Full size image
$$({\boldsymbol{\alpha }}_{\text{2v}}{)}_{02}={{\varvec{M}}}_{202}\cdot ({\boldsymbol{\alpha }}_{\text{2v}}{)}_{2},$$
(41)
$$({\boldsymbol{\alpha }}_{\text{2G}}{)}_{02}={{\varvec{M}}}_{202}\cdot ({\boldsymbol{\alpha }}_{\text{2G}}{)}_{2},$$
(42)
$$({{\varvec{n}}}_{2}{)}_{02}={{\varvec{M}}}_{202}\cdot ({{\varvec{n}}}_{2}^{*}{)}_{2}.$$
(43)

The angle velocity of the pinion is defined as |ω1|= 1 rad·s−1, and the relative angular velocity is represented in system S02 by.

$$({{\varvec{\omega}}}_{12}{)}_{02}=({{\varvec{\omega}}}_{1}{)}_{02}-({{\varvec{\omega}}}_{2}{)}_{02},\boldsymbol{ }$$
(44)
$$({{\varvec{\omega}}}_{1}{)}_{02}=({{\varvec{k}}}_{01}{)}_{02}={{\varvec{M}}}_{21}\cdot {{\varvec{k}}}_{01},$$
(45)
$$({{\varvec{\omega}}}_{2}{)}_{02}=-\frac{1}{{i}_{12}}({{\varvec{k}}}_{02}{)}_{02},$$
(46)

where i12 is the transmission ratio at point M, and.

$${{\varvec{M}}}_{21}=\left[\begin{array}{cc}\begin{array}{c}\mathit{cos}\left(-\Sigma \right)\\ 0\\ \begin{array}{c}-\mathit{sin}\left(-\Sigma \right)\\ 0\end{array}\end{array}& \begin{array}{ccc}0& \mathit{sin}\left(-\Sigma \right)& 0\\ 1& 0& 0\\ \begin{array}{c}0\\ 0\end{array}& \begin{array}{c}\mathit{cos}\left(-\Sigma \right)\\ 0\end{array}& \begin{array}{c}0\\ 1\end{array}\end{array}\end{array}\right].$$
(47)

The relative velocity of the pinion and gear at point M is represented by.

$$({{\varvec{v}}}_{12}{)}_{02}=({{\varvec{\omega}}}_{12}{)}_{02}\times ({{\varvec{r}}}_{2}{)}_{02}+({{\varvec{\omega}}}_{1}{)}_{02}\times \left(E\cdot {{\varvec{j}}}_{02}\right).$$
(48)

In the meshing process, surfaces Σ1 and Σ2 are in point contact continuously, and it can be assumed that imaginary tooth surfaces Σ2′ and Σ1′ is obtained from the envelopes of surfaces Σ1 and Σ2, and they are in line contact respectively. α1v and α2v are the vectors for the directions of the tooth trace of the pinion and the gear. At point M, α1v = α2v. Surfaces Σ2 and Σ1′, as shown in Fig. 7, are in line contact. Γ2 is the contact path. The relative positions of Σ1 and Σ2′are the same as those of Σ2 and Σ1′.

Tooth surface Σ1 is in conjugation with surface Σ2′; thus, the unit normal vector of the instantaneous contact line is obtained as.

$$({{\varvec{N}}}_{12}{)}_{02}={N}_{\text{12v}}\cdot ({\boldsymbol{\alpha }}_{\text{2v}}{)}_{02}+{N}_{12G}\cdot ({\boldsymbol{\alpha }}_{\text{2G}}{)}_{02},$$
(49)

Here,

$${N}_{\text{12v}}={\kappa }_{\text{1v}}({{\varvec{v}}}_{12}{)}_{02}\cdot ({\boldsymbol{\alpha }}_{\text{2v}}{)}_{02}+{\tau }_{\text{1v}}({{\varvec{v}}}_{12}{)}_{02}\cdot ({\boldsymbol{\alpha }}_{\text{2G}}{)}_{02}+({{\varvec{\omega}}}_{12}{)}_{02}\cdot ({\boldsymbol{\alpha }}_{\text{2G}}{)}_{02},$$
(50)
$${N}_{\text{12G}}={\tau }_{\text{1v}}({{\varvec{v}}}_{12}{)}_{02}\cdot ({\boldsymbol{\alpha }}_{\text{2v}}{)}_{02}+{\kappa }_{\text{1v}}({{\varvec{v}}}_{12}{)}_{02}\cdot ({\boldsymbol{\alpha }}_{\text{2G}}{)}_{02}-({{\varvec{\omega}}}_{12}{)}_{02}\cdot ({\boldsymbol{\alpha }}_{\text{2v}}{)}_{02}.$$
(51)

Tooth surface Σ2 is in conjugation with tooth surface Σ1′; thus, the unit normal vector of the instantaneous contact line is obtained as.

$$({{\varvec{N}}}_{21}{)}_{02}={N}_{\text{21v}}({\boldsymbol{\alpha }}_{\text{2v}}{)}_{02}+{N}_{\text{21G}}({\boldsymbol{\alpha }}_{\text{2G}}{)}_{02},$$
(52)

Here,

$${N}_{\text{21v}}=-{\kappa }_{\text{2v}}({{\varvec{v}}}_{12}{)}_{02}\cdot ({\boldsymbol{\alpha }}_{\text{2v}}{)}_{02}-{\tau }_{\text{2v}}({{\varvec{v}}}_{12}{)}_{02}\cdot ({\boldsymbol{\alpha }}_{\text{2G}}{)}_{02}-({{\varvec{\omega}}}_{12}{)}_{02}\cdot ({\boldsymbol{\alpha }}_{\text{2G}}{)}_{02},$$
(53)
$${N}_{\text{21G}}=-{\tau }_{\text{2v}}({{\varvec{v}}}_{12}{)}_{02}\cdot ({\boldsymbol{\alpha }}_{\text{2v}}{)}_{02}-{\kappa }_{\text{2v}}({{\varvec{v}}}_{12}{)}_{02}\cdot ({\boldsymbol{\alpha }}_{\text{2G}}{)}_{02}+({{\varvec{\omega}}}_{12}{)}_{02}\cdot ({\boldsymbol{\alpha }}_{\text{2v}}{)}_{02}.$$
(54)

The unit vectors tangent to the contact path at point M are denoted by α1 and α2 for the pinion and gear tooth surface, shown as Fig. 8, respectively. The direction angle of αi to α2v is defined as νi (i = 1, 2):

Figure 8
figure 8

Position of the direction angle of the contact path.

Full size image
$${\boldsymbol{\alpha }}_{i}=\mathit{cos}{v}_{i}\cdot {\boldsymbol{\alpha }}_{\text{2V}}+\mathit{sin}{v}_{i}\cdot {\boldsymbol{\alpha }}_{\text{2G}}.$$
(55)

The area around reference point M meets the geometry condition of the tooth contact along the contact path: reference point M is the common point of both tooth surfaces, and a common normal line for both tooth surfaces exists at reference point M. Accordingly, angle νi is obtained by the following equations:

$${\mathit{tan}\nu }_{2}=\frac{-\left({\kappa }_{12V}+{\tau }_{12V}\right)\mathit{tan}{\theta }_{12}}{{\kappa }_{12G}\mathit{tan}{\theta }_{12}+{\tau }_{12V}},$$
(56)
$${\mathit{tan}\nu }_{1}=\frac{-\left({\kappa }_{12V}+{\tau }_{12V}\right)\mathit{tan}{\theta }_{21}}{{\kappa }_{12G}\mathit{tan}{\theta }_{21}+{\tau }_{12V}},$$
(57)

Where

$$\mathit{tan}{\theta }_{12}=\frac{{N}_{12V}}{{N}_{12G}},$$
(58)
$$\mathit{tan}{\theta }_{21}=\frac{{N}_{21V}}{{N}_{21G}}.$$
(59)

Influence of the Angular Setting of the Head Cutter on the Direction of the Contact Path

In the Spirac system, the installment of the head cutter is determined by parameters Exi and qi for the gear if i = 2 and for the pinion if i = 122. Exi is corrected to satisfy the requirement of the spiral angle at the reference point, whereas qi is not corrected. To further satisfy the requirement of the direction angle of the contact path, one more parameter is required. Thus, q1 is chosen, and its influence on the contact path is investigated.

A numerical example is considered to analyze the influence, and Table 1 shows the main design parameters of the gear and the pinion.

Table 1 Design parameters for the numerical example.
Full size table

Figure 9 shows the result of the contact path on the gear tooth surfaces obtained by correcting the value of q1. The dotted lines with “ + ” signify the contact paths when △q1 =  + 0.0003 rad, the dotted lines with “ − ” signify the contact paths when △q1 =  − 0.0003 rad, and the solid lines signify the contact paths when the value is not corrected.

Figure 9
figure 9

Influence of q4 on the contact path.

Full size image

In Fig. 9, the positive correction of q1 increases the angles between the contact path and the tooth trace on the concave and convex tooth surfaces simultaneously, whereas the negative correction decreases the angles. Meanwhile, the positive correction makes the contact paths on the concave and convex tooth surfaces move to the tooth heel simultaneously, whereas the negative correction has the reverse effect.

The result proves the validity of the angular setting of the head cutter q1 to control the direction of the contact path. Considering its influence on the contact path, q1 is added to control the symmetry of the contact paths on the concave and convex tooth surfaces of the gear.

Building equations

In the face hobbing method, the concave and convex tooth surfaces of the pinion or the gear are cut simultaneously under a single set of machine tool settings. Equations (1–60), described above, can be applied to evaluate the concave tooth surfaces of the pinion and the gear with the replacement of parameters u1i, ψ1i, and α1i, and u2e, ψ2e, and α2e with the original parameters (u1, ψ1, and α1, and u2, ψ2, and α2) and the convex tooth surfaces with the replacement of parameters u1e, ψ 1e, and α1e, and u2i, ψ2i, and α2i with the original parameters (u1, ψ1, and α1, and u2, ψ2, and α2).

If the contact paths of the concave and convex tooth surfaces are symmetrical, parameters ν1e and ν1i will be related by the following equation:

$${\nu }_{\text{1e}}=-{\nu }_{\text{1i}}.$$
(60)

The current computation of machine tool settings for the Spirac hypoid gears is based on three conditions at the reference point: (a) the reference point is at the prescribed location, (b) the pressure angle at the reference point is equal to the theoretical value, and (c) the spiral angle at the reference point is equal to the theoretical value. The equations are.

$$\left\{\begin{array}{c}{r}_{mjk}^{r}={r}_{m2}\\ {r}_{mjk}^{n}=0\\ {\alpha }_{mjk}={\alpha }_{mk}\\ {\beta }_{mjk}={\beta }_{m2}\end{array}\right.\left(j=\text{4,2};k=i,e\right),$$
(62)

Where \({r}_{mjk}^{r}\) and \({r}_{mjk}^{n}\) are the radial and axial positions of the reference point, respectively, on tooth surface Σj in coordinate system Sj; rm2 is the radius of the reference circle at point M; αm4i and αm4e, and αm2e and αm2i are the normal pressure angles of the concave and convex tooth surfaces of the generating gear of pinion and the gear at the reference point, respectively; αmi and αme are the theoretical values of the normal pressure angles; βm4i and βm4e, and βm2e and βm2i are the spiral angles of the concave and convex tooth surfaces of the generating gear of pinion and the gear at the reference point, respectively; βm2 is the theoretical value of the spiral angle at the reference point.

Equation (61) consists of 16 nonlinear equations, which contain 16 unknowns, u1k, ψ1k, u2k, ψ2k, Ex1, Ex2, α1k, α2k, δ40, and δM2, for solving for a set of values. To achieve symmetry of the contact paths, angle q1 is taken as an unknown, and Eq. (60) is used for another function. Overall, 17 equations obtained from Eqs. (60) and (61) are applied to solve for the 17 unknowns to achieve the final values of the machine tool settings.

Analysis of the symmetry of the contact path

Table 1 lists the design parameters for the example hypoid gear pair. By the original method which is currently used for calculation22, the values of the machine tool settings are obtained and listed in Tables 2, and 3 lists the results of the conditions. The output of the tooth contact analysis (TCA) is shown in Fig. 10a.

Table 2 Machine tool settings by the original method for the numerical example.
Full size table
Table 3 Results obtained by the original method for the numerical example.
Full size table
Figure 10
figure 10

TCA outputs with the (a) original and (b) new methods.

Full size image

By the new method proposed in this paper, the values of the machine tool settings are obtained and listed in Tables 4, and 5 lists the results obtained under the different conditions. The outputs of the TCA are shown in Fig. 10b.

Table 4 Machine tool settings obtained by the proposed method.
Full size table
Table5 Results obtained by the proposed method.
Full size table

Tables 2 and 4 show that the machine tool settings for the gear are modified and determined to be equal, whereas the machine tool settings for the pinion change. Tables 3 and 5 show that the values obtained by the two methods, related to the position of the reference point, the pressure angle, and the spiral angle, are both equal to the theoretical values. Table 3 shows that the direction angle of the contact paths on the concave tooth surface is not equal to the angle on the convex by the original method. In order to obtain a good meshing performance, they need to be modified artificially and repeatedly by correcting the machine tool settings. However, the direction angles of the contact paths on the concave and convex tooth surfaces of the gear obtained by the proposed method are equal in Table 5. This method is practicable and effective for impacting the meshing performance.

In Fig. 10a, there are significant differences in the tooth contact quality and the motion error between the concave and convex tooth surfaces: (i) both contact paths are not symmetrical; (ii) the convex tooth surface of the gear has a small rotation angle error but a long contact zone, which increases the gear sensitivity; and (iii) although the concave tooth surface has a good contact zone, it has a large rotation angle error.

In Fig. 10b, the contact paths on the concave and convex tooth surfaces are approximately symmetrical, the motion errors are approximately equal, and the meshing characteristics are approximate. Thus, the proposed method for controlling the direction angle of the contact path at the reference point is effective, and it can improve the tooth contact quality and the transmission performance.

Conclusion

In this paper, a novel optimization method is presented for determining machine tool settings specific to Spirac hypoid gears, aiming to achieve optimal meshing performance with greater efficiency.

In the existing Spirac system, the pinion is cut by the generated method, the gear is cut by the non-generated method, which provides a higher production, but the meshing performance cannot be predicted and controlled. It needs to be modified artificially and repeatedly by correcting the machine tool settings during the tooth contact analysis. In the proposed method, the symmetry of the contact paths on the concave and convex tooth surfaces of the gear is controlled to achieve optimal meshing performance with greater efficiency. The direction angles of the two contact paths are equated to estimate their symmetry, achieved by modifying the angular setting of the head cutter when cutting the pinion. The results show that the contact paths on the concave and convex tooth surfaces are approximately symmetrical and the transmission errors of both sides are comparable.