Optimizing of particle accelerated rotor parameters using the discrete element method

Abstract

The acceleration capability of a centrifugal jet rotor plays a crucial role in achieving a high injection velocity of powder particles in the centrifugal impact moulding process. In this regard, the focus of this article is on optimization of the runner shape. To this end, the lengths of the first and second acceleration sections (L₁ and L₂), and the angles between the first and second acceleration sections and between the second and third sections (α₁ and α₂) are considered as the rotor parameters. Simulations were conducted using multiple discrete elements to explore the influence of multiple input parameters on the response value, and a regression model was established between the parameters and the particle injection rate. The experimental results show that the selected parameters significantly affect the rate of particle injection, and the interactions between the parameters L₁ and L₂, and between L₂ and α₂ have the largest effects. The results reveal that applying the optimized parameters improves the particle injection speed by 7.85% when compared to the pre-optimization model. This improvement in the rotor acceleration provides the basis for improving the efficiency of centrifugal impact moulding of metal powders.

Introduction

Studies show that accelerated powder particles impinging on a solid-state substrate can provide a coating on the substrate surface by producing a large plastic strain deposit^1,2,3,4,5. In this technology, the velocity of the particles is the key factor in combining the particle with the substrate after impact. Currently, the common particle acceleration methods include the airflow acceleration method, mechanical acceleration method, electromagnetic acceleration method, ultrasonic acceleration method and electrostatic acceleration method. It is worth noting that each method has advantages and limitations and can be employed in various applications. In this context, the airflow acceleration method has attracted many researchers focusing on the optimization of jet structures to increase the acceleration capacity of particles. Wan⁶ studied the effect of the various parameters of the powder jet on the impact velocity and particle distribution and developed a mathematical hydrodynamic model. Gao⁷ proposed the degree of aggregation (PAD) concept and analysed the effects of the nozzle geometry on the powder flow. Cao⁸ designed the nozzle geometry based on the selected particles and propellant gases for ejected particles to reach the maximum impact velocity. Furthermore, Buhl⁹ established an analytical model, analysed the motion of the particles, and modified the nozzle structure based on CFD simulation results. Forero-Sossa¹⁰ investigated the effect of the nozzle geometry on the deposition of hydroxy-apatite particles in LPCS and demonstrated that the nozzle geometry affects the coating uniformity. Zavalan¹¹ employed an objective multi-optimization method to optimize the nozzle structure and improve nozzle performance. Klinkov¹² employed a cylindrical barrel with a double-edged bevelled exit vortex to generate a high-speed two-phase flow. This approach was suggested as an alternative to cold spray nozzles. To resolve the shortcomings of conventional DeLaval nozzles in the cold-air dynamic spraying process, Liao¹³ proposed a modified nozzle structure and verified its acceleration performance through numerical simulations. In all the aforementioned studies, it was observed that the internal structure of the flow channel exhibits a substantial influence on the acceleration effect of powder particles.

Based on the performed literature survey, the focus of present study is on investigating the mechanical acceleration of powder particles using centrifugal throw rotors. To this end, the acceleration process involving the throwing of rotors with variously shaped runners is simulated using EDEM discrete-element software. The main objective of this article is to analyse the influences of the runner control parameters on the injection velocity of particles, establish a model to numerically analyse the influencing factors, and optimize the control parameters of the runner to improve the rotor acceleration performance.

Materials and methods

In this article, the discrete element method is chosen as the simulation technique. This selection is made primarily because the perturbation of the particle motion caused by the airflow is often neglected when analysing the effect of the flow channel structure on the particle acceleration performance^14,15,16,17. The fundamental idea behind the discrete element method is to consider the medium as a discrete body. Then the structure is discretized into independent elements and particles, where each particle is assumed to Newton's second law of motion. In this approach, the macroscopic motion of the entire medium is calculated by iteratively solving the governing equation^18,19. To simulate the particle motion using the discrete unitary method, vibrational equations of motion are used to model particle‒particle collisions and the motion of particles at boundaries^20,21.

Modelling particle accelerating rotors

The rotor’s internal structure of the runner consists of two elements: the runner modelling line and the section contour line, as shown in Fig. 1A, the former determines the structural characteristics of the runner and the latter determines the cross-sectional shape of the runner .The runner modelling line is composed of multi-segment lines, and the following five parameters are implemented for line control: the lengths of the first acceleration section (L₁), the lengths of the second acceleration section (L₂), the lengths of the third acceleration section (L₃), the angle between the first and second acceleration sections (α₁) and the angle between the second and third accelerating sections (α₂). These parameters, which are referred to as shape parameters, are shown in Fig. 1B. The parameter L₃ can be calculated from L₁, L₂, α₁, α₂ and the known rotor radius (R) using Eq. (1). Therefore, the rotor optimization design is tested with the four key parameters L₁, L₂, α₁, and α₂ in a vehicle.

Figure 1

Rotor internal runner structure and its moulding control parameters. This figure consists of two plots. Two components of the runner inside the rotor are shown in Plot (a): the runner moulding line and the cross-section contour line. Moreover, the control parameters of the flow to the molding line are shown in Plot (b).

$$L_{3} = \sqrt {R^{2} - [\sin \left( {\alpha_{1} + \alpha_{2} } \right)L_{1} + \sin \alpha_{2} L_{2} ]^{2} } - \cos (\alpha_{1} + \alpha_{2} )L_{1} - \cos \alpha_{2} L_{2}$$

(1)

The rotor is modelled using the SolidWorks software platform, and its internal and external structures are illustrated in Fig. 2. The parameter for the rotor are shown in Table 1, and the material properties are provided in Table 2.

Figure 2

Rotor structure diagram. This figure shows the internal and external structure of the particle acceleration rotor.

Table 1 Table of the rotor model parameters.

Table 2 Table of rotor material parameters.

Powder particulate model

Powder particles are usually spherical with smooth surfaces. To simplify the simulation, the hard-sphere model was employed in this study. The shape parameters and material properties are provided in Table 3.

Table 3 Pellet shape and material parameters.

Contact pattern

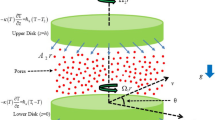
Several contact models, including the Hertz‒Mindlin no-slip contact model, the Hertz‒Mindlin adhesion contact model, the linear adhesion contact model, the kinematic contact model at the surface, the linear elastic contact model, and the frictional loaded contact model, are commonly used²². Since the powder particles are spherical and there is no adhesion on their surfaces, the Hertz‒Mindlin no-slip contact model is selected to simulate particle‒particle and particle-rotor contacts. This model is schematically illustrated in Fig. 3. As shown in this figure, the contact forces between two particles fundamentally simplify into springs (with normal stiffness $k_{n}$ and tangential stiffness $k_{t}$), dampers (with normal damping $d_{n}$ and tangential damping $d_{t}$) and a slider (with friction coefficient $\mu$)²³.

Figure 3

Hertz‒Mindlin no-slip contact mechanics model. This figure illustrates the Hertz‒Mindlin no-slip contact mechanics model.

In this model, the normal force between the particles, tangential force, normal damping force, and tangential damping force can be calculated using the following equations:

$$F_{n} = \frac{4}{3}E^{*} \sqrt {R^{*} \alpha^{3} }$$

(2a)

$$F_{t} = - S_{t} \delta$$

(2b)

$$F_{n}^{d} = - 2\sqrt{\frac{5}{6}} \beta \sqrt {S_{n} m^{*} } \upsilon_{n}^{rel}$$

(2c)

$$\frac{1}{{R^{*} }} = \frac{1}{{R_{A} }} + \frac{1}{{R_{B} }}$$

(2d)

$$\frac{1}{{E^{*} }} = \frac{{1 - \nu_{A}^{2} }}{{E_{A} }} + \frac{{1 - \nu_{B}^{2} }}{{E_{B} }}$$

(2e)

$$\alpha = R_{A} + R_{B} - \left| {{\mathbf{r}}_{A} - {\mathbf{r}}_{B} } \right|$$

(2f)

$$S_{t} = 8G^{*} \sqrt {R^{*} \alpha }$$

(2g)

$$S_{n} = 2E^{*} \sqrt {R^{*} \alpha }$$

(2h)

$$\beta = \frac{\ln \varepsilon }{{\sqrt {\ln^{2} \varepsilon + \pi^{2} } }}$$

(2i)

$$m^{*} = \frac{{m_{A} m_{B} }}{{m_{A} + m_{B} }}$$

(2j)

$$\upsilon_{n}^{rel} = \left( {{{\varvec{\upupsilon}}}_{A} - {{\varvec{\upupsilon}}}_{B} } \right)n$$

(2k)

$$G^{*} = \frac{{2 - \upsilon_{A}^{2} }}{{G_{A} }} + \frac{{2 - \upsilon_{B}^{2} }}{{G_{B} }}$$

(2l)

$${\mathbf{n}} = \frac{{{\mathbf{r}}_{A} - {\mathbf{r}}_{B} }}{{\left| {{\mathbf{r}}_{A} - {\mathbf{r}}_{B} } \right|}}$$

(2m)

$$T_{i} = - \mu_{r} F_{n} R_{i} \omega_{i}$$

(2n)

The parameters in the above equation are defined as follows:

$E^{*}$ is the equivalent modulus of elasticity, Pa; $R^{*}$ is the equivalent particle radius, m; $\alpha$ is the normal overlap, m; $\delta$ is the tangential overlap, m; $S_{t}$ is the tangential stiffness, N/m; $S_{n}$ is the normal stiffness, N/m; $m^{*}$ is the equivalent mass, kg; $\upsilon_{n}^{rel}$ is the normal relative velocity, m/s; $\upsilon_{t}^{rel}$ is the tangential relative velocity, m/s; $\nu_{A}$,$\nu_{B}$ is the Poisson's ratio of the particles A&B; $E_{A}$,$E_{B}$ is the elastic modulus of the particle A&B, Pa; $R_{A}$,$R_{B}$ is the radius of the particle A&B, m; ${\mathbf{r}}_{A}$,${\mathbf{r}}_{B}$ is the spherical central position vector of the particle A&B, m; ${{\varvec{\upupsilon}}}_{A}$,${{\varvec{\upupsilon}}}_{B}$ is the velocity vector of the particles A&B before collision, m/s; ${\mathbf{n}}$ is the normal unit vector at the collision of the particles A&B; $G^{*}$ is the equivalent shear modulus, Pa; $\varepsilon$ is the recovery coefficient; $G_{A}$,$G_{B}$ is the shear modulus of the particle A&B, Pa; $\mu_{r}$ is the rolling friction factor; $R_{i}$ is the distance from the mass centre to the contact point, mm; ${{\varvec{\upomega}}}_{{\mathbf{i}}}$ is the Unit angular velocity vector of the object at the contact point, rad/s.

Simulation parameters

In the simulation, the rotor rotation speed is set to 30,000 rpm. A total of 5,000 powder particles were used in the analysis, and the simulation time was set to 0.05 s. Depending on the material of the rotor and particle, the coefficient of restitution, coefficient of static friction, and coefficient of rolling friction were selected as 0.1, 1.05, and 1.4, respectively. The Rayleigh wave method was utilized to determine the time step. Since the focus of this paper is on the launch speed and velocity of particles as they leave the rotor body, the annular grid area shown in Fig. 4 was used as the data acquisition area. In this area, is the instantaneous velocity of the particles can be determined as they are accelerated by the rotor. Figure 4 shows the configuration of the simulation model.

Figure 4

Simulation model. This figure illustrates the rotor-particle simulation modelling system utilized in this paper.

Box‒Behnken design (BBD)

The BBD method is typically used to design response surface tests and perform an accurate statistical analysis of the test data to obtain an image with continuous features so that the mapping between the factors and the response values can be investigated visually²⁴. In this article, a regression model needs to be developed using the particle ejection velocity V as the target quantity and the rotor parameters L₁, L₂, α₁, and α₂ as input factors. Then, the optimized design of the rotor can be achieved by solving the model. The use of the BBD response surface method allows complex unknown functional relationships between the target quantity and input factors to be fitted with simple primary or quadratic polynomial models over a small area, which is computationally easier and ensures the continuity of the predictive model. Using this method and performing ANOVA on their experimental data, this regression model can be obtained and solved for the optimal combination of parameters can be determined.

The empirical levels were determined based on the results obtained from the BBD tests shown in Table 4. Additionally, a preliminary analysis of the individual factors and a comprehensive consideration of their effects on acceleration was performed. To minimize measurement errors, each test was repeated three times and the mean values were recorded. The obtained results for each parameter level group are presented in Table 5.

Table 4 Factor ranges and levels.

Table 5 BBD experimental design and results.

Results

Based on the results of ANOVA presented in Table 6, the obtained P-value for the regression model is less than 0.0001, indicating that the regression model is highly significant. In the meantime, the obtained P-value for the model is more than 0.05, indicating that the model misfit is not significant and that the regression model fit is high. Furthermore, based on the contents of Table 7, the R² and adjusted R² values in the model are all close to one, indicating a good fit of the regression model. The predicted R² reasonably agrees with the adjusted R², with a difference of less than 0.2. The coefficient of variation and precision are 0.25% and 27.23, respectively, indicating that the fitted regression model has a high degree of reliability.

Table 6 Analysis of the variance for model.

Table 7 Fit statistics.

The P-values in Table 6 for the parameters L₁, L₂, α₁, and α₂ indicate that all four test factors have a highly significant effect on the injection velocity of particles. Among them, the effects of L₁, α₁, and α₂ are more significant compared to that of L₂. The presented results in Table 6 obtained from the one-way ANOVA confirm that the parameters L₁, α₁, and α₂ significantly affect the particle injection rate, while the effect of the parameter L₂ is relatively smaller.

The parameters L₁, L₂, α₁, and α₂ were selected as independent variables and denoted as x₁, x₂, x₃, and x₄, respectively. Moreover, the injection velocity of particles, denoted as V, was selected as the target variable. The least-squares method was employed to optimize the regression model. In the optimization process, four groups of single-factor first-order terms, four groups of single-factor second-order terms, and six groups of interactive-factor second-order terms were considered. Since the P-value reflects the significance of each factor in the model, when P ≤ 0.01, the factor is considered highly significant; when 0.01 < P < 0.05, the factor is significant; and when P ≥ 0.05, the factor is not significant. The model can be optimized according to the P-value of each factor. Consequently, the terms BC (interaction terms for L₂ and α₁) and B² (the quadratic term for L₂) with P > 0.05 were excluded from the model. The regression model for the injection rate V can be expressed as follows:

$$\begin{aligned} V & = 420.22 + 1.9488x_{1} + 0.0897x_{2} + 3.2078x_{3} + 4.3585x_{4} \\ & \;\;\; + 0.0037x_{1} x_{2} - 0.0257x_{1} x_{3} - 0.0279x_{1} x_{4} - 0.0115x_{2} x_{4} - 0.0306x_{3} x_{4} \\ & \;\;\; - 0.0047x_{1}^{2} - 0.0175x_{3}^{2} - 0.0344x_{4}^{2} \\ \end{aligned}$$

(3)

Discussion

The influence of the runners' shape parameters on the injection rate

The effect of the individual parameters on the injection velocity

Figure 5 provides insights into the influence of individual design parameters on the injection velocity. Figure 5a depicts the effect of L₁ on the injection rate when L₂, α₁, and α₂ are held constant at their median values. Similarly, Fig. 5b shows the impact of L₂ on the injection rate while maintaining L₁, α₁, and α₂ at their median values. Figure 5c demonstrates the influence of α₁ on the injection rate with L₁, L₂, and α₂ set at their median values. Finally, Fig. 5d illustrates the effect of α₂ on injection velocity when L₁, L₂, and α₁ are held constant at their median values.

Figure 5

Effects of the individual parameters on the injection speed. This figure illustrates the influence of the multi-model parameter interactions on the injection rate. Plot (a) shows the impact of L₁ on the injection rate while maintaining L₂, α₁, and α₂ at their median values. Plot (b) shows the impact of L₂ on the injection rate while maintaining L₁, α₁, and α₂ at their median values. Plot (c) shows the impact of α₁ on the injection rate while maintaining L₁, L₂, and α₂ at their median values. Plot (d) shows the impact of α₂ on the injection rate while maintaining L₁, L₂, and α₁ at their median values.

In general, the design parameters L₁, α₁, and α₂ exhibit a negative correlation with the injection velocity, while the parameter L₂ shows a positive correlation. The trend for each parameter can be described as follows:

• As the parameter L₁ increases from 40 to 60 mm, the injection velocity increases slightly. However, when L₁ exceeds 60 mm, the ejecta velocity decreases.

• When the parameter L₂ varies in the range of 20 mm to 60 mm, there is a positive correlation between L₂ and the ejection velocity.

• When the design parameters α₁ and α₂ increase from 30 to 50 and from 10 to 30, respectively, the ejection velocity decreases.

The results reveal that L₁, L₂, α₁, and α₂ affect the particle injection velocity. The optimized design involves setting the parameter L₁ around the median value (60 mm), selecting the maximal value of 60 mm for L₂, and choosing the minimum values (30 and 10) for α₁ and α₂, respectively. Meanwhile, it is necessary to analyse the interaction between various factors.

The influence of the multi-model parameter interactions on the injection rate

Design-Expert13 software was utilized to generate 3D response surface plots depicting the interaction effects of each shape parameter. The results align with those of the ANOVA analysis: $P_{{L_{1} \alpha_{2} }} (0.0001)$ < $P_{{L_{1} \alpha_{1} }} (0.0001)$ < $P_{{\alpha_{1} \alpha_{2} }} (0.0007)$ < $P_{{L_{2} \alpha_{2} }} (0.0058)$ < $P_{{L_{1} L_{2} }} (0.0196)$. The interaction between the L₁ and L₂ parameters exhibits the most substantial impact on the particle injection velocity among the various parameter interactions. Then the interaction between the parameters L₂ and α₂ has a comparatively smaller effect, while the interaction between the parameters α₁ and α₂ has a much smaller effect. Last, the interactions between the parameters L₂ and parameters α₂ and L₂ and α₂ exhibit the weakest effects. The interaction effects of the pair of parameters L₁ and L₂, L₂ and α₂, and α₁ and α₂ are analysed.

The interaction between the parameters L₁ (ranging from 40 to 90 mm) and L₂ (ranging from 20 to 60 mm) is illustrated in Fig. 6a, b. It is observed that as the values of L₁ increase and the values of L₂ decrease, the contour lines become along the 135 contour. This indicates a decrease in the jet velocity, which gradually transitions to an acceleration effect. Based on the distribution of the contours, the entire response surface has a maximum point of approximately 70 mm for L₁ and 50 mm for L₂. This implies that the length of each acceleration section should be relatively constant in a multi-segment model and that the difference in length should be minimized. For example, when L₁ = 90 mm and L₂ = 20 mm, the particle jet velocity reaches its minimum value.

Figure 6

Mapping of the interaction effects of the parameters L₁ and L₂. This figure consists of two pictures. Plot (a) shows the response surface of the parameters L₁ and L₂, and Plot (b) shows the contour plots of the parameters L₁ and L₂, both of which reflect the interaction between the two parameters.

Figure 7a, b illustrate the interaction effect of the parameters L₂ (20 mm to 60 mm) and α₂ (10–30). It is observed that for the parameter L₂ with a value of 60 mm and α₂ with a value of 10, the peak of the entire response surface is at the top right. Furthermore, the contours gradually concentrate in the direction of the lower right-hand corner, and the degree of curvature increases gradually indicating that as the value of α₂ is increased from 30 to 10, the effect on the L₂ increases gradually. This result demonstrates that a too-large angle between the acceleration sections affects the overall acceleration effect of the rotor.

Figure 7

Mapping of the interaction effects of the parameters L₂ and α₂. This figure consists of two plots. Plot (a) shows the response surface of the parameters L₂ and α₂, and Plot (b) shows the contour plots of the parameters L₂ and α₂, both of which reflect the interaction between the two parameters.

Figure 8a, b illustrate the interaction analysis of the parameters α₁ and α₂. When the parameters α₁ and α₂ vary in the range of 30 to 40 and 10 to 20, respectively, the value of the response face has a high level of significance. The results also show a decreasing contour that thickens along 45, indicating that the particle jet velocity drops significantly as large values are selected for the parameters α₁ and α₂. This finding further confirms that the angle between the accelerating sections should not be too large.

Figure 8

Mapping of the interaction effects of the parameters α₁ and α₂. This figure consists of two plots. Plot (a) shows the response surface of the parameters α₁ and α₂, and Plot (b) shows the contour plots of the parameters α₁ and α₂, both of which reflect the interaction between the two parameters.

Through the discussion of the independent effect of a single parameter and the interaction of multiple parameters on the spraying speed, we can conclude that the internal flow channel structure of the rotor has an important influence on the acceleration process of particles in which there exists a quantitative relationship between the structural parameters and the particle spraying speed (the acceleration capacity of the particles), which can be solved through the establishment of a mathematical model of this relationship. This change in acceleration is characterized by the acceleration process of powder particles in cold spraying^{25,26,27,28,29}, which can be achieved by changing the nozzle structure to increase the acceleration capacity. However, due to the lack of analysis of the overall force on the acceleration process of individual particles in the current study, it is not yet possible to completely correspond the change in the runner structure to the acceleration process of the particles, and therefore, the current acquisition of the mathematical model is still based on the statistical foundations.

Optimum parameters and verification

Based on the solution of the regression model with the injection velocity as a condition, the optimal parameters are L₁ = 77.37, L₂ = 58.67, α₁ = 39.74, and α₂ = 10.11. The regression prediction of the injection velocity based on these parameters was 585.439 m/s, as illustrated in Fig. 9. Subsequently, using these optimal parameters to model the throwing rotor and conducting EDEM simulation tests, a jet speed of 587.841 was obtained, with a 0.408% error compared to the model prediction. This indicates that the established regression model can effectively predict the velocity of the particle jet based on the rotor runner parameters. Simultaneously, the EDEM simulation test of the rotor with a through-hole runner showed a particle injection speed of 545.00 m/s as illustrated in Fig. 10. By optimizing the runner design, the particle injection speed was increased by 7.85%, demonstrating that the capability of the jet rotor can be improved through runner optimization.

Figure 9

Acceleration of particles by the rotor after parameters optimization. This figure illustrates the acceleration of the particles by the rotor after shape parameter optimization.

Figure 10

Acceleration of particles by the rotor with a through-hole runner. This figure illustrates the acceleration of the particles by the rotor with a through-hole runner.

Conclusions

In this paper, the particle accelerating rotor was used as a research object to investigate the effect of rotor parameters on its accelerating performance. Simulations of the particle acceleration by rotors with different parameters were conducted based on the discrete cell method. In addition, the rotor acceleration performances before and after parameter optimization were compared. The main conclusions can be summarized as follows.

• (1) In this study, the accelerated rotor is modelled using SolidWorks and its acceleration performance is simulated using EDEM. By analysing the simulation results of 25 groups of rotors, a multivariate nonlinear regression model is established for the first time based on rotor parameters.

• (2) By analysing the regression model, it is proven that all four modelling parameters have significant effects on the particle ejection velocity. It was found that L₁, α₁, and α₂ are negatively correlated with the injection speed, while L₂ exhibits a positive correlation. The interaction between L₁ and L₂ had the largest effect, followed by the interaction between L₂ and α₂, whereas the interaction between α₁ and α₂ had a smaller effect, and the interaction of the other factors was not significant.

• (3) The accelerating rotor parameters were optimized using a regression model for parametric optimization. By analysing the simulation results, the improvement in the rotor acceleration capacity before and after optimization is 7.85%.

The results show that the optimization of the rotor parameters can enhance the acceleration capacity for particles, which provides a feasible solution for improving the quality and efficiency of the centrifugal impact caused by metal powders. However, further improvement of this forming method requires in-depth studies of more complex rotor structures and forming environmental conditions, as well as the optimization of the forming process control strategies.