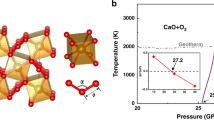
Abstract
Orthorhombic Ca2CO4 is a recently discovered orthocarbonate whose high-pressure physical properties are critical for understanding the deep carbon cycle. Here, we study the structure, elastic and seismic properties of Ca2CO4-Pnma at 20–140 GPa using first-principles calculations, and compare them with the results of CaCO3 polymorphs. The results show that the structural parameters of Ca2CO4-Pnma are in good agreement with the experimental results. It could be the potential host of carbon in the Earth's mantle subduction slab, and its low wave velocity and small anisotropy may be the reason why it cannot be detected in seismic observation. The thermodynamic properties of Ca2CO4-Pnma at high temperature and high pressure are obtained using the quasi-harmonic approximation method. This study is helpful in understanding the behavior of Ca-carbonate in the Earth’s lower mantle conditions.
Similar content being viewed by others
Introduction
As the most important carbonate, CaCO3 is transported to the deep mantle by subduction slab and plays a crucial role in the global long-term carbon cycle1. It is also a mineral that plays a key role in biomineralization2. However, CaCO3 undergoes a series of phase transitions under high temperature and high pressure, forming various structures and polymorphs. So far, the predicted structures are mainly calcite, aragonite, post-aragonite, and pyroxene-like3,4,5,6,7,8,9, and these structures and polymorphs have been experimentally verified3,4,6,9,10,11,12,13,14,15. Some studies also considered the reaction of calcium carbonate with MgO, SiO2, and MgSiO37,10,16,17, while ignoring the reaction with CaO. Previously, Al-Shemali and Boldyrev18 mentioned the possible formation of calcium orthocarbonate Ca2CO4 in the CaCO3 + CaO system under high pressure. Recently, using AIRSS19 and USPEX20 crystal structure prediction methods, Sagatova et al.21 discovered a new structure of calcium orthocarbonate Ca2CO4 (space group Pnma) stable at 13–50 GPa and 2000 K, the carbon atoms in this phase are fourfold coordinated, and the structure is similar to high temperature and high pressure α'H-Ca2SiO4 phase22. Afterward, they found that Ca2CO4-Pnma was stable in the pressure and temperature range of 20–100 GPa and 1000–2000 K using the density functional theory within quasi-harmonic approximation23. Subsequently, Binck et al.24 verified the results of Sagatova et al.23 with single-crystal diffraction experiments. In addition, other alkaline earth orthocarbonates, Mg2CO4-Pnma25, Mg2CO4-P21/c25, Sr2CO4-Pnma26, and Ba2CO4-Pnma26 have also been predicted, of which Sr2CO4-Pnma27 and Mg2CO4-P21/c28 have been experimentally verified.
The elastic, seismic, and thermodynamic properties of Ca2CO4-Pnma under high pressure have not been investigated so far. Even the elastic constants of CaCO3 polymorphs were only the experimental results of calcite29,30,31,32 and aragonite33,34 at ambient conditions. Using the first-principles method, Belkofsi et al. calculated the elastic constants of three calcite polymorphs(calcite-III, calcite-IIIb, calcite-VI)35, and Huang et al. studied the elastic properties of aragonite, post-aragonite and P21/c36. The thermal expansion coefficient37,38,39,40,41,42 and heat capacity37,43,44,45 of calcite and aragonite were measured at ambient conditions, where there was a large difference between the fitted thermal expansion coefficient.
In this work, the structural properties, elastic properties, and seismic properties of Ca2CO4-Pnma at 20–140 GPa are studied using the first-principles calculations based on density functional theory and are compared with the results of CaCO3 polymorphs. The thermodynamic properties of Ca2CO4-Pnma are obtained by quasi-harmonic approximation method.
Methods
First-principles calculations are done with using the VASP package46,47 with projector-augmented wave48. The exchange–correlation interactions adopt the Perdew-Burke-Ernzerhof functional within the generalized gradient approximation49. The electronic configurations of the atoms are Ca: 3s23p64s2, C: 2s22p2, O: 2s22p4, respectively. The cutoff energy of the plane-wave basis is set to 900 eV. The k-point mesh generation and data processing are obtained by vaspkit program50. The k-points mesh of Ca2CO4-Pnma, calcite, aragonite, P21/c-l, post-aragonite, P21/c-h and C2221 are set to 5 × 7 × 4, 9 × 9 × 2, 7 × 4 × 6, 7 × 10 × 3, 8 × 7 × 8, 8 × 10 × 4, and 6 × 5 × 10 using the Monkhorst–Pack scheme51, respectively. The convergence criteria for energy and force are 1.0⨯10–8 eV and 0.02 eV/Å, respectively. Based on the optimized lattice structure, the stress–strain method is used to obtain the elastic stiffness tensor. In order to ensure the accuracy of the elastic constants of Ca2CO4-Pnma, the elastic constants of calcite and aragonite are calculated and compared with the available experimental results32,33. As shown in Table S1 (see Supplementary Material), the calculated results are in good agreement with the experimental results32,33. The thermodynamic properties are calculated using the quasi-harmonic approximation method52 of the PHONOPY program53,54, and the force constants are calculated using the density functional perturbation theory55. The supercells of aragonite and Ca2CO4-Pnma adopt 2 × 2 × 2 and 2 × 2 × 1 unit cells, respectively. The convergence tests of the phonon spectrum calculations of aragonite and Ca2CO4-Pnma are shown in Tables S2, S3, and Figs. S1–S8 (see Supplementary Material).
Results and discussion
Structural properties
The lattice parameters and equations of state for Ca2CO4-Pnma are presented in Fig. 1. It is found that the calculated results are in good agreement with the available experimental24 and previous theoretical results21,24, indicating the validity of the structure. The sensitivity of the axis to compression is c > b > a. The unit-cell volume at 0 GPa is 303.38 Å3 and the bulk modulus and its first pressure derivative are K0 = 113.40 GPa and K0′ = 4.00 by fitting the third-order Birch–Murnaghan equation, respectively, which are consistent with the results (V0 = 302.0(3) Å3, K0 = 108(1) GPa, and K0′ = 4.43(3)) of Binck et al.24.
In order to better understand the elastic and seismic properties of Ca2CO4-Pnma, the candidate CaCO3 structures (aragonite, P21/c-l, post-aragonite, P21/c-h, C2221, ‘− l = low pressure’, ‘− h = high pressure’) in the Earth's mantle are considered. The relative stabilities of the CaCO3 polymorphs considered in this work are evaluated from their enthalpies. According to Fig. S9 (see Supplementary Material), P21/c-l stabilizes above 30 GPa and retains its stability up to 46 GPa, while P21/c-h stabilizes above 75 GPa and retains its stability up to at least 140 GPa, which are consistent with the experimental and previous theoretical results3,5. CaCO3-C2221 above 137 GPa is stable relative to post-aragonite, but this does not make any sense5,56. Because in this interval, the modification P21/c-h is more favorable. For comparison with calcium orthocarbonate, four modifications of CaCO3 must be considered, namely aragonite (20–35 GPa), P21/c-l (35–45 GPa), post-aragonite (45–75 GPa) and P21/c-h (75–140 GPa).
Elastic properties
The calculated elastic constants of Ca2CO4-Pnma are shown in Fig. 2 and Table 1. Within the studied pressure range, \(c_{11} > c_{22} > c_{33}\), indicating that compression is easier along the c-axis than along the a- and b-axes. These results are consistent with those of Fig. 1, where the lattice parameter c decreases faster than the lattice parameters a and b with increasing pressure. The calculated elastic constants of CaCO3 polymorphs are shown in Figs. S10–S13 and Tables S4–S7 (see Supplementary Material), respectively. Therefore, we believe that the calculated elastic constants are correct, but experimental verification is required.
The bulk modulus (B) and shear modulus (G) of Ca2CO4-Pnma can be obtained by the Voigt57-Reuss58-Hill59 scheme. As can be seen from Fig. 3 and Table 1, B is greater than G, indicating that with the change of volume, Ca2CO4-Pnma is more and more difficult to be compressed, and G is the main factor for the deformation of Ca2CO4-Pnma. The B and G of Ca2CO4-Pnma at < 75 GPa are larger than those of CaCO3 polymorphs. The B of Ca2CO4-Pnma at 75–140 GPa is equal to that of P21/c-h, and the G is slightly larger and almost parallel.
In order to evaluate the elastic anisotropy of Ca2CO4-Pnma, we adopt the scheme of Ravindran et al.60. The shear anisotropic factors of A100 in (100) plane, A010 in (010) plane, and A001 in (001) plane can be obtained from the following expression:
The variation of shear anisotropic factors A100, A010 and A001 of Ca2CO4-Pnma with pressure is displayed in Fig. 4 and Table 1. A010 and A001 gradually decrease with increasing pressure, A100 first increases with the increase of pressure, and then gradually decreases at > 40 GPa. It can also be found that the elastic anisotropy of Ca2CO4-Pnma in the lower mantle conditions is very small, and the anisotropy of the (010) plane between [101] and [001] directions is the smallest.
The compressional and shear wave velocities of minerals can be calculated from the elastic constants and densities. The compressional (VP) and shear (VS) wave velocities of Ca2CO4-Pnma and CaCO3 polymorphs can be obtained from the Navier's equations61:
The densities and wave velocities of Ca2CO4-Pnma, CaCO3 polymorphs and the Preliminary Reference Earth Model (PREM)62 are displayed in Fig. 5 and Table 1. From Fig. 5a, it is found that the densities of Ca2CO4-Pnma in the lower mantle is less than those of PREM, and greater than those of CaCO3 polymorphs. As shown in Fig. 5b, the VP and VS of CaCO4-Pnma and CaCO3 polymorphs are lower than those of PREM, and the VP and VS of Ca2CO4-Pnma are greater than those of P21/c-l and post-aragonite, which are almost the same as those of P21/c-h. The wave velocities in various crystallographic directions can be obtained by solving the Christoffel equation \(\left| {C_{ijkl} n_{j} n_{l} - \rho V^{2} \delta_{ik} } \right| = 0\)63. Figure 6 shows the wave velocities of Ca2CO4-Pnma along different crystallization directions at various pressures. The VP of Ca2CO4-Pnma propagates the fastest in the [100] direction. The shear fast-wave velocity propagates the slowest in the [001] direction. With the increase of pressure, the propagation in the [100] and [010] directions become slower. The shear slow-wave velocity in [100] direction propagates more and more slowly as pressure increases.
Wave velocities of Ca2CO4-Pnma along different crystallization directions at various pressures. Made using the AWESoMe program64.
The anisotropy AP of the compressional waves and the polarization anisotropy AS of the shear waves are defined as65:
Figure 7 and Table 1 show the AP and AS of Ca2CO4-Pnma and CaCO3 polymorphs. It can be seen that the seismic anisotropy AP and AS of Ca2CO4-Pnma are less than those of CaCO3 polymorphs, and decrease with the increase of pressure, and gradually increase at > 45 GPa. The nonlinear dependence of seismic anisotropy on pressure can be attributed to the nonlinear pressure sensitivity of the wave velocity, which is caused by the nonlinear pressure dependence of its elastic modulus, especially the shear modulus.
The seismic properties of Ca2CO4-Pnma indicate that it could be the potential host of carbon in the subduction slab and coexists with CaCO3 polymorphs, as suggested by Sagatova et al.21,23. It was also verified by Binck et al.24. The low wave velocity and small anisotropy of Ca2CO4-Pnma may be one of the reasons why it is impossible to detect the presence of carbonate in the lower mantle during the seismic observation of the subduction slab.
Thermodynamic properties
The thermodynamic parameters of minerals are a prerequisite for deriving the thermal state of the Earth's interior. In order to obtain the variation of thermodynamic parameters of Ca2CO4-Pnma with temperature and pressure, we first verify the constant pressure heat capacity CP of aragonite at 0 GPa, and find that the calculated results are in good agreement with the experimental results44(Fig. 8). On this basis, the predicted heat capacity and thermal expansion coefficient \(\alpha\) of Ca2CO4-Pnma are shown in Figs. 9 and 10, respectively.
Figure 9 shows that the constant capacity heat capacity CV increases sharply with increasing temperature at low temperatures. Due to the suppression of non-harmonic effects under high pressure, the constant volume heat capacity CV under high pressure and high temperature is very close to the Dulong Petit limit. The constant pressure heat capacity CP is very close to the constant capacity heat capacity CV. In addition, the effects of temperature and pressure on constant capacity heat capacity CV and constant pressure heat capacity CP are opposite, and the impact of temperature is more noteworthy.
It can be seen from Fig. 10 that thermal expansion coefficient α at low temperature increases rapidly with the increase of temperature and tends to flatten rapidly with the increase of temperature. With the increase of pressure, the thermal expansion coefficient \(\alpha\) decreases rapidly, and the influence of temperature becomes less and less obvious, resulting in linear high temperature behavior.
Conclusions
On the basis of the determination of the stability for CaCO3 polymorphs in the lower mantle conditions and the verification of the structural parameters of Ca2CO4-Pnma, we study the elastic, seismic and thermodynamic properties of Ca2CO4-Pnma, and compared the results with those of CaCO3 polymorphs. The research shows that the densities of Ca2CO4-Pnma in the lower mantle are greater than those of CaCO3 polymorphs, and the seismic anisotropies are less than those of CaCO3 polymorphs. The wave velocities of Ca2CO4-Pnma and CaCO3 polymorphs are relatively low, and the wave velocities of Ca2CO4-Pnma and CaCO3-P21/c-h are almost the same. This means that the presence of carbonate in the lower mantle is unlikely to be detected by seismic observations of subducted slab. By verifying the constant pressure heat capacity of aragonite at 0 GPa, the thermodynamic properties of Ca2CO4-Pnma at high temperature and high pressure are calculated using the quasi-harmonic approximation method. The results of this study are helpful to better understand the behavior of calcium carbonate in the lower mantle conditions.
Data availability
The datasets used and/or analyzed during the current study available from the corresponding author on reasonable request.
References
Gao, J., Wu, X., Yuan, X. & Su, W. Fate of carbonates in the Earth’s mantle (10–136 GPa). Front. Earth Sci. 10, 837775 (2022).
Lowenstam, H. A. & Weiner, S. On Biomineralization (Oxford University Press, 1989).
Gavryushkin, P. N. et al. Aragonite-II and CaCO3-VII: New high-pressure, high-temperature polymorphs of CaCO3. Cryst. Growth Des. 17, 6291–6296 (2017).
Oganov, A. R., Glass, C. W. & Ono, S. High-pressure phases of CaCO3: Crystal structure prediction and experiment. Earth Planet. Sci. Lett. 241, 95–103 (2006).
Pickard, C. J. & Needs, R. J. Structures and stability of calcium and magnesium carbonates at mantle pressures. Phys. Rev. B 91, 104101 (2015).
Smith, D. et al. Postaragonite phases of CaCO3 at lower mantle pressures. Phys. Rev. Mater. 2, 013605 (2018).
Zhang, Z. G., Mao, Z., Liu, X., Zhang, Y. G. & Brodholt, J. Stability and reactions of CaCO3 polymorphs in the Earth’s deep mantle. J. Geophys. Res. 123, 6491–6500 (2018).
Gavryushkin, P. N., Sagatov, N., Belonoshko, A. B., Banaev, M. V. & Litasov, K. D. Disordered aragonite: The new high-pressure, high-temperature phase of CaCO3. J. Phys. Chem. C 124, 26467–26473 (2020).
Bayarjargal, L., Fruhner, C. J., Schrodt, N. & Winkler, B. CaCO3 phase diagram studied with Raman spectroscopy at pressures up to 50 GPa and high temperatures and DFT modeling. Phys. Earth Planet. Inter. 281, 31–45 (2018).
Li, X. et al. New high-pressure phase of CaCO3 at the topmost lower mantle: Implication for the deep-mantle carbon transportation. Geophys. Res. Lett. 45, 1355–1360 (2018).
Ono, S., Kikegawa, T., Ohishi, Y. & Tsuchiya, J. Post-aragonite phase transformation in CaCO3 at 40 GPa. Am. Mineral. 90, 667–671 (2005).
Lobanov, S. S. et al. Raman spectroscopy and x-ray diffraction of sp3 CaCO3 at lower mantle pressures. Phys. Rev. B 96, 104101 (2017).
Ono, S., Kikegawa, T. & Ohishi, Y. High-pressure transition of CaCO3. Am. Mineral. 92, 1246–1249 (2007).
Lv, M., Liu, J., Greenberg, E., Prakapenka, V. & Dorfman, S. Thermal equation of state of post-aragonite CaCO3-Pmmn. Am. Mineral. 105, 1365–1374 (2020).
Druzhbin, D., Rashchenko, S. V., Shatskiy, A. & Crichton, W. A. New high-pressure and high-temperature CaCO3 polymorph. ACS Earth Space Chem. 6, 1506–1513 (2022).
Seto, Y., Hamane, D., Nagai, T. & Fujino, F. Fate of carbonates within oceanic plates subducted to the lower mantle, and a possible mechanism of diamond formation. Phys. Chem. Miner. 35, 223–229 (2008).
Drewitt, J. W. E. et al. The fate of carbonate in oceanic crust subducted into earth’s lower mantle. Earth Planet. Sci. Lett. 511, 213–222 (2019).
Al-Shemali, M. & Boldyrev, A. I. Search for ionic orthocarbonates: Ab initio study of Na4CO4. J. Phys. Chem. A 106, 8951–8954 (2002).
Pickard, C. J. & Needs, R. J. Ab initio random structure searching. J. Phys.: Condens Matter 23, 053201 (2011).
Oganov, A. R. & Glass, C. W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 124, 244704 (2006).
Sagatova, D., Shatskiy, A., Sagatov, N., Gavryushkin, P. N. & Litasov, K. D. Calcium orthocarbonate, Ca2CO4-Pnma: A potential host for subducting carbon in the transition zone and lower mantle. Lithos 370–371, 105637 (2020).
Belmonte, D., Ottonello, G. & Zuccolini, M. V. Ab initio-assisted assessment of the CaO–SiO2 system under pressure. Calphad 59, 12–30 (2017).
Sagatova, D. N., Shatskiy, A. F., Gavryushkin, P. N., Sagatov, N. E. & Litasov, K. D. Stability of Ca2CO4-Pnma against the main mantle minerals from ab initio computations. ACS Earth Space Chem. 5, 1709–1715 (2021).
Binck, J. et al. Synthesis of calcium orthocarbonate, Ca2CO4-Pnma at P-T conditions of Earth’s transition zone and lower mantle. Am. Mineral. 107, 336–342 (2022).
Gavryushkin, P. N., Sagatova, D. N., Sagatov, N. & Litasov, K. D. Formation of Mg-orthocarbonate through the reaction MgCO3+MgO=Mg2CO4 at Earth’s lower mantle P–T conditions. Cryst. Growth Des. 21, 2986–2992 (2021).
Gavryushkin, P. N., Sagatova, D. N., Sagatov, N. & Litasov, K. D. Orthocarbonates of Ca, Sr, and Ba-the appearance of sp3-hybridized carbon at a low pressure of 5 GPa and dynamic stability at ambient pressure. ACS Earth Space Chem. 5, 1948–1957 (2021).
Spahr, D. et al. Tetrahedrally coordinated sp3-hybridized carbon in Sr2CO4 orthocarbonate at ambient conditions. Inorg. Chem. 60, 5419–5422 (2021).
Gavryushkin, P. N. et al. First experimental synthesis of Mg orthocarbonate by the MgCO3+MgO=Mg2CO4 reaction at pressures of the Earth’s lower mantle. JETP Lett. 116, 477–484 (2022).
Chen, C.-C., Lin, C.-C., Liu, L.-G., Sinogeikin, S. V. & Bass, J. D. Elasticity of single-crystal calcite and rhodochrosite by Brillouin spectroscopy. Am. Mineral. 86, 1525–1529 (2001).
Dandekar, D. P. Variation in the elastic constants of calcite with temperature. J. Appl. Phys. 39, 3694–3699 (1968).
Dandekar, D. P. Pressure dependence of the elastic constants of calcite. Phys. Rev. 172, 873–877 (1968).
Hearmon, R. F. S., The elastic constants of crystals and other anisotropic materials. K. H. Hellwege, A. M. Hellwege, Eds., Landolt-Bornstein Tables,III/11 (Springer-Verlag, 1979).
Liu, L.-G., Chen, C.-C., Lin, C.-C. & Yang, Y.-J. Elasticity of single-crystal aragonite by Brillouin spectroscopy. Phys. Chem. Minerals 32, 97–102 (2005).
Hearmon, R. F. S. The elastic constants of anisotropic minerals. Rev. Mod. Phys. 8, 409–440 (1946).
Belkofsi, R., Adjaoud, O. & Belabbas, I. Pressure induced phase transitions and elastic properties of CaCO3 polymorphs: a density functional theory study. Modell. Simul. Mater. Sci. Eng. 26, 065004 (2018).
Huang, D. et al. Elastic properties of CaCO3 high pressure phases from first principles. Chin. Phys. B 26, 089101 (2017).
Litasov, K. D. et al. P-V-T equation of state of CaCO3 aragonite to 29 GPa and 1673 K: In situ X-ray diffraction study. Phys. Earth Planet. Inter. 265, 82–91 (2017).
Palaich, S. E. M. et al. High-pressure compressibility and thermal expansion of aragonite. Am. Mineral. 101, 1651–1658 (2016).
Li, Y. et al. P-V-T equation of state and high-pressure behavior of CaCO3 aragonite. Am. Mineral. 100, 2323–2329 (2015).
Antao, S. M. & Hassan, I. Temperature dependence of the structural parameters in the transformation of aragonite to calcite, as determined from in situ synchrotron powder X-ray-diffraction data. Can. Mineral. 48, 1225–1236 (2010).
Matas, J., Gillet, P., Ricard, Y. & Martinez, I. Thermodynamic properties of carbonates at high pressures from vibrational modelling. Eur. J. Mineral. 12, 703–720 (2000).
Martinez, I., Zhang, J. & Reeder, R. J. In situ X-ray diffraction of aragonite and dolomite at high pressure and high temperature: Evidence for dolomite breakdown to aragonite and magnesit. Am. Mineral. 81, 611–624 (1996).
Lucas, A., Mouallem-Bahout, M., Carel, C., Gaude, J. & Matecki, M. Thermal expansion of synthetic aragonite condensed review of elastic properties. J. Solid State Chem. 146, 73–78 (1999).
Staveley, L. A. K. & Linford, R. G. The heat capacity and entropy of calcite and aragonite, and their interpretation. J. Chem. Thermodyn. 1, 1–11 (1969).
Robie, R. A., Hemingway, B. S. & Fisher, J. R., Thermodynamic properties of minerals and related substances at 298.15 K and 1 bar (105 pascals) pressure and at higher temperatures. Bulletin (U.S. G.P.O, 1978).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total enery calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Wang, V., Xu, N., Liu, J. C., Tang, G. & Geng, W. T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 267, 108033 (2021).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Togo, A., Chaput, L., Tanaka, I. & Hug, G. First-principles phonon calculations of thermal expansion in Ti3SiC2, Ti3AlC2, and Ti3GeC2. Phys. Rev. B 81, 174301 (2010).
Togo, A. & Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 108, 1–5 (2015).
Togo, A. First-principles phonon calculations with phonopy and phono3py. J. Phys. Soc. Jpn. 92, 012001 (2023).
Gonze, X. & Lee, C. Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory. Phys. Rev. B 55, 10355–10368 (1997).
Yao, X., Xie, C., Dong, X., Oganov, A. R. & Zeng, Q. Novel high-pressure calcium carbonates. Phys. Rev. B 98, 014108 (2018).
Voigt, W. Lehrbuch der Kristallphysik-mit Ausschluß der Kristalloptik (Vieweg+Teubner Verlag, 1966).
Reuss, A. Calulation of yielding mixed crystals plasticity condition for single crystals. Z. Angew. Math. Mech. 9, 49–58 (1929).
Hill, R. The elastic behavior of a crystalline aggregate. Proc. Phys. Soc. Lond. 65A, 349–354 (1952).
Ravindran, P. et al. Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi2. J. Appl. Phys. 84, 4891–4904 (1998).
Anderson, O. L. A simplified method for calculating the debye temperature from elastic constants. J. Phys. Chem. Solids 24, 909–917 (1963).
Dziewonski, A. M. & Anderson, D. L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 25, 297–356 (1981).
Every, A. G. General closed-form expressions for acoustic waves in elastically anisotropic solids. Phys. Rev. B 22, 1746–1760 (1980).
Muñoz-Santiburcio, D. & Hernández-Laguna, A. AWESoMe 1.1: A code for the calculation of phase and group velocities of acoustic waves in homogeneous solids. Comput. Phys. Commun. 217, 212–214 (2017).
Kiefer, B., Stixrude, L., Hafner, J. & Kresse, G. Structure and elasticity of wadsleyite at high pressures. Am. Mineral. 86, 1387–1395 (2001).
Acknowledgements
This work is supported by the Industrial Support and Guidance Project of Colleges and Universities of Gansu Province (No. 2022CYZC-37), the Key Natural Science Foundation of Gansu Province (No. 20JR5RA211) and the Talent Innovation and Entrepreneurship Project of Lanzhou City (No. 2020-RC-18).
Author information
Authors and Affiliations
Contributions
Z.-J.L. designed the calculations and wrote the manuscript. X.-W.S., C.-R.Z. and Z.-L.L analyzed the results. T.L., T.S. and X.-D.W. performed partial calculations. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, ZJ., Li, T., Sun, XW. et al. First-principles study on the high-pressure physical properties of orthocarbonate Ca2CO4. Sci Rep 13, 11422 (2023). https://doi.org/10.1038/s41598-023-38604-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-023-38604-w
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.