Abstract
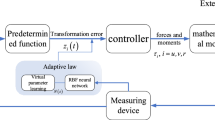
An adaptive finite time trajectory tracking control method is presented for underactuated unmanned marine surface vessels (MSVs) by employing neural networks to approximate system uncertainties. The proposed algorithm is developed by combining event-triggered control (ETC) and finite-time convergence (FTC) techniques. The dynamic event-triggered condition is adopted to avert the frequent acting of actuators using an adjustable triggered variable to regulate the minimal inter-event times. While solving the system uncertainties and asymmetric input saturation, an adaptive neural networks based backstepping controller is designed based on FTC under bounded disturbances. In addition, via Lyapunov approach it is proved that all signals in the closed-loop system are semi-global uniformly ultimately bounded. Finally, simulations results are shown to demonstrate the effectiveness of this proposed scheme.
Similar content being viewed by others
Introduction
Ships sailing under complex sea conditions have great dynamic uncertainty. The unknown time-varying interference and the limited communication resources affect the trajectory tracking of underactuated surface ships. There are many urgent problems in the trajectory tracking control and actual navigation engineering. An effective control scheme is very important for MSVs1,2,3,4,5, which is conducive to improving the tracking accuracy of ships and enabling them to complete the tracking task safely and efficiently. To make the control scheme easier to implement in engineering practice, many practical factors need to be considered, such as input saturation, state constraints, communication resource constraints, etc.
The MSV trajectory tracking system is a classical nonlinear control system. The increased efforts have been taken to research the motion control of this system in the past decades. Control laws are designed for MSV to track the time referenced trajectory or virtual objects6. It is significant to apply trajectory tracking in scenarios of way-point navigation, reconnaissance and surveillance. Attentions have been paid to trajectory tracking control both in theory and practice7,8,9. The paper10 studied the robust tracking control of underactuated surface vessels with parameters uncertainties using sliding mode control technique. The paper11 constructed an observer to estimate unknown disturbances and design a robust trajectory tracking controller through backstepping method for MSVs. Lekkas12 applied a tracking guidance system for MSVs considering unknown ocean currents. Moreover, linear algebra method13, sampled-data approach14 and model predictive nonlinear control15 have been adopted to design the trajectory tracking controller for MSVs.
When designing the trajectory tracking controller, difficulties caused by external disturbances and dynamic uncertainty need to be conquered. Thus, neural networks16,17,18, fuzzy logic19,20,21,22,23, sliding mode24 and adaptive backstepping25,26,27 have been continuously integrated and applied for the trajectory tracking control of MSVs. Adaptive control based on neural networks was used to approximate uncertainty and disturbance of nonlinear system28,29. The update laws of parameters were designed based on Lyapunov theorem.
The tracking ability of MSVs within limited time help to avoid collision with target ships and obstacles urgently and reasonably and improve the safety in complex environment. For realizing fast tracking control, finite time control of MSVs is designed to track desired trajectory within a limited time. The paper30 proposed a novel hyperbolic tangent guidance method to cooperatively control the course of the ship, and designed the controller using terminal non-singular sliding mode technology. The finite time control scheme greatly improves the convergence speed of the system. However, with the improvement of control accuracy, high energy consumption is often required and it also undoubtedly increase the wear and tear of the thrusters and controllers. In order to solve such problems, event-triggered technology has been applied. Tabuada31 first developed an event-triggered control scheme with static trigger conditions. The applications of event-triggered in ship motion and control have been further developed in papers32,33.
This paper presents a trajectory tracking control algorithm for unmanned MSVs with external disturbances considering saturation problem of actuators. The contributions of this paper have been summarized.
-
(1)
Gaussian error functions are introduced to explore saturation non-linearity which is represented by the continuous derivative formulation.
-
(2)
Based on finite time control, RBF neural networks is applied for the adaptive backstepping control method of MSVs with disturbances and actuator saturation.
-
(3)
Stability analysis is provided for the closed-loop systems. It proves all the states are semi-globally uniformly ultimately bounded. Tracking error converges to a small neighborhood of origin.
This paper is organized as follows. Section “Preliminaries and problem statements” states some useful preliminaries and problem formulation. Section “Controller design” is devoted to the algorithm of designing the trajectory tracking for MSVs. Simulations of the proposed control approach are introduced in Section “Stability proof”. Finally in Section “Simulation”, we make conclusions and propose further work.
Preliminaries and problem statements
Preliminaries
Notations
In this paper, \(\left| \cdot \right|\) denotes the absolute value of a scalar or each component for a vector. For example, \({\text{x}} \in {\mathbb{R}}^{n}\) is a vector, \(\left| x \right| = \left[ {\left| {x_{{1}} } \right|,\left| {x_{2} } \right|,....\left| {x_{n} } \right|} \right]^{T}\). \(\left\| \cdot \right\|\) denotes the Euclidean norm of a vector or the Frobenius norm of a matrix. \({\text{tr}}\left( X \right)\) represents its trace with the property \({\text{tr}}\left( {X^{{\text{T}}} X} \right) = \left\| X \right\|^{2}\) for a matrix \(X \in {\mathbb{R}}^{n \times n}\) and \(a < b\) represents \(a_{i} < b_{i} ,\;\)\(i = 1,2,...,n\) for any vectors \(a \in {\mathbb{R}}^{n}\) and \(b \in {\mathbb{R}}^{n}\).
RBFNNs approximation
By using RBFNNs34, an unknown smooth nonlinear function \(f\left( x \right)\), \({\mathbb{R}}^{m} \to {\mathbb{R}}\) can be approximated in a compact set \(\Omega \subseteq {\mathbb{R}}^{m}\) as bellow
where \(\Delta\) is the approximation error that is bounded over \(\Omega\), namely, \(\Delta \le \overline{\Delta }\), \(\overline{\Delta }\) is an unknown constant. \(\omega^{*} \in {\mathbb{R}}^{l}\) represents the optimal weight vector, \(l\) the node number of the NNs.
\(\omega^{*} \in {\mathbb{R}}^{l}\) is defined as
where \(\hat{\omega }\) is the estimation of \(\omega^{*}\). \(\Phi \left( x \right) = \left[ {\Phi_{{1}} \left( x \right),...,\Phi_{l} \left( x \right)} \right]^{T}\): \(\Omega \to {\mathbb{R}}^{l}\) represents the RBF vector and elements are chosen as the Gaussian functions
where \(\mu_{i} \in {\mathbb{R}}^{m}\) is the center and \(\varepsilon_{i} \in {\mathbb{R}}^{m}\) is the spread.
Asymmetric inputs saturation
An auxiliary system is designed to describe the inputs saturation nonlinearity for backstepping method. This smooth auxiliary system with the asymmetric saturation nonlinearity is formulized as
where \(\tau_{i}^{ + }\),\(\tau_{i}^{ - }\) are the upper and lower bounds of the actuator,\({\text{sign}} \left( {\varphi_{i} } \right)\) is the standard sign function, and \(erf{(} \cdot {)}\) is a Gaussian error function with \(erf{(}x{) = }\frac{2}{\sqrt \pi }\int_{{0}}^{x} {e^{{ - t^{2} }} } dt\). It shows the saturation limitation with smooth form in Fig. 2, with \(\tau_{i}^{ + } = 5\),\(\tau_{i}^{ - } = - 2.5\), and the input signal \(\varphi \left( t \right) = 10{\text{sin}}\left( {2t} \right)\).
Remark 1
For the lower and upper bounds of \(\tau_{i}^{ + }\),\(\tau_{i}^{ - }\), if \(\left| {\tau_{i}^{ + } } \right| = \left| {\tau_{i}^{ - } } \right|\),the saturation model is symmetric, else if \(\left| {\tau_{i}^{ + } } \right| \ne \left| {\tau_{i}^{ - } } \right|\) means the actuator has asymmetric saturation.
MSV model
Neglecting the motions in heave, pitch and roll, the three degrees-of-freedom nonlinear mathematical model of the MSV with disturbances can be considered as Ref.11
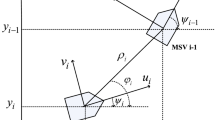
where \(\left( {x,\,y} \right)\) is the position of the ship,\(\psi\) is yaw angle. \(u\), \(v\), and \(r\) are the surge, the sway and the angular velocity of yaw, respectively.
Their derivatives are shown as
where \(\begin{array}{*{20}l} \tau \hfill \\ \end{array}_{u} = \varphi_{u} + \sigma {(}\varphi_{u} {)}\) and \(\begin{array}{*{20}l} \tau \hfill \\ \end{array}_{r} = \varphi_{r} + \sigma {(}\varphi_{r} {)}\) are the inputs, \(d_{u}\),\(d_{u}\) and \(d_{u}\) are unknown dynamics and disturbances. \(f_{u} \left( {u,v,r} \right)\), \(f_{v} \left( {u,v,r} \right)\) and \(f_{r} \left( {u,v,r} \right)\) are the terms of high order dynamics.
Assumption 1
The reference signal is a desired smooth function \(\eta_{r} \left( {x_{r} ,\,y_{r} ,\,\psi_{r} } \right)\) which are bounded and have the bounded first and second times of derivatives \(\dot{\eta }_{r} ,\,\ddot{\eta }_{r}\).There exists a positive constant \(B_{{0}}\) with such condition that \(\left\| {\eta_{r} } \right\|^{2} + \;\left\| {\dot{\eta }_{r} } \right\|^{2} + \left\| {\ddot{\eta }_{r} } \right\|^{2} \le B_{{0}}\).
Assumption 2
Assume that the control command \(\tau\), the unknown disturbances \(d\) and the optimal weight vector \(\omega^{*}\) are bounded.
Definition 1
(35). Given a nonlinear system \(\dot{x} = f\left( {x,t} \right),\;x \in {\mathbb{R}}^{n} ,\;t \ge t_{{0}}\), the solution of the above system is semi-globally uniformly ultimately bounded if for any \(\Omega_{{0}}\), a compact subset of \({\mathbb{R}}^{n}\) and all \(\dot{x}\left( {t_{{0}} } \right) = f\left( {x,t} \right),\;x \in \Omega_{{0}}\), there exists \(S > {0}\) and a number \(T\left( {S,X\left( {t_{{0}} } \right)} \right)\) such that \(\left\| {X\left( t \right)} \right\| \le S\) for all \(t \ge t_{{0}} + T\).
Lemma 1
(35). The condition \(\dot{V}\left( x \right) + \lambda_{1} V\left( x \right) + \lambda_{2} V^{l} \left( x \right) \le 0\) is satisfied by the existence of real number \(\lambda_{1} > 0,\lambda_{2} > 0,l \in \left( {0,1} \right)\) and an open-loop neighborhood near the origin. Then the origin is stable in finite time, and the stable time is
Lemma 2
(36). For any constant \(a > {0}\) and \(x \in R\), it satisfies \({0 < }\left| x \right| - x{\text{tanh}}\left( \frac{x}{a} \right) \le 0.2785a\).
Controller design
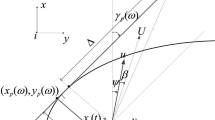
In this section, we design the trajectory tracking controller for the MSV model as stated in Section “Preliminaries and problem statements”, all states of the MSV are assume to be measurable. Firstly, define tracking error of underactuated MSV as
Then let
Thus, derivatives can be obtained as
where \(g_{u} \left( \varphi \right) = \left[ \begin{gathered} \cos \left( \varphi \right) \hfill \\ \sin \left( \varphi \right) \hfill \\ \end{gathered} \right]\), \(g_{v} \left( \varphi \right) = \left[ \begin{gathered} - \sin \left( \varphi \right) \hfill \\ \, \cos \left( \varphi \right) \hfill \\ \end{gathered} \right]\).
According to formula (11), the virtual control law is designed as
The speed, heading rate and heading angle are expected as
Define the following error variables:
Take the derivative of Eq. (14), it has
where the unknown dynamics are approximated by using RBF neural networks
Thus, the following control law is designed
where \(\delta_{u} = \varepsilon_{u} + \tau_{d,u}\), \(\delta_{r} = \varepsilon_{r} + \tau_{d,r}\), \(\hat{\overline{\delta }}_{u} ,\hat{\overline{\delta }}_{r}\) are the estimations of the upper bounds.
The adaptive law is designed as follows
Define errors as
Design trigger conditions
where \(\dot{\eta }_{u} \left( t \right) = - h_{11} \eta_{u} \left( t \right) + h_{12} \left| {\omega_{u} \left( t \right)} \right| - h_{13} \left| {e_{u} \left( t \right)} \right|\), \(\dot{\eta }_{r} \left( t \right) = - h_{21} \eta_{r} \left( t \right) + h_{22} \left| {\omega_{r} \left( t \right)} \right| - h_{23} \left| {e_{r} \left( t \right)} \right|\), the event-triggered interval is \(\left[ {t_{k} ,t_{k + 1} } \right)\), \(\omega_{u} \left( t \right) - \delta_{u} \left( t \right) \le l_{u} ,\,\,\omega_{r} \left( t \right) - \delta_{r} \left( t \right) \le l_{r}\).
Stability proof
The following Lyapunov function is selected for the underactuated ship kinematics.
where \(\tilde{\overline{\delta }}_{u} = \overline{\delta }_{u} - \hat{\overline{\delta }}_{u} ,\tilde{\overline{\delta }}_{r} = \overline{\delta }_{r} - \hat{\overline{\delta }}_{r}\).
Then, the derivation of (23) is obtained as
where \(\kappa_{11} = \min \left\{ {k_{11} ,k_{31} } \right\}\),\(\Delta_{e} = ug_{u} \left( \psi \right) - u^{*} g_{u} \left( {\psi^{*} } \right)\).\(u_{e} \dot{u}_{e} - \tilde{\overline{\delta }}_{u} \dot{\hat{\delta }}_{u}\) and \(r_{e} \dot{r}_{e} - \tilde{\overline{\delta }}_{r} \dot{\hat{\delta }}_{r}\) can be expressed as
According to lemma \(0 < \left| x \right| - x{\text{tanh(}}\frac{x}{a}{)} \le {0}{\text{.2785a}}\), obtain
Then, the following inequation is derived from formula (25), (26), (27) and (28),
Substitute formula (25), (26), (27), (28), (29), (31) and (32) into formula (23)
where \(\Lambda = \frac{1}{4}\Theta_{u}^{2} + \frac{1}{4}\Theta_{r}^{2} { + }\frac{5}{2}\left\| {\Delta_{e} } \right\|^{2}\),\(\kappa_{12} = \min \left\{ {k_{12} ,k_{32} } \right\}\),\(\kappa_{21} = \min \left\{ {k_{21} + 0.5,k_{41} + 0.5} \right\}\),\(\kappa_{22} = \min \left\{ {k_{22} ,k_{42} } \right\}\).
By young's inequality, we get
Then obtain
We can get a result according to formula (35)
where \(\iota = \min \left\{ {\iota_{{1}} ,\iota_{{2}} } \right\}\), \({0} < \iota < {1}\).
According to formula (28), if \(V > \theta /\iota \rho_{1}\), we have
According to Lemma 1, the system will stabilize to the region in finite time \(\Omega_{V} = \left\{ {V:V \le \theta /\imath \rho_{1} } \right\}\) and the stability time is
where \(V\left( {0} \right)\) is the initial value of \(V\).
For formula (42), it guarantees the system converge in finite time \(\forall t \ge T\), that has
Further, it can be obtained smooth continuous differentiable functions of \(\delta_{u}\) and \(\delta_{r}\).
Since all variables in \(\dot{\delta }_{u}\) and \(\dot{\delta }_{r}\) are globally bounded, there exists constants \(\vartheta_{u} > 0\),\(\vartheta_{r} > 0\), such that the condition \(\left| {\dot{\omega }_{u} } \right| < \vartheta_{u} ,\;\left| {\dot{\omega }_{r} } \right| < \vartheta_{r}\) are satisfied. When \(t = t_{k}\),\(e_{u} \left( {t_{k} } \right)\) and \(e_{r} \left( {t_{k} } \right)\) are 0,\(\mathop {\lim }\limits_{t \to \infty } e_{u} \left( t \right) = \vartheta_{u}\),\(\mathop {\lim }\limits_{t \to \infty } e_{r} \left( t \right) = \vartheta_{r}\). Therefore, there is time \(t^{*}\) interval satisfaction \(t^{*} \ge l_{i} /\vartheta_{i}\),\(i = u,r\), so zeno behavior does not occur.
Simulation
In the simulation, the length of ship is \(L = 1.255m\),\(M = 23.8kg\) and other parameters are referred to paper37. The designed parameters are set as \(k_{11} = 0.1\), \(k_{12} = 0.1\), \(k_{21} = 0.2\), \(k_{22} = 0.1\), \(k_{31} = 0.2\), \(k_{32} = 0.05\), \(k_{41} = 0.4\), \(k_{42} = 0.05\).The simulation results are shown in Figs. 1, 2, 3, 4, 5, 6 and 7.
The simulations have been implemented and results of the method adopted in this paper have been shown in the figures using dashed lines.The comparison is provided for the proof of validity. The method without considering asymmetric input saturation is taken as comparison that displayed in solid line mode.
Figure 1 shows the tracking effect of the actual and expected trajectories of the control scheme, and the tracking effect of the control scheme designed in this study is good. Both control schemes can make the actual cures track the reference, and meet the control requirements of the system. However, the finite-time trajectory tracking control scheme designed in this paper considers the existence of asymmetric input saturation when the fault occurs, and still achieves high tracking accuracy.
Figure 2 shows the tracking of the ship's actual position and actual heading angle. Both control schemes realize the tracking of reference position and reference heading. The control scheme designed in this paper shows good robustness in the tracking process of position and heading angle, and has high tracking accuracy for the desired position and heading angle.
Figure 3 shows the speed tracking of the ship, indicating that this research scheme can track the desired speed in a limited time. The changes of the actual speed of the ship and the tracking effect of the reference speed of the two control schemes tend to be similar with time, and the tracking of the reference speed is achieved.
The change of posture error with time and the change of heading error with time are displayed in Fig. 4. Even there is input saturation, the error at the beginning is limited in a small range. Finally the convergence rate of tracking error is almost the same.
Figure 5 shows the comparison effect of tracking errors of ship velocity. The upper and lower bounds of the errors of the two control schemes are small, which shows the effectiveness of the control scheme designed in this paper.
Figure 6 shows the comparison curves of the control inputs. The oscillation amplitude of the control inputs in this study are limited by asymmetric input saturation \(- {100} \le \varphi_{u} \le {200}\), \(- {10} \le \varphi_{r} \le {20}\). In addition, by analyzing the tracking situation of the reference trajectory of the control scheme in this study, the finite-time trajectory tracking control scheme proposed in this study has strong robustness.
The introduction of event triggering mechanism effectively reduces the update times of controller as show in Fig. 7. By reconstructing the dynamic uncertainty of the ship through the neural networks, the problem of finite time trajectory tracking control is solved considering asymmetric saturation. The tracking effect of the system is guaranteed, and the introduction of the event triggering mechanism effectively saves the communication resources.
Conclusion
A finite-time trajectory tracking control scheme based on adaptive neural networks with minimum learning parameters and asymmetric input saturation is proposed for underactuated surface ships affected by dynamic uncertainties and external unknown disturbances. The unknown dynamic uncertainty of the ship is approximated by neural network, and the computational complexity is reduced by combining the minimum learning parameter, and the controller structure is simplified. Then, an adaptive law is designed to approximate the upper bound of the composite disturbance to solve the asymmetric input saturation limit problem. Finally, the simulation results show that the proposed control scheme can make all signals in the closed-loop trajectory tracking system bounded, and ensure that the actual trajectory of the ship can track the desired trajectory in finite time. The control scheme designed in this study has good performance and is more suitable for application in engineering practice (The framework of the adaptive finite time trajectory tracking control method, and more simulation results are provided in the Supplementary Figures).
Data availability
All data generated or analysed during this study are included in this published article [and its supplementary information files]. Besides, the datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Zhao, Z., He, W. & Ge, S. S. Adaptive neural network control of a fully actuated marine surface vessel with multiple output constraints. IEEE Trans. Control Syst. Technol. 22(4), 1536–1543 (2014).
Do, K. D. Global robust adaptive path-tracking control of underactuated ships under stochastic disturbances. Ocean Eng. 111, 267–278 (2016).
Xie, W. et al. A simple robust control for global asymptotic position stabilization of underactuated surface vessels. Int. J. Robust Nonlinear Control https://doi.org/10.1002/rnc.3845 (2017).
Shojaei, K. Observer-based neural adaptive formation control of autonomous surface vessels with limited torque. Robot. Auton. Syst. 78, 83–96 (2016).
Peng, Z. & Wang, J. Output-feedback path-following control of autonomous underwater vehicles based on an extended state observer and projection neural networks. IEEE Trans. Syst. Man Cybern. 99, 1–10 (2017).
Zuo, Z. & Tie, L. Distributed robust finite-time nonlinear consensus protocols for multi-agent systems. Int. J. Syst. Sci. 47(6), 1366–1375 (2016).
Xiang, X., Lapierre, L. & Jouvencel, B. Smooth transition of AUV motion control: From fully-actuated to under-actuated configuration, robot. Robot. Autonom. Syst. 67, 14–22 (2015).
Wang, N. et al. Adaptive robust finite-time trajectory tracking control of fully actuated marine surface vehicles. IEEE Trans. Control Syst. Technol. 24(4), 1454–1462 (2016).
Zheng, Z., Huang, Y., Xie, L. & Zhu, B. Adaptive trajectory tracking control of a fully actuated surface vessel with asymmetrically constrained input and output. IEEE Trans. Control Syst. Technol. 26(5), 1851–1859 (2017).
Yu, R., Yu, Q., Xia, G. & Liu, Z. Sliding mode tracking control of an underactuated surface vessel. IET Control Theory Appl. 6(3), 461–466 (2012).
Yang, Y. et al. A trajectory tracking robust controller of surface vessels with disturbance uncertainties. IEEE Trans. Control Syst. Technol. 22(4), 1511–1518 (2014).
Lekkas, A. M. & Lekkas, T. I. Trajectory tracking and ocean current estimation for marine underactuated vehicles. In IEEE Conference on Control Applications Vol. 20 905–910 (IEEE, 2014).
Serrano, M. E. et al. Trajectory tracking of underactuated surface vessels: a linear algebra approach. IEEE Trans. Control Syst. Technol. 22(3), 1103–1111 (2014).
Katayama, H. & Aoki, H. Straight-line trajectory tracking control for sampled data underactuated ships. IEEE Trans. Control Syst. Technol. 22(4), 1638–1645 (2014).
Guerreiro, B. J. et al. Trajectory tracking nonlinear model predictive control for autonomous surface craft. IEEE Trans. Control Syst. Technol. 22(6), 2160–2175 (2014).
Zhu, G. et al. Event-triggered adaptive neural fault-tolerant control of underactuated MSVs with input saturation. IEEE Trans. Intell. Transp. Syst. 99, 1–13 (2021).
Peng, Z. et al. Adaptive dynamic surface control for formations of autonomous surface vehicles with uncertain dynamics. IEEE Trans. Control Syst. Technol. 21(2), 513–520 (2013).
Park, B. S., Kwon, J. W. & Kim, H. Neural network-based output feedback control for reference tracking of underactuated surface vessels. Automatica 77, 353–359 (2017).
Wang, N. & He, H. Dynamics-level finite-time fuzzy monocular visual servo of an unmanned surface vehicle. IEEE Trans. Industr. Electron. 67(11), 9648–9658 (2020).
Cheng, Y. et al. Fuzzy categorical deep reinforcement learning of a defensive game for an unmanned surface vessel. Int. J. Fuzzy Syst. 21(2), 592–606 (2019).
Lu, Y. Adaptive-fuzzy control compensation design for direct adaptive fuzzy control. IEEE Trans. Fuzzy Syst. 26(6), 3222–3231 (2018).
Wang, N. et al. Fuzzy unknown observer-based robust adaptive path following control of underactuated surface vehicles subject to multiple unknowns. Ocean Eng. 176, 57–64 (2019).
Deng, Y. et al. Adaptive fuzzy tracking control for underactuated surface vessels with unmodeled dynamics and input saturation. ISA Trans. 103, 332–346 (2020).
Mu, D., Wang, G. & Fan, Y. Trajectory tracking control for underactuated unmanned surface vehicle subject to uncertain dynamics and input saturation. Neural Comput. Appl. 6, 236–255 (2021).
Wang, N. et al. Reinforcement learning-based optimal tracking control of an unknown unmanned surface vehicle. IEEE Trans. Neural Netw. Learn. Syst. 99, 665–677 (2020).
Qiu, B. et al. Path following of underactuated unmanned surface vehicle based on trajectory linearization control with input saturation and external disturbances. Int. J. Control Autom. Syst. 18(4), 1–12 (2020).
Wang, Y. & Jiang, T. Way-point tracking control of underactuated USV based on GPC path planning. Fundam. Design Autom. Technol. Offshore Robot. https://doi.org/10.1016/B978-0-12-820271-5.00016-X (2020).
Li, T. S., Dan, W., Gang, F. & Tong, S. C. A DSC approach to robust adaptive NN tracking control for strict-feedback nonlinear systems. Syst. Man Cybern. B 40(3), 915–927 (2010).
Ma, Y., Zhu, G. & Li, Z. Error-driven-based nonlinear feedback recursive design for adaptive NN trajectory tracking control of surface ships with input saturation. IEEE Intell. Transp. Syst. Mag. 2, 1–10 (2019).
Wang, N. & Ahn, C. K. Hyperbolic-tangent LOS guidance-based finite-time path following of underactuated marine vehicles. IEEE Trans. Industr. Electron. 99, 677–690 (2019).
Tabuada, P. Event-triggered real-time scheduling of stabilizing control tasks. IEEE Trans. Autom. Control 52(9), 1680–1685 (2007).
Gao, S. et al. Coordinated target tracking by multiple unmanned surface vehicles with communication delays based on a distributed event-triggered extended state observer. Ocean Eng. 227(4), 108283 (2021).
Yoo, S. J. & Park, B. S. Guaranteed connectivity based distributed robust event-triggered tracking of multiple underactuated surface vessels with uncertain nonlinear dynamics. Nonlinear Dyn. 99(3), 2233–2249 (2020).
Huang, J. T. Global tracking control of strict-feedback systems using neural networks. IEEE Trans. Neural Netw. Learn. Syst. 23(11), 1714–1725 (2012).
Ge, S. S., Hang, C. C., Hang, T. H. & Zhang, T. Stable Adaptive Neural Network Control (Kluwer, 2002).
Chen, M., Ge, S. S. & Ren, B. Adaptive tracking control of uncertain MIMO nonlinear systems with input constraints. Automatica 47(3), 452–465 (2011).
Skjetne, R., Fossen, T. I. & Kokotović, P. V. Adaptive maneuvering, with experiments, for a model ship in a marine control laboratory. Automatica 41(2), 289–298 (2005).
Acknowledgements
This work is partially supported by the Natural Science Foundation of China (No. 52101375), the Shandong Provincial Natural Science Foundation (No. ZR2021QG022, No. ZR2022ME087), the Hebei Province Natural Science Foundation (No. E2021203142) and Shandong Jiaotong University PhD Startup foundation of Scientific Research (No. BS201902052).
Author information
Authors and Affiliations
Contributions
Y.H. and Q.Z. wrote the main manuscript text and mathematical methods. Y.L. checked the grammar and figures. X.M. prepared the programing. All authors reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hu, Y., Zhang, Q., Liu, Y. et al. Event trigger based adaptive neural trajectory tracking finite time control for underactuated unmanned marine surface vessels with asymmetric input saturation. Sci Rep 13, 10126 (2023). https://doi.org/10.1038/s41598-023-37331-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-023-37331-6
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.