Abstract
Mathematically study mass transfer phenomena involving chemical reactions in the flow of Sisko Ferro nanofluids through the porous surface. Three ferronano particles, manganese-zinc ferrite (Mn1/2Zn1/2Fe2O4), cobalt ferrite (CoFe2O4), and nickel–zinc ferrite (Ni–Zn Fe2O4) are considered with water (H2O) and ethylene glycol (C2H6O2) as base liquids. Appropriate resemblance transitions are used to convert the governing system of a nonlinear PDE to a linear ODE. The Runge–Kutta method, as extended by the shooting technique, is used to accomplish the reduction governing equations. The effects of various associated parameters on fluid concentration and mass transfer rate are investigated: magnetic criterion (M), Siskofluid material factor (A), Solid volume fraction (ϕ) for nanofluids, permeability parameter (Rp), Chemical reaction criterion (γ), Brownian motion factor (Nb), and Thermophoretic parameters (Nt). The current findings indicate that the diffusion proportion of Sisko Ferronanofluid Ni–Zn Fe2O4–H2O and CoFe2O4–H2O is higher than that of Ni–Zn Fe2O4–C2H6O2 and CoFe2O4–C2H6O2 respectively but it is opposite in the case of Mn–Zn ferrite. The comparison study was carried out to validate the precision of the findings.
Similar content being viewed by others
Introduction
A framework is made up of one or more elements, the number of which varies from system to system. Mass is also routed, reducing intensity differences within the framework. The field of mass transfer encounters some of the most unusual solutions in substance engineering. The ability to develop and operate used to make preparations for responding elements is what distinguishes a synthetic expert. Factors caused the isolation of production knowledge. One such potential seems to be highly dependent on mastery of mass transfer research. The strategies of inertia and heat transition are widely used in a variety of engineering fields, but absorption has typically been confined to bioengineering. These significant ones include fabrication systems and, more recently, the elevated airliner configuration.
Ordinary diffusion and convection have been selected for study among a number of physical processes that can move and transfer a chemical species through a system through the boundaries of the system. Mass diffusion, which happens when a gradient in species concentration develops, is comparable to heat conduction. In terms of fundamentals, mass convection and heat convection are the same; a fluid flow that carries heat can also convey a chemical species. Heat transmission and mass transfer have very similar fundamental mechanisms. It is well known that non-Newtonian fluid mechanics pose Engineers, Physicists, and Mathematicians with a special challenge. In recent years various scientists have proposed several models of non-Newtonian fluids to investigate the flow behavior of such engineering and non-engineering systems. This is because of their varying rheological characteristics. The Sisko model was commonly used by these models to model industrial and non-industrial problems.
Buongiorno's model is used to investigate the steady flow of a nanofluid of heat, thermal, and condensation mechanisms with provisional slip effects1. Primarily concerned with a symmetric elasticized sheet with a mixed convection MHD flow of cross fluid2. Fluid dynamic resilience of the Couette flow of a fluid that conducts electricity going to flow in an analogous link with a typical magnetism across a porous channel was investigated3. Williamson nanofluid MHD shear layer progression across a stretch sheet of the porous layer while accounting for acceleration and radiative deterioration. The goal of this model is to investigate the conditions of heat and mass transit using thermophoresis and Brownian acceleration with an approximate solution4. Study examines the impact of radiant heat, chemical thermolysis, and source of heat on the flow of MHD Casson fluid across a nonlinear inclined stretching surface with velocity slip in a porous medium5.The primary goal of this work is to quantitatively alleviate a Cross nanofluid surging across a perpetually broadening horizontal cylinder under non-Newtonian uncertain conditions6. Diffusion and heat conduction of a designed nanomaterial model is possible within existence besides a binary decomposition solution, radiation, as well as nanofluid, assuming Brownian motion and thermophoresis occurrences. Deals the magnetohydrodynamics of a Casson nanofluid flowing toward a stretched sheet. Additionally, the interaction between the Arrhenius activation energy, nonlinear radiation, and the current mass flow theory is examined7. Describes how Brownian motion and thermophoresis affect the flow of non-Newtonian power-law nanofluids in an expanding surface at a mixed convective-magneto-hydrodynamic interface8. In rectangular tubes with protrusions, the properties of the non-Newtonian stream and heat transport are quantitatively explored9. We investigate the MHD fluid Casson flow using a temperature diffusion heat absorber. It is investigated how synthetic reactivity and Joule heating function when thermal radiation passes through a porous sloped extended sheet of MHD Casson nanofluid10. When thermal radiation occurs through a porous sloped extended sheet of MHD Casson nanofluid, the role that chemical reaction and Joule heating play is explored in work, ramping power electromagnetic fluids stream is used thru a sloped parabolic shaped Riga area11,12. The Riga surface's electrically conducting viscoelastic fluid characteristics are also carefully examined, with an emphasis on time-dependent density and temperature changes.
Sisko fluid models successfully predict flow behaviour in the power law region, upper Newtonian region, and higher peak intensities.The model first learned oil flow but was later discovered to also exhibit flow behavior such as concrete glue. The manufactured products are a combination of water-based paints, flat oils, and concrete slurries. Studied the Sisko fluid boundary layer flow with entropy generation13. The analysis is performed on the unsteady MHD thin-film flow of Sisko Fluids when thermal radiation is applied to the expansive surface quantitative studies have been done on how heat and mass transfer affect non-Newtonian Sisko fluid flow in crooked, spongy, sloping tubes14,15. The movement of nanomaterials by radially contracting or extending the surface with zero mass flux, as well as the impact of magnetic fields on the movement of the Sisko liquids, were explored16.
Colloidal liquids called ferrofluids contain nanoscale or ferromagnetic particles floating in a carrier fluid. Ferrofluids are a unique class of nanofluids created by dispersing iron-containing nanoparticles into regular base liquids in a colloidal suspension. These liquids are extraordinary materials with fluid, magnetic, and strong thermal conductivity qualities. The Ferrofluid's strength is in its ability to control fluid flow.
In the domains of nautical technology, aviation, bioliquids, and medicinal and fibre manufacturing, it has a wide range of applications. To enhance microscale mass transfer, a dilute Ferrofluid is employed along with a non-uniform magnetic flux major objective of the work was the experimental investigation of the fluid and thermally transport characteristics of a ferrofluid depending on turbine oil and iron nanomaterial, magnetic field application17,18. The flow of MHD nanofluids made of water and kerosene over a porous surface with a predetermined heat flux is examined19.
An attenuated ferrofluid and a non-uniform magnetic flux are used to improve atomic level absorption20. An exploratory analysis of the motion and radiative transport properties of a ferrofluid relying on turbine oil and a ferrous nanomaterial, magnetic system, was the main objective of the work21.
As far as the author is aware, the current study is examining the mass transfer on flow through a permeable surface saturated with Sisko ferro nanofluid. With the required surface mass flux, the altered governing equations have a solution. For an explanation of the concentration profiles, numerical findings are shown on graphs. Table entries were used to display the excess surface concentration gradient connected to the mass flux distributions (Nt) for special values of the Siskofluid variation (A), magnetic factor (M), permeability criterion (Rp), nanoparticle volume fraction (ϕ), Brownian motion criterion (Nb), and thermophoresis parameter (Nt).
Formulation of the problem
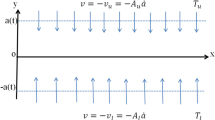
The impact of chemical reaction mass transfer in Sisko Ferronanofluid through a linearly expanding permeable surface is examined in this paper while prescribed mass flux conditions are present. The Ferrofluid model combines Brownian motion and thermophoresis to describe non-Newtonian fluid dynamics. Three Ferroparticles nickel zinc ferrite (Ni–Zn Fe2O4), cobalt ferrite (CoFe2O4), manganese zinc ferrite (Mn1/2Zn1/2Fe2O4), and two base fluids ethylene glycol and water are considered. The Ferronanofluids' physical, and thermal characteristics are shown in Table 1. The graphical abstract of the proposed research work is shown in Fig. 1. Here, the Sisko Ferro nanofluid's governing flow equations are written in the system of Cartesian coordinates. For the isotropic incompressible flow of a Sisko fluid, the rheological equation of state is given by22.
The problem's governing hypothesis under the aforementioned conditions23.
The conservation equations governing the flows
In which L ‘is characteristic length, ‘s’ is power-law velocity index,‘c’ is constant and \({ }^{\prime } {\text{m}}_{{\text{w }}}^{\prime }\) is surface mass flux.
The following similar transformations (Malik24).
\({\text{Q}}^{^{\prime}} = - {\text{d Q f}}\left( {\upeta } \right)\) Seems to be the parametric proportion of a thermal regression model.
Transformed equations of (2), (3), and (4)
As for model parameters
where \(\phi_{1} = 1 - \phi + { }\phi \frac{{{\uprho }_{{\text{s}}} }}{{{\uprho }_{{\text{f}}} }}\), \(\phi_{2} = { }\left( {1 - \phi } \right)^{2.5}\), \(A = \frac{{R_{{e_{b} }}^{{\frac{2}{n + 1}}} }}{{R_{{e_{a} }} }}\) is Sisko fluid parameter \(R_{{e_{a} }} = \frac{{\rho_{f} x U}}{a}\) and \(R_{{e_{b} }} = \frac{{\rho_{f } x U^{2 - n} }}{b}\) are Reynolds number, \(\lambda = \frac{{V_{0} }}{{U R_{{e_{b} }}^{{\frac{ - 1}{{n + 1}}}} }}\) is a suction parameter, \(R_{p} = \frac{{K_{P} U}}{{\nu_{f} x}}\) is permeability parameter, \(M = \frac{{\sigma B_{0 x}^{2} }}{{\rho_{f U} }}\) is a magnetic parameter, \(P_{r} = \frac{{x U R_{{e_{b} }}^{{\frac{ - 2}{{n + 1}}}} }}{{\alpha_{f} }}\) is Prandtl number, \(\gamma = {\kern 1pt} \frac{{k_{1} x}}{U}\) (chemical reaction parameter), \(\mathop L\nolimits_{e} = \;{\kern 1pt} \frac{{\mathop \alpha \nolimits_{f} }}{{\mathop D\nolimits_{B} }}\) (Lewis number),\(N_{b} = \frac{{\left( {\rho C_{p} } \right)_{p} }}{{\left( {\rho C_{p} } \right)_{f} }} \frac{{D_{B } \left( {C_{f } - C_{\infty } } \right)}}{{\alpha_{f} }}\) is Brownian motion parameter, \(N_{t} = \frac{{\left( {\rho C_{p} } \right)_{p} }}{{\left( {\rho C_{p} } \right)_{f} }} \frac{{D_{T } \left( {T_{f } - T_{\infty } } \right)}}{{T_{\infty } \alpha_{f} }}\) is thermophoresis parameter.
The physical quantity Sherwood number is defined from the relation
Using Eqs. (4), (5), and (9), the dimensionless Sherwood number can be written as
Numerical methods
In this study, we investigate the flow of MHD Sisko ferronano fluids under the influence of chemical reactions and specific mass flow rates. The Runge–Kutta method extended by the shooting technique is used for solving Eqs. (7) to (9) for a range of values of some specific parameters. To select a good initial approximation, the models have evolved into first-order nonlinear equations25.
Define a new set of variables as
Equation (13) is imposed on Eqs. (7)–(9), resulting in a method of seven ordinary differential equations as
To solve Eqs. (7) and (9) using (10) as the initial value problem, no initial values for fʺ(0), g(0) and h(0) are given. Then use the shooting estimation technique to change the attributes of fʺ(0) and g(0) = 0 and assess the observed attributes of f′ and g with given parameters \({\text{f}}^{\prime } \left( {{\upeta }_{\infty } } \right) = 0{ }\) and \({\text{g}}\left( {{\upeta }_{\infty } } \right) = 0.\) This process continues until the findings are accurate and meet the convergence parameter24,26,27,28,29,30.
Results and discussion
This research looks at the fluid of MHD Sisko's ferro nanofluids through a porous stretched surface using chemical reactions. The aforementioned numerical scheme is used for the conceptual evaluation of different flow parameters. The effects of parameters such as the magnetic parameter (M), the material parameter (A) for Siskofluid, the solid volume fraction (ϕ) for nanofluids, the permeability parameter (Rp), the thermophoretic parameters (Nt), the Brownian motion factor (Nb), and the chemical reaction criterion (γ) on concentration and Sherwood quantity are shown graphically and tabulated31.
A comparison study was conducted using Table 2 to validate the accuracy of results obtained from previously published data. In a few specific cases, the current h(0) findings have been found to be in good accordance to previously published work.
Figure 2 depicts the characterization of the material parameter Siskofluid Parameter A in a diffusion coefficient. The graph illustrates that the consistency decreases as the value of A increases. A measure of the viscosity of a fluid that slows it down and reduces the concentration layer thickness.
Figure 3 illustrates how the magnetic field affects Concentration. It can be demonstrated that the concentration rises as the value of M rises. The Lorentz force is a resistive force that results from the transverse magnetic field's actions on an electrically conducting fluid. This force aids in slowing the fluid's velocity and improving its concentration profile. Given that the magnetic field slows the mixed convection flow, this discovery qualitatively fits forecasts. A driving force that slows down the fluid's motion and thickens its boundary layer. The magnetic field causes high collisions between the ferro nanoparticles in the inter-particles, which raises the concentration. Figure 4 illustrates how the permeability parameter Rp affects the absorption profile. And is obvious further that the existence of a porous material increases the flow's constraint, which slows the fluid down. The velocity drops as a result of the impermeability parameter increasing the resistance to fluid motion. Figure 5 illustrates the chemical reaction parameter γ impact on concentration. The value of chemical reaction parameter γ is seen to be optimised when concentration is shown to grow. A rise in the reaction rate parameter causes a high collision of ferro nanoparticle inter-particles, which raises the concentration. The study's findings suggest that water-based ferro nanofluids increase concentration when compared to those based on ethylene glycol33,34,35,36,37.
Figures 6, 7, 8 show the effect of the Brownian motion parameter Nb, the thermophoresis parameter (Nt), and the ferro nanoparticle solid volume fraction (ϕ) on the Sherwood number is shown in Figs. 6, 7, 8. Thermotransport is a crucial step in increasing Ferrofluid's thermal conductivity and is facilitated by the Brownian motion of ferroparticles. It is clear that a rise in the Brownian motion parameter Nb is the cause of the mass transfer rate's drop. The above results have a physical explanation that involves an improvement in fluid intermolecular collisions, increased Nb and decreased Sherwood number.
Figure 7 shows how the thermophoresis parameter Nt affects the ferro nanoparticle Sherwood number. The Sherwood number's profile is immediately raised by the increase in Nt. Physically, the higher mass flux that significantly raises the Sherwood number is associated to the higher value of Nt. Figure 8 demonstrates that the Sherwood number profile declines as a result of increasing values. This is because more nanoparticles cause fluid friction, which slows the flow as their volume increases. This illustration shows how this agreement and physical behaviour are related.When the Sherwood number falls,the volume fraction of nanoparticles does as well. It is well known that when Nt increases in value, the Sherwood number also rises. However, the Nb and ϕ affects both lower the Sherwood number. Mn–Zn Fe2O4–H2O and CoFe2O4–H2O are found to have lower and higher Sherwood numbers than Mn–Zn Fe2O4–C2H6O2 and CoFe2O4–C2H6O2, respectively.
For particular values of Nb, Nt, M Rp, and A, Table 3 shows the Sherwood number of the Siskoferronanofluids Mn–Zn–Fe2O4–H2O, Mn–Zn Fe2O4–C2H6O2, CoFe2O4–H2O, and CoFe2O4–C2H6O2. This table shows that the Sherwood number rises with M and Nt and falls with A, Rp, and Nb. Mn–Fe2O4–H2O and CoFe2O4–H2O are found to have lower and higher Sherwood numbers than Mn–Fe2O4–C2H6O2 and CoFe2O4–C2H6O2, respectively.
Conclusion
The characteristics of variables influencing the mechanisms of concern are used to forecast action in a specific physical state. The assumption might be whether any of these amounts will affect the outcome of the change effort in geometrical, mass flow, flow characteristics, and so on. The primary goal of this research is to develop a mathematical framework of assumptions for mass transfer, fluid flow, and related operations. In short, of all estimation strategies, the mathematical approach has the most intention.
The effectiveness of Sisko ferro nanofluid mass transfer using the ferro particles manganese zinc ferrite (Mn1/2Zn1/2Fe2O4), cobalt ferrite (CoFe2O4) and nickel zinc ferrite (Ni–Zn Fe2O4) with water (H2O) and ethylene glycol (C2H6O2) as the base fluid on a porous surface is examined. The effects of parameters related to concentration and Sherwood number are illustrated using figures and tables. Following is a summary of this study.
-
1.
The fluid's concentration rises with an increase in M and γ and falls with a reduction in A and Rp.
-
2.
The Sisko ferro nanofluids' Sherwood number rises with M and Nt and falls with ϕ, A, Rp, Nb.
-
3.
Siskoferronanofluid based on ethylene glycol has a lower mass transfer rate than that of water-based Siskoferronanofluid containing ferro particles nickel–zinc ferrite (Ni–ZnFe2O4) and cobalt ferrite (CoFe2O4), manganese–zinc. Ferrite (Mn1/2Zn1/2Fe2O4).
Current analyzes are directly relevant to next-generation mass transfer technology, vertical surface material processing, the chemical industry and all processes strongly influenced by mass transfer principles. This research enabled engineers to understand the most important processes in chemical processes. The use of mass transfer fluids incorporating ferro particle suspensions in Siskofluids to resolve the cooling issue in thermal systems is one scientific application of ferro particles with enormous potential. As a result, the coexistence of Brownian motion and thermophoretic subatomic condensation on magnetic field sisko ferrofluids is critical for both basic and applied sciences worldwide.
Data availability
The datasets used and analyzed during the current study are available from the corresponding author on request.
Abbreviations
- \(K_{p}\) :
-
Permeability of the medium (m2)
- Q’:
-
Volumetric rate of heat absorption
- T :
-
Temperature of the fluid (K)
- \(T_{\infty }\) :
-
Temperature away from the surface
- \({\text{D}}_{{\text{B}}}\) :
-
Brownian diffusion coefficient (m2/s)
- \({\text{D}}_{{\text{T}}}\) :
-
Thermophoresis diffusion coefficient (m2/s)
- E0,1 :
-
Positive constant
- ϕ:
-
Solid volume nanoparticle fraction (mol/m3)
- knf :
-
Thermal conductivity of nanofluid (W/mK)
- kf :
-
Thermal conductivity of base fluid (W/mK)
- kp :
-
Thermal conductivity of nanoparticle (W/mK)
- μnf :
-
Dynamic viscosity of nanofluid (Ns/m2)
- μf :
-
Dynamic viscosity of base fluid (Ns/m2)
- μp :
-
Dynamic viscosity of nanoparticle(Ns/m2)
- ρnf :
-
Density of nanofluid (kg/m3)
- ρf:
-
Density of base fluid(kg/m3)
- ρp :
-
Density of nanoparticle(kg/m3)
- νnf :
-
Kinematic viscosity of nanoparticle (m2/s)
- νf :
-
Kinematic viscosity of base fluid(m2/s)
- νp :
-
Kinematic viscosity of nanoparticle(m2/s)
- (CP)nf:
-
Specific capacity of nanofluid (J/kg K)
- (CP)f:
-
Specific capacity of base fluid(J/kg K)
- (CP)p:
-
Specific capacity of nanoparticle(J/kg K)
- a:
-
Viscosity parameter
- m&n:
-
Power low index
- b:
-
Consistency index
- P:
-
Pressure
- I:
-
The identity tensor
- A1 :
-
The kinematic tensor
- S:
-
Extra stress tensor
- τ:
-
Cauchy stress tensor
References
Shahzad, M. et al. Theoretical analysis of cross-nanofluid flow with nonlinear radiation and magnetohydrodynamics. Indian J. Phys. 95, 481–488 (2021).
Sultan, F. et al. Physical assessments on variable thermal conductivity and heat generation/absorption in cross magneto-flow model. J. Therm. Anal. Calorim. 140, 1069–1078 (2020).
Hussain, Z. et al. Instability of magneto hydro dynamics couette flow for electrically conducting fluid through porous media. Appl. Nanosci. 10, 5125–5134 (2020).
Reddy, Y. D., Mebarek-Oudina, F., Goud, B. S., et al. Radiation, velocity and thermal slips effect toward MHD boundary layer flow through heat and mass transport of williamson nanofluid with porous medium. Arab. J. Sci. Eng. (2022).
Bejawada, S. G., Reddy, Y. D., Nisar, K. S., Alharbi, A. N. & Chouikh, R. Radiation effect on MHD Casson fluid flow over an inclined non-linear surface with chemical reaction in a Forchheimer porous medium. Alexandria Eng. J. 61, 8207–8220 (2022).
Ali, M. et al. Numerical analysis of chemical reaction and non-linear radiation for magneto-cross nanofluid over a stretching cylinder. Appl. Nanosci. 10, 3259–3267 (2020).
Khan, S. et al. Numerical simulation for MHD flow of casson nanofluid by heated surface. Appl. Nanosci. 10, 5391–5399 (2020).
Madhu, M. & Kishan, N. Magnetohydrodynamic mixed convection stagnation-point flow of a power-law non-Newtonian nanofluid towards a stretching surface with radiation and heat source/sink. J. Fluids 2015, (2015).
Xie, Y., Zhang, Z., Shen, Z. & Zhang, D. Numerical investigation of non-Newtonian flow and heat transfer characteristics in rectangular tubes with protrusions. Math. Probl. Eng. 2015, (2015).
Saritha, K. & Palaniammal, P. MHD viscous cassonfluid flow in the presence of a temperature gradient dependent heat sink with prescribed heat and mass flux. Front. Heat Mass Transf. 10, (2018).
Reddy, Y. D., Goud, B. S., Chamkha, A. J. & Kumar, M. A. Influence of radiation and viscous dissipation on MHD heat transfer casson nanofluid flow along a nonlinear stretching surface with chemical reaction. Heat Transf. Res. 51, 3495–3511 (2022).
Asogwa, K. K., Goud, B. S. & Reddy, Y. D. Non-Newtonian electromagnetic fluid flow through a slanted parabolic started Riga surface with ramped energy. Heat Transf. Res. 51, 5589–5609 (2022).
Khan, M. I., Qayyum, S., Hayat, T., Alsaedi, A. & Khan, M. I. Investigation of Sisko fluid through entropy generation. J. Mol. Liq. 257, 155–163 (2018).
Khan, A. S., Nie, Y. & Shah, Z. Impact of thermal radiation on magnetohydrodynamic unsteady thin film flow of Sisko fluid over a stretching surface. Processes 7, 369 (2019).
Asghar, Z., Ali, N., Ahmed, R., Waqas, M. & Khan, W. A. A mathematical framework for peristaltic flow analysis of non-Newtonian Sisko fluid in an undulating porous curved channel with heat and mass transfer effects. Comput. Methods Programs Biomed. 182, 105040 (2019).
Khan, U., Zaib, A., Shah, Z., Baleanu, D. & Sherif, E.-S.M. Impact of magnetic field on boundary-layer flow of Sisko liquid comprising nanomaterials migration through radially shrinking/stretching surface with zero mass flux. J. Mater. Res. Technol. 9, 3699–3709 (2020).
Hejazian, M., Phan, D.-T. & Nguyen, N.-T. Mass transport improvement in microscale using diluted ferrofluid and a non-uniform magnetic field. RSC Adv. 6, 62439–62444 (2016).
Paulovičová, K. et al. Rheological and thermal transport characteristics of a transformer oil based ferrofluid. Acta Phys. Pol. A 133, 564–566 (2018).
Saritha, K. & Palaniammal, S. MHD viscous nanofluid flow with base fluids’ water and kerosene in the presence of a temperature gradient dependent heat sink with prescribed heat flux. Lat. Am. Appl. Res. 48, 139–144 (2018).
Palaniammal, S. & Saritha, K. Heat and mass transfer of a casson nanofluid flow over a porous surface with dissipation, radiation, and chemical reaction. IEEE Trans. Nanotechnol. 16, 909–918 (2017).
Sharma, R. K. & Bisht, A. Effect of buoyancy and suction on Sisko nanofluid over a vertical stretching sheet in a porous medium with mass flux condition. Indian J. Pure Appl. Phys. 58, 178–188 (2020).
Saritha, K., Muthusami, R. & Rameshkumar, M. The effect of viscous dissipation and thermal radiation in siskoferronanofluid flow over a porous medium. Int. J. Eng. Res. Afr. 54, 118–131 (2021).
Prasannakumara, B. C., Gireesha, B. J., Krishnamurthy, M. R. & Kumar, K. G. MHD flow and nonlinear radiative heat transfer of Sisko nanofluid over a nonlinear stretching sheet. Inform. Med. Unlocked 9, 123–132 (2017).
Malik, R., Khan, M., Munir, A. & Khan, W. A. Flow and heat transfer in Sisko fluid with convective boundary condition. PLoS ONE 9, e107989 (2014).
Khan, Z. H., Khan, W. A., Qasim, M. & Shah, I. A. MHD stagnation point ferrofluid flow and heat transfer toward a stretching sheet. IEEE Trans. Nanotechnol. 13, 35–40 (2013).
Ahmad, L., Munir, A. & Khan, M. Locally non-similar and thermally radiative Sisko fluid flow with magnetic and Joule heating effects. J. Magn. Magn. Mater. 487, 165284 (2019).
Dawar, A., Wakif, A., Thumma, T. & Shah, N. A. Towards a new MHD non-homogeneous convective nanofluid flow model for simulating a rotating inclined thin layer of sodium alginate-based Iron oxide exposed to incident solar energy. Int. Commun. Heat Mass Transf. 130, 105800 (2022).
Hayat, T., Tanveer, A. & Alsaedi, A. Numerical analysis of partial slip on peristalsis of MHD Jeffery nanofluid in curved channel with porous space. J. Mol. Liq. 224, 944–953 (2016).
Zhang, L., Arain, M. B., Bhatti, M. M., Zeeshan, A. & Hal-Sulami, H. Effects of magnetic Reynolds number on swimming of gyrotactic microorganisms between rotating circular plates filled with nanofluids. Appl. Math. Mech. 41, 637–654 (2020).
Ramzan, M., Chung, J. D. & Ullah, N. Radiative magnetohydrodynamic nanofluid flow due to gyrotactic microorganisms with chemical reaction and non-linear thermal radiation. Int. J. Mech. Sci. 130, 31–40 (2017).
Hayat, T., Sajjad, L., Khan, M. I., Khan, M. I. & Alsaedi, A. Salient aspects of thermo-diffusion and diffusion thermo on unsteady dissipative flow with entropy generation. J. Mol. Liq. 282, 557–565 (2019).
Anjalidevi, S. P. & Kayalvizhi, M. Nonlinear hydromagnetic flow with radiation and heat source over a stretching surface with prescribed heat and mass flux embedded in a porous medium. J. Appl. Fluid Mech. 6, 157–165 (2013).
Awais, M., Malik, M. Y., Bilal, S., Salahuddin, T. & Hussain, A. Magnetohydrodynamic (MHD) flow of Sisko fluid near the axisymmetric stagnation point towards a stretching cylinder. Results Phys. 7, 49–56 (2017).
Gholinia, M., Gholinia, S., Hosseinzadeh, K. & Ganji, D. D. Investigation on ethylene glycol nano fluid flow over a vertical permeable circular cylinder under effect of magnetic field. Results Phys. 9, 1525–1533 (2018).
Shamshuddin, M. D., Salawu, S. O., Ogunseye, H. A. & Mabood, F. Dissipative power-law fluid flow using spectral quasi linearization method over an exponentially stretchable surface with Hall current and power-law slip velocity. Int. Commun. Heat Mass Transf. 119, 104933 (2020).
Bhatti, M. M. & Michaelides, E. E. Study of Arrhenius activation energy on the thermo-bioconvection nanofluid flow over a Riga plate. J. Therm. Anal. Calorim. 143, 2029–2038 (2021).
RevannaLalitha, K., Veeranna, Y., ThimmappaSreenivasa, G. & Ashok Reddy, D. Active and passive control of nanoparticles in ferromagnetic Jeffrey fluid flow. Heat Transf. 51, 998–1018 (2022).
Author information
Authors and Affiliations
Contributions
Conceptualization, S.K., M.R., M.N., N.N. and K.R.; Data curation, S.K., M.R., M.N., N.N. and K.R.; Analysis and Validation, S.K, M.R., M.N., N.N. and K.R.; Formal analysis, S.K., M.R., M.N., N.N. and K.R.; Investigation, S.K., M.R., M.N., N.N. and K.R.; Methodology, S.K., M.R., M.N., N.N. and K.R.; Project administration, K.R.; Resources, S.K., M.R., M.N., N.N. and K.R.; Software, S.K., M.R., M.N., N.N. and K.R., Supervision, K.R.; Validation, S.K., M.R., M.N., N.N. and K.R.; Visualization, S.K., M.R., M.N., N.N. and K.R.; Writing—original draft, S.K., M.R., M.N., N.N. and K.R., Data Visualization, Editing and Rewriting, S.K., M.R., M.N., N.N. and K.R.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Saritha, K., Muthusami, R., Manikandan, N. et al. A mathematical analysis of mass transfer phenomena with chemical reaction over the flow of Sisko ferronanofluid across a permeable surface. Sci Rep 13, 336 (2023). https://doi.org/10.1038/s41598-022-27214-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-27214-7
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.