Partial differential equations of entropy analysis on ternary hybridity nanofluid flow model via rotating disk with hall current and electromagnetic radiative influences

Abstract

The flow of a fluid across a revolving disc has several technical and industrial uses. Examples of rotating disc flows include centrifugal pumps, viscometers, rotors, fans, turbines, and spinning discs. An important technology with implications for numerous treatments utilized in numerous sectors is the use of hybrid nanofluids (HNFs) to accelerate current advancements. Through investigation of ternary nanoparticle impacts on heat transfer (HT) and liquid movement, the thermal properties of tri-HNFs were to be ascertained in this study. Hall current, thermal radiation, and heat dissipation have all been studied in relation to the use of flow-describing equations. The ternary HNFs under research are composed of the nanomolecules aluminum oxide (Al₂O₃), copper oxide (CuO), silver (Ag), and water (H₂O). For a number of significant physical characteristics, the physical situation is represented utilizing the boundary layer investigation, which produces partial differential equations (PDEs). The rheology of the movement is extended and computed in a revolving setting under the assumption that the movement is caused by a rotatingfloppy. Before the solution was found using the finite difference method, complicated generated PDEs were transformed into corresponding ODEs (Keller Box method). A rise in the implicated influencing factors has numerous notable physical impacts that have been seen and recorded. The Keller Box method (KBM) approach is also delivered for simulating the determination of nonlinear system problems faced in developing liquid and supplementary algebraic dynamics domains. The rate of entropy formation rises as the magnetic field parameter and radiation parameter increase. Entropy production rate decreases as the Brinkman number and Hall current parameter become more enriched. The thermal efficiency of ternary HNFs compared to conventional HNFs losses to a low of 4.8% and peaks to 5.2%.

Introduction

The generation, utilization, conversion, and exchange of heat through physical configurations are the topics of heat transfer (thermal transform) (TT), an area of contemporary engineering. Heat is transferred through a variety of techniques, including heat transmission, convection current, current radiation, and energy loss via phase variations. Engineers likewise consider the all types of transfers (heat, mass amd heat-mass) of different chemical classes in order to realize TT (mentioned to as physical announcement in the technique of the movement of a fluid, especially horizontally in the air or water, to transmit heat or substance). These developments are different, although they regularly happen instantaneously in the identical scheme. A variety of TT problematic examples are currently being measured by investigators. The neural networks are selected by Cai et al.¹ for TT experiments. Mousa et al.² presented a review investigation in which they improved methods by eating TT. In the research of Li et al.³, transformed properties are promoted in combination with TT. The effort of Khodadadi et al.⁴ requires the effectiveness of TT and electrical performance calculation of possessions. Sheikholeslami et al.⁵ developed a scientific demonstrating outline aimed at regulating TT. Nguyen et al.⁶ obtained a detailed assessment of TT. Mohankumar, et al.⁷ proposed TT through countless classes of geometries. Additional TT presentations can be found in solar researches⁹, magnetic fields⁸, and altering macroscopic¹⁰. Gao et al.¹¹, Jiaqiang et al.¹², and Mousavi et al.¹³ have recently reviewed the application of TT in the field of energy.

There are several simulations available to outbuilding light on the performance of hybrid nanofluids (HNFs), containing the controller regulation structure, Carreaus arrangement, Cross system, and Ellis pattern; however, the Williamson liquid strategy has received little attention from academics (WLS). Williamson (1929) supposed the flow of HNFs as a system of equations and then confirmed the results. Researchers suggested in a sophisticated gravitational analysis that a WLS's reverberating level should move to the conclusion of an inspired superficial. With respect to its molecular structure, a real fluid possesses together the deepest and maximum operational viscosities. The lowest and maximum thicknesses are measured together by the WLS. Said et al.¹⁴ invisaged a 3D-class of HNF in the event of a revolution in order to additional progress the amount of heat transfer (HT) by broadening slide. Investigative statistics were created using an artificial neural network by Mandal et al.¹⁵. Al-Chlaihawi et al.¹⁶, Saha et al.¹⁷ reported a research of HNFs' rheological and TT properties for refrigeration presentations. Researcheres in^18,19,20 have all published survey studies in this area. While a small investigation on mechanical revisions was performed in HNF by Dubey et al.²¹. The migration of an MHD tangent HNF across a stretched slip's boundary layer was examined by Syed and Jamshed²². Additionally, the demonstration of the prolonged TT of curvature hyperbolic liquids across a nonlinearly oscillating transparency incorporating HNFs was put to the test by Qureshi²³, Jamshed et al.²⁴, and Parvin et al.²⁵.

Three separate single nanofluid types were used to prepare tri-hybrid nanofluids (THNFs). Sahu et al.²⁶ investigated the stable‐formal and passing hydrothermal studies of solitary‐stage normal measure ring employing aquatic‐based THNFs. Safieiet al.²⁷ computed the possessions of THNFs going on shallow roughness and upsetting heat in close overwhelming procedure of aluminum mixture utilizing uncoated and covered sharp inserts with negligible amount lubricant technique. Manjunatha et al.²⁸ presented a hypothetical realization of convective TT in THNFs fluid past a extending slip. Gul and Saeed²⁹ introduced a varied convection pairpressure THNFs movement in a Darcy-Forchheimerabsorbentaverage via a nonlinear extending shallow. Ramadhan et al.^30,31,32 considered an investigational examination of thermo-physical possessions of THNFs in water-ethylene glycol assortment.

The result of converting the THNFs flow, wind, and current to the construction associate is an unsteady flow analysis (UFA), which develops in line with cyclone molting. In their numerical study of split-up and inactivity sites for stable and UFA via an elliptic cylinder next to aaffecting wall, Zhu and Holmedal³³ developed their methodology. In simplified and accurate iliac bifurcation replicas, Carvalho et al.³⁴ considered a numerical investigation of the UFA. The UFA field in the humanoid pulmonic was once again numerically reproduced by Ciloglu³⁵. In a rotating annulus area with a control law kernel, Javaid et al.³⁶ reported UFA of fractional Burgers' fluid. UFA in a side station pump with a curved blade was described by Zhang et al.³⁷. Phan and He³⁸ investigated UFA's efficiency when demonstrating for bladerows that were randomly misaligned and subjected to inlet modification. In arrow-shaped micro-mixers with various slope approaches, Mariotti et al.³⁹ presupposed UFA. Through distribution and deep-learning-based denoising, Gu et al.⁴⁰ prepared a deep study on UFA. UFA of a wavering piezoelectric fan blade at high Reynolds numbers was employed by Chen et al.⁴¹. Li et al.⁴² proposed a dynamic delayed detached-eddy model and an investigation of UFA's acoustic equivalency.

Rotating discs are a common component of many mechanical structures, containing flywheels, mechanisms, footbrakes, and gas turbine appliances. The level of force required to push the loop past frictional effort is determined by the shave pressures between the disk and the rotating liquid, and the local movement field will move TT. Numerous factors conspire haphazardly to prevent any common analysis, therefore it is important to take movement aspects and the contiguity of limited geometry into consideration. Suliman et al.⁴³ used the inside helical flippers on revolving discs enhanced the competence and PEC of a parabolic solar collector including THNFs. The dynamism propensity founded by means of THNFs and altered via a strong magnetic field across rotating discs was analyzed using finite elements by Hafeez et al.⁴⁴. A mathematical preparation on TT and mass transmission in Maxwell liquid with THNFs was presented by Haneef et al.⁴⁵ utilizing spinning discs. THNFs with TT over vertical heated cylinder were the subject of an investigation by Nazir et al.^46,47. Darcy THNFs movement over a scattering pipe with beginning possessions remained computationally valued in the effort of Alharbi et al.⁴⁸.

Thermal radiation (TR) is electromagnetic energy that is created through a material as a consequence of its temperature and whose physiognomies depend on the material's temperature. An example of TR is the infrared radiation given off by a conventional internal radiator or electric heater. A review paper on HS, TR, and heat transmission of NFs in porous media was offered by Xu et al.⁴⁹. Alumina-copper oxide hybrid NFs' thermo-magneto-hydrodynamic constancy was examined by Wakifet al.⁵⁰ by looking at the TR properties. Studying the impact of NFs aggregation on NFs' TR holdings was done by Chen et al.⁵¹. The flow of Al₂O₃ NFs with TR and HS effects was controlled by Agrawal et al.⁵² over an expanse of seemingly entrenched porous material. Magnetic NFs with TR and properties of heat-dependent viscidity were pumped using peristaltic motion by Prakash et al.⁵³. Khan et al.⁵⁴ created a magnetic dipole and TR influences on stagnation point movement of micropolar based NFs across a precipitously extending slip using the finite element approach. In light of TR and motive energy, Ali et al.⁵⁵ offered a comparative study of trembling MHD Falkner-Skan wedge flow for non-Newtonian NFs. For any Prandtl number, Shaw et al.⁵⁶ used the MHD movement of Cross HNFs influenced by linear, nonlinear, and quadratic TR.

The current, which is recognized as a Hall current, is present constantly but an electric field is applied to an electrode that likewise has an MHD (HC: after the Hall Upshot). Ramzan et al.⁵⁷ investigated the migration of THNFs derived from mildly ionized kerosene oil over a convectively animated rotating surface. In ethylene glycol, Wang et al.⁵⁸ provided a method for combining THNFs that included moveable diffusion and current conductivity utilizing a non-scheme. Fourier's A study of THNFs distributionclasses and energy transmission in materials affected by input energy and heat source was recommended by Sohail et al.^59,60. A large manufacturing of current energy in partially ionized hyperbolic tangent material formulated by ternary THNFs was disclosed by Nazir et al.⁶¹.

Recently, many researchers utilized THNFs with viscous dissipation (VD). Khan et al.⁶² studied the movement and TT of bio–convective THNFs stratification effects. Zainal et al.⁶³ described the VD and MHD THNFs flow towards an exponentially stretching/shrinking surface. Hou et al.⁶⁴ presented the dynamics of THNFs in the rheology of pseudo-plastic liquid with some material effects. Khan and Haleema⁶⁵ studied the thermal performance in THNFs under the influence of mixed convection and VD by using a numerical investigation. Munawar and Saleem⁶⁶ varied convective cilia activatedwatercourse of magneto ternary THNFs by elastic pump and VD using the entropy analysis.

It is well knowledge that the entropy, a consequence of any thermal activity, measures the degree of irreversibility. Cooling and warming are key cases that are usually employed in energy and electrical equipment in a number of industrial engineering research disciplines⁶⁷. Shahsavar et al.⁶⁸ conducted a statistical analysis of the entropy generation of the HNF flow. Significant improvements in NFs properties relative to straight fluids have contributed to the quick development of using HNFs for TT as proposed by Hussien et al.⁶⁹. The effects of MHD and TT movement with maximal entropy is presented by Ellahi et al.⁷⁰. While, Lu et al.⁷¹ investigated the nonlinear heating system by using the entropy concept in the movement of HNF done by a slip. The maximization of entropy is used in recent research by Sheikholeslami et al.⁷², Khan et al.⁷³, Zeeshan et al.⁷⁴, Ahmad et al.⁷⁵, and Moghadasi et al.⁷⁶. Entropy was recommended by Jamshed et al.^24,77,78 to optimize thermal applications, while Shahzad et al.⁷⁹ used it to growth the currenteffectiveness of a solar water pump used in NFs movement. References^{80,81,82,83,84,85,86} did similar work.

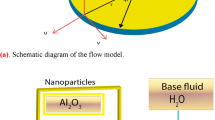
The TT of tri-HNFs over a rotating disk by means of linear dynamism, Hall movement, and heat depravities, or else the collaborating of ternary HNFs in MHD movement, have not been studied before. The ternary HNFs under research are composed of the nanomolecules aluminum oxide (Al₂O₃), copper oxide (CuO), silver (Ag), and water (H₂O). In the current study, the novel combination Al₂O₃–CuO–Ag–H₂O was applied for the first time. This unique combination aids in environmental purification and the cooling of other appliances. Once the regulatory PDEs system has been transformed into linear ODEs utilizing the correspondence method, the robust KBM is employed to obtain numerical solutions. Tables and statistics displaying numerical results are utilizd to sustenance the observations. Entropy production has also been investigated for the modelled problem. It has been well addressed how particle morphologies are affected, as well as the convective slide boundary condition, current radiative movement, and smooth velocity.

Physical aspects and construction of system

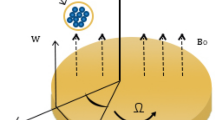
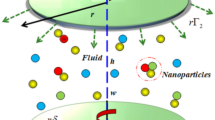
In the cylindrical coordinate scheme (r,φ, z), we reflect an unstable magnetohydrodynamic (MHD) electrically guiding movement of THNFs through a stretchable turning floppy. As seen in Fig. 1, the disk switches with an angular velocity Ω while being positioned at z = 0 and laterally the z-axis. A fixed magnetic field, called B₀, is employed laterally the z-axis. It is supposed that the heat on the disk's shallow is ${\mathrm{\yen }}_{\infty }$, while the outside temperature is ${\mathrm{\yen }}_{\infty }$. Widening velocities, disk rotation, and temperature profiles all depend on both space and time.

Figure 1

Diagramillustration of the movementmodel.

To make the situation simpler, the following assumptions were made:

$$u=\frac{cr}{(1-bt)},\quad v=\frac{c\Omega }{(1-bt)},\quad B(t)=\frac{{B}_{0}}{\sqrt{(1-bt)}},\quad {\mathrm{\yen }}_{s}={\mathrm{\yen }}_{0}-{\mathrm{\yen }}_{Ref}\left(\frac{{r}^{2}\Omega }{\nu (1-bt{)}^\frac{3}{2}}\right).$$

(1)

The flow contains three different kinds of nanoparticles, including Ag, CuO, and Al₂O₃. It is anticipated that a sufficient strong magnetic field will influence the Hall movement. The full application of Ohm's law is as follows in the presence of an electric field:

$$\mathrm{J}+\frac{{{\tau }_{e}\omega }_{e}}{{B}_{0}}(\mathrm{J}\times \mathrm{B})=\sigma {\mu }_{e}(\mathrm{V}\times \mathrm{B})+\frac{\sigma }{e{n}_{e}}\nabla {p}_{e},$$

(2)

assuming that for poorly ionized gas, the thermoelectric pressure and ion slideenvironments are unimportant. The aforesaid equations, in the following more condensed form:

$${J}_{r}=\frac{\sigma {\mu }_{e}{B}_{0}}{1+{m}^{2}}(mv-u),{J}_{\varphi }=\frac{\sigma {\mu }_{e}{B}_{0}}{1+{m}^{2}}(mu+v),$$

(3)

where $c$, $b$, $\Omega$, ${\mathrm{\yen }}_{s}$, ${\mathrm{\yen }}_{0}$, ${\mathrm{\yen }}_{ref}$, ${\omega }_{e}$, ${\tau }_{e}$, $Pe$, ${n}_{e}$, ${\mu }_{e}$, $m$, $\sigma$, ${B}_{0}$, $u$ an d $v$ are the splayed quantity, progressive static quantity, disk rotating quantity, superficial thermal, source thermal, continual direction thermal, cyclotron incidence of electrons, electron crash period, electron pressure, quantity of viscosity of electrons, magnetic permeability, Hall current bound, electrical conductivity of fluid, magnetic field influence, radiating and azimuthal velocities devices, correspondingly. The Hall factor is indicated here as $m={{\tau }_{e}\omega }_{e}$, while liquid electrical conductivity is indicated as

$$\sigma =\frac{{e}^{2}{n}_{e}{t}_{e}}{{m}_{e}}.$$

(4)

A flow diagram of the ternary hybrid nanoparticles TiO₂, Al₂O₃, and Ag is shown in Fig. 2, with water (H₂O) being considered as an inappropriate fluid in the current issue.

Figure 2

Organized attitude of tri-hybrid nanoparticles.

Mathematical modeling system of eqautions

The representation figure in cylindrical coordinates (r,$\varphi ,$ z) for the continuous circling movement of the nanofluid through a stretchable and fixed disk is exposed in Fig. 1. The rounded disk by means of fixed heat ($\mathrm{\yen }$ _s) at z = 0 can be strained consistently in the radial direction by the side of an extending amount of (c). Henceforward, the leading calculations⁸⁷ of continuousness, momentum and dynamism are

$$\frac{1}{r}\frac{\partial }{\partial r}(ur)+\frac{\partial w}{\partial z}=0,$$

(5)

$$\left(\frac{\partial u}{\partial t}-\frac{{v}^{2}}{r}+w\frac{\partial u}{\partial z}+u\frac{\partial u}{\partial r}\right)={\nu }_{thnf}\left(\frac{{\partial }^{2}u}{\partial {z}^{2}}\right)-\frac{{\sigma }_{thnf}{B}_{0}^{2}}{{\rho }_{thnf}(1+m{a}^{2})\sqrt{1-bt}}\left[u-mav\right],$$

(6)

$$\left(\frac{\partial v}{\partial t}+\frac{uv}{r}+u\frac{\partial v}{\partial r}+w\frac{\partial v}{\partial z}\right)={\nu }_{thnf}\left(\frac{{\partial }^{2}v}{\partial {z}^{2}}\right)-\frac{{\sigma }_{thnf}{B}_{0}^{2}}{{\rho }_{thnf}(1+m{a}^{2})\sqrt{1-bt}}\left[v+mau\right],$$

(7)

$$\left(\frac{\partial \mathrm{\yen }}{\partial t}+u\frac{\partial \mathrm{\yen }}{\partial r}+w\frac{\partial \mathrm{\yen }}{\partial z}\right)=\frac{{\kappa }_{thnf}}{(\rho {C}_{p}{)}_{thnf}}\left(\frac{{\partial }^{2}\mathrm{\yen }}{\partial {z}^{2}}\right)+\frac{{\mu }_{thnf}}{(\rho {C}_{p}{)}_{thnf}}\left[{\left(\frac{\partial u}{\partial z}\right)}^{2}-{\left(\frac{\partial v}{\partial z}\right)}^{2}\right]-\frac{1}{(\rho {C}_{p}{)}_{thnf}}\frac{\partial {q}_{r}}{\partial z}.$$

(8)

where $\mathrm{\yen }$, ${\nu }_{thnf}$, ${\sigma }_{thnf}$, ${\rho }_{thnf}$, ${\kappa }_{thnf}$, $(\rho {C}_{p}{)}_{thnf}$, and ${q}_{r}$ are the liquefied temperature, kinematic viscosity, tri-HNF electrical directing, thickness of tri-HNF, current conductivity of tri-HNF, full heat of tri-HNF and radiative temperature fluidity. In this instance, the radiative temperature fluctuation may perhaps be situated via employing Rosseland estimate through incomes of:

$${q}_{r}=-\frac{4{\sigma }^{*}}{3{k}^{*}}\frac{\partial {\mathrm{\yen }}^{4}}{\partial Z}=-\frac{16{\sigma }^{*}{\mathrm{\yen }}_{\infty }^{3}}{3{k}^{*}}\frac{\partial \mathrm{\yen }}{\partial z},$$

(9)

Here, ${\sigma }^{*}$ is the Boltzmann constant and ${k}^{*}$ is the concentration number. In view of Eqs. (9) and (8), it can be communicated as

$$\left(\frac{\partial \mathrm{\yen }}{\partial t}+u\frac{\partial \mathrm{\yen }}{\partial r}+w\frac{\partial \mathrm{\yen }}{\partial z}\right)=\frac{{\kappa }_{thnf}}{(\rho {C}_{p}{)}_{thnf}}\left(\frac{{\partial }^{2}\mathrm{\yen }}{\partial {z}^{2}}\right)+\frac{{\mu }_{thnf}}{(\rho {C}_{p}{)}_{thnf}}\left[{\left(\frac{\partial u}{\partial z}\right)}^{2}-{\left(\frac{\partial v}{\partial z}\right)}^{2}\right]+\frac{16{\sigma }^{*}{\mathrm{\yen }}_{\infty }^{3}}{(\rho {C}_{p}{)}_{thnf}3{k}^{*}}\frac{{\partial }^{2}\mathrm{\yen }}{\partial {z}^{2}}.$$

(10)

The relevant boundary conditions are:

$$\left.\begin{array}{l}(u,v,w,\mathrm{\yen })=\left(\frac{cr}{(1-bt)},\frac{r\Omega }{(1-bt)},0,{\mathrm{\yen }}_{s}\right)\quad \mathrm{at}\,\, z=0,\\ u=v=0,\mathrm{\yen }\to {\mathrm{\yen }}_{\infty }\quad as \,\, z\to \infty .\end{array}\right\}$$

(11)

The functioning attitude of tri-HNFs is the rearrangement of tri-various categories of nanoparticles in the improper fluid. This advances the TTcompetences of the normal fluids plus verifies a superior heat supporter than the HNFs. Methodical expressions on the subject of the thermophysical properties for ternary HNF⁸⁸ arestated inferior to

$$\left. {\begin{array}{*{20}l} {\mu_{thnf} = \frac{{\mu_{f} }}{{(1 - \phi_{1} )^{2.5} (1 - \phi_{2} )^{2.5} (1 - \phi_{3} )^{2.5^{\prime}} }}} \hfill \\ {\rho_{thnf} = [(1 - \phi_{1} )\{ (1 - \phi_{2} )[(1 - \phi_{3} )\rho_{f} + \rho_{3} \phi_{3} ] + \rho_{2} \phi_{2} \} + \rho_{1} \phi_{1} ],} \hfill \\ \begin{gathered} (\rho C_{p} )_{thnf} = (1 - \phi_{1} )\{ (1 - \phi_{2} )[(1 - \phi_{3} )(\rho C_{p} )_{f} + (\rho C_{p} )_{3} \phi_{3} ] \hfill \\ + \qquad (\rho C_{p} )_{2} \phi_{2} \} + (\rho C_{p} )_{1} \phi_{1} , \hfill \\ \end{gathered} \hfill \\ {\frac{{k_{thnf} }}{{k_{hnf} }} = \frac{{k_{1} + 2k_{nf} - 2\phi_{1} (k_{nf} - k_{1} )}}{{k_{1} + 2k_{nf} + \phi_{1} (k_{nf} - k_{1} )}},} \hfill \\ {\frac{{k_{hnf} }}{{k_{nf} }} = \frac{{k_{2} + 2k_{nf} - 2\phi_{2} (k_{nf} - k_{2} )}}{{k_{2} + 2k_{nf} + \phi_{2} (k_{nf} - k_{2} )}},} \hfill \\ {\frac{{k_{nf} }}{{k_{f} }} = \frac{{k_{3} + 2k_{nf} - 2\phi_{3} (k_{nf} - k_{3} )}}{{k_{3} + 2k_{nf} + \phi_{3} (k_{nf} - k_{3} )}},} \hfill \\ \begin{gathered} \frac{{\sigma_{thnf} }}{{\sigma_{hnf} }} = \frac{{\sigma_{1} (1 + 2\phi_{1} ) - \phi_{hnf} (1 - 2\phi_{1} )}}{{\sigma_{1} (1 - \phi_{1} ) + \sigma_{hnf} (1 + \phi_{1} )}} \hfill \\ \frac{{\sigma_{hnf} }}{{\sigma_{nf} }} = \frac{{\sigma_{2} (1 + 2\phi_{2} ) + \varphi_{nf} (1 - 2\phi_{2} )}}{{\sigma_{2} (1 - \phi_{2} ) + \sigma_{nf} (1 + \phi_{2} )}} \hfill \\ \end{gathered} \hfill \\ {\frac{{\sigma_{nf} }}{{\sigma_{f} }} = \frac{{\sigma_{3} (1 + 2\phi_{3} ) + \varphi_{f} (1 - 2\phi_{3} )}}{{\sigma_{3} (1 - \phi_{3} ) + \sigma_{f} (1 + \phi_{3} )}}.} \hfill \\ \end{array} } \right\}$$

In which, ${\mu }_{thnf}$, ${\rho }_{thnf}$, $\rho ({C}_{p}{)}_{thnf}$,${\kappa }_{thnf}$ and ${\sigma }_{thnf}$ indicated the crescendos stickiness, thickness, specific temperature measurements of the THNF's thermal conductivity and electrical conductivity. $\phi ={\phi }_{1}+{\phi }_{2}+{\phi }_{3}$ is the nanoparticle capacity growth constant aimed at THNF and ${\phi }_{1}={\phi }_{{\mathrm{Al}}_{2}{O}_{3}},{\phi }_{2}={\phi }_{CuO},$ and ${\phi }_{3}={\phi }_{Ag}$ are the capacity fraction of the first, second, and third nanoparticles. ${\mu }_{f}$, ${\rho }_{f}$, $({C}_{p}{)}_{f}$,${\kappa }_{f}{\sigma }_{f}$ and are self-motivatedviscidness, intensity, explicittemperaturecapability, current conductivity and electrical conductivity of the foundationliquid. ${\rho }_{1}$, ${\rho }_{2}$,${\rho }_{3}$, $({C}_{p}{)}_{1}$, $({C}_{p}{)}_{2}$, $({C}_{p}{)}_{3}$, ${\kappa }_{1}$, ${\kappa }_{2}$, ${\kappa }_{3}$, ${\sigma }_{1}$, ${\sigma }_{2}$ and ${\sigma }_{3}$ are the thicknesses, specific thermal measurements, thermal conductivities and electrical conductivitiesof the nanoparticles.

The physicalpossessions of the base liquidwaterand various nanoparticles being utilized in the existenttraining are illustratedin Table 1.

Table 1 Thermal properties^89,90 of nanoparticles (Al₂O₃, CuO and Ag) in H₂O.

The result to the problem

Take into account the similarity transformations below:

$$\left.\begin{array}{l}u=\frac{r\Omega }{(1-bt)}{F}^{*{^{\prime}}}, v=\frac{r\Omega }{(1-bt)}{G}^{*}, w=-2\sqrt{\frac{r\Omega }{(1-bt)}}{F}^{*},\\ \chi =\sqrt{\frac{\Omega }{\nu (1-bt)}z},\mathrm{\yen }={\mathrm{\yen }}_{0}-{\mathrm{\yen }}_{ref}\frac{\Omega {r}^{2}}{\nu (1-bt{)}^\frac{3}{2}}{\theta }^{*}.\end{array}\right\}$$

(12)

Paid to the above resemblance variables, Eqs. (4–7) and Eqs. (10, 11) are concentrated as:

$$\frac{{D}_{1}}{{D}_{2}}{F}^{*{^{\prime}}{^{\prime}}{^{\prime}}}+({G}^{*2}+2{F}^{*}{F}^{*{^{\prime}}{^{\prime}}}-({F}^{*{^{\prime}}}{)}^{2})-{A}^{*}(\frac{\chi }{2}{F}^{*{^{\prime}}{^{\prime}}}+{F}^{*{^{\prime}}})-\frac{{D}_{3}}{{D}_{2}(1+m{a}^{2})}Ha({F}^{*{^{\prime}}}-ma{G}^{*})=0,$$

(13)

$$\frac{{D}_{1}}{{D}_{2}}{G}^{*{^{\prime}}{^{\prime}}}-2({F}^{*}{G}^{*{^{\prime}}}-{G}^{*}{F}^{*{^{\prime}}})-{A}^{*}(\frac{\chi }{2}{G}^{*{^{\prime}}}+{G}^{*})-\frac{{D}_{3}}{{D}_{2}(1+m{a}^{2})}Ha({G}^{*}-ma{G}^{*{^{\prime}}})=0,$$

(14)

$${D}_{4}\left({D}_{5}+\frac{4}{3}Nr\right){\theta }^{*{^{\prime}}{^{\prime}}}+Pr{A}^{*}\left(\frac{\chi }{2}{\theta }^{*{^{\prime}}}+\frac{3}{2}{\theta }^{*}\right)+2Pr\left(F{\theta }^{*}{^{\prime}}-{F}^{*}{^{\prime}}{\theta }^{*}\right)-\frac{{D}_{4}}{{D}_{1}}Prhc\left(({F}^{*{^{\prime}}{^{\prime}}}{)}^{2}+({G}^{*{^{\prime}}}{)}^{2}\right)=0,$$

(15)

with conditions

$$\left.\begin{array}{l}{F}^{*}(0)=0,{F}^{*{^{\prime}}}(0)=\omega , {\theta }^{*}(0)=1={G}^{*}(0)\quad \mathrm{at} \,\, \chi =0\\ {F}^{*}{^{\prime}}(\chi )=0,{G}^{*}(\chi )\to 0,{\theta }^{*}(\chi )\to 0,\quad as\,\, \chi \to \infty \end{array}\right\}$$

(16)

where $\omega$, ${A}^{*}$, $Ha$, $ma$, $Nr$, $Pr,$ and $hc$ are rotation parameter, the quantity of trembling, magnetic field aspect, Hallcurrent factor, radiation aspect, Prandtl number and Eckert number, correspondingly. These uni-dimensional limitations and measured forms of the coefficients.

${D}_{1}$, ${D}_{2}$, ${D}_{3}$, ${D}_{4}$ and ${D}_{5}$ can be expressed as:

$$\left.\begin{array}{l}{D}_{1}=\frac{{\mu }_{thnf}}{{\mu }_{f}},{D}_{2}=\frac{{\rho }_{thnf}}{{\rho }_{f}},{D}_{3}=\frac{{\sigma }_{thnf}}{{\sigma }_{f}},{D}_{4}=\frac{(\rho {C}_{p}{)}_{f}}{(\rho {C}_{p}{)}_{thnf}},\\ {D}_{5}=\frac{{\kappa }_{thnf}}{{\kappa }_{f}}, \omega =\frac{\Omega }{c},{A}^{*}=\frac{b}{\Omega }, Ha=\frac{{\sigma }_{f}{B}_{0}^{2}}{{\rho }_{f}\Omega }, ma={{\omega }_{e}}_{e},\\ Nr=\frac{4{\sigma }^{*}{\mathrm{\yen }}_{\infty }^{3}}{{\kappa }^{*}{\kappa }_{f}}, Pr=\frac{{\mu }_{f}(\rho {C}_{p}{)}_{f}}{{\rho }_{f}{\kappa }_{f}}, hc=\frac{{r}^{2}{\Omega }^{2}}{(1-bt{)}^{2}({\mathrm{\yen }}_{s})}.\end{array}\right\}$$

(17)

Skin friction and Nusselt number

Skin friction and Nusselt number are fairlyappreciated for manufacturing purposes at the nano-level. The presentsomatic problem, skin friction,isformulated by:

$${\text{Re}}^{\frac{1}{2}} Cf_{r} = \frac{{F*^{\prime\prime}(0)}}{{(1 - \phi_{1} )^{2.5} (1 - \phi_{2} )^{2.5} (1 - \phi_{3} )^{2.5^{\prime}} }}$$

(18)

$${\text{Re}}^{\frac{1}{2}} Cg_{r} = \frac{{G*^{\prime}(0)}}{{(1 - \phi_{1} )^{2.5} (1 - \phi_{2} )^{2.5} (1 - \phi_{3} )^{2.5^{\prime}} }}$$

(19)

and Nusselt number is given by

$$\begin{array}{l}N{u}_{r}R{e}^{-\frac{1}{2}}=-\frac{{\kappa }_{thnf}}{{\kappa }_{f}}\left(1+\frac{4}{3}Nr\right){\theta }^{*{^{\prime}}}(0),\end{array}$$

(20)

where $Re=\frac{{r}^{2}\Omega }{{\nu }_{f}(1-bt)}$ is the Reynolds number.

Entropy generation analysis

The data presented by Bejan⁹¹ are used to formulate the volumetric entropy generation rate with the effects of TT and liquid friction

$${E}_{G}=\frac{1}{{\mathrm{\yen }}_{0}^{2}}\left({k}_{thnf}+\frac{16}{3}\frac{{\sigma }^{*}{\mathrm{\yen }}_{0}^{3}}{{\kappa }^{*}}\right){\left(\frac{\partial \mathrm{\yen }}{\partial z}\right)}^{2}+\frac{{\mu }_{thnf}}{{\mathrm{\yen }}_{0}}\left({\left(\frac{\partial u}{\partial z}\right)}^{2}+{\left(\frac{\partial v}{\partial z}\right)}^{2}\right)+\frac{{\sigma }_{thnf}{B}_{0}^{2}\left({u}^{2}+{v}^{2}\right)}{k{\mathrm{\yen }}_{0}\left(1+m{a}^{2}\right)\left(1-bt\right)}.$$

(21)

The reduced entropy generation equation is as follows:

$${N}_{G}={\alpha }_{a}\left({D}_{5}+\frac{4}{3}Nr\right){\theta }^{*\mathrm{^{\prime}}2}+{D}_{1}Br\left({F}^{*\mathrm{^{\prime}}\mathrm{^{\prime}}2}+{G}^{*\mathrm{^{\prime}}2}\right)+\frac{{D}_{3}MBr}{\left(1+m{a}^{2}\right)\left({F}^{*\mathrm{^{\prime}}2}+{G}^{*2}\right)}.$$

(22)

Here ${\alpha }_{a}=\frac{\mathrm{\Delta \yen }}{{\mathrm{\yen }}_{0}}$ is the dimensionless temperature difference, in which $\mathrm{\Delta \yen }={\mathrm{\yen }}_{ref}\left(\frac{{r}^{2}\Omega }{\nu (1-bt{)}^\frac{3}{2}}\right),Br=\frac{{\mu }_{f}{r}^{2}{\Omega }^{2}}{{k}_{f}\left({\mathrm{\yen }}_{w}-{\mathrm{\yen }}_{\infty }\right)}$ is the Brinkman number, $\omega =\frac{{\mathrm{\yen }}_{w}-{\mathrm{\yen }}_{\infty }}{{\mathrm{\yen }}_{\infty }}$ is the dimensionless temperature gradient and ${N}_{G}=\left(\frac{{\mathrm{\yen }}_{0}{E}_{G}\nu (1-bt)}{{\kappa }_{f}\mathrm{\Omega \Delta \yen }}\right)$ is the entropy generation rate.

Numerical implementation

Here, the Keller box technique^92,93 is utilized using the algebraic database Matlab for different principles of the relevant parameters to address the nonlinear ordinary differential Eqs. (14)–(16) with respect to the endpoint condition (Eq. 17). Despite recent advances in other numerical approaches, this method appears to be the most flexible of the popular methods and remains a powerful and extremely accurate solution for parabolic boundary layer flows. It can also solve equations of any order and is absolutely stable on the results. The flow process chart (see Fig. 3) represents the step-by-step Keller box scheme procedure as follows:

Figure 3

Current diagram demonstratingthe Keller box technique.

Adaptation of ODEs

We begin by including renewed independent variables: ${\xi }_{1}(x,\chi ),{\xi }_{2}(x,\chi ),{\xi }_{3}(x,\chi ),{\xi }_{4}(x,\chi )$, ${\xi }_{5}(x,\chi )$, ${\xi }_{6}(x,\chi )$ and ${\xi }_{7}(x,\chi )$ with ${\xi }_{1}={F}^{*}, {\xi }_{2}={F}^{*{^{\prime}}}, {\xi }_{3}={F}^{*{^{\prime}}{^{\prime}}}, {\xi }_{4}=G, {\xi }_{5}={G}^{*{^{\prime}}}, {\xi }_{6}={\theta }^{*}$ and ${\xi }_{7}={\theta }^{*{^{\prime}}}$. This transformation causes Eqs. (10–12) to decrease to the subsequent first-order formula

$$\frac{d{\xi }_{1}}{d\chi }={\xi }_{2},$$

(23)

$$\frac{d{\xi }_{2}}{d\chi }={\xi }_{3},$$

(24)

$$\frac{d{\xi }_{4}}{d\chi }={\xi }_{5},$$

(25)

$$\frac{d{\xi }_{6}}{d\chi }={\xi }_{7},$$

(26)

$$\frac{{D}_{1}}{{D}_{2}}\frac{d{\xi }_{3}}{d\chi }+({\xi }_{4}^{2}+2{\xi }_{1}{\xi }_{3}-{\xi }_{2}^{2})-{A}^{*}(\frac{\chi }{2}{\xi }_{3}+{\xi }_{2})-\frac{{D}_{3}}{{D}_{2}(1+m{a}^{2})}Ha({\xi }_{2}-ma{\xi }_{4})=0,$$

(27)

$$\frac{{D}_{1}}{{D}_{2}}\frac{d{\xi }_{5}}{d\chi }-2({\xi }_{1}{\xi }_{5}-{\xi }_{2}{\xi }_{4})-{A}^{*}(\frac{\chi }{2}{\xi }_{5}+{\xi }_{4})-\frac{{D}_{3}}{{D}_{2}(1+m{a}^{2})}Ha({\xi }_{4}-ma{\xi }_{2})=0,$$

(28)

$$\left.\begin{array}{ll}& {D}_{4}\left({D}_{5}+\frac{4}{3}Nr\right)\frac{d{\xi }_{7}}{d\chi }-Pr{A}^{*}\left(\frac{\chi }{2}{\xi }_{7}+\frac{3}{2}{\xi }_{6}\right)+2Pr\left({\xi }_{1}{\xi }_{7}-{\xi }_{2}{\xi }_{6}\right)\\ & -\frac{{D}_{4}}{{D}_{1}}Prhc\left({\xi }_{3}^{2}+{\xi }_{5}^{2}\right)=0,\end{array}\right\}$$

(29)

$$\left.\begin{array}{l}{\xi }_{1}(0)=0,{\xi }_{2}(0)=\omega , {\xi }_{4}(0)=1={\xi }_{6}(0)\quad \mathrm{at}\,\, \chi =0\\ {\xi }_{2}(\chi )=0,{\xi }_{4}(\chi )\to 0,{\xi }_{6}(\chi )\to 0, \quad as\,\, \chi \to \infty \end{array}\right\}$$

(30)

Dominiondiscretization and difference equations

Additionally, area discretization in $x-\chi$ plane is characterized in Fig. 4. According to this arguments, we have

Figure 4

Representative grid structure for modification evaluations.

${\chi }_{0}=0,{\chi }_{j}={\chi }_{j-1}+{h}_{j}, j=\mathrm{0,1},\mathrm{2,3}...,J,{\chi }_{J}=1$ where, ${h}_{j}$ is the step-magnitude. Applying central difference construction at the midpoint ${\chi }_{j-0.5}$

Employing the central difference preparation at the medium point ${\xi }_{j-1/2}$

$$({\xi }_{1}{)}_{j}-({\xi }_{1}{)}_{j-1}=0.5*{h}_{j}(({\xi }_{2}{)}_{j}+({\xi }_{2}{)}_{j-1}),$$

(31)

$$({\xi }_{2}{)}_{j}-({\xi }_{2}{)}_{j-1}=0.5*{h}_{j}(({\xi }_{3}{)}_{j}+({\xi }_{3}{)}_{j-1}),$$

(32)

$$({\xi }_{4}{)}_{j}-({\xi }_{4}{)}_{j-1}=0.5*{h}_{j}(({\xi }_{5}{)}_{j}+({\xi }_{5}{)}_{j-1}),$$

(33)

$$({\xi }_{6}{)}_{j}-({\xi }_{6}{)}_{j-1}=0.5*{h}_{j}(({\xi }_{7}{)}_{j}+({\xi }_{7}{)}_{j-1}),$$

(34)

$$\left.\begin{array}{l}\frac{{D}_{1}}{{D}_{2}}\frac{(({\xi }_{3}{)}_{j}-({\xi }_{3}{)}_{j-1})}{{h}_{j}}+( \frac{(({\xi }_{4}{)}_{j}+({\xi }_{4}{)}_{j-1}{) }^{2}}{4}\\ +2\times \left(\frac{({\xi }_{1}{)}_{j}+({\xi }_{1}{)}_{j-1}}{2}\right)\left(\frac{({\xi }_{3}{)}_{j}+({\xi }_{3}{)}_{j-1}}{2}\right)-{\left(\frac{({\xi }_{2}{)}_{j}+({\xi }_{2}{)}_{j-1}}{2}\right)}^{2} )\\ -{A}^{*}(\frac{\chi }{2}\left(\frac{({\xi }_{3}{)}_{j}+({\xi }_{3}{)}_{j-1}}{2}\right)+\left(\frac{({\xi }_{2}{)}_{j}+({\xi }_{2}{)}_{j-1}}{2}\right))\\ -\frac{{D}_{3}}{{D}_{2}(1+m{a}^{2})}Ha\left(\left(\frac{({\xi }_{2}{)}_{j}+({\xi }_{2}{)}_{j-1}}{2}\right)-ma\left(\frac{({\xi }_{4}{)}_{j}+({\xi }_{2}{)}_{j-1}}{4}\right)\right)=0,\end{array}\right\},$$

(35)

$$\left.\begin{array}{l}\frac{{D}_{1}}{{D}_{2}}\frac{(({\xi }_{5}{)}_{j}-({\xi }_{5}{)}_{j-1})}{{h}_{j}}-2\left(\left(\frac{({\xi }_{1}{)}_{j}+({\xi }_{1}{)}_{j-1}}{2}\right)\left(\frac{({\xi }_{5}{)}_{j}+({\xi }_{5}{)}_{j-1}}{2}\right)-\left(\frac{({\xi }_{2}{)}_{j}+({\xi }_{2}{)}_{j-1}}{2}\right)\right.\\ \left.\left(\frac{({\xi }_{4}{)}_{j}+({\xi }_{4}{)}_{j-1}}{2}\right)\right)-{A}^{*}\left(\frac{\chi }{2}\left(\frac{({\xi }_{5}{)}_{j}+({\xi }_{5}{)}_{j-1}}{2}\right)+\left(\frac{({\xi }_{4}{)}_{j}+({\xi }_{4}{)}_{j-1}}{2}\right)\right)\\ -\frac{{D}_{3}}{{D}_{2}(1+m{a}^{2})}Ha\left(\left(\frac{({\xi }_{4}{)}_{j}+({\xi }_{4}{)}_{j-1}}{2}\right)-ma\left(\frac{({\xi }_{2}{)}_{j}+({\xi }_{2}{)}_{j-1}}{2}\right)\right)=0,\end{array}\right\},$$

(36)

$$\left.\begin{array}{l}{D}_{4}\left({D}_{5}+\frac{4}{3}Nr\right)\frac{(({\xi }_{7}{)}_{j}-({\xi }_{7}{)}_{j-1})}{{h}_{j}}-Pr{A}^{*}\left(\frac{\chi }{2}\left(\frac{({\xi }_{7}{)}_{j}+({\xi }_{7}{)}_{j-1}}{2}\right)+\frac{3}{2}\left(\frac{({\xi }_{6}{)}_{j}+({\xi }_{6}{)}_{j-1}}{2}\right)\right)\\ +2Pr\left(\left(\frac{({\xi }_{1}{)}_{j}+({\xi }_{1}{)}_{j-1}}{2}\right)\left(\frac{({\xi }_{7}{)}_{j}+({\xi }_{7}{)}_{j-1}}{2}\right)-\left(\frac{({\xi }_{2}{)}_{j}+({\xi }_{2}{)}_{j-1}}{2}\right)\left(\frac{({\xi }_{6}{)}_{j}+({\xi }_{6}{)}_{j-1}}{2}\right)\right)\\ -\frac{{D}_{4}}{{D}_{1}}Prhc\left({\left(\frac{({\xi }_{3}{)}_{j}+({\xi }_{3}{)}_{j-1}}{2}\right)}^{2}+{\left(\frac{({\xi }_{5}{)}_{j}+({\xi }_{5}{)}_{j-1}}{2}\right)}^{2}\right)=0,\end{array}\right\}$$

(37)

Newton technique

The Newton linearization method is used to linearize Eqs. (28)–(34) in this formula.

$$\left.\begin{array}{ll}& ({\xi }_{1}{)}_{j}^{m+1}=({\xi }_{1}{)}_{j}^{m}+(\delta {\xi }_{1}{)}_{j}^{m},({\xi }_{2}{)}_{j}^{m+1}=({\xi }_{2}{)}_{j}^{m}+(\delta {\xi }_{2}{)}_{j}^{m},\\ & ({\xi }_{3}{)}_{j}^{m+1}=({\xi }_{3}{)}_{j}^{m}+(\delta {\xi }_{3}{)}_{j}^{m},({\xi }_{4}{)}_{j}^{m+1}=({\xi }_{4}{)}_{j}^{m}+(\delta {\xi }_{4}{)}_{j}^{m},\\ & ({\xi }_{5}{)}_{j}^{m+1}=({\xi }_{5}{)}_{j}^{m}+(\delta {\xi }_{5}{)}_{j}^{m},({\xi }_{6}{)}_{j}^{m+1}=({\xi }_{6}{)}_{j}^{m}+(\delta {\xi }_{6}{)}_{j}^{m},\\ & ({\xi }_{7}{)}_{j}^{m+1}=({\xi }_{7}{)}_{j}^{m}+(\delta {\xi }_{7}{)}_{j}^{m}.\end{array}\right\}$$

(38)

The resulting set of equations is generated by substituting the expressions found in Eqs. (28) via (34) and reducing the square and upper powers of:

$$((\delta {\xi }_{1}{)}_{j }-(\delta {\xi }_{1}{)}_{j-1})-0.5*{h}_{j}((\delta {\xi }_{2}{)}_{j }+(\delta {\xi }_{2}{)}_{j-1})=({r}_{1}{)}_{j},$$

(39)

$$((\delta {\xi }_{2}{)}_{j }-(\delta {\xi }_{2}{)}_{j-1})-0.5*{h}_{j}((\delta {\xi }_{3}{)}_{j }+(\delta {\xi }_{3}{)}_{j-1})=({r}_{2}{)}_{j},$$

(40)

$$((\delta {\xi }_{4}{)}_{j }-(\delta {\xi }_{4}{)}_{j-1})-0.5*{h}_{j}((\delta {\xi }_{5}{)}_{j }+(\delta {\xi }_{5}{)}_{j-1})=({r}_{3}{)}_{j},$$

(41)

$$((\delta {\xi }_{6}{)}_{j }-(\delta {\xi }_{6}{)}_{j-1})-0.5*{h}_{j}((\delta {\xi }_{7}{)}_{j }+(\delta {\xi }_{7}{)}_{j-1})=({r}_{4}{)}_{j},$$

(42)

$$\left.\begin{array}{l}({C}_{1}{)}_{j}(\delta {\xi }_{1}{)}_{j}+({C}_{2}{)}_{j}(\delta {\xi }_{1}{)}_{j-1}+({C}_{3}{)}_{j}(\delta {\xi }_{2}{)}_{j}+({C}_{4}{)}_{j}\delta {\xi }_{2}{)}_{j-1}+({C}_{5}{)}_{j}(\delta {\xi }_{3}{)}_{j}\\ +({C}_{6}{)}_{j}(\delta {\xi }_{3}{)}_{j-1}+({C}_{7}{)}_{j}(\delta {\xi }_{4}{)}_{j}+({C}_{8}{)}_{j}(\delta {\xi }_{4}{)}_{j-1}=({r}_{5}{)}_{j},\end{array}\right\}$$

(43)

$$\left.\begin{array}{l}({D}_{1}{)}_{j}(\delta {\xi }_{1}{)}_{j}+({D}_{2}{)}_{j}(\delta {\xi }_{1}{)}_{j-1}+({D}_{3}{)}_{j}(\delta {\xi }_{2}{)}_{j}+({D}_{4}{)}_{j}(\delta {\xi }_{2}{)}_{j-1}+({D}_{5}{)}_{j}(\delta {\xi }_{4}{)}_{j}\\ +({D}_{6}{)}_{j}(\delta {\xi }_{4}{)}_{j-1}+({D}_{7}{)}_{j}(\delta {\xi }_{5}{)}_{j}+({D}_{8}{)}_{j}(\delta {\xi }_{5}{)}_{j-1}=({r}_{6}{)}_{j},\end{array}\right\}$$

(44)

$$\left.\begin{array}{l}({E}_{1}{)}_{j}(\delta {\xi }_{1}{)}_{j}+({E}_{2}{)}_{j}(\delta {\xi }_{1}{)}_{j-1}+({E}_{3}{)}_{j}(\delta {\xi }_{2}{)}_{j}+({E}_{4}{)}_{j}(\delta {\xi }_{2}{)}_{j-1}+({E}_{5}{)}_{j}(\delta {\xi }_{3}{)}_{j}\\ +({E}_{6}{)}_{j}(\delta {\xi }_{3}{)}_{j-1}+({E}_{7}{)}_{j}(\delta {\xi }_{5}{)}_{j}+({E}_{8}{)}_{j}(\delta {\xi }_{5}{)}_{j-1}+({E}_{9}{)}_{j}(\delta {\xi }_{6}{)}_{j}+({E}_{10}{)}_{j}(\delta {\xi }_{6}{)}_{j-1}\\ +({E}_{11}{)}_{j}(\delta {\xi }_{7}{)}_{j}+({E}_{12}{)}_{j}(\delta {\xi }_{7}{)}_{j-1}=({r}_{7}{)}_{j},\end{array}\right\}$$

(45)

where

$$\left.\begin{array}{ll}& ({C}_{1}{)}_{j}=2{h}_{j}\left(\frac{({\xi }_{3}{)}_{j}+({\xi }_{3}{)}_{j-1}}{4}\right)=({C}_{2}{)}_{j},\\ & ({C}_{3}{)}_{j}=-\frac{\delta LS}{2}-{h}_{j}\left(\frac{({\xi }_{2}{)}_{j}+({\xi }_{2}{)}_{j-1}}{2}\right)-\frac{{h}_{j}M{B}_{3}}{2{B}_{2}(1+m{a}^{2})}=({C}_{4}{)}_{j},\\ & ({C}_{5}{)}_{j}=-\frac{{h}_{j}{A}^{*}\xi }{4}+\frac{{D}_{1}}{{D}_{2}}+2\delta L\left(\frac{({\xi }_{1}{)}_{j}+({\xi }_{1}{)}_{j-1}}{4}\right),\\ & ({C}_{6}{)}_{j}=-\frac{{h}_{j}{A}^{*}\xi }{4}-\frac{{D}_{1}}{{D}_{2}}+2\delta L\left(\frac{({\xi }_{1}{)}_{j}+({\xi }_{1}{)}_{j-1}}{4}\right),\\ & ({C}_{7}{)}_{j}={h}_{j}\left(\frac{({\xi }_{4}{)}_{j}+({\xi }_{4}{)}_{j-1}}{2}\right)+\frac{{h}_{j}mM{B}_{3}}{2{B}_{2}(1+m{a}^{2})}=({C}_{8}{)}_{j},\end{array}\right\}$$

(46)

$$\left.\begin{array}{l}({r}_{5}{)}_{j}=-\frac{{D}_{1}}{{D}_{2}}\frac{(({\xi }_{3}{)}_{j}-({\xi }_{3}{)}_{j-1})}{{h}_{j}}-\left(\frac{(({\xi }_{4}{)}_{j}+({\xi }_{4}{)}_{j-1}{)}^{2}}{4}\right.\\ \left.\qquad\quad -2\left(\frac{({\xi }_{1}{)}_{j}+({\xi }_{1}{)}_{j-1}}{2}\right)\left(\frac{({\xi }_{3}{)}_{j}+({\xi }_{3}{)}_{j-1}}{2}\right)+{\left(\frac{({\xi }_{2}{)}_{j}+({\xi }_{2}{)}_{j-1}}{2}\right)}^{2}\right)\\ \qquad\quad+{A}^{*}\left(\frac{\chi }{2}\left(\frac{({\xi }_{3}{)}_{j}+({\xi }_{3}{)}_{j-1}}{2}\right)+\left(\frac{({\xi }_{2}{)}_{j}+({\xi }_{2}{)}_{j-1}}{2}\right)\right)\\ \qquad \quad+\frac{{D}_{3}}{{D}_{2}(1+m{a}^{2})}Ha\left(\left(\frac{({\xi }_{2}{)}_{j}+({\xi }_{2}{)}_{j-1}}{2}\right)+ma\left(\frac{({\xi }_{4}{)}_{j}+({\xi }_{2}{)}_{j-1}}{4}\right)\right),\end{array}\right\}$$

(47)

$$\left.\begin{array}{ll}& ({D}_{1}{)}_{j}=2{h}_{j}\left(\frac{({\xi }_{5}{)}_{j}+({\xi }_{5}{)}_{j-1}}{4}\right)=({D}_{2}{)}_{j},\\ & ({D}_{3}{)}_{j}=2{h}_{j}\left(\frac{({\xi }_{4}{)}_{j}+({\xi }_{4}{)}_{j-1}}{4}\right)-\frac{{h}_{j}M{B}_{3}}{2{B}_{2}(1+m{a}^{2})}=({D}_{4}{)}_{j},\\ & ({D}_{5}{)}_{j}=-\frac{{h}_{j}{A}^{*}}{2}-\frac{{h}_{j}{A}^{*}\xi }{4}+2{h}_{j}\left(\frac{({\xi }_{2}{)}_{j}+({\xi }_{2}{)}_{j-1}}{4}\right)+\frac{{h}_{j}mM{B}_{3}}{2{B}_{2}(1+m{a}^{2})}=({D}_{6}{)}_{j},\\ & ({D}_{7}{)}_{j}=-\frac{{h}_{j}}{2}+\frac{{D}_{1}}{{D}_{2}}-2{h}_{j}\left(\frac{({\xi }_{1}{)}_{j}+({\xi }_{1}{)}_{j-1}}{4}\right),\\ & ({D}_{8}{)}_{j}=-\frac{{h}_{j}}{2}-\frac{{D}_{1}}{{D}_{2}}-2{h}_{j}\left(\frac{({\xi }_{1}{)}_{j}+({\xi }_{1}{)}_{j-1}}{4}\right),\end{array}\right\}$$

(48)

$$\left.\begin{array}{l}({r}_{6}{)}_{j}=-\frac{{D}_{1}}{{D}_{2}}\frac{(({\xi }_{5}{)}_{j}-({\xi }_{5}{)}_{j-1})}{{h}_{j}}+2\left(\left(\frac{({\xi }_{1}{)}_{j}+({\xi }_{1}{)}_{j-1}}{2}\right)\left(\frac{({\xi }_{5}{)}_{j}+({\xi }_{5}{)}_{j-1}}{2}\right)\right.\\ \left.\qquad\quad -\left(\frac{({\xi }_{2}{)}_{j}+({\xi }_{2}{)}_{j-1}}{2}\right)\left(\frac{({\xi }_{4}{)}_{j}+({\xi }_{4}{)}_{j-1}}{2}\right)\right)+{A}^{*}\frac{\chi }{2}\left(\frac{({\xi }_{5}{)}_{j}+({\xi }_{5}{)}_{j-1}}{2}\right)\\ \qquad\quad +{A}^{*}\left(\frac{({\xi }_{4}{)}_{j}+({\xi }_{4}{)}_{j-1}}{2}\right)+\frac{{D}_{3}}{{D}_{2}(1+m{a}^{2})}Ha\left(\left(\frac{({\xi }_{4}{)}_{j}+({\xi }_{4}{)}_{j-1}}{2}\right)-ma\left(\frac{({\xi }_{2}{)}_{j}+({\xi }_{2}{)}_{j-1}}{2}\right)\right),\end{array}\right\}$$

(49)

$$\left.\begin{array}{ll}& ({E}_{1}{)}_{j}=2{h}_{j}Pr\left(\frac{({\xi }_{7}{)}_{j}+({\xi }_{7}{)}_{j-1}}{4}\right)=({E}_{2}{)}_{j},\\ & ({E}_{3}{)}_{j}=-2{h}_{j}Pr\left(\frac{({\xi }_{6}{)}_{j}+({\xi }_{6}{)}_{j-1}}{4}\right),\\ & ({E}_{5}{)}_{j}=-\frac{hc{h}_{j}Pr{B}_{4}}{2{B}_{1}}=({E}_{6}{)}_{j},\\ & ({E}_{7}{)}_{j}=-\frac{hc{h}_{j}Pr{B}_{4}}{2{B}_{1}}=({E}_{8}{)}_{j},\\ & ({E}_{9}{)}_{j}=-\frac{3}{4}{h}_{j}Pr{A}^{*}-2{h}_{j}Pr\left(\frac{({\xi }_{2}{)}_{j}+({\xi }_{2}{)}_{j-1}}{4}\right)=({E}_{10}{)}_{j},\\ & ({E}_{11}{)}_{j}=-\frac{1}{4}{h}_{j}nPrS+{D}_{4}\left({D}_{5}+4/3Rd\right)+2{h}_{j}Pr\left(\frac{({\xi }_{1}{)}_{j}+({\xi }_{1}{)}_{j-1}}{4}\right),\\ & ({E}_{12}{)}_{j}=-\frac{1}{4}{h}_{j}nPrS-{D}_{4}\left({D}_{5}+4/3Rd\right)+2{h}_{j}Pr\left(\frac{({\xi }_{1}{)}_{j}+({\xi }_{1}{)}_{j-1}}{4}\right),\end{array}\right\}$$

(50)

$$\left. {\begin{array}{*{20}l} {(r_{7} )_{j} = - D_{4} \left( {D_{5} + \frac{4}{3}Nr} \right)\frac{{((\xi_{7} )_{j} - (\xi_{7} )_{j - 1} )}}{{h_{j} }}} \hfill \\ \qquad\quad { + \Pr A*\left( {\frac{\chi }{2}\left( {\frac{{(\xi_{7} )_{j} + (\xi_{7} )_{j - 1} }}{2}} \right) + \frac{3}{2}\left( {\frac{{(\xi_{6} )_{j} + (\xi_{6} )_{j - 1} }}{2}} \right)} \right)} \hfill \\ \qquad\quad { - 2\Pr \left( {\frac{{(\xi_{1} )_{j} + (\xi_{1} )_{j - 1} }}{2}} \right)\left( {\frac{{(\xi_{7} )_{j} + (\xi_{7} )_{j - 1} }}{2}} \right)} \hfill \\ \qquad\quad { + 2\Pr \left( {\frac{{(\xi_{2} )_{j} + (\xi_{2} )_{j - 1} }}{2}} \right)\left( {\frac{{(\xi_{6} )_{j} + (\xi_{6} )_{j - 1} }}{2}} \right)} \hfill \\ \qquad\quad { + \frac{{D_{4} }}{{D_{1} }}\Pr hc\left( {\left( {\frac{{(\xi_{3} )_{j} + (\xi_{3} )_{j - 1} }}{2}} \right)^{2} + \left( {\frac{{(\xi_{5} )_{j} + (\xi_{5} )_{j - 1} }}{2}} \right)^{2} } \right).} \hfill \\ \end{array} } \right\}$$

(51)

Block tridiagonal structure

The linearized scheme's subsequent block tridiagonal construction is as follows.

$$A\Delta =S,$$

(52)

where

$$A = \left[ {\begin{array}{*{20}{l}} {\left[ {A_1^*} \right]}&{\left[ {C_1^*} \right]}&{}&{}&{}&{}&{}\\ {}&{\left[ {A_2^*} \right]}&{\left[ {C_2^*} \right]}&{}&{}&{}&{}\\ {}&{}&{}& \ddots &{}&{}&{}\\ {}&{}&{}& \ddots &{}&{}&{}\\ {}&{}&{}& \ddots &{}&{}&{}\\ {}&{}&{}&{}&{\left[ {B_{J - 1}^*} \right]}&{\left[ {A_{J - 1}^*} \right]}&{\left[ {C_{J - 1}^*} \right]}\\ {}&{}&{}&{}&{}&{\left[ {B_{J~}^*} \right]}&{\left[ {A_{J~}^*} \right]} \end{array}} \right],\,\,\Delta = \left[ {\begin{array}{*{20}{l}} {\left[ {{\Delta _1}} \right]}\\ {\left[ {{\Delta _2}} \right]}\\ \vdots \\ \vdots \\ \vdots \\ {\left[ {{\Delta _{J - 1}}} \right]}\\ {\left[ {{\Delta _J}} \right]} \end{array}} \right]{\rm{and}}~~S = \left[ {\begin{array}{*{20}{l}} {\left[ {{S_1}} \right]}\\ {\left[ {{S_2}} \right]}\\ \vdots \\ \vdots \\ \vdots \\ {\left[ {{S_{J - 1}}} \right]}\\ {\left[ {{S_J}} \right]} \end{array}} \right].$$

where the features demarcated in Eq. (52) be situated, as follows:

$$\left[\begin{array}{l}{A}_{1}^{*}\end{array}\right]=\left[\begin{array}{lllllll}0& 0& 0& 1& 0& 0& 0\\ -0.5*{h}_{j}& 0& 0& 0& -0.5*{h}_{j}& 0& 0\\ 0& -0.5*{h}_{j}& 0& 0& 0& -0.5*{h}_{j}& 0\\ 0& 0& -0.5*{h}_{j}& 0& 0& 0& -0.5*{h}_{j}\\ ({C}_{6}{)}_{1}& 0& 0& ({C}_{1}{)}_{1}& ({C}_{5}{)}_{1}& 0& 0\\ 0& ({D}_{8}{)}_{1}& 0& ({D}_{1}{)}_{1}& 0& ({D}_{7}{)}_{1}& 0\\ ({E}_{6}{)}_{1}& ({E}_{8}{)}_{1}& ({E}_{12}{)}_{1}& ({E}_{1}{)}_{1}& ({E}_{5}{)}_{1}& ({E}_{7}{)}_{1}& ({E}_{11}{)}_{1}\\ & & & & & & \end{array}\right],$$

$$\left[\begin{array}{l}{A}_{\mathrm{j}}^{*}\end{array}\right]=\left[\begin{array}{lllllll}-0.5*{h}_{j}& 0& 0& 1& 0& 0& 0\\ -1& 0& 0& 0& -0.5*{h}_{j}& 0& 0\\ 0& -1& 0& 0& 0& -0.5*{h}_{j}& 0\\ 0& 0& -1& 0& 0& 0& -0.5*{h}_{j}\\ ({C}_{4}{)}_{j}& ({C}_{8}{)}_{j}& 0& ({C}_{1}{)}_{j}& ({C}_{5}{)}_{j}& 0& 0\\ ({D}_{4}{)}_{j}& ({D}_{6}{)}_{j}& 0& ({D}_{1}{)}_{j}& 0& ({D}_{7}{)}_{j}& 0\\ ({E}_{4}{)}_{j}& 0& ({E}_{10}{)}_{j}& ({E}_{1}{)}_{j}& ({E}_{5}{)}_{j}& ({E}_{7}{)}_{j}& ({E}_{11}{)}_{j}\\ & & & & & & \end{array}\right], 2\le j\le J$$

$$\left[ {B_{j}^{*} } \right] = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 0 \hfill & { - 1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - 0.5*h_{j} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - 0.5*h_{j} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - 0.5*h_{j} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {(C_{2} )_{j} } \hfill & {(C_{6} )_{j} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {(D_{2} )_{j} } \hfill & 0 \hfill & {(D_{8} )_{j} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {(E_{2} )_{j} } \hfill & {(E_{6} )_{j} } \hfill & {(E_{8} )_{j} } \hfill & {(E_{12} )_{j} } \hfill \\ \end{array} } \right],\,\,2 \le j \le J$$

$$\left[ {C_{j}^{*} } \right] = \left[ {\begin{array}{*{20}l} { - 0.5*h_{j} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {(C_{3} )_{j} } \hfill & {(C_{7} )_{j} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {(D_{3} )_{j} } \hfill & {(D_{5} )_{j} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {(E_{3} )_{j} } \hfill & 0 \hfill & {(E_{9} )_{j} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right],\,\,\,1 \le j \le J - 1.$$

Currently, the factorization of A can be viewed as follows:

$$A=LU,$$

(53)

where

$$L=\left[\begin{array}{llllll}[{\Gamma }_{1}^{*}]& & & & & \\ & [{\Gamma }_{2}^{*}]& & & & \\ & & & \ddots & & \\ & & & \ddots & [{\Gamma }_{J-1}^{*}]& \\ & & & & [{B}_{J }^{*}]& [{\Gamma }_{J }^{*}]\end{array}\right],U=\left[\begin{array}{llllll}[I]& [{\alpha }_{1}^{*}]& & & & \\ & [I]& [{\alpha }_{2}^{*}]& & & \\ & & \ddots & \ddots & & \\ & & & [I]& [{\alpha }_{J-1}^{*}]& \\ & & & & [I]& \end{array}\right],$$

where the entire magnitude of matrix $A$ is $J\times J$ by means of all block magnitude of super-vectors actuality $7\times 7$ plus $[I]$, $[{\Gamma }_{i}^{*}]$ and $[{\alpha }_{i}^{*}]$ are the matrices of degree 7. Applying $LU$ decomposition procedure aimed at the resolution of $\Delta$. Aimed at scientific valuation, a netting magnitude of $\Delta {h}_{j}$= 0.01 is presumedobtainable to remain suitable, and the consequences remain assimilated consuming an error broadmindedness of $1{0}^{-6}$.

Cryptogramauthentication

It is noted that the results of the current study are approximations based on the Keller box approach. Table 2 provides a summary of the results' coherence with relation to results from earlier methodologies. In the absence of the unsteadiness parameter, Hall current parameter, magnetic parameter, radiation parameter, Prandtl number parameter, and Eckert number parameter presented in Table 3, a comparison table is created. Table 3 shows numerical value comparisons between the present literature and those of Bachok et al.⁹⁴ and Turkyilmazoglu⁹⁵. The table shows that the current study has been compared and that the results are quite dependable.

Table 2 A comparison of the ${F}^{*}{^{\prime}}(0)$, −${G}^{*}{^{\prime}}(0)$ and −${\theta }^{*}{^{\prime}}(0)$ on static Pr = 6.2 through Refs.^94,95.

Table 3 Comparison models among NFs, HNFs and tri-HNFs of skin frictions.

Outcomes and discussion

The possessions of the factors corresponding to magnetic field parameter $Ha$, Hall current parameter $ma$, Brinkman number $Br$, Radiation parameter $Nr$, rotation parameter $\omega$, solid volume fraction parameters ${\phi }_{1}, {\phi }_{2}, {\phi }_{3}$, Prandtl number $Pr$, Eckert number $hc$, and measure of unsteadiness parameter ${A}^{*}$ on the dimensionless profiles of Entropy ${N}_{G}\left(\chi \right)$, velocity components $\left({F{^{\prime}}}^{*}\left(\chi \right), {G}^{*}\left(\chi \right)\right)$ and temperature ${\theta }^{*}\left(\chi \right)$ are analyzed in this section. In order to produce results in the form of figures and tables, the parameter values must be between $0.5\le Ha\le 1.5$, $1\le ma\le 3$, $5\le Br\le 15$, $0.4\le Nr\le 1.2$, $0.4\le \omega \le 1.5$, $0.01\le \phi \le 0.03$, $0.5\le {A}^{*}\le 2.5$, $0.5\le hc\le 2.5$ and 5 ≤ Pr ≤ 7.

The entropy profile ${N}_{G}\left(\chi \right)$ in Fig. 5 is decaying for growing estimations of the magnetic parameter $Ha$. When Ha is higher, the resistive Lorentzian force is formed, slowing the fluid velocity. Furthermore, when a stronger magnetic field is present, the temperature rises owing to Ohmic heating, resulting in the input of considerable heat. As a consequence, Entropy increases. The entropy profile ${N}_{G}\left(\chi \right)$ decreases in Fig. 6 for larger Hall current parameter $ma$. The decreasing effects look similar for all nanoparticles. The escalation in Brinkmann's number causes a decrease in Entropy (see Fig. 7). It is emphasised that the parameter Br contributes to fluid erosion in the dissipative flow pattern. Upon increasing the radiation parameter, the entropy production escalates along $\chi$ in Fig. 8. It is because of rising emissions, which raise frictional irreversibility and promote entropy production.

Figure 5

Conclusion of $Ha$ on ${N}_{G}(\chi )$.

Figure 6

Influence of $ma$ on ${N}_{G}(\chi )$.

Figure 7

Impression of $Br$ on ${N}_{G}(\chi )$.

Figure 8

Control of $Nr$ on ${N}_{G}(\chi )$.

The consequences of the magnetic parameter $Ha$ on the velocity components (radial ${F{^{\prime}}}^{*}\left(\chi \right)$ and azimuthal ${G}^{*}\left(\chi \right)$)and temperature ${\theta }^{*}\left(\chi \right)$ are displayed in Figs. 9, 10 and 11. It is experienced both components are decaying along $\chi$ whereas as temperature escalates for diverse estimations of the parameter $Ha$. As the magnetic parameter grows, the thickness of the velocity boundary layer rises. This occurs because the Lorentz force is put in motion by the transverse magnetic field, which causes a retarding force to act on the velocity field. As a consequence, the retarding force and consequently the velocity decreases as the estimations of $M$ rise. Also, more heat is generated during this process, and hence temperature grows.Upon enhancing rotation parameter $\omega ,$ the velocity and temperature profiles are observed to increase along $\chi$ in Figs. 12, 13, 14 for momo, hybrid and tri-HNFs. Figure 12 displays that through higher estimations of the parameter $\omega ,$ the radial velocity tends to rise, and the viscosity of the energy boundary layer declines. It demonstrates that centrifugal force causes the nanofluid particles to be pushed in the radial direction. As a consequence, the velocity in this direction enhances. The profiles of azimuthal speed and heat inside the boundary layer escalate with the escalating estimations of the parameter $\omega$, as seen in Figs. 13 and 14. Additionally, it is observed that when the disk's rotation speed enhances, the thickness of the thermal boundary layer decays. The inspiration of Hall's current parameter $ma$ at the velocity and temperature distributions isrevealed in Figs. 15, 16, 17. It is checked that the distributions are escalating with growing estimations of the parameter $ma$. This suggests that the radial and azimuthal flows are accelerated throughout the boundary layer domain. Also, the enhancement in temperature in Fig. 17 for tri-HNF is slightly further than the memo and HNFs. The effects of the solid volume fraction of memo ${\phi }_{1}$, hybrid ${\phi }_{2}$ and tri-hybrid ${\phi }_{3}$ nanofluids on the velocity and temperature profiles are described in Figs. 18, 19, 20. The radial, azimuthal and temperature profiles are observed to enhance upon the enhancing values of parameters ${\phi }_{1}, {\phi }_{2}$ and ${\phi }_{3}$. Physically, this is understood to mean that as the quantity of nanoparticles rises, so does the thermal conductivity as determined by Brinkman with the thermal conductivity model called the Maxwell model. As a consequence, the thermal boundary layer escalates. The escalation in the Prandtl number $Pr$ in Fig. 21 leads to a decrement in the temperature profile. The thickness of the boundary layer reduces as the parameter $Pr$ grows. The Prandtl number is generally the proportion of the heat diffusivity to momentum diffusivity. In heat transmission problems,$Pr$ regulates the relative thickness of momentum and thermal boundary layers. Upon higher estimations of the radiation parameter $Nr$, the temperature escalates in Fig. 22. The increment in the radiation parameter means the reduction in the mean preoccupation coefficient, which provides extra heat towards fluid and, as a consequence, fluid temperature grows. The rise in the Eckert number $hc$ causes an increment in temperature in Fig. 23. This occurs because frictional heating causes heat to be created within the fluid as $hc$ rises. Eckert number in terms of physics is the ratio of kinetic energy to the particular enthalpy difference between fluid and wall. As a result, a rise in the parameter $hc$ results in work being done against the viscous fluid stresses, which converts kinetic energy into internal energy. An augmentation in the parameter $hc$ implies a conversion of the kinetic energy into internal energy through the effort against the viscous fluid stresses. As a consequence, rising $hc$ rises the fluid's temperature. The impression of the measure of unsteadiness parameter ${A}^{*}$ proceeding the velocity and temperature curves are described in Figs. 24, 25, 26 along $\chi$. In Figs. 24 and 25, it is shown that as the parameter ${A}^{*}$ grows, the velocity profiles decelerate, whereas temperature accelerates. In the case of radial velocity in Fig. 24, the decrease for a hybrid is slightly higher, whereas, for azimuthal velocity in Fig. 25, the decrease for tri-hybrid is more.

Figure 9

Inspiration of $Ha$ on ${F}^{*{^{\prime}}}(\chi )$.

Figure 10

Impression of $Ha$ on ${G}^{*}(\chi )$.

Figure 11

Effect of $Ha$ on ${\theta }^{*}(\chi )$.

Figure 12

Control of $\omega$ on ${F}^{*{^{\prime}}}(\chi )$.

Figure 13

Power of $\omega$ on ${G}^{*}(\chi )$.

Figure 14

Stimulus of $\omega$ on ${\theta }^{*}(\chi )$.

Figure 15

Impression of $ma$ on ${F}^{*{^{\prime}}}(\chi )$.

Figure 16

Effect of $ma$ on ${G}^{*}(\chi )$.

Figure 17

Control of $ma$ on ${\theta }^{*}(\chi )$.

Figure 18

Impact of $\phi$ on ${F}^{*{^{\prime}}}(\chi )$.

Figure 19

Encouragement of $\phi$ on ${G}^{*}(\chi )$.

Figure 20

Power of $\phi$ on ${\theta }^{*}(\chi )$.

Figure 21

Control of $Pr$ on ${\theta }^{*}(\chi )$.

Figure 22

Result of $Nr$ on ${\theta }^{*}(\chi )$.

Figure 23

Bearing of $hc$ on ${\theta }^{*}(\chi )$.

Figure 24

Impact of ${A}^{*}$ on ${F}^{*{^{\prime}}}(\chi )$.

Figure 25

Impression of ${A}^{*}$ on ${G}^{*}(\chi )$.

Figure 26

Effect of ${A}^{*}$ on ${\theta }^{*}(\chi )$.

Table discussion

The numerical values of the radial and azimuthal direction skin friction coefficients (surface drag forces) are calculated for NF, HNF and tri-HNF. The values are calculated for diverse ranges of the parameters $\phi , {A}^{*}, ma, Ha$ and $\omega$. Also, the local Nusselt number (heat transfer amount) is numerically calculated in Tables 3 and 4 for the parameters $\phi , hc, Nr, Ha$ and $ma,$ and the results are compared fornanofluid, hybrid nanofluid and tri-hybrid nanofluid.

Table 4 Comparison imitations among NF, HNFs and tri-HNFs of Nusselt number.

Final outcomes

The current theoretical analysis is keen to analyze the stagnant time-dependent flow of simple nanofluid, HNF and THNFs movement over a rotatory stretchable disk. Heat transmission is likewise examined in MHD, thermal radiation, heat dissipation and Hall current. The boundary layer approximation is utilized to design the liquid movement dynamics in PDEs. The governing PDEs are transfigured into ODEs through precise resemblance variables. The resultant ODEs are mathematically confronted via the efficient Keller Box method. The following outcomes may be depicted from the present investigation:

• The entropy production is increased for the parameters $Ha$ and $Nr,$ but it is decreased for $ma$ and $Br$.

• The radial and azimuthal velocities are in the similar increasing pattern for the parameters $\omega , ma$ and $\phi ,$ whereas decreasing for $Ha$ and ${A}^{*}$.

• The temperature is escalated for the parameters $Ha, \omega , ma, \phi , Nr, hc, {A}^{*}$ and decayed for $Pr$.

• As a result of an incremental change in the volume fraction of nanoparticles, the heat delivery rate of fluid increases in the case of trihybrid nanomolecules compared to dihybrid nanomolecules.

• It has been discovered that the Nusselt number of ternary hybrid nanofluid is increasing when compared to unitary NF and HNF.

• The skin frictions rise by increasing nanoparticles volume fraction values and decrease with increasing values of Hall current parameter.

Future direction

The current theoretical investigation is presented over a disk geometry. The same investigation can be done over different surfaces like a cylinder, cone and Riga. In the future, a range of physical and technical difficulties might be addressed using the KBM technique^{96,97,98,99,100,101,102,103,104,105,106,107}.

Date availability

All data generated or analyzed during this study are included in this published article.